图像基本运算
《数字图像处理教学课件》第3章图像的基本运算(2)

实例
源图像
(b)双线性插值方法的结果
实例
用最近邻插值和双线性插值的方法分别将老虎放大 1.5倍。
实例
采用最近邻插值放大1.5倍 采用双线性插值放大1.5倍
比例变换中对应图像的确定
比例变换中对应图像的确定
假设输出图像的宽度为W,高度为H; 输入图像的宽度为w高度为h,要将输入图像的尺度拉伸或压
枕形失真
由镜头引起的画面向中间“收缩”的现象。
6.图像变形
图像变形(Image Warping) 图像变形合成(Image morphing )
参数化(全局)变形(warping)
参数化变形实例
Translation 平移
Rotation 旋转
Aspect 缩放
Affine 仿射变换
Perspective 透视变换
x' a b c x y' d e f y 1 0 0 1 1
x' ax by c
y'
dx
ey
f
将三对对应点的坐标代入上面公式,
可以求得变换的
对于内的任意一个像素点,再计算其新的坐标,然后 颜色映像
三角变形实例
四边形区域的变换方法
图像变形的几何校正
用控制点及插值过程定义,通常具有较为复杂的数学 变换函数
投影变换
投影变换是下列变换的组合
仿射变换 投影变形
投影变换的性质:
原点无需变换至原点 线变换为线 比例不保持 平行线无需保持平行
x' a b c x y' d e f y w' g h i w
举例:三角变形
B
源图像
?
B’ 目标图像
T(x,y)
图像基本运算实验指导
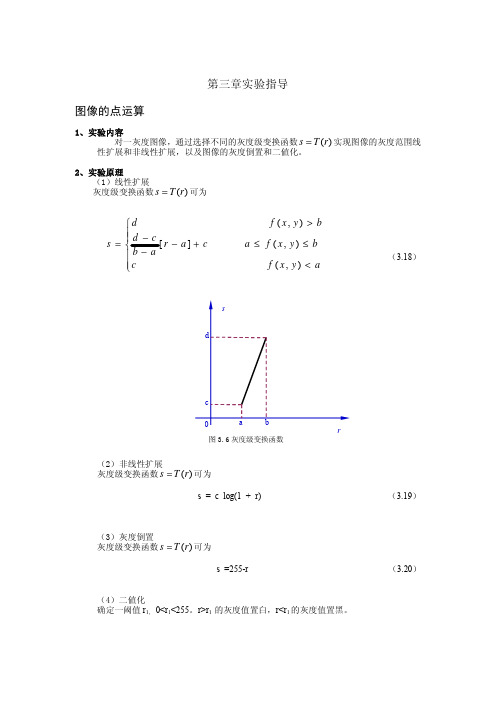
图像的缩放
1 、实验内容 对一幅图像实现按比例缩小和不按比例任意缩小的效果,以及图像的成倍放大和 不按比例放大效果。 2 、实验原理 数字图像的比例缩放是指将给定的图像在 x 方向和 y 方向按相同的比例缩放 a 倍, 从而 获得一幅新的图像,又称为全比例缩放。如果 x 方向和 y 方向缩放的比例不同,则图像的比 例缩放会改变原始图像像素间的相对位置,产生几何畸变。设原始图像中的点 A0 ( x0 , y0 ) 比 例缩放后,在新图中的对应点为 A1 ( x 1 , y1 ) ,则 A0 ( x0 , y0 ) 和 A1 ( x 1 , y1 ) 之间坐标关系可表 示如下:
J = i m 2 d o u b l e ( J ) ; K = I + 0 . 3 * J ; % 两幅图像相加 s u b p l o t ( 1 , 3 , 1 ) ; i m s h o w ( I ) ; t i t l e ( ' 人物图' ) ; s u b p l o t ( 1 , 3 , 2 ) ; i m s h o w ( J ) ; t i t l e ( ' 背景图' ) ; s u b p l o t ( 1 , 3 , 3 ) ; i m s h o w ( K ) ; t i t l e ( ' 相加后的图' ) ; i m w r i t e ( K , ' i _ l e n a 1 . j p g ' ) ; (2 )选取一幅混合图像,如上图相加得到的图像 i _ l e n a . j p g , 将混合图像与背景图像 做减法运算,程序如下,结果如图(b ) 。 A = i m r e a d ( ' i _ l e n a 1 . j p g ' ) ; B = i m r e a d ( ' r i c e . p n g ' ) ; C = A 0 . 3 * B ; % 混合图减去背景图 s u b p l o t ( 1 , 3 , 1 ) ; i m s h o w ( A ) ; t i t l e ( ' 混合图' ) ; s u b p l o t ( 1 , 3 , 2 ) ; i m s h o w ( B ) ; t i t l e ( ' 背景图' ) ; s u b p l o t ( 1 , 3 , 3 ) ; i m s h o w ( C ) ; t i t l e ( ' 分离后的图' ) ; (3 )选取一幅尺寸为 2 5 6 ×2 5 6 的灰度图,如 i _ l e n a . j p g 。设置掩膜模板,对于需要 保留下来的区域,掩膜图像的值置为 1,而在需要被抑制掉的区域,掩膜图像的值置为 0。 程序如下,结果如图(c) 。 A = i m r e a d ( ' i _ l e n a . j p g ' ) ; A = i m 2 d o u b l e ( A ) ; s u b p l o t ( 1 , 2 , 1 ) ; i m s h o w ( A ) ; t i t l e ( ' 原图' ) ; B = z e r o s ( 2 5 6 ) ; % 设置模板 B ( 4 0 : 2 0 0 , 4 0 : 2 0 0 ) = 1 ; K = A . * B ; % 两幅图像相乘 s u b p l o t ( 1 , 2 , 2 ) ; i m s h o w ( K ) ; t i t l e ( ' 局部图' ) ; 4 、实验结果与分析 (1 ) 、实验结果如图 3 . 8 所示。
数字图像处理-图像基本运算
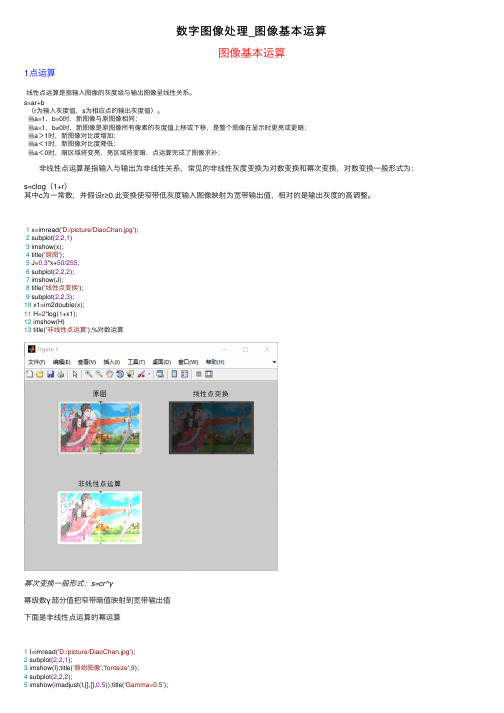
数字图像处理_图像基本运算图像基本运算1点运算线性点运算是指输⼊图像的灰度级与输出图像呈线性关系。
s=ar+b(r为输⼊灰度值,s为相应点的输出灰度值)。
当a=1,b=0时,新图像与原图像相同;当a=1,b≠0时,新图像是原图像所有像素的灰度值上移或下移,是整个图像在显⽰时更亮或更暗;当a>1时,新图像对⽐度增加;当a<1时,新图像对⽐度降低;当a<0时,暗区域将变亮,亮区域将变暗,点运算完成了图像求补; ⾮线性点运算是指输⼊与输出为⾮线性关系,常见的⾮线性灰度变换为对数变换和幂次变换,对数变换⼀般形式为:s=clog(1+r)其中c为⼀常数,并假设r≥0.此变换使窄带低灰度输⼊图像映射为宽带输出值,相对的是输出灰度的⾼调整。
1 x=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1)3 imshow(x);4 title('原图');5 J=0.3*x+50/255;6 subplot(2,2,2);7 imshow(J);8 title('线性点变换');9 subplot(2,2,3);10 x1=im2double(x);11 H=2*log(1+x1);12 imshow(H)13 title('⾮线性点运算');%对数运算幂次变换⼀般形式:s=cr^γ幂级数γ部分值把窄带暗值映射到宽带输出值下⾯是⾮线性点运算的幂运算1 I=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1);3 imshow(I);title('原始图像','fontsize',9);4 subplot(2,2,2);5 imshow(imadjust(I,[],[],0.5));title('Gamma=0.5');7 imshow(imadjust(I,[],[],1));title('Gamma=1');8 subplot(2,2,4);9 imshow(imadjust(I,[],[],1.5));title('Gamma=1.5');2代数运算和逻辑运算加法运算去噪处理1 clear all2 i=imread('lenagray.jpg');3 imshow(i)4 j=imnoise(i,'gaussian',0,0.05);5 [m,n]=size(i);6 k=zeros(m,n);7for l=1:1008 j=imnoise(i,'gaussian',0,0.05);9 j1=im2double(j);10 k=k+j1;11 End12 k=k/100;13 subplot(1,3,1),imshow(i),title('原始图像')14 subplot(1,3,2),imshow(j),title('加噪图像')15 subplot(1,3,3),imshow(k),title(‘求平均后的减法运算提取噪声1 I=imread(‘lena.jpg’);2 J=imnoise (I,‘lena.jpg’,0,0.02);3 K=imsubtract(J,I);4 K1=255-K;5 figure;imshow(I);7 figure;imshow(K1);乘法运算改变图像灰度级1 I=imread('D:/picture/SunShangXiang.jpg')2 I=im2double(I);3 J=immultiply(I,1.2);4 K=immultiply(I,2);5 subplot(1,3,1),imshow(I);subplot(1,3,2),imshow(J);6 subplot(1,3,3);imshow(K);逻辑运算1 A=zeros(128);2 A(40:67,60:100)=1;3 figure(1)4 imshow(A);5 B=zeros(128);6 B(50:80,40:70)=1;7 figure(2)8 imshow(2);9 C=and(A,B);%与10 figure(3);11 imshow(3);12 D=or(A,B);%或13 figure(4);14 imshow(4);15 E=not(A);%⾮16 figure(5);17 imshow(E);3⼏何运算平移运算实现图像的平移1 I=imread('lenagray.jpg');2 subplot(1,2,1);3 imshow(I);4 [M,N]=size(I);g=zeros(M,N);5 a=20;b=20;6for i=1:M7for j=1:N8if((i-a>0)&(i-a<M)&(j-b>0)&(j-b<N)) 9 g(i,j)=I(i-a,j-b);10else11 g(i,j)=0;12 end13 end14 end15 subplot(1,2,2);imshow(uint8(g));⽔平镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(i,N-j+1);7 end8 end9 subplot(122);imshow(uint8(g));垂直镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(M-i+1,j);7 end8 end9 subplot(122);imshow(uint8(g));图像的旋转1 x=imread('D:/picture/DiaoChan.jpg');2 imshow(x);3 j=imrotate(x,45,'bilinear');4 k=imrotate(x,45,'bilinear','crop');5 subplot(1,3,1),imshow(x);6 title(‘原图')7 subplot(1,3,2),imshow(j);8 title(‘旋转图(显⽰全部)')9 subplot(1,3,3),imshow(k);10 title(‘旋转图(截取局部)')⼏种插值法⽐较1 i=imread('lena.jpg');2 j1=imresize(i,10,'nearest');3 j2=imresize(i,10,'bilinear');4 j3=imresize(i,10,'bicubic');5 subplot(1,4,1),imshow(i);title(‘原始图像')6 subplot(1,4,2),imshow(j1);title(‘最近邻法')7 subplot(1,4,3),imshow(j2);title(‘双线性插值法')8 subplot(1,4,4),imshow(j3);title(‘三次内插法')放缩变换1 x=imread('D:/picture/ZiXia.jpg')2 subplot(2,3,1)3 imshow(x);4 title('原图');5 Large=imresize(x,1.5);6 subplot(2,3,2)7 imshow(Large);8 title('扩⼤为1.5');9 Small=imresize(x,0.1);10 subplot(2,3,3)11 imshow(Small);12 title('缩⼩为0.3');13 subplot(2,3,4)14 df=imresize(x,[600700],'nearest');15 imshow(df)16 title('600*700');17 df1=imresize(x,[300400],'nearest');18 subplot(2,3,5)19 imshow(df1)20 title('300*400');后记:(1)MATLAB基础知识回顾1:crtl+R是对选中的区域注释,ctrl+T是取消注释2:有的代码中点运算如O=a.*I+b/255 ,其中b除以255原因是:灰度数据有两种表式⽅法:⼀种是⽤unit8类型,取值0~255;另⼀种是double类型,取值0~1。
实验1 图像基本运算

实验一图像基本运算实验目的:1.熟悉Matlab的使用和矩阵运算;2.掌握图片的读写显示;3.熟悉图像的算术运算。
实验内容:1、以下两个矩阵A和B:(1)>>A=[100;110;001]A=100110001>>B=[234;567;8910]B=2345678910 >>plus(A,B)ans=3346778911>>minus(A,B)ans=-1-3-4-4-5-7-8-9-9 >>times(A,B)ans=2005600010 >>mtimes(A,B)ans=23479118910>>rdivide(A,B)ans=0.5000000.20000.16670000.1000>>mrdivide(A,B)Warning:Matrix is singular to working precision. ans=NaN Inf-InfNaN-Inf InfNaN Inf-Inf(2)>>A&Bans=100110001 >>A|Bans=111111111 >>~Aans=011001110 >>~Bans=000000000 (3)>>C=[444;444;444]C=444444444>>B>Cans=000111111(1)计算A+B、A-B、A.*B、A*B、A./B和A/B。
(2)计算A&B、A|B、~A和~B。
(3)判断B中哪些元素值大于4,将其置1,其它点置0。
以上题目先自己简单计算一下,如果Matlab得到的结果和自己算的不一样,分析原因。
2、(1)仿照课本例2.1(a),读入肺部图片lung.bmp,并显示出来。
>>f=imread('W:\学校\大三上学期\图像处理课件和实验软件\实验1\实验1\image\lung.bmp');>>whos fName Size Bytes Classf582x584x31019664uint8arrayGrand total is1019664elements using1019664bytes>>imshow(f)Warning:Image is too big to fit on screen;displaying at75%scale.>In truesize>Resize1at308In truesize at44In imshow at161(2)直接读入chest.tif并显示,效果怎样?如何改进图片效果?动态范围较低>>f=imread('W:\学校\大三上学期\图像处理课件和实验软件\实验1\实验1\image\chest.tif');>>imshow(f)>>imshow(f,[])3、仿照课本例2.5,对一幅图像进行反转,提取图像的一部分和二次取样。
图像的几何运算

图像的⼏何运算@⽬录图像的⼏何运算是指引起图像⼏何形状发⽣改变的变换。
与点运算不同的是,⼏何运算可以看成是像素在图像内的移动过程,该移动过程可以改变图像中物体对象之间的空间关系。
1.图像的插值图像插值是指利⽤已知邻近像素点的灰度值来产⽣位置像素点的灰度值,以便由原始图像再⽣成具有更⾼分辨率的图像。
插值是在不⽣成新的像素的情况下对原图像的像素重新分布,从⽽改变像素数量的⼀种⽅法。
在图像放⼤过程中,像素也相应的增加,增加的过程就是‘插值’发⽣作⽤的过程,‘’插值程序⾃动选择信息较好的像素作为增加、弥补空⽩像素的空间,⽽并⾮只使⽤近邻的像素,所以在放⼤图像时,图像看上去会⽐较平滑、⼲净。
⽆论使⽤何种插值⽅法,⾸先都需要找到与输出图像像素相对应的输⼊图像点,然后再通过计算该点附近某⼀像素集合的权平均值来指定输出像素的灰度值。
像素的权是根据像素到点的距离来⽽定的,不同插值⽅法的区别就在于考虑的像素集合不同。
最常见的插值⽅法如下:(1)向前映射法:通过输⼊图像像素的位置,计算输出图像对应像素的位置,将该位置像素的灰度值按某种⽅式分配到输出图像相邻的四个像素。
(2)向后映射法:通过输出图像像素位置,计算输⼊图像对应像素的位置,根据输⼊图像相邻四个像素的灰度值计算该位置像素的灰度值。
(3)最近邻插值:表⽰输出像素将被指定为像素点所在位置处的像素值。
(4)双线性插值:表⽰输出像素值是像素2×2邻域内的平均值。
(5)双三次插值:表⽰输出像素值是像素4×4邻域内的权平均值。
在MATLAB中,interp2函数⽤于对图像进⾏插值处理,该函数的调⽤⽅法如下:A=interp2(X,Y,Z,IX,IY):Z为要插值的原始图像,IX和IY为图像的新⾏和新列clear allclose allclcI2=imread('eight.tif');subplot(231)imshow(I2)title('原始图像')Z1=interp2(double(I2),2,'nearest');%最近邻插值法Z1=uint8(Z1);subplot(232)imshow(Z1)title('最近邻插值')Z2=interp2(double(I2),2,'linear');%线性插值法Z2=uint8(Z2);subplot(232)imshow(Z2)title('线性插值法')Z3=interp2(double(I2),2,'spline');%三次样条插值法Z3=uint8(Z3);subplot(234)imshow(Z3);title('三次样条插值');Z4=interp2(double(I2),2,'cubic');%⽴⽅插值法Z4=uint8(Z4);subplot(235);imshow(Z4);title('⽴⽅插值')2.旋转与平移变换旋转变换的表达式为⽤齐次矩阵表⽰为在MATLAB中,使⽤imrotate函数来旋转⼀幅图像,调⽤格式如下:B=imrotate(A,ANGLE,METHOD,BBOX)其中,A是需要旋转的图像;ANGLE是旋转的⾓度,正值为逆时针;METHOD是插值⽅法;BBOX表⽰旋转后的显⽰⽅式。
图像基本运算-幻灯片
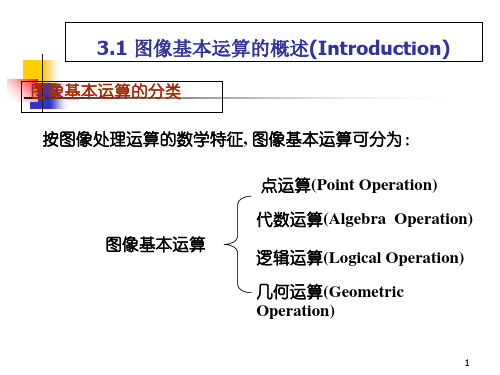
代数运算的四种基本形式
C ( x ,y ) A ( x ,y ) B ( x ,y ) C ( x ,y ) A ( x ,y ) B ( x ,y ) C ( x ,y ) A ( x ,y ) B ( x ,y )
20
3.3代数运算与逻辑运算 (Algebra and Logical Operation) 逻辑运算
主要应用举例: 图像的局部显示 改变图像的灰度级
图像的局部显示
36
3.3.3乘法运算(Multiplication)
改变图像的灰度级
(a) 原图
(b) 乘以1.2 图3.8 乘法运算结果
(c) 乘以2
37
3.3.4除法运算(Division)
除法运算 C ( x ,y ) A ( x ,y ) B ( x ,y )
输 L-1 出
灰
度
级 L/2
s
=0.04
=0.1 =0.4 =1 =2.5
=10.0
=25.0
0
L/2
L-1
输入灰度级r
不同的s=cr曲线及图像变换结果
加暗、减亮图像
=1.5
原始图像
=0.66
加亮、减暗图像
17
3.2.2非线性点运算(Non-Linear Point Operation)
加暗、减亮图像
32
图像相减——运动检测
33
3.3.2减法运算 (Subtraction )
混合图像的分离
(a)混合图像 (b)被减图像 (c)差影图
像
图3.6 差影法进行混合图像的分离
34
3.3.2减法运算 (Subtraction )
图像的基本运算

图像的基本运算图像的基本运算包括以下几类:图像的点运算;图像的代数运算;图像的几何运算;图像的逻辑运算和图像的插值。
下面将依次介绍这几种运算。
一、点运算点运算是指对一幅图像中每个像素点的灰度值进行计算的方法。
点运算通过对图像中每个像素值进行计算,改善图像显示效果的操作,也称对比度增强,对比度拉伸,灰度变换,可以表示为B(x,y)=f(A(x,y))。
这是一种像素的逐点运算,是原始图像与目标图像之间的映射关系,不改变图像像素的空间关系。
可以提高图像的对比度,增加轮廓线等。
可分为:(1)线性点运算:输出灰度级与输入灰度级之间呈线性关系。
(2)非线性点运算:输出灰度级与输入灰度级之间呈非线性关系。
二、代数运算代数运算是指将两幅或多幅图像通过对应像素之间的加、减、乘、除运算得到输出图像的方法。
对于相加和相乘的情形,可能不止有两幅图像参加运算。
如果记A(x,y)和B(x,y)为输入图像,C(x,y)为输出图像。
那么,四种代数运算的数学表达式如下:(1)C(x,y)=A(x,y)+B(x,y)加法运算可以实现以下两个目的:1.1去除叠加性随机噪声;1.2生成图像叠加效果。
(2)C(x,y)=A(x,y)-B(x,y)减法运算可以实现以下两个目的:2.1消除背景影响;2.2检查同一场景两幅图像之间的变化。
(3)C(x,y)=A(x,y)*B(x,y)乘法运算可以实现以下两个目的:3.1图像的局部显示;3.2图像的局部增强。
(4)C(x,y)=A(x,y)/B(x,y)乘法运算可以实现以下三个目的:4.1遥感图像的处理中;4.2消除图像数字化设备随空间变化的影响。
4.3校正成像设备的非线性影响。
还可以通过适当的组合形成涉及几幅图像的复合代数运算。
三、几何运算几何运算就是改变图像中物体对象(像素)之间的空间关系。
从变换性质来分,几何变换可以分为图像的位置变换(平移、镜像、旋转)、形状变换(放大、缩小)以及图像的复合变换等。
图像处理课后习题答案

第一章绪论1.模拟图像处理与数字图像处理主要区别表现在哪些方面?(什么是图像?什么是数字图像?什么是灰度图像?模拟图像处理与数字图像处理主要区别表现在哪些方面?)图像:是对客观对象的一种相似性的、生动性的描述或写真。
数字图像:一种空间坐标和灰度均不连续的、用离散数字(一般用整数)表示的图像。
灰度图像:在计算机领域中,灰度数字图像是每个像素只有一个采样颜色的图像。
在数字图像领域之外,“黑白图像”也表示“灰度图像”,例如灰度的照片通常叫做“黑白照片”。
模拟图像处理与数字图像处理主要区别:模拟图像处理是利用光学、照相方法对模拟图像的处理。
(优点:速度快,一般为实时处理,理论上讲可达到光的速度,并可同时并行处理。
缺点:精度较差,灵活性差,很难有判断能力和非线性处理能力)数字图像处理(称计算机图像处理,指将图像信号转换成数字格式并利用计算机对数据进行处理的过程)是利用计算机对数字图像进行系列操作,从而达到某种预期目的的技术.(优点:精度高,内容丰富,可进行复杂的非线性处理,灵活的变通能力,一只要改变软件就可以改变处理内容)2.图像处理学包括哪几个层次?各层次间有何区别和联系?数字图像处理可分为三个层次:狭义图像处理、图像分析和图像理解。
狭义图像处理是对输入图像进行某种变换得到输出图像,是一种图像到图像的过程。
图像分析主要是对图像中感兴趣的目标进行检测和测量,从而建立对图像目标的描述,图像分析是一个从图像到数值或符号的过程。
图像理解则是在图像分析的基础上,基于人工智能和认知理论研究图像中各目标的性质和它们之间的相互联系,对图像内容的含义加以理解以及对原来客观场景加以解译,从而指导和规划行动。
区别和联系:狭义图像处理是低层操作,它主要在图像像素级上进行处理,处理的数据量非常大;图像分析则进入了中层,经分割和特征提取,把原来以像素构成的图像转变成比较简洁的、非图像形式的描述;图像理解是高层操作,它是对描述中抽象出来的符号进行推理,其处理过程和方法与人类的思维推理有许多类似之处。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
23
3.3.1加法运算(Addition)
去除“叠加性”噪音
对于原图象f(x,y),有一个噪音图像集 { g i (x ,y) } i =1,2,...M
其中:g i (x ,y) = f(x,y) + ei(x,y)
gx,y f x,y ex,y
27
未加噪声的图像
加 噪 声 后 的 图 像
求平均后的图像
28
3.3.1加法运算(Addition)
相加
M=1
Addition:
averaging for noise reduction
M=2
M=4
M=16
29
3.3.1加法运算(Addition)
生成图象叠加效果:可以得到各种图像合成的效果,也可以 用于两张图片的衔接。
30
3.3.2减法运算 (Subtraction )
减法运算 将同一景物在不同时间拍摄的图像或同一景物在不同波段 的图像相减,这就是图像的减法运算。实际中常称为差影法。
C(x, y) A(x, y) B(x, y) 差值图像提供了图像间的差值信息,能用于指导动态监测 、运动目标的检测和跟踪、图像背景的消除及目标识别等。
12
3.2.1线性点运算(Linear Point Operation)
分段线性点运算的应用
g(x,y) Mg
d
变换前
c
f(x,y)
0
ab
Mf
变换后
13
3.2.2非线性点运算(Non-Linear Point Operation)
1、非线性点运算 非线性点运算的输出灰度级与输入灰度级呈非线性关
系,常见的非线性灰度变换为对数变换和幂次变换。
M个图像的均值为: 混入噪声
g(x, y)
的
1
图像
M
M i1
原始图像 随机噪声
fi (x, y) ei (x, y)
f (x, y) 1 M
M
ei (x, y)
i 1
当:噪音ei(x,y)为互不相关,且均值为0时,上述图象均值将 降低噪音的影响。
24
3.3.1加法运算(Addition)
非线性点运算应用实例3
输 L-1 出
灰
度
级 L/2
s
=0.04
=0.1 =0.4 =1 =2.5
=10.0
=25.0
0
L/2
L-1
输入灰度级r
不同的s=cr曲线及图像变换结果
加暗、减亮图像
=1.5
原始图像
=0.66
加亮、减暗图像
18
3.2.2非线性点运算(Non-Linear Point Operation)
2)、幂次变换
幂次变换的一般形式为: s cr
其中C和 为正常数。
0.04
0 1
0.1 0.2 0.4
0.67
s
加亮、减暗图像
1 1.5
2.5
5
10 25
r
1
加暗、减亮图像
17
3.2.2非线性点运算(Non-Linear Point Operation)
则灰度变换函数可简化表示为: s T [r ]
25 s
5
s
255 218
非线性灰度变换
0 48
r
178 255
3.1 对比度增大
0
r
128 255
3.2 加亮、减暗图像
点运算可以改变图像数据所占据的灰度值范围,
从而改善图像显示效果。
6
3.2 点运算 (Point Operation)
2.点运算的分类 点运算又称为“对比度增强”、“对比度拉伸”、“灰度
g(x, y) 1
M
M
fi (x, y) ei (x, y)
i 1
f (x, y) 1 M
M
ei (x, y)
i 1
则 gx, y 是 f x, y 的无偏估计
Eg
x,
y
E
1 M
M gi x, y
i 1
1
M
M
Egi x, y
i1
1 M
M
E fi
i 1
x,
y
Eei
x,
y
1 M
几何运算 几何运算就是改变图像中物体对象(像
素)之间的空间关系。 从变换性质来分,几何变换可以分为图
像的位置变换(平移、镜像、旋转)、形 状变换(放大、缩小)以及图像的复合变 换等。
4
3.2 点运算 (Point Operation)
1.点运算的定义 设输入图像的灰度为f(x,y),输出图像的灰度为g(x,y),
M i 1
fi x, y
f x, y
利用同一景物的多幅图像取平均、消除噪声。取M 个图像相加求平均得到1幅新图像,一般选8幅取平均。
25
当:噪音e(x,y)i为互不相关,且均值为0时,上述图像均值将 降低噪音的影响。 【例3.1】把一幅图像加上高斯噪声,再通过100次求平均的方法 去除噪声,其MATLAB程序如下: I=imread('eight.tif'); %读取一幅图片 J=imnoise(I,'gaussian',0,0.02); %向这幅图片加入高斯噪 声 subplot(1,2,1),imshow(I); %显示图片 subplot(1,2,2),imshow(J); %显示图片
255 142
变换前
0
255
3.5 降低对比度
变换后
10
3.2.1线性点运算(Linear Point Operation)
3)如果a为负值,暗区域将变亮,亮区域将变暗
255
0 变换前
255 变换后
11
3.2.1线性点运算(Linear Point Operation)
2、分段线性点运算
将感兴趣的灰度范围线性扩展,相对抑制不感兴趣的灰度区域。
2
3.1 图像基本运算的概述(Introduction)
点运算 点运算是指对一幅图像中每个像素点的灰度值进行计算的
方法。
代数运算、逻辑运算 代数运算或逻辑运算是指将两幅或多幅图像通过对应像
素之间的加、减、乘、除运算或逻辑与、或、非运算得到输 出图像的方法。
3
3.1 图像基本运算的概述(Introduction)
设f(x,y)灰度范围为[0,Mf],g(x,y)灰度范围为[0,Mg],
g(x,y)
Mg
M
f
d b
[
f
(x,
y)
b]
d
b f (x, y) M f
Mg
d
g
(x,
y)
d b
c a
[
f
(
x,
y)
a]
c
c
a
f
(x,
y)
a f (x, y) b 0 f (x, y) a
c
0
ab
f(x,y) Mf
1)、对数变换
对数变换的一般表达式为: s = c log(1 + r)
其中C是一个常数。
低灰度区扩展,高灰度区压缩。 图像加亮、减暗。
s
s=log(1+r)
非线性拉伸不是对图像的整个灰
度范围进行扩展,而是有选择地对某
一灰度值范围进行扩展,其他范围的
r
灰度值则有可能被压缩。
图3.9 对数曲线图
14
3.2.2非线性点运算(Non-Linear Point Operation) 非线性点运算应用实例1
1
3.1 图像基本运算的概述(Introduction)
图像基本运算的分类
按图像处理运算的数学特征, 图像基本运算可分为:
图像基本运算
点运算(Point Operation) 代数运算(Algebra Operation)
逻辑运算(Logical Operation) 几何运算(Geometric Operation)
变换”等,按灰度变换函数T[ ]的性质,可将点运算分为:
线性灰度变换(线性点运算)
点运算
灰度变换增强 分段线性灰度变换(分段线性点运算)
非线性灰度变换(非线性点运算) 直方图增强(基于直方图处理的图像增强)
7
rs ar b
3.2.1线性点运算(Linear Point Operation)
1、线性点运算
主要应用举例: 差影法(检测同一场景两幅图像之间的变化) 混合图像的分离
31
3.3.2减法运算 (Subtraction )
检测同一场景两幅图像之间的变化
设:时刻1的图像为 T1(x,y), 时刻2的图像为 T2(x,y) g(x,y) = T2 (x,y) - T1(x,y)
=
-
g(x,y)
T1(x,y)
线性点运算的灰度变换函数形式可以采用线性方程描述,即
s ar b
黑线: 0 a 1, b 0 红线: a 1, b 0
输出灰度压 缩 输出灰度不变
45º
图 3.3线性点运算
蓝线: a 1, b 0 绿线: 0 a 1, b 0
输出灰度扩展 整体变亮 输出灰度压 缩,整体变 暗
T2(x,y)
32
3.3.2减法运算 (Subtraction )
差影法在自动现场监测中的应用
1、在银行金库内,摄像头每隔一固定时间拍摄一幅图像,并与上 一幅图像做差影,如果图像差别超过了预先设置的阈值,则表明可 能有异常情况发生,应自动或以某种方式报警; 2、用于遥感图像的动态监测,差值图像可以发现森林火灾、洪水泛滥, 监测灾情变化等; 3、也可用于监测河口、海岸的泥沙淤积及监视江河、湖泊、海岸等的污染; 4、利用差值图像还能鉴别出耕地及不同的作物覆盖情况。
