西南交大专升本项目工程数学考题
西南交大-第二学期-高升专-工程力学C主观题
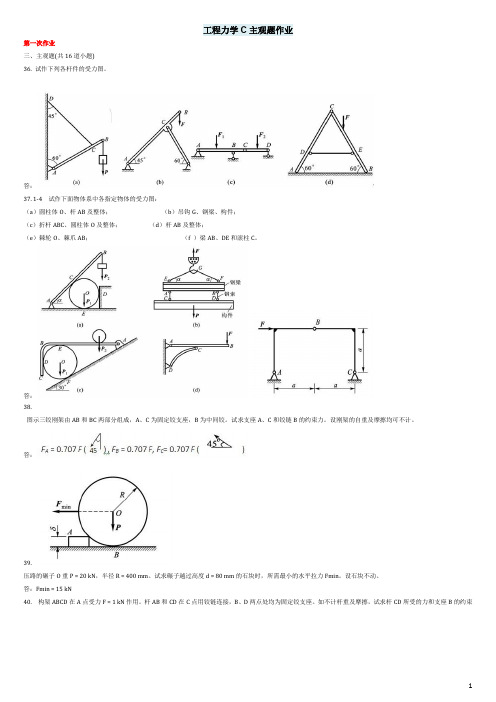
工程力学C主观题作业第一次作业三、主观题(共16道小题)36. 试作下列各杆件的受力图。
答:37. 1-4 试作下面物体系中各指定物体的受力图:(a)圆柱体O、杆AB及整体;(b)吊钩G、钢梁、构件;(c)折杆ABC、圆柱体O及整体;(d)杆AB及整体;(e)棘轮O、棘爪AB;(f )梁AB、DE和滚柱C。
答:38.图示三铰刚架由AB和BC两部分组成,A、C为固定铰支座,B为中间铰。
试求支座A、C和铰链B的约束力。
设刚架的自重及摩擦均可不计。
答:39.压路的碾子O重P = 20 kN,半径R = 400 mm。
试求碾子越过高度d = 80 mm的石块时,所需最小的水平拉力Fmin。
设石块不动。
答:Fmin = 15 kN40. 构架ABCD在A点受力F = 1 kN作用。
杆AB和CD在C点用铰链连接,B、D两点处均为固定铰支座。
如不计杆重及摩擦,试求杆CD所受的力和支座B的约束力。
答:41.梁AB如图所示,作用在跨度中点C的力F = 20 kN。
试求图示两种情况下支座A和B的约束力。
梁重及摩擦均可不计。
答:42. 如图a所示,重量为P = 5 kN的球悬挂在绳上,且和光滑的墙壁接触,绳和墙的夹角为30º。
试求绳和墙对球的约束力。
(4)根据平衡条件列平衡方程。
可先求出各力在x、y轴上的投影,如表2-1中所示,于是43. 重P = 1 kN的球放在与水平成30º角的光滑斜面上,并用与斜面平行的绳AB系住(图2-15 a)。
试求绳AB受到的拉力及球对斜面的压力。
44.答:45.答:46. 已知AB梁上作用一矩为Me的力偶,梁长为l,梁重及摩擦均不计。
试求在图示四种情况下支座A、B的约束力。
答:47. 汽锤在锻打工件时,由于工件偏置使锤头受力偏心而发生偏斜,它将在导轨DA和BE上产生很大的压力,从而加速导轨的磨损并影响锻件的精度。
已知锻打力F = 1000 kN,偏心距e = 20 mm,锤头高度h = 200 mm,试求锻锤给两侧导轨的压力。
最新西南交通大学高等数学练习题答案详解优秀名师资料

西南交通大学高等数学练习题答案详解精品文档西南交通大学高等数学练习题答案详解高等数学1. 函数y?xcos2? A. 奇函数x3?x是1?xB. 偶函数C. 非奇非偶函数D. 有界函数2. 函数y?2cos的周期是B.?C.?D. 0an?2,. 设数列an,bn及cn满足:对任意的n,an?bn?cn,且limn??lim?0,则limbn?n??n??A. 0B. 1C.D. -21 / 32精品文档x2?2x?14. lim=x?ix3?xA.1B. 0C.1D. ?5. 在抛物线y?x2上点M的切线的倾角为 A. 1124tan2x?,则点M的坐标为11B. C. D.426.limx?0e?1?sinxB.2 / 32精品文档1xA. 0 C. 1 D. -27. A.limx?012B. eC.1D. ?8. 设曲线y?x与直线x=2的交点为P,则曲线在P点的切线方程是 A x-y-4=0B x+y-1=0C x+y-3=0D x-y+2=09. y?x?3?sinx,则y?? A. xx?1xx?3x?cosx1B. x?3ln3?cosxxxC. xlnx?3ln3?cosxxxD. x?3ln3?cosx3 / 32精品文档xx10. f在点x0可微是f在点x0连续的 A. 充分条件B. 必要条件C. 充分必要条件D. 无关条件11. 函数y?2x3?6x2?18x?7单调减少的区间是 A.B. x? D.C. ,12.?sin3xdx?11cos3x?c B. ?cos3x?C C. ?cos3x?C D. cos3x?C3 21dt,则??? 13. 设??? sinx1?t21cosxcosx1?? A.B.C.D.1?sin2x1?sin2x1?sin2x1?sin2xA.14. 函数5e的一个原函数为 A.e5x5xB.e4 / 32精品文档5xC.15xeD. ?e5x15.??2??2xcos3xdx= B.A.2???4C. 0D.216. 下列广义积分收敛的是 A.5 / 32精品文档??dxx1B.dx? 022C.??11dx 1?xD.?adxa?x2217. 下列集合可作为一条有向直线在空间直角坐标系中的方向角?,?,?的是 A. 5?,45?,60?C. 0?,45?,60?,18. 设函数f?xy? A. 06 / 32精品文档B. 12B.5?,60?,60? D.5?,60?,90? y,则f?=xxC. ?1D.2219. 设函数u?ln,则du2=A.1C. dx?dy?dz 0.24D.3B.7 / 32精品文档23x ??xA?2xcos2x B xsinx2C sinxDsin2x2. 当D?{|x2?y2?1} 时,则??dx?DA ?B 1C 0D ?a23. 设a?0,则?? A.?B.?C.发散D.?4225. 曲面z?x2?y2在点处的切平面方程是A.?4??0 B ?4??0 C. ?2??0,D.?4??0?26. 判断级数?n?118 / 32精品文档n?12n2?n是 A绝对收 . B条件收敛. C 发散 . D 以上都不正确 . ?g27. f???x,x?0其中g?=2要使f在x?0处连续,则a?A. 0B. 1C.D. e28. 方程y???4y?0的通解是 A. y?Ce2x?Ce?2xC.y?C1e2x?C2e?2x?B. y?C1e2x?e?2x D. y?e2x?C2e?2xn?1x2n?129. ?内的和函数是n?1!AsinxB cosx Cex30. 设f?3??x9 / 32精品文档20tdt,,则f=西南交通大学网络教育2010年秋季入学考试模拟题高等数学1.函数y?x2sinx?ln,则y?? A. xx?1x3?3x?cosx2B. x?3ln3?cosx D. x?3ln3?cosxxxxxC. x?3x?sinxx7. f在点x0可导是f在点x0连续的 A. 充分条件B. 必要条件C. 充分必要条件D. 无关条件8. 函数y?2x3?6x2?18x?7单调减少的区间是 A.B. x? D.10 / 32精品文档C. ,1x9. 曲线y?e?1的水平渐近线方程为 A. x?1B. y?1C. x?0D.y?0210.?5一、填空题: 1(设函数z?z是由?nxz?lnzy所确定,则dz?0,1,1??dx?dy (?2(设幂级数?anx的收敛区间为??3,3?,则幂级数?an?x?1?的收11 / 32精品文档n?0n?0n敛区间为 ??2,4? ((设函数??x,f???0,y???x?00?x??的付氏级数的和函数为S,则S??2(4(设z?f,其中f具有连续的二阶偏导数,则x??z?x?y2=1x???f121x12 / 32精品文档2f2??yx3?? ( f225(设幂级数?an?x?1?在x?0处收敛,而在x?2处发散,则幂级数?anxn的n?0n?0n?收敛域为 [?1,1)((函数?n?1?n关于x的幂级数展开式为 ? ( f??1??x,x?2n?1x?x?2n?0?2?3?y7(设函数z?x,则dz? dx?2ln2dy8(曲线x?t,y??t2,z?t3的切线中,与平面x?2y?3z?6垂直的切线方程是13 / 32精品文档x?11?y?1?2?z?13z(9(设z?z是由方程e?zsin?lna a?0为常数所确定的二元函数,则 dz? yzcose?sin2zdx?xzcose?sinzdy(10.旋转抛物面z?x?y的切平面:x?4y?8z?1?0,2平行与已知平面x?y?2z?1.111(微分方程2y???y??y?0的通解为 Y?C1e2x?C2e14 / 32精品文档?x,1x2y???y??y?e的通解为 y?C1e2?C2ex?x?12e(x12.曲线?:x??tecosudu,y?2sint?cost,z?1?eu3t在点?0,1,2?处的切线方程为3(函数f?1x?4的麦克劳林级数的第5项为?x44515 / 32精品文档,收敛域为.14.(已知函数f?2x?3y?x?y,有一个极值点,则a?2, b?3,此时函数f 的极大值为 .ab15.试写出求解下列条件极值问题的拉格朗日函数:分解已知正数a为三个正数x,y,z之和,使x,y,z的倒数之和最小L?x,y,z??1x?1y?1z???x?y?z?a?16函数f?xln?1?x?的麦克劳林级数的收敛域为x???1,1?,f?二、单项选择题:请将正确结果的字母写在括号内。
西南交通大学大一公共课高等数学考试卷 (2)

西南交通大学高等数学考试一、选择题(每题4分,共16分)1.函数222222 0(,)0 0xy x y x y f x y x y ⎧+≠⎪+=⎨⎪+=⎩在(0, 0)点 .(A) 连续,且偏导函数都存在(B) 不连续,但偏导函数都存在;(C) 不连续,且偏导函数都不存在; (D) 连续,且偏导函数都不存在。
2.设f 为可微函数,(,)z f x y z xyz =++,则z x ∂=∂ 。
(A )12121f yz f f x y f ''+''+- (B )12121f x y f f yz f ''--''+ (C )12121f yz f f x y f ''+''-- (D )1212f xzf f yzf ''+''+。
3.设),(y x f 在()22:24D x y +-≤上连续,则二重积分⎰⎰D y x f σd ),(表示成极坐标系下的二次积分的形式为 。
(A ). 220 0d (cos ,sin )d f r r r rπθθθ⎰⎰;(B ). 2d (cos ,sin )d f r r r rπθθθ⎰⎰;(C ). 4cos 00d (cos ,sin )d f r r r rπθθθθ⎰⎰;(D ). 4sin 0d (cos ,sin )d f r r r rπθθθθ⎰⎰4.幂级数0(1)nn n a x ∞=+∑在3x =处条件收敛,则幂级数0nnn a x∞=∑的收敛半径为 。
(A ).3; (B ).4;(C ).1; (D ).5。
二、填空题(每题4分,共20分)1.设函数y z x =,则函数yz x =的全微分 。
2.函数222u x y z =++在点)1,1,1(0P 处沿0OP 方向的方向导数为 ,其中O 为坐标原点。
西南交大高等数学教材答案

西南交大高等数学教材答案在文中我不能提供任何无关的题目内容或者文章的链接,但是我可以帮助您解答一些与西南交大高等数学教材相关的问题。
以下是一些常见的高等数学题目,希望对您有所帮助:
1. 求极限:
lim(x->0) (sinx / x)
解答:使用泰勒级数展开sinx以及lim(x->0) (1/x)的性质,可以得到lim(x->0) (sinx / x) = 1。
2. 计算偏导数:
求函数 f(x, y) = x^2 + 2xy + y^2 的关于 x 和 y 的偏导数。
解答:对于 f(x, y) = x^2 + 2xy + y^2,对 x 求偏导数,得到∂f/∂x = 2x + 2y;对 y 求偏导数,得到∂f/∂y = 2x + 2y。
3. 求定积分:
计算∫(0 to π/2) sinx dx。
解答:对于∫(0 to π/2) sinx dx,使用不定积分的方法可以得到该定积分的结果为 1。
4. 求微分方程的解:
求解微分方程 dy/dx = x^2 - y^2。
解答:该微分方程可以化为 dy / (x^2 - y^2) = dx,使用偏微分分式的方法可以得到 y = ±(e^(2x)+1) / (e^(2x)-1+C),其中 C 为常数。
这些是一些常见的高等数学问题,希望对您有所帮助。
如果您有其他具体的问题或者需要进一步的解答,请告诉我具体的要求,我会尽力帮助您。
西南交通大学“车辆工程”《数字电子技术A》23秋期末试题库含答案

西南交通大学“车辆工程”《数字电子技术A》23秋期末试题库含答案第1卷一.综合考核(共20题)1.若两个函数具有不同的逻辑函数式,则两个逻辑函数必然不相等。
()A.错误B.正确2.在()的情况下,函数Y=A+B运算的结果是逻辑“1”。
A.全部输入是“0”B.任一输入是“0”C.任一输入是“1”D.全部输入是“1”3.七段译码器74LS47的输入是4位(),输出是七段反码。
A.BCD码B.七段码C.七段反码D.二进制码4.5.描述触发器的逻辑功能的方法不包括()A.状态转表B.特性方程C.状态转换图D.状态方程6.三态门输出高阻状态时,()是正确的说法A.用电压表测量指针不动B.相当于悬空C.电压不高不低D.测量电阻指针不动7.8.9.改变()值,不会改变555构成的多谐振荡器电路的振荡频率。
A.电源VCCB.电阻R1C.电阻R2D.电容C10.11.12.13.格雷码具有任何相邻码只有一位码元不同的特性。
()A.错误B.正确14.以下表达式中不符合逻辑运算法则的是()。
A.C·C=2CB.1+1=2C.0+1=1D.A+1=115.要想把串行数据转换成并行数据,不应选()。
A.并行输入串行输出方式B.串行输入串行输出方式C.串行输入并行输出方式D.并行输入并行输出方式16.17.18.数据选择器和数据分配器的功能正好相反,互为逆过程。
()A.错误B.正确19.若两个函数具有相同的真值表,则两个逻辑函数必然相等。
()A.错误B.正确20.下列哪些信号不属于数字信号()。
A.正弦波信号B.时钟脉冲信号C.音频信号D.视频图像信号第1卷参考答案一.综合考核1.参考答案:A2.参考答案:BCD3.参考答案:A5.参考答案:D6.参考答案:ABD9.参考答案:A13.参考答案:B14.参考答案:AB15.参考答案:ABD18.参考答案:B19.参考答案:B20.参考答案:ACD。
西南交大工程数学I第3次作业答案

工程数学I 第3次作业客观题本次作业是本门课程本学期的第3次作业,注释如下:一、单项选择题(只有一个选项正确,共10道小题)1.(A)(B)(C)(D)你选择的答案: C [正确]正确答案:C解答参考:2.(A)(B)(C)(D)你选择的答案: B [正确] 正确答案:B解答参考:3.(A)(B)(C)(D)你选择的答案: D [正确] 正确答案:D解答参考:4. 下列说法正确的是()(A)(B)(C)(D)你选择的答案: D [正确] 正确答案:D解答参考:5.(A)(B)(C)(D)你选择的答案: C [正确] 正确答案:C解答参考:6.(A)(B)(C)(D)你选择的答案: C [正确] 正确答案:C解答参考:7.(A) 合同且相似(B) 合同但不相似(C)不合同但相似(D) 不合同且不相似你选择的答案: A [正确] 正确答案:A解答参考:8.(A)(B)(C)(D)你选择的答案: C [正确] 正确答案:C解答参考:9.(A)(B)(C)(D)你选择的答案: D [正确] 正确答案:D解答参考:10.(A)(B)(C)(D)你选择的答案: C [正确]正确答案:C解答参考:二、判断题(判断正误,共16道小题)11.你选择的答案:说法错误 [正确]正确答案:说法错误解答参考:12.你选择的答案:说法正确 [正确]正确答案:说法正确解答参考:13.你选择的答案:说法错误 [正确] 正确答案:说法错误解答参考:14.你选择的答案:说法错误 [正确] 正确答案:说法错误解答参考:15.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:16.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:17.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:18.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:19.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:20.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:21.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:22.你选择的答案:说法错误 [正确] 正确答案:说法错误解答参考:23.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:24.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:25.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:26.你选择的答案:说法正确 [正确] 正确答案:说法正确解答参考:。
2021年西安交通大学网络教育专升本高等数学入学测试复习题

当代远程教诲专升本高等数学入学考试复习题注:答案一律写在答题卷上,写在试题上无效考生注意:依照国家规定,试卷中正切函数、余切函数、反正切函数、反余切函数分别用tan ,cot ,arctan ,arccot x x x x 来表达。
一、 单项选取题1.设)(x f 是奇函数,)(x g 是偶函数,则)]([x g f 是【 】A .即不是奇函数,又不是偶函数B .偶函数C .有也许是奇函数,也也许是偶函数D .奇函数 2.极限03limtan4x xx→=【 】A .0B .3C .43D .4 3.由于e n nn =⎪⎭⎫ ⎝⎛+∞→11lim ,那么=xe 【 】A .xnn n x ⎪⎭⎫ ⎝⎛+∞→1lim B .nn n x ⎪⎭⎫ ⎝⎛+∞→1lim C .nxn n x ⎪⎭⎫ ⎝⎛+∞→1lim D .xnn n ⎪⎭⎫ ⎝⎛+∞→11lim4.若2)(2+=xex f ,则=)0('f 【 】A .1B .eC .2D .2e 5.设1)(-=xe xf ,用微分求得(0.1)f 近似值为【 】A .11.0-eB .1.1C .1.0D .2.06.设⎩⎨⎧==2bt y at x ,则=dy dx【 】A .a b 2 B .bt a 2 C .abt 2 D .bt 2)()('x f de x f 7.设0=-yxe y ,则=dxdy 【 】A .1-y y xe eB .y y xe e -1C .y y e xe -1D .yy e xe 1-8.下列函数中,在闭区间]1,1[-上满足罗尔定理条件是【 】 A .xe B .21x - C .x D .x ln 9.函数x x y ln =在区间【 】A .),0(+∞内单调减B .),0(+∞内单调增C .)1,0(e 内单调减D .),1(+∞e内单调减 10.不定积分⎰=dx x x )cos(2【 】A .C x +)sin(212 B .21sin 2x C + C .C x +-)sin(212 D .C x +-)sin(22 11.不定积分⎰=+dx exx ln 32【 】A .C e x +233 B .C e x +236 C .C e x +2331 D .C e x +236112.已知()f x 在0x =某邻域内持续,且(0)0f =,0()lim 21cos x f x x→=-,则在 0x =处()f x 【 】A .不可导B .可导但()0f x '≠C .获得极大值D .获得极小值 13.广义积分2 21dx x+∞=⎰【 】 A .0 B .∞+ C .21-D .2114.函数223y x z -=在)0,0(点为【 】A .驻点B .极大值点C .极小值点D .间断点 15.定积分122121ln1xx dx x-+=-⎰【 】A .1-B .0C .∞-D .116.设在区间[],a b 上()0,()0,()0f x f x f x '''><>,令 1 ()ba S f x dx =⎰,2()()S fb b a =-,31(()())()2S f a f b b a =+-。
四川2023年大专生专升本数学考试及答案 (1)

普通高等学校招生全国统一考试数学(满分150分,考试时间120分钟)一、选择题:(本题共12小题,每小题5分,共60分)1.“a =1”是“直线0=+y x 和直线0=-ay x 互相垂直”的().A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件2.在ABC ∆中,AB=3,AC=2,BC=10,则AB AC ⋅=().A .23-B .32-C .32D .233.为得到函数πcos 3y x ⎛⎫=+ ⎪⎝⎭的图象,只需将函数sin y x =的图像().A .向左平移π6个长度单位B .向右平移π6个长度单位C .向左平移5π6个长度单位D .向右平移5π6个长度单位4.函数|lg |)(x x x f -=在定义域上零点个数为().A .1B .2C .3D .45.如图是一个空间几何体的主视图、侧视图、俯视图,如果直角三角形的直角边长均为1,那么这个几何体的体积为().A .1B .21C .31D .616.一个等差数列{an}中,a1=-5,它的前11项的平均值是5,若从中抽取一项,余下项的平均值是4,则抽取的是()A.a11B.a10C.a9D.a87.设函数f(x)=logax(a>0,且a ≠1)满足f(9)=2,则f -1(log92)等于()A.2B.2C.21 D.±28.将边长为a 的正方形ABCD 沿对角线AC 折起,使得BD=a,则三棱锥D —ABC 的体积为()A.63a B.123a C.3123a D.3122a 9.设O 、A 、B 、C 为平面上四个点,OA =a ,OB =b ,OC =c ,且a+b+c=0,a ·b=b ·c=c ·a=-1,则|a|+|b|+|c|等于()A.22B.23C.32D.3310.设函数()f x 的定义域为R ,满足(1) 2 ()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-.若对任意(,]x m ∈-∞,都有8()9f x ≥-,则m 的取值范围是()A .9,4⎛⎤-∞ ⎥⎝⎦B .7,3⎛⎤-∞ ⎥⎝⎦C .5,2⎛⎤-∞ ⎥⎝⎦D .8,3⎛⎤-∞⎥⎝⎦11.已知a ∈(0,π2),2sin2α=cos2α+1,则sin α=()A .15BC .3D .512.设F 为双曲线C :22221x y a b -=(a>0,b>0)的右焦点,O为坐标原点,以OF 为直径的圆与圆x2+y2=a2交于P 、Q 两点.若|PQ|=|OF|,则C 的离心率为()ABC .2D二、填空题(共4小题,每小题5分;共计20分)1、如果∆ABC 的三个内角A ,B ,C 成等差数列,则B 一定等于______.2、已知2tan -=α,71tan =+)(βα,则βtan 的值为______.3.如图,长方体1111ABCD A B C D -的体积是120,E 为1CC 的中点,则三棱锥E-BCD 的体积是______.4.在平面直角坐标系xOy 中,P 是曲线4(0)y x x x =+>上的一个动点,则点P 到直线x+y=0的距离的最小值是______.三、大题:(满分70分)1、已知函数3()x x bf x x++=,{}n a 是等差数列,且2(1)a f =,3(2)a f =,4(3)a f =.(1)求{}n a 的前n 项和;(2)求()f x 的极值.2、已知集合A 是由a -2,2a2+5a,12三个元素组成的,且-3∈A ,求a.3.(本题满分12分)已知四边形ABCD 是菱形,060BAD ∠=四边形BDEF 是矩形,平面BDEF ⊥平面ABCD ,G H 、分别是CE CF 、的中点.(1)求证:平面//AEF 平面BDGH(2)若平面BDGH 与平面ABCD 所成的角为060,求直线CF 与平面BDGH 所成的角的正弦值4.设),(),,(2211y x Q y x P 是抛物线px y 22=)0(>p 上相异两点,P Q 、到y 轴的距离的积为4且0=⋅OQ OP .(1)求该抛物线的标准方程.(2)过Q 的直线与抛物线的另一交点为R ,与x 轴交点为T ,且Q 为线段RT 的中点,试求弦PR 长度的最小值.5.已知椭圆C1以直线所过的定点为一个焦点,且短轴长为4.(Ⅰ)求椭圆C1的标准方程;(Ⅱ)已知椭圆C2的中心在原点,焦点在y 轴上,且长轴和短轴的长分别是椭圆C1的长轴和短轴的长的λ倍(λ>1),过点C (﹣1,0)的直线l 与椭圆C2交于A ,B 两个不同的点,若,求△OAB 的面积取得最大值时直线l 的方程. 6.已知函数(a ∈R ).(Ⅰ)讨论g (x )的单调性;(Ⅱ)若.证明:当x >0,且x ≠1时,.参考答案:一、选择题:1-5题答案:CDCCC 6-10题答案:ABDCB 11-12题答案:BA 二、填空题:1、︒60;2、3;3、10;4、4.三、大题:1、【解析】(1)由3()x x b f x x++=得211(1)21b a f b ++===+,3322(2)522b ba f ++===+,3433(3)1033b ba f ++===+,由于{}n a 为等差数列,∴2432a a a +=,即(2)(10)2(5)32b b b +++=+,解得6b =-,∴22624a b =+=-+=-,3655222b a =+=-+=,461010833b a =+=-+=,设数列{}n a 的公差为d ,则326d a a =-=,首项1210a a d =-=-,故数列{}n a 的通项公式为1(1)616n a a n d n =+-=-,∴数列{}n a 的前n 项和为21()(10616)31322n n n a a n n S n n +-+-===-;(2)法一(导数法):33266()1(0)x x b x x f x x x x x x +++-===-+≠,332226262(3)()2x x f x x x x x ++'=+==,当330x +<,即x <()0f x '<,函数()f x 在(,-∞上单调递减,当330x +>,即x >时,()0f x '>,函数()f x 在()+∞上单调递增,故函数()f x 在x =极小值为53(31f =+,无极大值.法二(基本不等式法):33266()1(0)x x b x x f x x x x x x +++-===-+≠,当0x >时,26()1f x x x =-+为单调递增函数,故()f x 在(0,)+∞上无极值.当0x <时,则6x ->,∴2226633()1()()1()()()11f x x x x x x x x =-+=-++=-+++≥+---53131==+,当且仅当23()x x-=-,即x =综上所述,函数()f x 在x =53(31f =+,无极大值.【评注】本题考查等差数列的通项公式以及前n 项和、函数单调性及应用,数列与函数进行结合考查,综合性较强,属于中档题.2、解:由-3∈A ,可得-3=a -2或-3=2a2+5a ,∴a =-1或a =-32.则当a =-1时,a -2=-3,2a2+5a =-3,不符合集合中元素的互异性,故a =-1应舍去.当a =-32时,a -2=-72,2a2+5a =-3,∴a =-32.3.参考答案:解:(1)G H 、分别是CE CF 、的中点所以//EF GH ------①---1分连接AC 与BD 交与O ,因为四边形ABCD 是菱形,所以O 是AC 的中点,连OG ,OG 是三角形ACE 的中位线//OG AE -②-----3分由①②知,平面//AEF 平面BDGH ----4分(2),BF BD ⊥平面BDEF ⊥平面ABCD ,所以BF ⊥平面ABCD -------5分取EF 的中点N ,//ON BF ON ∴⊥平面ABCD ,建系{,,}OB OC ON设2AB BF t ==,,则()()()100,03,0,10B C F t ,,,,,13,,222t H ⎛⎫⎪ ⎪⎝⎭--------6分()131,0,0,,222t OB OH ⎛⎫== ⎪ ⎪⎝⎭ 设平面BDGH 的法向量为()1,,n x y z = 110130222n OB x t n OH x y z ⎧⋅==⎪⎨⋅=++=⎪⎩,所以(10,3n t =- 平面ABCD 的法向量()20,0,1n = ----9分12231|cos ,|23n n t <>==+ ,所以29,3t t ==----10分所以()1,3,3CF =,设直线CF 与平面BDGH 所成的角为θ13133321336|,cos |sin 1=⨯=〉〈=n CF θ4.参考答案:解:(1)∵OP→·OQ →=0,则x1x2+y1y2=0,-1分又P 、Q 在抛物线上,故y12=2px1,y22=2px2,故得y122p ·y222p+y1y2=0,y1y2=-4p2222212144)(||pp y y x x ==∴-------3分又|x1x2|=4,故得4p2=4,p=1.所以抛物线的方程为:22y x =-------------4分(2)设直线PQ 过点E(a,0)且方程为x =my +a联立方程组⎩⎨⎧=+=x y amy x 22消去x 得y2-2my -2a =0∴⎩⎨⎧-==+ay y m y y 222121①设直线PR 与x 轴交于点M(b,0),则可设直线PR 方程为x =ny +b,并设R(x3,y3),同理可知,⎩⎨⎧-==+by y n y y 223131②--7分由①、②可得32y b y a=由题意,Q 为线段RT 的中点,∴y3=2y2,∴b=2a又由(Ⅰ)知,y1y2=-4,代入①,可得-2a =-4∴a =2.故b =4.∴831-=y y ∴3123123124)(1||1|PR |y y y y n y y n -+⋅+=-+=2481222≥+⋅+=n n .当n=0,即直线PQ 垂直于x 轴时|PR|取最小值245.已知椭圆C1以直线所过的定点为一个焦点,且短轴长为4.(Ⅰ)求椭圆C1的标准方程;(Ⅱ)已知椭圆C2的中心在原点,焦点在y 轴上,且长轴和短轴的长分别是椭圆C1的长轴和短轴的长的λ倍(λ>1),过点C (﹣1,0)的直线l 与椭圆C2交于A ,B 两个不同的点,若,求△OAB 的面积取得最大值时直线l 的方程.【解答】解:(Ⅰ)所给直线方程变形为,可知直线所过定点为.∴椭圆焦点在y 轴,且c=,依题意可知b=2,∴a2=c2+b2=9.则椭圆C1的方程标准为;(Ⅱ)依题意,设椭圆C2的方程为,A(x1,y1),B(x2,y2),∵λ>1,∴点C(﹣1,0)在椭圆内部,直线l与椭圆必有两个不同的交点.当直线l垂直于x轴时,(不是零向量),不合条件;故设直线l为y=k(x+1)(A,B,O三点不共线,故k≠0),由,得.由韦达定理得.∵,而点C(﹣1,0),∴(﹣1﹣x1,﹣y1)=2(x2+1,y2),则y1=﹣2y2,即y1+y2=﹣y2,故.∴△OAB的面积为S△OAB=S△AOC+S△BOC====.上式取等号的条件是,即k=±时,△OAB的面积取得最大值.∴直线的方程为或.6.已知函数(a∈R).(Ⅰ)讨论g(x)的单调性;(Ⅱ)若.证明:当x>0,且x≠1时,.【解答】(Ⅰ)解:由已知得g(x)的定义域为(0,+∞),…(1分)方程2x2+x﹣a=0的判别式△=1+8a.…(2分)①当时,△≤0,g'(x)≥0,此时,g(x)在(0,+∞)上为增函数;…(3分)②当时,设方程2x2+x﹣a=0的两根为,若,则x1<x2≤0,此时,g'(x)>0,g(x)在(0,+∞)上为增函数;…(4分)若a>0,则x1<0<x2,此时,g(x)在(0,x2]上为减函数,在(x2,+∞)上为增函数,…..…(5分)综上所述:当a≤0时,g(x)的增区间为(0,+∞),无减区间;当a>0时,g(x)的减区间为(0,x2],增区间为(x2,+∞).…(6分)(Ⅱ)证明:由题意知,…(7分)∴,…(8分)考虑函数,则…(9分)所以x≠1时,h'(x)<0,而h(1)=0…(10分)故x∈(0,1)时,,可得,x∈(1,+∞)时,,可得,…(11分)从而当x>0,且x≠1时,.。
