等效电压源定理(高中物理精品)
戴维南定理典型例子_戴维南定理解题方法

戴维南定理典型例子_戴维南定理解题方法什么是戴维南定理戴维南定理(又译为戴维宁定理)又称等效电压源定律,是由法国科学家L·C·戴维南于1883年提出的一个电学定理。
由于早在1853年,亥姆霍兹也提出过本定理,所以又称亥姆霍兹-戴维南定理。
其内容是:一个含有独立电压源、独立电流源及电阻的线性网络的两端,就其外部型态而言,在电性上可以用一个独立电压源V和一个松弛二端网络的串联电阻组合来等效。
在单频交流系统中,此定理不仅只适用于电阻,也适用于广义的阻抗。
戴维南定理在多电源多回路的复杂直流电路分析中有重要应用。
戴维南定理(Thevenin‘stheorem):含独立电源的线性电阻单口网络N,就端口特性而言,可以等效为一个电压源和电阻串联的单口网络。
电压源的电压等于单口网络在负载开路时的电压uoc;电阻R0是单口网络内全部独立电源为零值时所得单口网络N0的等效电阻。
戴维南定理典型例子戴维南定理指出,等效二端网络的电动势E等于二端网络开路时的电压,它的串联内阻抗等于网络内部各独立源和电容电压、电感电流都为零时,从这二端看向网络的阻抗Zi。
设二端网络N中含有独立电源和线性时不变二端元件(电阻器、电感器、电容器),这些元件之间可以有耦合,即可以有受控源及互感耦合;网络N的两端ɑ、b接有负载阻抗Z(s),但负载与网络N内部诸元件之间没有耦合,U(s)=I(s)/Z(s)。
当网络N中所有独立电源都不工作(例如将独立电压源用短路代替,独立电流源用开路代替),所有电容电压和电感电流的初始值都为零的时候,可把这二端网络记作N0。
这样,负载阻抗Z(s)中的电流I(s)一般就可以按下式1计算(图2)式中E(s)是图1二端网络N的开路电压,亦即Z(s)是无穷大时的电压U(s);Zi(s)是二端网络N0呈现的阻抗;s是由单边拉普拉斯变换引进的复变量。
和戴维南定理类似,有诺顿定理或亥姆霍兹-诺顿定理。
按照这一定理,任何含源线性时不变二端网络均可等效为二端电流源,它的电流J等于在网络二端短路线中流过的电流,并联内阻抗同样等于看向网络的阻抗。
4.3等效电源定理

U
s
得
Req
Us I
1
1
0.8
225
300 720
20 中北大学国家级电工电子实验教学示范中心
戴维南定理例题3
③戴维南等效电路如图示,则得电流解
I4
U 225
0.03A
该例题用戴维南定理求解电流,
同时涵盖了含受控源电路之回
路方程的概念和外加电源求解
戴维南定理是有源单口网路的基本属性。
7 中北大学国家级电工电子实验教学示范中心
戴维南定理例题1
[例]图示电路中已知Us2 = 9V , Uab = 9V , Is = 6A , R1 = 1Ω, R2 = 2Ω, R3 = 3Ω,R4 = 4Ω, 试求Us1
解一:用戴维南定理化简ab 端口右边的网路。 ①求ab端的开路电压Uoc,如图 (a)所示,先求Icb再求Uoc最 为捷径,因为
18 中北大学国家级电工电子实验教学示范中心
戴维南定理例题3
可列回路方程解电流 I 3
R1 R2 R3 I3 R2I3 U s
I3
R1
R2
Us
R3
R2
36
420 300 300 0.2 300
0.0375A
Uoc U seq R3I3 300 0.0375 11.25V
(Req RL ) R0 RL
6 中北大学国家级电工电子实验教学示范中心
戴维南定理的证明
结论:前式 i i i uoc useq
(Req RL ) R0 RL
该式正是含内阻电压源的电流表达式。它表明: 从端口上看,有源单口网路对外电路的作用,可 以用一个含内阻的电压源来等效代替。该电压源 的源电压等于有源单口网路的开路电压,其内电 阻R0就是有源单口网路去源后的等效电阻。故戴 维南定理得证。此刻应该认识到:
电分第4章-3,4节等效电源定理

6Ω
I + 4V -
U OC ∴ RO = = 8Ω I SC
③一步法求解 (直接求端口VAR)
例:试求图示电路的戴维南等效电路。 解:法一:U OC
⎧U ' = (4 + 8) I 1 ⎪ ⎨U ' = 4 I 2 − 12 I ' ⎪I + I = I ' U ' = −6 I ' 2 ⎩ 1
-
-
方法六:实验测量法(限于直流电路): ①测开路电压UOC ; ②允许短路时测ISC ,则RO =UOC/ISC ; 否则用一R作为外电路并测其U、I,
U OC − U RO = I
I a + U b
N
R
例:用等效电源定理求图示电路中的I。考虑 R = 2.14Ω 和 R = 4.14Ω 两种情况。 a 法一:戴维南定理 + 60V
§4-3 戴维南定理和诺顿定理(等效电源定理)
一. 二端网络及其等效电路 二端网络:互连的一组元件可看作一个整体,当这 个整体只有两个端钮与外部电路相连接时,称 之为二端网络。 又因从一端钮流进的电流必然等于另一端钮流出 的电流,故也可称为一端口(单口)网络。 有源二端网络 :内部含电源的二端网络。 无源二端网络 :内部不含电源的二端网络。
U=6-6I
+ 4Ω U 12 I −
+
a
b
+
-
a
6V
b
−6Ω
例:用戴维南定理求图示电路中的电流 I 。 R2 解:1) R1 + US
-
I A IS B R
高中物理竞赛辅导讲义-第篇-稳恒电流(精品)

高中物理竞赛辅导讲义第8篇 稳恒电流【知识梳理】一、基尔霍夫定律(适用于任何复杂电路) 1. 基尔霍夫第一定律(节点电流定律)流入电路任一节点(三条以上支路汇合点)的电流强度之和等于流出该节点的电流强度之和。
即∑I =0。
若某复杂电路有n 个节点,但只有(n −1)个独立的方程式。
2. 基尔霍夫第二定律(回路电压定律)对于电路中任一回路,沿回路环绕一周,电势降落的代数和为零。
即∑U =0。
若某复杂电路有m 个独立回路,就可写出m 个独立方程式。
二、等效电源定理1. 等效电压源定理(戴维宁定理)两端有源网络可以等效于一个电压源,其电动势等于网络的开路端电压,其内阻等于从网络两端看除源(将电动势短路,内阻仍保留在网络中)网络的电阻。
2. 等效电流源定理(诺尔顿定理)两端有源网络可等效于一个电流源,电流源的电流I 0等于网络两端短路时流经两端点的电流,内阻等于从网络两端看除源网络的电阻。
三、叠加原理若电路中有多个电源,则通过电路中任一支路的电流等于各个电动势单独存在时,在该支路产生的电流之和(代数和)。
四、Y−△电路的等效代换如图所示的(a )(b )分别为Y 网络和△网络,两个网络中的6个电阻满足一定关系时完全等效。
1. Y 网络变换为△网络122331123R R R R R R R R ++=, 122331231R R R R R R R R ++=122331312R R R R R R R R ++=2. △网络变换为Y 网络12311122331R R R R R R =++,23122122331R R R R R R =++,31233122331R R R R R R =++五、电流强度与电流密度 1.电流强度 (1)定义式:q I t∆=∆。
(2)宏观决定式:U I R=。
(3)微观决定式:I neSv =。
2.电流密度在通常的电路问题中,流过导线截面的电流用电流强度描述就可以了,但在讨论大块导体中电流的流动情况时,用电流强度描述就过于粗糙了。
第3.3节 等效电源定理

+ +
b
R1两端的电压为0(虚短),即 I1 0 U 0 等效电阻 Ri U I 0
a
I2
R1
a
I
Ri U
b
U OC
b
不可以等效成诺顿电路
3.3 等效电源定理
【例题】图示电路中,N为线性含源电阻网络。已知 i1=2A时,i2=1/3A。当R增加10Ω时,i1=1.5A, i2=1/2A。当R减少10Ω时,试求支路电流i2。
戴维南定理:线性含源一端口网络的对外作用可以用 一个电压源串联电阻的电路来等效代替。其中电压源 的源电压等于此一端口网络的开路电压,而电阻等于 此一端口网络内部各独立电源置零后所得无独立源一 端口网络的等效电阻。
3.3 等效电源定理
Ri
U oc
I
U
I SC
U OC Ri
I sc
I
U
R
U OC 2 ( R 10 ) 10 22.5W i ( U OC ) 2 20 20W Ri 20
Ri R
Ri
U OC
R
U
Ri 10 U OC 30V 联立解得 当 R 30 时 2 30V U OC 2 PR ( ) 30 30 16.9W Ri 30 (10 30)
戴维南定理

例题 以电桥电路为例,试用戴维南定理 求解。 电桥电路如下图所示,已知R1 = 3Ω, R2 = 5Ω,R3 = R4=4Ω, E = 8V (内阻不计), R5 = 0.125Ω,试求 电阻R5上 通过的电流。
解:(1)先移开R5支路,求开路电压Uab
E I1 I 2 1A, R1 R2 E I3 I 4 1A R3 R4
注意
1. 戴维南定理只适用于线性有源二端网络, 若有源二端网络内含有非线性电阻,则不能 应用戴维南定理。 2. 在画等效电路时,电压源的参考方向应与 选定的有源二端网络开路电压参考方向一致。
诺顿定理
任何一个有源二端线性网络都可以用一个电流为 IS的理想电流源和内阻 R0 并联的电源来等效代 aI 替。 a I + 有源 + IS RL R0 U U 二端 RL – – 网络 等效电源 b b 等效电源的电流 IS 就是有源二端网络的短路电流, 即将 a 、b两端短接后其中的电流。 等效电源的内阻R0等于有源二端网络中所有电源 均除去(理想电压源短路,理想电流源开路)后所 得到的无源二端网络 a 、b两端之间的等效电阻。
任何具有两个引出端的电路(也称网络)都可 称为二端网络。若在这部分电路中含有电源,就 称为有源二端网络,否则称无源二端网络。
无源 二端 网络
a R b + _E a
a 无源二端网络可 化简为一个电阻 b 电压源 (戴维南定理)
有源 二端 网络
a
b
R0 b a
IS R0
有源二端网络可 化简为一个电源 电流源 (诺顿定理)
Байду номын сангаас 小结
1、二端网络的有关概念:任何具有两个引出
戴维南定理

戴维南定理戴维南定理(Thevenin's theorem):含独立电源的线性电阻单口网络N,就端口特性而言,可以等效为一个电压源和电阻串联的单口网络。
电压源的电压等于单口网络在负载开路时的电压uoc;电阻R0是单口网络内全部独立电源为零值时所得单口网络N0的等效电阻。
简介戴维南定理(又译为戴维宁定理)又称等效电压源定律,是由法国科学家L·C·戴维南于1883年提出的一个电学定理。
由于早在1853年,亥姆霍兹也提出过本定理,所以又称亥姆霍兹-戴维南定理。
其内容是:一个含有独立电压源、独立电流源及电阻的线性网络的两端,就其外部型态而言,在电性上可以用一个独立电压源V和一个松弛二端网络的串联电阻组合来等效。
在单频交流系统中,此定理不仅只适用于电阻,也适用于广义的阻抗。
对于含独立源,线性电阻和线性受控源的单口网络(二端网络),都可以用一个电压源与电阻相串联的单口网络(二端网络)来等效,这个电压源的电压,就是此单口网络(二端网络)的开路电压,这个串联电阻就是从此单口网络(二端网络)两端看进去,当网络内部所有独立源均置零以后的等效电阻。
u oc 称为开路电压。
R o称为戴维南等效电阻。
在电子电路中,当单口网络视为电源时,常称此电阻为输出电阻,常用R o表示;当单口网络视为负载时,则称之为输入电阻,并常用R i 表示。
电压源u oc和电阻R o的串联单口网络,常称为戴维南等效电路。
当单口网络的端口电压和电流采用关联参考方向时,其端口电压电流关系方程可表为:U=R0i+uoc[1]戴维南定理和诺顿定理是最常用的电路简化方法。
由于戴维南定理和诺顿定理都是将有源二端网络等效为电源支路,所以统称为等效电源定理或等效发电机定理。
证明戴维南定理可以在单口外加电流源i,用叠加定理计算端口电压表达式的方法证明如下。
戴维南定理证明在单口网络端口上外加电流源i,根据叠加定理,端口电压可以分为两部分组成。
等效电压源定理及其在高中物理中应用
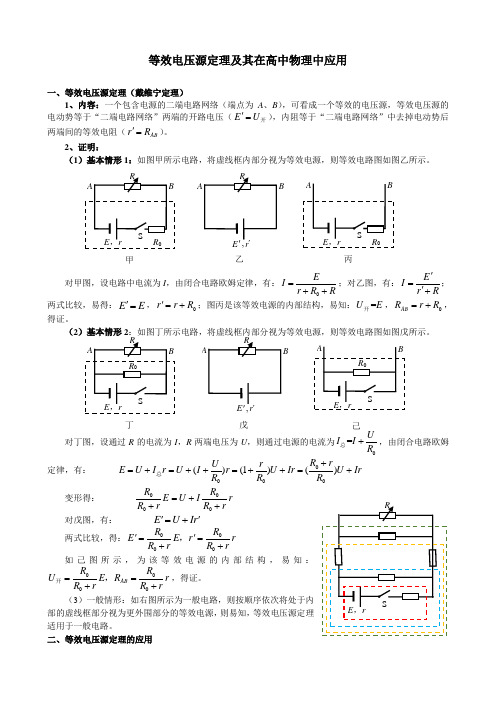
等效电压源定理及其在高中物理中应用一、等效电压源定理(戴维宁定理)1、内容:一个包含电源的二端电路网络(端点为A 、B ),可看成一个等效的电压源,等效电压源的电动势等于“二端电路网络”两端的开路电压(E U '=开),内阻等于“二端电路网络”中去掉电动势后两端间的等效电阻(AB r R '=)。
2、证明:(1)基本情形1:如图甲所示电路,将虚线框内部分视为等效电源,则等效电路图如图乙所示。
对甲图,设电路中电流为I ,由闭合电路欧姆定律,有:0EI r R R=++;对乙图,有:E I r R '='+;两式比较,易得:E E '=,0r r R '=+;图丙是该等效电源的内部结构,易知:=U E 开,0AB R r R =+,得证。
(2)基本情形2:如图丁所示电路,将虚线框内部分视为等效电源,则等效电路图如图戊所示。
对丁图,设通过R 的电流为I ,R 两端电压为U ,则通过电源的电流为0=UI I R +总,由闭合电路欧姆定律,有:0000()(1)()R r U rE U I r U I r U Ir U Ir R R R +=+=++=++=+总 变形得: 0000R R E U I r R r R r=+++对戊图,有:E U Ir ''=+ 两式比较,得:0000R R E E r r R r R r''==++,如己图所示,为该等效电源的内部结构,易知:0000AB R R U E R r R r R r==++开,,得证。
(3)一般情形:如右图所示为一般电路,则按顺序依次将处于内部的虚线框部分视为更外围部分的等效电源,则易知,等效电压源定理适用于一般电路。
二、等效电压源定理的应用乙ARE ',r 'B甲R 0ARE ,rSB丙R 0AE ,rSB丁R 0A R E ,r SB 戊A R E ',r ' BR 0 A E ,r S B 己E ,rSR1、电源电动势和内阻测量的系统误差分析该实验的理论依据是Ir U E +=,其中U 为电源的端电压,I 为通过电源的电流;如图所示为该实验的两种测量电路。
