【精品课件】1.2充分与必要条件
合集下载
1.2.1 充分条件与必要条件1.2.2 充要条件课件人教新课标

1.2 充分条件与必要条件 1.2.1 充分条件与必要条件
1.2.2 充要条件
课标要求:1.理解充分、必要、充要条件的意义.2.会判断条件与结论之间 的充分(必要、充要)性.
自主学习
知识探究
1.充分条件与必要条件 一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由 p可推出q,记作p⇒q,并且说p是q的充分条件,q是p的必要条件.
即时训练1-1:(1)(202X·山东卷)已知直线a,b分别在两个不同的平面α,β
内.则“直线a和直线b相交”是“平面α和平面β相交”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
解析:(1)若a,b相交,则α,β一定相交;若α,β相交,则不能得出a,b相交.故选 A.
方法技能一般地,证明“p成立的充要条件为q”时,在证充分性时应以q为 “已知条件”,p是该步中要证明的“结论”,即q⇒p;证明必要性时则是 以p为“已知条件”,q为该步中要证明的“结论”,即p⇒q.
即时训练 2-1:(1)已知 x,y 都是非零实数,且 x>y,求证: 1 < 1 的充要条件是 xy>0; xy
1b
所以“ab=1”是“l1∥l2”的必要不充分条件,③正确.
④中,y=x2+mx+m+3有两个不同零点⇔Δ=m2-4(m+3)>0⇔m<-2或 m>6. 所以是充要条件,④正确. 答案:(3)①③④
方法技能 充分、必要、充要条件的判断方法 若 p⇒ q,q p,则 p 是 q 的充分不必要条件; 若 p q,q⇒ p,则 p 是 q 的必要不充分条件; 若 p⇒ q,q⇒ p,则 p 是 q 的充要条件; 若 p q,q p,则 p 是 q 的既不充分也不必要条件.
1.2.2 充要条件
课标要求:1.理解充分、必要、充要条件的意义.2.会判断条件与结论之间 的充分(必要、充要)性.
自主学习
知识探究
1.充分条件与必要条件 一般地,“若p,则q”为真命题,是指由p通过推理可以得出q.这时,我们就说,由 p可推出q,记作p⇒q,并且说p是q的充分条件,q是p的必要条件.
即时训练1-1:(1)(202X·山东卷)已知直线a,b分别在两个不同的平面α,β
内.则“直线a和直线b相交”是“平面α和平面β相交”的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
解析:(1)若a,b相交,则α,β一定相交;若α,β相交,则不能得出a,b相交.故选 A.
方法技能一般地,证明“p成立的充要条件为q”时,在证充分性时应以q为 “已知条件”,p是该步中要证明的“结论”,即q⇒p;证明必要性时则是 以p为“已知条件”,q为该步中要证明的“结论”,即p⇒q.
即时训练 2-1:(1)已知 x,y 都是非零实数,且 x>y,求证: 1 < 1 的充要条件是 xy>0; xy
1b
所以“ab=1”是“l1∥l2”的必要不充分条件,③正确.
④中,y=x2+mx+m+3有两个不同零点⇔Δ=m2-4(m+3)>0⇔m<-2或 m>6. 所以是充要条件,④正确. 答案:(3)①③④
方法技能 充分、必要、充要条件的判断方法 若 p⇒ q,q p,则 p 是 q 的充分不必要条件; 若 p q,q⇒ p,则 p 是 q 的必要不充分条件; 若 p⇒ q,q⇒ p,则 p 是 q 的充要条件; 若 p q,q p,则 p 是 q 的既不充分也不必要条件.
上课1.2《充分条件与必要条件》课件 (共20张PPT)

2
(充要条件) 4)同旁内角互补 " "是 " 两直线平行 "的
5)" x 5" 是 " x 3"的
(必要不充分条件) 6)" a b " 是 " a c b c "的 (充要条件)
7)已知ABC不是直角三角形, "A<B" 是 "tan A tan B "的 (既不充分也不必要条件)
定义: 对于命题“若p则q”
1.若p q, q p, 则p是q的充分不必要条件. q是p的必要不充分条件.
2.若p q, q p,即p q, 则p是q充分必要条件, 简称充要条件 . 也说p与q互为充要条件 .
3.若p q, q p, 则p是q的既充分不必要条件. q是p的既必要不充分条件.
作业:
• P.15 A组 第4题 B组第2题
真
2 0 ac 00 (5方程有 )若ab ax ,则 ; 假 bx (a 0) 两个不等的实数解 b 2 4ac 0
(6) 若两三角形全等 ,则两三角形面积相等; 两三角形全等
真
两三角形面积相等
定义:
充分条件与必要条件:一般地,如果已知 p q , 即命题“若p则q” 为真命题,那么就说,p 是q 的充分条件, q 是p 的必要条件.
1 1 当x 0, y 0时,有: . x y
必要性(q p) 1 1 yx 若 , 则有: 0,即xy( y x) 0. x y xy x y y x 0 xy 0.
例2、已知ab 0, 求证:a b 1的充要条件是 a 3 b3 ab a 2 b 2 0.
(充要条件) 4)同旁内角互补 " "是 " 两直线平行 "的
5)" x 5" 是 " x 3"的
(必要不充分条件) 6)" a b " 是 " a c b c "的 (充要条件)
7)已知ABC不是直角三角形, "A<B" 是 "tan A tan B "的 (既不充分也不必要条件)
定义: 对于命题“若p则q”
1.若p q, q p, 则p是q的充分不必要条件. q是p的必要不充分条件.
2.若p q, q p,即p q, 则p是q充分必要条件, 简称充要条件 . 也说p与q互为充要条件 .
3.若p q, q p, 则p是q的既充分不必要条件. q是p的既必要不充分条件.
作业:
• P.15 A组 第4题 B组第2题
真
2 0 ac 00 (5方程有 )若ab ax ,则 ; 假 bx (a 0) 两个不等的实数解 b 2 4ac 0
(6) 若两三角形全等 ,则两三角形面积相等; 两三角形全等
真
两三角形面积相等
定义:
充分条件与必要条件:一般地,如果已知 p q , 即命题“若p则q” 为真命题,那么就说,p 是q 的充分条件, q 是p 的必要条件.
1 1 当x 0, y 0时,有: . x y
必要性(q p) 1 1 yx 若 , 则有: 0,即xy( y x) 0. x y xy x y y x 0 xy 0.
例2、已知ab 0, 求证:a b 1的充要条件是 a 3 b3 ab a 2 b 2 0.
1.2充分条件与必要条件课件人教新课标3
[解析] x>0⇒|x|>0,但|x|>0⇒/ x>0,故选 A.
4.已知函数f(x)=x+bcosx,其中b为常数.那 么“b=0”是“f(x)为奇函数”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
[答案] C
[解析] 当b=0时,f(x)=x为奇函数,故满足 充分性;当f(x)为奇函数时,f(-x)=-f(x), ∴-x+bcosx=-x-bcosx,从而2bcosx=0,∵ 此式对任意x∈R都成立,∴b=0,故满足必要 性,选C.
典例探究学案
充分条件
已知 p:2x+m>0,q:x2-4x>0,若 p 是 q 的充 分条件,则实数 m 的取值范围是________.
[解析] p:x>-m2 ,q:x<0 或 x>4,由条件知 p⇒q, ∴-m2 ≥4,∴m≤-8.
[方法规律总结] 1.判断p是q的充分条件,就是 判断命题“若p,则q”为真命题.
∴-m2 =1,∴m=-2,故选 A.
• [答案] A
[方法规律总结] 1.充要条件
一般地,如果有p⇒q,那么p是q的充分条件; 如果还有q⇒p,那么p又是q的必要条件,则称p 是q的充要条件.显然p和q能互相推出,所以q 也是p的充要条件.记为:p⇔q(“⇔”表示p 与q等价).
2.充分条件、必要条件、充要条件与命题的 真假之间关系:
2.在下列横线上填上“充分”或“必要”.
(1)a>1是a>2的__必__要____条件. (2)a<1是a<2的__充__分____条件.
• 充要条件新知导学
3.如果既有 p⇒q,又有 q⇒p,则 p 是 q 的__充__要__条__件__, 记为___p_⇔__q____.
4.已知函数f(x)=x+bcosx,其中b为常数.那 么“b=0”是“f(x)为奇函数”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
[答案] C
[解析] 当b=0时,f(x)=x为奇函数,故满足 充分性;当f(x)为奇函数时,f(-x)=-f(x), ∴-x+bcosx=-x-bcosx,从而2bcosx=0,∵ 此式对任意x∈R都成立,∴b=0,故满足必要 性,选C.
典例探究学案
充分条件
已知 p:2x+m>0,q:x2-4x>0,若 p 是 q 的充 分条件,则实数 m 的取值范围是________.
[解析] p:x>-m2 ,q:x<0 或 x>4,由条件知 p⇒q, ∴-m2 ≥4,∴m≤-8.
[方法规律总结] 1.判断p是q的充分条件,就是 判断命题“若p,则q”为真命题.
∴-m2 =1,∴m=-2,故选 A.
• [答案] A
[方法规律总结] 1.充要条件
一般地,如果有p⇒q,那么p是q的充分条件; 如果还有q⇒p,那么p又是q的必要条件,则称p 是q的充要条件.显然p和q能互相推出,所以q 也是p的充要条件.记为:p⇔q(“⇔”表示p 与q等价).
2.充分条件、必要条件、充要条件与命题的 真假之间关系:
2.在下列横线上填上“充分”或“必要”.
(1)a>1是a>2的__必__要____条件. (2)a<1是a<2的__充__分____条件.
• 充要条件新知导学
3.如果既有 p⇒q,又有 q⇒p,则 p 是 q 的__充__要__条__件__, 记为___p_⇔__q____.
1.2充分条件与必要条件ppt课件
如果若p则q为假命题,那么由p推不 出q,记作p q。此时,我们就说p不 是q的充分条件,q不是p的必要条件。
5
例2: 下 列 “ 若p, 则q” 形 式 的 命 题 中 , 哪 些命 题 中 的 q是p的 必 要 条 件 ?
(1)若x y,则x2 y2; (2) 若 两 个 三 角 形 全 等 ,则 这 两 个 三 角 形 的 面 积相 等; (3) 若a b, 则ac bc.
条件。
2
6
5.设p、r都是q的充分条件,s是q的充分必要条件,t是s 的必要条件,t是r的充分条件,那么p是t的__充__分___条件, r是t的___充__要___条件。
17
习题1.2
4.求圆(x-a)2+(y-b)2=r2经过原点的充要条件。
2.求证:△ABC是等边三角形的充要条件是 a2+b2+c2=ab+ac+bc, 这里a,b,c是△ABC的三条边。
如果p q,那么p与q互为充要条件。
练习:p:三角形的三条边相等; q:三角形的三个角相等.
8
学习小结: “” 表示: “充分”的意义; “” 表示: “必要”的意义;
你会发现有四种类型的条件:
⑴充分但不必要条件(如 p q 且 p 緌 q )
⑵不充分但必要条件(如 p 縬 q 且 p q )
2.x>2的一个必要而不充分条件是____x_>__1______。
3.条件p:“直线l在y轴上的截距是在x轴上截距的2倍”,
条件q:“直线l的斜率为-2”,则p是q的充__分__而__不__必__要___ 条件。
4.“cos 3”是“ 2k 5 , k Z”的必__要__而__不__充__分_
5
例2: 下 列 “ 若p, 则q” 形 式 的 命 题 中 , 哪 些命 题 中 的 q是p的 必 要 条 件 ?
(1)若x y,则x2 y2; (2) 若 两 个 三 角 形 全 等 ,则 这 两 个 三 角 形 的 面 积相 等; (3) 若a b, 则ac bc.
条件。
2
6
5.设p、r都是q的充分条件,s是q的充分必要条件,t是s 的必要条件,t是r的充分条件,那么p是t的__充__分___条件, r是t的___充__要___条件。
17
习题1.2
4.求圆(x-a)2+(y-b)2=r2经过原点的充要条件。
2.求证:△ABC是等边三角形的充要条件是 a2+b2+c2=ab+ac+bc, 这里a,b,c是△ABC的三条边。
如果p q,那么p与q互为充要条件。
练习:p:三角形的三条边相等; q:三角形的三个角相等.
8
学习小结: “” 表示: “充分”的意义; “” 表示: “必要”的意义;
你会发现有四种类型的条件:
⑴充分但不必要条件(如 p q 且 p 緌 q )
⑵不充分但必要条件(如 p 縬 q 且 p q )
2.x>2的一个必要而不充分条件是____x_>__1______。
3.条件p:“直线l在y轴上的截距是在x轴上截距的2倍”,
条件q:“直线l的斜率为-2”,则p是q的充__分__而__不__必__要___ 条件。
4.“cos 3”是“ 2k 5 , k Z”的必__要__而__不__充__分_
1.2《充分条件和必要条件》课件

(3)若p q,且q p,则p是q的充要条件; (4)若p / q,且q / p,则p既不是q的充分条件 也不是q必要条件;
引申 ②从集合角度看 ⑴p是q的充分条件,相当于 P Q,即:
或 ⑵p是q的必要条件,相当于 P Q ,即:
或
q p等价于p q
⑶q P相当于P=Q , 即 : 互
2、写出命题“若a=0,则a·b=0”的逆命题,并判断真 假。
逆命题:若a·b=0 ,则a=0 (假命题) a b 0 a 0 原命题:若a=0,则a·b=0 (真命题) a 0 a b 0
二、新课讲授 1、一般地:若p则q为真,记作:p q 或 q p
若p则q为假,记作:p q
(2) p : x2 y2 0 q:x y0
(3)p:两个角是对顶角, q:两个角相等
(4)p:a·b=0 q:a=0 (5)p:两个三角形全等,
q:两个三角形面积相等
解
(1)由 p q即 x y x2 y2
知: p是q的充分条件, q是p的 必要条件.
(2) p是q的充分条件, q是p的 必要条件.
二、新课讲授
2、充分条件与必要条件
一般地,如果已知 p q那么我们就说
p是q的充分条件, q是p的必要条件。
例 两个三形全等 两三角形面积相等。
如
“两个三形全等”是“两三角形面积相 等”的充分条件 “两三角形面积相等”是“两个三形全 等 ”的必要条件
一般地,如果已知p q,那么我们说, p是q的充分条件,q是p的必要条件。 注意:(1) p q即“若p则q”为真 是定义成立的唯一前提条件。
为充要的两个条件表示的 是——同一事物。
q:三角形有一个角等于60º (2)p不是q的充分条件也
引申 ②从集合角度看 ⑴p是q的充分条件,相当于 P Q,即:
或 ⑵p是q的必要条件,相当于 P Q ,即:
或
q p等价于p q
⑶q P相当于P=Q , 即 : 互
2、写出命题“若a=0,则a·b=0”的逆命题,并判断真 假。
逆命题:若a·b=0 ,则a=0 (假命题) a b 0 a 0 原命题:若a=0,则a·b=0 (真命题) a 0 a b 0
二、新课讲授 1、一般地:若p则q为真,记作:p q 或 q p
若p则q为假,记作:p q
(2) p : x2 y2 0 q:x y0
(3)p:两个角是对顶角, q:两个角相等
(4)p:a·b=0 q:a=0 (5)p:两个三角形全等,
q:两个三角形面积相等
解
(1)由 p q即 x y x2 y2
知: p是q的充分条件, q是p的 必要条件.
(2) p是q的充分条件, q是p的 必要条件.
二、新课讲授
2、充分条件与必要条件
一般地,如果已知 p q那么我们就说
p是q的充分条件, q是p的必要条件。
例 两个三形全等 两三角形面积相等。
如
“两个三形全等”是“两三角形面积相 等”的充分条件 “两三角形面积相等”是“两个三形全 等 ”的必要条件
一般地,如果已知p q,那么我们说, p是q的充分条件,q是p的必要条件。 注意:(1) p q即“若p则q”为真 是定义成立的唯一前提条件。
为充要的两个条件表示的 是——同一事物。
q:三角形有一个角等于60º (2)p不是q的充分条件也
【精品课件】1.2充分条件与必要条件

鱼生存是生存环境有 水的充分不必要条件 生存环境有水是鱼生 存的必要不充分条件
学期 派思 创想墨 始家子 人,战 。墨国 家初
历史文化
我国战国时期,墨子所著《墨经》 充分条件:有之则必然,无之则未必不然; 必要条件:无之则必不然,有之则未必然 。
• 1、学习逻辑学有助于提高人们的逻辑思维
能力,一个人的逻辑思维能力越强,对知识 的理解越透,掌握的越牢固,运用就越灵 活。 • 2、学习逻辑学有助于人们正确地表达思想。 • 3、学习逻辑学有助于人们提高工作效率。 • 4、学习逻辑学有助于人们获取新知识。
总结提高
课堂小结
一、知识内容:
1、充分条件与必要条件的概念; 2、充分条件与必要条件的判断; 3、充分条件和必要条件与集合之间的联系.
二、过程方法:
学会观察、归纳、总结,进行探索发现,注意逻 辑推理的合理性和严密性.
概念理解
新知体会
必要性:若生存环境没有水,则鱼不生存。 真命题 就是说,要使鱼生存,必须生存环境有水。 所以生存环境有水是鱼生存必要条件。
概念理解例如:若x a 源自b ,则x 2ab。2 2
真
那么,x a 2 b 2是x 2ab的充分条件, x 2ab是x a 2 b 2的必要条件。
充分性:x a 2 b2成立能够充分说明 x 2ab成立。
必要性:由于“若 x 2ab,则x a 2 b 2 ”为真命题, 就是说,要使 x a 2 b 2成立,就必须有 x 2ab成立。
知识联系
任意x A, 则x B, 即:A B
如果 p : x A, q : x B ,则有 p q
A
B
A、 B
概念理解
高中数学1.1.2充分条件与必要条件课件选修一

05
习题与解答
习题
判断下列命题的真假
如果 $p$,则 $q$(充分不必要条件)
如果 $q$,则 $p$(必要不充分条件)
习题
如果 $lnot p$,则 $lnot q$( 充要条件)
如果 $lnot q$,则 $lnot p$( 既不充分也不必要条件)
已知 $p: x > 1$,$q: x > 2$, 判断 $p$ 是 $q$ 的什么条件。
举反例法
通过举反例来说明某个条 件不是必要条件。
充分必要条件的应用实例
逻辑推理
在逻辑推理中,充分必要条件常常用于判断推理是否成立。例如,在三段论中,大前提和 小前提之间的关系就是充分必要条件。
数学证明
在数学证明中,充分必要条件也经常被用到。例如,在证明一个数学命题时,需要先证明 充分条件,再证明必要条件,才能得出结论。
THANKS
感谢观看
要点二
如果 $lnot q$,则 $lnot p$( 既不…
即使 $lnot q$ 成立,$lnot p$ 也可能不成立;反之亦然 。因此,这是既不充分也不必要条件。
解答
• 当 $x > 1$ 时(即 $p$ 成立),不一定要求 $x > 2$(即 $q$ 成立),但当 $x > 2$ 时(即 $q$ 成立),一定要求 $x > 1$(即 $p$ 成立)。因此,这是必要不充分条件。
条件。
06
总结与回顾
本章总结
01 02
充分条件与必要条件的定义
充分条件指的是某事件发生时,另一事件也必然发生;必要条件指的是 某事件发生时,另一事件不一定发生,但若不发生,则该事件也不发生 。
充分条件与必要条件的逻辑关系
《充分条件与必要条件》课件(共38张PPT)

1.对充分条件的理解 充分条件是某一个结论成立应具备的条件,当命题具备此条件 时,就可以得出此结论;或要使此结论成立,只要具备此条件就 足够了,当命题不具备此条件时,结论也有可能成立.例如,x=6 ⇒x2=36,但是,当x≠6时,x2=36也可以成立,所以“x=6”是“x2 =36成立”的充分条件.
(2)命题判断法:①如果命题:“若p,则q”为真命题,那么p是q 的充分条件,同时q是p的必要条件. ②如果命题:“若p,则q”为假命题,那么p不是q的充分条件,同 时q也不是p的必要条件.
【变式训练】已知p:|x|=|y|,q:x=y,则p是q的什么条件?
【解题指南】解答本题的关键是判断命题“若|x|=|y|,则
1.判一判(正确的打“√”,错误的打“×”) (1)若p是q的必要条件,则q是p的充分条件.( (2)若p是q的充分条件,则﹁p是﹁q的充分条件.( ) ) )
(3)“两角不相等”是“两角不是对顶角”的必要条件.(
【解析】(1)正确.若p是q的必要条件,即p⇐q,所以q是p的充分 条件. (2)错误.若p是q的充分条件,即p⇒q,其逆否命题为﹁p⇐﹁q,所 以﹁p是﹁q的必要条件. (3)错误.“对顶角相等”的逆否命题为“不相等的两个角不是
3 2 2 3
所以p是q的充分条件,但p不是q的必要条件. ②因为(x+1)(x-2)=0 x+1=0,但x+1=0⇒(x+1)(x-2)=0,所 以p是q的必要条件,但p不是q的充分条件.
【方法技巧】充分条件、必要条件的两种判断方法 (1)定义法:①确定谁是条件,谁是结论. ②尝试从条件推结论,若条件能推出结论,则条件为充分条件, 否则就不是充分条件. ③尝试从结论推条件,若结论能推出条件,则条件为必要条件, 否则就不是必要条件.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C、充要条件
D、既不充分也不必要条件
3、已知A是B的充分条件,则 ┒A是┒B的 ┒B是┒A的 必要 充分 条件; 条件。
当难判断原命题真假时,可以先判断逆否 命题。
①若┒A是B 的必要不充分条件,则A是┒B 的( ) A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件 ②条件p:x>2,或y>3;是q:x+y>5 的 必要不充分条件 条件。
复习
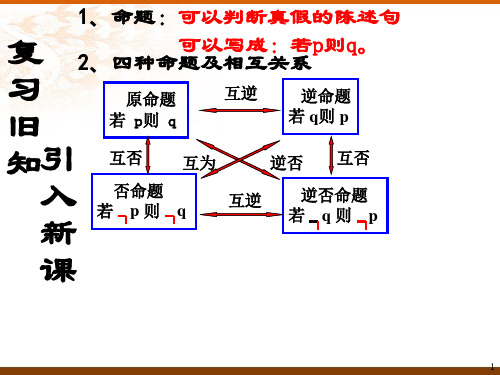
命题:我们把用语言、符号或式子表达的,可 以判断真假的陈述句称为命题。 原命题 若 A则 B 互逆 互为 逆否 互逆 逆命题 若 B则 A 互 否 逆否命题 若┐B则┐A
互 否
否命题 若┐A则┐B
我们对每一个命题的四种命题的 真假情况进行归纳,得出: ①互为逆否的两个命题同真假; ②互否或互逆的两个命题的真假性无关。 举例:判断下列命题的四种命题的真假。
新授课
1、充分条件与必要条件:一般地,如果已 知 p q那么就说,p 是q 的充分条件,q 是p 的 必要条件.
x 1 x 1 2 x 1是x 1的充分条件 2 x 1是x 1的必要条件
2
典型例题
例1 .指出下列各组命题中,p是q的什么条件,q是 p的什么条件:
2 2 p : x y ; q : x y (1)
①复数x+yi (x,y∈R)为纯虚数的充要条件 是 。
1、已知集合A={x|x>1},B={x|x>2}, 则x∈A是x∈B的 必要不充分 条件。
方法二、用命题的等价转化判断两条件 的关系
2、已知条件p:x+y≠2, 条件q:x,y不都是1,则p是q的( ) A、充分不必要条件 B、必要不充分条件
简称充要条件,记作 p q .
3.判断充分、必要条件的基本步骤: (1)认清条件和结论; (2)考察 若p 则q 和 若q则p的真假。
典型例题
例2.填表
p q p是q的什么条件 q是p的什么条件 充分不必要 充分不必要 充分不必要 必要不充分 充分 必要 充分不必要 必要不充分 必要不充分 必要不充分 必要不充分 充分不必要 必要 充分 必要不充分 充分不必要
(2)p:三角形的三条边相等; q:三角形的三个角相等.
解: (1) x=y是x2=y2的充分不必要条件. x2=y2是 x=y的必要不充分条件. (2) p是q的充分条件且是必要条件. q是p充分条件且是必要条件.
2. 充分必要条件 如果p是q的充分条件, p又是q的必 要条件,则称 p是q的充分必要条件,
1.求证:一元二次方程ax bx c 0
2
有一正根和一负根的充要条件是ac<0.
2m-3 2.在直角坐标系中,点(2m+3-m , ) 2-m 在第四象限,则实数m的取值范围是? 2 2m-3 变式.在直角坐标系中,点(2m+3-m , ) 2-m 在第四象限的充要条件是?
2
充要条件的证明与应用
(C)充分且必要条件,(D)既不充分也不必要条件
3 .如图所示,在下列电路图中闭合开关A是灯泡 B亮的什么条件?
(1)开关A闭合是灯泡B亮的 充分不必要条件 条件; (2)开关A闭合是灯泡B亮的 必要不充分条件 条件; 充要条件 (3)开关A闭合是灯泡B亮的 条件; (4)开关A闭合是灯泡B亮的既不充分也不必要条件 条件.
N M
a
1
2
a≤1
7、方程 x 2 x m 0无实根是 m 0 的什么条件? 8、(1)若 (2)若 (3)若
p q ,则 p q p,则 p p q ,则 p
是 是 是
q 的什么条件? q 的什么条件?
q 的什么条件?
9、设甲、乙、丙是三个命题,如果甲是乙的必要条件; 丙是乙的充分不必要条件,那么丙是甲的 (A)充分不必要条件,(B)必要不充分条件,
p q 且q p p是q的既不充分也不必要条件的含义:————
3.从集合角度理解:
pq
,相当于 P Q ,即
或
p q,相当于 P Q ,即
充要条件的证明与应用
例题:求证:ABC是等边三角形的充要条件是 a2 b 2 c 2 ab ac bc 其中a, b, c是 ABC的三条边。
方法三、从集合的角度判断两条件 的关系
4.已知: p : 0 x 5, q : x 2 3 ,则p 是q的( A )
A.充分不必要条件 B.必要不充分条件 C.既充分又必要条件 D.既不充分也不必要条件
①已知集合M={x|1<x<2},N={x|x>a},
若x∈M是x∈N的充分不必要条件,则求 实数a的取值范围。
a0
m,n全是奇数 m+n是偶数
x A且x B ab 0
( x 1)( y 2) 0 x 1且y 2
巩固与提高
p q 1.若p则q为真 ,记作_____________; pq 若p则q为假 ,记作_____________. p q 且q p 2. p是q的充分不必要条件的含义:————。 p q 且q p p是q的必要不充分条件的含义:—————。 p q 且q p ( p q ) p是q的充要条件的含义:—————。
2
若p则q为真 ,记作 p q 若p则q为假,记作 p q
(1)若 x 1 ,则 x 2 1 ;真 x≥1 x2≥1 真 (3)全等三角形的面积相等; 两三角形全等
2 2
(2)若x y,则x
两三角形面积相等 2 2 x y x y 假 y;
(4)对角线互相垂直的四边形是菱形; 假 四边形对角线互相垂直 四边形是菱形;
)
正难 则反
⑶在△ABC中,若A≠B,则sinA≠sinB。
利用原命题与其逆否命题同真假的关系证 明一些问题。
例3、证明:若a2-b2+2a-4b-3≠0,则a-b≠1。
其逆否命题是:
若a-b=1,则a2-b2+2a-4b-3=0
1.1.2 充分条件与必要条件
判断下列命题是真命题还是假命题:
(1)若 x 1 ,则 x 1 ; 真 2 x y ; 假 (2)若 x 2 y ,则 (3)全等三角形的面积相等; 真 假 (4)对角线互相垂直的四边形是菱形;
课 堂 小 结
(1)充分条件、必要条件、充分必要条件的概念. (2)判断充分、必要条件的基本步骤: ①认清条件和结论; ②考察 p q 和 q p 的真假。 (3)判别技巧: ① 可先简化命题; ② 否定一个命题只要举出一个反例即可; ③ 将命题转化为等价的逆否命题后再判 断。
命题 原命题 逆命题 否命题 逆否命题
若x>2,则x>0
若x2-3x+2=0,则x=2
真 假
假 真
假 真
真 假
结论:判断一个命题的四种命题的真假,
其实只须判断其中的两个即可。
例1、若一个命题M的逆命题是假命题,则( A、命题M是真命题 B、命题M的否命题是假命题 C、命题M的否命题是真命题 D、命题M的逆否命题是真命题 例2、判断下列命题的真假。 ⑴若x+y≤5,则x≤2或y≤3; ⑵若x≠0,或y≠0,则xy≠0;
