r语言上级实验一
大数定律和中心极限定理的r语言实验报告

大数定律和中心极限定理是概率论中的两个重要概念。
大数定律描述了在独立重复试验中,当试验次数趋于无穷时,某一事件发生的频率趋于其概率。
中心极限定理则指出,无论试验中的个体之间的差异有多大,当试验次数足够多时,试验结果的平均值将接近正态分布。
以下是一个简单的R语言实验报告,用于演示大数定律和中心极限定理。
大数定律和中心极限定理的R语言实验
实验目的:通过模拟实验,观察大数定律和中心极限定理的现象。
实验原理:
1.大数定律:在大量独立重复试验中,某一事件的相对频率趋近于该事件的概率。
2.中心极限定理:无论个体之间的差异有多大,当试验次数足够多时,试验结果的平均值将接近正态分布。
实验步骤:
1.生成1000个0到1之间的随机数,模拟1000次掷硬币试验(正面概率为0.5)。
2.计算正面朝上的频率。
3.使用R语言绘制频率直方图和正态分布曲线。
4.重复步骤1-3多次(例如100次),观察频率的稳定性。
5.计算100次试验中每次试验得分的平均值的频数分布,并绘制直方图和正态分布曲线。
实验结果:
1.正面朝上的频率逐渐稳定于0.5。
2.频率直方图接近正态分布。
3.平均值的频数分布也接近正态分布。
实验分析:
实验结果验证了大数定律和中心极限定理。
在大量独立重复试验中,正面朝上的频率趋近于0.5,符合大数定律。
同时,试验结果的平均值分布接近正态分布,符合中心极限定理。
结论:通过R语言模拟实验,我们观察到了大数定律和中心极限定理的现象,加深了对这两个定理的理解。
R语言实验报告—回归分析在女性身高与体重的应用

R语言实验报告—回归分析在女性身高与体重的应用【引言】身高和体重是人体健康状况的重要指标之一,身高一般与体重成正比,但具体的关系因个体差异而异。
为了探究女性身高与体重之间的关系,并通过回归分析建立二者之间的数学模型,本实验使用R语言进行实验。
【数据获取与处理】从网上收集了100名女性的身高和体重数据作为样本。
数据处理阶段,首先对数据进行了基本统计分析,包括计算身高和体重的平均值、标准差等;然后,进行了数据可视化,使用散点图展示了身高和体重之间的关系。
【回归建模】接下来,使用R语言进行回归分析建模。
假设身高为自变量x,体重为因变量y,建立线性回归模型y=β0+β1x+ε,其中ε为误差项。
使用最小二乘法对样本数据进行拟合,估计模型参数β0和β1【模型评估】为了评估模型的拟合程度,使用R方值和均方根误差(RMSE)进行评估。
R方值越接近1表示模型拟合效果越好,RMSE值越小表示模型预测结果与实际数据越接近。
【结果讨论】根据回归分析得到的模型参数估计值,可以判断女性身高和体重之间存在正相关关系。
同时,R方值为0.8,表明模型拟合效果较好。
但是,RMSE为3.2,表示模型的预测误差较大,可能存在其他影响体重的因素未考虑。
【结论】回归分析可以帮助我们了解女性身高和体重之间的关系,并建立数学模型预测体重。
本实验结果显示女性的身高与体重存在正相关关系。
但是,模型的预测效果可能还可以改进,需要进一步考虑其他可能的影响因素,例如年龄、饮食习惯等。
[2] Guo SS, Chumlea WC. Tracking of body mass index in children in relation to overweight in adulthood. Am J Clin Nutr, 1999, 70(1):145S-148S.【附录】实验中使用的R代码如下:```R#数据处理与可视化data <- read.csv("data.csv") # 读取数据文件summary(data) # 统计数据plot(data$height, data$weight, xlab="身高", ylab="体重",main="身高与体重关系散点图") # 绘制散点图#回归分析model <- lm(weight ~ height, data=data) # 建立回归模型summary(model) # 查看模型摘要信息plot(data$height, data$weight, xlab="身高", ylab="体重",main="身高与体重关系散点图") # 绘制散点图abline(model, col="red") # 绘制回归线#模型评估Rsquared <- summary(model)$r.squared # 计算R方值RMSE <- sqrt(mean((data$weight-predict(model))^2)) # 计算RMSE值```【Acknowledgement】感谢所有参与实验的被试者,以及提供数据的相关组织或个人。
R语言实验报告
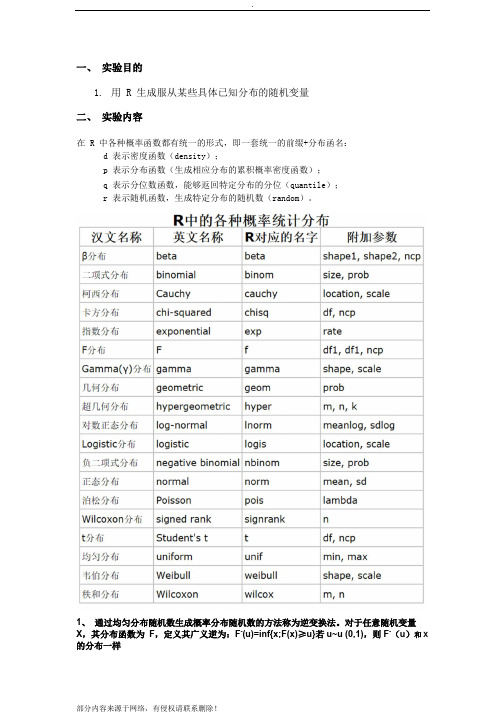
一、实验目的1.用 R 生成服从某些具体已知分布的随机变量二、实验内容在 R 中各种概率函数都有统一的形式,即一套统一的前缀+分布函名:d 表示密度函数(density);p 表示分布函数(生成相应分布的累积概率密度函数);q 表示分位数函数,能够返回特定分布的分位(quantile);r 表示随机函数,生成特定分布的随机数(random)。
1、通过均匀分布随机数生成概率分布随机数的方法称为逆变换法。
对于任意随机变量X,其分布函数为F,定义其广义逆为:F-(u)=inf{x;F(x)≥u}若u~u (0,1),则F-(u)和X 的分布一样Example 1 如果X~Exp(1)(服从参数为 1 的指数分布),F(x)=1-e-x。
若u=1-e-x并且u~u(0,1),则X=-logU~Exp(1)则可以解出x=-log(1-u)通过随机数生成产生的分布与本身的指数分布结果相一致R 代码如下:nsim = 10^4U = runif(nsim)X = -log(U)Y = rexp(nsim)X11(h=3.5)Xpar(mfrow=c(1,2),mar=c(2,2,2,2))hist(X,freq=F,main="Exp from Uniform",ylab="",xlab="",ncl=150,col="grey",xlim=c(0,8))curve(dexp(x),add=T,col="sienna",lwd=2)hist(Y,freq=F,main="Exp from R",ylab="",xlab="",ncl=150,col="grey",xlim=c(0,8))curve(dexp(x),add=T,col="sienna",lwd=2)2、某些随机变量可由指数分布生成。
R语言综合实验报告

学号:2013310200629姓名:王丹学院:理学院专业:信息与计算科学成绩:日期:年月日基于工业机器人能否准确完成操作的时间序列分析摘要:时间序列分析是预测领域研究的重要工具之一,它描述历史数据随时间变化的规律,并用于预测数据。
本文首先介绍了一些常用的时间序列模型,包括建模前对数据的预处理、模型的识别以及模型的预测等。
通过多种方法分析所得到的数据,实现准确建模,可以得出正确的结论。
关键词:自回归(AR)模型,滑动平均(MA)模型,自回归滑动平均(ARMA)模型,ARMA最优子集一、问题提出,问题分析随着社会日新月异的发展,不断创新的科技为我们的生活带来了越来越多的便利。
机器人也逐渐走向了我们的生活,工厂里使用机器人去工作也可以大大减少生产成本,但为了保证产品质量,工厂使用的机器人应该多次测试,确保动作准确无误。
现有一批数据,包含了来自工业机器人的时间序列(机器人需要完成一系列的动作,与目标终点的距离以英寸为单位被记录下来,重复324次得到该时间序列),对于这些离散的数据,我们期望从中发掘一些信息,以便对机器人做更好的改进或者确定机器人是否可以投入使用。
但我们从中并不能看出什么,需要借助工具做一些处理,对数据进行分析。
时间序列分析是通过直观的数据比较或作图观测,去寻找序列中包含的变化规律,这种分析方法称为描述性时序分析。
在物理、天文、海洋学等科学领域,这种描述性时序分析方法经常能够使人们发现一些意想不到的规律,操作起来十分简单而且直观有效,因此从史前到现在一直被人们广泛使用,它也是我们进行统计时序分析的第一步。
我们将利用自回归(AR)模型、滑动平均(MA)模型以及自回归滑动平均(ARMA)模型去解决遇到的问题。
二、数据描述和初步分析下面是我们接收到的数据,数据来源:/~kchan/TSA.htm0.0011 0.0011 0.0024 0.0000 -0.0018 0.0055 0.0055 -0.00150.0047 -0.0001 0.0031 0.0031 0.0052 0.0034 0.0027 0.00410.0041 0.0034 0.0067 0.0028 0.0083 0.0083 0.0030 0.00320.0035 0.0041 0.0041 0.0053 0.0026 0.0074 0.0011 0.0011-0.0001 0.0008 0.0004 0.0000 0.0000 -0.0009 0.0038 0.00540.0002 0.0002 0.0036 -0.0004 0.0017 0.0000 0.0000 0.00470.0021 0.0080 0.0029 0.0029 0.0042 0.0052 0.0056 0.00550.0055 0.0010 0.0043 0.0006 0.0013 0.0013 0.0008 0.00230.0043 0.0013 0.0013 0.0045 0.0037 0.0015 0.0013 0.00130.0029 0.0039 -0.0018 0.0016 0.0016 -0.0003 0.0000 0.00090.0017 0.0017 0.0030 -0.0001 0.0070 -0.0008 -0.0008 0.00090.0025 0.0031 0.0002 0.0002 0.0022 0.0020 0.0003 0.00330.0033 0.0044 -0.0010 0.0048 0.0019 0.0019 0.0031 0.00200.0017 0.0014 0.0014 0.0039 0.0052 0.0020 0.0012 0.00120.0031 0.0022 0.0040 0.0038 0.0038 0.0007 0.0016 0.00240.0003 0.0003 0.0057 0.0006 0.0009 0.0040 0.0040 0.00350.0032 0.0068 0.0028 0.0028 0.0048 0.0035 0.0042 -0.0020-0.0020 0.0023 -0.0011 0.0062 -0.0021 -0.0021 0.0000 -0.0019-0.0005 0.0048 0.0048 0.0027 0.0009 -0.0002 0.0079 0.00790.0017 0.0034 0.0030 0.0025 0.0025 0.0004 0.0031 0.0057-0.0003 -0.0003 0.0006 0.0018 0.0022 0.0042 0.0042 0.0055-0.0005 -0.0053 0.0028 0.0028 0.0005 0.0036 0.0017 -0.0043-0.0043 0.0066 -0.0016 0.0055 -0.0011 -0.0011 -0.0049 0.00470.0056 0.0057 0.0057 -0.0002 0.0056 0.0037 0.0012 0.00120.0018 -0.0025 -0.0011 0.0027 0.0027 0.0039 0.0058 0.00030.0040 0.0040 0.0042 0.0000 0.0056 -0.0029 -0.0029 -0.00260.0016 0.0019 0.0015 0.0015 0.0007 0.0007 -0.0044 -0.0030-0.0030 0.0013 0.0029 -0.0010 0.0009 0.0009 -0.0016 0.00000.0000 0.0014 0.0014 -0.0003 0.0009 -0.0068 0.0003 0.0003-0.0012 0.0037 -0.0019 0.0023 0.0023 -0.0033 -0.0002 -0.00100.0021 0.0021 0.0026 -0.0002 0.0011 0.0028 0.0028 -0.00040.0026 -0.0015 0.0002 0.0002 0.0018 -0.0005 0.0004 -0.0008-0.0008 0.0018 0.0019 0.0029 -0.0022 -0.0022 0.0010 -0.00330.0020 0.0000 0.0000 0.0003 0.0007 -0.0009 -0.0035 -0.00350.0010 0.0007 0.0028 -0.0008 -0.0008 -0.0034 -0.0010 -0.0018-0.0021 -0.0021 -0.0006 -0.0018 -0.0046 -0.0017 -0.0017 -0.0001-0.0029 0.0020 -0.0049 -0.0049 -0.0021 -0.0027 -0.0018 -0.0015-0.0015 0.0051 -0.0002 0.0000 -0.0006 -0.0006 -0.0012 0.00120.0000 0.0021 0.0021 -0.0001 0.0022 0.0055 -0.0010 -0.00100.0048 0.0006 0.0026 0.0004 0.0004 0.0000 0.0000 0.00080.0044 0.0044 0.0002 0.0036这一群数目庞大的数据,以我们直观的判断,它们错综复杂,且毫无规律可言,根本不能从中得到有用的消息。
r语言实验报告

r语言实验报告R语言实验报告介绍•本文旨在对R语言实验报告进行相关介绍和指导。
准备工作•在开始编写R语言实验报告之前,需要进行一些准备工作:–安装R语言环境–确保安装必要的R包–理解实验要求和相关数据集实验报告结构•一个完整的R语言实验报告通常包含以下几个部分:1. 标题•实验报告的标题应简明扼要地描述实验内容。
2. 引言•引言部分应包含以下内容:–实验的背景和目的–实验所采用的数据集和方法的简要介绍3. 数据分析•数据分析部分是实验报告的重点,应包含以下内容:–数据的读取和预处理–数据的可视化–统计分析方法的应用–结果的解释和讨论4. 结论•结论部分应总结实验的结果,并对实验的目的和方法进行评价。
5. 参考文献•参考文献部分应列举实验报告中所引用的相关文献。
编写要点•在编写R语言实验报告时,需要遵守以下要点:1. 语法规范•使用清晰、准确的语法表达实验过程和结果。
2. 结果的解释•对于结果的解释,应该尽量采用简洁明了的语言,避免使用过于专业的术语或过于复杂的句子结构。
3. 图表的使用•图表是实验报告中常用的可视化工具,应合理使用图表来展示数据和结果,并配以简洁明了的图题和注解。
4. 逻辑性和连接性•实验报告应具有良好的逻辑性和连接性,各部分之间应有明确的联系和衔接,以确保整篇报告的连贯性。
结语•编写一份规范、完整的R语言实验报告需要系统的学习和实践,希望本文对您有所帮助。
参考文献•[参考文献1]•[参考文献2]继续编写一份更详细的R语言实验报告:R语言实验报告介绍•本文旨在对R语言实验报告进行相关介绍和指导。
准备工作•在开始编写R语言实验报告之前,需要进行一些准备工作:–安装R语言环境:确保在电脑上成功安装R语言的最新版本。
–确保安装必要的R包:根据实验需求,安装并加载所需的R包,例如ggplot2、dplyr等。
–理解实验要求和相关数据集:认真阅读实验要求,理解实验的目的和需求,并熟悉所使用的数据集。
R语言 上机实验一 EXCEL的应用
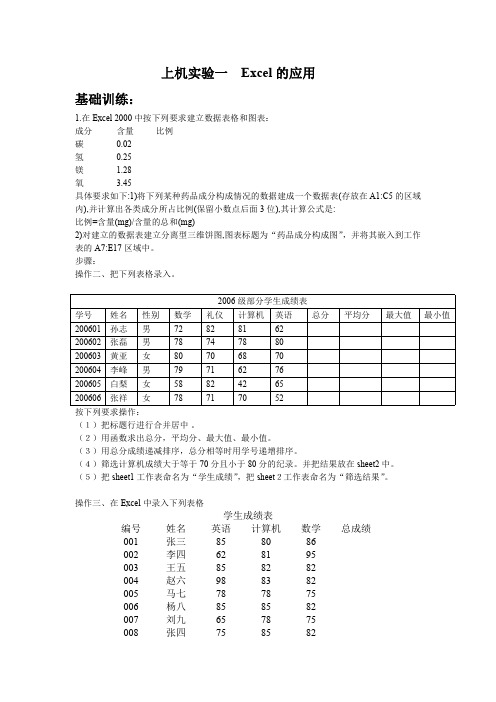
上机实验一Excel的应用基础训练:1.在Excel2000中按下列要求建立数据表格和图表:成分含量比例碳0.02氢0.25镁 1.28氧 3.45具体要求如下:1)将下列某种药品成分构成情况的数据建成一个数据表(存放在A1:C5的区域内),并计算出各类成分所占比例(保留小数点后面3位),其计算公式是:比例=含量(mg)/含量的总和(mg)2)对建立的数据表建立分离型三维饼图,图表标题为“药品成分构成图”,并将其嵌入到工作表的A7:E17区域中。
步骤:操作二、把下列表格录入。
2006级部分学生成绩表学号姓名性别数学礼仪计算机英语总分平均分最大值最小值200601孙志男72828162200602张磊男78747880200603黄亚女80706870200604李峰男79716276200605白梨女58824265200606张祥女78717052按下列要求操作:(1)把标题行进行合并居中。
(2)用函数求出总分,平均分、最大值、最小值。
(3)用总分成绩递减排序,总分相等时用学号递增排序。
(4)筛选计算机成绩大于等于70分且小于80分的纪录。
并把结果放在sheet2中。
(5)把sheet1工作表命名为“学生成绩”,把sheet2工作表命名为“筛选结果”。
操作三、在Excel中录入下列表格学生成绩表编号姓名英语计算机数学总成绩001张三858086002李四628195003王五858282004赵六988382005马七787875006杨八858582007刘九657875008张四758582009李十359565010王六755875平均分最高分按要求操作:1、设置工作表行、列:标题行:行高30;其余行高为20。
2、设置单元格:(1)标题格式:字体:楷书;字号:20;字体颜色为红色;跨列居中;底纹黄色。
(2)将成绩右对齐;其它各单元格内容居中。
3、设置表格边框:外边框为双线,深蓝色;内边框为细实心框,黑色。
R语言实验报告

R语言实验报告一、试验目的R是用于统计分析、绘图的语言和操作环境。
R是属于GNU系统的一个自由、免费、源代码开放的软件,它是一个用于统计计算和统计制图的优秀工具。
本次试验要求掌握了解R语言的各项功能和函数,能够通过完成试验内容对R语言有一定的了解,会运用软件对数据进行分析。
二、试验环境Windows系统,RGui(32-bit)三、试验内容模拟产生电商专业学生名单(学号区分),记录高数、英语、网站开发三科成绩,然后进行统计分析。
假设有的100名学生,起始学号为210222001,各科成绩取整,高数成绩为均匀分布随机数,都在75分以上。
英语成绩为正态分布,平均成绩80,标准差为7。
网站开发成绩为正态分布,平均成绩83,标准差为18。
把正态分布中超过100分的成绩变成100分。
1把上述信息组合成数据框,并写到文本文件中;2计算各种指标:平均分,每个人的总分,最高分,最低分,(使用apply函数)3求总分最高的同学的学号4绘各科成绩直方图、散点图、柱状图丶饼图丶箱尾图(要求指定颜色和缺口)5画星相图,解释其含义6画脸谱图,解释其含义,7画茎叶图、qq图四、试验实现(一)按要求随机生成学号,和对于的高数、英语、网站开发三科成绩。
A、生成学号B、生成高数成绩高数成绩要求:高数成绩为均匀分布随机数,都在75分以上均匀分布函数:runif(n,min=0,max=1)其中,n为产生随机值个数(长度),min为最小值,max为最大值。
C、生成英语成绩英语成绩要求:正态分布,平均成绩80,标准差为7正态分布函数:rnorm(n,mean=0,sd=1)其中,n为产生随机值个数(长度),mean是平均数,sd是标准差。
D、生成网站开发成绩网站开发成绩要求:网站开发成绩为正态分布,平均成绩83,标准差为18。
其中大于100的都记为100。
(二)把上述信息组合成数据框,并写到文本文件中;计算各种指标:平均分,每个人的总分,最高分,最低分,(使用apply函数)A、生成文本文件B、打开数据框C、在数据框中命名变量D、计算各种指标:平均分,每个人的总分,最高分,最低分平均分(x4):总分(x5):最低分(x6):最高分(x7):(三)将生成成绩写入文本文件中(四)求总分最高的同学的学号(五)绘各科成绩直方图、散点图、柱状图丶饼图丶箱尾图(要求指定颜色和缺口)直方图散点图柱状图饼图箱尾图(要求指定颜色和缺口)(六)画星相图,解释其含义(七)画脸谱图,解释其含义(八)画茎叶图(九)qq图五、试验总结 这次试验是我第一次接触R 语言,刚开始遇到了很多困难,对于R语言一窍不通,后来经过老师的悉心指导,以及自己积极的去查找资料,对R语言有了进一步的了解。
武汉理工大学R语言实验报告

第二部分:实验过程记录(可加页)(包括实验原始数据记录,实验现象
记录,实验过程发现的问题等)
原始数据(E:/fire.txt):
xy
3.4 26.2
1.8 17.8
4.6 31.3
2.3 23.1
3.1 27.5
5.5 36
0.7 14.1
3 22.3
2.6 19.6
4.3 31.3
2.1 24
1.1 17.3
6.1 43.2
4.8 36.4
3.8 26.1
打开 R 软件后依次按一下程序输入函数命令进行回归分析
1.数据准备
fire <- read.table('E:/fire.txt', head = T)
#读取数据
2.回归分析
plot(fire$y ~ fire$x)
#散点图:
fire.reg <- lm(fire$y ~ fire$x, data = fire)
summary(fire.reg)
#回归分析表:
#回归拟合
anova(fire.reg)
#方差分析表
abline(fire.reg, col = 2, lty = 2)
#拟合直线
3.残差分析 fire.res <- residuals(fire.reg) #残差 fire.sre <- rstandard(fire.reg) #学生化残差 plot(fire.sre) abline(h = 0) text(11, fire.sre[11], label = 11, adj = (-0.3), col = 2) #标注点
2. 一旦我们将时间序列读入 R,下一步通常是用这些数据绘制时间序列图,我 们可以使用 R 中的 plot.ts()函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理学院实验报告班级:学号:姓名:实验编号:01实验一:初识R软件一、实验目的与要求:1、了解R软件的安装、启动和退出。
2、掌握软件包的安装和载入。
3、掌握R软件帮助功能。
4、会使用R的集成开发环境Tinn-R或Rstudio。
5、掌握用R进行基本的代数运算。
6、掌握用R生成向量、矩阵、数据框和列表的方法。
7、掌握提取数据子集的方法。
二、实验内容:1.按N的不同取值,计算∑=-Nii12)12(1,并求其与log(N)+1.0的距离,其中N=100,500,1000,1500.#计算其值> N<-c(100,500,1000,1500)> for(k in 1:length(N))+ {+ s=0+ for(i in 1:N[k]){+ s=s+1/(2*i-1)^2+ }+ print(s)+ }[1] 1.231201[1] 1.233201[1] 1.233451[1] 1.233534#求距离> y<-abs(s-(log(N)+1.0))> y[1] 4.371636 5.981074 6.674221 7.0796872.联合命令rep()和seq()生成(1,2,3,4,5,2,3,4,5,6,3,4,5,6,7,4,5,6,7,8,5,6,7,8,9). #用rep生成> rep(1:5,5)+rep(0:4,rep(5,5))[1] 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 5 6 7 8 9 #用seq 生成> rep(seq(1,5),5)+rep(seq(0,4),rep(5,5))[1] 1 2 3 4 5 2 3 4 5 6 3 4 5 6 7 4 5 6 7 8 5 6 7 8 93. 利用命令matrix()将矩阵⎪⎪⎪⎭⎫ ⎝⎛=4912011411435A 输入变量A ,并求A 的行列式、逆矩阵,T AA (转置命令为t())、A A T .#输入变量A> A<-matrix(c(35,14,1,4,11,0,12,9,4),nrow=3,ncol=3,byrow=T) > A[,1] [,2] [,3][1,] 35 14 1 [2,] 4 11 0 [3,] 12 9 4#计算A 值 > det(A) [1] 1220#计算A 逆> solve (A) %*%A[,1] [,2] [,3] [1,] 1.000000e+00 -5.551115e-17 0.000000e+00 [2,] -1.387779e-17 1.000000e+00 -1.734723e-18 [3,] -4.440892e-16 -4.440892e-16 1.000000e+00#计算AA T > A%*%t(A)[,1] [,2] [,3] [1,] 1422 294 550 [2,] 294 137 147 [3,] 550 147 241#计算A T A> t(A)%*%A[,1] [,2] [,3] [1,] 1385 642 83 [2,] 642 398 50[3,] 83 50 174. (1)利用命令data.frame()将下表数据读入变量sea,Season Salinity(盐度) Temperature winter 29.19 4 winter 27.37 6 spring24.997.3spring 28.79 8.2 spring 33.28 9.1 summer 32.69 18.1 summer 31.9 17 summer NA 21 autumn 32.53 15.1 autumn32.53 13.8>Season<-c("winter","winter","spring","spring","spring","summer","summer","summer","autu mn","autumn")> Salinity<-c(29.19,27.37,24.99,28.79,33.28,32.69,31.9,NA,32.53,32.53) > Temperature<-c(4,6,7.3,8.2,9.1,18.1,17,21,15.1,13.8) > sea<-data.frame(Season,Salinity,Temperature) > seaSeason Salinity Temperature 1 winter 29.19 4.0 2 winter 27.37 6.0 3 spring 24.99 7.3 4 spring 28.79 8.2 5 spring 33.28 9.1 6 summer 32.69 18.1 7 summer 31.90 17.0 8 summer NA 21.0 9 autumn 32.53 15.1 10 autumn 32.53 13.8 > class(sea)[1] "data.frame"(2)将盐度的标准化变量加到这个数据框中;(标准化公式:ni s x x ,x 是样本均值,n s 是样本方差);#将标准化变量加入> sea<-data.frame(Season,Salinity,Temperature,scale(Salinity))> seaSeason Salinity Temperature scale.Salinity.1 winter 29.19 4.0 -0.40437122 winter 27.37 6.0 -1.03160603 spring 24.99 7.3 -1.85183624 spring 28.79 8.2 -0.54222505 spring 33.28 9.1 1.00518406 summer 32.69 18.1 0.80184977 summer 31.90 17.0 0.52958848 summer NA 21.0 NA9 autumn 32.53 15.1 0.746708110 autumn 32.53 13.8 0.7467081(3)从数据框sea提取包含season和temperature变量的子数据框存入变量sea1,并计算温度的平均值和标准差;> sea1<-data.frame(sea$Season,sea$Temperature)> sea1Season Temperature1 winter 4.02 winter 6.03 spring 7.34 spring 8.25 spring 9.16 summer 18.17 summer 17.08 summer 21.09 autumn 15.110 autumn 13.8> mean(Temperature)[1] 11.96> sd(Temperature)[1] 5.782963(4) 从数据框sea提取包含season和salinity变量的子数据框存入变量sea2,并计算盐度的平均值和标准差(结果不能为NA);> sea2<-data.frame(sea$Season,sea$Salinity)> sea2sea.Season sea.Salinity1 winter 29.192 winter 27.373 spring 24.994 spring 28.795 spring 33.286 summer 32.697 summer 31.908 summer NA9 autumn 32.5310 autumn 32.53> mean(Salinity,na.rm=T)[1] 30.36333> sd(Salinity,na.rm=T)[1] 2.901625(5)利用命令list() 将上表读入变量sea.list, 再将盐度的标准化变量加入到这个列表中,并比较该方法与数据框方法的区别。
#利用list读表> sea.list<-list(Season,Salinity,Temperature)> sea.list[[1]][1] "winter" "winter" "spring" "spring" "spring" "summer" "summer" "summer" "autumn" "autumn"[[2]][1] 29.19 27.37 24.99 28.79 33.28 32.69 31.90 NA 32.53 32.53[[3]][1] 4.0 6.0 7.3 8.2 9.1 18.1 17.0 21.0 15.1 13.8#将盐度标准化变量加入> list(Season,Salinity,Temperature,scale(Salinity))[[1]][1] "winter" "winter" "spring" "spring" "spring" "summer" "summer" "summer" "autumn" "autumn"[[2]][1] 29.19 27.37 24.99 28.79 33.28 32.69 31.90 NA 32.53 32.53[[3]][1] 4.0 6.0 7.3 8.2 9.1 18.1 17.0 21.0 15.1 13.8[[4]][,1] [1,] -0.4043712 [2,] -1.0316060 [3,] -1.8518362 [4,] -0.5422250 [5,] 1.0051840 [6,] 0.8018497 [7,] 0.5295884 [8,] NA [9,] 0.7467081 [10,] 0.7467081attr(,"scaled:center")[1] 30.36333attr(,"scaled:scale")[1] 2.901625。
