倍数解决问题..
人教版五年级上册解决问题专项训练题-倍数问题

人教版五年级上册解决问题专项训练题-倍数问题一、已知倍数和1倍的量,求多倍的量。
(建议用算术方法解答)1.图书室有400本科技书,文艺书的本数比科技书的4倍少24本。
问文艺书有多少本?解答:设文艺书的本数为x,则有x+24=4×400,解得x=376.所以文艺书有376本。
2.公园里有160盆菊花,月季花的盆数比菊花的4倍少20盆。
问月季花有多少盆?解答:设月季花的盆数为x,则有x+20=4×160,解得x=620.所以月季花有60盆。
二、已知倍数和多倍的量,求1倍的量。
(建议用方程解答)1.图书室有400本科技书,比文艺书的4倍少24本。
问文艺书有多少本?解答:设文艺书的本数为x,则有4x-24=400,解得x=106.所以文艺书有106本。
2.公园里有160盆菊花,比月季花的4倍少20盆。
问月季花有多少盆?解答:设月季花的盆数为x,则有4x-20=160,解得x=45.所以月季花有45盆。
3.XXX的体重是34.5千克,比小军的2倍轻11.7千克。
问小军的体重是多少千克?解答:设小军的体重为x,则有2x-34.5=11.7,解得x=23.1.所以小军的体重是23.1千克。
三、已知倍数,分别求两个量。
(建议用方程解答,一般设1倍的量为X)1.公园里有菊花和月季花共880盆,菊花的盆数是月季花的4.5倍,菊花和月季花各有多少盆?解答:设月季花的盆数为x,则菊花的盆数为4.5x,所以有x+4.5x=880,解得x=160,所以月季花有160盆,菊花有720盆。
2.市场运来一批水果,其中苹果质量是梨的4倍,已知苹果和梨共重270千克,苹果和梨各重多少千克?解答:设梨的重量为x千克,则苹果的重量为4x千克,所以有x+4x=270,解得x=45,所以苹果重180千克,梨重90千克。
3.市场运来一批水果,其中苹果质量是梨的4倍,已知苹果比梨重270千克,苹果和梨各重多少千克?解答:设梨的重量为x千克,则苹果的重量为4x千克,所以有4x-x=270,解得x=90,所以苹果重360千克,梨重90千克。
利用倍数关系解决实际问题

利用倍数关系解决实际问题倍数关系在解决实际问题中具有重要的作用,它可以帮助我们计算和比较不同物体或数量之间的关系。
本文将通过几个实际问题的例子来说明如何利用倍数关系解决问题。
一、购物打折问题假设商店正在进行一次打折活动:原价为100元的商品现在以8折的价格出售。
我们可以通过倍数关系来计算打折后的价格。
8折相当于原价的80%,即0.8倍,所以打折后的价格为100元 × 0.8 = 80元。
二、速度和时间问题假设一辆汽车以每小时60公里的速度行驶,我们想知道在不同时间段内汽车行驶的距离。
可以利用倍数关系来计算。
例如,在2小时内,汽车行驶的距离为60公里/小时 × 2小时 = 120公里。
三、货币兑换问题假设我们需要将人民币兑换成美元,兑换比例为1美元兑换成6.5人民币。
可以利用倍数关系将人民币转换成美元。
例如,兑换100人民币,即100人民币 × 1美元/6.5人民币≈ 15.38美元。
四、食谱比例问题假设我们有一份蛋糕的食谱,需要根据不同的人数来调整所需的材料。
比如,原本的食谱是适用于10人份量,现在需要调整为20人份。
可以利用倍数关系计算每种材料的用量。
例如,每种材料的用量乘以2即可得到适用于20人份的食谱。
五、人口增长问题假设一个城市的人口每年以2%的速度增长,我们想知道未来几年的人口增长情况。
可以利用倍数关系来计算未来的人口数量。
例如,在10年后,人口数量将增长为原来的1.02^10倍。
通过以上几个例子,我们可以看到倍数关系在解决实际问题中的应用。
无论是购物打折、速度和时间、货币兑换、食谱比例还是人口增长问题,倍数关系都可以帮助我们计算和比较不同物体或数量之间的关系。
这种解决问题的方法简单直观,且易于理解和应用。
在解决实际问题时,我们需要注意对问题进行适当的分析和理解,找到合适的倍数关系来解决问题。
同时,我们还需要关注所用的数值单位和问题的精确度,以确保计算结果的准确性。
倍数问题解题技巧和方法

倍数问题是指在数学中,求一个数是另一个数的几倍或者求一个数是另一个数的倍数的问题。
解决倍数问题有以下几种技巧和方法:
1. 倍数的基本原理:
-已知甲数是乙数的几倍和乙数,求甲数:用乙数乘以倍数即可得到甲数。
-已知甲数是乙数的几倍和甲数,求乙数:用甲数除以倍数即可得到乙数。
2. 数字2、3、5的倍数问题:
- 2的倍数:所有偶数都是2的倍数,尾数是0、2、4、6、8的数都是2的倍数。
- 3的倍数:各个数位上的数字相加之和是3的倍数,那么这个数一定是3的倍数。
- 5的倍数:个位数是0或5的数都是5的倍数。
3. 浓度问题:
浓度问题实际上是百分率的问题。
已知溶液的浓度和体积,求溶质质量或溶液的体积。
解题方法:利用浓度、体积和溶质质量之间的关系进行计算。
4. 求最大公约子和最小公倍数:
-最大公约数:两个数的最大公约数是这两个数公有的质因数的乘积。
-最小公倍数:两个数的最小公倍数是这两个数公有的质因数和各自独有的质因数的乘积。
5. 分数倍数问题:
-求一个数是另一个数的几倍,可以用除法计算。
-求一个数的几分之几,可以用乘法计算。
6. 解题思路和方法:
-分析题目,确定需要求解的是倍数还是其他数学关系。
-根据已知条件,运用相应的数学公式和原理进行计算。
-注意检查计算过程和结果,确保准确性。
通过以上技巧和方法,可以更好地解决倍数问题。
在实际解题过程中,要根据题目要求和条件,灵活运用这些方法。
小学三年级用倍数解决问题

小学三年级用倍数解决问题在小学三年级的数学学习中,倍数是一个重要的概念,通过使用倍数可以解决一些实际生活中的问题。
本文将讨论小学三年级使用倍数解决问题的方法和技巧。
一、倍数的概念和意义倍数是指一个数可以整除另一个数的情况。
例如,2是4的倍数,因为4可以被2整除。
理解倍数的概念对于解决一些数学问题至关重要。
通过使用倍数,可以简化运算,提高解决问题的效率。
二、使用倍数解决问题的方法1.找到最小公倍数解决一些涉及到多个数的问题时,需要找到最小公倍数。
最小公倍数是指多个数中同时能整除的最小数。
例如,对于数3和5,最小公倍数是15。
通过找到最小公倍数,可以将多个数的问题转化为单个数的问题,更加简化计算过程。
2.寻找规律在解决一些字符串或图形问题时,可以通过寻找倍数的规律来简化解题过程。
例如,如果要将一个长度为8厘米的纸条分成相等的长度为2厘米的小段,可以使用倍数的概念,找到最小的倍数8,然后将纸条等分成4段。
3.倍数问题的实际应用倍数问题在实际生活中也有广泛应用。
例如,购物时遇到打折优惠,可以通过计算倍数来快速判断折扣后的价格。
又如,在种地和养殖等农业生产中,通过计算倍数可以确定农作物的生长周期和动物的繁殖周期。
4.深化应用:数的整除性质倍数与数的整除有密切关系。
当一个数是另一个数的倍数时,也就意味着这个数可以整除另一个数,即没有余数。
通过理解整除的概念,可以更好地理解倍数的含义和应用。
三、例题及解答1.例题1:某校聚会分组,男生组女生组各需要准备相同的礼物,男生组有6人,女生组有4人,请问最少准备多少个礼物?解答:根据题意可知,男生组和女生组分别需要相同数量的礼物,而6和4的最小公倍数为12。
所以,最少需要准备12个礼物。
2.例题2:某班同学分组,每组有8人,现在有32个同学,请问最多能分成几个完整的小组?解答:根据题意可知,每个小组需要8人,而32可以被8整除,所以最多能分成4个完整的小组。
四、小结小学三年级的学生通过使用倍数来解决问题可以提高他们的数学思维能力和计算能力。
倍数问题详解
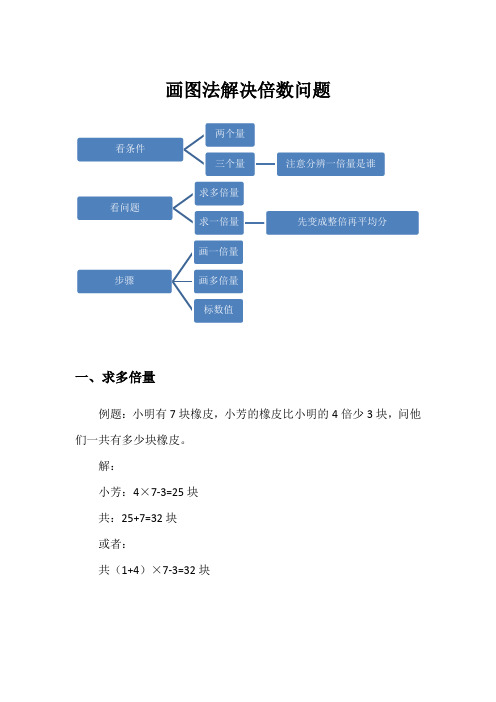
画图法解决倍数问题一、求多倍量例题:小明有7块橡皮,小芳的橡皮比小明的4倍少3块,问他们一共有多少块橡皮。
解:小芳:4×7-3=25块共:25+7=32块或者:共(1+4)×7-3=32块二、求一倍量例题:苹果有45个,苹果的数量比橘子的5倍多5个,苹果和橘子一共有多少个?解:45-5=40个40÷5=8个共45+8=53个例题:有一个数加上20后,变成自己的3倍,再增加多少,变成自己原来的6倍?解:自己:一倍量自己+20:3倍所以:20=2倍一倍量=10,因此,这个数是10.变成自己的6倍,就是60,要再增加30三、有多个量例题:有一些气球,黄气球的数量是红气球的2倍,蓝气球的数量比黄气球的2倍多2个,蓝气球有38个,一共有多少个气球?解:红:黄:蓝:一份有:(38-2)÷4=9个一共有:3×9+38=65个例题:有一些花,牡丹花的数量是月季花的3倍,百合花的数量比牡丹花和月季花数量之和的2倍多2束,百合花有66束,共有多少花?解:月季花:一倍量牡丹花:3倍百合花:8倍+2=66一倍量=(66-2)÷8=8束共4×8+66=98束四、混合题目例题:被除数和除数的和是64,商是7,被除数和除数各是多少?解:除数:一倍量被除数:7倍共:8倍=64所以除数是64÷8=8 被除数是64-8=56例题:有两袋大米,甲袋大米重34千克,甲袋比乙袋的5倍多4千克,要使两袋大米重量相同,应从甲袋中取出多少千克给乙袋?解:乙袋:一倍量甲袋:5倍+4=34所以:一倍量=(34-4)÷5=6乙袋有6,甲袋有34,甲给乙(34-6)÷2=14千克。
巧妙运用倍数关系解决问题

巧妙运用倍数关系解决问题解决问题是我们在日常生活和学习中经常遇到的事情。
有时候,我们可能会遇到一些复杂的问题,需要用到一些巧妙的方法。
本文将介绍一种解决问题的方法——巧妙运用倍数关系。
通过运用倍数关系,我们可以在解决问题时更加高效和准确。
下面将从几个不同场景出发,详细介绍如何巧妙运用倍数关系来解决问题。
一、货物运输问题在货物运输中,我们经常会遇到计算运输量、运费等问题。
如果我们知道某种货物的运输量,希望计算出其他种类货物的运输量,倍数关系就可以派上用场了。
假设我们知道A种货物的运输量为100吨,且知道B种货物的运输量是A种货物的2倍,那么B种货物的运输量就是200吨。
此外,倍数关系还可以用于计算运费。
如果我们知道A种货物的运费是10元/吨,且知道B种货物的运费是A种货物的1.5倍,那么B种货物的运费就是15元/吨。
二、比例问题在生活中,比例问题也十分常见。
比例问题可以通过巧妙运用倍数关系得到解决。
例如,某种物品每件售价100元,我们想要计算出买n件需要支付的金额。
由于售价是批量销售的,我们可以假设想要购买的件数是原售价的倍数,假设是m倍。
那么,买n件需要支付的金额就是m*100元。
同样的,倍数关系也可以用于计算折扣。
如果某品牌衣服原价500元,打7折出售,那么打折后的价格就是500*0.7元。
三、时间问题在时间计算中,我们也可以灵活运用倍数关系。
例如,如果我们要计算一个事件需要的时间,已知某个过程需要的时间是60分钟,且另一个过程需要的时间是第一个过程的1.5倍,那么第二个过程需要的时间就是90分钟。
另外,倍数关系还可以用于计算速度。
如果我们已经知道某个人的速度是10千米/小时,且另一个人的速度是第一个人的0.8倍,那么他的速度就是8千米/小时。
四、面积和体积问题在解决面积和体积问题时,倍数关系同样适用。
例如,我们想要计算一个正方形的面积,已知另外一个正方形的面积是它的2倍,那么第二个正方形的面积就是第一个正方形的面积的2倍。
解决问题倍数问题PPT课件

第9页/共17页
例 2: 椅子的单价是课桌的3/5, 一张课桌比一把椅子贵 20 元。 求课桌和 椅子的单价。
• 分析: 把
看作 1 份,
就是(3/5) 份,课桌单价比椅子单价多
•
份,也就是20 元是
份, 先求一份, 再求3/5 份。
• (1) 课桌单价:
(元) 。
• (2) 椅子单价:
(元)
• 你能用方程的方法解答吗?
第14页/共17页
巩固练习 2:
• 1、 果园里有梨树和苹果树共 320 棵, 其中苹果树比梨树多 2 倍。 两种树各有多少棵? • 梨树:320÷(2+1+1)=80(棵)苹果树:320-80=240(棵) • 2、 甲数与乙数的和是 840, 甲数除以乙数的商是 7,甲、 乙两数各是多少? • 乙:840÷(7+1)=105 甲:840-105=735 • 3、女运动员每分钟可跑 300 米, 比男运动员每分钟的2/3还少 20 米, 男运动员每分钟跑多少米? • 男:(300+20)÷2/3=480(米) • 4、粮店运来大米和面粉共 96 袋,大米和面粉袋数的比是 5: 3.运来大米和面粉各多少袋?
•1 、部分与整体的比较, 整体或总数是单 位“1” 的量。
• 2、 两种数量比较, 被比较的那个量是单
位“1”的量, 即在“比”、“是”、
“占”、“相当于” 这些关键字后面的那
一个量。
第2页/共17页
解决分数应用题的一般方法
• 1、求一个数的几分之几(几倍)是多少。即求比较量,用乘法
•
单位“1”的量 ×比较量对应的分率(或倍数)=比较量
• 列方程解答:
• 解: 设课桌单价是
倍数解决问题

起来有多少高?
1、42÷7=6(倍) 2、12×6=72(毫米)
答:全班42本数学练习本摞起来有72毫米。
2、一个长方形的面积是256平方厘米,如果长缩小4倍,宽扩大4倍
,这个长方形九变成了正方形。这个正方形的面积是多少?边长是多少?
1、长×宽=256(平方米) 2、(长÷4)×(宽×4)=256(平方米) 3、(16 )×( 16)=256(平方米)
答:应付32元。
4、胜利街的一块长方形地域是下图,现在要把长增加到96米,宽不变。扩大后
的面积是多少? 1、96÷32=3(倍) 2、480×3=1440(平方米)
480平方米 32米
综合算式:
480×(96÷32)ቤተ መጻሕፍቲ ባይዱ= 480×3 =1440(平方米)
答:扩大后的面积是1440平方米。
答:这个正方形的面积是256平方米。边长是16米。
3、冰淇淋:6元可以买4个,雪糕:5元可以买3个。小强他们打算买8个 冰淇淋和12支雪糕,应付多少钱?
1、8÷4=2(倍) 2、6×2=12(元)
5、 12+20=32(元)
3、12÷3=4(倍) 4、 5×4=20(元)
综合算式:
6×(8÷4)+ 5×(12÷3) = 6×2 + 5×4 =12 +20 =32(元)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、在○里填上“>”、“<”或 “=”
(1)0.76×1.02 ○ 0.76×1.05 (2)4.87×0.6 ○ 48.7×0.06 (3)0.98×1.02 ○ 1.02 (4)0.84 ○ 0.84×0.84
1、判断对错,并把错的改正过来
(1)19.8×0.7=68.6
(2)6.45×0.8=5.16 (3)3.47×60=20.82
•教学目标; 学会倍数是小数的 解题方法,并会正确解 决有关实际问题。
• 自学指导: • 请同学们认真看课本第 6 页例 5 内 容,并独立思考以下几个问题; • 求一个的倍数用什么方法? • 怎样验算你小数乘法 ? 有几种验算 方法? • 5 分钟后,指名学生回答以上马的最长寿命是52岁, 蓝鲸的最长寿命是河马的1.7倍, 蓝鲸的最长奉命是多少?
布置作业:
1、哥哥上大学,要坐6.4小时的火车, 火车的平均速度是70.5千米/时,他坐火 车走了多少千米? 2、小娟加印了14张照片,每张照片0.55 元,她一共花了多少钱? 3、地球直径1.28万千米,月球到地球的 距离是地球直径的30倍,月球到地球有 多远?
讨论:
1、内容:自学指导中的问题。 2、要求:对桌讨论,大号讲, 小号听,大号不会, 小号及时补 充或纠正。 3分钟以后看谁展示的更精彩!
非洲野狗的最高速 度是56千米/时。
鸵鸟的最高速度是非洲野狗的1.3倍, 鸵鸟的最高速度是多少千米/时?
验算方法:
A、把两个因数交换位置再乘一遍; B、用计算器验算; C、用原式再做一遍; D、观察法:因为第二个因数大于 1,所以积一定大于第一个因数。
72.8 72.8
结论:
一个数(0除外)乘大于1的 数,积比原来的数大。 一个数(0除外)乘小于1的 数,积比原来的数小。 用途: 我们可以根据它们的这种关 系初步判断小数乘法的正误。
2.4×
3 5 1.5
7.2 = 12 3.6
0.4 1.2× 0.11 0.35
0.48 = 0.132 0.42
• 1. 13.65扩大到原来的(100)倍是1365,6.8 缩小到原来的(1/100)是0.068。 • 2. 8.25684保留整数约是(8),精确到千 分位是约是(8.257)。 • 3. 4.09×0.05的积是(4)位小数。
