MATLAB实验报告 (2)
实验二MATLAB绘制图形

grid on %在所画出的图形坐标中加入栅格
绘制图形如下
50
10
1
0.8
40
10
0.6
0.4
30
10
0.2
0
1020
-0.2
-0.4
1010
-0.6
-0.8
0
10
-1
-2
0
2
-2
0
2
10
10
10
10
10
10
如果在图中不加栅格
程序如下:
clear x=logspace(-1,2);%在10^(-1)到10^2之间产生50个 对数等分的行向量 subplot(121); loglog(x,10*exp(x),'-p') subplot(122); semilogx(x,cos(10.^x))
(2)plot(x,y): 基本格式,x和y可为向量或矩阵. 1. 如果x,y是同维向量,以x元素为横坐标,以y元素 为纵坐标绘图. 2. 如果x是向量,y是有一维与x元素数量相等的矩阵, 则以x为共同横坐标, y元素为纵坐标绘图,曲线数目 为y的另一维数. 3. 如果x,y是同维矩阵,则按列以x,y对应列元素为 横、纵坐标绘图,曲线数目等于矩阵列数.
y=2*exp(-0.5*x).*cos(4*pi*x);
2
plot(x,y)
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
1
2
3
4
5
6
7
例4 绘制曲线
t=(0:0.1:2*pi);
x=t.*sin(3*t);
y=t.*sin(t).*sin(t);
matlab实验二

北京工业大学Matlab实验报告**: ***学号: ************: **实验二、Matlab 的基本计算(一)实验目的1.掌握建立矩阵的方法。
2.掌握Matlab 各种表达式的书写规则以及常用函数的使用。
3.能用Matlab 进行基本的数组、矩阵运算。
4.掌握矩阵分析的方法以及能用矩阵运算或求逆法解线性方程组。
5.掌握Matlab 中的关系运算与逻辑运算。
(二)实验环境1.计算机2.MATLAB7.0集成环境(三)实验内容及要求1、熟练操作MATLAB7.0运行环境;2、自主编写程序,必要时参考相关资料;3、实验前应写出程序大致框架或完整的程序代码;4、完成实验报告。
(四)实验程序设计1.利用diag 等函数产生下列矩阵。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=032570800a ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=804050702b2.利用reshape 函数将1题中的a 和b 变换成行向量。
3.产生一个均匀分布在(-5,5)之间的随机矩阵(10×2),要求精确到小数点后一位。
4.已知:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=76538773443412A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=731203321B求下列表达式的值:(1) B A K *611+=和I B A K +-=12(其中I 为单位矩阵)(2) B A K *21=和B A K *.22=(3) 331^A K =和3.32^A K =(4) B A K /41=和A B K \42=(5) ],[51B A K =和]2:);],3,1([[52^B A K = 5.下面是一个线性方程组:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡52.067.095.03216/15/14/15/14/13/14/13/12/1x x x(1)求方程的解(矩阵除法和求逆法)(2)将方程右边向量元素3b 改为0.53,再求解,并比较3b 的变化和解的相对变化。
matlab计算机实验报告

matlab计算机实验报告Matlab计算机实验报告引言Matlab是一种强大的计算机软件,广泛应用于科学计算、数据分析和工程设计等领域。
本实验报告旨在介绍我对Matlab的实验研究和应用。
通过实验,我深入了解了Matlab的功能和特点,并通过实际案例展示了其在科学计算和数据处理中的应用。
实验一:基本操作和语法在本实验中,我首先学习了Matlab的基本操作和语法。
通过编写简单的程序,我熟悉了Matlab的变量定义、赋值、运算符和条件语句等基本语法。
我还学习了Matlab的矩阵操作和向量化计算的优势。
通过实例演示,我发现Matlab在处理大规模数据时具有高效性和便捷性。
实验二:数据可视化数据可视化是Matlab的重要应用之一。
在本实验中,我学习了如何使用Matlab绘制各种图表,如折线图、散点图、柱状图和饼图等。
我了解了Matlab 的绘图函数和参数设置,并通过实例展示了如何将数据转化为直观的图形展示。
数据可视化不仅可以帮助我们更好地理解数据,还可以用于数据分析和决策支持。
实验三:数值计算和优化Matlab在数值计算和优化方面具有强大的功能。
在本实验中,我学习了Matlab 的数值计算函数和工具箱,如数值积分、微分方程求解和线性代数运算等。
通过实例研究,我发现Matlab在求解复杂数学问题和优化算法方面具有出色的性能。
这对于科学研究和工程设计中的数值分析和优化问题非常有用。
实验四:图像处理和模式识别Matlab在图像处理和模式识别领域也有广泛的应用。
在本实验中,我学习了Matlab的图像处理工具箱和模式识别算法。
通过实例演示,我了解了如何使用Matlab进行图像滤波、边缘检测和特征提取等操作。
我还学习了一些常见的模式识别算法,如支持向量机和神经网络等。
这些技术在计算机视觉和模式识别中具有重要的应用价值。
实验五:信号处理和系统建模Matlab在信号处理和系统建模方面也有广泛的应用。
在本实验中,我学习了Matlab的信号处理工具箱和系统建模工具。
南华大学《MATLAB及应用》实验报告2

核科学技术学院实验报告实验项目名称MATLAB符号计算所属课程名称MATLAB及应用实验类型上机实验实验日期12月日指导教师谢芹班级学号姓名成绩一、实验名称MATLAB符号计算二、实验目的(1)掌握定义符号对象的方法(2)掌握符号表达式的运算法则以及符号矩阵运算(3)掌握求符号函数极限及导数的方法(4)掌握求符号函数定积分和不定积分的方法三、实验原理1. 函数极限及导数的方法(1)函数极限:limit(F,x,a) 求符号函数f(x)的极限值。
即计算当变量x趋近于常数a时,f(x)函数的极限值。
(2)limit(f):求符号函数f(x)的极限值。
符号函数f(x)的变量为函数findsym(f)确定的默认变量;没有指定变量的目标值时,系统默认变量趋近于0,即a=0的情况。
(3)limit(f,x,a,'right'):求符号函数f的极限值。
'right'表示变量x从右边趋近于a。
(4)limit(f,x,a,‘left’):求符号函数f的极限值。
‘left’表示变量x从左边趋近于a。
2. 微分:diff(s):没有指定变量和导数阶数,则系统按findsym函数指示的默认变量对符号表达式s求一阶导数。
diff(s,'v'):以v为自变量,对符号表达式s求一阶导数。
diff(s,n):按findsym函数指示的默认变量对符号表达式s求n阶导数,n为正整数。
diff(s,'v',n):以v为自变量,对符号表达式s求n阶导数。
3. 函数定积分和不定积分的方法:int(s):没有指定积分变量和积分阶数时,系统按findsym函数指示的默认变量对被积函数或符号表达式s求不定积分。
int(s,v):以v为自变量,对被积函数或符号表达式s求不定积分。
int(s,v,a,b):求定积分运算。
a,b分别表示定积分的下限和上限。
梯形法:trapz(x,y):x为分割点构成的向量,y为被积函数在分割点上的函数值构成的向量;抛物线法:quad(f,a,b,tol),f 是被积函数,[a,b]是积分区间,tol 是精度。
MATLAB实验报告

实验二MATLAB语言基础一、实验目的基本掌握MA TLAB向量、矩阵、数组的生成及其基本运算(区分数组运算和矩阵运算)、常用的数学函数。
了解字符串的操作。
二、实验内容1.向量的生成与运算;2.矩阵的创建、引用和运算;3.多维数组的创建及运算;4.字符串的操作。
三、实验步骤1.向量的生成与运算①向量的生成向量的生成有三种方法:直接输入法:生成行向量、列向量;冒号表达式法:变量=初值:间隔(可正可负):终值函数法:使用linspace线性等分函数,logspace对数等分函数。
格式为:linspace(初值,终值,个数)Logspace(初值,终值,个数), 初值及终值均为10的次幂。
②向量的运算A=[1 2 3 4 5],b=3:7,计算两行向量的转置,两行向量人加、减,两列向量的加、减;向量的点积与叉积。
a=[1 2 3 4 5];b=3:7;a =1 2 3 4 5b =3 4 5 6 7at=a',bt=b'at =12345bt =34567e1=a+b,e2=a-be1 =4 6 8 10 12 e2 =-2 -2 -2 -2 -2 f1=at+bt,f2=at-btf1 =4561012f2 =-2-2-2-2-2g1=dot(a,b),g2=a*bt>> g1=dot(a,b),g2=a*btg1 =85g2 =85g4=a.*b>> g4=a.*bg4 =3 8 15 24 35A=1:3;B=4:6;g3=cross(A,B)>> g3=cross(a,b)g3 =-3 6 -3注意:g1和g2的结果是否相同,为什么?g4的结果与g1和g2结果是否一样,为什么?g1和g2的结果相同,因为两者是同一种运算;g4与g1和g2不相同,因为两者一个是点乘一个是叉乘,运算不一样。
2.矩阵的创建、引用和运算矩阵是由n×m元素构成的矩阵结构。
实验二MATLAB程序设计含实验报告

实验二 MATLAB 程序设计一、 实验目的1.掌握利用if 语句实现选择结构的方法。
2.掌握利用switch 语句实现多分支选择结构的方法。
3.掌握利用for 语句实现循环结构的方法。
4.掌握利用while 语句实现循环结构的方法。
5.掌握MATLAB 函数的编写及调试方法。
二、 实验的设备及条件计算机一台(带有MATLAB7.0以上的软件环境)。
M 文件的编写:启动MATLAB 后,点击File|New|M-File ,启动MATLAB 的程序编辑及调试器(Editor/Debugger ),编辑以下程序,点击File|Save 保存程序,注意文件名最好用英文字符。
点击Debug|Run 运行程序,在命令窗口查看运行结果,程序如有错误则改正三、 实验内容1.编写求解方程02=++c bx ax 的根的函数(这个方程不一定为一元二次方程,因c b a 、、的不同取值而定),这里应根据c b a 、、的不同取值分别处理,有输入参数提示,当0~,0,0===c b a 时应提示“为恒不等式!”。
并输入几组典型值加以检验。
(提示:提示输入使用input 函数)2.输入一个百分制成绩,要求输出成绩等级A+、A 、B 、C 、D 、E 。
其中100分为A+,90分~99分为A ,80分~89分为B ,70分~79分为C ,60分~69分为D ,60分以下为E 。
要求:(1)用switch 语句实现。
(2)输入百分制成绩后要判断该成绩的合理性,对不合理的成绩应输出出错信息。
(提示:注意单元矩阵的用法)3.数论中一个有趣的题目:任意一个正整数,若为偶数,则用2除之,若为奇数,则与3相乘再加上1。
重复此过程,最终得到的结果为1。
如:2?13?10?5?16?8?4?2?16?3?10?5?16?8?4?2?1运行下面的程序,按程序提示输入n=1,2,3,5,7等数来验证这一结论。
请为关键的Matlab 语句填写上相关注释,说明其含义或功能。
MATLAB实验报告第二章
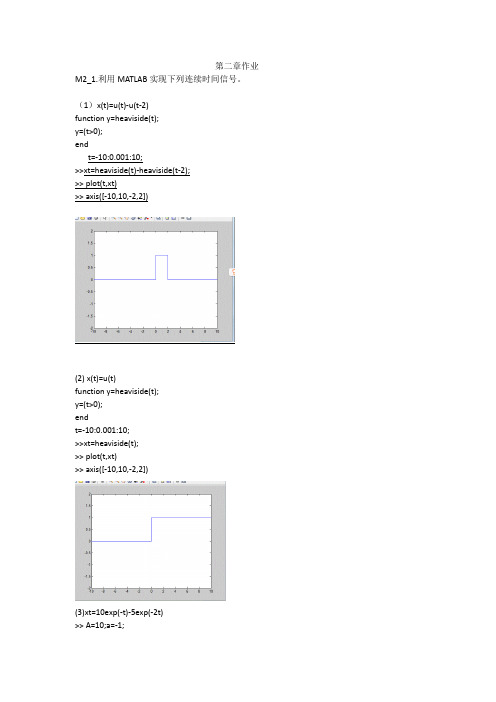
第二章作业M2_1.利用MATLAB实现下列连续时间信号。
(1)x(t)=u(t)-u(t-2)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t)-heaviside(t-2);>>plot(t,xt)>>axis([-10,10,-2,2])(2) x(t)=u(t)function y=heaviside(t);y=(t>0);endt=-10:0.001:10;>>xt=heaviside(t);>>plot(t,xt)>>axis([-10,10,-2,2])(3)xt=10exp(-t)-5exp(-2t)>> A=10;a=-1;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=5;a=-2;>> t=0:0.001:10;>> x2t=A*exp(a*t);>>xt=x1t-x2t;>>plot(t,xt)(4)xt=tu(t)>> t=-10:0.001:10;>>xt=t.*heaviside(t);>>plot(t,xt)(5)xt=2|sin(10pit+pi/3)| >> A=2;w0=10*pi;phi=pi/3; >> t=0:0.001:1;>>xt=A*abs(sin(w0*t+phi)); >>plot(t,xt)>>axis([0,1,-4,4])Xt=cost+sin(2pit)>> A=1;w0=1;phi=0; >> t=0:0.002:10;>> x1t=A*cos(w0*t+phi); >> A=2;w0=2*pi;phi=0; >> t=0:0.002:10;>> x2t=A*sin(w0*t+phi); >>xt=x1t+x2t;>>plot(t,xt)(7)xt=4exp(-0.5t)cos(2pit) >> A=5;a=-0.5;>> t=0:0.001:10;>> x1t=A*exp(a*t);>> A=1;w0=2*pi;phi=0; >> t=0:0.001:10;>> x2t=A*cos(w0*t+phi); >>xt=x1t.*x2t;>>plot(t,xt)(8)Sa(pit)cos(30t)A=1;w0=30;phi=0;>> t=0:0.001:3;>> x1t=A*cos(w0*t+phi);>> t=0:0.001:3;>> x2t=sinc(t);>>xt=x1t.*x2t;>>plot(t,xt)M2-3,写出书中图示波形函数,并画出xt,x0.5t,x(2-0.5t)的图像function yt=x2_3(t)yt=t.*(t>=0&t<2)+2*(t>=2&t<3)+(-1)*(t>=3&t<=5); end>> t=0:0.001:5;>>xt=x2_3(t);>>title('x(t)');>>plot(t,xt)>>axis([0,6,-2,3])>> t=0:0.001:10;xt=x2_3(0.5*t); >>plot(t,xt)>>title('x(0.5t)')>>axis([0,10,-2,3])x(0.5t)>> t=-10:0.001:10;>>xt=x2_3(2-0.5*t);>>plot(t,xt)>>title('x(2-0.5t)')>>axis([-10,10,-2,3])M2-4画出图示的奇分量和偶分量。
matlab实验报告2

第二次上机作业准备&要求:1、 运行课件第三章(课本第四章)讲过的例子,掌握Matlab 的流程控制语句、函数及脚本文件的编程、调试方法。
2、 本次作业(4~12题)要求全部写M 文件;3、 题目要求未明确要求写脚本文件还是函数文件的,学生自己决定是写脚本文件还是函数文件。
只要能够实现要求。
4、 列出第二章课堂上出现过的所有函数,知道它们的作用并试着调用这些函数。
作业:1. 继续完成第一次上机实验未完成的作业。
2. 分析脚本M 文件及函数M 文件的区别。
(1)脚本文件没有输入参数,也不返回输出参数,而函数文件可以带输入参数,也可以返回输出参数。
(2)脚本文件对MATLAB 工作空间中的变量进行操作,文件中所有命令的执行结果也完全返回到工作空间中,而函数文件中定义的变量为局部变量,当函数文件执行完毕时。
这些变量被清除。
(3)脚本文件可以直接运行。
在MATLAB 命令行窗口输入脚本文件的名字,就会顺序执行脚本文件中的命令。
而函数文件不能直接运行,要以函数调用的方式来调用。
3. 已知⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=7613870451A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=023352138B ,求下列表达式的值,并注意第(2)(3)小题表达式的结果有何特点:(1)B A 6+ 、I B A +-2(其中I 为单位阵);>> A+6*Bans =47 23 -1012 37 26-15 73 7>> A^2-B+Ians =-18 -217 1722 533 10921 867 526(2)A*B、A.*B、B*A、B.*A;>> A*Bans =14 14 16-10 51 21125 328 180>> A.*Bans =-8 15 40 35 24-9 122 0>> B*Aans =-11 0 -157 228 533 -1 28>> B.*Aans =-8 15 40 35 24-9 122 0(3)A/B、B\A、A./B、B.\A;A/Bans =1.2234 -0.92552.9787-0.9468 2.3511 -0.95744.6170 3.8723 13.8936>> B\Aans =-0.5106 -8.6170 -1.12770.7340 17.5745 1.8085-0.8830 -21.2128 0.4043>> A./Bans =-0.1250 1.6667 4.00000 1.4000 2.6667-1.0000 30.5000 Inf>> B.\Aans =-0.1250 1.6667 4.00000 1.4000 2.6667-1.0000 30.5000 Inf(4)[A, B]、[A([1 3],:);B^2]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
仲恺农业工程学院实验报告纸_自动化学院_(院、系)_工业自动化_专业_144_班_Matlab仿真控制实践课程实验一MATLAB绘图基础一、实验目的了解MATLAB常用命令和常见的内建函数使用。
熟悉矩阵基本运算以及点运算。
掌握MATLAB绘图的基本操作:向量初始化、向量基本运算、绘图命令plot,plot3,mesh,surf 使用、绘制多个图形的方法。
二、实验内容建立并执行M文件multi_plot.m,使之画出如图的曲线。
三、实验方法四、实验要求1.分析给出的MA TLAB参考程序,理解MA TLAB程序设计的思维方法及其结构。
2.添加或更改程序中的指令和参数,预想其效果并验证,并对各语句做出详细注释。
对不熟悉的指令可通过HELP查看帮助文件了解其使用方法。
达到熟悉MA TLAB画图操作的目的。
3.总结MATLAB中常用指令的作用及其调用格式。
五、实验思考1、实现同时画出多图还有其它方法,请思考怎样实现,并给出一种实现方法。
(参考程序如下)2、思考三维曲线(plot3)与曲面(mesh, surf)的用法,(1)绘制参数方程233,)3cos(,)3sin()(t z e t t y e t t t x t t ===--的三维曲线;(2)绘制二元函数xyy x ex x y x f z ----==22)2(),(2,在XOY 平面内选择一个区域(-3:0.1:3,-2:0.1:2),然后绘制出其三维表面图形。
(以下给出PLOT3和SURF 的示例)绘制题目要求曲面:%绘制二元函数,在XOY平面内选择一个区域(-3:0.1:3,-2:0.1:2)仲恺农业工程学院实验报告纸_自动化学院_(院、系)_工业自动化_专业_144_班_Matlab 仿真控制实践 课 程实验二:基于Simulink 的控制系统仿真实验目的1. 掌握MATLAB 软件的Simulink 平台的基本操作; 2. 能够利用Simulink 平台研究PID 控制器对系统的影响;实验原理PID (比例-积分-微分)控制器是目前在实际工程中应用最为广泛的一种控制策略。
PID 算法简单实用,不要求受控对象的精确数学模型。
1.模拟PID 控制器典型的PID 控制结构如图1所示。
`图1 典型PID 控制结构 连续系统PID 控制器的表达式为()()()()tp I Dde t x t K e t K e d K dt ττ=++⎰ (1)式中,P K ,IK 和DK 分别为比例系数,积分系数和微分系数,分别是这些运算的加权系数。
对式(7-21)进行拉普拉斯变换,整理后得到连续PID 控制器的传递函数为1()(1)I C P D P D I K G s K K s K T s s T s =++=++ (2)显然P K ,IK 和DK 这3个参数一旦确定(注意/,/I P I D D PT K K T K K ==),PID 控制器的性能也就确定下来。
为了避免微分运算,通常采用近似的PID 控制器,气传递函数为1()(1)0.11D C P I D T s G s K T s T s =+++ (3)实验过程PID 控制器的P K ,I K 和D K 这3三个参数的大小决定了PID 控制器的比例,积分和微分控制作用的强弱。
下面请通过一个直流电动机调速系统,利用MA TLAB 软件中的Simulink 平台,使用期望特性法来确定这3个参数的过程。
并且分析这3个参数分别是如何影响控制系统性能的。
【问题】某直流电动机速度控制系统如图2所示,采用PID 控制方案,使用期望特性法来确定P K ,IK 和DK 这3三个参数。
期望系统对应的闭环特征根为:-300,-300,-30+j30和-30-j30。
请建立该系统的Simulink 模型,观察其单位阶跃响应曲线,并且分析这3个参数分别对控制性能的影响。
图2 直流电动机PID 控制系统 (1)使用期望特性法来设计PID 控制器。
首先,假设PID 控制器的传递函数为:()IC PD K G s K K s s =++,其中P K ,I K 和D K 这3个参数待定。
图2所示的系统闭环的传递函数为2432113120550()()660(36801357447)(4860001357447)1357447D P I B D P I K s K s K G s s s K s K s K ⨯++=++++++如果希望闭环极点为:-300,-300,-30+j30和-30-j30,则期望特征多项式为:4326660127800648000016210s s s s ++++⨯。
对应系数相等,可求得:0.067D K =, 4.4156P K =,119.34I K =。
在命令窗口中输入这3个参数值,并且建立该系统的Simulink模型,如图3所示。
图3直流电动机PID 控制系统的Simulink 仿真模型输入信号为单位阶跃信号,在t=1s 时从0变化到1。
系统响应曲线如图4所示。
(2)分析比例系数PK 对控制性能的影响在119.34I K =和0.067D K =保持不变的情况下,PK 分别取值0.5,5和20,系统的响应曲线如图5所示。
可见,当PK 取值较小时系统的响应较慢,而当PK取值较大时图4直流电动机PID 控制系统响应曲线系统的响应速度较快,但超调量增加。
(3)分析积分系数IK 对控制性能的影响在0.067D K =和4.4156P K =保持不变的情况下,IK 分别取值20,120,300,系统的响应曲线如图6所示。
可见,当IK 取值较小时系统响应进入稳态的速度较慢。
而当IK 取较大值时系统的响应进入稳态的速度较快,但超调量增加。
图5 改变P K 时的系统响应曲线(分别取0.5、5、20)(4)分析微分系数DK 对控制性能的影响 在4.4156P K =和119.34I K =保持不变的情况下,DK 分别取值0.01,0.07,0.2,系统的响应曲线如图7所示。
可见,当DK 取值较小时系统响应对变化趋势的调节较慢。
超调量较大。
而当DK 取值较大时系统的响应进入稳态的速度较快。
但是超调量增加。
当DK 取值过大时,对变化趋势的调节过强,阶跃响应的初期出现尖脉冲。
图6 改变IK 时的系统响应曲线(分别取20、120、300)实验总结比例控制器的控制规律为)()(t e K t u p p =当偏差e(t)不为0,比例控制器就会产生控制作用,比例系数Kp 决定控制作用的强弱,增大比例系数Kp 可提高控制灵敏度,加快系统动态响应速度,减小稳态误差,但是无法消除静差。
此外,Kp 过大会降低系统的动态品质,引起被控量的振荡,甚至导致闭环系统不稳定。
积分控制器的控制规律为⎰⨯=ti p i dtt e T K t u 0)(1)(其中,积分时间常数Ti 表示积分速度的快慢,Ti 越大,积分速度越慢,积分作用越弱,反之则越强。
它可以消除静差,但积分作用缓慢,不能及时克服扰动的影响,降低了系统的快速性,一半不单独使用。
微分控制器的控制规律为dtt de T K t d p d )()(u ⨯= 微分控制作用与偏差的变化速度成正比,能够预测偏差的变化,从而产生超前控制作用,以阻止偏差的变化。
微分时间常数Td 表示微分速度的快慢,Td 越大,微分作用越强,反之则越弱。
微分控制可以加快系统的动态响应,减少超调量,但不能消除静差,且只在偏差刚刚出现时产生控制作用。
根据以上可知,理想的控制系统是PID 控制,综合了P 、I 、D 三种控制的优点,既有比例控制的迅速调节,又有积分控制消除稳态误差的能力,还有微分控制的超前控制作用,只要合理选择控制参数Kp 、Ti 、Td ,便可发挥三种控制规律的优点,得到很好的控制效果。
仲恺农业工程学院实验报告纸_自动化学院_(院、系)_工业自动化_专业_144_班_Matlab 仿真控制实践 课 程实验三 控制系统数学模型转换及MATLAB 实现一、实验目的熟悉MATLAB 的实验环境。
掌握MATLAB 建立系统数学模型的方法。
二、实验内容用MA TLAB 做如下练习。
(1)用2种方法建立系统2)(2+=s s G 的多项式模型。
(2)用2种方法建立系统)10)(5)(1()1(10)(++++=s s s s s G 的零极点模型和多项式模型。
(3)如图,已知G (s )和H (s )两方框对应的微分方程是:)(20)(10)(6t e t c dt t dc =+ )(10)(5)(20t c t b dtt db =+且初始条件为零。
试求传递函数C(s)/R(s)及E(s)/R(s)。
三、实验思考1、如何灵活选择函数的各种不同调用方法。
答:当传递函数的分子、分母都是多项式的形式或分子、分母含有的分式较为简单并且易化简时,多采用多项式模型来建立系统传递函数模型。
其中,多项式模型又有两种方法(详见实验内容(1)),第一种方式需要先求出分子分母多项式,再将其作为tf函数的参数使用,第二种方式需先定义Laplace算子,将传递函数直接赋给对象。
当传递函数含有较多分式(即零极点)时,一般采用零极点模型来建立传递函数模型,它又包含两种方式,一种是直接将零极点向量和增益值赋给zpk函数;另一种是先定义零极点形式的Laplace算子,再输入零极点模型。
2、复杂系统如何用MA TLAB建立系统模型,如何对结构图进行化简。
答:对于复杂的系统,一般不采用上述的零极点模型或传递函数模型,而是采用Simulink来进行图形化系统建模,只要知道各模块的参数便可以建立相应模型,还可以在Simulink中进行仿真。
结构图的化简主要有以下的变换方式:1)串联方框连接及其等效变换;2)并联方框连接及其等效变换;3)方框反馈链接及其等效变换;4)引出点前后移动等效变换;5)相邻引出点之间的移动变换;6)综合点前后移动等效变换;7)相邻综合点之间的移动等效变换;3、求系统传递函数有哪些方法?各有何特点?适用于什么情况。
答:个人认为,在Matlab中有两种方法求传递函数,第一种是利用传递函数模型和零极点模型,建立各部分传递函数模型,然后利用Matlab自带的传递函数化简函数进行化简,最后输出,该方法适用于环节不多且没有较为复杂反馈环节的情况下;第二种是在Simulink中建立方框图模型,利用Simulink来求传递函数和化简。
在环节较多且较为复杂是,使用Simulink可以节省很多时间。
仲恺农业工程学院实验报告纸_自动化学院_(院、系)_工业自动化_专业_144_班_Matlab 仿真控制实践 课 程实验四 控制系统的MATLAB 辅助分析一、实验目的熟悉基于MATLAB 的系统稳定性分析。
