第3章例题
第3章数据的集中趋势和离散程度(十四大题型)(原卷版)

项目
在线学习
知识竞赛
演讲比赛
甲
84
96
90
乙
89
99
85
(1)若将在线学习、知识竞赛与演讲比赛三项成绩的平均分作为最后成绩,谁将会获得冠军?
(2)若将在线学习、知识竞赛与演讲比赛的成绩按2:3:5的比例计算最后成绩,谁将会获得冠军?
解题技巧提炼
首先通过计算加权平均数,然后比较平均数的大小,最后进行决策.
普通话
主题
得分
90
80
88
评总分时,按服装占15%,普通话占35%,主题占50%,她的总得分是( )
A.86B.85.5C.86.5D.88
【变式25】(2021春•房山区期末)已知数据x1,x2,x3,x4,x5的平均数为k1;数据x6,x7,x8,x9,x10的平均数为k2;k1与k2的平均数是k;数据x1,x2,x3,…,x8,x9,x10的平均数为m,那么k与m的关系是( )
A.k>mB.k=mC.k<mD.不能确定
【例题3】(2023•宁波一模)为深入学习贯彻习近平法治思想,推动青少年宪法学习宣传教育走深走实,教育部组织开展第七届全国学生“学宪法讲宪法”系列活动.某校积极响应教育部的号召,开展了宪法知识在线学习、知识竞赛与演讲比赛三项活动,表是参加冠亚军决赛的两名选手的各项测试成绩(单位:分).
A.15B.16C.17D.18
【变式12】在计算100个数的平均数时,将其中的一个数100错看成了1000,则此时计算出来的平均数比实际结果多( )
A.9B.10C.19D.2
【变式13】(2023•湖州)某住宅小区6月1日~6月5日每天用水量情况如图所示,那么这5天平均每天的用水量是( )
第三章 PLC例题作业解答
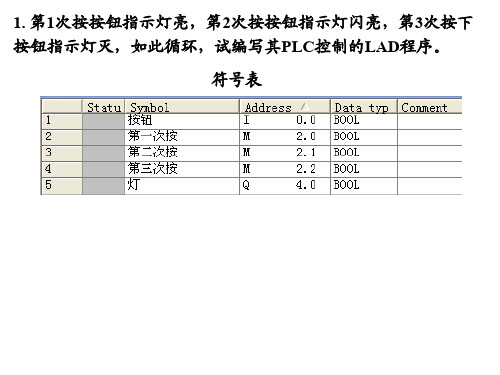
1. 第1次按按钮指示灯亮,第2次按按钮指示灯闪亮,第3次按下 按钮指示灯灭,如此循环,试编写其PLC控制的LAD程序。 符号表
2. 用一个按钮控制2盏灯,第1次按下时第1盏灯亮,第2盏灯灭; 第2次按下时第1盏灯灭,第2盏灯亮;第3次按下时2盏灯都灭。
3. 编写PLC控制程序,使Q4.0输出周期为5s,。鼓风机系统一般有引风机和鼓风 机两级构成。要求: (1).按下起动按钮后首先起动引风机,引风机指示灯亮, 10s后鼓风机自动起动,鼓风机指示灯亮;按下停止按钮后首先 关断鼓风机,鼓风机指示灯灭,经20s后自动关断引风机和引风 机指示灯。 (2).起动按钮接I0.0,停止按钮接I0.1。鼓风机及其指示由 Q4.1和Q4.2驱动,引风机及其指示由Q4.3和Q4.4驱动。
符号表
5. 某设备有3台风机,当设备处于运行状态时,如果有2台或2 台以上风机工作,则指示灯常亮,指示“正常”;如果仅有1台 风机工作,则该指示灯以0.5Hz的频率闪烁,指示“一级报警”; 如果没有风机工作了,则指示灯以2Hz的频率闪烁,指示“严重 警报”。当设备不运转时,指示灯不亮。试用STL及LAD编写符 合要求的控制程序。 提示:本题要点是如何实现“一灯多用”功能。指示灯指示 了4种状态:“正常、一级报警、严重警报、设备停止”。
第3章 高频调谐功率放大器(含例题)

两者工作频率与相对频宽不同 低频功率:工作频率低,但相对 频带宽度很宽。 如:低频(音频):20Hz~20kHz
高:工作频率高(由几百KHZ一直到几百、 几千甚至几万MHZ),但相对频带窄。
如:AM广播信号: 535kHz~1605kHz,BW=10kHz
f max 1000 f min
BW 20k 2 f0 10k
uCE E C U cm cost
Ucm
t
vCE VCC Vcm cost
v
i V
CE
min i vCE
c max
1 T P i v dt 晶体管集电极平均耗散功率: c T 0 C CE 1.利用谐振回路的选频作用,将失真的集电极脉冲电流变换 2. iC 脉冲最大时,vCE最小。 3、如何减小集电极耗散功率Pc 故:要想获得高的集电极效率,谐振功率放大器的集电极电流 4.如果失谐,则损耗快速增加!? 可见使ic在vCE最低的时候才能通过,那么,集电极耗散功率自然会大为 成不失真的余弦电压输出。 应该是脉冲状。导通角小于180,处于丙类工作状态。 减小。效率就提高。而且导通角和vCEmin越小,Pc越小;
6. 功放设计中各方面的折中关系
提高输出功率
减小失真(线性度)
管子的保护 提高效率
遗留问题: (1) 丙类导通角<180o,何时最优?
(2) 放大、临界、饱和,何处最优?
7.分析方法 高频功率放大器工作于丙类,属于非线性电路,所以不 能够用线性等效电路来分析. 因此,谐振功率放大器的分析方法: ●图解法 ●解析近似分析法(折线法)
为什么采用折线法?
1、由于功率放大器工作在大信号状态下,如果考虑晶 体管的非线性特性,将使计算变得复杂。 2、采用折线近似分析法,利用折线段来”代替“晶体管
第3章 傅里叶变换-例题全文编辑修改

1 2
Sa
4
1 e j
π n π
n
π
sin n
4
2 n n π
1 ejnπ n π
4
2
n
sin n π 4
n
1
(1)n
n
π
方法二:利用周期信号的傅里叶级数求解
f(t)的傅里叶级数为
1
Fn T
f (t ) e jn1td t
T
12sin3212nπG12
(
t
下面用三种方法求解此题。
方法一:利用傅里叶变换的微分性质 方法二:利用傅里叶变换的积分性质 方法三:线性性质
方法一:利用傅里叶变换的微分性质
要注意直流,设fA(t)为交流分量, fD(t)为直流分量,则
f t fA t fD t
F FA ω FD ω
f t
2 1
O1
t
f (t) 3/2 D
将 f (t)看成是信号1 cos t 经过窗函数 G2π t 的
截取,即时域中两信号相乘
f (t) 1 cos t G2π(t)
根据频域卷积定理有
F
ω
1
2
F
1
cos t F
G2 π
t
1 2π
2
π
δ
ω
π
δ
ω
1
π
δ
ω
1
2
sinπ ω
ω
2sinπ ω ω ω2 1
例3-8
求信号f (t) Sa(100t)的频宽(只计正频率部分), 若对f (t)进行均匀冲激抽样,求奈奎斯特频率fN 和奈奎斯特周期TN。
(1)要求出信号的频宽,首先应求出信号的傅里
四川省部分中学2023高中生物第3章细胞的基本结构知识总结例题

四川省部分中学2023高中生物第3章细胞的基本结构知识总结例题单选题1、豆固醇为大豆细胞的组分,不能被人体肠道吸收,其结构与胆固醇相似。
饭后服用豆固醇能抑制肠黏膜对胆固醇的吸收。
下列关于固醇的说法不正确的是()A.豆固醇可以作为降低人体内胆固醇含量的药物B.豆固醇与糖类、磷脂的组成元素相同C.肠道能吸收胆固醇,不能吸收豆固醇,体现了细胞膜控制物质进出细胞的功能D.维生素D也是固醇类物质,可以促进人体肠道对钙和磷的吸收答案:B分析:脂质分为脂肪、磷脂和固醇,固醇包括胆固醇、性激素和维生素D,与糖类相比,脂肪分子中的氢含量多,氧含量少,氧化分解时产生的能量多,因此是良好的储能物质,磷脂双分子层构成生物膜的基本骨架,固醇中的胆固醇是动物细胞膜的重要组成成分,也参与脂质在血液中的运输。
A、因为豆固醇能抑制肠黏膜对胆固醇的吸收,因此,豆固醇可以作为降低人体内胆固醇含量的药物,A正确;B、胆固醇的组成元素只有C、H、O,糖类的组成元素也基本只有C、H、O,而磷脂的组成元素是有C、H、O、N、P,又知豆固醇与胆固醇相似,据此可推测,豆固醇与糖类的组成元素相同,B错误;C、肠道能吸收胆固醇,不能吸收豆固醇,是细胞膜控制物质进出细胞功能的体现,C正确;D、维生素D属于固醇类物质,可以促进人体肠道对钙和磷的吸收,因此在补充钙的同时可以同时补充维生素D,D正确。
故选B。
2、下列关于真核细胞的结构与功能的叙述,正确的是()A.根据细胞代谢需要,线粒体可在细胞质基质中移动和增殖B.细胞质基质、线粒体基质和叶绿体基质所含核酸的种类相同C.人体未分化的细胞中内质网非常发达,而胰腺外分泌细胞中则较少D.高尔基体与分泌蛋白的合成、加工、包装和膜泡运输紧密相关答案:A分析:细胞在生命活动中发生着物质和能量的复杂变化,细胞内含有多种细胞器,各种细胞器的形态、结构不同,在功能上也各有分工。
解答本题需要掌握细胞内各种细胞器的结构和功能特性,然后分析选项中的关键点A、线粒体是细胞的“动力车间”,根据细胞代谢的需要,线粒体可以在细胞质基质中移动和增殖,A正确;B、细胞质基质中含有RNA,不含DNA,而线粒体基质和叶绿体基质中含有DNA和RNA,所含核酸种类不同,B 错误;C、内质网是蛋白质等大分子物质合成、加工的场所和运输通道,在未分化的细胞中数量较少,而胰腺外分泌细胞由于能合成并分泌含消化酶的胰液,细胞中的内质网数量较多,C错误;D、分泌蛋白是在附着在内质网上的核糖体上合成的,高尔基体与分泌蛋白的加工、包装和膜泡运输紧密相关,D错误。
化工热力学例题与解答(7)

第三章 例题一、空题一、空题1. 状态方程P V b RT ()-=的偏离焓和偏离熵分别是bP dP P R T b P RT dP T V T V H H P PP ig =úûùêëé-+=úûùêëé÷øöçè涶-=-òò00和0ln 0000=úûùêëé-=úûùêëé÷øöçè涶-=+-òòdP P R P R dP T V P R P P R S S P P P ig;若要计算()()1122,,P T H P T H -和()()1122,,P T S P T S -还需要什么性质?ig P C ;其计算式分别是()()1122,,P T H P T H -()()[]()()[]()()[]()dTC P P b dT C bP bP T H T H T H P T H T H P T H T T igP T T igP igig ig ig òò+-=+-=-+---=2121121212111222,,和()()1122,,P T S P T S -()()[]()()[]()()[]dT TC P P R dT T C P P R P P R P T S P T S P T S P T S P T S P T S T T ig P T T ig P igigigigòò+-=++-=-+---=2121120102010201110222ln ln ln ,,,,,,。
第三章 例题

dU (V ) E p=− +γ dV V
式中P是压强, E 为所有模式的振动能量,即
hωs (q ) ⎞ ⎛1 E = ∑ ⎜ hωs (q ) + hωs ( q ) kBT ⎟ e −1 ⎠ q ,s ⎝ 2
γ 为格林爱森常数
dl n ω s ( q ) γ =− dl n V
定义为简正模式频率对体积的对数导数的负值,和 点阵振动的非线性有关。在德拜模型下,有
5. 中子(或光子)的非弹性散射
声子对中子的非弹性散射可以用来测量声子能谱 (晶格振动谱)。该实验方法所依据的基本原理是 散射过程遵守能量守恒和动量(波矢)守恒定律。
′ ± hωs (q ) 能量守恒定律要求: E = En
i n
′ 是散射前后中子的能量, ωs (q ) 是吸收或 式中 Eni 和 En 发射的声子的频率。
在德拜模型下有式中p是压强为所有模式的振动能量即例1初基晶胞含有两个原子的一维点阵考虑一个双原子链其中两种具有相同质量m的离子交错排列只考虑近邻原子间的相互作用设力常数分别为ca证明简正模式的色散关系是b讨论在下列极限情况下色散关系的形式及简正模式的性质分别表示第s个初基晶胞中两个原子相对于平衡位置的位移
7. 爱因斯坦模型和德拜模型
爱因斯坦模型假定晶体中所有简正模式都具有 ω = ωE 相同的频率: 于是爱因斯坦模型的模式密度为
g E (ω ) = 3nδ (ω − ωE )
⎝ V ⎠
N⎞ 式中 n 是单原子点阵的原子密度 ⎛ n = ⎜ ⎟ ω = ν q ,声速 ν 为常数。另外,假定波矢q取 在波矢空间中半径为 qD 的球(称为德拜球)内, 而不是取第一布里渊区中的所有q值。
相应地点阵热容为
第3章动量守恒
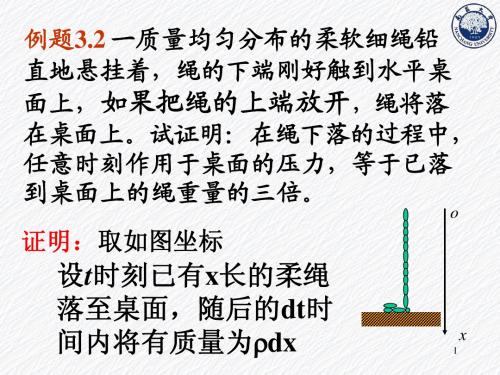
注意
内力不改变质点系的动量
初始速度
v g 0 = v b 0 = 0 m b = 2m g
且方向相反
推开后速度 v g = 2 v b 推开前后系统动量不变
v v p = p0
v 则 p0 = 0 v 则 p =0
8
一质量为0.05kg、速率为 的刚球,以与 例 3.3 一质量为 、速率为10m·s-1的刚球 以与 钢板法线呈45º角的方向撞击在钢板上 角的方向撞击在钢板上,并以相同的速 钢板法线呈 角的方向撞击在钢板上 并以相同的速 设碰撞时间为0.05s.求在此时间内 率和角度弹回来 .设碰撞时间为 设碰撞时间为 求在此时间内 钢板所受到的平均冲力. 钢板所受到的平均冲力 建立如图坐标系, 解 建立如图坐标系 由动量定理得
2
而 v = 2 gx
2
而已落到桌面上的柔绳的重量为: 而已落到桌面上的柔绳的重量为:
M mg = gx L
所以总F为 所以总 为:
2 Mgx Mgx ∑ F = F + mg = L + L = 3mg
4
§3.2 质点系动量定理
质点系: 有相互作用的若干质点组成的系统。 质点系 有相互作用的若干质点组成的系统。 r 质点系内质点之间的相互作用力。 内力 f : 质点系内质点之间的相互作用力。
o
证明: 证明:取如图坐标
时刻已有x长的柔绳 设t时刻已有 长的柔绳 时刻已有 落至桌面,随后的dt时 落至桌面,随后的 时 间内将有质量为ρ 间内将有质量为ρdx
x
1
M 质量为ρ 质量为ρdx 即: dx L
o
的柔绳以dx/dt的速率碰到 的速率碰到 的柔绳以 桌面而停止, 桌面而停止,它的动量变 化率为: 化率为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章例题
例1.袋内装有五个白球,三个黑球。
从中任取两个球,求取出的两个球都是白球的概率。
解:试验的基本事件总数2
35+=C n ,组成所求事件A(取到两个白球)的基本事件数
2
5C m =,因此, 357
.0)(14528
25===
=
C C n
m
A P
例2.一百个产品中有60个一等品,30个二等品,10个废品。
规定一、二等品都为合格品。
从中抽取一个产品,问抽到合格品的概率是多少? 解:设事件A 、B 分别表示产品为一等品和二等品。
则:
10060)(=A P ,10030)(=B P ,10090100
3060)(==
++B A P 。
由此可以得
出结论:
)()()(B P A P B A P +=+
例3.50个产品中有46个合格品与4个废品,从中一次抽取三个,求其中有废品的概率。
解:设事件A 、B 、C 分别表示取到一个、两个、三个废品,则:
2112.0)(196004140350
24614===
∙C C C A P
0141.0)(19600276350
1
4624===
∙C C C B P
0002.0)(196004
350
3
4
===C C C P
2255
.00002.00141.02112.0)()()(=++=++C P B P A P
例4.(教材P116练习题2)某技术小组有12人,他们的性别和职称如下表所示。
现要产生一名幸运者,试求这位幸运者分别是以下几种可能的概率:(1)女性;
P (A )= P (B )= P (AB )= P (A +B )=
例5.设随机事件A 发生的概率为0.5,事件B 发生的概率为0.6,在事件A 发生的条件下B 发生的概率为0.8。
试求:
(1)“A 发生或B 发生”这一随机事件的概率; (2)在B 事件发生的条件下A 发生的概率。
解(1):已知,P(A)=0.5 P(B)=0.6 P(B |A)=0.8
P(A ∪B)=P(A)+P(B)-P(AB)
P(AB)=P(A)ΧP(B|A)=0.5Χ0.8=0.40
P(A ∪B)=P(A)+P(B)-P(AB)=0.5+0.6-0.4=0.7
解(2):∵P(AB)=P(B)P(A|B)
∴P(A|B)=P(AB)/P(B)=0.40/0.6=2/3
例6. 已知某地区男子寿命超过55岁的概率为84%,超过70岁的概率为63%。
试求任一位刚过55岁生日的男子将会活到70岁以上的概率为多少。
解:设A=活到55岁,B=活到70岁。
所求概率为
P(B|A)=P(AB)/P(A)=P(B)/P(A)=63%/84%=0.75=75%
例7.一个具有n=64个观察值的随机样本抽自于均值等于20、标准差等于16的总体。
求下列情况的概率。
(1) ;(2) ;(3) 落在16和22之间。
解:根据题意,n=64 μ=20 σ=16,样本均值服从正态分布。
样本均值的数学期望等于总体均值,即()
20==μx E 。
样本均值的标准差为264
16==
=
n
x σσ
(1)224
64
/162016/-====
=
----n
x x x
x
x
z σμσμ
0227.09773.01)2(1)2()16(=-=Φ-=-Φ=<x P
16<x 23>x x
(2)
5.123
64
/162023/
=====---n
x x x
x
x
z σμσμ 0668
.09332.01)5.1(1)23(1)23(=-=Φ-=≤-=>x P x P (3)
}{
8186
.018413.09773.01)1()2()2()1()12()2216(64
/1620
2264/162016=-+=-Φ+Φ=
-Φ-Φ=<<-=<<=<<--z P z P x P
例8.某厂生产的某种节能灯管的使用寿命服从正态分布,对某批产品测试的结果,平均使用寿命为1050小时,标准差为200小时。
试求:
(1)使用寿命在500小时以下的灯管占多大比例? (2)使用寿命在850~1450小时的灯管占多大比例?
(3)以均值为中心,95%的灯管的使用寿命在什么范围内? 解:设X=“该种节能灯管的使用寿命”,根据题意:X ~N(1050,2
200),因此,
(1)
{}
00298.099702.01)75.2(175.2)500(200
1050
500=-=Φ-=-=<
=<-Z P X P
由此可知该种节能灯管使用寿命在500小时以下的灯管约占0.298%。
(2)8186
.015865.097725.0)1()2()21()()1450850(200
1050
14502001050850=-=-Φ-Φ=≤≤-=
≤≤=≤≤--Z P Z P X P
由此可知该种节能灯管使用寿命在850~1450小时的灯管约占81.86%。
(3)95.0)(=≤K Z P ,由标准正态分布函数值表可知,K=1.96,即有:
{
}
{}95.0392105096.11050=≤-=≤=
-X P Z P X
95%的灯管的使用寿命在均值左右392小时(即658~1442小时)的范围内。
例9:总体的均值为50,标准差为8,现从该总体中随机抽取容量为64的样本,则样本均值和抽样分布的标准差分别是多少?
解:现从某一不知如何分布的总体中抽取容量为64的样本,可以断定该样本均值服从正态分布。
因此,样本均值的数学期望等于总体均值,即:
50)(==μx E
而样本均值抽样分布的标准差为,164
8==
=
n
x σ
σ
例10:某快餐店记录了过去5年每天的营业额,每天营业额的均值为2500元,标准差为400元。
由于在某些节日的营业额偏高,所以每天营业额的分布是右偏的。
假设现从这5年中随机抽取100天,并计算这100天的平均营业额,则样本均值的抽样分布是什么?
解:根据中心极限定理,对于一个抽自任意总体(均值为μ,标准差为σ)样本容量为n 的随机样本。
当n 充分大(n ≥30)时,样本均值 的抽样分布将近似于一个具有均值
和标准差 的正态分布。
因此, 样本均值的数学期望就是总体均值
而,标准差 最后得到样本均值的抽样分布是服从均值为2500元,标准差为40元的正态分布。
x μμ=x n x σσ
=2500==μμx 4010400
100400====n x σσ。
