江西省吉安市凤凰中学2020高二数学 第8讲 点线面之间的位置关系小题训练 新人教A版
副题04 空间点线面的位置关系(理)(解析版)

2020届高考数学23题对对碰【二轮精品】 第一篇副题4 空间点线面的位置关系(理)【副题考法】本副题考题形式为选择题或填空题,以简单几何体与球的切接为载体考查球的几何性质与求得表面积与体积计算,以棱柱、棱锥、棱台或其简单组合体为载体主要考查对线线、线面与面面平行和垂直判定与性质和利用空间向量知识计算异面直线角、线面角、二面等问题,考查空间想象能力、逻辑推理能力、运算求解能力,难度为中等,分值为5分.【主题考前回扣】1. 球的性质:球被一个平面所截, (1)截面是圆;(2)球心与截面圆圆心的连线与截面圆垂;(3)若球心到截面的距离为d ,球的半径为R ,截面圆的半径为r ,则222d r R +=. 2. 线面平行(1)判定:平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行.(2)性质:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行. 3.面面平行(1)判定:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行. (2)性质:①若两个平面平行,则一个平面内一条直线与另一个平面平行.②如果两个平行平面同时和第三个平面相交,那么它们的交线平行.4.线面垂直(1)定义:如果直线l 与平面α内的任意一条直线都垂直,我们就说直线l 与平面α互相垂直.记作:l ⊥α. (2)判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直. (3)性质定理:①垂直于同一个平面的两条直线平行.②若两条平行线中的一条垂直于一个平面,则另一条也垂直于这个平面. 5.面面垂直(1)定义:两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.平面α与平面β垂直,记作αβ⊥.(2)判定定理:一个平面过另一个平面的垂线,则这两个平面垂直.(3)性质定理:两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.6.直线与平面所成的角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角..,叫做这条直线和这个平面所成的角.规定:一条直线垂直于平面,我们说它们所成的角等于90;一条直线和平面平行,或在平面内,我们说它们所成的角等于0.(.2.)直线与平面所成的角..........α.的范围是....π[0,]2. 7二面角(1)二面角的定义:平面内的一条直线把平面分成两部分,这两部分通常称为半平面.从一条直线出发的两个半平面所组成的图形叫做二面角....这条直线叫做二面角的棱,这两个半平面叫做二面角的面. (2)二面角的平面角的定义:在二面角的棱上任取一点,以该点为垂足,在两个半平面内分别作垂直于棱的射线,则这两条射线构成的角叫做这个二面角的平面角.学*科网 (3)二面角的范围:[0,π]8.异面直线所成的角(1)定义:已知b a ,是异面直线,O 是空间任意一点,过O 作b b a a //,//'',则b a '',所成的锐角或直角叫异面直线b a ,所成的角. (2)范围:]2,0(π.【易错点提醒】1.不清楚空间线面平行与垂直关系中的判定定理和性质定理,忽视判定定理和性质定理中的条件,导致判断出错.如由α⊥β,α∩β=l ,m ⊥l ,易误得出m ⊥β的结论,就是因为忽视面面垂直的性质定理中m ⊂α的限制条件.2.空间向量求角时易忽视向量的夹角与所求角之间的关系,如求解二面角时,不能根据几何体判断二面角的范围,忽视向量的方向,误以为两个法向量的夹角就是所求的二面角,导致出错.【副题考向】考向一 球与简单几何体的切接问题【解决法宝】①涉及球与棱柱、棱锥的切、接问题时,一般过球心及多面体中的特殊点(一般为接、切点)或线作截面,把空间问题化归为平面问题,再利用平面几何知识寻找几何体中元素间的关系或只画内切、外接的几何体的直观图,确定球心的位置,弄清球的半径(直径)与该几何体已知量的关系,列方程(组)求解,球内接正棱锥、正棱柱、圆柱、圆锥的球心在高上,球的截面性质是求解此类问题重要工具.②若球面四点P ,A ,B ,C 构成的线段PA ,PB ,PC 两两垂直,且PA =a ,PB =b ,PC =c ,则22224c b a R ++=,把有关元素“补形”为一个球内接长方体(或其他图形),从而显示出球的数量特征,这种方法是一种常用的好方法.例1【2020届江西吉安期末】如图,三棱锥P ABC -的体积为24,又90PBC ABC ∠=∠=︒,3BC =,4AB =,410PB =,且二面角P BC A --为锐角,则该三棱锥的外接球的表面积为( )A .169πB .144πC .185πD .80π【分析】首先根据题中条件可以求出三棱锥各边长,然后证出PA ⊥平面ABC ,则可以找出外接球球心,求出半径,最后利用球体表面积公式求出答案即可.【解析】因90PBC ABC ∠=∠=︒,所以BC ⊥平面PAB ,且PBA ∠为二面角P BC A --的平面角,又3BC =,4AB =,410PB =13PC =,5AC =,因为1sin 8102PAB S PB AB PBA PBA ∆⋅=⋅∠=∠,所以三棱锥的体积1181032433PAB V S BC PBA ∆=⋅=⨯∠⨯=,解得310sin 10PBA ∠=,又PBA ∠为锐角,所以10cos 10PBA ∠=,在PAB ∆中,由余弦定理得210160162441014410PA =+-⨯⨯=,即12PA =,则222PB PA AB =+,故PA AB ⊥,由BC ⊥平面PAB 得BC PA ⊥,故PA ⊥平面ABC ,即PA AC ⊥,取PC 中点O ,在直角PAC ∆和直角PBC ∆中,易得OP OC OA OB ===,故O 为外接球球心,外接圆半径11322R PC ==,故外接球的表面积24169S R ππ==,故选A. 考向二 空间点线面位置关系的判定【解决法宝】解决空间点、线、面位置关系的组合判断题,主要是根据平面的基本性质、空间位置关系的各种情况,以及空间线面垂直、平行关系的判定定理和性质定理进行判断,必要时可以利用正方体、长方体、棱锥等几何模型辅助判断或将笔作直线,书做平面,利用实验进行判断,同时要注意平面几何中的结论不能完全引用到立体几何中.例2 【2020届四川蓉城名校联盟第二次联考】已知,αβ是空间中两个不同的平面,,m n 是空间中两条不同的直线,则下列说法正确的是( ) A .若,m n αβ⊂⊂,且αβ⊥,则 m n ⊥ B .若,m n αα⊂⊂,且//,//m n ββ,则//αβ C .若,//m n αβ⊥,且αβ⊥,则 m n ⊥ D .若,//m n αβ⊥,且//αβ,则m n ⊥【分析】利用线面平行和垂直的判定定理和性质定理,对选项做出判断,举出反例排除. 【解析】对于A ,当,m n αβ⊂⊂,且αβ⊥,则m 与n 的位置关系不定,故错; 对于B ,当//m n 时,不能判定//αβ,故错;对于C ,若,//m n αβ⊥,且αβ⊥,则m 与n 的位置关系不定,故错; 对于D ,由,//m βαα⊥可得m β⊥,又//n β,则m n ⊥故正确. 故选D .考向三 简单几何体中点线面位置关系的判定【解决法宝】对简单几何体中点线面位置关系的判定问题,首先要熟记空间线线、线面、面面平行与垂直的定义、判定与性质,掌握线线、线面、面面平行的相互转化及线线、线面、面面垂直的相互转化,其次认真阅读试题,理清题中的条件和结论,然后利用相关知识和方法,对每个结论认真分析,即可找出正确的结论,例3【2020陕西省汉中3月线上模拟】正方体1111ABCD A B C D -的棱长为2,E ,F ,G 分别为BC ,1CC ,1BB 的中点,则( )A .直线1D D 与直线AF 垂直B .直线1A G 与平面AEF 不平行C .平面AEF 截正方体所得的截面面积为92D .点C 与点G 到平面AEF 的距离相等【分析】根据条件对选项进行逐一分析, A.若有1D D AF ⊥,则能得到1DD ⊥平面AEF ,进一步得到1CC EF ⊥,显然不成立,可判断. B.取11B C 的中点Q ,连接1A Q ,GQ ,可得平面1//A GO 平面AEF ,从而可判断. C.连接1D F ,1D A ,延长1D F ,AE 交于点S ,由条件可得1//EF AD ,截面即为梯形1AEFD ,再计算其面积. D.用等体积法分别求出点C 和点G 到平面AEF 的距离,从而判断.【解析】A.若1D D AF ⊥,又因为1D D AE ⊥且AE AF A ⋂=,所以1DD ⊥平面AEF ,所以1DD EF ⊥,所以1CC EF ⊥,显然不成立,故结论错误; B.如图所示,取11B C 的中点Q ,连接1A Q ,GQ ,由条件可知://GQ EF ,1//A Q AE ,且1GQ AQ Q =,EF AE E =,所以平面1//A GO 平面AEF ,又因为1AG ⊂平面1A GQ ,所以1//AG 平面AEF ,故结论不正确; C.如图所示,连接1D F ,1D A ,延长1D F ,AE 交于点S ,因为E ,F 为1C C ,BC 的中点,所以1//EF AD ,所以A ,E ,F ,1D 四点共面,所以,截面即为梯形1AEFD又因为2214225D S AS ==+=,122AD =,所以()1221222225622AD S S ∆⎛⎫=⨯⨯-= ⎪ ⎪⎝⎭,所以139642AEFD S =⨯=梯形,故结论正确; D.记点C 与点G 到平面AEF 的距离分别为1h ,2h ,因为11111123323C AEF AEF A CEF V S h V --⨯=⋅⋅==⋅⋅=,又因为2112222333G AEF AEF A GEF V S h V --⨯=⋅⋅==⋅⋅=,所以12h h ≠,故结论错误,故选C. 考向四 折叠问题【解决法宝】(1)解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量.一般情况下,折线同一侧线段的长度是不变量,而位置关系往往会发生变化,抓住不变量是解决问题的突破口.(2)在解决问题时,要综合考虑折叠前后的图形,既要分析折叠后的图形,也要分析折叠前的图形 例4 【2020河北邯郸网上检测】在ABC ∆中,AB AC =,120A ∠=,D 为BC 中点,DE AC ⊥,将CDE ∆沿DE 翻折,得到直二面角C DE B --,连接BC ,F 是BC 中点,连接AF ,则下列结论正确的是( )A .AD CD ⊥B .//AF DEC .DE ⊥平面ACED .//AF 平面CDE【分析】设AB AC a ==,在折叠前在ABC ∆中,AB AC a ==,120A ∠=,根据余弦定理可得:3CB a =,结合已知,逐项判断,即可求得答案.【解析】设AB AC a ==,在折叠前在ABC ∆中,AB AC a ==,120A ∠=, 根据余弦定理可得:3CB a =,D 为BC 中点,DE AC ⊥,故32CD DB a ==又Rt CDE ∆中,30C ︒∠=,∴33,44ED a CE a ==,可得14EA a =,在折叠前图形中取BD 中点M ,连接,FM AMAD CB⊥,3DM a=,2aDA=,∴232tan33aADDMADMa∠===,又tan tan603CDE︒∠==,∴AM不平行DE——①对于C,DE AC⊥,将CDE∆沿DE翻折,得到直二面角C DE B--,∴AE DE⊥,CE DE⊥,故ED⊥面CEA,故C正确;对于A,在Rt EDA∆,由222222314416AD ED EA a a a⎛⎫⎛⎫=+=+=⎪ ⎪⎪⎝⎭⎝⎭,在Rt CAE∆,22222231104416CA EA EC a a a⎛⎫⎛⎫=+=+=⎪ ⎪⎝⎭⎝⎭,又222312=16CD a a⎛⎫= ⎪⎪⎝⎭,∴222CD AD CA≠+,故AD不垂直CD,故A错误;对于B,F是BC中点,BD中点M,∴//MF CD,假设//AF DE,可得面//AFM面CDE,进而可得//AM ED,与结论①相矛盾,故假设错误,故B错误.对于D,F是BC中点,BD中点M,∴//MF CD,假设//AF平面CDE,可得面//AFM面CDE,进而可得//AM ED,与结论①相矛盾,故假设错误,故D错误,综上所述,正确的是C,故选C.考向五异面直线所成角的问题【解决法宝】求解两异面直线所成的角时,往往经历“作(平行线)——证(平行)——算(解三角形)”的过程,其中作平行线是关键,一般借助平面几何中中位线,平行四边形、平行线分线段成比例定理推论等知识解决,也可以利用空间向量计算两条异面直线的方向向量的夹角来计算,注意向量夹角与异面直线角的关系.例5 【2019河南南阳一高期末】平面过正方体的顶点A,平面,平面,则直线m与直线BC所成角的正弦值为A.B.C.1 D.【分析】根据题意作出几何体,找到直线,由图像可得即等于直线m与直线BC所成的角,进而可求出结果. 【解析】如图:平面,平面,可知:,是直线m 与直线BC 所成角或所成角的补角,,,,.直线m 与直线BC 所成角的正弦值为,故选B .考向六 线面角问题【解决法宝】在求解线面角时,有两种思路,思路1,几何法,根据线面角的定义,先在图中有没有线面角,若没有,作出线面角,证明是线面角,再通过解三角形解出来;思路2,向量法,求出线面夹角问题中已知直线的方向向量m 和平面法向量n ,设线面角为θ,则直线方向向量m 在平面法向量n 方向上的投影的长度|•|m n |n |与直线方向向量m 的模之|m |比||•|m n |m |n |就是线面夹角的正弦值,即sin θ=||•|m n |m |n |. 例6【2020届西北工业大学附中3月月考】已知在斜三棱柱111ABC A B C -中,点E ,F 分别在侧棱1AA ,1BB 上(与顶点不重合),11AE BFEA FB =,14AA =,ABC 的面积为5,截面1C EF 与截面CEF 将三棱柱111ABC A B C -分成三部分.若中间部分的体积为4,则1AA 与底面所成角的正弦值为( )A .12B .35C .45D 3【分析】由题意可得中间部分的体积为原三棱柱体积的三分之一,得到原三棱柱的体积,设1AA 与底面所成角为α,由棱柱体积公式列式求得sin α的值.【解析】由点E ,F 分别在侧棱1AA ,1BB 上(与顶点不重合),11AE BFEA FB =则//EF AB ,过EF 作平面//EFG 底面ABC ,如图. 则111113C EFG A B CEFG V V --=, 13C EFG ABC EFG V V --=. 所以中间部分的体积1111143E FCC ABC A B C V V --== 所以11112ABC A B C V -=,设三棱柱111ABC A B C -的高为h111512ABC A B C ABC V S h h -=⨯==△,则125h =, 设1AA 与底面所成角为α,则11235sin 45h AA α=== ,故选B考向七 二面角问题【解决法宝】对求二面角l αβ--的大小问题,思路1,几何法,先在几何图形中找一找有没有一个角的顶点在二面角的棱上,两边分别在两个半平面内与棱垂直,若有则该角是二面角的平面角,若没有需要作,用垂线法或垂面法或三垂线法作二面角,然后证明所找(作)的角是二面角的平面角,再通过解三角形求出该角;若坐标系容易建立,也可以用向量法计算二面角的大小,即先求出平面α、β的法向量m 、n ,再求出m 、n 的夹角,在α内取一点A ,在β内取一点B ,设二面角l αβ--大小为θ,若AB •n 与AB•m 同号,则θ=m,n ,若AB •n 与AB •m 异号,则θ=π-m,n ,注意二面角大小与法向量夹角的关系. 例7【2020山西晋城一中期中】已知矩形ABCD 中23AB =2AD =,沿对角线AC 将面ADC 翻折,使得三棱锥D ABC -体积最大时,二面角D BC A --大小的正切值为( ) A .23B .33C .23D .32【分析】依题意可知当平面ADC ⊥平面ABC 时,三棱锥D ABC -的高最大,此时三棱锥D ABC -的体积最大,过点D 作DE AC ⊥交AC 于点E ,过E 作EF BC ⊥交BC 于点F ,连接DF ,由面面垂直的性质可知DE ⊥面ABC ,则EFD ∠为二面角D BC A --的平面角,利用三角形的相关性质求出EF ,DE 即可求出二面角D BC A --大小的正切值.【解析】矩形ABCD ,23AB =,2AD =,将ADC∆沿对角线AC 进行翻折,得到三棱锥D ABC -,则在翻折的过程中,当平面ADC ⊥平面ABC 时,三棱锥D ABC -的高最大,此时三棱锥D ABC -的体积最大,过点D 作DE AC ⊥交AC 于点E ,过E 作EF BC ⊥交BC 于点F ,连接DF , 由面面垂直的性质可知DE ⊥面ABC ,则EFD ∠为二面角D BC A --的平面角, 23AB =,2AD =,224AC AB AD ∴=+=,AD DC DE AC ⋅=⋅,3DE ∴=,1AD =,3CE =, ABC EFC ∆∆∽,CE EF CA AB ∴=,33EF ∴=, 32tan 333DE EFD EF ∴∠===,故选C【副题集训】1.【2020福建省3月考】已知不同直线l 、m 与不同平面α、β,且l α⊂,m β⊂,则下列说法中正确的是( ) A .若//αβ,则l//m B .若αβ⊥,则l m ⊥ C .若l β⊥,则αβ⊥ D .若αβ⊥,则m α⊥【答案】C【解析】对于A ,若//αβ,则,l m 可能为平行或异面直线,A 错误; 对于B ,若αβ⊥,则,l m 可能为平行、相交或异面直线,B 错误;对于C ,若l β⊥,且l α⊂,由面面垂直的判定定理可知αβ⊥,C 正确; 对于D ,若αβ⊥,只有当m 垂直于,αβ的交线时才有m α⊥,D 错误,故选C .2.【2020湖南株洲一中期中】已知正四棱锥S ABCD -的侧棱长与底面边长都相等,E 是SB 的中点,则AE SD ,所成的角的余弦值为( )A .13B .23C .3 D .23【答案】C【解析】设AC BD 、的交点为O ,连接EO ,则AEO ∠为,AE SD 所成的角或其补角;设正四棱锥的棱长为a ,则312,,2AE a EO a OA a ===,所以222cos 2AE OA EO AEO AE OA +-∠=⋅ 222312()()()3222312()()a a a a a +-==⨯⋅,故选C . 3. 【2020河北省衡水中学六调】如图,已知四棱锥P ABCD -的底面是平行四边形,AC 交BD 于点, O E 为AD 的中点,点F 在PA 上,AP AF λ=,//PC 平面BEF ,则λ的值为( )A .1B .32C .2D .3【答案】D【解析】如下图所示,设AO 交于BE 于点G ,连接FG ,E 为AD 的中点,则1122AE AD BC ==⋅,四边形ABCD 是平行四边形,//AD BC ,AEG △∽CBG ,12AG AE GC BC =∴=,13AG AC ∴=,又//PC 平面BEF ,PC ⊂平面PAC ,平面 BEF ⋂平面PAC GF =.//GF PC ∴,3AP ACAF AGλ∴===,故选D .4.【2020重庆八中3月月考】如图,四棱柱ABCD ﹣A 1B 1C 1D 1中,ABCD 为平行四边形,E ,F 分别在线段DB ,DD 1上,且112DE DF EB FD ==,G 在CC 1上且平面AEF ∥平面BD 1G ,则1CGCC =( )A .12B .13C .23D .14【答案】 B【解析】∵四棱柱ABCD ﹣A 1B 1C 1D 1中,ABCD 为平行四边形,E ,F 分别在线段DB ,DD 1上,且112DE DF EB FD ==,∴EF ∥BD 1,平面ADD 1A 1∥平面BCC 1B 1,∵G 在CC 1上且平面AEF ∥平面BD 1G ,∴AF ∥BG ,∴1113CG DE CC DD ==,故选B . 5.【2019届广东省汕头市一模】在正方体中,点是四边形的中心,关于直线,下列说法正确的是( ) A . B .平面 C .D .平面【答案】B【解析】由题意,在正方体中,点是四边形的中心,所以,因为,所以平面平面,因为平面,所以平面,故选B.6.【2020江西宜春昌黎实验学校月考】在正四棱锥S ABCD -中,E ,M ,N 分别是BC ,CD ,SC 的中点.动点P 在线段MN 上运动时,下列四个结论,不一定成立的为( )①EP ⊥AC ;②EP BD ∥;③EP ∥平面SBD ;④EP ⊥平面SAC . A .①③ B .③④C .①②D .②④【答案】D【解析】作出如图的辅助线,对①,再正四棱锥S ABCD -中,因为AC BD ⊥, AC SO ⊥, BD ⊂面SBD ,SO ⊂面SBD ,且SO BD O ⋂=,故AC ⊥面SBD .又因为E ,M ,N 分别是BC ,CD ,SC 的中点,故面//EMN 面SBD ,故AC ⊥面EMN ,因为EP ⊂面EMN ,故EP ⊥AC 成立.故①成立. 对②,当且仅当P 与M 重合时, EP BD ∥.故②不一定成立.对③,由①有面//EMN 面SBD ,又EP ⊂面EMN ,故EP ∥平面SBD .故③成立. 对④, 当且仅当P 与M 重合时, 才有EP ⊥平面SAC .故④不一定成立,故选D7. 【2020广西桂林一中期末】已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 上的射影为BC 的中点,则异面直线AB 与1CC 所成的角的余弦值为( ) A 3B .34C.5D.54【答案】B【解析】如图,设BC的中点为D,连接1A D、AD、1A B,易知1A AB∠即为异面直线AB与1CC所成的角(或其补角),设三棱柱111ABC A B C-的侧棱与底面边长均为1,则3AD=,112A D=,12A B=,由余弦定理,得222111111132cos22114A A AB A BA ABA A AB+-+-∠===⋅⨯⨯,故选B.8.【2020届西北工业大学附中第三次适应性考】如图,在三棱柱111ABC A B C-中,侧棱1AA⊥底面111A B C,底面ABC是正三角形E是BC的中点,则下列叙述正确的是()A.1CC与1B E是异面直线B.AC⊥平面11ABB AC.11AE B C⊥D.11//A C平面1AB E【答案】C【解析】对于A选项,由于11,CC B E都含于平面11BCC B,所以不是异面直线,故A选项错误.对于B选项,由于3CABπ∠=,所以AC与平面11ABB A不会垂直,故B选项错误.对于C选项,在等边三角形ABC中,AE BC⊥,根据直三棱柱中易得1AE AA⊥,所以AE⊥平面11BCC B,所以11AE B C ⊥,所以C 选项正确.对于D 选项,由于11//A C AC ,而AC 与平面1AB E 相交,所以直线11A C 与平面1AB E 不平行,故D 选项错误,故选C9.【2020届浙江省温州新力量联盟期末】正四面体ABCD 中,CD 在平面α内,点E 是线段AC 的中点,在该四面体绕CD 旋转的过程中,直线BE 与平面α所成角的余弦值不可能是( )A .16B .36C .13D .1【答案】A【解析】考虑相对运动,让四面体ABCD 保持静止,平面α绕着CD 旋转,∴其垂线也绕着CD 旋转,如右图,取AD 中点F ,连结EF ,则//EF CD ,等价于平面α绕着EF 旋转,设正四面体ABCD 中棱长为2,在BEF ∆中,3BE BF ==,1EF =,3133cos 6231BEF +-∠==⨯⨯,如下图示,将问题抽象为如下几何模型,平面α的垂线可视为圆锥的底面半径EP ,绕着圆锥的轴EF 旋转,显然22BEF PEB BEF ππ-∠≤∠≤+∠,则3sin 16PEB ≤∠≤,设BE 与平面α所成的角为θ,则可得3cos 1θ≤≤,故选A10.【2020福建省闽侯六中期末】在菱形ABCD 中, 60,3A AB ∠=︒=,将ABD ∆折起到PBD ∆的位置,若三棱锥P BCD -的外接球的体积为776π,则二面角P BD C --的正弦值为( )A.13 B. 12 C. 3 D. 7 【答案】C【解析】设菱形对角线交点为O ,则POC ∠为二面角P BD C --的平面角,设外接球1O 半径为R ,则347773R R ππ=∴=,所以2211971+-1441cos =32212O O R OB O OC =-=∴∠=⨯⨯, 123,sin 332O OC POC POC ππ∴∠=∴∠=∠=,选C 11.【2019届西安市一质检】已知,,在球的球面上,,,,直线与截面所成的角为,则球的表面积为( ) A .B .C .D .【答案】D 【解析】在中,由余弦定理得到求得,由勾股定理得为直角,∴中点即所在小圆的圆心, ∴平面,且小圆半径为1,又直线与截面所成的角为,∴在直角三角形中,球的半径为,∴球的表面积为,故选D.12.【20200湖北黄冈中学一诊】如图,在三棱锥P ABC -中,已知底面ABC 是正三角形,2AB AP =,且AP ⊥平面PBC ,则直线PA 与平面ABC 所成角的余弦值为( )A .6 B .5 C .23D .3 【答案】D【解析】三棱锥P ABC -中,已知底面ABC 是正三角形,2AB AP =,且AP ⊥平面PBC ,取BC 中点M ,连接,PM AM ,如下图所示,设2,AB =则1AP =,3PB PC ==,2,3PM AM ==,因为222PM A M P A +=,所以三角形APM 为直角三角形,且AP PM ⊥,则PAM ∠即为直线PA 与平面ABC 所成的角,所以3cos 33PA PAM PM ∠===,故选D.13.【2019届广东省广州市天河区综合测试(二)】如图是一几何体的平面展开图,其中四边形ABCD 为矩形,E ,F 分别为P A ,PD 的中点,在此几何体中,给出下面4个结论:直线BE 与直线CF 异面;直线BE 与直线AF 异面;直线平面PBC ;平面平面P AD .其中正确的结论个数为A .4个B .3个C .2个D .1个 【答案】C【解析】将平面展开图还原后可得立体图形如图所示:①为中点,又四边形为矩形 , 四点共面,直线与共面,不是异面直线,即①错误 ②平面,平面,,平面,直线与直线为异面直线,即②正确③,平面,平面,平面,即③正确④假设平面平面,即平面平面,又平面平面,作,垂足为,可得平面,但实际无法证得平面,故假设不成立,即④错误,故选14.【2020届浙江省高中发展共同体期末】如图,在三棱台111ABC A B C -中,M 是棱11A C 上的点,记直线AM 与直线BC 所成的角为α,直线AM 与平面ABC 所成的角为β,二面角M AC B --的平面角为γ,则( )A .αβ≥,≤βγB .αβ≤,≤βγC .αβ≥,βγ≥D .αβ≤,βγ≥【答案】A 【解析】在三棱台111ABC A B C -中,M 是棱11A C 上的点,记直线AM 与直线BC 所成的角为α,直线AM 与平面ABC 所成的角为β,二面角M AC B --的平面角为γ,由于β是直线AM 与平面ABC 内所有直线所成角中最小的角,故αβ≥,排除B 、D 选项;若2πγ≥,由于02πβ<≤,则≤βγ,排除C选项,故选A.15.【2019届江西省红色七校二联考】如图,单位正方体的对角面上存在一动点,过点作垂直于平面的直线,与正方体表面相交于两点.则的面积最大值为 ( )A .B .C .D .【答案】A 【解析】连接,则当M,N 在正方体侧面上(非棱上)运动时,分别过M ,N 作M ⊥面,N ⊥面,则MN=,此时面积小于的面积,故当MN 在面上时,面积最大,当M ∈,设则MN=BM=MN=为等腰三角形,底边MN 上的高为,的面积为≤,当x=1时取等;同理当M ∈, 设, 则MN=BM=MN=为等腰三角形,底边MN上的高为,的面积为,令f(x)==4x()≥0,故f(x)单调递增,当x=1 取最大值为,故选:A16.【2020年云南省师范大学附属中学期中】四边形ABDC 是菱形,60BAC ∠=,3AB =沿对角线BC 翻折后,二面角A BC D --的余弦值为13-,则三棱锥D ABC -的外接球的体积为( ) A 5π B 6πC 7πD .22π【答案】B【解析】如下图所示,取BC 的中点为M ,设球心O 在平面ABC 内的射影为1O ,在平面BCD 内的射影为2O ,则二面角A BC D --的平面角为AMD ∠,3AB =32DM =,2213DO DM ==,212O M =,设2AMD θ∠=,则21cos 22cos 13θθ=-=-,21cos 3θ∴=,则22sin 3θ=,2tan 2θ∴=,tan 2θ∴=222tan OO O M θ∴=⋅=O 的半径22226R DO OO =+=,所求外接球的体积为246632V ππ⎛⎫=⋅= ⎪ ⎪⎝⎭,故选B.17.【2020届河南平顶山许昌济源第一次质检】在直角梯形ABCD 中,//AB CD ,AD CD ⊥,1AB AD ==,2CD =.沿BD 将ABCD 折成60︒ 的二面角A BD C --,则折后直线AC 与平面BCD 所成角的正弦值为( ) A .24B 3C 6D .14【答案】B【解析】由题意,取CD 的中点E ,连接,AE BD 交于点O ,在图(1)中,正方形ABCD ,则AC BD ⊥,即在图(2)中,,AO BD EO BD ⊥⊥,所以AOE ∠为二面角A BD C --的平面角,即60AOE =︒∠,又在AOE ∆中,2260AO EO AOE ==∠=︒,所以AOE ∆等边三角形,取EO 的中点F ,则AF EO ⊥,且2362AF ==,由面面垂直的性质定理,可得AF ⊥平面BCD ,所以ACF ∠为AC 与平面BCD 所成的角,设ACF θ∠=,在CEF ∆中,21,1354EF CE CEF ==∠=,由余弦定理可得22222222132cos135()121(8CF EF CE EF CE =+-=+-⨯=,解得26CF =,所以39tan 13AF CF θ==,所以13cos 4θ=,故选B .18.【2020广西北海一中二模】在等腰三角形中,,,将它沿边上的高翻折,使为正三角形,则四面体的外接球的表面积为__________.【答案】【解析】翻折后所得的四面体ABCD的直观图如图所示,易知AD⊥平面BCD,AD=,BD=BC=CD=3,设△BCD的重心为G,则DG=.则外接球的半径,从而外接球的表面积为.19.【2019届广东省模拟(一)】已知在三棱锥P﹣ABC中,PA=4,AC=,PB=BC=,PA⊥平面PBC,则三棱锥P﹣ABC的内切球的表面积为__________.【答案】【解析】由题意,已知PA⊥面PBC,且PA=4,PB=,AC=,由勾股定理得AB=,PC=,所以,△PBC为等边三角形,△ABC为等腰三角形,==S△PBC×PA=×××4=,表面积,设内切球半径为r,利用体积相等,即,所以=×,所以r=,所以三棱锥P﹣ABC的内切球的表面积为4π×= .20.【2020陕西、湖北、山西部分学校3月联考】在长方体1111ABCD A B C D -中,13,4AD AA AB ===,则异面直线1A B 与AC 所成角的余弦值为________.【答案】225【解析】如图,连接1CD ,1AD ,则1//A B CD ,所以1ACD ∠为异面直线1A B 与AC 所成角,由题意可得15AC AD ==,1142A B CD ==,则2221111cos 2AC CD AD ACD AC CD +-∠=⋅2542=⨯⨯225=.21.【2020届浙江省杭州学军中学3月月】在长方体1111ABCD A B C D -中,4AB BC ==,11AA =,E 是底面ABCD 的中心,又AF AB λ=(102λ≤≤),则当λ=____时,长方体过点1A ,E ,F 的截面面积的最小值为____. 【答案】110 551255【解析】如图所示,延长EF 交CD 于M ,由已知,有22AE =EF a =,(02)AF t t =≤≤, 在AEF ∆中,由余弦定理得2222cos EF AF AE AE AF EAF =+-⋅∠,即2284a t t =+-, 作AG 垂直于EF 于G ,T 为AB 中点,则AGF ∆与EFT ∆相似,且1A G EF ⊥,所以AG ET AF EF =,即2AG t a =,所以2t AG a =,故过点1A ,E ,F 的截面面积 21221()t S FM A G a a =⨯=+2222236454825(55a t t t t =+=-+=-+) 当25t =,即215410AE AB λ===时,min 36555S ==.22.【2019届安徽省合肥市二质检】已知半径为4的球面上有两点,,,球心为,若球面上的动点满足二面角的大小为,则四面体的外接球的半径为_______.【答案】【解析】设所在截面圆的圆心为,中点为,连接,OA =OB ,所以,OD ⊥AB ,同理O 1D ⊥AB ,所以,即为二面角的平面角,,因为,所以是等腰直角三角形,,在中,由cos60º=,得,由勾股定理,得:,因为O 1到A 、B 、C 三的距离相等,所以,四面体外接球的球心在直线上,设四面体外接球半径为,在中,,由勾股定理可得:,即,解得.23.【2020届四川蓉城名校联盟第二次联考】在四面体ABCD 中,41,34,5,,AB CD AC BD AD BC E F ======分别是,AD BC 的中点.则下述结论:①四面体ABCD 的体积为20; ②异面直线,AC BD 所成角的正弦值为2425; ③四面体ABCD 外接球的表面积为50π;④若用一个与直线EF 垂直,且与四面体的每个面都相交的平面α去截该四面体,由此得到一个多边形截面,则该多边形截面面积最大值为6.其中正确的有_____.(填写所有正确结论的编号) 【答案】①③④.【解析】根据四面体特征,可以补图成长方体设其边长为,,a b c ,222222413425c b c a b a ⎧+=⎪+=⎨⎪+=⎩,解得3,4,5a b c ===补成长,宽,高分别为3,4,5的长方体,在长方体中:①四面体ABCD 的体积为134********V ⨯⨯-⨯⨯⨯⨯==,故正确②异面直线,AC BD 所成角的正弦值等价于边长为5,3的矩形的对角线夹角正弦值,可得正弦值为1517,故错;③四面体ABCD 外接球就是长方体的外接球,半径2223455022R ++==,其表面积为50π,故正确; ④由于EF α⊥,故截面为平行四边形MNKL ,可得5KL KN +=,设异面直线BC 与AD 所成的角为θ,则sin sin HFB sin LKN θ∠∠==,算得2425sin θ=, 224••6225MNKL KL KN S NK KL sin NKL +⎛⎫∴∠≤⨯= ⎪⎝⎭=.故正确. 故答案为:①③④.。
高中数学 第二章 点、直线、平面之间的位置关系 2.2.3 直线与平面平行的性质练习(含解析)新人教

高中数学第二章点、直线、平面之间的位置关系2.2.3 直线与平面平行的性质练习(含解析)新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学第二章点、直线、平面之间的位置关系2.2.3 直线与平面平行的性质练习(含解析)新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学第二章点、直线、平面之间的位置关系2.2.3 直线与平面平行的性质练习(含解析)新人教A版必修2的全部内容。
直线与平面平行的性质班级:姓名:_____________1.过平面α外的直线l,作一组平面与α相交,如果所得的交线为a,b,c,…,则这些交线的位置关系为( )A.都平行B.都相交且一定交于同一点C.都相交但不一定交于同一点D。
都平行或都交于同一点【解析】选D。
当l与α相交时,设交点为A,则过l的平面与α的交线a,b,c,…都过点A,当l∥α时,由线面平行的性质得l∥a∥b∥c∥….2.已知m,n为两条不同的直线,α,β为两个不同的平面,则下列结论中正确的是( )A。
m∥α,m∥n⇒n∥αB.m∥α,n∥α⇒m∥nC.m∥α,m⊂β,α∩β=n⇒m∥nD.m∥α,n⊂α⇒m∥n【解析】选C。
A中,n还有可能在平面α内;B中m,n可能相交、平行、异面;由线面平行的性质定理可得C正确。
D中m,n可能异面.3.已知m∥n,m∥α,过m的平面β与α相交于a,则n与a的位置关系是()A.平行B。
相交 C.异面D。
以上均有可能【解析】选A。
因为m∥α,m⊂β,α∩β=a,所以m∥a,又m∥n,所以n∥a.4.如图,四棱锥P—ABCD中,M,N分别为AC,PC上的点,且MN∥平面PAD,则()A。
江西省吉安市凤凰中学2020高二数学 第8讲 点线面之间的位置关系小题训练 新人教A版
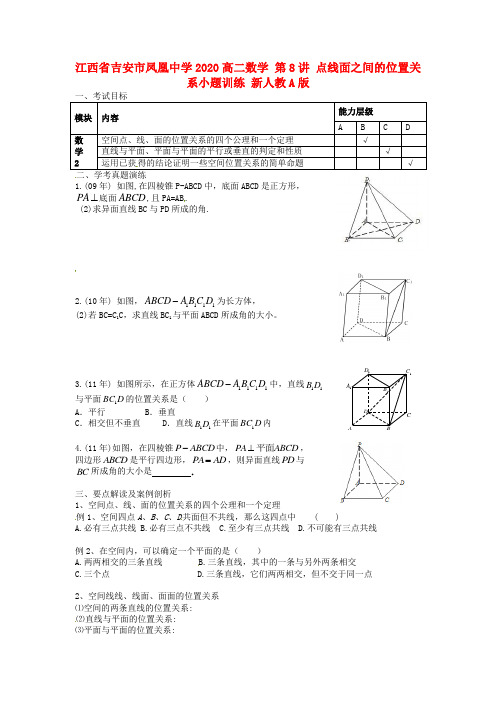
江西省吉安市凤凰中学2020高二数学 第8讲 点线面之间的位置关系小题训练 新人教A 版一、考试目标 模块 内容能力层级 A B C D 数学 2 空间点、线、面的位置关系的四个公理和一个定理 √ 直线与平面、平面与平面的平行或垂直的判定和性质 √ 运用已获得的结论证明一些空间位置关系的简单命题√二、学考真题演练1.(09年) 如图,在四棱锥P-ABCD 中,底面ABCD 是正方形, PA ⊥底面ABCD ,且PA=AB.(2)求异面直线BC 与PD 所成的角.2.(10年) 如图,1111ABCD A B C D -为长方体, (2)若BC=C 1C ,求直线BC 1与平面ABCD 所成角的大小。
3.(11年) 如图所示,在正方体1111ABCD A B C D -中,直线11B D与平面1BC D 的位置关系是( )A .平行B .垂直C .相交但不垂直D .直线11B D 在平面1BC D 内4.(11年)如图,在四棱锥P ABCD -中,PA ABCD ⊥平面, 四边形ABCD 是平行四边形,PA AD =,则异面直线PD 与 BC 所成角的大小是 .三、要点解读及案例剖析1、空间点、线、面的位置关系的四个公理和一个定理例1、空间四点A 、B 、C 、D 共面但不共线,那么这四点中 ( )A.必有三点共线B.必有三点不共线C.至少有三点共线D.不可能有三点共线例2、在空间内,可以确定一个平面的是( ) A.两两相交的三条直线 B.三条直线,其中的一条与另外两条相交 C.三个点 D.三条直线,它们两两相交,但不交于同一点2、空间线线、线面、面面的位置关系 ⑴空间的两条直线的位置关系: ⑵直线与平面的位置关系: ⑶平面与平面的位置关系:A BCD 1A 1B 1C 1D例3、在正方体1111ABCD A B C D -中,E F G H 、、、分别为1111AA AB BB B C 、、、的中点,则异面直线EF 与GH 所成的角为( )A 、︒45 B.︒60 C.︒90 D.︒120例4.(12年) 如图,在四棱柱1111ABCD A B C D -中,D 1D ⊥底面ABCD ,底面ABCD 是正方形,且AB=1,D 1D=2. (1)求直线D 1B 与平面ABCD 所成角的大小;四、达标练习1、下列四个命题中,正确命题的序号为________________ ①A 、B 是空间中两点,,,,A l A B l B αα∈∈∈∈,则α⊂l ;②A 、B 是空间中两点,α与β不重合,若βαβα∈∈∈∈B B A A ,,,,则AB =βαI ; ③两平面可以仅有一个公共点;④A,B,C 都在α内,A,B,C 都在β内,且A,B,C 不共线,则α与β重合。
高二数学点线面的位置关系试题

高二数学点线面的位置关系试题1.已知三个互不重合的平面且,给出下列命题:①则②则③若则④若则其中正确命题的个数为().A.1B.2C.3D.4【答案】C【解析】①如图三棱锥中,底面是正三角形,侧棱,所以①错误;②,,,即;④,,又,;③由④得一定相交,又且,;又,;故选C.【考点】直线与平面的平行与垂直的判定.2.如图所示,正三棱锥中,分别是的中点,为上任意一点,则直线与所成的角的大小是 ( )A.B.C.D.随点的变化而变化.【答案】B【解析】连接,因为为正三棱锥,所以,则有,所以,即直线与所成的角的大小是.【考点】(1)线面垂直的判定与性质应用;(2)线线角.3.如图,在中,,斜边.可以通过以直线为轴旋转得到,且二面角是直二面角.动点在斜边上.(1)求证:平面平面;(2)求与平面所成角的最大角的正切值.【答案】(1)见解析(2)【解析】(1)利用二面角的定义、线面与面面垂直的判定与性质即可得出;(2)利用线面角的定义及其含30°角的直角三角形的边角关系即可得出.试题解析:(1)证明:由题意,,∴是二面角的平面角,又二面角是直二面角,,又∵平面平面(2)解:由(1)知,,∴∠CDO是CD与平面AOB所成的角,且,当OD最小时,∠CDO最大,这时,OD⊥AB,垂足为D,,,CD与平面AOB所成的角最大时的正切值为.【考点】二面角的定义、线面与面面垂直的判定与性质、线面角的定义4.类比平面内“垂直于同一条直线的两条直线互相平行”的性质,可推出空间下列结论:①垂直于同一条直线的两条直线互相平行②垂直于同一个平面的两条直线互相平行③垂直于同一条直线的两个平面互相平行④垂直于同一个平面的两个平面互相平行,则正确的结论是( )A.①②B.②③C.③④D.①④【答案】B【解析】命题①不正确,垂直于同一条直线的两条直线可能相交或异面,在长方体中即可找到不平行的情形;对于命题②正确,符合线面垂直的性质定理;命题③正确,符合面面平行的判定定理;命题④不正确,垂直于同一个平面的两个平面还可能相交,比如课本打开立在桌面上,也可结合长方体和身边的事物来判断;故选B.【考点】1.空间中的平行关系;2.空间中的垂直关系.5.将边长为1的正方形ABCD延对角形AC折起,使平面平面,在折起后形成的三棱锥D-ABC中,给出下列三个命题:①面是等边三角形;②③三棱锥D-ABC的体积为其中正确命题的序号是_________(写出所有正确命题的序号)【答案】①②【解析】设正方形的边长为,取线段的中点,连接,则有,所以面,又面,从而,②正确,又平面平面,所以,且,所以,①正确,又=,③错误.【考点】1、面面垂直的性质;2、线面垂直的性质;3、几何体的体积.6.对两条不相交的空间直线a与b, 必存在平面a, 使得( )A. aÌa, bÌa B.aÌa, b//a C. a^a, b^a D.aÌa, b^a【答案】B【解析】当两条不相交的空间直线a与b异面时,A、C错;对D,仅当直线a与b异面垂直时成立,故不对;对B,当直线a与b平行时显然存在无数平面a使aÌa, b//a,当直线a与b异面时,将直线b平移到与a相交,确定的平面a使aÌa, b//a成立,故选B.【考点】1.直线与平面的位置关系;2.异面直线7.在棱长为的正方体中,错误的是()A.直线和直线所成角的大小为B.直线平面C.二面角的大小是D.直线到平面的距离为【答案】D【解析】根据题意,由于对于A.直线和直线所成角的大小为,利用平移法可知成立,对于B.由于,则可知直线平面成立。
高二数学点线面的位置关系试题

高二数学点线面的位置关系试题1.以下命题(其中a,b表示直线,a表示平面)①若a∥b,bÌa,则a∥a②若a∥a,b∥a,则a∥b③若a∥b,b∥a,则a∥a④若a∥a,bÌa,则a∥b其中正确命题的个数是 .【解析】①若a∥b,bÌa,可能a∥a或;②若a∥a,b∥a,则a与b平行,相交或异面③若a∥b,b∥a,则a∥a或。
④若a∥a,bÌa,则a∥b或a与b相交.【考点】直线与平面平行的判定及直线与平面平行的性质.2.如图,在正方体中,点为线段的中点。
设点在线段上,直线与平面所成的角为,则的取值范围是。
【答案】[,1]【解析】连结A1O,OP和PA1,不难知∠POA1就是直线OP与平面A1BD所成的角或其补角设正方体棱长为2,则AO=,A1O=,(1)当P点与C点重合时,PO=,A1P=2,且cosα=,此时α=∠A1OP为钝角,sinα=(2)当P点与C1点重合时,PO=A1O=,A1P=2,且cosα=,此时α=∠A1OP为锐角,sinα=(3)在从钝角逐渐变化到锐角的过程中,CC1上一定存在一点P,使得α=∠A1OP=90°,此时sinα=1由于<,综上,sinα的取值范围是[,1].【考点】直线与平面所成的角,空间想象能力3.二面角为60°,A、B是棱上的两点,AC、BD分别在半平面内,,,且AB=AC=,BD=,则CD的长为()A. B. C. D.【答案】A【解析】根据异面直线上两点间的距离公式,对于本题中,,,,,故.【考点】异面直线上两点间距离,空间想象能力.4.若正三棱柱的棱长均相等,则与侧面所成角的正切值为___.【答案】【解析】设棱长为1.取中点,连接,根据正三棱柱的特点,,根据线面角的定义可知,为与侧面所成角,在中,.【考点】线面角的定义.5.如图,AB是圆的直径,PA垂直圆所在的平面,C是圆周上的一点.(1)求证:平面PAC⊥平面PBC;(6分)(2)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.(6分)【答案】(1)答案见详解;(2)【解析】(1)通过线面垂直即BC⊥平面PAC,可得平面PAC⊥平面PBC;(2)建立空间坐标系,求出两平面的法向量求解或利用线面垂直性质,做出二面角平面角,再求解.试题解析:(1)证明由AB是圆的直径,得AC⊥BC,由PA⊥平面ABC,BC⊂平面ABC,得PA⊥BC.又PA∩AC=A,PA⊂平面PAC,AC⊂平面PAC,所以BC⊥平面PAC.因为BC⊂平面PBC,所以平面PBC⊥平面PAC.(5分)(2)解方法一过C作CM∥AP,则CM⊥平面ABC.如图,以点C为坐标原点,分别以直线CB、CA、CM为x轴,y轴,z轴建立空间直角坐标系.因为AB=2,AC=1,所以BC=.因为PA=1,所以A(0,1,0),B(,0,0),P(0,1,1).故C=(,0,0),C=(0,1,1).设平面BCP的法向量为n1=(x,y,z),则所以不妨令y=1,则n1=(0,1,-1).因为A=(0,0,1),A=(,-1,0),设平面ABP的法向量为n2=(x,y,z),则所以不妨令x=1,则n2=(1,,0).于是cos〈n1,n2〉==.所以由题意可知二面角C-PB-A的余弦值为.(10分)方法二过C作CM⊥AB于M,因为PA⊥平面ABC,CM⊂平面ABC,所以PA⊥CM,又PA∩AB=A,故CM⊥平面PAB.过M作MN⊥PB于N,连接NC,由三垂线定理得CN⊥PB,所以∠CNM为二面角C-PB-A的平面角.在Rt△ABC中,由AB=2,AC=1,得BC=,CM=,BM=,在R t△PAB中,由AB=2,PA=1,得PB=.因为Rt△BNM∽Rt△BAP,所以=,故MN=.又在Rt△CNM中,CN=,故cos∠CNM=. 所以二面角C-PB-A的余弦值为.(10分)【考点】1、面面垂直;2、二面角.6.已知三棱锥S-ABC,G1,G2分别为△SAB,△SAC的重心,则G1G2与△SBC,△ABC所在平面的位置关系是 ( )A.垂直和平行B.均为平行C.均为垂直D.不确定【答案】B【解析】根据题意,由于三棱锥S-ABC,G1,G2分别为△SAB,△SAC的重心,则G1G2与△SBC,△ABC所在平面的位置关系是,利用中位线性质定理,可知线线平行,得到线面平行,选B.【考点】线面平行点评:主要是考查了线面平行的判定,属于基础题。
2必修二-点线面之间的位置关系测试题-含答案-1130

第二章点、直线、平面之间的位置关系一、选择题1.设α,β为两个不同的平面,l,m为两条不同的直线,且l⊂α,m⊂β,有如下的两个命题:①若 α∥β,则l∥m;②若l⊥m,则 α⊥β.那么().A.①是真命题,②是假命题B.①是假命题,②是真命题C.①②都是真命题D.①②都是假命题2.如图,ABCD-A1B1C1D1为正方体,下面结论错误..的是().A.BD∥平面CB1D1B.AC1⊥BDC.AC1⊥平面CB1D1(第2题)D.异面直线AD与CB1角为60°3.关于直线m,n与平面 α,β,有下列四个命题:①m∥α,n∥β 且 α∥β,则m∥n;②m⊥α,n⊥β 且 α⊥β,则m⊥n;③m⊥α,n∥β 且 α∥β,则m⊥n;④m∥α,n⊥β 且 α⊥β,则m∥n.其中真命题的序号是().A.①②B.③④C.①④D.②③4.给出下列四个命题:①垂直于同一直线的两条直线互相平行②垂直于同一平面的两个平面互相平行③若直线l1,l2与同一平面所成的角相等,则l1,l2互相平行④若直线l1,l2是异面直线,则与l1,l2都相交的两条直线是异面直线其中假.命题的个数是().A.1 B.2 C.3 D.45.下列命题中正确的个数是().①若直线l上有无数个点不在平面 α 内,则l∥α②若直线l与平面 α 平行,则l与平面 α 内的任意一条直线都平行③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行④若直线l与平面 α 平行,则l与平面 α 内的任意一条直线都没有公共点A.0个B.1个C.2个D.3个6.两直线l1与l2异面,过l1作平面与l2平行,这样的平面().A.不存在B.有唯一的一个C.有无数个D.只有两个7.把正方形ABCD沿对角线AC折起,当以A,B,C,D四点为顶点的三棱锥体积最大时,直线BD和平面ABC所成的角的大小为().A.90°B.60°C.45°D.30°8.下列说法中不正确的....是().A.空间中,一组对边平行且相等的四边形一定是平行四边形B.同一平面的两条垂线一定共面C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线在同一个平面内D.过一条直线有且只有一个平面与已知平面垂直9.给出以下四个命题:①如果一条直线和一个平面平行,经过这条直线的一个平面和这个平面相交,那么这条直线和交线平行②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面③如果两条直线都平行于一个平面,那么这两条直线互相平行④如果一个平面经过另一个平面的一条垂线,那么些两个平面互相垂直其中真命题的个数是().A.4 B.3 C. 2 D.110.异面直线a,b所成的角60°,直线a⊥c,则直线b与c所成的角的范围为().A.[30°,90°]B.[60°,90°]C.[30°,60°] D.[30°,120°]二、填空题11.已知三棱锥P-ABC的三条侧棱PA,PB,PC两两相互垂直,且三个侧面的面积分别为S1,S2,S3,则这个三棱锥的体积为.12.P是△ABC所在平面 α 外一点,过P作PO⊥平面 α,垂足是O,连PA,PB,PC.(1)若PA=PB=PC,则O为△ABC的心;(2)PA⊥PB,PA⊥PC,PC⊥PB,则O是△ABC的心;(3)若点P到三边AB,BC,CA的距离相等,则O是△ABC的心;(4)若PA=PB=PC,∠C=90º,则O是AB边的点;(5)若PA=PB=PC,AB=AC,则点O在△ABC的线上.13.如图,在正三角形ABC中,D,E,F分别为各J边的中点,G,H,I,J分别为AF,AD,BE,DE的中点,将△ABC沿DE,EF,DF折成三棱锥以后,GH与IJ所成角的度数为.14.直线l与平面α 所成角为30°,l∩α=A,直线m∈α,则m与l所成角的取值范围是.15.棱长为1的正四面体内有一点P,由点P向各面引垂线,垂线段长度分别为d1,d2,d3,d4,则d1+d2+d3+d4的值为.16.直二面角 α-l-β 的棱上有一点A,在平面 α,β 内各有一条射线AB,AC与l成45°,AB⊂α,AC⊂β,则∠BAC=.三、解答题17.在四面体ABCD中,△ABC与△DBC都是边长为4的正三角形.(1)求证:BC⊥AD;(2)若点D到平面ABC的距离等于3,求二面角A-BC-D的正弦值;(第17题) (3)设二面角A-BC-D的大小为θ,猜想θ 为何值时,四面体A-BCD的体积最大.(不要求证明)18.如图,在长方体ABCD—A1B1C1D1中,AB=2,BB1=BC=1,E为D1C1的中点,连结ED,EC,EB和DB.(1)求证:平面EDB ⊥平面EBC ;(2)求二面角E -DB -C 的正切值.19*.如图,在底面是直角梯形的四棱锥S-ABCD 中,AD ∥BC ,∠ABC =90°,SA ⊥面ABCD ,SA =AB =BC =1,AD =21. (1)求四棱锥S —ABCD 的体积;(2)求面SCD 与面SBA 所成的二面角的正切值.(提示:延长 BA ,CD 相交于点 E ,则直线 SE 是所求二面角的棱.20*.斜三棱柱的一个侧面的面积为10,这个侧面与它所对棱的距离等于6,求这个棱柱的体积.(提示:在 AA 1 上取一点 P ,过 P 作棱柱的截面,使 AA 1 垂直于这个截面.)(第20题)答案:DDDDB BCDBA11.313212S S S . 12.外,垂,内,中,BC 边的垂直平分. 13.60°.14.[30°,90°]. 15.36. 16.60°或120°.三、解答题17.证明:(1)取BC 中点O ,连结AO ,DO .∵△ABC ,△BCD 都是边长为4的正三角形,(第18题)∴AO ⊥BC ,DO ⊥BC ,且AO ∩DO =O ,∴BC ⊥平面AOD .又AD ⊂平面AOD ,∴BC ⊥AD . (第17题)解:(2)由(1)知∠AOD 为二面角A -BC -D 的平面角,设∠AOD =θ,则过点D 作DE ⊥AD ,垂足为E .∵BC ⊥平面ADO ,且BC ⊂平面ABC ,∴平面ADO ⊥平面ABC .又平面ADO ∩平面ABC =AO ,∴DE ⊥平面ABC .∴线段DE 的长为点D 到平面ABC 的距离,即DE =3.又DO =23BD =23,在Rt △DEO 中,sin θ=DO DE =23,故二面角A -BC -D 的正弦值为23.(3)当 θ=90°时,四面体ABCD 的体积最大.18.证明:(1)在长方体ABCD -A 1B 1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1的中点.∴△DD 1E 为等腰直角三角形,∠D 1ED =45°.同理∠C 1EC =45°.∴︒=∠90DEC ,即DE ⊥EC . 在长方体ABC D -1111D C B A 中,BC ⊥平面11DCC D ,又DE ⊂平面11DCC D ,∴BC ⊥DE .又C BC EC = ,∴DE ⊥平面EBC .∵平面DEB 过DE ,∴平面DEB ⊥平面EBC .(2)解:如图,过E 在平面11DCC D 中作EO ⊥DC 于O .在长方体ABCD -1111D C B A 中,∵面ABCD ⊥面11DCC D ,∴EO ⊥面ABCD .过O 在平面DBC 中作OF ⊥DB 于F ,连结EF ,∴EF ⊥BD .∠EFO 为二面角E -D B -C 的平面角.利用平面几何知识可得OF =51, (第18题) 又OE =1,所以,tan ∠EFO =5.19*.解:(1)直角梯形ABCD 的面积是M底面=AB AD BC ⋅)(+21=43=1221+1⨯,∴四棱锥S —ABCD 的体积是V =31·SA ·M 底面=31×1×43=41.(2)如图,延长BA ,CD 相交于点E ,连结SE ,则SE 是所求二面角的棱.∵AD ∥BC ,BC =2AD ,∴EA =AB =SA ,∴SE ⊥SB∵SA ⊥面ABCD ,得面SEB ⊥面EBC ,EB 是交线.又BC ⊥EB ,∴BC ⊥面SEB ,故SB 是SC 在面SEB上的射影,∴CS ⊥SE ,∠BSC 是所求二面角的平面角.∵SB =22+AB SA =2,BC =1,BC ⊥SB ,∴tan ∠BSC =22=SB BC ,(第19题) 即所求二面角的正切值为22. 20*.解:如图,设斜三棱柱ABC —A 1B 1C 1的侧面BB 1C 1C 的面积为10,A 1A 和面BB 1C 1C 的距离为6,在AA 1上取一点P作截面PQR,使AA1⊥截面PQR,AA1∥CC1,∴截面PQR⊥侧面BB1C1C,过P作PO⊥QR于O,则PO⊥侧面BB1C1C,且PO=6.1·QR·PO·AA1∴V 斜=S△PQR·AA1=21·PO·QR·BB1=21×10×6=2=30.(第20题)第二章点、直线、平面之间的位置关系参考答案及解析A组一、选择题1.D 解析:命题②有反例,如图中平面 α∩平面 β=直线n,l⊂α,m⊂β,且l∥n,m⊥n,则m⊥l,显然平面 α 不垂直平面β, (第1题)故②是假命题;命题①显然也是假命题,2.D解析:异面直线AD与CB1角为45°.3.D解析:在①、④的条件下,m,n的位置关系不确定.4.D解析:利用特殊图形正方体我们不难发现①②③④均不正确,故选择答案D.5.B解析:学会用长方体模型分析问题,A1A有无数点在平面ABCD外,但AA1与平面ABCD相交,①不正确;A1B1∥平面ABCD,显然A1B1不平行于BD,②不正确;A1B1∥AB,A1B1∥平面ABCD,但AB⊂平面ABCD内,③不正确;l与平面α平行,则l与 α 无公共点,l与平面 α 内的所有直线都没有公共点,④正确,应选B.(第5题)6.B 解析:设平面 α 过l 1,且 l 2∥α,则 l 1上一定点 P 与 l 2 确定一平面 β ,β 与 α 的交线l 3∥l 2,且 l 3 过点 P . 又过点 P 与 l 2 平行的直线只有一条,即 l 3 有唯一性,所以经过 l 1 和 l 3 的平面是唯一的,即过 l 1 且平行于 l 2 的平面是唯一的.7.C 解析:当三棱锥D -ABC 体积最大时,平面DAC ⊥ABC ,取AC 的中点O ,则△DBO 是等腰直角三角形,即∠DBO =45°. 8.D 解析:A .一组对边平行就决定了共面;B .同一平面的两条垂线互相平行,因而共面;C .这些直线都在同一个平面内即直线的垂面;D .把书本的书脊垂直放在桌上就明确了.9.B 解析:因为①②④正确,故选B .10.A 解析:异面直线a ,b 所成的角为60°,直线c ⊥a ,过空间任一点 P ,作直线 a ’∥a , b ’∥b , c ’∥c . 若a ’,b ’,c ’ 共面则 b ’ 与 c ’ 成 30° 角,否则 b ’ 与 c ’ 所成的角的范围为(30°,90°],所以直线b 与c 所成角的范围为[30°,90°] . 二、填空题 11.313212S S S .解析:设三条侧棱长为 a ,b ,c .则 21ab =S 1,21bc =S 2,21ca =S 3 三式相乘:∴ 81a 2 b 2 c 2=S 1S 2S 3,∴ abc =23212S S S .∵ 三侧棱两两垂直, ∴ V =31abc ·21=313212S S S .12.外,垂,内,中,BC 边的垂直平分.解析:(1)由三角形全等可证得 O 为△ABC 的外心; (2)由直线和平面垂直的判定定理可证得,O 为△ABC 的垂心;(3)由直线和平面垂直的判定定理可证得,O 为△ABC 的内心;(4)由三角形全等可证得,O 为 AB 边的中点;(5)由(1)知,O 在 BC 边的垂直平分线上,或说 O 在∠BAC 的平分线上. 13.60°.解析:将△ABC 沿DE ,EF ,DF 折成三棱锥以后,GH 与IJ 所成角的度数为60°. 14.[30°,90°].解析:直线l 与平面 α 所成的30°的角为m 与l 所成角的最小值,当m 在 α 内适当旋转就可以得到l ⊥m ,即m 与l 所成角的的最大值为90°. 15.36.解析:作等积变换:4331⨯×(d 1+d 2+d 3+d 4)=4331⨯·h ,而h =36.16.60°或120°.解析:不妨固定AB ,则AC 有两种可能. 三、解答题17.证明:(1)取BC 中点O ,连结AO ,DO . ∵△ABC ,△BCD 都是边长为4的正三角形, ∴AO ⊥BC ,DO ⊥BC ,且AO ∩DO =O , ∴BC ⊥平面AOD .又AD ⊂平面AOD , ∴BC⊥AD . (第17题)解:(2)由(1)知∠AOD 为二面角A -BC -D 的平面角,设∠AOD =θ,则过点D 作DE ⊥AD ,垂足为E . ∵BC ⊥平面ADO ,且BC ⊂平面ABC ,∴平面ADO ⊥平面ABC .又平面ADO ∩平面ABC =AO , ∴DE ⊥平面ABC .∴线段DE 的长为点D 到平面ABC 的距离,即DE =3. 又DO =23BD =23,在Rt △DEO 中,sin θ=DODE =23,故二面角A -BC -D 的正弦值为23.(3)当 θ=90°时,四面体ABCD 的体积最大.18.证明:(1)在长方体ABCD -A 1B 1C 1D 1中,AB =2,BB 1=BC =1,E 为D 1C 1的中点.∴△DD 1E 为等腰直角三角形,∠D 1ED =45°.同理∠C 1EC =45°.∴︒=∠90DEC ,即DE ⊥EC .在长方体ABC D -1111D C B A 中,BC ⊥平面11DCC D ,又DE ⊂平面11DCC D ,∴BC ⊥DE .又C BC EC = ,∴DE ⊥平面EBC .∵平面DEB 过DE ,∴平面DEB ⊥平面EBC .(2)解:如图,过E 在平面11DCC D 中作EO ⊥DC 于O .在长方体ABCD -1111D C B A 中,∵面ABCD ⊥面11DCC D ,∴EO ⊥面ABCD .过O 在平面DBC 中作OF ⊥DB 于F ,连结EF ,∴EF ⊥BD .∠EFO 为二面角E -D B -C 的平面角.利用平面几何知识可得OF =51,(第18题)又OE =1,所以,tan ∠EFO =5.19*.解:(1)直角梯形ABCD 的面积是M底面=AB AD BC ⋅)(+21=43=1221+1⨯,∴四棱锥S —ABCD 的体积是V =31·SA ·M 底面=31×1×43=41. (2)如图,延长BA ,CD 相交于点E ,连结SE ,则SE 是所求二面角的棱.∵AD ∥BC ,BC =2AD , ∴EA =AB =SA ,∴SE ⊥SB∵SA ⊥面ABCD ,得面SEB ⊥面EBC ,EB 是交线. 又BC ⊥EB ,∴BC ⊥面SEB ,故SB 是SC 在面SEB 上的射影,∴CS ⊥SE ,∠BSC 是所求二面角的平面角.∵SB =22+AB SA =2,BC =1,BC ⊥SB ,∴tan ∠BSC =22=SB BC ,(第19题)即所求二面角的正切值为22.20*.解:如图,设斜三棱柱ABC —A 1B 1C 1的侧面BB 1C 1C 的面积为10,A 1A 和面BB 1C 1C 的距离为6,在AA 1上取一点P 作截面PQR ,使AA 1⊥截面PQR ,AA 1∥CC 1,∴截面PQR ⊥侧面BB 1C 1C ,过P 作PO ⊥QR 于O ,则PO ⊥侧面BB 1C 1C ,且PO =6. ∴V 斜=S △PQR ·AA 1=21·QR ·PO ·AA 1=21·PO ·QR ·BB 1=21×10×6 =30.(第20题)。
高二数学点线面的位置关系试题
高二数学点线面的位置关系试题1.在长方体中,已知,为的中点,则直线与平面的距离是___________.【答案】9.【解析】过作,因为,所以,则,的长度即为直线与平面的距离;在中,,;在中,,,,即直线与平面的距离为9.【考点】直线到平面的距离.2.两条异面直线所成的角为θ,则θ的取值范围是 .【答案】【解析】两条异面直线,经过空间任一点作两条异面平行线,把这两条相交直线所成锐角(或直角)叫做这两条异面直线所成的角,因此,θ【考点】异面直线所成的角的定义3.过所在平面外一点,作,垂足为,连接.若则点()A.垂心B.外心C.内心D.重心【答案】B【解析】由于,点外心【考点】三角形外心的概念.4.如图所示,正三棱锥中,分别是的中点,为上任意一点,则直线与所成的角的大小是 ( )A.B.C.D.随点的变化而变化.【答案】B【解析】连接,因为为正三棱锥,所以,则有,所以,即直线与所成的角的大小是.【考点】(1)线面垂直的判定与性质应用;(2)线线角.5.已知a,b,c是三条互不重合的直线,α,β是两个不重合的平面,给出四个命题:①a∥b,b∥α,则a∥α;②a,b⊂α,a∥β,b∥β,则α∥β;③a⊥α,a∥β,则α⊥β;④a⊥α,b∥α,则a⊥b.其中正确的命题个数是 ( )A.1B.2C.3D.4【答案】B【解析】①中a∥α需a⊄α,此条件不一定成立;②中α∥β时需a,b相交,此条件不一定成立;③中β内平行于a的直线一定垂直于α,正确;④中a与b所成角为90°,正确.6.如图,在矩形中,点为边上的点,点为边的中点,,现将沿边折至位置,且平面平面.(1) 求证:平面平面;(2) 求二面角的大小.【答案】(1)详见解析;(2).【解析】(1) 利用直角三角形,先证明折前有,折后这个垂直关系没有改变,然后由平面平面的性质证明平面,最后由面面垂直的判定定理即可证明平面平面;(2)为方便计算,不妨设,先以为原点,以方向为轴,以方向为轴,以与平面向上的法向量同方向为轴,建立空间直角坐标系,写给相应点的坐标,然后分别求出平面和平面的一个法向量,接着计算出这两个法向量夹角的余弦值,根据二面角的图形与计算出的余弦值,确定二面角的大小即可.试题解析:(1) 证明:由题可知:折前,这个垂直关系,折后没有改变故折后有(2)不妨设,以为原点,以方向为轴,以方向为轴,以与平面向上的法向量同方向为轴,建立空间直角坐标系 7分则设平面和平面的法向量分别为,由及可得到即,不妨取又由及可得到即不妨取 9分11分综上所述,二面角大小为 12分.【考点】1.线线垂直的证明;2. 线面垂直、面面垂直的判定与性质;3.空间向量在解决空间角中的运用问题.7.用M表示平面,表示一条直线,则M内至少有一直线与()A.平行;B.相交;C.异面;D.垂直。
高中数学必修二 点线面间的位置关系检测题及参考答案
高中数学必修二阶段质量检测(二)点、直线、平面之间的位置关系(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.分别在两个平行平面内的两条直线间的位置关系不可能为()A.平行B.相交C.异面D.垂直【答案】B。
【解析】因为两平行平面没有公共点,所以两直线没有公共点,所以两直线不可能相交.2.设BD1是正方体ABCD-A1B1C1D1的一条对角线,则这个正方体中面对角线与BD1异面的有()A.0条B.4条C.6条D.12条【答案】C。
【解析】每个面中各有一条对角线与BD1异面,它们是:AC,A1C1,B1C,A1D,AB1,DC1.3.下列说法不正确的是()A.空间中,一组对边平行且相等的四边形一定是平行四边形B.同一平面的两条垂线一定共面C.过直线上一点可以作无数条直线与这条直线垂直,且这些直线都在同一平面内D.过一条直线有且只有一个平面与已知平面垂直【答案】D。
【解析】如图所示,在正方体ABCD-A1B1C1D1中,AD⊥平面DCC1D1,因此平面ABCD、平面AA1D1D均与平面DCC1D1垂直,而且平面AA1D1D∩平面ABCD=AD,显然选项D不正确,故选D.4.已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是() A.若α,β垂直于同一平面,则α与β平行B.若m,n平行于同一平面,则m与n平行C.若α,β不平行,则在α内不存在与β平行的直线D.若m,n不平行,则m与n不可能垂直于同一平面【答案】D。
【解析】A项,α,β可能相交,故错误;B项,直线m,n的位置关系不确定,可能相交、平行或异面,故错误;C项,若m⊂α,α∩β=n,m∥n,则m∥β,故错误;D项,假设m,n垂直于同一平面,则必有m∥n,所以原命题正确,故正确.5.如图所示,在正方体ABCD-A1B1C1D1中,若E是A1C1的中点,则直线CE垂直于()A.AC B.BD C.A1D D.A1D1【答案】选B【解析】CE⊂平面ACC1A1,而BD⊥AC,BD⊥AA1,∴BD⊥平面ACC1A1,∴BD⊥CE.6.已知在四面体ABCD中,E,F分别是AC,BD的中点,若AB=2,CD=4,EF ⊥AB,则EF与CD所成的角的度数为()A.90°B.45°C.60°D.30°【答案】D【解析】取BC的中点G,连接EG,FG,则EG=1,FG=2,EF⊥EG,则EF与CD所成的角等于∠EFG,为30°.7.如图,在三棱柱ABC-A1B1C1中,AA1⊥底面ABC,D,E分别是棱BC,AB的中点,点F在棱CC1上,AB=BC=CA=CF=2,AA1=3,则下列说法正确的是() A.设平面ADF与平面BEC1的交线为l,则直线EC1与l相交B.在棱A1C1上存在点N,使得三棱锥N-ADF的体积为3 7C.设点M在BB1上,当BM=1时,平面CAM⊥平面ADFD.在棱A1B1上存在点P,使得C1P⊥AF【答案】C【解析】连接CE交AD于点O,则O为△ABC的重心,连接OF.由已知得OF∥EC1,则EC1∥l,故A错;若在A1C1上存在点N,则V N-ADF=V D-AFN,当N与C1重合时,V D-AFN取最小值为36,故B错;当BM=1时,可证得△CBM≌△FCD,则∠BCM+∠CDF=90°,即CM⊥DF.又∵AD⊥平面CBB1C1,CM⊂平面CBB1C1,∴AD⊥CM.∵DF∩AD=D,∴CM⊥平面ADF.∵CM⊂平面CAM,∴平面CAM⊥平面ADF,故C正确;过C1作C1G∥FA交AA1于点G.若在A1B1上存在点P,使得C1P⊥AF,则C1P⊥C1G.又∵C1P⊥GA1,C1G∩GA1=G,∴C1P⊥平面A1C1G.∵A1C1⊂平面A1GC1,∴C1P⊥A1C1,矛盾,故D错.故选C.8.在四面体ABCD 中,已知棱AC 的长为 2 ,其余各棱长都为1,则二面角A -CD -B 的余弦值为( ) A.12 B.13 C.33 D.23【答案】C【解析】取AC 的中点E ,CD 的中点F ,则EF =12,BE =22,BF =32, ∴△BEF 为直角三角形,cos θ=EF BF =33. 9.如图,平面α⊥平面β,A ∈α,B ∈β,AB 与平面α,β所成的角分别为45°和30°,过A ,B 分别作两平面交线的垂线,垂足分别为A ′,B ′,若AB =12,则A ′B ′等于( )A .4B .6C .8D .9【答案】B【解析】连接AB ′,BA ′,则∠BAB ′=45°,∠ABA ′=30°.在Rt △ABB ′中,AB =12,可得BB ′=6 2.在Rt △ABA ′中,可得BA ′=6 3.故在Rt △BA ′B ′中,可得A ′B ′=6.10.矩形ABCD 中,AB =4,BC =3,沿AC 将矩形ABCD 折成一个直二面角B -AC -D ,则四面体ABCD 的外接球的体积为( )A.125π12B.125π9C.125π6D.125π3【答案】C【解析】球心O 为AC 中点,半径为R =12AC =52,V =43πR 3=125π6. 11.如图,四边形ABCD 中,AD ∥BC ,AD =AB ,∠BCD =45°,∠BAD =90°,将△ABD 沿BD 折起,使平面ABD ⊥平面BCD ,构成四面体ABCD ,则在四面体ABCD 中,下列结论正确的是( )A .平面ABD ⊥平面ABCB .平面ADC ⊥平面BDCC .平面ABC ⊥平面BDCD .平面ADC ⊥平面ABC【答案】D【解析】易知△BCD中,∠DBC=45°,∴∠BDC=90°,又平面ABD⊥平面BCD,而CD⊥BD,∴CD⊥平面ABD,∴AB⊥CD,而AB⊥AD,CD∩AD=D,∴AB⊥平面ACD,∴平面ABC⊥平面ACD.12.(2019·全国卷Ⅲ)如图,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则()A.BM=EN,且直线BM,EN是相交直线B.BM≠EN,且直线BM,EN是相交直线C.BM=EN,且直线BM,EN是异面直线D.BM≠EN,且直线BM,EN是异面直线【答案】B【解析】如图,取CD的中点F,DF的中点G,连接EF,FN,MG,GB.∵△ECD是正三角形,∴EF⊥CD.∵平面ECD⊥平面ABCD,平面ECD∩平面ABCD=CD,EF⊂平面ECD,∴EF⊥平面ABCD.∴EF⊥FN.不妨设AB=2,则FN=1,EF=3,∴EN=FN2+EF2=2.∵EM=MD,DG=GF,∴MG∥EF且MG=12EF,∴MG⊥平面ABCD,∴MG⊥BG.∵MG=12EF=32,BG=CG2+BC2=2235222⎛⎫+=⎪⎝⎭,∴BM=MG2+BG2=7,∴BM≠EN.连接BD,BE,∵点N是正方形ABCD的中心,∴点N在BD上,且BN=DN,∴BM,EN是△DBE的中线,∴BM,EN必相交.二、填空题(本大题共4小题,每小题5分,共20分)13.设正三角形ABC的边长为a,PA⊥平面ABC,PA=AB,则A到平面PBC的距离为________. 【答案】217a 【解析】如图所示,取BC 中点E ,连接AE ,PE ,则AE ⊥BC ,又BC ⊥PA ,∴BC ⊥平面PAE .∴平面PAE ⊥平面PBC .在平面PAE 内过A 作AF ⊥PE ,垂足为F ,则AF ⊥平面PBC .则AF =PA ·AE PE =217a . 14.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M ,N 分别是棱AA 1和AB 上的点,若∠B 1MN 是直角,则∠C 1MN 等于________.【答案】90°【解析】∵B 1C 1⊥平面A 1ABB 1,MN ⊂平面A 1ABB 1,∴B 1C 1⊥MN ,又∠B 1MN 为直角.∴B 1M ⊥MN ,而B 1M ∩B 1C 1=B 1.∴MN ⊥平面MB 1C 1,又MC 1⊂平面MB 1C 1,∴MN ⊥MC 1,∴∠C 1MN =90°.15.如图,圆锥SO 中,AB 、CD 为底面圆的两条直径,AB ∩CD =O ,且AB ⊥CD ,SO =OB =2,P 为SB 的中点,则异面直线SA 与PD 所成角的正切值为________.【答案】 2【解析】连接PO ,则PO ∥SA ,∴∠OPD 即为异面直线SA 与PD 所成的角,且△OPD 为直角三角形,∠POD 为直角,∴tan ∠OPD =OD OP =22= 2. 16.(2019·全国卷Ⅰ)已知∠ACB =90°,P 为平面ABC 外一点,PC =2,点P 到∠ACB 两边AC ,BC 的距离均为3,那么P 到平面ABC 的距离为________.【答案】 2【解析】如图,过点P 作PO ⊥平面ABC 于O ,则PO 为P 到平面ABC 的距离.再过O 作OE ⊥AC 于E ,OF ⊥BC 于F ,连接PC,PE,PF,则PE⊥AC,PF⊥BC.又PE=PF=3,所以OE=OF,所以CO为∠ACB的平分线,即∠ACO=45°.在Rt△PEC中,PC=2,PE=3,所以CE=1,所以OE=1,所以PO=PE2-OE2=(3)2-12= 2.三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)如图,在四面体ABCD中,CB=CD,AD⊥BD,且E、F分别是AB、BD的中点.求证:(1)EF∥平面ACD;(2)平面EFC⊥平面BCD.证明:(1)∵E,F分别是AB,BD的中点,∴EF是△ABD的中位线,∴EF∥AD,∵EF⊄平面ACD,AD⊂平面ACD,∴EF∥平面ACD.(2)∵AD⊥BD,EF∥AD,∴EF⊥BD.∵CB=CD,F是BD的中点,∴CF⊥BD.又EF∩CF=F,∴BD⊥平面EFC.∵BD⊂平面BCD,∴平面EFC⊥平面BCD.18.(本小题满分12分)(2019·全国卷Ⅰ)如图,直四棱柱ABCD -A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.解:(1)证明:连接B1C,ME.因为M,E分别为BB1,BC的中点,所以ME∥B1C,且ME=12B1C.又因为N为A1D的中点,所以ND=12A1D.由题设知A1B1綊DC,可得B1C綊A1D,故ME綊ND,因此四边形MNDE为平行四边形,所以MN∥ED.又MN⊄平面C1DE,所以MN∥平面C1DE.(2)过点C作C1E的垂线,垂足为H.由已知可得DE⊥BC,DE⊥C1C,所以DE⊥平面C1CE,故DE⊥CH.从而CH⊥平面C1DE,故CH的长即为点C到平面C1DE的距离.由已知可得CE=1,C1C=4,所以C1E=17,故CH=41717.从而点C到平面C1DE的距离为41717.19.(本小题满分12分)矩形ABCD中,AB=2,AD=1,E为CD的中点,沿AE将△DAE折起到△D1AE的位置,使平面D1AE⊥平面ABCE.(1)若F为线段D1A的中点,求证:EF∥平面D1BC;(2)求证:BE⊥D1A.证明:(1)取AB的中点G,连接EG、FG,则EG∥BC,FG∥D1B,且EG∩FG=G,EG、FG⊂平面EFG;D1B∩BC=B,D1B、BC⊂平面D1BC.∴平面EFG∥平面D1BC,注意到EF⊂平面EFG,∴EF∥平面D1BC.(2)易证BE⊥EA,平面D1AE⊥平面ABCE,平面D1AE∩平面ABCE=AE,∴BE⊥平面D1AE,且D1A⊂平面D1AE,∴BE⊥D1A.20.(本小题满分12分)在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC且分别交AC、SC于D、E,又SA=AB,SB=BC.(1)求证:BD⊥平面SAC;(2)求二面角E-BD-C的大小.解:(1)证明:如图,∵DE⊥SC,且E为SC的中点,又SB=BC,∴BE⊥S C.又DE∩BE=E,根据直线与平面垂直的判定定理知SC⊥平面BDE,BD⊂平面BDE,∴SC⊥BD.又SA⊥平面ABC,BD⊂平面ABC,∴SA⊥BD.又SA∩SC=S,∴BD⊥平面SAC.(2)由(1)知∠EDC为二面角E-BD-C的平面角,又△SAC∽△DEC,∴∠EDC=∠ASC.在Rt△SAB中,∠SAB=90°,设SA=AB=1,则SB= 2.由SA⊥BC,AB⊥BC,AB∩SA=A,∴BC⊥平面SAB,SB⊂平面SAB,∴BC⊥SB.在Rt△SBC中,SB=BC=2,∠SBC=90°,则SC=2.在Rt△SAC中,∠SAC=90°,SA=1,SC=2.∴cos∠ASC=SASC=12.∴∠ASC=60°,即二面角E-BD-C的大小为60°.21.(本小题满分12分)如图,正方形ABCD和四边形ACEF所在的平面互相垂直,EF ∥AC,AB=2,CE=EF=1.(1)求证:AF∥平面BDE;(2)求证:CF⊥平面BDE.证明:(1)设AC与BD交于点O,连接EO,∵EF∥AC,且EF=1,AO=12AC=1,∴四边形AOEF为平行四边形,∴AF∥OE.∵OE⊂平面BDE,AF⊄平面BDE,∴AF∥平面BDE.(2)连接FO,∵EF∥CO,EF=CO=1,且CE=1,∴四边形CEFO为菱形,∴CF⊥EO.∵四边形ABCD为正方形,∴BD⊥AC.又平面ACEF⊥平面ABCD,且平面ACEF∩平面ABCD=AC,∴BD⊥平面ACEF,∴CF⊥BD. 又BD∩EO=O,∴CF⊥平面BDE.22.(本小题满分12分)如图,已知空间几何体ABCDE中,△BCD与△CDE均为边长为2的等边三角形,△ABC为腰长为3的等腰三角形,平面CDE⊥平面BCD,平面ABC ⊥平面BCD.(1)试在平面BCD内作一条直线,使得直线上任意一点F与E的连线EF均与平面ABC平行,并给出详细证明;(2)求三棱锥E-ABC的体积.解:(1)取DC的中点N,取BD的中点M,连接MN,EN,EM,则直线MN即为所求.取BC的中点H,连接AH,∵△ABC为腰长为3的等腰三角形,H为BC的中点,∴AH⊥BC.又平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,AH⊂平面ABC,∴AH⊥平面BCD,同理,可证EN⊥平面BCD,∴EN∥AH.∵EN⊄平面ABC,AH⊂平面ABC,∴EN∥平面ABC.又M,N分别为BD,DC的中点,∴MN∥BC.∵MN⊄平面ABC,BC⊂平面ABC,∴MN∥平面ABC.又MN∩EN=N,MN⊂平面EMN,EN⊂平面EMN,∴平面EMN∥平面ABC.又EF⊂平面EMN,∴EF∥平面ABC.(2)连接DH,取CH的中点G,连接NG,则NG∥DH,NG=12DH,由(1)可知,EN∥平面ABC,∴点E到平面ABC的距离与点N到平面ABC的距离相等.又△BCD是边长为2的等边三角形,∴DH⊥BC,又平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,DH⊂平面BCD,∴DH⊥平面ABC,∴NG⊥平面ABC.又DH=3,∴NG=3 2.又AC=AB=3,BC=2,∴AH=22,∴S△ABC=12·BC·AH=22,∴V E-ABC=V N-ABC=13·S△ABC·NG=63.。
最新整理点线面之间的位置关系练习题.doc
点、线、面之间的位置关系及线面平行应用练习1、 平面L =⋂βα,点βαα∈∈∈C B A ,,,且L C ∈,又R L AB =⋂,过A 、B 、C 三点确定的平面记作γ,则γβ⋂是( )A .直线ACB .直线BC C .直线CRD .以上都不对2、空间不共线的四点,可以确定平面的个数是( )A .0B .1C .1或4D .无法确定3、在三角形、四边形、梯形和圆中,一定是平面图形的有 个4、正方体1111D C B A ABCD -中,P 、Q 分别为11,CC AA 的中点,则四边形PBQ D 1是( )A .正方形B .菱形C .矩形D .空间四边形5、在空间四边形ABCD 中,点E 、F 、G 、H 分别为AB 、BC 、CD 、DA 的中点,若AC=BD , 且BD AC ⊥,则四边形EFGH 为6、下列命题正确的是( )A . 若βα⊂⊂b a ,,则直线b a ,为异面直线B . 若βα⊄⊂b a ,,则直线b a ,为异面直线C . 若∅=⋂b a ,则直线b a ,为异面直线D . 不同在任何一个平面内的两条直线叫异面直线7、在空间中:①若四点不共面,则这四点中任何三点都不共线;②若两条直线没有公共点,则这两条直线是异面直线,以上两个命题中为真命题的是8、过直线L 外两点作与直线L 平行的平面,可以作( )A .1个B .1个或无数个C .0个或无数个D .0个、1个或无数个9、b a //,且a 与平面α相交,那么直线b 与平面α的位置关系是( )A .必相交B .有可能平行C .相交或平行D .相交或在平面内10、直线与平面平行的条件是这条直线与平面内的( )A .一条直线不相交B .两条直线不相交C .任意一条直线不相交D .无数条直线不相交11、如果两直线b a //,且//a 平面α,则b 与平面α的位置关系是( )A .相交B .α//bC .α⊂bD .α//b 或α⊂b12、已知直线a 与直线b 垂直,a 平行于平面α,则b 与平面α的位置关系是( )A .α//bB .α⊂bC .b 与平面α相交D .以上都有可能13、若直线a 与直线b 是异面直线,且//a 平面α,则b 与平面α的位置关系是( )A .α//bB .b 与平面α相交C .α⊂bD .不能确定14、已知//a 平面α,直线α⊂b ,则直线a 与直线b 的关系是( )A .相交B .平行C .异面D .平行或异面15、平面⋂α平面a =β,平面⋂β平面b =γ,平面⋂γ平面c =α,若b a //,则c 与b a ,的位置关系是( )A .c 与b a ,异面B .c 与b a ,相交C .c 至少与b a ,中的一条相交D .c 与b a ,都平行16、b a ,是异面直线,则过a 且与b 平行的平面有____个17、正方体1111D C B A ABCD -的棱长为a ,求异面直线1BD 和11C B 所成的角的余弦值18、已知E 、F 、G 、M 分别是四面体的棱AD 、CD 、BD 、BC 的中点,求证:AM //面EFG19、在正方体1111D C B A ABCD -中,E 为1DD 的中点,求证:1BD ∥面AEC20、在正方体1111D C B A ABCD -中,E 、F 分别为BC 、11D C 的中点,求证:EF//平面11B BDD21、已知在正方体1111D C B A ABCD -中,E 、F 分别是11,CC AA 的中点,求证:平面//BDF 平面E D B 1122、过正方体1111D C B A ABCD -的棱1BB 作一平面交平面11C CDD 于1EE ,求证:1BB //1EE23、如图,四边形ABCD 是矩形,∉P 面ABCD ,过BC 作平面BCFE 交AP 于E , 交DP 于F ,求证:四边形BCFE 是梯形点、线、面之间的位置关系及线面平行应用练习答案1、C2、C3、34、B5、正方形6、D7、①8、D (提示:当α⊂L 时,就为 0个)9、A 10、C 11、D 12、D 13、D 14、D 15、D 16、1 17、33 18、提示:连结MD 交GF 于H ,则点H 为MD 的中点19、提示:连接BD 交AC 于点O ,连接EO ,则EO//1BD ,又⊂EO 面AEC , 故1BD //面AEC20、提示:取11D B 的中点为1O ,连接11,BO FO ,则BE FO //1且BE FO =1,则 四边形1BEFB 是平行四边形,故EF BO //121、提示:11//D B BD ,取1BB 的中点H ,连接EH ,H C 1,有EH D C EH D C =1111,// 所以四边形11D EHC 是平行四边形,所以E D H C 11//,又BF H C //1, 所以BF E D //122、分析:因为1BB //⊄11,BB CC 面11C CDD ,所以1BB //面11C CDD23、分析:因为AD BC //,所以BC//面ADP ,所以BC//EF ,所以EF//AD ,但EF 的长度 小于AD 的长度,而AD BC =,所以EF 的长度小于BC 的长度。
点线面位置关系例题与练习(含答案)
点、线、面的位置关系● 知识梳理 (一).平面公理1:如果一条直线上有两点在一个平面内,那么直线在平面内。
公理2:不共线...的三点确定一个平面. 推论1:直线与直线外的一点确定一个平面. 推论2:两条相交直线确定一个平面. 推论3:两条平行直线确定一个平面.公理3:如果两个平面有一个公共点,那么它们还有公共点,这些公共点的集合是一条直线 (二)空间图形的位置关系1.空间直线的位置关系:相交,平行,异面1.1平行线的传递公理:平行于同一条直线的两条直线互相平行。
1.2等角定理:如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补。
1.3异面直线定义:不同在任何一个平面内的两条直线——异面直线;1.4异面直线所成的角:(1)范围:(]0,90θ∈︒︒;(2)作异面直线所成的角:平移法.2.直线与平面的位置关系: 包含,相交,平行3.平面与平面的位置关系:平行,相交(三)平行关系(包括线面平行,面面平行) 1.线面平行:①定义:直线与平面无公共点.②判定定理:////a b a a b ααα⎫⎪⊄⇒⎬⎪⊂⎭③性质定理:////a a a b b αβαβ⎫⎪⊂⇒⎬⎪=⎭ 2.线面斜交: ①直线与平面所成的角(简称线面角):若直线与平面斜交,则平面的斜线与该斜线在平面内射影的夹角。
范围:[]0,90θ∈︒︒ 3.面面平行:①定义://αβαβ=∅⇒;②判定定理:如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行; 符号表述:,,,//,////a b ab O a b ααααβ⊂=⇒判定2:垂直于同一条直线的两个平面互相平行.符号表述:,//a a αβαβ⊥⊥⇒.③面面平行的性质:(1)////a a αββα⎫⇒⎬⊂⎭;(2)////a a b b αβαγβγ⎫⎪=⇒⎬⎪=⎭(四)垂直关系(包括线面垂直,面面垂直)1.线面垂直①定义:若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江西省吉安市凤凰中学2020高二数学 第8讲 点线面之间的位置关
系小题训练 新人教A 版
一、考试目标 模块 内容
能力层级 A B C D 数
学 2 空间点、线、面的位置关系的四个公理和一个定理 √ 直线与平面、平面与平面的平行或垂直的判定和性质 √ 运用已获得的结论证明一些空间位置关系的简单命题
√
二、学考真题演练
1.(09年) 如图,在四棱锥P-ABCD 中,底面ABCD 是正方形, PA ⊥底面ABCD ,且PA=AB.
(2)求异面直线BC 与PD 所成的角.
2.(10年) 如图,1111ABCD A B C D -为长方体, (2)若BC=C 1C ,求直线BC 1与平面ABCD 所成角的大小。
3.(11年) 如图所示,在正方体1111ABCD A B C D -中,直线11B D
与平面1BC D 的位置关系是( )
A .平行
B .垂直
C .相交但不垂直
D .直线11B D 在平面1BC D 内
4.(11年)如图,在四棱锥P ABCD -中,PA ABCD ⊥平面, 四边形ABCD 是平行四边形,PA AD =,则异面直线PD 与 BC 所成角的大小是 .
三、要点解读及案例剖析
1、空间点、线、面的位置关系的四个公理和一个定理
例1、空间四点A 、B 、C 、D 共面但不共线,那么这四点中 ( )
A.必有三点共线
B.必有三点不共线
C.至少有三点共线
D.不可能有三点共线
例2、在空间内,可以确定一个平面的是( ) A.两两相交的三条直线 B.三条直线,其中的一条与另外两条相交 C.三个点 D.三条直线,它们两两相交,但不交于同一点
2、空间线线、线面、面面的位置关系 ⑴空间的两条直线的位置关系: ⑵直线与平面的位置关系: ⑶平面与平面的位置关系:
A B
C
D 1
A 1
B 1
C 1
D
例3、在正方体1111ABCD A B C D -中,E F G H 、、、分别为1111AA AB BB B C 、、、的中点,则异面直线EF 与GH 所成的角为( )
A 、︒45 B.︒60 C.︒90 D.︒120
例4.(12年) 如图,在四棱柱1111ABCD A B C D -中,D 1D ⊥底面
ABCD ,底面ABCD 是正方形,且AB=1,D 1D=2. (1)求直线D 1B 与平面ABCD 所成角的大小;
四、达标练习
1、下列四个命题中,正确命题的序号为________________ ①A 、B 是空间中两点,,,,A l A B l B αα∈∈∈∈,则α⊂l ;
②A 、B 是空间中两点,α与β不重合,若βαβα∈∈∈∈B B A A ,,,,则AB =βαI ; ③两平面可以仅有一个公共点;
④A,B,C 都在α内,A,B,C 都在β内,且A,B,C 不共线,则α与β重合。
2.正方体1111ABCD A B C D -中,E F 、分别是边1111A B B C 、的中点,求异面直线11DB EF 、所成角的大小。
3.在正方体1111ABCD A B C D -中
(1)求1AC 与平面1111A B C D 所成角的正切值; (2)求面对角线1A B 与对角面11BB D D 所成的角。
