双线性插值-matlab实现
matlab在两个数据点之间插值一条曲线的方法

一、插值的定义在数学和计算机科学中,插值是指在已知数据点的基础上,利用插值算法来估算出在这些数据点之间未知位置上的数值。
插值可以用于生成平滑的曲线、曲面或者函数,以便于数据的分析和预测。
二、matlab中的插值方法在matlab中,有多种插值方法可以用来在两个数据点之间插值一条曲线。
这些方法包括线性插值、多项式插值、样条插值等。
下面我们将逐一介绍这些方法及其使用场景。
1. 线性插值线性插值是最简单的插值方法之一。
它的原理是通过已知的两个数据点之间的直线来估算未知位置上的数值。
在matlab中,可以使用interp1函数来进行线性插值。
该函数的调用格式为:Y = interp1(X, Y, Xq, 'linear')其中X和Y分别是已知的数据点的横纵坐标,Xq是待估算数值的位置,'linear'表示使用线性插值方法。
使用线性插值可以快速地生成一条近似直线,但是对于非线性的数据分布效果可能不佳。
2. 多项式插值多项式插值是利用多项式函数来逼近已知数据点之间的曲线。
在matlab中,可以使用polyfit和polyval函数来进行多项式插值。
polyfit函数用于拟合多项式曲线的系数,polyval函数用于计算多项式函数在给定点的数值。
多项式插值的优点是可以精确地通过已知数据点,并且可以适用于非线性的数据分布。
3. 样条插值样条插值是一种比较常用的插值方法,它通过在每两个相邻的数据点之间拟合一个低阶多项式,从而保证整条曲线平滑且具有良好的拟合效果。
在matlab中,可以使用splinetool函数来进行样条插值。
样条插值的优点是对于非线性的数据分布可以有较好的拟合效果,且能够避免多项式插值过拟合的问题。
4. 三角函数插值三角函数插值是一种常用的周期性数据插值方法,它利用三角函数(如sin和cos)来逼近已知数据点之间的曲线。
在matlab中,可以使用interpft函数来进行三角函数插值。
Matlab插值

(2)由图形可见,若可由 散点图得到时间和温度 的函数关系(一元函 数),则问题得解!
35
30
散
25
点
20
图
15
10
5
0
2
4
6
8 10 12
显然,找时间和温度间的函数关系是很难的!
那我们是否可以找到一条经过每一个点的简单函数 作为它的近似呢?
3
插值
在离散数据的基础上补插连续函数,使得 这条连续曲线通过全部给定的离散数据点。插 值是离散函数逼近的重要方法,利用它可通过 函数在有限个点处的取值状况,估算出函数在 其他点处的近似值。
返回 17
三次样条插值 是一种分段插值,比分段线性插值更光滑!
y
a
xi-1 xi
bx
在数学上,光滑程度的定量描述是:函数(曲线) 的k阶可导且连续,则称该曲线具有k阶光滑性。
光滑性的阶次越高,则越光滑。为了得到具有
较高阶光滑性的分段低次插值多项式,我们介绍三 次样条插值。
18
1、了解插值的基本内容。 2、掌握用Matlab软件包求解插值问题。
[1] 问题的提出 [2] 一维插值 [3] 二维插值
2
问题1
在1-12的11小时内,每隔1小时测量一次温度,测得的温度 依次为:5,8,9,15,25,29,31,30,22,25,27,24 试估计每隔1/10小时的温度值。
分析:
y0
x x1
x0 x0
x x2 x1 x2
y1
x x2
x0 x0
利用双线性插值法实现图像放大
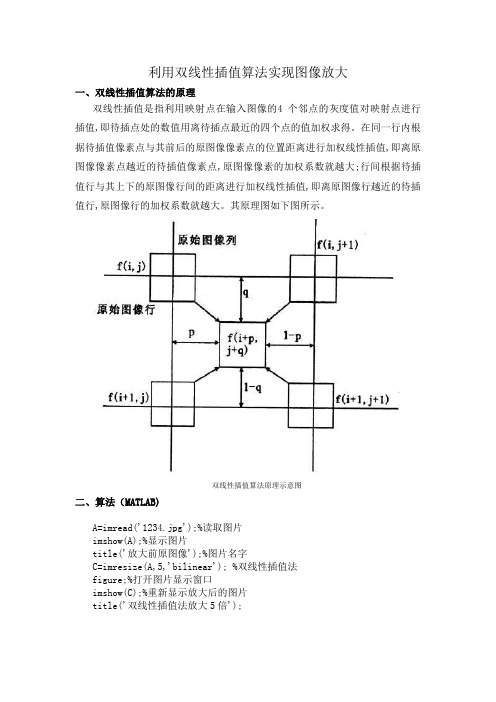
利用双线性插值算法实现图像放大
一、双线性插值算法的原理
双线性插值是指利用映射点在输入图像的4 个邻点的灰度值对映射点进行插值,即待插点处的数值用离待插点最近的四个点的值加权求得。
在同一行内根据待插值像素点与其前后的原图像像素点的位置距离进行加权线性插值,即离原图像像素点越近的待插值像素点,原图像像素的加权系数就越大;行间根据待插值行与其上下的原图像行间的距离进行加权线性插值,即离原图像行越近的待插值行,原图像行的加权系数就越大。
其原理图如下图所示。
双线性插值算法原理示意图
二、算法(MATLAB)
A=imread('1234.jpg');%读取图片
imshow(A);%显示图片
title('放大前原图像');%图片名字
C=imresize(A,5,'bilinear'); %双线性插值法
figure;%打开图片显示窗口
imshow(C);%重新显示放大后的图片
title('双线性插值法放大5倍');
三、程序运行结果截图。
用MATLAB作函数插值

1.先在三维坐标画出原始数据,画出粗糙的温度分布曲面图. 输入以下命令: x=1:5; y=1:3; temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86]; mesh(x,y,temps) 2.以平滑数据,在x、y方向上每隔0.2个单位的地方进行插值.
figure(5) subplot(1,3,1),contour(xi,yi,z1i,10,'r'); subplot(1,3,2),contour(xi,yi,z2i,10,'r'); subplot(1,3,3),contour(xi,yi,z3i,10,'r');
用MATLAB作散点数据的插值计算
例
已知飞机下轮廓线上数据如下,求x每改变0.1时的y值。
X Y
0 3 5 7 9 1 1 1 1 1 1 2 3 4 5 0 12 17 20 21 20 18 12 10 16 . . . . . . . . .
机翼下 轮廓线 y
x
x0=[0 3 5 7 9 11 12 13 14 15 ]; y0=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6 ]; x=0:0.1:15; y1=lagr1(x0,y0,x); y2=interp1(x0,y0,x); y3=interp1(x0,y0,x,'spline'); subplot(3,1,1) plot(x0,y0,'k+',x,y1,'r') grid title('lagrange') subplot(3,1,2) plot(x0,y0,'k+',x,y2,'r') grid title('piecewise linear') subplot(3,1,3) plot(x0,y0,'k+',x,y3,'r') grid title('spline')
图像插值技术——双线性插值法

图像插值技术——双线性插值法在图像处理中,如果需要对图像进⾏缩放,⼀般可以采取插值法,最常⽤的就是双线性插值法。
本⽂⾸先从数学⾓度推导了⼀维线性插值和⼆维线性插值的计算过程,并总结了规律。
随后将其应⽤到图像的双线性插值上,利⽤Matlab编程进⾏图像的缩放验证,实验证明,⼆维线性插值能够对图像做出较好的缩放效果。
数学⾓度的线性插值⼀维线性插值假设有⼀个⼀元函数 y=f(x) , 已知曲线上的两点,A 和 B 的坐标分别为 (x0,y0) 、(x1,y1) 。
现在要在A 和 B 之间通过插值计算出⼀个点 P ,若已知 P点的横坐标 x,如何求出 P点的纵坐标 y ?这⾥我们的插值之所以叫做线性插值,就是因为我们假定了 P 点落在 A 点和 B 点的连线上,使得他们的坐标之间满⾜线性关系。
所以,根据初中的知识,可以得到下⾯的等式:y−y0 y1−y0=x−x0 x1−x0这⾥我们令:α=x−x0 x1−x0于是,我们可以得到P点的纵坐标 y 的表达式:y=(1−α)f(x0)+αf(x1)⼆维线性插值⼀维线性插值可以扩展到⼆维的情况。
假设有⼀个⼆元函数 z=f(x,y) , 已知曲⾯上的四点,A 、B 、C、D的坐标分别为 (x0,y0) 、(x1,y0) 、(x1,y1)、(x0,y1) 。
现在要在A 、B 、C、D之间通过插值计算出⼀个点 P ,若已知 P点的坐标 (x,y),如何求出 P点的函数值坐标 z ?这⾥我们依旧可以仿照⼀维线性插值,进⾏计算。
假设先计算 y 轴⽅向的插值点 P0 和 P1 ,则根据上⾯的推导过程,且令α=y−y0 y1−y0则, P0 的取值 z0为:z0=(1−α)f(x0,y0)+αf(x0,y1) P1 的取值 z1为:z1=(1−α)f(x1,y0)+αf(x1,y1)再计算 x 轴⽅向的插值点 P,令β=x−x0 x1−x0则 P 的取值 z为:z=(1−β)z0+βz1整理得到下⾯的式⼦:z =(1−β)(1−α)f x 0,y 0+αf x 0,y 1+β(1−α)f x 1,y 0+αf x 1,y 1=(1−β)(1−α)f x 0,y 0+(1−β)αf x 0,y 1+β(1−α)f x 1,y 0+βαf x 1,y 1⼩结由⼀维线性插值过渡到⼆维线性插值,我们发现,⼆者在表达式上有相似的规律:⼀维线性插值:y =f (x )α=x p −x 0x 1−x 0y p =(1−α)f x 0+αf x 1⼆维线性插值:z =f (x ,y )α=x p −x 0x 1−x 0,β=y p −y 0y 1−y 0z p =(1−β)(1−α)f x 0,y 0+(1−β)αf x 0,y 1+β(1−α)f x 1,y 0+βαf x 1,y 1图像中的双线性插值我们可以⽤函数来表⽰⼀幅图像(假设为单通道)。
matlab几何纠正,间接法,双线性内插

matlab几 何 纠 正 , 间 接 法 , 双 线 性 内 插
超简洁,超级快,两个文件 datapre.m文件代码: global X; global Y; global A; global l; global i; global I; global m; global n; global k; global dx;
['待纠正图像Y: ',num2str(Y)]}; i=i+1; if(rem(i,2)==1) k=(i+1)/2; A(k,1)=1; A(k,2)=X; A(k,3)=Y; else
l(i/2,1)=X; l(i/2,2)=Y; end [m,n]=size(l); if(m==4) datacursormode off; dx=inv(A'*A)*(A'*l); [m,n,k]=size(I); dis=sqrt((A(2,2)-A(1,2))*(A(2,2)-A(1,2))+(A(2,3)-A(1,3))*(A(2,3)-A(1,3))); dist=sqrt((l(2,1)-l(1,1))*(l(2,1)-l(1,1))+(l(2,2)-l(1,2))*(l(2,2)-l(1,2))); sca=dist/dis; cosa=(dx(2,1)+dx(3,2))/(2*sca); sina=(-dx(2,2)+dx(3,1))/(2*sca); alfa=atan(sina/cosa); alfa=alfa*180/3.1415926; ResImage=imresize(I,sca,'bilinear'); ResImage=imrotate(ResImage,alfa,'bilinear');
(完整版)Matlab学习系列13.数据插值与拟合

13. 数据插值与拟合实际中,通常需要处理实验或测量得到的离散数据(点)。
插值与拟合方法就是要通过离散数据去确定一个近似函数(曲线或曲面),使其与已知数据有较高的拟合精度。
1.如果要求近似函数经过所已知的所有数据点,此时称为插值问题(不需要函数表达式)。
2.如果不要求近似函数经过所有数据点,而是要求它能较好地反映数据变化规律,称为数据拟合(必须有函数表达式)。
插值与拟合都是根据实际中一组已知数据来构造一个能够反映数据变化规律的近似函数。
区别是:【插值】不一定得到近似函数的表达形式,仅通过插值方法找到未知点对应的值。
【拟合】要求得到一个具体的近似函数的表达式。
因此,当数据量不够,但已知已有数据可信,需要补充数据,此时用【插值】。
当数据基本够用,需要寻找因果变量之间的数量关系(推断出表达式),进而对未知的情形作预测,此时用【拟合】。
一、数据插值根据选用不同类型的插值函数,逼近的效果就不同,一般有:(1)拉格朗日插值(lagrange插值)(2)分段线性插值(3)Hermite(4)三次样条插值Matlab 插值函数实现:(1)interp1( ) 一维插值(2)intep2( ) 二维插值(3)interp3( ) 三维插值(4)intern( ) n维插值1.一维插值(自变量是1维数据)语法:yi = interp1(x0, y0, xi, ‘method’)其中,x0, y0为原离散数据(x0为自变量,y0为因变量);xi为需要插值的节点,method为插值方法。
注:(1)要求x0是单调的,xi不超过x0的范围;(2)插值方法有‘nearest’——最邻近插值;‘linear’——线性插值;‘spline’——三次样条插值;‘cubic’——三次插值;默认为分段线性插值。
例1 从1点12点的11小时内,每隔1小时测量一次温度,测得的温度的数值依次为:5,8,9,15,25,29,31,30,22,25,27,24.试估计每隔1/10小时的温度值。
matlab插值(详细 全面)

Matlab中插值函数汇总和使用说明MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,'method')其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量, 'method'表示采用的插值方法,MATLAB提供的插值方法有几种: 'method'是最邻近插值, 'linear'线性插值; 'spline'三次样条插值; 'cubic'立方插值.缺省时表示线性插值注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
例如:在一天24小时内,从零点开始每间隔2小时测得的环境温度数据分别为12,9,9,10,18 ,24,28,27,25,20,18,15,13,推测中午12点(即13点)时的温度.x=0:2:24;y=[12 9 9 10 18 24 28 27 25 20 18 15 13];a=13;y1=interp1(x,y,a,'spline')结果为: 27.8725若要得到一天24小时的温度曲线,则:xi=0:1/3600:24;yi=interp1(x,y,xi, 'spline');plot(x,y,'o' ,xi,yi)命令1 interp1功能一维数据插值(表格查找)。
该命令对数据点之间计算内插值。
它找出一元函数f(x)在中间点的数值。
其中函数f(x)由所给数据决定。
x:原始数据点Y:原始数据点xi:插值点Yi:插值点格式(1)yi = interp1(x,Y,xi)返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。
参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。
yi是阶数为length(xi)*size(Y,2)的输出矩阵。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双线性插值算法
张俊飞一、算法简介
假设c[a]到c[a+1]之间是线性变化的,那么对于浮点数
x( a <= x < a+1)
c(x) = c[a+1]*( x - a) + c[a]*( 1 + a - x);
c(x) = c[a] + [ (c[a+1]-c[a])/(b-a)]*( x - a);
b = a+1;
c(x) = c[a] + [ c[a+1] - c[a]]*( x - a);
把这种插值方式扩展到二维情况:对于一个二维数组c,
我们假设对于任意一个浮点数i,c(a,i)到c(a+1,i)之间是线性变化的,c(i,b)到c(i,b+1)之间也是线性变化的(a,b都是整数) ,
那么对于浮点数的坐标(x,y)满足(a <= x < a+1, b <= y < b+1),可以先分别求出c(x,b)和c(x,b+1):
c(x,b) = c[a+1][b]*( x - a) + c[a][b]*( 1 + a - x);
c(x,b+1) = c[a+1][b+1]*( x - a) + c[a][b+1]*( 1 + a - x);
现在已经知道c(x,b)和c(x,b+1)了,而根据假设c(x,b)到c(x,b+1)也是线性变化的,所以: c(x,y) = c(x,b+1)*( y - b) + c(x,b)*( 1 + b - y)
二、matlab实现
在command窗口输入chahzi('cameraman.tif',2),这里cameraman.tif为灰度图片,得到结果如下:
origin image
result image
在command窗口输入chahzi('a.jpg',0.5),这里a.jpg为彩色图片,得到结果为:
origin image
result image
由以上结果可知,该算法的鲁棒性较强,图片伸缩插值保真度高。
三、代码
function []=chahzi(str,k)
% str input image
% k zoo in or out k times
% clear all
% clc
% k=2;
I=imread(str);
% if size(I,3)~=1
% I=rgb2gray(I);
% end
figure,imshow(I);
title('origin image');
I=double(I);
[rows cols tongdao]=size(I);
x_new=rows*k;
y_new=cols*k; %缩放至k倍。
I_new=zeros(x_new,y_new,tongdao );
for rgb=1:tongdao
for i=1:x_new
for j=1:y_new
x=i/k;a=floor(x); y=j/k;b=floor(y);
%% 双线性插值算法
if
a>0&&b>0&&a<rows&&b<cols
cxb=I(a+1,b,rgb)*(x-a)+I(a,b,rg b)*(1+a-x);
cxb1=I(a+1,b+1,rgb)*(x-a)+I(a,b +1,rgb)*(1+a-x);
I_new(i,j,rgb)=round(cxb1*(y-b) +cxb*(1+b-y));
end
end
end
end
% iftongdao==1%如果输入是灰度图,则% I_new=I_new(:,:,1);
% end
figure,imshow(uint8(I_new))
title('result image');。
