分式复习课件.
合集下载
分式-复习课件-(共34张PPT)

x2
1 x2
2
9
变: 已知 x2 – 3x+1=0 ,求 x2+
x
x
的1x2值. 的1x2 值.
变:已知 x+ 1=3 ,求
x
x2 /x2 的值. x4+x2+1 /x2
1
x2
1 x2
1
两个分式相乘,把分子相乘的积作为积的分子, 把分母相乘的积作为积的分母。
用符号语言表达: a c ac b d bd
27xy2
-2(a-b)2 -8(b-a)3
关键找出分子和 分母的公因式
m2+4m+4
(3)
m2 - 4
关键找出分母的
2.通分
最简公分母
(1) x 与 y (2)
6a2b
9ab2c
a-1
6
a2+2a+1 与 a2-1
约分与通分的依据都是: 分式的基本性质
整体代入法化简思想:
【【例例11】】已已知知::1x
a0 1
an
1
an
(a 0)
(1)(3)3 1 (3)3
1 27
(2)(3a)2 b2 (a2b2 )3 解:原式= 32 a2b2 a6b6
6、用科学记数法表示:
例: 0.00065 6.5104
(1) 0.000030
3.0 105
7、约分
:
例(1)
6x2y 12 xy 2
(2) x 1 2x 1 3x 2 x 1 1 x x 1
复习回顾一:
1.解分式方程的思路是:
分式 方程
去分母
整式 方程
2.解分式方程的一般步骤
分式 复习课 教学课件(两课时)

4.分式的混合运算的顺序是 先乘方、再乘除、后加减,如有括号,先算括号内。 注意:分式运算的结果要化为最简分式。
小试牛刀:
a b c 2b , , 12a 1、分式 2b 3a 2 4ab 的最简公分母是 1 1 1 1 1 , , 2 , 2 2、分式 , x x 1 x 1 x 1 x 2 x 的最简公分母是 1
一展身手:
1.不改变分式的值,使下列分 式的分子与分母的最高次项的 系数是正数:
x (1) 2 1 x
(2)
y y (3) 2 y y
2
2 x 2 x 3
2.不改变分式的值,把下列各式的分子 与分母中最高次项的系数都化为正整数。
1 1 a 2 (1) 1 a 3
a 0.2a (2) 2 3 a 0.3a
2
3、若将分式 a、b的值分别扩大为原来的2倍,则分式的值 为( ) 1 A.扩大为原来的2倍 B.缩小为原来的 2 C.不变 D.缩小为原来的 1
ab (a 、 b 均为正数)中的字母 ab
4 2 x2 4 1 m 3x 1 , , , (a b), , 4、下列各式中, 3x 2 2 y 3 x2
( A B 1) x (2 A B 5) 0
A B 1 0 2 A B 5 0
A 2 解得: B 1
例6、某工程要求限期完成,甲队独做正好 按期完成,乙队独做则要误期3天,现甲、乙 两队合做2天后,余下的工程由乙队独做,正 好按期完成,问该工程限期多少天? 例7、正在修建的西塔(西宁~塔尔寺)高速 公路上,有一段工程,若甲、乙两个工程队单 独完成,甲工程队比乙工程队少用10天;若甲、 乙两队合作,12天可以完成.若设甲单独完成 这项工程需要x天.则根据题意,可列方程为 _______________-
第三章整理《分式》(复习)ppt课件

顺水速=静水速+水流速 逆水速=静水速-水流速
设是水流速为xkm/ h
则 水 为 20 + x)km/ h 顺 速 (
逆 速 (20 - x)km/ h 水 为
72 48 = 20 + x 20 − x
A.扩大3倍 B.扩大9倍C.扩大4倍D.不变 扩大3 扩大9 扩大4
3、 填空: x ( x − y ) = ( x − 2
y)
x + xy
x+y
例1:化简求值 :
a−2 a −1 a−4 ( 2 − 2 )÷ a + 2a a + 4a + 4 a + 2 2 其中a满足:a + 2a − 1 = 0
1. 若分式
A、 A、x≠-1 C、x≠2 、
若有意义, 应满足( 若有意义,则x应满足( B ) 应满足
B、 ≠-1且 B、x ≠-1且x ≠2 D、x ≠-1或x ≠2 、 或
x −4 ( x + 1)( x − 2)
若值为0, 应满足( 若值为 ,则x应满足( B ) 应满足
A、x=2 、 C、 、
1km
中点 18km }
xkm / h
甲 A
乙 B
甲走了总共20km 甲走了总共
设 乙的速度 xkm / h 则 甲的速度( x + 0.5)km / h
20 18 = x + 0.5 x
1、一项工程,若甲队单独做,恰好在规定的日期 、一项工程,若甲队单独做, 完成,若乙队单独做要超过规定日期3天完成 天完成; 完成,若乙队单独做要超过规定日期 天完成;现 在先由甲、乙合做2天 在先由甲、乙合做 天,剩下的工程再由乙队单独 也刚好在规定日期完成, 做,也刚好在规定日期完成,问规定的日期是多 少天? 少天? 1 甲每天的工作量 x 设 天 甲x
中考数学复习《分式》教学课件

00
2.分式的混合运算.
【例题 2】 (2013·衢州)化简:x2+x24-x+4 4-x-x 2. 分析:首先确定最简公分母为(x+2)(x-2);然后通分,
第二个分式的分子与分母同乘以(x+2);最后按同分母分
式的加减法法则进行加减,并化简.
解
原
式
=
x2+4x+4-2)
如果A、B表示_两__个__整__式_,并且B中含有_字__母_,那么式
子
A B
(B≠0)叫分式,(1)当_当__分__母__为__零_时,分式无意义;
(2)_____分__子__为__零__且__分__母__不__为时零,分式的值为零.
2.分式的基本性质 A×M A÷M
AB=_B_×__M__,AB=_B_÷__M__ (其中 A、B、M 为整式,且 M≠0)
解 原式=[(x+x(2)x-(2x)-2)-
x(x-1) x(x-2)
]×
(x-2)2 x-4
=
x2-4-x2+x x(x-2)
×
(x-2)2 x-4
=
x(xx--42)×(xx--24)2
=x-x 2,3x+7>1,3x>-6,x>-2, ∵x 是不等式 3x+7>1 的负整数解,∴x=-1,
第五讲 分 式
考纲要求
1.了解分式的概念; 2.知道什么时候分式的值为零,什么时候分式有
a b
意义;
3.会利用分式的基本性质进行约分和通分; 4.会进行简单的分式的加、减、乘、除及乘方运
c c
算;
5.掌握分式的混合运算; 6.会对分式先化简,再求值.
c c
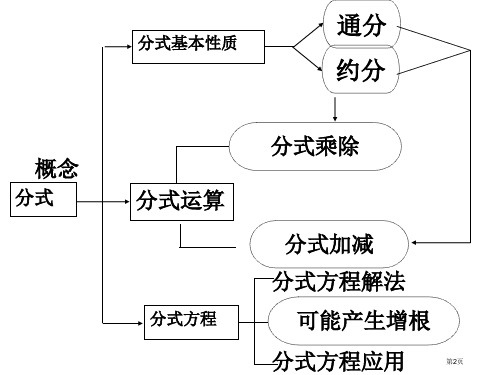
网络构建
分式的概念和基本性质
1.分式的概念
【即时应用 2】 计算:x-x 2+2-2 x=________. 答案 1
2.分式的混合运算.
【例题 2】 (2013·衢州)化简:x2+x24-x+4 4-x-x 2. 分析:首先确定最简公分母为(x+2)(x-2);然后通分,
第二个分式的分子与分母同乘以(x+2);最后按同分母分
式的加减法法则进行加减,并化简.
解
原
式
=
x2+4x+4-2)
如果A、B表示_两__个__整__式_,并且B中含有_字__母_,那么式
子
A B
(B≠0)叫分式,(1)当_当__分__母__为__零_时,分式无意义;
(2)_____分__子__为__零__且__分__母__不__为时零,分式的值为零.
2.分式的基本性质 A×M A÷M
AB=_B_×__M__,AB=_B_÷__M__ (其中 A、B、M 为整式,且 M≠0)
解 原式=[(x+x(2)x-(2x)-2)-
x(x-1) x(x-2)
]×
(x-2)2 x-4
=
x2-4-x2+x x(x-2)
×
(x-2)2 x-4
=
x(xx--42)×(xx--24)2
=x-x 2,3x+7>1,3x>-6,x>-2, ∵x 是不等式 3x+7>1 的负整数解,∴x=-1,
第五讲 分 式
考纲要求
1.了解分式的概念; 2.知道什么时候分式的值为零,什么时候分式有
a b
意义;
3.会利用分式的基本性质进行约分和通分; 4.会进行简单的分式的加、减、乘、除及乘方运
c c
算;
5.掌握分式的混合运算; 6.会对分式先化简,再求值.
c c
网络构建
分式的概念和基本性质
1.分式的概念
【即时应用 2】 计算:x-x 2+2-2 x=________. 答案 1
分式复习优质课市公开课一等奖省优质课获奖课件
1 x2 2x 1
3
x 2x2
2 1
2 x2 1 4x 4
x2
4 (π
x)2
第4页
2.分式基本性质:
分式分子和分母都乘以(或除以)同一个不等 于0整式,分式值不变.
A AM A AM
,
(其中M是不等于0整式)
B BM B BM
第5页
1.以下式子
(1) a x a (1 2)
b x b1
n ;na ,a 0
b ; a 1
ab
(3) x y x; y(4)
xy xy
ba ab ca ac
中正确是
()
A 、1个 B 、2 个 C、 3 个 D、 4 个
第9页
4b、值若分将别分扩式大为a原ab来b (2a倍、,b均则为分正式数值)为中(字)母a、
A.扩大为原来2倍 B.缩小为原来 1
C.不变
D.缩小为原来 2
x2 y2
B、 x y2
y2 x2 C、 x y
x2 y2 D、 x 2 y xy 2
第13页
1.计算:
第14页
第15页
5. a2 b2 (1 a2 b2 )
a2b ab2
2ab
6. x 3 (x 2 5 )
x2
x2
第16页
3.化简并求值:
x2
x2
2x
x2
x 1 4x 4
x y z
4.分式
,
,
5b2c 10a 2b 2ac
最简公分母是
;
3
y
x 2 y y 3 , xy x 2
最简公分母是
.
第11页
4.什么是最简分式? 一个分式分子和分母没有公因式时叫做最
数学中考专题复习分式市公开课一等奖课件名师大赛获奖课件

分式有意义的条件:分母不为零
分式值为零的条件:分子等于零且分母不等于零
例题:当 x 1 =______时,分式 x2 1 的值为0。
x 1
x2 1 0
分析:
x 1 0
x 1 x 1
2.分分式式的的基基本本性 性质质:
表达式:AB=AB× ×M M,AB=AB÷ ÷M M(M 是不等于 0 的整式). 约分:把分式的分子与分母中的公因式约去,叫做分式的 约分. 通分:利用分式的基本性质,使分子和分母同时乘以适当 的整式,不改变分式的值,把异分母化成同分母的分式, 这样的分式变形叫做分式的通分.
的
值代入求值。
解析:原式=
(x x
1 1
1 ) x 1
x2
x2 1 4x 4
x2 x 1
(x 1)(x 1) (x 2)2
x 1 x2
当 x 1 时,上式= 2 (错解)
发现:x可以取除1、-1、2以外的任意整数
正解:当 x 3 时,上式=4
例3:先化简,再求值:3mm2
3 6m
(m
x2 x2 xy xy y2 x y
y2 x y
原式=
x2 x y
x
y
方法2
xx22
((xx y)
xx yy
x2 (x y)(x y)
x y
x y
x2 (x2 y2) x y
y2 x y
例2:先化简
(1
1) x 1
x2
4x x2 1
4
,然后选一个你喜欢的整数作为
x
2
m
5
2
)
,其中
m 是方程
x 2 3x 1 0的根。
初中数学《分式》课件(同步+复习+名师=精选课件)

(4)当x =-3时,
x 4 ∴当x = 2时分式 的值为零。 x2
2
x 2 4 (3) 2 4 x2 3 2 5
1.填空:
(1)当 x≠2
1 x 时,分式 4 x 8 有意义;
时,分式
(2)当
x=3
3 x 9 x 2 的值是零;
Байду номын сангаас
xa (3)当x=2时,分式 x b 没有意义,则 b= -2
七年级
(下 册)
义务教育教科书
学科网
1、下列代数式中,哪些是整式?哪些是分式?
3 4
2
b 3 2a
y -1 x
m( n p ) 7
4 5b c
m 7
x 2 xy y 2 2 x 1
a 1 2、 对于分式 2a
(1)当a=1时,求分式的值 (2)当a取何值时,分式无意义? 当a取何值时,分式有意义? (3)当a取何值时,分式值为零?
2 y 1 x
4 5b c
3
m 7 m 7
x xy y 2 x 1
2
2
整式有: 分式有:
3 2 b 3 2 a 1
m( n p ) 7
3
4 5b c
x 2 xy y 2 2 x 1
b 分式 分母中的字母能取任何实数吗? a
为什么?分式
2x 3 中的字母x呢? x2
:
我们已经知道:
2 3 16 36
= =
25 3 5
=
10 15
;
4 9
16 4 36 4
=
这是根据分数的基本性质:
分数的分子与分母都乘以或除以同 一个不等于零的数,分数的值不变.
x 4 ∴当x = 2时分式 的值为零。 x2
2
x 2 4 (3) 2 4 x2 3 2 5
1.填空:
(1)当 x≠2
1 x 时,分式 4 x 8 有意义;
时,分式
(2)当
x=3
3 x 9 x 2 的值是零;
Байду номын сангаас
xa (3)当x=2时,分式 x b 没有意义,则 b= -2
七年级
(下 册)
义务教育教科书
学科网
1、下列代数式中,哪些是整式?哪些是分式?
3 4
2
b 3 2a
y -1 x
m( n p ) 7
4 5b c
m 7
x 2 xy y 2 2 x 1
a 1 2、 对于分式 2a
(1)当a=1时,求分式的值 (2)当a取何值时,分式无意义? 当a取何值时,分式有意义? (3)当a取何值时,分式值为零?
2 y 1 x
4 5b c
3
m 7 m 7
x xy y 2 x 1
2
2
整式有: 分式有:
3 2 b 3 2 a 1
m( n p ) 7
3
4 5b c
x 2 xy y 2 2 x 1
b 分式 分母中的字母能取任何实数吗? a
为什么?分式
2x 3 中的字母x呢? x2
:
我们已经知道:
2 3 16 36
= =
25 3 5
=
10 15
;
4 9
16 4 36 4
=
这是根据分数的基本性质:
分数的分子与分母都乘以或除以同 一个不等于零的数,分数的值不变.
《分式方程复习》课件

详细描述
在金融和经济领域,分式方程可以用来描述和预测市场行为、投资回报和成本效益分析等。在交通领 域,分式方程可以用来解决交通流量和路线规划问题。在工程领域,分式方程可以用来描述机械运动 、热传导和电路等问题。
04 分式方程的解题 技巧
转化思想
总结词
转化思想是将复杂问题转化为简单问 题,将未知问题转化为已知问题的一 种解题策略。
详细描述
分式方程与整式方程的主要区别在于分母中是否含有未知数。分式方程的分母中 含有未知数,而整式方程的分母中不含有未知数。此外,分式方程的解法通常需 要更多的技巧和注意事项,例如需要处理分母为零的情法
01
02
03
04
直接求解法
通过对方程进行化简,直接求 出方程的解。
详细描述
在解分式方程时,通过对方程进行适 当的变形和转化,可以将分式方程转 化为整式方程或更容易解决的形式, 从而简化解题过程。
整体思想
总结词
整体思想是从整体角度出发,将 问题看作一个整体,从而简化问 题的一种解题策略。
详细描述
在解分式方程时,可以将方程中 的某些项看作一个整体,通过对 方程进行整体变形和运算,从而 简化解题过程。
代数方法
总结词
代数方法是利用代数性质和定理,对方 程进行变形和求解的一种解题策略。
VS
详细描述
在解分式方程时,可以利用代数性质和定 理,如乘法分配律、合并同类项等,对方 程进行变形和简化,从而找到方程的解。
05 分式方程的易错 点分析
概念理解不清
总结词
概念理解不清晰
详细描述
分式方程的基本概念和定义是解题的基础,如果对分式方程的概念理解不清晰,会导致 解题思路出现偏差,甚至无法正确列出方程。
在金融和经济领域,分式方程可以用来描述和预测市场行为、投资回报和成本效益分析等。在交通领 域,分式方程可以用来解决交通流量和路线规划问题。在工程领域,分式方程可以用来描述机械运动 、热传导和电路等问题。
04 分式方程的解题 技巧
转化思想
总结词
转化思想是将复杂问题转化为简单问 题,将未知问题转化为已知问题的一 种解题策略。
详细描述
分式方程与整式方程的主要区别在于分母中是否含有未知数。分式方程的分母中 含有未知数,而整式方程的分母中不含有未知数。此外,分式方程的解法通常需 要更多的技巧和注意事项,例如需要处理分母为零的情法
01
02
03
04
直接求解法
通过对方程进行化简,直接求 出方程的解。
详细描述
在解分式方程时,通过对方程进行适 当的变形和转化,可以将分式方程转 化为整式方程或更容易解决的形式, 从而简化解题过程。
整体思想
总结词
整体思想是从整体角度出发,将 问题看作一个整体,从而简化问 题的一种解题策略。
详细描述
在解分式方程时,可以将方程中 的某些项看作一个整体,通过对 方程进行整体变形和运算,从而 简化解题过程。
代数方法
总结词
代数方法是利用代数性质和定理,对方 程进行变形和求解的一种解题策略。
VS
详细描述
在解分式方程时,可以利用代数性质和定 理,如乘法分配律、合并同类项等,对方 程进行变形和简化,从而找到方程的解。
05 分式方程的易错 点分析
概念理解不清
总结词
概念理解不清晰
详细描述
分式方程的基本概念和定义是解题的基础,如果对分式方程的概念理解不清晰,会导致 解题思路出现偏差,甚至无法正确列出方程。
