一笔画成的数学
浅谈一笔画问题

浅谈一笔画问题公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]浅谈一笔画问题摘要:一笔画问题是一个几何问题,传统意义上的几何学是研究图形的形状大小等性质,而存在一些几何问题,它们所研究的对象与图形的形状和线段的长短没关系,而只和线段的数目和它们之间的连接关系有关,比如一笔画问题就是如此。
一笔画问题是一个简单的数学游戏,即平面上由曲线段构成的一个图形能不能一笔画成,使得在每条线段上都不重复例如汉字‘日’和‘中’字都可以一笔画的,而‘田’和‘目’则不能。
关键词:一笔画规律原理早在18世纪,瑞士的着名数学家欧拉就找到了一笔画的规律。
欧拉认为,能一笔画的图形必须是连通图。
连通图就是指一个图形各部分总是有边相连的.但是,不是所有的连通图都可以一笔画的。
能否一笔画是由图的奇、偶点的数目来决定的。
一笔画问题是图论中一个着名的问题。
一笔画问题起源于柯尼斯堡七桥问题。
数学家欧拉在他1736年发表的论文《柯尼斯堡的七桥》中不仅解决了七桥问题,也提出了一笔画定理,顺带解决了一笔画问题。
一般认为,欧拉的研究是图论的开端。
与一笔画问题相对应的一个图论问题是哈密顿问题。
一、一笔画规律数学家欧拉找到一笔画的规律是:(一)凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
(二)凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
画时必须把一个奇点为起,,另一个奇点终点。
(三)其他情况的图都不能一笔画出。
(有偶数个奇点除以二便可算出此图需几笔画成)比如附图:(a)为(1)情况,因此可以一笔画成;(b)(c)(d)则没有符合以上两种情况,所以不能一笔画成。
补充:相关名词的含义◎顶点与指数:设一个平面图形是由有限个点及有限条弧组成的,这些点称为图形的顶点,从任一顶点引出的该图形的弧的条数,称为这个顶点的指数。
◎奇顶点:指数为奇数的顶点。
◎偶顶点:指数为偶数的顶点。
第九讲 一笔画问题 PPT

• 解答:图(1)中无奇点,能一笔画出,从任意点开始再回到这一点, 仅举一例:A→B→C→N→F→G→H→M→D→N→E→M→H;
• 图(2)有两个奇点,可以从B开始到E结束,也可以从E开始到B结束, 如:B→C→D→E→A→B→E;
• 图(3)不能一笔画出有4个奇点,要想一笔画出至少应该添一笔,可 以连接A、B,如图1,其它的任何两个奇点都可以。共有多少连法呢, 你能列举出来吗?共有6种分别为AB、AC、AD、BC、BD、CD;
重复.从上图中容易看出:能一笔画出的图首先必须是连
通图.但是否所有的连通图都可以一笔画出呢?下面,我
们就来探求解决这个问题的方法。
•
为了叙述的方便,我们把与奇数条边相连的结点叫做
奇点,把与偶数条边相连的点称为偶点.如上图(a)中的
八个结点全是奇点,上图(b)中E、F为奇点,G为偶点。
•
容易知道,上图(b)可以一笔画出,即从奇点E出发,
得出了一个非常重要的结论,你想知道吗?其实
这就是“一笔画”问题,也是一种数学游戏,学
完了下面的内容,也许你就能像欧拉那样解决
“七桥问题”了。
• 欧拉解决这个问题的方法非常巧妙.他认为: 人们关心的只是一次不重复地走遍这七座桥,而 并不关心桥的长短和岛的大小,因此,岛和岸都 可以看作一个点,而桥则可以看成是连接这些点 的一条线.这样,一个实际问题就转化为一个几何 图形能否一笔画出的问题了.
都有一条通路(即可以从其中一点出发,沿着图 的边走到另一点,如A到I的通路为A→H→I或 A→D→I…),这样的图,我们称为连通图;而 下图中(c)的一些结点之间却不存在通路(如M 与N),像这样的图就不是连通图。
•
所谓图的一笔画,指的就是:从图的一点出发,笔不
世界数学难题——一笔画
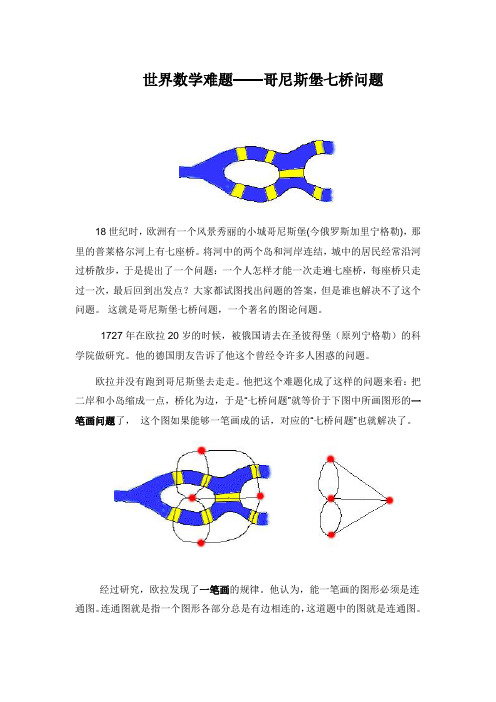
世界数学难题——哥尼斯堡七桥问题18世纪时,欧洲有一个风景秀丽的小城哥尼斯堡(今俄罗斯加里宁格勒),那里的普莱格尔河上有七座桥。
将河中的两个岛和河岸连结,城中的居民经常沿河过桥散步,于是提出了一个问题:一个人怎样才能一次走遍七座桥,每座桥只走过一次,最后回到出发点?大家都试图找出问题的答案,但是谁也解决不了这个问题。
这就是哥尼斯堡七桥问题,一个著名的图论问题。
1727年在欧拉20岁的时候,被俄国请去在圣彼得堡(原列宁格勒)的科学院做研究。
他的德国朋友告诉了他这个曾经令许多人困惑的问题。
欧拉并没有跑到哥尼斯堡去走走。
他把这个难题化成了这样的问题来看:把二岸和小岛缩成一点,桥化为边,于是“七桥问题”就等价于下图中所画图形的一笔画问题了,这个图如果能够一笔画成的话,对应的“七桥问题”也就解决了。
经过研究,欧拉发现了一笔画的规律。
他认为,能一笔画的图形必须是连通图。
连通图就是指一个图形各部分总是有边相连的,这道题中的图就是连通图。
但是,不是所有的连通图都可以一笔画的。
能否一笔画是由图的奇、偶点的数目来决定的。
那么什么叫奇、偶点呢?与奇数(单数)条边相连的点叫做奇点;与偶数(双数)条边相连的点叫做偶点。
如下图中的①、④为奇点,②、③为偶点。
1.凡是由偶点组成的连通图,一定可以一笔画成。
画时可以把任一偶点为起点,最后一定能以这个点为终点画完此图。
例如下图都是偶点,画的线路可以是:①→③→⑤→⑦→②→④→⑥→⑦→①2.凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。
画时必须把一个奇点为起点,另一个奇点终点。
例如下图的线路是:①→②→③→①→④3.其他情况的图都不能一笔画出。
一笔画问题

一笔画问题画一个图案,如果用笔既不重复也不遗漏,纸不离笔,一笔画成,那么就称这个图案是一笔画图案.现在我们来研究的问题是:(1)怎样的图案才能一笔画成?(2)如果一个图案能一笔画成,那么该从哪里起笔到哪里收笔?需提醒大家的是,这些问题与图案中的“奇点”的个数有关.何谓奇点呢?我们知道,任何图案都是由线条(直线或曲线)连成的.在图案中,由三条或三条以上的方向各不相同的线连接在一起的点叫做图案点,通过图案点的线是奇数条就称奇点(当然,通过图案点的线是偶数条就称偶点,现在只需回答前面的问题而与偶点无关).例如,在下面各图案中的奇点个数见统计表(请读者对照图案辨认奇点).统计表:接着就请读者朋友拿起你的笔来逐个试画以上各图案,看能否一笔画成,将结论填在统计表内.并注意体会能一笔画的图案应该怎样画.最后,请根据上表归纳出前面两个问题的答案.【规律】(1)奇点数为0或2的图案可以一笔画成.奇点数多于2的图案不能一笔画成.(2)画奇数为0的图案时,可以选择任意点起笔都能一笔画成;画奇数为2的图案时,必须选择其中的一个奇点起笔,而到另一个奇点收笔才能一笔画成.【练习】1.下面各图案,能一笔画出来吗?试一试.2.容易看出,下面的两个图案都不能一笔画成,请在每个图案上各补画一条线就能使新图案一笔画成了.会吗?3.这是大数学家欧拉曾经研究过的一个著名数学问题----七桥问题.东普士的多尼斯堡城中有一条横贯城区的河流,河上有两个岛,两岸和两岛之间共架有七座桥、如下图所示:问人们能不重复地走遍这七座桥吗?4.回龙州公园的游览点与路线示意图如下.如果要使游人游完所有的游览点而不重复行走的路线,请问入口处和出口处应该设在什么位置?如果一个图形可以用笔在纸上连续不断而且不重复地一笔画成,那么这个图形就叫一笔画。
显然,在下面的图形中,(1)(2)不能一笔画成,故不是一笔画,(3)(4)可以一笔画成,是一笔画。
同学们可能会问:为什么有的图形能一笔画成,有的图形却不能一笔画成呢?一笔画图形有哪些特点?关于这个问题有一个著名的数学故事——哥尼斯堡七桥问题。
小学数学一笔画课件

THANKS FOR WATCHING
感谢您的观看
03
一笔画问题的解题方法
逐步推理法
总结词
通过逐步推理,按照一定的逻辑顺序,确定笔画的路径。
详细描述
逐步推理法是一种常用的解题方法,它通过逐步分析图形的特点和规律,推断出 笔画的路径。这种方法需要有一定的逻辑推理能力,对于一些较为复杂的图形, 需要仔细分析其结构,找出正确的笔画路径。
奇偶点分析法
拉回路是指一条通过图形的每条边且每条边只通过一次的闭合路径。
02
奇点与偶点
在图形中,如果一个节点发出的线条数是奇数,则该节点称为奇点;如
果一个节点发出的线条数是偶数,则该节点称为偶点。
03
哈密顿路径和哈密顿回路
哈密顿路径是指一条通过图形的每条边且每条边只通过一次的路径,但
不一定是闭合路径;哈密顿回路是指一条通过图形的每条边且每条边只
计算机科学
一笔画问题在计算机科学 中也有广泛应用,例如在 计算机图形学、算法设计 等领域。
实际应用
一笔画问题在现实生活中 也有很多应用,如地图的 绘制、电路设计、交通规 划等。
02
一笔画问题的数学原理
欧拉公式
欧拉公式
对于一个连通图,其边数和顶点数的关系可以用公式(V - E + F = 2)来表示,其中(V)表示顶点数,(E)表示边数,(F)表示面 数。这个公式是解决一笔画问题的重要依据。
问题的能力。
创新的一笔画问题
总结词
创意问题,挑战性
VS
详细描述
创新的一笔画问题通常涉及更为复杂和创 意的图形,如不规则多边形、立体图形等 ,这类问题旨在激发学生的创造力和挑战 精神。同时,这类问题也可能涉及到数学 中的其他知识点,如平面几何、立体几何 等。
小学二年级益智数学 九、一笔画成

九、一笔画成学习导航:在我们的生活和学习过程中,我们经常碰到一些能够一笔就画成的图形或图案。
这就是今天我们要研究的一笔画的问题。
它是一种有趣的数学游戏。
所谓一笔画,就是从图形上某点出发,笔不离开纸,而且每条线都只画一次不重复。
我们知道,任何图形都是由点和线组成的,图形中的点分为两大类:(1)从一点出发的线的条数是双数,这点称为双数点。
(2)从一点出发的线的条数是单数,这点称为单数点。
一个图形能否一笔画成,关键在于图中的单数点的多少。
图形中没有单数点的,一定可以一笔画成;图形中只有两个单数点的,也一定可以一笔画成;其他情况的图形,都不能一笔画成。
单数点在一笔画中只能作为起点或终点。
例1.你能从下面图形中有小黑点的地方开始画,不重复、不遗漏,一笔就把每个图形画出来吗?为什么?(1)(2)(3)例2.下面的图形可以一笔画成吗?为什么?能的话,应从什么位置起笔?(1)(2)(3)例3.观察下面图形,哪个可以一笔画成?怎样画?(3)例4.右图是某地区所有街道的平面图,甲、乙两人同时分别从A、B两地出发,以相同的速度走遍所有的街道,最后到达C点,问两人谁能最先到达C?练习题:1.判断下面各图哪个可以一笔画成?试一试。
(3)2.请你一笔画成下面的图形,并标明应从哪里起笔。
(1)(2)(3)3.判断下面哪些图形可以一笔画成?为什么?能画得请在图中标明起点位置。
(1)(2)(3)(4)(5)4.下图是一个公园的平面图,要是游客走遍每条路而不重复,出入口应设在哪里? BA5.下图是商场的平面图,顾客可以从六个门进出商场,怎样走才能不重复的走遍商场的每条通道?。
一笔画问题

一笔画问题
1.瑞士大数学家欧拉在七桥问题的过程中,发现了一笔画原理,这一原理被命名为“欧拉定理”:
(1)能一笔画的图形必须是连通的。
(2)凡是只由偶顶点组成的连通图形,一定可以一笔画出,画时可以由任一偶顶点为起点,最后仍回到这点。
(3)凡是只有两个奇顶点的连通图形一定可以一笔画出,画时必须以一个奇顶点为起点,以另一个奇顶点为终点。
(4)奇顶点个数超过两个的图形不能一笔画出。
2.能一笔画出的图形的奇顶点数目是2或0,如果图形有奇顶点2N(n为正整数)个,那么图形最少要用N笔画出。
苏教版二年级下册奥数培优 第10讲 一笔画成
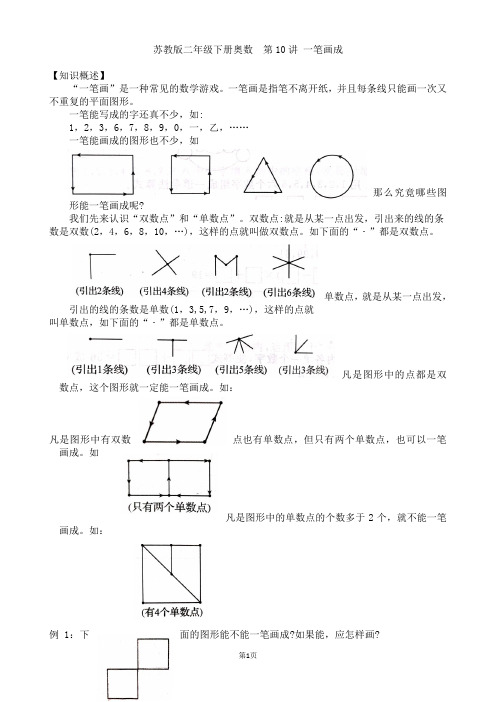
苏教版二年级下册奥数第10讲一笔画成【知识概述】“一笔画”是一种常见的数学游戏。
一笔画是指笔不离开纸,并且每条线只能画一次又不重复的平面图形。
一笔能写成的字还真不少,如:1,2,3,6,7,8,9,0,一,乙,……一笔能画成的图形也不少,如那么究竟哪些图形能一笔画成呢?我们先来认识“双数点”和“单数点”。
双数点:就是从某一点出发,引出来的线的条数是双数(2,4,6,8,10,…),这样的点就叫做双数点。
如下面的“・”都是双数点。
单数点,就是从某一点出发,引出的线的条数是单数(1,3,5,7,9,…),这样的点就叫单数点,如下面的“・”都是单数点。
凡是图形中的点都是双数点,这个图形就一定能一笔画成。
如:凡是图形中有双数点也有单数点,但只有两个单数点,也可以一笔画成。
如凡是图形中的单数点的个数多于2个,就不能一笔画成。
如:例1:下面的图形能不能一笔画成?如果能,应怎样画?练习一:1.下面两个图形能一笔画成吗?如果能,请一笔画成功。
2.下面的图形能不能一笔画成?如果能,应怎样画?3.下面的图形能不能一笔画成?为什么?例2:下面的图形能不能一笔画成?如果能,应该怎样画?练习二:1.下面的图形能不能一笔画成?如果能,应该怎样画?如果不能,请说明理由。
2.下面的图形能不能一笔画成?如果能,应该怎样画?3.下面的图形能不能一笔画成?如果能,应该怎样画?例3:有一条河,河中有两个小岛,河上有7座桥,把这两个岛与河岸联系起来,能不能不重复地走遍七座桥,最后又回到出发点?练习三:1.下图是一个迷阵图,箭头指出了迷阵的入口和出口。
请你画线表示从入口进入迷阵,从出口走出来。
能不能走通?2.下图是某展览馆的平面图,相邻两个展室之间有一个门相通,每个展室都有一扇门通往馆外。
一个参观者怎样走才能不重复地走过每一扇门?如果这种走法不存在,应关闭展览室的哪扇门才能实现上述走法?3.下图中有11个邮递员的投递点,邮递员叔叔要向这11个地点送信,邮递员能不能不重复地一次走遍各个点?如果能应怎样走?例4:下面的图形中有6个单数点,因此不能一笔画成功。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、什么是一笔画问题?
下面这些图形能不能一笔画完,而且每一条线只描绘一次,不得重复?
这类题目就叫做一笔画问题,在这些图形中有偶数点和奇
数点。
二、柯尼斯堡的七座桥
18世纪,东普鲁士的首府哥尼斯堡是一座景色迷人的城市,普莱格尔河横贯城区,使这座城市锦上添花,显得更加风光旖旋。
这条河有两条支流,在城中心汇成大河,在河的中央有一座美丽的小岛。
河上有七座各具特色的桥把岛和河岸连接起来。
每到傍晚,许多人都来此散步。
人们漫步于这七座桥之间,久而久之,就形成了这样一个问题:能不能既不重复又不遗漏地一次相继走遍这七座桥?这就是闻名遐迩的“哥尼斯堡七桥问题。
”每一个到此游玩或散心的人都想试一试,可是,对于这一看似简单的问题,没有一个人能符合要求地从七座桥上走一遍。
这个问题后来竟变得神乎其神,说是有一支队伍,奉命要炸毁这七座桥,并且命令要他们按照七桥问题的要求去炸。
七桥问题也困扰着哥尼斯堡大学的学生们,在屡遭失败之后,他们给当时著名数学家欧拉写了一封信,请他帮助解决这个问题。
欧拉看完信后,对这个问题也产生了浓厚的兴趣。
他想,既然岛和半岛是桥梁的连接地点,两岸陆地也是桥梁的连接地点,那就不妨把这四处地方缩小成四个点,并且把这七座桥表示成七条线。
这样,原来的七桥问题就抽象概括成了如
下的关系图:这显然并没有改变问题的本质特征。
于是,七桥问题也就变成了一个一笔画的问题,即:能否笔不离纸,不重复地一笔画完整个图形。
这竟然与孩子们的一笔画游戏联系起来了。
接着,欧拉就对“一笔画”问题进行了数学分析。
一笔画有起点和终点,起点和终点重合的图形称为封闭图形,否则便称为开放图形。
除起点和终点外,一笔画中间可能出现一些曲线的交点。
欧拉注意到,只有当笔沿着一条弧线到达交点后,又能沿着另一条弧线离开,也就是交汇于这些点的弧线成双成对时,一笔画才能完成,这样的交点就称为“偶点”。
如果交汇于这些点的弧线不是成双成对,也就是有奇数条,则一笔画就不能实现,这样的点又叫做“奇点”。
欧拉通过分析,得到了下面的结论:若是一个一笔画图形,要么只有两个奇点,也就是仅有起点和终点,这样一笔画成的图形是开放的;要么没有奇点,也就是终点和起点连接起来,这样一笔画成的图形是封闭的。
由于七桥问题有四个奇点,所以要找到一条经过七座桥,但每座桥只走一次的路线是不可能的。
数学家欧拉:
1707年4月15日,欧拉诞生于瑞士的巴塞尔。
小时候他就特别喜欢数学,不满10岁就开始自学《代数学》。
这本书连他的几位老师都没读过,可小欧拉却读得津津有味,遇到不懂的地方,就用笔作个记号,事后再向别人请教。
1720年,13岁的欧拉靠自己的努力考入了巴塞尔大学。
这在当时是个奇迹,曾轰动了数学界。
小欧拉是这所大学,也是整个瑞士大学校园里年龄最小的学生。
欧拉大学毕业后到了俄国的首都彼得堡。
在他26岁时,担任了彼得堡科学院的数学教授。
1735年,年仅28岁的欧拉,由于要计算一个彗星的轨道,奋战了三天三夜,最后用他自己发明的新方法圆满地解决了这个难题。
过度的工作,使欧拉得了眼病,就在那一年他右眼失明了。
疾病没有吓倒他,他更加勤奋地工作,写出了几百篇论文,大量出色的研究成果,使他在欧洲科学界享有很高的声望。
在他59岁时,仅剩的一只左眼视力衰退,只能模糊地看到物体,最后双目失明。
但是工作就是他的生命,他决心用加倍的努力,来回答命运对他的挑战。
眼睛看不见,他就口述,由他的儿子记录,继续写作。
欧拉凭着他惊人的记忆力和心算能力,在黑暗中整整工作了17年。
欧拉的一生,是为数学发展而奋斗的一生,他那杰出的智慧,顽强的毅力,孜孜不倦的奋斗精神和高尚的科学道德,永远是值得我们学习的.欧拉还创设了许多数学符号,例如π(1736年),i(1777年),e(1748年),sin和cos(1748年),tg(1753年),
△x(1755年),Σ(1755年),f(x)(1734年)等.欧拉是18世纪最优秀的数学家,也是历史上最伟大的数学家之一。
1783年9月18日,在不久前才刚计算完气球上升定律的欧拉,在兴奋中突然停止了呼吸,享年76岁。
欧拉生活、工作过的三个国家:瑞士、俄国、德国,都把欧拉作为自己的数学家,为有他而感到骄傲。
三、认识奇数点和偶数点
有偶数条线通过的点,叫做偶数点。
有奇数条线通过的点,叫做奇数点。
四、能一笔画成的图形的特点
◆1.每一个图形的奇数点个数必定是偶数。
◆2.若一个图形可以一笔画成,它必为一个连通的图
形。
(连通图形:任何两点间都有路径可到)
◆3.至多有两个奇数点的图形,必可一笔画成。
◆4.若某图形只有两個奇数点,那么其中一个奇数点
必定是起点,另一个则是終点。
◆5.若某图形上的点都是偶数点,无论从哪一点开始
都可一笔画完。
◆6.若某图形可用一笔画成,那么只要掌握了起点,
而且未走完的图形仍是连通图形,这个图就一定可以一笔画成。
五、小试身手
下列哪些图形可以一笔画成?
六、我是智慧小达人
下列图形能一笔画成吗?
六、我是小小画家达人
这些图画我都能画。
七、欧拉图形的应用
可一笔画成、且起点与终点相同的图形,称之为欧拉图形。
这是数学家们为紀念欧拉在1736年所提出关于一笔画问题
的论文所命名的。
欧拉图形概念应用在:
1.英国数学家古德用欧拉图形设计计算机的储存器。
2.我国学者管梅谷教授应用在作业研究方面,而提出了
中国邮差问题。
3.塔克和包定应用在都市的清扫问题。
4.裴夫兹捺应用于決定DNA序列。
