专题05 四边形(名师点睛+能力提升)(原卷板)

合集下载

2020年中考数学备考专题能力提升训练卷：四边形

培优专题能力提升训练卷：《四边形》1．如图，现有一张矩形纸片ABCD ，AB ＝4，BC ＝8，点M ，N 分别在矩形的边AD ，BC 上，将矩形纸片沿直线MN 折叠，使点C 落在矩形的边AD 上，记为点P ，点D 落在G 处，连接PC ，交MN 丁点Q ，连接CM ．（1）求证：PM ＝PN ；（2）当P ，A 重合时，求MN 的值；（3）若△PQM 的面积为S ，求S 的取值范围．2．将矩形ABCD 绕点B 顺时针旋转得到矩形A 1BC 1D 1，点A 、C 、D 的对应点分别为A 1、C 1、D 1．（1）当点A 1落在AC 上时．①如图1，若∠CAB ＝60°，求证：AC ∥D 1B ；②如图2，AD 1交CB 于点O ．若∠CAB ≠60°，求证：DO ＝AO ；（2）①如图3，当A 1D 1过点C 时．若BC ＝15，CD ＝9，则A 1A 的长＝． ②当∠A 1BA ＝45°时，作A 1E ⏊AB ，△A 1EB 绕点B 转动，当直线A 1E 经过D 时，BC ＝15，CD ＝9，直线A 1E 交边AB 于N ，的值＝．3．（1）观察猜想，如图①点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE＝90°，AD＝AE，则BC、BD、CE之间的数量关系为；（2）问题解决，如图②，在Rt△ABC中，∠ABC＝90°，CB＝6，AB＝3，以AC为直角边向外作等腰Rt△DAC，连结BD，求BD的长；（3）拓展延伸如图③，在四边形ABCD中，∠ABC＝∠ADC＝90°，CB＝6，AB＝3，DC＝DA，请直接写出BD的长．4．已知：如图，在菱形ABCD中，AB＝2，∠B＝60°，把一个含60°角的三角尺与这个菱形叠合，使三角尺60°角的顶点与点A重合，将三角尺绕点A按逆时针方向旋转．（1）菱形ABCD的面积为．（2）如图1，当三角尺的两边分别与菱形的两边BC、CD相交于点E、F．①求证：CE+CF＝AB；②若点P是AF的中点，当点E由点B运动到点C时，点P运动的路线长为．（3）如图2，当三角尺的两边分别与菱形的两边BC、CD的延长线相交于点E、F．写出此时CE、CF、AB长度之间关系的结论．（不需要证明）5．如图①，已知△ABC是等腰直角三角形，∠BAC＝90°，点D是BC的中点．作正方形DEFG，使点A，C分别在DG和BE上，连接AE，BG．（1）试猜想线段BG和AE的数量关系，请直接写出你得到的结论；（2）将正方形DEFG绕点D逆时针方向旋转一定角度后（旋转角度大于0°，小于或等于360°），如图②，通过观察或测量等方法判断（1）中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由．（3）若BC＝DE＝10，在（2）的旋转过程中，求线段AE长的最大值和最小值．6．（1）【发现证明】如图1，在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF＝45°，求证：EF＝DF+BE．小明发现，当把△ABE绕点A顺时针旋转90°至△ADG，使AB与AD重合时能够证明，请你给出证明过程．（2）【类比引申】①如图2，在正方形ABCD中，如果点E，F分别是CB，DC延长线上的动点，且∠EAF＝45°，则（1）中的结论还成立吗？请写出证明过程．②如图3，如果点E，F分别是BC，CD延长线上的动点，且∠EAF＝45°，则EF，BE，DF之间的数量关系是（不要求证明）（3）【联想拓展】如图1，若正方形ABCD的边长为6，AE＝3，求AF的长．7．（1）问题：如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为BC边上一点（不与点B，C重合），连接AD，过点A作AE⊥AD，并满足AE＝AD，连接CE．则线段BD和线段CE的数量关系是，位置关系是．（2）探索：如图2，当D点为BC边上一点（不与点B，C重合），Rt△ABC与Rt△ADE 均为等腰直角三角形，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE．试探索线段BD2、CD2、DE2之间满足的等量关系，并证明你的结论；（3）拓展：如图3，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°，若BD＝3，CD＝1，请直接写出线段AD的长．8．如图，正方形ABCD的边长为4，点E，F分别在边AB，AD上，且∠ECF＝45°，CF的延长线交BA的延长线于点G，CE的延长线交DA的延长线于点H，连接AC，EF，GH．（1）填空：∠AHC∠ACG；（填“＞”或“＜”或“＝”）（2）线段AC，AG，AH什么关系？请说明理由；（3）设AE＝m，请直接写出使△CGH是等腰三角形的m值．9．如图1，平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC，若有PA2＝PB2+PC2则称点P为△ABC关于点A的勾股点．（1）如图2，在4×5的网格中，每个小正方形的长均为1，点A、B、C、D、E、F、G均在小正方形的顶点上，则点D是△ABC关于点的勾股点；在点E、F、G三点中只有点是△ABC关于点A的勾股点．（2）如图3，E是矩形ABCD内一点，且点C是△ABE关于点A的勾股点，①求证：CE＝CD；②若DA＝DE，∠AEC＝120°，求∠ADE的度数．（3）矩形ABCD中，AB＝5，BC＝6，E是矩形ABCD内一点，且点C是△ABE关于点A的勾股点，若△ADE是等腰三角形，直接写出AE的长．10．在正方形ABCD中，点E、F分别在边BC、AD上，DE＝EF，过D作DG⊥EF于点H，交AB 边于点G．（1）如图1，求证：DE＝DG；（2）如图2，将EF绕点E逆时针旋转90°得到EK，点F对应点K，连接KG，EG，若H 为DG中点，在不添加任何辅助线及字母的情况下，请直接写出图中所有与EG长度相等的线段（不包括EG）．11．如图，在矩形ABCD中，AB＝4，BC＝3，BD为对角线．点P从点B出发，沿线段BA向点A运动，点Q从点D出发，沿线段DB向点B运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到A时，两点都停止．设运动时间为t秒．（1）是否存在某一时刻t，使得PQ∥AD？若存在，求出t的值；若不存在，说明理由．（2）设四边形BPQC的面积为S，求S与t之间的函数关系式．（3）是否存在某一时刻t，使得S四边形BPQC ：S矩形ABCD＝9：20？若存在，求出t的值；若不存在，则说明理由．（4）是否存在某一时刻t，使得PQ⊥CQ？若存在，求出t的值；若不存在，则说明理由．12．已知，正方形ABCD的边长为4，点E是对角线BD延长线上一点，AE＝BD．将△ABE绕点A顺时针旋转α（0°＜α＜360°）得到△AB'E'，点B、E的对应点分别为B'、E'．（Ⅰ）如图1，当α＝30°时，求证：B'C＝DE；（Ⅱ）连接B′E、DE′，当B'E＝DE''时，请在图2中补全图形，并求出α的值；（Ⅲ）如图3，点P为AB的中点，点Q为线段B'E'上任意一点，试探究：在此旋转过程中，线段PQ长度的取值范围为．13．如图1正方形ABCD，边CD在等腰三角形DEF的边DE上，AB＝3，DE＝5，连接AE、CF，点M、N分别是AE、CF的中点，连DM、DN、MN．（1）直接写出AE与CF的关系和△DMN的形状．（2）如图2，将等腰直角三角形DEF绕点D顺时针旋转α°（0°≤α≤45°），连接AE、CF，点M、N分别是AE、CF的中点，连DM、DF、MN．此时（1）中的两个结论是否成立？若成立，给出证明；若不成立，说明理由．（3）在（2）的条件下，△ECF的面积在旋转过程中变化吗？若没有变化，请直接写出面积；若有变化，请直接写出它的最大值和最小值．14．已知：如图，在菱形ABCD中，对角线AC，BD交于点O，AC＝16cm，BD＝12cm，点P从点A出发，沿AD方向匀速运动，速度为1cm/s；同时，点Q从点D出发，沿DC方向匀速运动，速度为2cm/s；当一个点停止运动时，另一个点也停止运动，连接PO并延长，交BC于点E，过点Q作QF∥AC，交BD于点F，设运动时间为t（s）（0＜t＜5），解答下列问题：（1）当t为何值时，QE⊥AC？（2）设五边形OECQF的面积为S（cm2），试确定S与t的函数关系式；（3）在运动过程中，是否存在某一时刻t，使S五边形OECQF ：S菱形ABCD＝1：5？若存在，求出t的值；若不存在，请说明理由；15．如图1，长方形OABC的边OA、OC分别在x轴、y轴上，B点坐标是（8，4），将△AOC 沿对角线AC翻折得△ADC，AD与BC相交于点E．（1）求证：△CDE≌△ABE（2）求E点坐标；（3）如图2，动点P从点A出发，沿着折线A→B→C→O运动（到点O停止），是否存在点P，使得△POA的面积等于△ACE的面积，若存在，直接写出点P坐标，若不存在，说明理由．参考答案1．（1）证明：如图1中，∵四边形ABCD是矩形，∴PM∥CN，∴∠PMN＝∠MNC，∵∠MNC＝∠PNM，∴∠PMN＝∠PNM，∴PM＝PN．（2）解：点P与点A重合时，如图2中，设BN＝x，则AN＝NC＝8﹣x，在Rt△ABN中，AB2+BN2＝AN2，即42+x2＝（8﹣x）2，解得x＝3，∴CN＝8﹣3＝5，AC＝＝＝4，∴CQ＝AC＝2，∴QN＝＝＝，∴MN ＝2QN ＝2．（3）解：当MN 过点D 时，如图3所示，此时，CN 最短，四边形CMPN 的面积最小，则S 最小为S ＝S 菱形CMPN ＝×4×4＝4，当P 点与A 点重合时，CN 最长，四边形CMPN 的面积最大，则S 最大为S ＝×5×4＝5， ∴4≤S ≤5，2．（1）证明：①如图1中，∵∠BAC ＝60°，BA ＝BA 1， ∴△ABA 1是等边三角形， ∴∠AA 1B ＝60°， ∵∠A 1BD 1＝60°， ∴∠AA 1B ＝∠A 1BD 1， ∴AC ∥BD 1．②如图2中，连接BD 1，BD ，DD 1．∵BA ＝BA 1，BD ＝BD 1，∠ABA 1＝∠DBD 1， ∴∠BAA 1＝∠BDD 1， ∵∠BAA 1＝∠BDC ， ∴∠BDC ＝∠BDD 1，∴D ，C ，D 1共线，∵∠BCD 1＝∠BAD 1＝90°，BD 1＝D 1B ，BC ＝A 1D 1，∴Rt △BCD 1≌Rt △D 1A 1B （HL ），∴CD 1＝BA 1，∵BA ＝BA 1，∴AB ＝CD 1，∵AC ＝BD 1∴四边形ABD 1C 是平行四边形，∴OC ＝OB∵CD ＝BA ，∠DCO ＝∠ABO ，∴△DCO ≌△ABO （SAS ），∴DO ＝OA ．（2）①如图3中，作A 1E ⊥AB 于E ，A 1F ⊥BC 于F ．在Rt △A 1BC 中，∵∠CA 1B ＝90°，BC ＝15．AB ＝9，∴CA 1＝＝＝12， ∵•A 1C •A 1B ＝•BC •A 1F ，∴A 1F ＝，∵∠A 1FB ＝∠A 1EB ＝∠EBF ＝90°，∴四边形A 1EBF 是矩形，∴EB ＝A 1F ＝，A 1E ＝BF ＝＝＝， ∴AE ＝9﹣＝，在Rt △AA 1E 中，AA 1＝＝＝．故答案为．②如图4中，连接BD．∵四边形ABCD是矩形，∴∠DAN＝90°，AD＝BC＝15，CD＝AB＝9，在Rt△A1BE中，∵BA1＝BA＝9，∠A1BE＝45°，∴BE＝EA1＝，∵∠DAN＝∠BEN＝90°，∠AND＝∠BNE，∴△DAN∽△BEN，∴＝＝＝．故答案为．3．解：（1）观察猜想结论：BC＝BD+CE，理由是：如图①，∵∠B＝90°，∠DAE＝90°，∴∠D+∠DAB＝∠DAB+∠EAC＝90°，∴∠D＝∠EAC，∵∠B＝∠C＝90°，AD＝AE，∴△ADB≌△EAC（AAS），∴BD＝AC，EC＝AB，∴BC＝AB+AC＝BD+CE；故答案为：BC＝BD+CE；（2）问题解决如图②，过D作DE⊥AB，交BA的延长线于E，由（1）同理得：△ABC≌△DEA，∴DE＝AB＝3，AE＝BC＝6，Rt△BDE中，BE＝9，由勾股定理得：BD＝＝＝3；（3）拓展延伸如图③，过D作DE⊥BC于E，作DF⊥AB于F，同理得：△CED≌△AFD，∴CE＝AF，ED＝DF，设AF＝x，DF＝y，则，解得：，∴BF＝3+＝，DF＝，由勾股定理得：BD＝＝．4．解：（1）如图1，过点A作AE⊥BC于点E，∵菱形ABCD中，AB＝2，∠B＝60°，∴∠BAE＝30°，BC＝AB＝2，∴AE＝，∴S＝BC×．菱形ABCD故答案为：2；②如图2，连接AC．∵四边形ABCD是菱形，∴AB＝BC＝CD＝DA．∵∠B＝60°，∴∠D＝60°，∴△ABC、△ACD都是等边三角形，∴AB＝AC，∠BAC＝∠ACD＝∠B＝60°．∵∠EAF＝60°，∴∠BAC＝∠EAF＝60°，∴∠BAC﹣∠EAC＝∠EAF﹣∠EAC，即∠BAE＝∠CAF，在△BAE和△CAF中，，∴△BAE≌△CAF（ASA），∴BE＝CF，∴CE+CF＝CB＝AB．②由①知，当点E与点B重合时，点P为AC的中点，当点E由点B运动到点C时，点P运动路线为△ACD的中位线，长度为＝1．故答案为：1．（3）CF＝AB+CE．如图3，连接AC．∵四边形ABCD是菱形，∴AB＝BC＝CD＝DA．∵∠B＝60°，∴∠D＝60°，∴△ABC、△ACD都是等边三角形，∴AB＝AD＝AC，∠BAC＝∠ACB＝∠ADC＝∠ACD＝∠B＝60°．∴∠ACE＝∠ADF＝120°，∵∠EAF＝60°，∴∠CAD＝∠EAF＝60°，∴∠CAE＝∠DAF，在△ACE和△ADF中，，∴△ACE≌△ADF（ASA），∴CE＝DF，∴CF﹣CE＝CF﹣DF＝CD＝AB．即CF＝AB+CE．故答案为：CF＝AB+CE．5．解：（1）BG＝AE．理由：如图1，∵△ABC是等腰直角三角形，∠BAC＝90°，点D是BC的中点，∴AD⊥BC，BD＝CD，∴∠ADB＝∠ADC＝90°．∵四边形DEFG是正方形，∴DE＝DG．在△BDG和△ADE中，，∴△ADE≌△BDG（SAS），∴BG＝AE．故答案为：BG＝AE；（2）成立，BG＝AE．理由：如图2，连接AD，∵在Rt△BAC中，D为斜边BC中点，∴AD＝BD，AD⊥BC，∴∠ADG+∠GDB＝90°．∵四边形EFGD为正方形，∴DE＝DG，且∠GDE＝90°，∴∠ADG+∠ADE＝90°，∴∠BDG＝∠ADE．在△BDG和△ADE中，，∴△BDG≌△ADE（SAS），∴BG＝AE；（3）由（2）可得BG＝AE，当BG取得最大值时，AE取得最大值，如图3，当旋转角为270°时，BG＝AE．∵BC＝DE＝10，∴BG＝10+5＝15．∴AE＝15．如图4，当旋转角为90°时，AE取得最小值为5．6．（1）【发现证明】证明：把△ABE绕点A顺时针旋转90°至△ADG，如图1，∴∠BAE＝∠DAG，AE＝AG，∵∠EAF＝45°，∴∠BAE+∠FAD＝45°，∴∠DAG+∠FAD＝45°，∴∠EAF＝∠FAG，∵AF＝AF，∴△EAF≌△GAF（SAS），∴EF＝FG＝DF+DG，∴EF＝DF+BE；（2）【类比引申】①不成立，结论：EF＝DF﹣BE；证明：如图2，将△ABE绕点A顺时针旋转90°至△ADM，∴∠EAB＝∠MAD，AE＝AM，∠EAM＝90°，BE＝DM，∴∠FAM＝45°＝∠EAF，∵AF＝AF，∴△EAF≌△MAF（SAS），∴EF＝FM＝DF﹣DM＝DF﹣BE；②如图3，将△ADF绕点A逆时针旋转90°至△ABN，∴AN＝AF，∠NAF＝90°，∵∠EAF＝45°，∴∠NAE＝45°，∴∠NAE＝∠FAE，∵AE＝AE，∴△AFE≌△ANE（SAS），∴EF＝EN，∴BE＝BN+NE＝DF+EF．即BE＝EF+DF．故答案为：BE＝EF+DF．（3）【联想拓展】解：由（1）可知AE＝AG＝3，∵正方形ABCD的边长为6，∴DC＝BC＝AD＝6，∴＝＝3．∴BE＝DG＝3，∴CE＝BC﹣BE＝6﹣3＝3，设DF＝x，则EF＝DG＝x+3，CF＝6﹣x，在Rt△EFC中，∵CF2+CE2＝EF2，∴（6﹣x）2+32＝（x+3）2，解得：x＝2．∴DF＝2，∴AF＝＝＝2．7．解：（1）问题：在Rt△ABC中，AB＝AC，∴∠B＝∠ACB＝45°，∵∠BAC＝∠DAE＝90°，∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，即∠BAD＝∠CAE，在△BAD和△CAE中，，∴△BAD≌△CAE（SAS），故答案为：BD＝CE，BD⊥CE；（2）探索：结论：DE2＝BD2+CD2，理由是：如图2中，连接EC．∵∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，在△ABD和△ACE中，∵，∵△BAD≌△CAE（SAS），∴BD＝CE，∠B＝∠ACE＝45°，∴∠BCE＝∠ACB+∠ACE＝45°+45°＝90°，∴DE2＝CE2+CD2，∴DE2＝BD2+CD2；（3）拓展：如图3，将AD绕点A逆时针旋转90°至AG，连接CG、DG，则△DAG是等腰直角三角形，∴∠ADG＝45°，∵∠ADC＝45°，∴∠GDC＝90°，同理得：△BAD≌△CAG，∴CG＝BD＝3，Rt△CGD中，∵CD＝1，∴DG＝＝＝2，∵△DAG是等腰直角三角形，∴AD＝AG＝2．8．解：（1）∵四边形ABCD是正方形，∴AB＝CB＝CD＝DA＝4，∠D＝∠DAB＝90°，∠DAC＝∠BAC＝45°，∴AC＝4，∵∠DAC＝∠AHC+∠ACH＝45°，∠ACH+∠ACG＝∠ECF＝45°，∴∠AHC＝∠ACG．故答案为＝．（2）结论：AC2＝AG•AH．理由：∵∠AHC＝∠ACG，∠CAH＝∠CAG＝135°，∴△AHC∽△ACG，∴，∴AC2＝AG•AH．（3）如图1中，当GC＝GH时，易证△AHG≌△BGC，∵GC＝GH，∴∠GCH＝∠GHC＝45°，∴∠CGH＝90°，∴∠BGC+∠BGH＝90°，且∠BGC+∠BCG＝90°∴∠BGH＝∠BCG，且∠GBC＝∠GAH，GC＝GH，∴△BCG≌△AGH（AAS）∴AG＝BC＝4，AH＝BG＝8，∵BC∥AH，∴＝，∴AE＝AB＝；如图2中，当CH＝HG时，∵HC＝GH，∴∠GCH＝∠CGH＝45°，∴∠CHG＝90°，∴∠CHD+∠AHG＝90°，且∠CHD+∠DCH＝90°∴∠AHG＝∠DCH，且∠CDH＝∠GAH，CH＝GH，∴△DHC≌△AGH（AAS）∴AH＝CD＝4，∵BC∥AH，∴＝1，∴AE＝BE＝2．如图3中，当CG＝CH时，∵∠AHC＝∠ACG，∠ACH＝∠AGC，且CG＝CH，∴△ACH≌△AGC（ASA）∴AC＝AH＝4，AG＝AC，∵BC∥AH，∴＝，∴AE＝BE，∵BE+AE＝AB＝4，∴BE＝4﹣4，∴AE＝8﹣4，综上所述，满足条件的m的值为或2或8﹣4．9．解：（1）∵DA2＝12+22＝5，DB2＝12+32＝10，DC2＝DA2＝5 ∴DB2＝DC2+DA2∴点D是△ABC关于点B的勾股点∵EA2＝42+42＝32，EB2＝22+52＝29，EC2＝4∴点E不是△ABC的勾股点∵FA2＝32+42＝25，FB2＝22+42＝20，FC2＝12+22＝5∴FA2＝FB2+FC2∴点F是△ABC关于点A的勾股点∵GA2＝42+22＝20，GB2＝22+32＝13，GC2＝22+22＝8∴点G不是△ABC的勾股点故答案为：B；F．（2）①证明：如图3中，∵点C是△ABE关于点A的勾股点∴CA2＝CB2+CE2∵四边形ABCD是矩形∴AB＝CD，AD＝BC，∠ADC＝90°∴CA2＝AD2+CD2＝CB2+CD2∴CB2+CE2＝CB2+CD2∴CE＝CD②如图3中，设∠CED＝α，则∠CDE＝∠CED＝α∴∠ADE＝∠ADC﹣∠CDE＝90°﹣α∵∠AEC＝120°∴∠AED＝∠AEC﹣∠CED＝120°﹣α∵DA＝DE∴∠DAE＝∠DEA＝120°﹣α∵∠DAE+∠DEA+∠ADE＝180°∴2（120°﹣α）+（90°﹣α）＝180°解得：α＝50°∴∠ADE＝90°﹣50°＝40°（3）∵矩形ABCD中，AB＝5，BC＝6∴AD＝BC＝6，CD＝AB＝5∵点C是△ABE关于点A的勾股点∴CE＝CD＝5i）如图1，若DE＝DA，则DE＝6过点E作MN⊥AB于点M，交DC于点N∴∠AME＝∠MND＝90°∴四边形AMND是矩形∴MN＝AD＝6，AM＝DN设AM＝DN＝x，则CN＝CD﹣DN＝5﹣x∵Rt△DEN中，EN2+DN2＝DE2；Rt△CEN中，EN2+CN2＝CE2∴DE2﹣DN2＝CE2﹣CN2∴62﹣x2＝52﹣（5﹣x）2解得：x＝，∴EN＝＝＝，AM＝DN＝，∴ME＝MN﹣EN＝6﹣＝，∴Rt△AME中，AE＝＝＝．ii）如图2，若AE＝DE，则E在AD的垂直平分线上过点E作PQ⊥AD于点P，交BC于点Q∴AP＝DP＝AD＝3，∠APQ＝∠PQC＝90°∴四边形CDPQ是矩形∴PQ＝CD＝5，CQ＝PD＝3∴Rt△CQE中，EQ＝＝＝4∴PE＝PQ﹣EQ＝1∴Rt△APE中，AE＝＝＝iii）如图3，若AE＝AD＝6，则AE2+CE2＝AD2+CD2＝AC2∴∠AEC＝90°取AC中点O，则点A、B、C、D在以O为圆心、OA为半径的⊙O上∴点E也在⊙O上∴点E不在矩形ABCD内部，不符合题意综上所述，若△ADE是等腰三角形，AE的长为或．10．解：（1）∵四边形ABCD是正方形，∴AD＝DC，AD∥BC，∠DAG＝∠DCE＝90°，∴∠DEC＝∠EDF，∵DE＝EF，∴∠EFD＝∠EDF，∴∠EFD＝∠DEC，∵DG⊥EF于H，∴∠GHF＝90°，∴∠AGH+∠AFH＝180°，∵∠AFH+∠EFD＝180°，∴∠DGA＝∠EFD＝∠DEC，在△DAG和△DCE中：∴△DAG≌△DCE（AAS），∴DG＝DE．（2）∵KE⊥EF，DG⊥EF，∴KE∥DG，且DG＝EF＝KE＝DE，∴四边形KEDG是平行四边形，且DG＝DE，∴四边形KEDG是菱形，∴GK＝DG＝KE＝DE，∵DG⊥EF，H是DG的中点，∴EG＝DE，∴EG＝DE＝DG＝GK＝KE＝EF．11．解：（1）∵四边形ABCD是矩形，∴∠A＝90°，∵AB＝4，AD＝BC＝3，∴BD＝＝＝5，由题意BP＝t，DQ＝t，∵PQ∥AD，∴＝，∴＝，∴t＝，∴满足条件的t的值为．（2）作OE⊥AB于E，OF⊥BC于F．∵QE∥AD，∴＝，∴＝，∴QE＝（5﹣t），∵QF∥CD，∴＝，∴＝，∴QF＝（5﹣t），∴S＝S△PBQ +S△BCQ＝•PB•QE+•BC•QF＝•t•（5﹣t）+×3×（5﹣t）＝﹣t2+t+6．（3）由题意：（﹣t2+t+6）：12＝9：20，整理得：t2﹣t﹣2＝0，解得t＝2或﹣1（舍弃），∴满足条件的t的值为2．（4）如图1中，作OE⊥AB于E，OF⊥BC于F．当PQ⊥QC时，△QEP∽△QFC，则＝，∴＝，解得t＝，∴满足条件的t的值为．12．解：（1）如图1，连接AC交BD于O，连接B′C．∵四边形ABCD是正方形，∴AB＝AD，AC⊥BD，AC＝BD＝2OA，∠CAB＝ADB＝45°，∵AE＝BD，∴AC＝AE＝2OA，在Rt△AOE中，∠AOE＝90°，AE＝2OA，∴∠E＝30°，∴∠DAE＝∠ADB﹣∠E＝45°﹣30°＝15°，由旋转有，AD＝AB＝AB′∠BAB′＝30°，∴∠DAE＝15°，在△ADE和△AB′C中，，∴△ADE≌△AB′C（SAS），∴DE＝B′C．（2）补充图形如图2所示：由旋转得，AB′＝AB＝AD，AE′＝AE，在△AEB′和△AE′D中，，∴△AEB′≌△AE′D（SSS），∴∠DAE′＝∠EAB′，∴∠EAE′＝∠DAB′，由旋转得，∠EAE′＝∠BAB′，∴∠BAB′＝∠DAB′，∵∠BAB′+∠DAB′＝90°，∴α＝∠BAB′＝45°，或α＝360°﹣90°﹣45°＝225°．（3）如图3，连接AC交BD于O，∵正方形ABCD的边长为4，∴AC＝BD＝4，OA＝OD＝OC＝OB＝2在旋转过程中，△ABE在旋转到边B'E'⊥AB于Q，此时PQ最小，由旋转知，△ABE≌△AB'E'，∴AQ＝OA＝2（全等三角形对应边上的高相等），∴PQ＝AQ﹣AP＝2﹣2在旋转过程中，△ABE在旋转到点E在BA的延长线时，点Q和点E'重合时，PQ的值最大，∴AE'＝AE＝4，∴PE'＝AE'+AP＝4+2，∴2﹣2≤PQ≤4+2故答案为2﹣2≤PQ≤4+2．13．解：（1）如图1中，结论：AE＝CF，AE⊥CF，△DMN是等腰直角三角形．理由：延长FC交AE于H．∵四边形ABCD是正方形，∴AD＝DC，∠ADC＝90°，∵△DEF是等腰直角三角形，∴DE＝DF，∠DEF＝90°，∵AD＝DC，∠ADE＝∠CDE，DE＝DF，∴△ADE≌△CDF（SAS），∴AE＝CF，∠DCF＝∠EAD，∵∠EAD+∠AED＝90°，∠HCE＝∠DCF，∴∠HCE+∠AED＝90°，∴∠CHE＝90°，∴AE⊥CF，∵AM＝EM，CN＝NF，∴DM＝AE＝AM＝ME，DN＝CF＝CN＝NF，∴DM＝DN，∠ADM＝∠MAD，∠DCN＝∠NDC，∴∠ADM＝∠CDN，∴∠NDM＝∠ADC＝90°，∴△MDN是等腰直角三角形．（2）如图2中，结论成立．理由：延长FC交AE于H．∵∠ADC＝∠EDF＝90°，∴∠ADE＝∠CDF，∵AD＝DC，DE＝DF，∴△ADE≌△CDF（SAS），∴AE＝CF，∠DCF＝∠EAD，∵∠DCF+∠DCH＝180°，∴∠DAH+∠DCH＝180°，∴∠ADC+∠AHC＝180°，∵∠ADC＝90°，∴∠AHC＝90°，∴AE⊥CF，∵△ADE≌△CDF，DM，DN是三角形的中线，∴DM＝DN，AM＝CN，∵AD＝DC，∴△ADM≌△CDN（SSS），∴∠ADM＝∠CDN，∴∠NDM＝∠ADC＝90°，∴△MDN是等腰直角三角形．（3）如图3中，△ECF的面积在旋转过程中有变化．①当DE与DC重合时，DM的长最小，此时△DMN的值最小，DM最小值＝•＝•＝，此时△DMN的面积＝××＝．②当旋转角为45°时，DM的值最大，此时△DMN的面积最大．如图3中，DA＝3，DE＝5，∠ADM＝45°，作EH⊥DA交DA的延长线于H，MK⊥AH于K．则HE＝DH＝，∵MK∥EH，AM＝ME，∴AK＝KH＝（DH﹣AD）＝（﹣3），MK＝EH＝，∴DM2＝MK2+DK2＝（）2+[3+（﹣3）]2＝+，∴△DMN的面积的最大值＝DM2＝+．14．解：（1）∵四边形ABCD是菱形，∴AC⊥BD，OA＝OC＝8cm，OD＝OB＝6cm，∴AD＝＝＝10cm，∵0＜t＜5，∴点Q在线段DC数运动，点P在线段AD上运动，∵AP∥EC，∴∠APO＝∠CEO，∵∠AOP＝∠EOC，OA＝OC，∴△AOP≌△COE（AAS），∴PA＝EC＝t，∵QE⊥AC，BD⊥AC，∴QE∥BD，∴＝，∴CD＝CB，∴CQ＝EC，∴10﹣2t＝t，∴t＝，∴t＝时，QE⊥AC．（2）作OH⊥BC于H．∵•OB•OC＝•BC•OH，∴OH＝，∵FQ∥OC，∴＝＝，∴DF ＝t ，FQ ＝t ，∴S ＝S △ECO +S 梯形CQFO ＝×t ×+（t +8）•（6﹣t ）＝﹣t 2+t +24（0＜t ＜5）．（3）由题意：（﹣t 2+t +24）：96＝1：5，整理得：2t 2﹣5t ﹣10＝0，解得t ＝或（舍弃），∴满足条件的t 的值为．15．解：（1）证明：∵四边形OABC 为矩形， ∴AB ＝OC ，∠B ＝∠AOC ＝90°，∴CD ＝OC ＝AB ，∠D ＝∠AOC ＝∠B ，又∠CED ＝∠ABE ，∴△CDE ≌△ABE （AAS ），∴CE ＝AE ；（2）∵B （8，4），即AB ＝4，BC ＝8．∴设CE ＝AE ＝n ，则BE ＝8﹣n ，可得（8﹣n ）2+42＝n 2，解得：n ＝5，∴E （5，4）；（3）∵S △ACE ＝•CE •AB ＝×5×4＝10， ∴S △POA ＝•OA •y P ＝10，P∴y P＝，∴满足条件的点P的坐标为（8，）或（0，）．。

四边形的相关概念、判定及性质(压轴突破)(原卷版)—2024年中考数学【高分突破】压轴题培优专题精练

A ．134,55æöç÷èø2．已知点P 在矩形ABCD A ．若PD BC =，则C ．若PC PD =，则A ．35B ．45C ．324．如图，菱形ABCD 中，60A Ð=°，4AB =，点M E 、F ，若点A 与点M 关于直线EF 对称，则:DE BFA ．2B ．65A ．两问都正确B ．两问都不正确C ．第（1）问正确，第（2）问错误D ．第（1）问错误，第（2）问正确6．如图，▱OABC 的顶点()0,0O ，()4,0A ，点()5,1E 是边AB 的中点，则对角线AC ，标为（）A ．()3,1B ．7．如图，在矩形ABCD 中，连接AE 、CF ．甲说：图中若A ．先是平行四边形，平移3个单位长度后是菱形B ．先是平行四边形，平移3个单位长度后是矩形，再平移2C ．先是平行四边形，平移3个单位长度后是矩形，再平移3D ．在Rt BCD V 平移的过程中，依次出现平行四边形、矩形、菱形、正方形二、填空题9．矩形OABC 在平面直角坐标系如图所示，12OA =，24OC =，点10．如图，沿EF 折叠菱形纸片则12．如图，将一副三角板放置在盒子中，动，12cm AC EF ==，则线段13．如图在矩形ABCD 中，AB 向右下方向平移到IHC V 的位置，新组成的矩形CFGH 与矩形ABCD14．如图，点G 是矩形ABCD 对应点分别是点E ，F ，且点6AD =，4AB =，当G ，E15．如图，在平面直角坐标系中，正方形2B ，3B 都在x 轴上，点C (1,1)，则点4C 的坐标为16．如图，点G 是正方形ABCD 边AB 上的一点，连接过点E 作EF CE ^，过点G 作GF CG ^，EF 和AD 为边作矩形ADHI ．记CEH △的面积为S 4AB =，1233S S S +-=，则CE = ．三、解答题17．阅读下面的例题及点拨，并解决问题：例题：如图①，已知四边形ABCD H 是AF 的中点，连接DH ，HE ，求证：点拨1：如图②，延长EH 交AD 于点M ，由题意可知AD EF P ，易证：()AAS AMH FEH V V ≌，可得AM EF =，又因为DM AD AM =-，=-DE CD CE ，且CE EF =，所以DM DE =，所以点角三角形MDE 斜边ME 上的中点，所以DH HE ^且1DH HE=．点拨2：如图③，延长使得HM DH =，连接、，，可证得四边形(1)求证：AG GF =(2)若6AB =，AD =19．如图，正方形ABCD 于点F ，过E 作EG过点C 作CN AM ∥交DE 的延长线于点N ，则四边AMNC 是平行四边形（依据利用“等积变形”可得：ADEC AMNCS S =正方形平行四边形将AMNC Y 沿直线MQ 向下平移MA 的长度得到A M N C ¢¢¢¢Y 若点A ¢恰好与点Q 重合，即MA AQ =，则A M N C ¢¢¢¢Y 即为QACC ¢Y 延长CC ¢交QP 于点H ，利用“等积变形”可得：QACC QATHS S ¢=四边形四边形ADEC QATHS S =正方形四边形同理：BCFG BPHTS S =正方形四边形(1)上述证明过程中的依据是___________．(2)根据小明的思路，请你帮助小明证明“若点A¢恰好与点Q重合”这一猜想．(3)已知：（如图2）正方形ABCD的边长为8，E是边CD上的一个动点，以CE为一边在正方形ABCD外作正方形CEFG，连接BD，BF，点E在运动的过程中，DBFV的面积是否发生变化，若变化说出变化的理由，若不变，请直接写出DBFV的面积．。

中考数学三轮冲刺专题05 四边形(名师点睛+能力提升)(解析版)

中考考点总动员之三轮冲刺聚焦考点+名师点睛+能力提升专题05 四边形讲练测模块一：平行四边形【例1】如果一个四边形的两条对角线相等，那么称这个四边形为“等对角线四边形”．写出一个你所学过的特殊的等对角线四边形的名称____________．【难度】★【答案】答案不唯一，例：矩形，正方形，等腰梯形．【解析】考查常见的四边形的性质．【例2】下列判断错误的是( )A．对角线互相垂直且相等的平行四边形是正方形B．对角线互相垂直平分的四边形是菱形C．对角线相等的四边形是矩形D．对角线互相平分的四边形是平行四边形【难度】★【答案】C【解析】对平行四边形，矩形，正方形，菱形的性质的考查．【例3】下列命题中，真命题是( )A．菱形的对角线互相平分且相等B．矩形的对角线互相垂直平分C．对角线相等且垂直的四边形是正方形D．对角线互相平分的四边形是平行四边形【难度】★【答案】D【解析】考查菱形，矩形，正方形，平行四边形的性质．【例4】如图，在ABCD 中，AC 、BD 相交于点O ，请添加一个条件________________，可得ABCD 是矩形．【难度】★【答案】BD AC =或90DAB ∠=︒．【解析】矩形是有一个角为直角的平行四边形，或者矩形是对角线平分且相等的四边形．【总结】考查矩形的判定．【例5】已知四边形ABCD 是平行四边形，对角线AC 与BD 相交于点O ，那么下列结论中正确的是( )A ．当AB = BC 时，四边形ABCD 是矩形 B ．当AC ⊥BD 时，四边形ABCD 是矩形 C ．当OA = OB 时，四边形ABCD 是矩形 D ．当ABD CBD ∠=∠时，四边形ABCD 是矩形【难度】★★ 【答案】C【解析】矩形是对角线平分且相等的四边形．【例6】已知在四边形ABCD 中，AC 与BD 相交于点O ，那么下列条件中能判定这个四边形是正方形的是( )A ．AC = BD ，AB // CD ，AB = CD B ．AD // BC ，A C ∠=∠ C ．AO = BO = CO = DO ，AC BD ⊥D ．AO = CO ，BO = DO ，AB = BC【难度】★★ 【答案】C【解析】正方形是对角线互相垂直平分且相等的四边形．【例7】如果点K 、L 、M 、N 分别是四边形ABCD 的四条边AB 、BC 、CD 、DA 的中点，且四边形KLMN 是菱形，那么下列选项正确的是( )A ．AB BC ⊥ B ．AC BD ⊥C ．AB BC =D ．AC BD =【难度】★★ 【答案】D【解析】连接AC 、BD ，点K 、L 、M 、N 分别是四边形ABCD 的四条边AB 、BC 、CD 、DA 的中点，所以得四边形KLMN 为平行四边形，又它为菱形则相邻两边相等，而邻边正好是四边形ABCD 的对角线的中位线，所以AC=BD ．ABC DO【总结】考查三角形中位线定理的运用．【例8】从①AB // CD ，②AD // B C ，③AB = CD ，④AD = BC 四个关系中，任选两个作为条件，那么选到能够判定四边形ABCD 是平行四边形的概率是______．【难度】★★ 【答案】23．【解析】四种选2中共有6种情况，两组对边平行的四边形、两组对边相等的四边形、一组对边平行且相等的四边形均是平行四边形，共有4种情况，所以概率是42=63．【总结】考查平行四边形的判定及概率的综合运用．【例9】在平行四边形ABCD 中，BC = 24，AB = 18，ABC ∠和BCD ∠的平分线交AD 于点E 、F ，则EF =______．【难度】★★ 【答案】12．【解析】由平行线和角平分线可知△ABE 和△CDF 都是等腰三角形，所以18AE AB ==，18DF DC ==，所以18182412EF AE DF AD =+-=+-=．【总结】本题主要考查“平行线+角平分线推出等腰三角形”的基本模型的运用．【例10】如图，在四边形ABCD 中，90ABC ∠=︒，对角线AC 、BD 交于点O ，AO = CO ，AOD ADO ∠=∠，E是DC 边的中点．下列结论中，错误的是( ) A ．12OE AD = B ．12OE OB =C ．12OE OC =D ．12OE BC =【难度】★★ 【答案】DF EDCBAAB C D EO【解析】由AOD ADO ∠=∠得到AO OD =，又AO = CO ，得AO =AD =OC ，因为O 、E 都是中点，所以OE 是中位线，即12OE AD =，又90ABC ∠=︒且O 为中点，则AO =OC =OB ，所以A 、B 、C 正确，D 错误．【总结】本题主要考查直角三角形的性质与三角形中位线的综合运用．【例11】设边长为3的正方形的对角线长为a ．下列关于a 的四种说法：①a 是无理数；②a 可以用数轴上的一个点来表示；③34a <<；④a 是18的一个平方根．其中，所有正确说法的序号是( )A ．①④B ．②③C ．①②④D ．①③④【难度】★★ 【答案】C【解析】勾股定理可得：a = 一对应，所以②是对的，故选C ．【总结】本题主要考查勾股定理及对实数的认识．【例12】如图，在ABC ∆中，点D 、E 分别在AB 、AC 上，ADE C ∠=∠，如果AE = 2，ADE ∆的面积是4，四边形BCDE 的面积是5，那么AB 的长是______．【难度】★★ 【答案】3．【解析】因为ADE C A A ∠=∠=∠，，所以ADEACB ∆∆．因为4ADE S ∆=，459ABC S ∆=+=，根据相似三角形面积比等于相似比的平方，得：249ADE ABC S DE AB S ∆∆⎛⎫== ⎪⎝⎭，得：23DE AB =，因为AE = 2，所以AB=3．【总结】本题主要考查相似三角形的性质的运用．【例13】已知：如图，在四边形ABCD 中，AB // CD ，点E 是对角线AC 上一点，DEC ABC ∠=∠，且2CD CE CA =．（1）求证：四边形ABCD 是平行四边形；（2）分别过点E 、B 作AB 和AC 的平行线交于点F ，联结CF ，若FCE DCE ∠=∠，求证：四边形EFCD 是菱形．【难度】★★ 【答案】略．【解析】证明：（1）∵AB // CD ，∴BAC ECD ∠=∠， ∵DEC ABC ∠=∠，∴CDE ACB ∆~∆，∴CD CEAC AB=． ∴CD AB CE CA ⋅=⋅，又∵2CD CE CA =，∴AB =CD ，又因为AB // CD ，所以四边形ABCD 为平行四边形；（2）∵//AE BF ，//AB EF ，∴四边形ABFE 是平行四边形，∴//AB EF 且AB EF =，又∵ABCD 为平行四边形，∴//AB CD 且AB CD = ∴//EF CD 且EF CD =，∴四边形EFCD 为平行四边形，∵//EF CD ，∴FEC ECD ∠=∠，∵FCE DCE ∠=∠，∴FEC FCE ∠=∠， ∴EF =CF ，∴四边形EFCD 为菱形．【总结】本题主要考查相似三角形与菱形性质的综合运用．【例14】如图，在ABC ∆中，AB = AC ，点D 在边AC 上，AD = BD =DE ，联结BE ，72ABC DBE ∠=∠=︒．（1）联结CE ，求证：CE = BE ；（2）分别延长CE 、AB 交于点F ，求证：四边形DBFE 是菱形．【难度】★★ 【答案】见解析．A B C DEO A BCD EF【解析】证明：（1）设DE 与BC 的交点为O ， ∵72ABC DBE ∠=∠=︒，AB = AC ，AD = BD =DE ，∴36ABD DBA DBC ∠=∠=∠=，72ABC ACB BDC DBE DEB ∠=∠=∠=∠=∠=， ∴BCD DBE ∆≅∆，∴DE =BC ，CD =DO =BO ，∴OC =OE ， ∴36CEO OCE CBE ∠=∠=∠=︒，∴BE =CE ．（2）∵36BDE CED ∠=∠=︒，∴//BD CF ，∵36ABD EDB ∠=∠=︒，∴//DE AB ， ∴四边形DBFE 为平行四边形，又∵BD =DE ，∴四边形DBFE 为菱形．【总结】本题主要考查等腰三角形的性质与菱形判定的综合运用．【例15】已知：如图，在Rt ABC ∆中，90ACB ∠=︒，AC = BC ，点E 在边AC 上，延长BC 至D 点，使CE = CD ，延长BE 交AD 于F ，过点C 作CG // BF ，交AD 于点G ，在BE 上取一点H ，使HCE DCG ∠=∠．（1）求证：BCE ∆≌ACD ∆；（2）求证：四边形FHCG 是正方形．【难度】★★ 【答案】略．【解析】证明：（1）∵90ACB ACD ∠=∠=︒，CE =CD ，AC =BC ， ∴BCE ∆≌ACD ∆；（2）∵BCE ∆≌ACD ∆，∴CEB CDA ∠=∠，又∵HCE DCG ∠=∠，CE =CD ，∴CEH CDG ∆≅∆，∴CH =CG ， ∵HCE DCG ∠=∠且90ACB ∠=︒，∴90HCG CHF CGF ∠=︒=∠=∠，∴四边形FHCG 为矩形，又∵CH =CG ，∴四边形FHCG 为正方形．【总结】本题主要考查矩形和正方形性质的综合运用．【例16】如图，在四边形ABCD 中，AB // DC ，E 、F 为对角线BD 上两点，且BE = DF ，AF // EC ．（1）求证：四边形ABCD 是平行四边形；（2）延长AF ，交边DC 于点G ，交边BC 的延长线于点H ，求证：AD DC BH DG =．【难度】★★★ 【答案】略．【解析】证明：（1）∵BE =DF ，∴BF =DF ， ∵//AB DC ，∴ABF EDC ∠=∠，BAF AGD ∠=∠，∵AF // EC ，∴AGD ECD BAF ∠=∠=∠，∴AFB CED ∆≅∆， ∴AB =CD ，且AB // DC ，∴四边形ABCD 为平行四边形；（2）∵四边形ABCD 为平行四边形，∴HAB AGD ∆∆，∴AD DGBH AB=，又∵CD =AB ，∴AD DC BH DG =．【总结】本题主要考查平行四边形的性质及相似的性质的综合运用．【例17】如图，已知在矩形ABCD 中，过对角线AC 的中点O 作AC 的垂线，分别交射线AD 和CB 于点E 、F ，交边DC 于点G ，交边AB 于点H ．联结AF 、CE ．（1）求证：四边形AFCE 是菱形；（2）如果OF = 2GO ，求证：2GO DG GC =．A BCDEF H【难度】★★★ 【答案】略．【解析】（1）∵四边形ABCD 为矩形，∴AO =OC ，//AE DF ， ∴EOA FOC ∆≅∆，∴OE =OF ，又∵EF AC ⊥，且AO =OC ，∴四边形AFCE 为菱形；（2）∵四边形AFCE 为菱形，∴90EOC EDC ∠=∠=︒， ∵EGD CGO ∠=∠，∴EGDCGO ∆∆，∴DG GOEG CG=， ∵OF = 2GO =OE ，∴OG =EG ，∴2GO DG GC =．【总结】本题主要考查矩形及菱形性质的综合运用．【例18】已知：如图，Rt ABC ∆和Rt CDE ∆中，90ABC CDE ∠=∠=︒，且BC 与CD 共线，联结AE ，点M为AE 中点，联结BM ，交AC 于点G ，联结MD ，交CE 于点H ．（1）求证：MB = MD ；（2）当AB = BC ，DC = DE 时，求证：四边形MGCH 为矩形．【难度】★★★ 【答案】略．【解析】（1）过点M 作MN BD ⊥于N ，∵90ABC CDE ∠=∠=︒，且BC 与CD 共线，∴////AB MN DE ，又∵M 为AE 中点，∴N 也为BD 中点， ∴BM D ∆为等腰三角形，∴BM =MD ；（2）延长BM 交DE 延长线于点P ，∵//AB PE ，M 为AE 中点，∴AB =PE ，∵AB =BC ，DC =DE ，∴Rt ABC ∆和Rt CDE ∆都是等腰直角三角形，∴45CED ACB ∠=∠=︒， ∴CED P ∠=∠，ACB BDM ∠=∠，∴//CE BP ，//AC DM ，A BCDE M HN P∴四边形MGCH 为平行四边形，又∵90GMH ∠=︒，∴四边形MGCH 为矩形．【总结】本题主要考查等腰直角三角形性质和矩形判定的综合运用．【例19】如图，在正方形ABCD 中，点E 在对角线AC 上，点F 在边BC 上，联结BE 、DF ，DF 交对角线AC于点G ，且DE = DG ．（1）求证：AE = CG ；（2）求证：BE // DF ．【难度】★★★ 【答案】略．【解析】（1）取AC 中点O ，连接DO∵AD =CD ，∴DO AC ⊥．又∵DE =DG ，∴EO =OG ，∴AE =CG ；（2）∵正方形ABCD ，∴45BAC ACD ∠=∠=︒，∵AE =CG ，AB =CD ，∴EAB CGD ∆≅∆，∴ABE GDC ∠=∠，又∵90DFC FDC EBC ABE ∠+∠=∠+∠=︒，∴DFC EBF ∠=∠，∴BE // DF ．【总结】本题主要考查正方形性质的运用．【例20】已知：如图1，在平行四边形ABCD 中，点E 、F 分别在BC 、CD 上，且AE = AF ，AEC AFC ∠=∠．（1）求证：四边形ABCD 是菱形；（2）如图2，若AD = AF ，延长AE 、DC 交于点G ，求证：2AF AG DF =．（3）在第（2）小题的条件下，连接BD ，交AG 于点H ，若HE = 4，EG = 12，求AH 的长．A BCD E FOA BCD EF【难度】★★★ 【答案】略【解析】（1）∵AEC AFC ∠=∠， ∴AEB AFD ∠=∠，又∵四边形ABCD 为平行四边形，∴B D ∠=∠，又∵AE = AF ，∴ABE ADF ∆≅∆，∴AB =AD ，∴四边形ABCD 为菱形；（2）∵四边形ABCD 为菱形，∴BAG AGD FAD ∠=∠=∠，又∵D D ∠=∠， ∴AFDGDA ∆∆，∴AD FDGA AD=，又∵AD =AF ，∴2AF AG DF =；（3）∵//AB DC ，//AD BC ，∴AH BH HG HD =，BH EH HD AH =，∴AH EHHG AH=，又∵HE =4，EG =12，∴416AH AH=，∴AH =8．【总结】本题主要考查菱形的性质及相似性质的综合运用．【巩固1】（2019春•浦东新区校级月考）已知四边形ABCD ，在①//AB CD ；②AD BC =；③AB CD =；④A C ∠=∠四个条件中，不能推出四边形ABCD 是平行四边形的条件是( ) A ．①②B ．①③C ．①④D ．②③【分析】根据平行四边形的判定定理：有一组对边平行且相等的四边形是平行四边形；有两组对边相互平行的四边形是平行四边形；即可得出结论．【解答】解：根据“有一组对边平行且相等的四边形是平行四边形”可以选①③和①④；根据两组对边分别相等的四边形是平行四边形，选②③；所以不能推出四边形ABCD 为平行四边形的是①②；故选：A ．【巩固2】（2019春•浦东新区校级月考）在平行四边形ABCD 中，对角线AC ，BD 交于点O ，若10BD =，14AC =，那么BC 的取值范围为．【分析】根据平行四边形的性质可得BO 、CO 的长，然后再根据三角形的三边关系可得BC 的取值范围．【解答】解：如图：四边形ABCD 是平行四边形，12BO BD ∴=，12CO AC =，10BD =，14AC =， 5BO ∴=，7CO =， 212BC ∴<<，故答案为：212BC <<．【巩固3】（2018春•浦东新区期中）如图，以BC 为底边的等腰ABC ∆，点D ，E ，G 分别在BC ，AB ，AC 上，且//EG BC ，//DE AC ，延长GE 至点F ，使得BE BF =．（1）求证：四边形BDEF 为平行四边形；（2）当45C ∠=︒，4BD =时，联结DF ，求线段DF 的长．【分析】（1）由等腰三角形的性质得出ABC C ∠=∠，证出AEG ABC C ∠=∠=∠，四边形CDEG 是平行四边形，得出DEG C ∠=∠，证出F DEG ∠=∠，得出//BF DE ，即可得出结论；（2）证出BDE ∆、BEF ∆是等腰直角三角形，由勾股定理得出BF BE ===作FM BD ⊥于M ，连接DF ，则BFM ∆是等腰直角三角形，由勾股定理得出2FM BM ===，得出6DM =，在Rt DFM ∆中，由勾股定理求出DF 即可．【解答】（1）证明：ABC ∆是等腰三角形， ABC C ∴∠=∠，//EG BC ，//DE AC ，AEG ABC C ∴∠=∠=∠，四边形CDEG 是平行四边形， DEG C ∴∠=∠，BE BF =，BFE BEF AEG ABC ∴∠=∠=∠=∠，F DEG ∴∠=∠， //BF DE ∴，∴四边形BDEF 为平行四边形；（2）解：45C ∠=︒，45ABC BFE BEF ∴∠=∠=∠=︒，BDE ∴∆、BEF ∆是等腰直角三角形，BF BE ∴=== 作FM BD ⊥于M ，连接DF ，如图所示：则BFM ∆是等腰直角三角形，2FM BM ∴===， 6DM ∴=，在Rt DFM ∆中，由勾股定理得：DF即D ，F 两点间的距离为【巩固4】（2018•上海）已知平行四边形ABCD ，下列条件中，不能判定这个平行四边形为矩形的是( ) A ．A B ∠=∠B ．AC ∠=∠C ．AC BD =D ．AB BC ⊥【分析】由矩形的判定方法即可得出答案．【解答】解：A 、A B ∠=∠，180A B ∠+∠=︒，所以90A B ∠=∠=︒，可以判定这个平行四边形为矩形，正确；B 、AC ∠=∠不能判定这个平行四边形为矩形，错误；C 、AC BD =，对角线相等，可推出平行四边形ABCD 是矩形，故正确；D 、AB BC ⊥，所以90B ∠=︒，可以判定这个平行四边形为矩形，正确；故选：B ．【巩固5】（2018•上海）对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上，且该图形与矩形的每条边都至少有一个公共点（如图1)，那么这个矩形水平方向的边长称为该图形的宽，铅锤方向的边长称为该图形的高．如图2，菱形ABCD 的边长为1，边AB 水平放置．如果该菱形的高是矩形的宽的23，那么矩形的宽的值是．【分析】先根据要求画图，设矩形的宽AF x =，则23CF x =，根据勾股定理列方程可得结论．【解答】解：在菱形上建立如图所示的矩形EAFC ，设AF x =，则23CF x =，在Rt CBF ∆中，1CB =，1BF x =-，由勾股定理得：222BC BF CF =+，22221(1)()3x x =-+，解得：1813x =或0（舍)，即它的宽的值是1813，故答案为：1813．【巩固6】（2017•上海）已知：如图，四边形ABCD 中，//AD BC ，AD CD =，E 是对角线BD 上一点，且EA EC =．（1）求证：四边形ABCD 是菱形；（2）如果BE BC =，且:2:3CBE BCE ∠∠=，求证：四边形ABCD 是正方形．【分析】（1）首先证得ADE CDE ∆≅∆，由全等三角形的性质可得ADE CDE ∠=∠，由//AD BC 可得ADE CBD ∠=∠，易得CDB CBD ∠=∠，可得BC CD =，易得AD BC =，利用平行线的判定定理可得四边形ABCD 为平行四边形，由AD CD =可得四边形ABCD 是菱形；（2）由BE BC =可得BEC ∆为等腰三角形，可得BCE BEC ∠=∠，利用三角形的内角和定理可得1180454CBE ∠=⨯=︒，易得45ABE ∠=︒，可得90ABC ∠=︒，由正方形的判定定理可得四边形ABCD 是正方形．【解答】证明：（1）在ADE ∆与CDE ∆中， AD CD DE DE EA EC =⎧⎪=⎨⎪=⎩， ADE CDE ∴∆≅∆，ADE CDE ∴∠=∠， //AD BC ， ADE CBD ∴∠=∠， CDE CBD ∴∠=∠，BC CD ∴=， AD CD =， BC AD ∴=，∴四边形ABCD 为平行四边形，AD CD =，∴四边形ABCD 是菱形；（2）BE BC =BCE BEC ∴∠=∠，:2:3CBE BCE ∠∠=，218045233CBE ∴∠=⨯=︒++，四边形ABCD 是菱形， 45ABE ∴∠=︒， 90ABC ∴∠=︒，∴四边形ABCD 是正方形．【巩固7】（2019•杨浦区二模）已知：如图，在ABC ∆中，AB BC =，90ABC ∠=︒，点D 、E 分别是边AB 、BC 的中点，点F 、G 是边AC 的三等分点，DF 、EG 的延长线相交于点H ，连接HA 、HC ．求证：（1）四边形FBGH 是菱形；（2）四边形ABCH 是正方形．【分析】（1）由三角形中位线知识可得//DF BG ，//GH BF ，根据菱形的判定的判定可得四边形FBGH 是菱形；（2）连结BH ，交AC 于点O ，利用平行四边形的对角线互相平分可得OB OH =，OF OG =，又AF CG =，所以OA OC =．再根据对角线互相垂直平分的平行四边形得证四边形ABCH 是菱形，再根据一组邻边相等的菱形即可求解．【解答】证明：（1）点F 、G 是边AC 的三等分点， AF FG GC ∴==．又点D 是边AB 的中点， //DH BG ∴．同理：//EH BF ．∴四边形FBGH 是平行四边形，连结BH ，交AC 于点O ， OF OG ∴=， AO CO ∴=，=，AB BC∴⊥，BH FG∴四边形FBGH是菱形；（2）四边形FBGH是平行四边形，=．∴=，FO GOBO HO==，又AF FG GC=．AF FO GC GO∴+=+，即：AO CO∴四边形ABCH是平行四边形．=，AC BH⊥，AB BC∴四边形ABCH是正方形．模块二：梯形【例21】顺次联结等腰梯形各边中点所得的四边形是__________形．【难度】★【答案】菱形．【解析】连接对角线，得出新的四边形的每条边为对角线的中位线且分别平行对角线，得出四边形为平行四边形，由因为等腰梯形的对角线相等，所以新的四边形为菱形．【总结】本题主要考查三角形中位线的运用．【例22】如果梯形的下底长为7，中位线长为5，那么其上底长为______．【难度】★【答案】3．【解析】梯形中位线等于上底加下底和的一半．【总结】本题主要考查梯形中位线的运用．【例23】梯形ABCD中，AD // BC，AD = 2，BC = 6，点E是边BC上的点，如果AE将梯形ABCD的面积平分，那么BE的长是______．【难度】★★【答案】4．【解析】设梯形的高为h，则1(26)42ABCDS h h=⨯+⨯=梯形，因为AE将梯形ABCD的面积平分，所以114222ABES BE h h h =⨯⨯=⨯=，所以4BE=．【总结】本题主要考查梯形的面积及三角形面积的运用．【例24】如果梯形ABCD中，AD // BC，E、F分别是AB、CD的中点，AD = 1，BC = 3，那么四边形AEFD与四边形EBCF的面积比是______．【难度】★★【答案】35．【解析】因为EF为梯形ABCD的中位线，所以EF=2，又因为四边形AEFD与EBCF为梯形，且他们的高相等，所以面积之比等于123 235 +=+．【总结】本题主要考查梯形中位线及面积的综合运用．【例25】如图，在梯形ABCD中，AD // BC，AB⊥BC，已知AD = 2，4cot3ACB∠=，梯形ABCD的面积是9．（1）求AB的长；（2）求tan ACD∠的值．【难度】★★【答案】（1）3；（2）617．E D CBAA B CDH【解析】（1）设AB x =，则43BC x =，梯形面积等于42392x x ⎛⎫+ ⎪⎝⎭=，解得：3x =，即AB 的长为3；（2）过D 作DH AC ⊥于H ，∵AD // BC ，∴ACB CAD ∠=∠，∴4cot cot 3CAD ACB ∠=∠=， ∴65DH =，85AH =，∵AC=5，∴175CH =， ∴6tan 17DH ACD CH ∠==．【总结】本题主要考查梯形的面积与锐角三角比的综合运用．【例26】已知，如图，在梯形ABCD 中，AD // BC ，点E 是边CD 的中点，点F 在边BC 上，EF // AB ．求证：()12BF AD BC =+．【难度】★★ 【答案】略．【解析】取AB 的中点G ，连接EG ，∵点E 是边CD 的中点，∴EG 为梯形ABCD 的中位线，∴()12EG AD BC =+，又∵//EF AB ，且//EG BC ，∴四边形BFEG 为平行四边形， ∴BF =EG ，∴()12BF AD BC =+．【总结】本题主要考查梯形的中位线和平行四边形性质的综合运用．【例27】如图，在直角梯形纸片ABCD 中，DC // AB ，AB >CD >AD ，90A ∠=︒，将纸片沿过点D 的直线翻折，使点A 落在边CD 上的点E 处，折痕为DF ，联结EF 并展开纸片；AB C D EF GAB C D EF GA BC DH（1）求证：四边形ADEF 为正方形；（2）取线段AF 的中点G ，联结GE ，当BG = CD 时，求证：四边形GBCE 为等腰梯形．【难度】★★★ 【答案】略．【解析】（1）∵//CD AB ，∴90ADE A ∠=∠=︒，由翻折性质，知ADF EDF ∆≅∆，∴90A DEF ∠=∠=︒， ∴四边形ADEF 为矩形，∵45ADF FDE ∠=∠=︒，∴DA =AF ， ∴四边形ADEF 为正方形；（2）连接DG ，EG ，∵BG =CD ，//AB CD ，∴四边形DGBC 为平行四边形，∴BC =DG ，又∵AG =GF ，AD =EF ，90A EFA ∠=∠=︒，∴AGD FGE ≅，∴EG =DG ， ∴BC =EG ，∵//BG CE 且不相等，∴四边形GBCE 为等腰梯形．【总结】本题综合性较强，一方面考查翻折的性质，另一方面考查特殊的平行四边形的性质的运用．【例28】如图，在ABC ∆中，D 、E 分别是AC 、BC 边上的点，AE 与BD 交于点O ，且CD = CE ，12∠=∠．（1）求证：四边形ABED 是等腰梯形；（2）若EC = 2，BE = 1，21AOD ∠=∠，求AB 的长．【难度】★★★ 【答案】（1）略；（2）32．【解析】（1）∵C C ∠=∠，CD = CE ，12∠=∠， ∴ACE BCD ∆≅∆，∴BC =AC ，∴AD =BE ，CAB ABC ∠=∠，∴ABC DEC ∠=∠，∴//DE AB ，又∵DE AB ≠，∴四边形ABED 为等腰梯形；A BC DE 1 2 O AB CD E FGA B CD E FG（2）∵四边形ADEB 为等腰梯形，∴ADE BED ∠=∠．∵12∠=∠，∴EDO OED ∠=∠，又∵21AOD ∠=∠，∴1ODE ∠=∠， ∴DE =BE =1，∵//DE AB ，∴DE EC AB BC =，∴32AB =．【总结】本题一方面考查等腰梯形的判定，另一方面考查三角形一边平行线性质定理的运用．【例29】如图，已知ABC ∆和ADE ∆都是等边三角形，点D 在边BC 上，点E 在边AD 的右侧，联结CE ．（1）求证：60ACE ∠=︒；（2）在边AB 上取一点F ，使BF = BD ，联结DF 、EF ．求证：四边形CDEF 是等腰梯形．【难度】★★★ 【答案】略．【解析】（1）∵ABC ∆和ADE ∆都是等边三角形， ∴60BAC DAE ∠=∠=︒，AB =AC ，AD =AE ， ∴BAD CAE ∠=∠，∴ABD ACE ∆≅∆， ∴60ACE ABC ∠=∠=︒；（2）∵CE =BD ，BF =BD ，60B ∠=︒，∴BDF ∆为等边三角形， ∴DF =BD =CE ，∵ACE ACB B ∠=∠=∠，∴120BCE ∠=︒， ∴180B BCE ∠+∠=︒，∴//BF CE ，∵BF =CE ，∴四边形BFEC 为平行四边形，∴//CD EF 且DF =CE ， ∴四边形CDFE 为等腰梯形．【总结】本题主要考查等边三角形的性质与等腰梯形判定的综合运用．【例30】如图，在梯形ABCD 中，AB // CD ，AD = BC ，E 是CD 的中点，BE 交AC 于F ，过点F 作FG // AB ，AB C D EF交AE 于点G ．（1）求证：AG = BF ；（2）当2AD CA CF =时，求证：AB AD AG AC =．【难度】★★★ 【答案】略．【解析】（1）∵四边形ABCD 为等腰梯形， ∴AD BC =，D BCE ∠=∠．又∵E 是CD 的中点，∴DE =CE ，∴ADE BCE ∆≅∆，∴AE =BE ． ∵//GF AB ，∴EGF ∆和AEB ∆均为等腰三角形，∴AG =BF ；（2）∵AD =BC ，且2AD CA CF =，∴2BC CA CF =，又∵BCF FCB ∠=∠，∴BCFACB ∆∆，∴AB ACBF BC=．又∵AD =BC ，AG =BF ，∴AB AD AG AC =．【总结】本题主要考查等腰梯形性质与相性质的综合运用．【巩固1】（2018•青浦区一模）在梯形ABCD 中，//AD BC ，下列条件中，不能判断梯形ABCD 是等腰梯形的是( )A ．ABC DCB ∠=∠ B ．DBC ACB ∠=∠C ．DAC DBC ∠=∠D ．ACD DAC ∠=∠【分析】等腰梯形的判定定理有：①有两腰相等的梯形是等腰梯形，②对角线相等的梯形是等腰梯形，③在同一底上的两个角相等的梯形是等腰梯形，根据以上内容判断即可．【解答】解：A 、ABC DCB ∠=∠， BD BC ∴=，∴四边形ABCD 是等腰梯形，故本选项错误；B 、DAC DBC ∠=∠，//AD BC ，ADB DBC ∴∠=∠，DAC ACB ∠=∠， OBC OCB ∴∠=∠，OAD ODA ∠=∠OB OC ∴=，OD OA =，AC BD ∴=，∴四边形ABCD 是等腰梯形，故本选项错误；C 、ADB DAC ∠=∠，//AD BC ， ADB DAC DBC ACB ∴∠=∠=∠=∠，OA OD ∴=，OB OC =， AC BD ∴=， //AD BC ，∴四边形ABCD 是等腰梯形，故本选项错误；D 、根据ACD DAC ∠=∠，不能推出四边形ABCD 是等腰梯形，故本选项正确．故选：D ．【巩固2】（2019•浦东新区二模）已知梯形的上底长为5厘米，下底长为9厘米，那么这个梯形的中位线长等于厘米．【分析】根据梯形中位线定理计算，得到答案．【解答】解：梯形的中位线长1(59)72=⨯+=（厘米）故答案为：7．【巩固3】（2019春•浦东新区期末）已知，在梯形ABCD 中，//AD BC ，5AD =，6AB CD ==，60B ∠=︒，那么下底BC 的长为．【分析】首先过A 作//AE DC 交BC 与E ，可以证明四边形ADCE 是平行四边形，进而得到4CE AD ==，再证明ABE ∆是等边三角形，进而得到6BE AB ==，从而得到答案．【解答】解：如图，过A 作//AE DC 交BC 与E ， //AD BC ，∴四边形AECD 是平行四边形，5AD EC ∴==，AE CD =， 6AB CD ==，6AE AB ∴==，60B ∠=︒，ABE ∴∆是等边三角形，6BE AB ∴==， 6511BC ∴=+=．故答案为：11．1．（2019春•嘉定区期末）如果平行四边形ABCD 两条对角线的长度分别为8AC m =，12BD cm =，那么BC 边的长度可能是( ) A ．2BC cm =B ．6BC cm =C ．10BC cm =D ．20BC cm =【分析】根据平行四边形的对角线互相平分确定对角线的一半的长，然后利用三角形的三边关系确定边长的取值范围，从该范围内找到一个合适的长度即可．【解答】解：设平行四边形ABCD 的对角线交于O 点， 4OA OC ∴==，6OB OD ==，6464BC ∴-<<+ 210BC ∴<<， 6cm ∴符合，故选：B ．2．（2019春•浦东新区期中）下列条件中不能判定一定是平行四边形的有( ) A ．一组对角相等，一组邻角互补B ．一组对边平行，另一组对边相等C ．两组对边相等D ．一组对边平行，且一条对角线平分另一条对角【分析】平行四边形的五种判定方法分别是：（1）两组对边分别平行的四边形是平行四边形；（2）两组对边分别相等的四边形是平行四边形；（3）一组对边平行且相等的四边形是平行四边形；（4）两组对角分别相等的四边形是平行四边形；（5）对角线互相平分的四边形是平行四边形．根据平行四边形的判定逐一验证．【解答】解：A 、能用两组对角相等的四边形是平行四边形判定平行四边形；B 、不能判定平行四边形，如等腰梯形；C 、能用两组对边相等的四边形是平行四边形判定平行四边形；D 、能用两组对边分别平行的四边形是平行四边形判定平行四边形；故选：B ．3．（2019春•杨浦区期中）如图，在平行四边形ABCD 中，对角线AC BD ⊥，10AC =，24BD =，则AD = ．【分析】利用平行四边形的性质和勾股定理易求AO 的长．【解答】解：ABCD 的对角线AC 与BD 相交于点O ，1122BO DO BD ∴===，152AO CO AC ===，AB AC ⊥，13AD ∴，故答案为：13．4．（2019•嘉定区二模）如图，平行四边形ABCD 的对角线AC 、BD 交于点O ，过点O 的线段EF 与AD 、BC 分别交于点E 、F ，如果4AB =，5BC =，32OE =，那么四边形EFCD 的周长为．【分析】根据平行四边形的性质知，4AB CD ==，5AD BC ==，AO OC =，OAD OCF ∠=∠，AOE ∠和COF ∠是对顶角相等，根据全等三角形的性质得到 1.5OF OE ==，CF AE =，所于是得到结论．【解答】解：四边形ABCD 平行四边形，4AB CD ∴==，5AD BC ==，AO OC =，OAD OCF ∠=∠，AOE COF ∠=∠，()OAE OCF AAS ∴∆≅∆， 1.5OF OE ∴==，CF AE =，∴四边形EFCD 的周长ED CD CF OF OE =++++ED AE CD OE OF =++++ AD CD OE OF =+++45 1.5 1.5=+++12=．故答案为：12．5．（2019春•浦东新区校级月考）如图，在平行四边形ABCD 中，60ABC ∠=︒，28BC AB ==，点C 关于AD 的对称点为E ，连接BE 交AD 于点F ，点G 为CD 的中点，连接EG ，BG ，则BEG S ∆= ．【分析】如图，取BC 中点H ，连接AH ，连接EC 交AD 于N ，作EM CD ⊥交CD 的延长线于M ．构建BEG BCE ECG BCG S S S S ∆∆∆=+-计算即可；【解答】解：如图，取BC 中点H ，连接AH ，连接EC 交AD 于N ，作EM CD ⊥交CD 的延长线于M ．2BC AB =，BH CH =，60ABC ∠=︒，BA BH CH ∴==，ABH ∴∆是等边三角形，HA HB HC ∴==， 90BAC ∴∠=︒，30ACB ∴∠=︒，EC BC ⊥，180120BCD ABC ∠=︒-∠=︒， 60ACE ∴∠=︒，30ECM ∠=︒， 28BC AB ==，4CD ∴=，CN EN ==，EC ∴=EM =， BEG BCE ECG BCG S S S S ∆∆∆∴=+-11182224ABCD S =⨯⨯⨯⨯平行四边形==故答案为．6．（2019春•杨浦区期中）如果一个平行四边形的一个内角的平分线分它的一边为1:2两部分，那么称这样的平行四边形为“协调平行四边形”，称该边为“协调边”，当协调边为6时，它的周长为．【分析】由平行四边形的性质和角平分线的定义得出AB AE =；分两种情况：①当2AE =，4DE =时；②当4AE =，2DE =时；即可求出平行四边形ABCD 的周长．【解答】解：如图所示：①当2AE =，4DE =时，四边形ABCD 是平行四边形， 6BC AD ∴==，AB CD =，//AD BC ， AEB CBE ∴∠=∠，BE 平分ABC ∠，ABE CBE ∴∠=∠，ABE AEB ∴∠=∠，2AB AE ∴==，∴平行四边形ABCD 的周长2()16AB AD =+=；②当4AE =，2DE =时，同理得：4AB AE ==，∴平行四边形ABCD 的周长2()20AB AD =+=；故答案为：16或20．7．（2019春•金山区期末）已知：如图，ABCD 中，AE 、CF 分别是BAD ∠和BCD ∠的角平分线，分别交边DC 、AB 于点E 、F ，求证：AE CF =．【分析】根据平行四边形的性质及角平分线的定义，证明ADE CBF ∆≅∆即可判断AE CF =．【解答】解：四边形ABCD 是平行四边形， DAB DCB ∴∠=∠，D B ∠=∠，AD BC =．AE 、CF 分别是BAD ∠和BCD ∠的角平分线，DAE BCF ∴∠=∠．()ADE CBF ASA ∴∆≅∆． AE CF ∴=．8．（2019春•杨浦区期中）在平行四边形ABCD 中，45A ∠=︒，BD AD ⊥，2BD =．（1）求平行四边形ABCD 的周长和面积；（2）求A 、C 两点间的距离．【分析】（1）由等腰直角三角形的性质得出2AD BD ==，由勾股定理求出AB =行四边形的性质得出DC AB ==，2BC AD ==，即可得出平行四边形的周长和面积；（2）连接AC ，与BD 相交于点O ，由平行四边形的性质得出112OD BD ==，2AC AO =，由勾股定理求出OA ，得出AC =【解答】（1）解：90BD AD ADB ⊥∴∠=︒ 又45452A ABD AD BD ∠=︒∴∠=︒∴==，AB ∴=，四边形ABCD 是平行四边形，DC AB ∴==2BC AD ==，∴()22224ABCD C AB AD =+==平行四边形，224ABCD S AD BD ∴=⨯=⨯=平行四边形；（2）解：连接AC ，与BD 相交于点O ，如图所示：四边形ABCD 是平行四边形， ∴112OD BD ==，2AC AO =，在Rt AOD ∆中，90ADO ∠=︒，∴OA∴AC =所以A 、C 两点间的距离为．9．（2018秋•黄浦区校级月考）已知：如图，在ABCD 中，4AC =，6BD =，CA AB ⊥，求ABCD 的周长和面积．【分析】依据平行四边形的对角线互相平分，即可得到2AO =，3BO =，再根据勾股定理即可得出AB 与BC 的长，进而得到ABCD 的周长和面积．【解答】解：如图所示，4AC =，6BD =，2AO ∴=，3BO =，又CA AB ⊥，Rt AOB ∴∆中，AB ==Rt ABC ∴∆中，BC ，ABCD ∴的周长==，ABCD 的面积4AB AC =⨯=．10．（2018春•金山区期中）已知，如图，在等边ABC ∆中，D 是BC 边上一点，F 为AB 边上一点，且CD BF =，以AD 为边作等边ADE ∆，联结EF 、FC ．求证：（1）ADC CFB ∆≅∆；（2）四边形EFCD 是平行四边形．【分析】（1）ACD ∆和CBF ∆中，已知的条件有：AC BC =，CD BF =，60ACD CBF ∠=∠=︒；根据SAS 即可判定两个三角形全等．（2）由（1）的全等三角形知：AD CF =，即DE CF AD ==；因此只需判断DE 与CF 是否平行即可，由（1）的全等三角形，可得DAC BCF ∠=∠，而60BCF ACG ∠+∠=︒，即60CAD ACG ∠+∠=︒；根据三角形外角的性质，可得60AGF CGD ∠=︒=∠，由此可判定//DE FC ，即可得出四边形CDEF 的形状．【解答】证明：（1）ABC ∆为等边三角形， AC BC ∴=， 60ACD B ∠=∠=︒，CD BF =，()ACD CBF SAS ∴∆≅∆；（2）四边形CDEF 为平行四边形； ACD CBF ∆≅∆；DAC BCF ∴∠=∠，CF AD =；AED ∆是等边三角形； AD DE ∴=；CF DE ∴=①；60ACG BCF ∠+∠=︒； 60ACG DAC ∴∠+∠=︒；180()120AGC ACG DAC ∴∠=︒-∠+∠=︒； 120DGF AGC ∴∠=∠=︒；AED ∆是等边三角形；60ADE ∴∠=︒；180DGF ADE ∴∠+∠=︒；//CF DE ∴②；综合①②可得四边形CDEF 是平行四边形．11．（2018春•浦东新区期中）如图，ABCD 中，E 、F 是直线AC 上两点，且AE CF =．求证：（1）BE DF =；（2）//BE DF【分析】（1）利用平行四边形的性质借助全等三角形的判定与性质得出即可；（2）利用全等三角形的性质结合平行线的判定方法得出即可．【解答】证明：（1）四边形ABCD 是平行四边形， AD BC ∴=，//AD BC ， DAC BCA ∴∠=∠，DAF BCE ∴∠=∠， AE CF =， AF EC ∴=，在FAD ∆和ECB ∆中， AF CE FAD ECB AD BC =⎧⎪∠=∠⎨⎪=⎩， ()FAD ECB SAS ∴∆≅∆，BE DF ∴=；（2）FAD ECB ∆≅∆，F E ∴∠=∠，//BE DF ∴．12．（2018春•浦东新区期中）在平行四边形ABCD 中，分别以AD 、BC 为边向内作等边ADE ∆和等边BCF ∆，连接BE 、DF ．求证：四边形BEDF 是平行四边形．【分析】由题意先证60DAE BCF ∠=∠=︒，再由SAS 证DCF BAE ∆≅∆，继而题目得证．【解答】证明：四边形ABCD 是平行四边形， CD AB ∴=，AD CB =，DAB BCD ∠=∠．又ADE ∆和CBF ∆都是等边三角形，DE BF ∴=，AE CF =．60DAE BCF ∠=∠=︒． DCF BCD BCF ∠=∠-∠，BAE DAB DAE ∠=∠-∠，DCF BAE ∴∠=∠．()DCF BAE SAS ∴∆≅∆．DF BE ∴=．∴四边形BEDF 是平行四边形．13.（2017•上海）已知平行四边形ABCD ，AC 、BD 是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是( )A ．BAC DCA ∠=∠B ．BAC DAC ∠=∠C ．BAC ABD ∠=∠ D ．BAC ADB ∠=∠【分析】由矩形和菱形的判定方法即可得出答案．【解答】解：A 、BAC DCA ∠=∠，不能判断四边形ABCD 是矩形；B 、BAC DAC ∠=∠，能判定四边形ABCD 是菱形；不能判断四边形ABCD 是矩形；C 、BAC ABD ∠=∠，能得出对角线相等，能判断四边形ABCD 是矩形；D 、BAC ADB ∠=∠，不能判断四边形ABCD 是矩形；故选：C ．14．（2019•杨浦区三模）如图，在四边形ABCD 中，AC 与BD 相交于点O ，90BAD ∠=︒，BO DO =，那么添加下列一个条件后，仍不能判定四边形ABCD 是矩形的是( )A ．90ABC ∠=︒B ．90BCD ∠=︒C ．AB CD =D ．//AB CD【分析】根据矩形的判定定理：有一个角是直角的平行四边形是矩形，对角线相等的平行四边形是矩形分。

高考文科数学三年真题分类汇编专题05 立体几何(选择题、填空题)(解析版)

专题05 立体几何（选择题、填空题）1．【2020年高考全国Ⅰ卷文数】埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为A BC D 【答案】C【解析】如图，设,CD a PE b ==，则PO ==由题意得212PO ab =，即22142a b ab -=，化简得24()210b b a a -⋅-=，解得b a =.故选C ．【点晴】本题主要考查正四棱锥的概念及其有关计算，考查学生的数学计算能力，是一道容易题.2．【2020年高考全国Ⅱ卷文数】已知△ABC 的等边三角形，且其顶点都在球O 的球面上．若球O 的表面积为16π，则O 到平面ABC 的距离为AB ．32C ．1D 【答案】C【解析】设球O 的半径为R ，则2416R ππ=，解得：2R =. 设ABC 外接圆半径为r ，边长为a ，ABC 的等边三角形，212a ∴=，解得：3a =，2233r ∴==∴球心O 到平面ABC 的距离1d ===.故选：C ．【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面. 3．【2020年高考全国Ⅲ卷文数】如图为某几何体的三视图，则该几何体的表面积是A．B ．C ．D ．【答案】C【解析】根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得：AB AD DB ===∴ADB △是边长为根据三角形面积公式可得：211sin 60222ADB S AB AD =⋅⋅︒=⋅=△∴该几何体的表面积是：632=⨯++故选：C ．【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题.4．【2020年高考全国Ⅰ卷文数】已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC △的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为 A ．64π B ．48πC ．36πD ．32π【答案】A【解析】设圆1O 半径为r ，球的半径为R ，依题意，得24,2r r ππ=∴=，ABC 为等边三角形，由正弦定理可得2sin60AB r =︒=，1OO AB ∴==根据球的截面性质1OO ⊥平面ABC ，11,4OO O A R OA ∴⊥====，∴球O 的表面积2464S R ππ==.故选：A【点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题.5．【2020年高考天津】若棱长为 A ．12π B ．24πC ．36πD ．144π【答案】C【解析】这个球是正方体的外接球，其半径等于正方体的体对角线的一半，即3R ==，所以，这个球的表面积为2244336S R πππ==⨯=. 故选：C ．【点睛】本题考查正方体的外接球的表面积的求法，求出外接球的半径是本题的解题关键，属于基础题.求多面体的外接球的面积和体积问题，常用方法有：（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果设计几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心. 6．【2020年高考北京】某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为A ．6+B ．6+C ．12D ．12+【答案】D【解析】由题意可得，三棱柱的上下底面为边长为2的等边三角形，侧面为三个边长为2的正方形，则其表面积为：()1322222sin 60122S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+ ⎪⎝⎭故选：D ．【点睛】(1)以三视图为载体考查几何体的表面积，关键是能够对给出的三视图进行恰当的分析，从三视图中发现几何体中各元素间的位置关系及数量关系．(2)多面体表面积是各个面的面积之和；组合体的表面积应注意重合部分的处理．(3)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展为平面图形计算，而表面积是侧面积与底面圆的面积之和．7．【2020年高考浙江】某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：cm 3）是A ．73B ．143C ．3D ．6【答案】A【解析】由三视图可知，该几何体是上半部分是三棱锥，下半部分是三棱柱，且三棱锥的一个侧面垂直于底面，且棱锥的高为1，棱柱的底面为等腰直角三角形，棱柱的高为2，所以几何体的体积为11117211212232233⎛⎫⎛⎫⨯⨯⨯⨯+⨯⨯⨯=+= ⎪ ⎪⎝⎭⎝⎭. 故选：A【点睛】本小题主要考查根据三视图计算几何体的体积，属于基础题.8．【2020年高考浙江】已知空间中不过同一点的三条直线l ，m ，n ．“l ，m ，n 共面”是“l ，m ，n 两两相交”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】B【解析】依题意,,m n l 是空间不过同一点的三条直线，当,,m n l 在同一平面时，可能////m n l ，故不能得出,,m n l 两两相交.当,,m n l 两两相交时，设,,m n A m l B n l C ⋂=⋂=⋂=，根据公理2可知,m n 确定一个平面α，而,B m C n αα∈⊂∈⊂，根据公理1可知，直线BC 即l α⊂，所以,,m n l 在同一平面.综上所述，“,,m n l 在同一平面”是“,,m n l 两两相交”的必要不充分条件. 故选：B【点睛】本小题主要考查充分、必要条件的判断，考查公理1和公理2的运用，属于中档题.9．【2020年新高考全国Ⅰ卷】日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为A ．20°B ．40°C ．50°D ．90°【答案】B【解析】画出截面图如下图所示，其中CD 是赤道所在平面的截线；l 是点A 处的水平面的截线，依题意可知OA l ⊥；AB 是晷针所在直线.m 是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直，根据平面平行的性质定理可得可知//m CD ，根据线面垂直的定义可得AB m ⊥..由于40,//AOC m CD ∠=︒，所以40OAG AOC ∠=∠=︒，由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与点A 处的水平面所成角为40BAE ∠=︒. 故选B.【点睛】本小题主要考查中国古代数学文化，考查球体有关计算，涉及平面平行，线面垂直的性质，属于中档题.10．【2019年高考全国Ⅱ卷文数】设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 B ．α内有两条相交直线与β平行 C ．α，β平行于同一条直线 D ．α，β垂直于同一平面【答案】B【解析】由面面平行的判定定理知：α内两条相交直线都与β平行是αβ∥的充分条件，由面面平行性质定理知，若αβ∥，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是αβ∥的必要条件，故选B ．【名师点睛】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若,,a b a b αβ⊂⊂∥，则αβ∥”此类的错误．11．【2019年高考全国Ⅱ卷文数】如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则A ．BM =EN ，且直线BM ，EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM ，EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线【答案】B【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线. 过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，M F ⊥平面ABCD ， MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知12EO ON EN ===,，5,22MF BF BM ==∴= BM EN ∴≠，故选B ．【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利用垂直关系，再结合勾股定理进而解决问题．12．【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V 柱体=Sh ，其中S 是柱体的底面积，h 是柱体的高．若某柱体的三视图如图所示（单位：cm ），则该柱体的体积（单位：cm 3）是A ．158B ．162C ．182D ．324【答案】B【解析】由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积为264633616222++⎛⎫⨯+⨯⨯= ⎪⎝⎭. 故选B.【名师点睛】本题首先根据三视图，还原得到几何体——棱柱，根据题目给定的数据，计算几何体的体积，常规题目.难度不大，注重了基础知识、视图用图能力、基本计算能力的考查.易错点有二，一是不能正确还原几何体；二是计算体积有误.为避免出错，应注重多观察、细心算.13．【2019年高考浙江卷】设三棱锥V –ABC 的底面是正三角形，侧棱长均相等，P 是棱VA 上的点（不含端点）．记直线PB 与直线AC 所成的角为α，直线PB 与平面ABC 所成的角为β，二面角P –AC –B 的平面角为γ，则 A ．β<γ，α<γB ．β<α，β<γC ．β<α，γ<αD ．α<β，γ<β【答案】B【解析】如图，G 为AC 中点，连接VG ，V 在底面ABC 的投影为O ，则P 在底面的投影D 在线段AO 上，过D 作DE 垂直于AC 于E ，连接PE ，BD ，易得PE VG ∥，过P 作PF AC ∥交VG 于F ，连接BF ，过D 作DH AC ∥，交BG 于H ，则,,BPF PBD PED αβγ=∠=∠=∠，结合△PFB ，△BDH ，△PDB 均为直角三角形，可得cos cos PF EG DH BDPB PB PB PBαβ===<=，即αβ>；在Rt △PED 中，tan tan PD PDED BDγβ=>=，即γβ>，综上所述，答案为B.【名师点睛】本题以三棱锥为载体，综合考查异面直线所成的角、直线与平面所成的角、二面角的概念，以及各种角的计算.解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小.而充分利用图形特征，则可事倍功半.常规解法下易出现的错误有，不能正确作图得出各种角，未能想到利用“特殊位置法”，寻求简便解法.14．【2018年高考全国Ⅱ卷文数】某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N 的路径中，最短路径的长度为A．1722B．5C．3D．2【答案】B【解析】根据圆柱的三视图以及其本身的特征，知点M在上底面上，点N在下底面上，且可以确定点M 和点N分别在以圆柱的高为长方形的宽，圆柱底面圆周长的四分之一为长的长方形的对角线的端点处，=B．【名师点睛】该题考查的是有关几何体的表面上两点之间的最短距离的求解问题，在解题的过程中，需要明确两个点在几何体上所处的位置，再利用平面上两点间直线段最短，所以处理方法就是将面切开平铺，利用平面图形的相关特征求得结果.15．【2018年高考全国Ⅱ卷文数】中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是【答案】A【解析】由题意知，题干中所给的是榫头，是凸出的几何体，求得是卯眼的俯视图，卯眼是凹进去的，即俯视图中应有一不可见的长方形，且俯视图应为对称图形.故选A.【名师点睛】本题主要考查空间几何体的三视图，考查考生的空间想象能力和阅读理解能力，考查的数学核心素养是直观想象.16．【2018年高考全国I 卷文数】在长方体1111ABCD A BC D -中，2AB BC ==，1AC 与平面11BBC C 所成的角为30︒，则该长方体的体积为A ．8B ．C ．D ．【答案】C【解析】在长方体1111ABCD A BC D -中，连接1BC ，根据线面角的定义可知130AC B ︒∠=，因为2AB =，所以1BC =，从而求得1CC =所以该长方体的体积为22V =⨯⨯= 故选C.【名师点睛】该题考查的是长方体的体积的求解问题，在解题的过程中，需要明确长方体的体积公式为长、宽、高的乘积，而题中的条件只有两个值，所以利用题中的条件求解另一条边的长就显得尤为重要，此时就需要明确线面角的定义，从而得到量之间的关系，最终求得结果.17．【2018年高考全国I 卷文数】已知圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为 A． B ．12π C．D ．10π【答案】B【解析】根据题意，可得截面是边长为所以其表面积为22π2π12πS =+=，故选B.【名师点睛】该题考查的是有关圆柱的表面积的求解问题，在解题的过程中，需要利用题的条件确定圆柱的相关量，即圆柱的底面圆的半径以及圆柱的高，在求圆柱的表面积的时候，一定要注意是两个底面圆与侧面积的和.18．【2018年高考浙江卷】某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是A ．2B ．4C ．6D ．8【答案】C俯视图正视图【解析】根据三视图可得几何体为一个直四棱柱，高为2，底面为直角梯形，上、下底分别为1，2，梯形的高为2，因此几何体的体积为()112226,2⨯+⨯⨯= 故选C.【名师点睛】先由几何体的三视图还原几何体的形状,再在具体几何体中求体积或表面积等.19．【2018年高考全国Ⅱ卷文数】设A B C D ，，，是同一个半径为4的球的球面上四点，ABC △为等边三角形且其面积为D ABC -体积的最大值为 A． B ．C．D ．【答案】B【解析】如图所示，设点M 为三角形ABC 的重心，E 为AC 中点，当点D 在平面ABC 上的射影为M 时，三棱锥D ABC -的体积最大，此时，4OD OB R ===，2ABC S AB ==△，6AB ∴=,点M 为三角形ABC 的重心，23BM BE ∴==Rt OBM ∴△中，有2OM ==，426DM OD OM ∴=+=+=，()max 163D ABC V -∴=⨯=，故选B.【名师点睛】本题主要考查三棱锥的外接球，考查了勾股定理，三角形的面积公式和三棱锥的体积公式，判断出当点D 在平面ABC 上的射影为三角形ABC 的重心时，三棱锥D ABC -体积最大很关键，由M 为三角形ABC 的重心，计算得到23BM BE ==OM ，进而得到结果，属于较难题型.20．【2018年高考全国Ⅱ卷文数】在正方体1111ABCD A BC D -中，E 为棱1CC 的中点，则异面直线AE 与CD 所成角的正切值为A BC D 【答案】C【解析】如图，在正方体1111ABCD A BC D -中，CD AB ∥，所以异面直线AE 与CD 所成角为EAB ∠，设正方体边长为2a ，则由E 为棱1CC 的中点，可得CE a =，所以BE =，则tan BE EAB AB ∠===．故选C ．【名师点睛】本题主要考查异面直线所成的角，考查考生的空间想象能力、化归与转化能力以及运算求解能力，考查的数学核心素养是直观想象、数学运算.求异面直线所成的角，需要将异面直线所成的角等价转化为相交直线所成的角，然后利用解三角形的知识加以求解.21．【2018年高考浙江卷】已知平面α，直线m ，n 满足m ⊄α，n ⊂α，则“m ∥n ”是“m ∥α”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】A【解析】因为,,m n m n ⊄⊂∥αα，所以根据线面平行的判定定理得m ∥α. 由m ∥α不能得出m 与α内任一直线平行，所以m n ∥是m ∥α的充分不必要条件，故选A. 【名师点睛】充分、必要条件的三种判断方法：（1）定义法：直接判断“若p 则q ”、“若q 则p ”的真假．并注意和图示相结合，例如“p ⇒q ”为真，则p 是q 的充分条件．（2）等价法：利用p ⇒q 与非q ⇒非p ，q ⇒p 与非p ⇒非q ，p ⇔q 与非q ⇔非p 的等价关系，对于条件或结论是否定式的命题，一般运用等价法．（3）集合法：若A ⊆B ，则A 是B 的充分条件或B 是A 的必要条件；若A ＝B ，则A 是B 的充要条件．22．【2018年高考浙江卷】已知四棱锥S −ABCD 的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为θ1，SE 与平面ABCD 所成的角为θ2，二面角S −AB −C 的平面角为θ3，则A ．θ1≤θ2≤θ3B ．θ3≤θ2≤θ1C ．θ1≤θ3≤θ2D ．θ2≤θ3≤θ1【答案】D【解析】设O 为正方形ABCD 的中心，M 为AB 中点，过E 作BC 的平行线EF ，交CD 于F ，过O 作ON 垂直EF 于N ，连接SO ，SN ，SE ，SM ，OM ，OE ，则SO 垂直于底面ABCD ，OM 垂直于AB ，因此123,,,SEN SEO SMO ∠=∠=∠=θθθ 从而123tan ,tan ,tan ,SN SN SO SOEN OM EO OM====θθθ 因为SN SO EO OM ≥≥，，所以132tan tan tan ,≥≥θθθ即132≥≥θθθ，故选D.【名师点睛】分别作出线线角、线面角以及二面角，再构造直角三角形，根据边的大小关系确定角的大小关系.23．【2018年高考北京卷文数】某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为A ．1B ．2C ．3D ．4【答案】C【解析】由三视图可得四棱锥P ABCD -如图所示，在四棱锥P ABCD -中，2,2,2,1PD AD CD AB ====，由勾股定理可知：3,PA PC PB BC ==== 则在四棱锥中，直角三角形有：,,PAD PCD PAB △△△，共3个，故选C.【名师点睛】此题考查三视图相关知识，解题时可将简单几何体放在正方体或长方体中进行还原，分析线面、线线垂直关系，利用勾股定理求出每条棱长，进而可进行棱长、表面积、体积等相关问题的求解.解答本题时，根据三视图还原几何体，利用勾股定理求出棱长，再利用勾股定理逆定理判断直角三角形的个数.24．【2020年高考全国Ⅱ卷文数】设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内． p 2：过空间中任意三点有且仅有一个平面． p 3：若空间两条直线不相交，则这两条直线平行． p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l ．则下述命题中所有真命题的序号是__________． ①14p p ∧ ②12p p ∧③23p p ⌝∨④34p p ⌝∨⌝【答案】①③④【解析】对于命题1p ，可设1l 与2l 相交，这两条直线确定的平面为α；若3l 与1l 相交，则交点A 在平面α内，同理，3l 与2l 的交点B 也在平面α内，所以，AB α⊂，即3l α⊂，命题1p 为真命题；对于命题2p ，若三点共线，则过这三个点的平面有无数个，命题2p 为假命题；对于命题3p ，空间中两条直线相交、平行或异面，命题3p 为假命题；对于命题4p ，若直线m ⊥平面α，则m 垂直于平面α内所有直线，直线l ⊂平面α，∴直线m ⊥直线l ，命题4p 为真命题. 综上可知，，为真命题，，为假命题，14p p ∧为真命题，12p p ∧为假命题，23p p ⌝∨为真命题，34p p ⌝∨⌝为真命题.故答案为：①③④.【点睛】本题考查复合命题的真假，同时也考查了空间中线面关系有关命题真假的判断，考查推理能力，属于中等题.25．【2020年高考全国Ⅲ卷文数】已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________．【解析】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，其中2,3BC AB AC ===，且点M 为BC 边上的中点，设内切圆的圆心为O ，由于AM =122S =⨯⨯△ABC 设内切圆半径为r ，则：ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()13322r =⨯++⨯= 解得：22r，其体积：3433V r π==.. 【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.26．【2020年高考浙江】已知圆锥的侧面积（单位：cm 2）为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：cm ）是_______．【答案】1【解析】设圆锥底面半径为r ，母线长为l ，则21222r l r l ππππ⨯⨯=⎧⎪⎨⨯⨯=⨯⨯⨯⎪⎩，解得1,2r l ==. 故答案为：1【点睛】本小题主要考查圆锥侧面展开图有关计算，属于基础题.27．【2020年高考江苏】如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2 cm ，高为2 cm ，内孔半轻为0.5 cm ，则此六角螺帽毛坯的体积是 ▲ cm.【答案】2π【解析】正六棱柱体积为262⨯圆柱体积为21()222ππ⋅=，所求几何体体积为2π.故答案为： 2π【点睛】本题考查正六棱柱体积、圆柱体积，考查基本分析求解能力，属基础题.28．【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∠BAD =60°．以1D 为半径的球面与侧面BCC 1B 1的交线长为________．【答案】2. 【解析】如图：取11B C 的中点为E ，1BB 的中点为F ，1CC 的中点为G ，因为BAD ∠=60°，直四棱柱1111ABCD A BC D -的棱长均为2，所以△111D B C 为等边三角形，所以1D E=111D E B C ⊥，又四棱柱1111ABCD A BC D -为直四棱柱，所以1BB ⊥平面1111D C B A ，所以111BB B C ⊥，因为1111BB B C B =，所以1D E ⊥侧面11BC CB ，设P 为侧面11BC CB 与球面的交线上的点，则1DE EP ⊥，1D E =，所以||EP ===，所以侧面11BC CB 与球面的交线上的点到E因为||||EF EG ==11BC CB 与球面的交线是扇形EFG 的弧FG ，因为114B EFC EG π∠=∠=，所以2FEG π∠=，所以根据弧长公式可得22FG π==.故答案为：2.【点睛】本题考查了直棱柱的结构特征，考查了直线与平面垂直的判定，考查了立体几何中的轨迹问题，考查了扇形中的弧长公式，属于中档题.29．【2019年高考全国Ⅱ卷文数】已知∠ACB=90°，P 为平面ABC 外一点，PC =2，点P 到∠ACB 两边AC ，BC P 到平面ABC 的距离为___________．【解析】作,PD PE 分别垂直于,AC BC ，PO ⊥平面ABC ，连接CO ，由题意可知,CD PD CD PO ⊥⊥，=PD PO P ，CD 平面PDO ，又OD ⊂平面PDO ，CD OD ∴⊥，PD PE ==2PC =，sin sin PCE PCD ∴∠=∠=， 60PCB PCA ︒∴∠=∠=，又易知PO CO ⊥，CO 为ACB ∠的平分线，451,,OCD OD CD OC ︒∴∠=∴===，又2PC =，PO ∴==【名师点睛】本题主要考查学生空间想象能力，合理画图成为关键，准确找到P 在底面上的射影，使用线面垂直定理，得到垂直关系，利用勾股定理解决．注意画图视角选择不当，线面垂直定理使用不够灵活，难以发现垂直关系，问题则很难解决，将几何体摆放成正常视角，是立体几何问题解决的有效手段，几何关系利于观察，解题事半功倍．30．【2019年高考全国Ⅱ卷文数】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．）【答案】261【解析】由图可知第一层（包括上底面）与第三层（包括下底面）各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有18826+=个面．如图，设该半正多面体的棱长为x ，则AB BE x ==，延长CB 与FE 的延长线交于点G ，延长BC 交正方体的棱于H ，由半正多面体对称性可知，BGE △为等腰直角三角形，,21)122BG GE CH x GH x x x ∴===∴=⨯+==，1x ∴==，1．【名师点睛】本题立意新颖，空间想象能力要求高，物体位置还原是关键，遇到新题别慌乱，题目其实很简单，稳中求胜是关键．立体几何平面化，无论多难都不怕，强大空间想象能力，快速还原图形． 31．【2019年高考全国Ⅱ卷文数】学生到工厂劳动实践，利用3D 打印技术制作模型．如图，该模型为长方体1111ABCD A BC D -挖去四棱锥O −EFGH 后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H分别为所在棱的中点，16cm 4cm AB=BC =AA =，，3D 打印所用原料密度为0.9 g/cm 3，不考虑打印损耗，制作该模型所需原料的质量为___________g.【答案】118.8【解析】由题意得，214642312cm 2EFGHS =⨯-⨯⨯⨯=四边形， ∵四棱锥O −EFGH 的高为3cm ， ∴3112312cm 3O EFGH V -=⨯⨯=．又长方体1111ABCD A BC D -的体积为32466144cm V =⨯⨯=，所以该模型体积为3214412132cm O EFGH V V V -=-=-=，其质量为0.9132118.8g ⨯=．【名师点睛】本题考查几何体的体积问题，理解题中信息联系几何体的体积和质量关系，从而利用公式求解．根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积，再求出模型的质量即可.32．【2019年高考北京卷文数】某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为__________．【答案】40【解析】如图所示，在棱长为4的正方体中，三视图对应的几何体为正方体去掉棱柱1111MPD A NQC B -之后余下的几何体，则几何体的体积()3142424402V =-⨯+⨯⨯=. 【名师点睛】本题首先根据三视图，还原得到几何体，再根据题目给定的数据，计算几何体的体积.属于中等题.(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解． 33．【2019年高考北京卷文数】已知l ，m 是平面α外的两条不同直线．给出下列三个论断：①l ⊥m ；②m ∥α；③l ⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．【答案】如果l ⊥α，m ∥α，则l ⊥m .【解析】将所给论断，分别作为条件、结论，得到如下三个命题：（1）如果l ⊥α，m ∥α，则l ⊥m ，正确；（2）如果l ⊥α，l ⊥m ，则m ∥α，不正确，有可能m 在平面α内；（3）如果l ⊥m ，m ∥α，则l ⊥α，不正确，有可能l 与α斜交、l ∥α. 故答案为：如果l ⊥α，m ∥α，则l ⊥m.【名师点睛】本题主要考查空间线面的位置关系、命题、逻辑推理能力及空间想象能力.将所给论断，分别作为条件、结论加以分析即可.34．【2019年高考天津卷文数】若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为__________. 【答案】π42=.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，一个底面的圆心为四棱锥底面的中心，故圆柱的高为1，圆柱的底面半径为12，故圆柱的体积为21ππ124⎛⎫⨯⨯= ⎪⎝⎭. 【名师点睛】本题主要考查空间几何体的结构特征以及圆柱的体积计算问题，解答时，根据棱锥的结构特点，确定所求的圆柱的高和底面半径.注意本题中圆柱的底面半径是棱锥底面对角线长度的一半、不是底边棱长的一半.35．【2019年高考江苏卷】如图，长方体1111ABCD A BC D -的体积是120，E 为1CC 的中点，则三棱锥E −BCD 的体积是 ▲ .。

2020中考数学一轮专项复习《四边形》能力提升卷及详细解答

2020中考数学一轮专项复习《四边形》能力提升卷及详细解答一．选择题1．（绵阳中考）如图，七边形ABCDEFG中，AB、ED的延长线交于点O，着∠1、∠2、∠3、∠4对应的邻补角和等于215°，则∠BOD的度数为（）A．30°B．35°C．40°D．45°2．一个正多边形的外角等于36°，则这个正多边形的内角和是（）A．1440°B．1080°C．900°D．720°3．（丽水中考）如图，在△ABC中，∠C＝90°，AC＝6，BC＝8，点P为斜边AB上一动点，过点P作PE⊥AC于点E，PF⊥BC于点F，连结EF，则线段EF的最小值为（）A．1.2 B．2.4 C．2.5 D．4.84．（武威中考）如图，矩形ABCD的对角线的交点为O，EF过点O且分别交AB，CD于点E，F，则图中阴影部分的面积是矩形ABCD的面积的（）A．B．C．D．5．（成都中考）如图，已知▱ABCD与正方形CEFG，其中E点在AD上．若∠EC D＝35°，∠AEF＝15°，则∠B的度数是（）A．75°B．70°C．55°D．50°6．如图，▱ABCD中，E，F分别是AB，C D的中点，则图中有（）个平行四边形．A ．7个B ．8个C ．9个D ．10个7．（兰州中考）如图，点E 、F 、G 、H 分别是四边形ABCD 边AB 、BC 、CD 、DA 的中点．则下列说法：①若AC ＝BD ，则四边形EFGH 为矩形；②若AC ⊥BD ，则四边形EFGH 为菱形；③若四边形EFGH 是平行四边形，则AC 与BD 互相平分；④若四边形EFGH 是正方形，则AC 与BD 互相垂直且相等．其中正确的个数是（）A ．1B ．2C ．3D ．48．（威海中考）如图，边长为2的正方形ABCD 中，点E 、F 分别在AD 、AB 上（点E 不与点D 重合），DE ＝AF ，DF 、CE 交于点G ，则AG 的取值范围是（）A ．﹣1≤AG ＜2B ．﹣1≤AG ＜2C ．1≤AG ＜2D ．﹣1≤AG ＜29．（凉山中考）如图，在平行四边形ABCD 中，CD ＝2AD ，BE ⊥AD 于点E ，F 为DC 的中点，连接EF 、BF ，下列结论： ①∠ABC ＝2∠ABF ；②EF ＝BF ；③S 四DEBC ＝2S △EFB ；④∠CFE ＝3∠DEF ；其中正确结论有（）A ．1个B ．2个C ．3个D ．4个10．如图，E 是边长为2的正方形ABCD 的对角线AC 上一点，且AE ＝AB ，F 为BE 上任意点，F G ⊥AC 于点G ，FH ⊥AB 于点H ，则FG +FH 的值是（）A．B．C．2 D．111．下列说法中，错误的是（）A．如果一个四边形绕对角线的交点旋转90°后，所得的图形能与原图形重合，那么这个四边形是正方形B．在一个平行四边形中，如果有一条对角线平分一个内角，那么该平行四边形是菱形C．在一个四边形中，如果有一条对角线平分一组内角，则该四边形是菱形D．两张等宽的纸条交叠在一起，重叠的部分是菱形12．如图：分别以Rt△ABC的直角边AC及斜边AB为边作等边△ACD及等边△ABE，已知∠BAC＝30°，EF⊥AB，垂足为F，连接DF交AC于点O．给出下列说法：①AC＝EF；②四边形ADFE是平行四边形；③△ABC≌△ADO；④2FO ＝BC；⑤∠EAD＝120°．其中正确结论的个数是（）A．2 B．3 C．4 D．5二．填空题13．已知，在梯形ABCD中，AD∥BC，AD＝4，AB＝CD＝6，∠B＝60°，那么下底BC的长为．14．如图，若∠A＝30°，则∠B+∠C+∠D+∠E＝．15．如图，长方形ABCD中，∠A＝∠ABC＝∠BCD＝∠D＝90°，AB＝CD＝5，AD＝BC＝13，点E为射线AD上的一个动点，若△ABE与△A'BE关于直线BE对称，当△A'BC为直角三角形时，AE的长为．16．小明用四根长度相同的木条制作了能够活动的菱形学具，他先活动学具成为图1所示菱形，并测得∠B＝60°，接着活动学具成为图2所示正方形，并测得正方形的对角线AC＝40cm，则图1中对角线AC的长为cm．17．如图，在平面直角坐标系中，正方形ABCD顶点A的坐标为（0，4），B点在x轴上，对角线AC，BD交于点M，OM＝6，则点C的坐标为．三．解答题18．在平面直角坐标系xOy中，四边形OADC为正方形，点D的坐标为（4，4），动点E沿边AO从A向O以每秒1cm 的速度运动，同时动点F沿边OC从O向C以同样的速度运动，连接AF、DE交于点G．（1）试探索线段AF、DE的关系，写出你的结论并说明理由；（2）连接EF、DF，分别取AE、EF、FD、DA的中点H、I、J、K，则四边形HIJK是什么特殊平行四边形？请在图①中补全图形，并说明理由．（3）如图②当点E运动到AO中点时，点M是直线EC上任意一点，点N是平面内任意一点，是否存在点N使以O，C、M、N为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．19．如图，在平行四边形ABCD中，连接AC，AD＝AC，过点D作DF⊥AC交BC于点F，交AC于点E，连接AF．（1）若AE＝4，DE＝2EC，求EC的长．（2）延长AC至点H，连接FH，使∠H＝∠EDC，若AB＝AF＝FH，求证：FD+FC＝AD．20．如图，在正方形ABCD中，M、N分别是射线CB和射线DC上的动点，且始终∠MAN＝45°．（1）如图1，当点M、N分别在线段BC、DC上时，请直接写出线段BM、MN、DN之间的数量关系；（2）如图2，当点M、N分别在CB、DC的延长线上时，（1）中的结论是否仍然成立，若成立，给予证明，若不成立，写出正确的结论，并证明；（3）如图3，当点M、N分别在CB、DC的延长线上时，若CN＝CD＝6，设BD与AM的延长线交于点P，交AN于Q，直接写出AQ、AP的长．21．【综合与实践】如图①，在正方形ABCD中，点E、F分别在射线CD、BC上，且BF＝CE，将线段FA绕点F顺时针旋转90°得到线段FG，连接EG，试探究线段EG和BF的数量关系和位置关系．【观察与猜想】任务一：“智慧小组”首先考虑点E、F的特殊位置如图②，当点E与点D重合，点F与点C重合时，易知：EG与BF的数量关系是，EG与BF的位置关系是．【探究与证明】任务二：“博学小组”同学认为E、F不一定必须在特殊位置，他们分两种情况，一种是点E、F 分别在CD、BC边上任意位置时（如图③）；一种是点E、F在CD、BC边的延长线上的任意位置时（如图④），线段EG与BF的数量关系与位置关系仍然成立．请你选择其中一种情况给出证明．【拓展与延伸】“创新小组”同学认为，若将“正方形ABCD”改为“矩形ABCD，且＝k（k≠1）”，点E、F分别在射线CD、BC上任意位置时，仍将线段FA绕点F顺时针旋转90°，并适当延长得到线段FG，连接EG（如图⑤），则当线段BF、CE、AF、FG满足一个条件时，线段EG与BF的数量关系与位置关系仍然成立．（请你在横线上直接写出这个条件，无需证明）参考答案一．选择题1．解：∵∠1、∠2、∠3、∠4的外角的角度和为215°，∴∠1+∠2+∠3+∠4+215°＝4×180°，∴∠1+∠2+∠3+∠4＝505°，∵五边形OAGFE内角和＝（5﹣2）×180°＝540°，∴∠1+∠2+∠3+∠4+∠BOD＝540°，∴∠BOD＝540°﹣505°＝35°，故选：B．2．解：∵一个正多边形的外角等于36°，∴这个正多边形是正十边形，∴内角和为（10﹣2）×180°＝1440°，故选：A．3．解：连接PC，∵PE⊥AC，PF⊥BC，∴∠PEC＝∠PFC＝∠C＝90°，∴四边形ECFP是矩形，∴EF＝PC，∴当PC最小时，EF也最小，即当CP⊥AB时，PC最小，∵AC＝6，BC＝8，∴AB＝10，∴PC的最小值为：．∴线段EF长的最小值为4.8．故选：D．4．解：∵矩形ABCD的边AB∥CD，∴∠ABO＝∠CDO，在矩形ABCD中，OB＝OD，在△BOE和△DOF中，，∴△BOE ≌△DOF （ASA ），∴S △BOE ＝S △DOF ，∴阴影部分的面积＝S △AOB ＝S 矩形ABCD ．故选：B ．5．解：∵四边形CEFG 是正方形，∴∠CEF ＝90°，∵∠CED ＝180°﹣∠AEF ﹣∠CEF ＝180°﹣15°﹣90°＝75°，∴∠D ＝180°﹣∠CED ﹣∠ECD ＝180°﹣75°﹣35°＝70°，∵四边形ABCD 为平行四边形，∴∠B ＝∠D ＝70°．故选：B ．6．解：E ，F 分别是AD ，BC 的中点，则有AE ＝FC ＝ED ＝BF ＝AD ＝BC∴四边形AECF ，EDFB ，是平行四边形，有∠FBE ＝∠EDF ＝∠AEB∵AE ∥BF∴EAF ＝∠AFB∴根据ASA 得出△MAE ≌△MFB ，∴AM ＝MF ，即点M 是AF 的中点．同理，点N 是FD 的中点，∴MN 是△EBC 和△AFD 的中位线，∴MN ＝AE ＝FC ＝ED ＝BF ＝AD ＝BC∴四边形AENM ，DEMN ，BMNF ，FCNM 是平行四边形∵EN ∥MF ，ME ∥FN∴四边形ENFM 是平行四边形，而四边形ABCD 也是平行四边形，共8个平行四边形．故选：B ．7．解：因为一般四边形的中点四边形是平行四边形，当对角线BD ＝AC 时，中点四边形是菱形，当对角线AC ⊥BD 时，中点四边形是矩形，当对角线AC ＝BD ，且AC ⊥BD 时，中点四边形是正方形，故④选项正确，故选：A ．8．解：∵AD ＝DC ，∠EDC ＝∠FAD ，DE ＝AF ，∴△DEC ≌△AFD （SAS ）．∴∠DCE ＝ADF ．∵∠DCE +∠DEC ＝90°，∴∠ADF+∠DEC＝90°，即∠DGE＝90°＝∠DGC．所以点G运动的轨迹在以DC为直径的圆上的一段弧，圆心在DC中点O处．当A、G、O三点共线时，AG最短，如图所示．此时AO＝＝＝，OG＝DC＝1，所以AG＝AO﹣OG＝﹣1．因为点E不与点D重合，所以AG＜2．所以﹣1≤AG＜2．故选：D．9．解：如图，延长EF交BC的延长线于G，取AB的中点H，连接FH．∵CD＝2AD，DF＝FC，∴CF＝CB，∴∠CFB＝∠CBF，∵CD∥AB，∴∠CFB＝∠FBH，∴∠CBF＝∠FBH，∴∠ABC＝2∠ABF．故①正确，∵DE∥CG，∴∠D＝∠FCG，在△DFE和△FCG中，∴△DFE≌△FCG（ASA），∴FE＝FG，∵BE⊥AD，∴∠AEB ＝90°，∵AD ∥BC ，∴∠AEB ＝∠EBG ＝90°，∴BF ＝EF ＝FG ，故②正确，∵S △DFE ＝S △CFG ，∴S 四边形DEBC ＝S △EBG ＝2S △BEF ，故③正确， ∵AH ＝HB ，DF ＝CF ，AB ＝CD ，∴CF ＝BH ，∵CF ∥BH ，∴四边形BCFH 是平行四边形，∵CF ＝BC ，∴四边形BCFH 是菱形，∴∠BFC ＝∠BFH ，∵FE ＝FB ，FH ∥AD ，BE ⊥AD ，∴FH ⊥BE ，∴∠BFH ＝∠EFH ＝∠DEF ，∴∠EFC ＝3∠DEF ，故④正确，故选：D ．10．解：如图，过点E 作EM ⊥AB ，连接AF ，∵四边形ABCD 是正方形， ∴∠ACB ＝45°，∴△AEM 是等腰直角三角形，∵AB ＝AE ＝2，∴EM ＝AE ×sin45°＝2×， ∵S △ABE ＝S △AEF +S △ABF ， ∴， ∴EM ＝FG +FH ＝，故选：B ．11．解：A ．如果一个四边形绕对角线的交点旋转90°后，所得的图形能与原图形重合，那么这个四边形是正方形，本选项正确；B．在一个平行四边形中，如果有一条对角线平分一个内角，那么该平行四边形是菱形，本选项正确；C．在一个四边形中，如果有一条对角线平分一组内角，则该四边形不一定是菱形，本选项错误；D．两张等宽的纸条交叠在一起，重叠的部分是菱形，本选项正确；故选：C．12．解：∵Rt△ABC中，∠BAC＝30°，∴AB＝2BC，又∵△ABE是等边三角形，EF⊥A B，∴AB＝2AF∴AF＝BC，在Rt△AFE和Rt△BCA中，，∴Rt△AFE≌Rt△BCA（HL），∴AC＝EF；故①正确∵△ACD是等边三角形，∴∠DAC＝60°，AC＝AD，∴∠DAB＝∠DAC+∠BAC＝90°又∵EF⊥AB，∴EF∥AD，∵AC＝EF，AC＝AD，∴EF＝AD，∴四边形ADFE是平行四边形．故②正确∵四边形ADFE是平行四边形∴AE＝DF＝AB，AE∥DF又∵AF＝BC，AD＝AC∴△ADF≌△CAB（SSS）∴△ABC与△ADO不全等故③错误∵AE∥DF∴BC＝2OF故④正确∵∠EAD＝∠BAE+∠BAC+∠CAD＝150°故⑤错误故选：B．二．填空题13．解：如图，过A作AE∥DC交BC与E，∵AD∥BC，∴四边形AECD是平行四边形，∴AD＝EC＝4，AE＝CD，∵AB＝CD＝6，∴AE＝AB＝6，∵∠B＝60°，∴△ABE是等边三角形，∴BE＝AB＝6，∴BC＝6+4＝10．故答案为：10．14．解：如图所示，AE与CD交于点M，AB与CD交于点N，∵∠ANC是△BCN的一个外角，∴∠ANM＝∠B+∠C，又∵∠DME是△AMN的一个外角，∴∠DME＝∠A+∠ANM，∴∠DME＝∠A+∠B+C，∴∠A+∠B+C+∠D+∠E＝180°，即30°+∠B+C+∠D+∠E＝180°，∴∠B+C+∠D+∠E＝180°﹣30°＝150°，故答案为：150°．15．解：若点E在线段AD上，∵若△ABE与△A′BE关于直线BE对称，∴AB＝A'B＝，5，∠EA'B＝90°，AE＝A'E∵△A'BC为直角三角形∴∠BA'C＝90°∴A'C＝＝＝12，∵∠EA'B＝90°，∠BA'C＝90°∴∠CA'E＝180°∴点E，点C，点A'共线在Rt△CDE中，DC2+DE2＝CE2．∴（A'E+12）2＝（13﹣AE）2+25，∴AE＝1，若点E在线段AD的延长线上，且点C在A'E上，如图所示：∵△ABE与△A′BE关于直线BE对称，∴AB＝A'B＝，5，∠A＝∠A'＝90°在Rt△A'BC中，A'C＝＝＝12，∵∠BCA'+∠DCE＝90°，∠DCE+∠DEC＝90°∵∠A'＝∠EDC＝90°，AB＝CD＝A'B，∴在△A'C和△DCE中，，∴△A'BC≌△DCE（AAS），∴DE＝A'C＝12，∴AE＝1AD+DE＝13+12＝25；故答案为：1或25．16．解：如图1，2中，连接AC．在图2中，∵四边形ABCD是正方形，∴AB＝BC，∠B＝90°，∵AC＝40°，∴AB＝BC＝20，在图1中，∵∠B＝60°，BA＝BC，∴△ABC是等边三角形，∴AC＝BC＝20，故答案为：20，17．解：过点C作CE⊥x轴于点E，过点M作MF⊥x轴于点F，连接EM，如图所示：∴∠MFO＝∠CEO＝∠AOB＝90°，AO∥MF∥CE，∵四边形ABCD是正方形，∴AB＝BC，∠ABC＝90°，AM＝CM，∴∠OAB＝∠EBC，OF＝EF，∴MF是梯形AOEC的中位线，∴MF＝（AO+EC），∵MF⊥OE，∴MO＝ME．∵在△AOB和△BEC中，，∴OB＝CE，AO＝BE．∴MF＝（BE+OB），又∵OF＝FE，∴△MOE是直角三角形，∵MO＝ME，∴△MOE是等腰直角三角形，∴OE＝＝12，∵A（0，4），∴OA＝4，∴BE＝4，∴OB＝CE＝OE﹣BE＝8．∴C（12，8）．故答案为：（12，8）．三．解答题18．解：（1）AF＝DE．理由如下：∵四边形OADC是正方形，∴OA＝AD，∠DAE＝∠AOF＝90°，由题意得：AE＝OF，在△AOF和△DAE中，，∴△AOF≌△DAE（SAS），∴AF＝DE．（2）四边形HIJK是正方形．理由如下：如图①所示：∵H、I、J、K分别是AE、EF、FD、DA的中点，∴HI＝KJ＝AF，HK＝IJ＝ED，HI∥AF，HK∥ED，∵AF＝DE，∴四边形HIJK是菱形，∵△AOF≌△DAE，∴∠ADE＝∠OAF，∵∠ADE+∠AED＝90°，∴∠OAF+∠AED＝90°，∴∠AGE＝90°，∴AF⊥ED，∵HI∥AF，HK∥ED，∴HI⊥HK，∴∠KHI＝90°，∴四边形HIJK是正方形．（3）存在，理由如下：∵四边形OADC为正方形，点D的坐标为（4，4），∴OA＝AD＝OC＝4，∴C（4，0），∵点E为AO的中点，∴OE＝2，E（0，2）；分情况讨论：如图②所示，①当OC是以O，C、M、N为顶点的菱形的对角线时，OC与MN互相垂直平分，则M为CE的中点，∴点M的坐标为（2，1），∵点M和N关于OC对称，∴N（2，﹣1）；②当OC是以O，C、M、N为顶点的菱形的边时，若M在y轴的左侧时，∵四边形OCM'N'是菱形，∴OM'＝OC＝4，M'N'∥OC，∴△M'FE∽△COE，∴＝＝2，设EF＝x，则M'F＝2x，OF＝x+2，在Rt△OM'F中，由勾股定理得：（2x）2+（x+2）2＝42，解得：x＝，或x＝﹣2（舍去），∴N'（，）；若M在y轴的右侧时，作N''P⊥OC于P，∵ON''∥CM''，∴∠PON''＝∠OCE，∴tan∠PON''＝＝tan∠OCE＝＝，设PN''＝y，则OP＝2y，在Rt△OPN''中，由勾股定理得：y2+（2y）2＝42，解得：y＝，∴PN''＝，OP＝，∴N''（，﹣）；综上所述，存在点N使以O，C、M、N为顶点的四边形是菱形，点N的坐标为（2，﹣1）或（，）或（，﹣）．19．（1）解：设EC＝x，则DE＝2x，AD＝AC＝AE+EC＝4+x，∵DF⊥AC，∴∠AED＝90°，在Rt△ADE中，由勾股定理得：（2x）2+42＝（4+x）2，解得：x＝，或x＝0（舍去），（2）证明：∵四边形ABCD是平行四边形，∴AB＝CD，∵AB＝AF＝FH，∴CD＝FH，∵DF⊥AC，∴∠DEC＝∠HEF＝90°，在△DEC和△HEF中，，∴△DEC≌△HEF（AAS），∴EC＝EF，DE＝EH，∵DF⊥AC，∴△CEF是等腰直角三角形，∴∠ECF＝45°，∵AF＝FH，DF⊥AC，∴AE＝HE＝DE，∴△ADE是等腰直角三角形，∴∠DAC＝45°，DE＝AD，∵AD＝AC，∴∠ADC＝∠ACD＝（180°﹣45°）＝67.5°，∴∠EDC＝∠H＝22.5°，∴∠CFH＝∠EF﹣∠H＝22.5°＝∠H，∴CF＝CH，∴EF+FC＝EC+CH＝EH＝DE，∴FD+FC＝DE+EF+FC＝DE+DE＝2DE＝AD．20．解：（1）BM+DN＝MN，理由如下：如图1，在MB的延长线上，截取BE＝DN，连接AE，∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠ABC＝∠D＝90°，∴∠ABE＝90°＝∠D，在△ABE和△ADN中，，∴AE＝AN，∠EAB＝∠NAD，∴∠EAN＝∠BAD＝90°，∵∠MAN＝45°，∴∠EAM＝45°＝∠NAM，在△AEM和△ANM中，，∴△AEM≌△ANM（SAS），∴ME＝MN，又∵ME＝BE+BM＝BM+DN，∴BM+DN＝MN；故答案为：BM+DN＝MN；（2）（1）中的结论不成立，DN﹣BM＝MN．理由如下：如图2，在DC上截取DF＝BM，连接AF，则∠ABM＝90°＝∠D，在△ABM和△ADF中，，∴△ABM≌△ADF（SAS），∴AM＝AF，∠BAM＝∠DAF，∴∠BAM+∠BAF＝∠BAF+∠DAF＝∠BAD＝90°，即∠MAF＝∠BAD＝90°，∵∠MAN＝45°，∴∠MAN＝∠FAN＝45°，在△MAN和△FAN中，，∴△MAN≌△FAN（SAS），∴MN＝NF，∴MN＝DN﹣DF＝DN﹣BM，∴DN﹣BM＝MN．（3）∵四边形ABCD是正方形，∴AB＝BC＝AD＝CD＝6，AD∥BC，AB∥CD，∠ABC＝∠ADC＝∠BCD＝90°，∴∠ABM＝∠MCN＝90°，∵CN＝CD＝6，∴AN＝＝＝6，∵AB∥CD，∴△ABQ∽△NDQ，∴＝＝＝＝，∴＝，∴AQ＝AN＝2；由（2）得：DN﹣BM＝MN．设BM＝x，则MN＝12﹣x，CM＝6+x，在Rt△CMN中，由勾股定理得：62+（6+x）2＝（12﹣x）2，解得：x＝2，∴BM＝2，∴AM＝＝＝2，∵BC∥AD，∴△PBM∽△PDA，∴＝＝＝，∴PM＝AM＝，∴AP＝AM+PM＝3．21．【观察与猜想】解：∵四边形ABCD是正方形，由旋转的性质得：GC＝AC，∠ACG＝90°，∴∠ACB＝∠GCD＝45°，在△ABC和△GDC中，，∴△ABC≌△GDC（SAS），∴AB＝GD，∠GDC＝∠B＝90°，∴DG∥BC，△CDG是等腰直角三角形，∴DG＝CD＝BC，∵点E与点D重合，点F与点C重合，∴EG＝BF，EG∥BF；故答案为：EG＝BF，EG∥BF；【探究与证明】证明：点E、F分别在CD、BC边上任意位置时，如图③所示：作GM⊥BC，交BC延长线于M，则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，由旋转的性质得：GF＝AF，∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，在△ABF和△FMG中，，∴△ABF≌△FMG（AAS），∴AB＝FM，BF＝MG，∵AB＝BC，∴BF＝CM，∵BF＝CE，∴MG＝CE，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；点E、F在CD、BC边的延长线上的任意位置时，如图④所示：作GM⊥BC，交BC延长线于M，则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，由旋转的性质得：GF＝AF，∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，在△ABF和△FMG中，，∴△ABF≌△FMG（AAS），∴AB＝FM，BF＝MG，∵AB＝BC，∴BF＝CM，∵BF＝CE，∴MG＝CE，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；【拓展与延伸】解：＝＝k（k≠1）时，线段EG与BF的数量关系与位置关系仍然成立；理由如下：作GM⊥BC，交BC延长线于M，如图⑤所示：则∠GMF＝90°，MG∥DC，∵四边形ABCD是正方形，∴AB＝BC，∠BCD＝∠B＝90°，∴∠BAF+∠BFA＝90°，∠B＝∠GMF，由旋转的性质得：∠AFG＝90°，∴∠BFA+∠MFG＝90°，∴∠BAF＝∠MFG，∴△ABF∽△FMG，∴＝＝，∵＝＝k，∴＝＝k，＝＝k，∴FM＝BC，GM＝CE，∴BF＝CM，∵MG∥CE，∴四边形CEGM是平行四边形，又∵∠GMF＝90°，∴四边形CEGM是矩形，∴EG＝CM，EG∥CM，∴EG＝BF，EG∥BF；故答案为：＝＝k（k≠1）．。

初中数学中考复习四边形综合复习(能力提升)

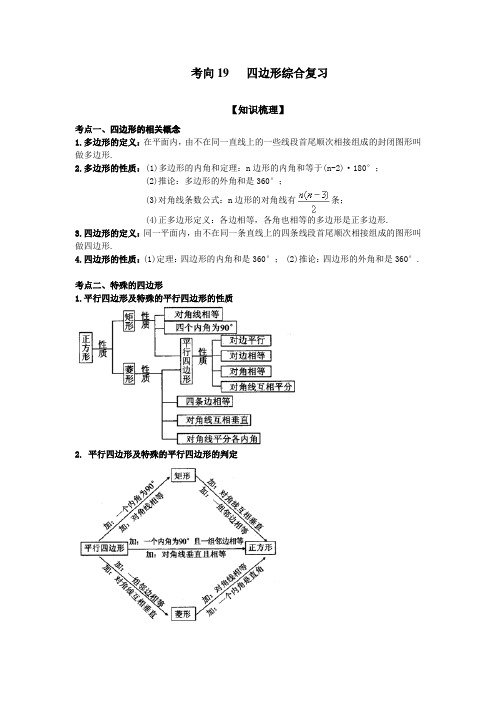
考向19 四边形综合复习【知识梳理】考点一、四边形的相关概念1.多边形的定义：在平面内，由不在同一直线上的一些线段首尾顺次相接组成的封闭图形叫做多边形.2.多边形的性质：(1)多边形的内角和定理：n边形的内角和等于(n-2)·180°；(2)推论：多边形的外角和是360°；(3)对角线条数公式：n边形的对角线有条；(4)正多边形定义：各边相等，各角也相等的多边形是正多边形.3.四边形的定义：同一平面内，由不在同一条直线上的四条线段首尾顺次相接组成的图形叫做四边形.4.四边形的性质：(1)定理：四边形的内角和是360°； (2)推论：四边形的外角和是360°.考点二、特殊的四边形1.平行四边形及特殊的平行四边形的性质2. 平行四边形及特殊的平行四边形的判定方法指导：面积公式：S 菱形 =21ab=ch （a 、b 为菱形的对角线,c 为菱形的边长，h 为c 边上的高）. S 平行四边形 =ah(a 为平行四边形的边，h 为a 上的高）.考点三、梯形1.梯形的定义：一组对边平行而另一组对边不平行的四边形叫做梯形.(1)互相平行的两边叫做梯形的底；较短的底叫做上底，较长的底叫做下底. (2)不平行的两边叫做梯形的腰. (3)梯形的四个角都叫做底角.2.直角梯形：一腰垂直于底的梯形叫做直角梯形.3.等腰梯形：两腰相等的梯形叫做等腰梯形.4.等腰梯形的性质：(1)等腰梯形的两腰相等； (2)等腰梯形同一底上的两个底角相等. (3)等腰梯形的对角线相等.5.等腰梯形的判定方法：(1)两腰相等的梯形是等腰梯形(定义)；(2)同一底上的两个角相等的梯形是等腰梯形； (3)对角线相等的梯形是等腰梯形.6.梯形中位线：连接梯形两腰中点的线段叫梯形的中位线.7.面积公式： S=(a+b)h(a 、b 是梯形的上、下底，h 是梯形的高).考点四、平面图形1.平面图形的镶嵌的定义：用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙，不重叠地铺成一片，这就是平面图形的镶嵌，又称做平面图形的密铺.2.平面图形镶嵌的条件：(1)同种正多边形镶嵌成一个平面的条件：周角是否是这种正多边形的一个内角的整倍数.在正多边形里只有正三角形、正四边形、正六边形可以镶嵌. (2)n 种正多边形组合起来镶嵌成一个平面的条件： ①n 个正多边形中的一个内角的和的倍数是360°； ②n 个正多边形的边长相等，或其中一个或n 个正多边形的边长是另一个或n 个正多边形的边长的整数倍.【专项训练】一、选择题1．如图，在中，，是上异于、的一点，则的值是（）．A．16 B．20 C．25 D．302. 如图1，在矩形中，动点从点出发，沿→→→方向运动至点处停止．设点运动的路程为，的面积为，如果关于的函数图象如图2所示，则当时，点应运动到（）.A．处B．处C．处D．处3．如图，在菱形ABCD中，∠A=60°，E、F分别是AB，AD的中点，DE、BF相交于点G，连接BD，CG．有下列结论：①∠BGD=120°；②BG+DG=CG；③△BDF≌△CGB；④S△ABD=AB2其中正确的结论有（）.A．1个 B．2个 C．3个 D．4个4.一个正方形纸片，用剪刀沿一条不过任何顶点的直线将其剪成两部分；拿出其中一部分，再沿一条不过任何顶点的直线将其剪成两部分；又从得到的三部分中拿出其中之一，还是沿一条不过任何顶点的直线将其剪成两部分……如此下去，最后得到了34个六十二边形和一些多边形纸片，则至少要剪的刀数是（）.A. 2004B. 2005C. 2006D. 20075．如图所示，已知菱形OABC，点C在x轴上，直线y=x经过点A，菱形OABC的面积是.若反比例函数的图象经过点B，则此反比例函数表达式为（）.A．B． C．D．6.如图，正方形ABCD的边长为1，将长为1的线段QR的两端放在正方形相邻的两边上同时滑动．如果点Q从点A出发，按A→B→C→D→A的方向滑动到A停止，同时点R从点B 出发，按B→C→D→A→B的方向滑动到B停止，在这个过程中，线段QR的中点M所经过的路线围成的图形面积为（）A．B．4﹣πC．πD．二、填空题7. 如图，将两张长为8，宽为2的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的周长有最小值8，那么菱形周长的最大值是_________．8. 如图，在等腰梯形中，，= 4=，=45°．直角三角板含45°角的顶点在边上移动，一直角边始终经过点，斜边与交于点．若为等腰三角形，则的长等于____________．9.如图，正方形A1B1B2C1，A2B2B3C2，A3B3B4C3，…，A n B n B n+1C n，按如图所示放置，使点A1、A2、A3、A4、…、A n在射线OA上，点B1、B2、B3、B4、…、B n在射线OB上．若∠AOB=45°，OB1=1，图中阴影部分三角形的面积由小到大依次记作S1，S2，S3，…，S n，则S n=______．10.如图，Rt△ABC中，∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5，OC=6，则另一直角边BC的长为．11.如图，已知正方形ABCD的边长为1，以顶点A、B为圆心，1为半径的两弧交于点E，以顶点C、D为圆心，1为半径的两弧交于点F，则EF的长为．12.如图，直角梯形ABCD中，∠A=90°，∠B=120°，AD=，AB=6．在底边AB上取点E，在射线DC上取点F，使得∠DEF=120°．若射线EF经过点C，则AE的长是．三、解答题13.如图，在边长为4cm的正方形ABCD中，点E，F，G，H分别按A⇒B，B⇒C，C⇒D，D⇒A的方向同时出发，以1cm/s的速度匀速运动．在运动过程中，设四边形EFGH的面积为S（cm2），运动时间为t（s）．（1）试证明四边形EFGH是正方形；（2）写出S关于t的函数关系式，并求运动几秒钟时，面积最小，最小值是多少？（3）是否存在某一时刻t，使四边形EFGH的面积与正方形ABCD的面积比是5：8？若存在，求出t的值；若不存在，请说明理由．14.如图,在矩形ABCD中，AB=3，AD=1，点P在线段AB上运动，设AP=x，现将纸片还原，使点D与P重合，得折痕EF（点E、F为折痕与矩形边的交点，再将纸片还原。

初中数学中考复习特殊的四边形(能力提升)

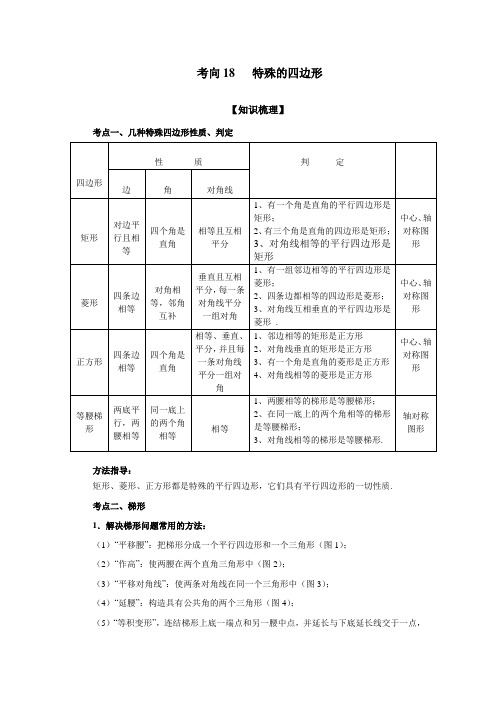
考向18 特殊的四边形【知识梳理】考点一、几种特殊四边形性质、判定方法指导：矩形、菱形、正方形都是特殊的平行四边形，它们具有平行四边形的一切性质.考点二、梯形1．解决梯形问题常用的方法：（1）“平移腰”：把梯形分成一个平行四边形和一个三角形（图1）；（2）“作高”：使两腰在两个直角三角形中（图2）；（3）“平移对角线”：使两条对角线在同一个三角形中（图3）；（4）“延腰”：构造具有公共角的两个三角形（图4）；（5）“等积变形”，连结梯形上底一端点和另一腰中点，并延长与下底延长线交于一点，构成三角形（图5）．图1 图2 图3 图4 图5 方法指导：解决梯形问题的基本思想和方法就是通过添加适当的辅助线，把梯形问题转化为已经熟悉的平行四边形和三角形问题来解决．在学习时注意它们的作用，掌握这些辅助线的使用对于学好梯形内容很有帮助．2.特殊的梯形（1）等腰梯形：两腰相等的梯形叫做等腰梯形．性质：①等腰梯形的同一底边上的两个角相等；等腰梯形的两条对角线相等．②同一底边上的两个角相等的梯形是等腰梯形．③等腰梯形是轴对称图形，它的对称轴是经过两底中点的一条直线．（2）直角梯形：有一个角是直角的梯形叫做直角梯形．考点三、中点四边形相关问题1.中点四边形的概念：把依次连接任意一个四边形各边中点所得的四边形叫做中点四边形．2.若中点四边形为矩形，则原四边形满足条件对角线互相垂直；若中点四边形为菱形，则原四边形满足条件对角线相等；若中点四边形为正方形，则原四边形满足条件对角线互相垂直且相等．方法指导：中点四边形的形状由原四边形的对角线的位置和数量关系决定．【专项训练】一、选择题1. 如图,E是边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ＋PR的值是( )．A．B．C．D．2．如图,在梯形ABCD中，AB∥CD，中位线MN = 7,对角线AC⊥BD,∠BDC = 30°，则梯形的高为（）．A．B．C．D．3. 四边形ABCD的对角线AC=BD，且AC⊥BD，分别过A、B、C、D作对角线的平行线，得到四边形EFGH，则它是（）.A．正方形B．菱形C．矩形D．任意四边形4. 如图，矩形ABCD中，其长为a，宽为b，如果，则的值为（）.A．B．C．D．5. 如图，在菱形ABCD中，，的垂直平分线FE交对角线AC于点F，E为垂足，连接DF．则等于（）．A．B．C．D．6. 如图，在正方形ABCD中，点P是AB上一动点（不与A、B重合），对角线AC、BD相交于点O，过点P分别作AC、BD的垂线，分别交AC、BD于点E、F，交AD、BC 于点M、N．下列结论：①△APE≌△AME；②PM+PN=AC；③PE2+PF2=PO2；④△POF∽△BNF；其中正确的结论有（）A．4个B．3个C．2个D．1个二、填空题7. 如图，点E、F、G、H分别为正方形ABCD的边AB、BC、CD、DA上的点，且AE=BF=CG=DH=AB，则图中阴影部分的面积与正方形ABCD的面积之比为___________．8. 如图，在等腰梯形ABCD中，AD∥BC，AC与BD相交于点O．下面结论正确的是_________．①AC=BD；②∠DAO=∠DBC；③S△BOC=S梯形ABCD；④△AOB≌△DOC．9. 如图，圆柱形玻璃杯，高为8cm，底面周长为12cm，在杯内离杯底2cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，求蚂蚁到达蜂蜜的最短距离是．10.如图，将正△ABC分割成m个边长为1的小正三角形和一个黑色菱形，这个黑色菱形可分割成n个边长为1的小三角形，若mn=4725，则△ABC的边长是_________.11.如图，在梯形ABCD中，AD∥BC，∠C=90°，BE平分∠ABC且交CD于E，E为CD的中点，EF∥BC交AB于F，EG∥AB交BC于G，当AD=2，BC=12时，四边形BGEF 的周长为_________．12.如图，以菱形ABCD各边的中点为顶点作四边形A1B1C1D1，再以A1B1C1D1各边的中点为顶点作四边形A2B2C2D2，…，如此下去，得到四边形A2011B2011C2011D2011，若ABCD对角线长分别为a和b，请用含a、b的代数式表示四边形A2011B2011C2011D2011的周长_________________.三、解答题13. 已知，如图，正方形ABCD的边长为6，菱形EFGH的三个顶点E，G，H分别在正方形ABCD边AB，CD，DA上，AH=2，连接CF．(1)当DG=2时，求△FCG的面积；(2)设DG=，用含的代数式表示△FCG的面积；(3)判断△FCG的面积能否等于1，并说明理由．14.在图1到图3中，点O是正方形ABCD对角线AC的中点，△MPN为直角三角形，∠MPN=90°．正方形ABCD保持不动，△MPN沿射线AC向右平移，平移过程中P点始终在射线AC上，且保持PM垂直于直线AB于点E，PN垂直于直线BC于点F．（1）如图1，当点P与点O重合时，OE与OF的数量关系为______；（2）如图2，当P在线段OC上时，猜想OE与OF有怎样的数量关系与位置关系？并对你的猜想结果给予证明；（3）如图3，当点P在AC的延长线上时，OE与OF的数量关系为_______；位置关系为_________．15．如图1，P是线段AB上的一点，在AB的同侧作△APC和△BPD，使PC=PA，PD=PB，∠APC=∠BPD，连接CD，点E、F、G、H分别是AC、AB、BD、CD的中点，顺次连接E、F、G、H．（1）猜想四边形EFGH的形状，直接回答，不必说明理由；（2）当点P在线段AB的上方时，如图2，在△APB的外部作△APC和△BPD，其他条件不变，（1）中的结论还成立吗？说明理由；（3）如果（2）中，∠APC=∠BPD=90°，其他条件不变，先补全图3，再判断四边形EFGH的形状，并说明理由．16. 如图，在平面直角坐标系中，点A（10，0），∠OBA=90°，BC∥OA，OB=8，点E 从点B出发，以每秒1个单位长度沿BC向点C运动，点F从点O出发，以每秒2个单位长度沿OB向点B运动．现点E、F同时出发，当点F到达点B时，E、F两点同时停止运动．（1）求梯形OABC的高BG的长；（2）连接E、F并延长交OA于点D，当E点运动到几秒时，四边形ABED是等腰梯形；（3）动点E、F是否会同时在某个反比例函数的图象上？如果会，请直接写出这时动点E、F运动的时间t的值；如果不会，请说明理由．答案与解析一.选择题1．【答案】A．2．【答案】B.3．【答案】A.4．【答案】A.【解析】由题意，，. 5．【答案】D.6．【答案】B.【解析】在正方形ABCD中，∠PAE=∠MAE=45°，在△APE和△AME中，，∴△APE≌△AME（ASA），故①正确；∴AP=AM，∴△APM是等腰直角三角形，∴PM=AP，同理可得PN=PB，∴PM+PN=AB，又∵AC=AB，∴PM+PN=AC，故②正确；∵PM⊥AC，PN⊥BD，AC⊥BD，∴四边形PEOF是矩形，∴PF=OE，在Rt△POE中，PE2+OE2=PO2，∴PE2+PF2=PO2，故③正确；∵矩形PEOF不一定是正方形，∴△POF是不一定等腰直角三角形，∵∠OBC=45°，BF⊥FN，∴△BNF是等腰直角三角形，∴△POF与△BNF相似不一定成立，故④错误；综上所述，正确的结论有①②③共3个．故选B．二．填空题7．【答案】2 5 .【解析】把△APD旋转到△DCM，把△ABF旋转到△BCN，则多边形PFBNMD的面积被分成10份，阴影部分占4份.8．【答案】①②④.9．【答案】10cm.【解析】如图：将杯子侧面展开，作A关于EF的对称点A′，连接A′C，则A′C即为最短距离，由题意可得出：A′D=6cm，CD=8cm，A′C==10（cm）．10.【答案】12.【解析】设正△ABC的边长为x，则高为32x，S△ABC=12x•32x=34x2，∵所分成的都是正三角形，∴结合图形可得黑色菱形的较长的对角线为32x-3，较短的对角线为（32x-3）33=12x-1，∴黑色菱形的面积=12（32x-3）（12x-1）=38（x-2）2，∴mn=22233(2)483(2)8x xx--=-4725，整理得，11x2-144x+144=0，解得x1=1211（不符合题意，舍去），x2=12，所以，△ABC的边长是12．11.【答案】28.【解析】先根据EF ∥BC 交AB 于F ，EG ∥AB 交BC 于G 得出四边形BGEF 是平行四边形，再由BE 平分∠ABC 且交CD 于E 可得出∠FBE=∠EBC ，由EF ∥BC 可知，∠EBC=∠FEB ，故∠FBE=FEB ，由此可判断出四边形BGEF 是菱形，再根据E 为CD 的中点，AD=2，BC=12求出EF 的长，进而可得出结论．12．【答案】10042a b+. 【解析】结合图形，脚码为奇数时，四边形A 2n-1B 2n-1C 2n-1D 2n-1是矩形，长为 2n a，宽为2nb ；脚码为偶数时，四边形A 2n B 2n C 2n D 2n 是菱形，边长为2212n a b ++ ， ∴四边形A 2010B 2010C 2010D 2010是菱形，边长为 2210062a b +，周长为 22100642a b +，即 2210042a b +． ∴四边形A 2011B 2011C 2011D 2011是矩形，长为10052a ，宽为10052b ，∴四边形A 2011B 2011C 2011D 2011的周长为：2（10052a +10052b ）=10042a b +．故答案为：10042a b+．三.综合题 13．【解析】(1).(2)作FM ⊥DC ，M 为垂足，连结GE ， ∵ AB ∥CD ，∴ ∠AEG=∠MGE ， ∵ HE ∥GF ，∴ ∠HEG=∠FGE ． ∴ ∠AEH=∠MGF.在△AHE 和△MFG 中，∠A=∠M=90°，HE=FG ， ∴ △AHE ≌△MFG . ∴ FM=HA=2，即无论菱形EFGH 如何变化，点F 的直线CD 的距离始终为定值2. 因此(3)若，由，得，此时在△DGH中，. 相应地，在△AHE中，，即点E已经不在边AB上.故不可能有.14．【解析】（1）OE=OF（相等）；（2）OE=OF，OE⊥OF；证明：连接BO，∵在正方形ABCD中，O为AC中点，∴BO=CO，BO⊥AC，∠BCA=∠ABO=45°，∵PF⊥BC，∠BCO=45°，∴∠FPC=45°，PF=FC．∵正方形ABCD，∠ABC=90°，∵PF⊥BC，PE⊥AB，∴∠PEB=∠PFB=90°．∴四边形PEBF是矩形，∴BE=PF．∴BE=FC．∴△OBE≌△OCF，∴OE=OF，∠BOE=∠COF，∵∠COF+∠BOF=90°，∴∠BOE+∠BOF=90°，∴∠EOF=90°，∴OE⊥OF．（3）OE=OF（相等），OE⊥OF（垂直）．15．【解析】（1）四边形EFGH是菱形．（2）成立．理由：连接AD，BC．∵∠APC=∠BPD，∴∠APC+∠CPD=∠BPD+∠CPD．即∠APD=∠CPB．又∵PA=PC，PD=PB，∴△APD≌△CPB（SAS）∴AD=CB．∵E、F、G、H分别是AC、AB、BD、CD的中点，∴EF、FG、GH、EH分别是△ABC、△ABD、△BCD、△ACD的中位线．∴EF=12BC，FG=12AD，GH=12BC，EH=12AD．∴EF=FG=GH=EH．∴四边形EFGH是菱形．（3）补全图形．判断四边形EFGH是正方形．理由：连接AD，BC．∵（2）中已证△APD≌△CPB．∴∠PAD=∠PCB．∵∠APC=90°，∴∠PAD+∠1=90°．又∵∠1=∠2．∴∠PCB+∠2=90°．∴∠3=90°．∵（2）中已证GH，EH分别是△BCD，△ACD的中位线，∴GH∥BC，EH∥AD．∴∠EHG=90°．又∵（2）中已证四边形EFGH 是菱形， ∴菱形EFGH 是正方形.16.【解析】（1）根据题意，AB=2222108AO OB -=-=6,∵2S △AOB =AB•OB=AO•BG ，∴BG=AB OB AO =6810⨯=4.8；（2）设当E 点运动到x 秒时，四边形ABED 是等腰梯形，则BE=x ，OF=2x ， ∵BC ∥OA ，∴BE OD =BF OF ，即x OD =822xx-，解得OD=24x x -，过E 作EH ⊥OA 于H ， ∵四边形ABED 是等腰梯形， ∴DH=AG=22226 4.8 3.6AB BG -=-=，HG=BE=x ，∴DH=10-24x x --x-3.6=3.6，解得x=2817；（3）会同时在某个反比例函数的图象上．根据题意，OG=AO-AG=10-3.6=6.4， ∴点E （6.4-t ，4.8）， ∵OF=2t ，∴2tcos ∠AOB=2t×810=85t ，2tsin ∠AOB=2t×610=65t ， ∴点F 的坐标为（85t ，65t ）假设能在同一反比例函数图象上，则85t×65t=（6.4-t ）×4.8，整理得：2t 2+5t-32=0，△=25-4×2×（-32）=281＞0，。

专题5.4四边形中的最值问题专项训练(30道)(举一反三)(浙教版)(原卷版)

专题5.4 四边形中的最值问题专项训练（30道）【浙教版】考卷信息：本套训练卷共30题，选择10题，填空10题，解答10题，题型针对性较高，覆盖面广，选题有深度，可强化学生对四边形中最值问题模型的记忆与理解！一．选择题（共10小题）1．（2022春•重庆期末）如图，矩形ABCD中，AB＝2√3，BC＝6，P为矩形内一点，连接P A，PB，PC，则P A+PB+PC的最小值是（）A．4√3+3B．2√21C．2√3+6D．4√52．（2022•灞桥区校级模拟）如图，平面内三点A、B、C，AB＝4，AC＝3，以BC为对角线作正方形BDCE，连接AD，则AD的最大值是（）√2A．5B．7C．7√2D．723．（2022春•中山市期末）如图，在边长为a的正方形ABCD中，E是对角线BD上一点，且BE＝BC，点P是CE上一动点，则点P到边BD，BC的距离之和PM+PN的值（）aA．有最大值a B．有最小值√22C．是定值a D．是定值√2a24．（2022春•三门峡期末）如图，在矩形ABCD中，AB＝2，AD＝1，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（）A．2B．4C．√2D．2√25．（2022春•滨湖区期末）如图，已知菱形ABCD的面积为20，边长为5，点P、Q分别是边BC、CD上的动点，且PC＝CQ，连接PD、AQ，则PD+AQ的最小值为（）A．4√5B．√89C．10D．7√26．（2022•泰山区一模）如图，M、N是正方形ABCD的边CD上的两个动点，满足AM＝BN，连接AC交BN于点E，连接DE交AM于点F，连接CF，若正方形的边长为2，则线段CF的最小值是（）A．2B．1C．√5−1D．√5−27．（2022•龙华区二模）如图，已知四边形ABCD是边长为4的正方形，E为CD上一点，且DE＝1，F为射线BC上一动点，过点E作EG⊥AF于点P，交直线AB于点G．则下列结论中：①AF＝EG；②若∠BAF＝∠PCF，则PC＝PE；③当∠CPF＝45°时，BF＝1；④PC的最小值为√13−2．其中正确的有（）A．1个B．2个C．3个D．4个8．（2022•南平校级自主招生）如图，在△ABC中，AB＝6，AC＝8，BC＝10，P为边BC上一动点（且点P不与点B、C重合），PE⊥AB于E，PF⊥AC于F．则EF的最小值为（）A．4B．4.8C．5.2D．69．（2022春•崇川区期末）如图，正方形ABCD边长为1，点E，F分别是边BC，CD上的两个动点，且BE＝CF，连接BF，DE，则BF+DE的最小值为（）A．√2B．√3C．√5D．√610．（2022•泰州）如图，正方形ABCD的边长为2，E为与点D不重合的动点，以DE为一边作正方形DEFG．设DE＝d1，点F、G与点C的距离分别为d2、d3，则d1+d2+d3的最小值为（）A．√2B．2C．2√2D．4二．填空题（共10小题）11．（2022春•江城区期末）如图，∠MON＝90°，矩形ABCD的顶点A、B分别在边OM、ON上，当B在边ON上运动时，A随之在OM上运动，矩形ABCD的形状保持不变，其中AB＝6，BC＝2．运动过程中点D到点O的最大距离是．12．（2022•东莞市校级一模）如图，在矩形ABCD中，AB＝6，AD＝5，点P在AD上，点Q在BC上，且AP＝CQ，连接CP，QD，则PC+DQ的最小值为．13．（2022•钱塘区一模）如图，在矩形ABCD中，线段EF在AB边上，以EF为边在矩形ABCD内部作正方形EFGH，连结AH，CG．若AB＝10，AD＝6，EF＝4，则AH+CG的最小值为．14．（2022春•东城区期中）在正方形ABCD中，AB＝5，点E、F分别为AD、AB上一点，且AE＝AF，连接BE、CF，则BE+CF的最小值是．15．（2022春•虎林市期末）如图，在Rt△ABC中，∠BAC＝90°，且BA＝12，AC＝16，点D是斜边BC 上的一个动点，过点D分别作DE⊥AB于点E，DF⊥AC于点F，点G为四边形DEAF对角线交点，则线段GF的最小值为．16．（2022•灞桥区校级三模）在菱形ABCD中，∠D＝60°，CD＝4，E为菱形内部一点，且AE＝2，连接CE，点F为CE中点，连接BF，取BF中点G，连接AG，则AG的最大值为．17．（2022春•靖江市校级期末）如图，线段AB的长为10，点D在AB上，△ACD是边长为3的等边三角形，过点D作与CD垂直的射线DP，过DP上一动点G（不与D重合）作矩形CDGH，记矩形CDGH 的对角线交点为O，连接OB，则线段BO的最小值为．18．（2022春•郫都区期末）如图，在矩形ABCD中，AB＝4，AD＝8，点E是BC边上一动点，作点B关于AE的对称点F，连接CF，点P为CF中点，则DP的最小值为．19．（2022春•江都区期中）如图，矩形ABCD中，AB＝4，AD＝2√3，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是．20．（2022春•如东县期中）如图，已知AB＝2√2，C为线段AB上的一个动点，分别以AC，CB为边在AB的同侧作菱形ACED和菱形CBGF，点C，E，F在一条直线上，∠D＝120°．P、Q分别是对角线AE，BF的中点，当点C在线段AB上移动时，点P，Q之间的距离最短为（结果保留根号）．三．解答题（共10小题）21．（2022•禹城市二模）（1）如图①，已知正方形ABCD的边长为4，点M和N分别是边BC，CD上两点，且BM＝CN，连AM和BN，交于点P．猜想AM与BN的位置关系，并证明你的结论．（2）如图②，已知正方形ABCD的边长为4．点M和N分别从点B、C同时出发，以相同的速度沿BC、CD方向向终点C和D运动，连接AM和BN，交于点P．求△APB周长的最大值．22．（2022春•东坡区校级月考）正方形ABCD中，E、F是AD上的两个点，AE＝DF，连CF交BD于点M，连AM交BE于点N，连接DN．如果正方形的边长为2．（1）求证：BE⊥AM；（2）求DN的最小值．23．（2022•黄埔区模拟）如图，在边长为4的菱形ABCD中，BD＝4，E、F分别是AD、CD上的动点（包含端点），且AE+CF＝4，连接BE、EF、FB．（1）试探究BE与BF的数量关系，并证明你的结论；（2）求EF的最大值与最小值．24．（2022春•洪山区期中）如图1，E，F是正方形ABCD的边上两个动点，满足AE＝DF，连接CF交BD于G，连接BE交AG于点H（1）求证：AG⊥BE；（2）如图2，连DH，若正方形的边长为4，则线段DH长度的最小值是．25．（2022•宁德）如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．（1）求证：△AMB≌△ENB；（2）①当M点在何处时，AM+CM的值最小；②当M点在何处时，AM+BM+CM的值最小，并说明理由；（3）当AM+BM+CM的最小值为√3+1时，求正方形的边长．26．（2022•南充模拟）如图，M，N是正方形ABCD的边CD上的两个动点，满足CM＝DN，AC，BM相交于点E，DE与AN相交于点F，连接CF．（1）求证：DE⊥AN．（2）若正方形ABCD的边长为4，求CF的最小值．27．（2022春•思明区校级期中）已知：在矩形ABCD中，AB＝8，BC＝12，四边形EFGH的三个顶点E、F、H分别在矩形ABCD的边AB、BC、DA上．（1）如图1，四边形EFGH为正方形，AE＝2，求GC的长．x．在（2）如图2，四边形EFGH为菱形，设BF＝x，△GFC的面积为S，且S与x满足函数关系S＝6−12自变量x的取值范围内，是否存在x，使菱形EFGH的面积最大？若存在，求x的值，若不存在，请说明理由．28．（2022•南岗区校级一模）已知菱形ABCD的对角线相交于O，点E、F分别在边AB、BC上，且BE ＝BF，射线EO、FO分别交边CD、AD于G、H．（1）求证：四边形EFGH为矩形；（2）若OA＝4，OB＝3，求EG的最小值．29．（2022春•戚墅堰区校级月考）如图，已知∠MON＝90°，线段AB长为6cm，AB两端分别在OM、ON上滑动，以AB为边作正方形ABCD，对角线AC、BD相交于点P，连接OC．（1）求OC的最大值；（2）求证：无论点A、点B怎样运动，点P都在∠AOB的平分线上；（3）若OP＝4√2cm，求OA的长．30．（2012秋•吴中区月考）如图①，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．（1）连接MN，△BMN是等边三角形吗？为什么？（2）求证：△AMB≌△ENB；（3）①当M点在何处时，AM+CM的值最小；②如图②，当M点在何处时，AM+BM+CM的值最小，请你画出图形，并说明理由．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020年中考考点总动员之三轮冲刺聚焦考点+名师点睛+能力提升专题05 四边形讲练测模块一：平行四边形【例1】如果一个四边形的两条对角线相等，那么称这个四边形为“等对角线四边形”．写出一个你所学过的特殊的等对角线四边形的名称____________．【例2】下列判断错误的是( )A．对角线互相垂直且相等的平行四边形是正方形B．对角线互相垂直平分的四边形是菱形C．对角线相等的四边形是矩形D．对角线互相平分的四边形是平行四边形【例3】下列命题中，真命题是( )A．菱形的对角线互相平分且相等B．矩形的对角线互相垂直平分C．对角线相等且垂直的四边形是正方形D．对角线互相平分的四边形是平行四边形【例4】如图，在ABCD中，AC、BD相交于点O，请添加一个条件________________，可得ABCD是矩形．【例5】已知四边形ABCD是平行四边形，对角线AC与BD相交于点O，那么下列结论中正确的是( ) A．当AB = BC时，四边形ABCD是矩形B．当AC BD时，四边形ABCD是矩形C．当OA = OB时，四边形ABCD是矩形A BCDOD ．当ABD CBD ∠=∠时，四边形ABCD 是矩形【例6】已知在四边形ABCD 中，AC 与BD 相交于点O ，那么下列条件中能判定这个四边形是正方形的是( )A ．AC = BD ，AB // CD ，AB = CDB ．AD // BC ，A C ∠=∠ C ．AO = BO = CO = DO ，AC BD ⊥ D ．AO = CO ，BO = DO ，AB = BC【例7】如果点K 、L 、M 、N 分别是四边形ABCD 的四条边AB 、BC 、CD 、DA 的中点，且四边形KLMN 是菱形，那么下列选项正确的是( )A ．AB BC ⊥B ．AC BD ⊥ C ．AB BC = D ．AC BD =【例8】从①AB // CD ，②AD // B C ，③AB = CD ，④AD = BC 四个关系中，任选两个作为条件，那么选到能够判定四边形ABCD 是平行四边形的概率是______．【例9】在平行四边形ABCD 中，BC = 24，AB = 18，ABC ∠和BCD ∠的平分线交AD 于点E 、F ，则EF =______．【例10】如图，在四边形ABCD 中，90ABC ∠=︒，对角线AC 、BD 交于点O ，AO = CO ，AOD ADO ∠=∠，E是DC 边的中点．下列结论中，错误的是( )A ．12OE AD =B ．12OE OB =C ．12OE OC =D ．12OE BC =【例11】设边长为3的正方形的对角线长为a ．下列关于a 的四种说法：①a 是无理数；②a 可以用数轴上的一个点来表示；③34a <<；④a 是18的一个平方根．其中，所有正确说法的序号是( )A ．①④B ．②③C ．①②④D ．①③④【例12】如图，在ABC ∆中，点D 、E 分别在AB 、AC 上，ADE C ∠=∠，如果AE = 2，ADE ∆的面积是4，四边形BCDE 的面积是5，那么AB 的长是______． A B C DE【例13】已知：如图，在四边形ABCD 中，AB // CD ，点E 是对角线AC 上一点，DEC ABC ∠=∠，且2CD CE CA =．（1）求证：四边形ABCD 是平行四边形；（2）分别过点E 、B 作AB 和AC 的平行线交于点F ，联结CF ，若FCE DCE ∠=∠，求证：四边形EFCD 是菱形．【例14】如图，在ABC ∆中，AB = AC ，点D 在边AC 上，AD = BD =DE ，联结BE ，72ABC DBE ∠=∠=︒．（1）联结CE ，求证：CE = BE ；（2）分别延长CE 、AB 交于点F ，求证：四边形DBFE 是菱形．【例15】已知：如图，在Rt ABC ∆中，90ACB ∠=︒，AC = BC ，点E 在边AC 上，延长BC 至D 点，使CE = CD ，延长BE 交AD 于F ，过点C 作CG // BF ，交AD 于点G ，在BE 上取一点H ，使HCE DCG ∠=∠． AB C DEABC DE FAB CDE O F（1）求证：BCE ∆≌ACD ∆；（2）求证：四边形FHCG 是正方形．【例16】如图，在四边形ABCD 中，AB // DC ，E 、F 为对角线BD 上两点，且BE = DF ，AF // EC ．（1）求证：四边形ABCD 是平行四边形；（2）延长AF ，交边DC 于点G ，交边BC 的延长线于点H ，求证：AD DC BH DG =．【例17】如图，已知在矩形ABCD 中，过对角线AC 的中点O 作AC 的垂线，分别交射线AD 和CB 于点E 、F ，交边DC 于点G ，交边AB 于点H ．联结AF 、CE ．（1）求证：四边形AFCE 是菱形；（2）如果OF = 2GO ，求证：2GO DG GC =． GF EDBA C HABC DEFG H【例18】已知：如图，Rt ABC∆和Rt CDE∆中，90ABC CDE∠=∠=︒，且BC与CD共线，联结AE，点M 为AE中点，联结BM，交AC于点G，联结MD，交CE于点H．（1）求证：MB = MD；（2）当AB = BC，DC = DE时，求证：四边形MGCH为矩形．【例19】如图，在正方形ABCD中，点E在对角线AC上，点F在边BC上，联结BE、DF，DF交对角线AC 于点G，且DE = DG．（1）求证：AE = CG；（2）求证：BE // DF．【例20】已知：如图1，在平行四边形ABCD中，点E、F分别在BC、CD上，且AE = AF，AEC AFC∠=∠．（1）求证：四边形ABCD是菱形；A BCDEFGOHAB CDEF（2）如图2，若AD = AF，延长AE、DC交于点G，求证：2AF AG DF=．（3）在第（2）小题的条件下，连接BD，交AG于点H，若HE = 4，EG = 12，求AH的长．【巩固1】（2019春•浦东新区校级月考）已知四边形ABCD，在①//AB CD；②AD BC=；③AB CD=；④A C∠=∠四个条件中，不能推出四边形ABCD是平行四边形的条件是()A．①②B．①③C．①④D．②③【巩固2】（2019春•浦东新区校级月考）在平行四边形ABCD中，对角线AC，BD交于点O，若10BD=，14AC=，那么BC的取值范围为．【巩固3】（2018春•浦东新区期中）如图，以BC为底边的等腰ABC∆，点D，E，G分别在BC，AB，AC 上，且//EG BC，//DE AC，延长GE至点F，使得BE BF=．（1）求证：四边形BDEF为平行四边形；（2）当45C∠=︒，4BD=时，联结DF，求线段DF的长．【巩固4】（2018•上海）已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是( )A．A B∠=∠B．A C∠=∠C．AC BD=D．AB BC⊥【巩固5】（2018•上海）对于一个位置确定的图形，如果它的所有点都在一个水平放置的矩形内部或边上，且该图形与矩形的每条边都至少有一个公共点（如图1)，那么这个矩形水平方向的边长称为该图形的宽，铅锤方向的边长称为该图形的高．如图2，菱形ABCD的边长为1，边AB水平放置．如果该菱形的高是矩形的宽的23，那么矩形的宽的值是．ACB DE FGACB DE F图1图2H【巩固6】（2017•上海）已知：如图，四边形ABCD中，//=，E是对角线BD上一点，AD BC，AD CD且EA EC=．（1）求证：四边形ABCD是菱形；（2）如果BE BC∠∠=，求证：四边形ABCD是正方形．=，且:2:3CBE BCE【巩固7】（2019•杨浦区二模）已知：如图，在ABC∠=︒，点D、E分别是边AB、ABC=，90∆中，AB BCBC的中点，点F、G是边AC的三等分点，DF、EG的延长线相交于点H，连接HA、HC．求证：（1）四边形FBGH是菱形；（2）四边形ABCH是正方形．模块二：梯形【例21】顺次联结等腰梯形各边中点所得的四边形是__________形．【例22】如果梯形的下底长为7，中位线长为5，那么其上底长为______．【例23】梯形ABCD 中，AD // BC ，AD = 2，BC = 6，点E 是边BC 上的点，如果AE 将梯形ABCD 的面积平分，那么BE 的长是______．【例24】如果梯形ABCD 中，AD // BC ，E 、F 分别是AB 、CD 的中点，AD = 1，BC = 3，那么四边形AEFD 与四边形EBCF 的面积比是______．【例25】如图，在梯形ABCD 中，AD // BC ，AB ⊥BC ，已知AD = 2，4cot 3ACB ∠=，梯形ABCD 的面积是9．（1）求AB 的长；（2）求tan ACD ∠的值．【例26】已知，如图，在梯形ABCD 中，AD // BC ，点E 是边CD 的中点，点F 在边BC 上，EF // AB ．求证：()12BF AD BC =+．【例27】如图，在直角梯形纸片ABCD 中，DC // AB ，E DC BA ABC D H ABC D E F GAB >CD >AD ，90A ∠=︒，将纸片沿过点D 的直线翻折，使点A 落在边CD 上的点E 处，折痕为DF ，联结EF 并展开纸片；（1）求证：四边形ADEF 为正方形；（2）取线段AF 的中点G ，联结GE ，当BG = CD 时，求证：四边形GBCE 为等腰梯形．【例28】如图，在ABC ∆中，D 、E 分别是AC 、BC 边上的点，AE 与BD 交于点O ，且CD = CE ，12∠=∠．（1）求证：四边形ABED 是等腰梯形；（2）若EC = 2，BE = 1，21AOD ∠=∠，求AB 的长．【例29】如图，已知ABC ∆和ADE ∆都是等边三角形，点D 在边BC 上，点E 在边AD 的右侧，联结CE ．（1）求证：60ACE ∠=︒；（2）在边AB 上取一点F ，使BF = BD ，联结DF 、EF ．求证：四边形CDEF是等腰梯形．AB CD E F G ABC D E 1 2OA B C D E F【例30】如图，在梯形ABCD中，AB // CD，AD = BC，E是CD的中点，BE交AC于F，过点F作FG // AB，交AE于点G．（1）求证：AG = BF；（2）当2AD CA CF=时，求证：AB AD AG AC=．【巩固1】（2018•青浦区一模）在梯形ABCD中，//AD BC，下列条件中，不能判断梯形ABCD是等腰梯形的是()A．ABC DCB∠=∠B．DBC ACB∠=∠C．DAC DBC∠=∠D．ACD DAC∠=∠【巩固2】（2019•浦东新区二模）已知梯形的上底长为5厘米，下底长为9厘米，那么这个梯形的中位线长等于厘米．【巩固3】（2019春•浦东新区期末）已知，在梯形ABCD中，//AD BC，5AD=，6AB CD==，60B∠=︒，那么下底BC的长为．1．（2019春•嘉定区期末）如果平行四边形ABCD两条对角线的长度分别为8AC m=，12BD cm=，那么BC 边的长度可能是()A．2BC cm=B．6BC cm=C．10BC cm=D．20BC cm=2．（2019春•浦东新区期中）下列条件中不能判定一定是平行四边形的有()A．一组对角相等，一组邻角互补B．一组对边平行，另一组对边相等C．两组对边相等ED CG FA BD ．一组对边平行，且一条对角线平分另一条对角3．（2019春•杨浦区期中）如图，在平行四边形ABCD 中，对角线AC BD ⊥，10AC =，24BD =，则AD = ．4．（2019•嘉定区二模）如图，平行四边形ABCD 的对角线AC 、BD 交于点O ，过点O 的线段EF 与AD 、BC 分别交于点E 、F ，如果4AB =，5BC =，32OE =，那么四边形EFCD 的周长为．5．（2019春•浦东新区校级月考）如图，在平行四边形ABCD 中，60ABC ∠=︒，28BC AB ==，点C 关于AD 的对称点为E ，连接BE 交AD 于点F ，点G 为CD 的中点，连接EG ，BG ，则BEG S ∆= ．6．（2019春•杨浦区期中）如果一个平行四边形的一个内角的平分线分它的一边为1:2两部分，那么称这样的平行四边形为“协调平行四边形”，称该边为“协调边”，当协调边为6时，它的周长为．7．（2019春•金山区期末）已知：如图，ABCD 中，AE 、CF 分别是BAD ∠和BCD ∠的角平分线，分别交边DC 、AB 于点E 、F ，求证：AE CF =．8．（2019春•杨浦区期中）在平行四边形ABCD 中，45A ∠=︒，BD AD ⊥，2BD =．（1）求平行四边形ABCD 的周长和面积；（2）求A 、C 两点间的距离．9．（2018秋•黄浦区校级月考）已知：如图，在ABCD 中，4AC =，6BD =，CA AB ⊥，求ABCD 的周长和面积．10．（2018春•金山区期中）已知，如图，在等边ABC ∆中，D 是BC 边上一点，F 为AB 边上一点，且CD BF =，以AD 为边作等边ADE ∆，联结EF 、FC ．求证：（1）ADC CFB ∆≅∆；（2）四边形EFCD 是平行四边形．11．（2018春•浦东新区期中）如图，ABCD 中，E 、F 是直线AC 上两点，且AE CF =．求证：（1）BE DF =；（2）//BE DF12．（2018春•浦东新区期中）在平行四边形ABCD 中，分别以AD 、BC 为边向内作等边ADE ∆和等边BCF ∆，连接BE 、DF ．求证：四边形BEDF 是平行四边形．13.（2017•上海）已知平行四边形ABCD ，AC 、BD 是它的两条对角线，那么下列条件中，能判断这个平行四边形为矩形的是( )A ．BAC DCA ∠=∠B ．BAC DAC ∠=∠ C ．BAC ABD ∠=∠ D ．BAC ADB ∠=∠14．（2019•杨浦区三模）如图，在四边形ABCD 中，AC 与BD 相交于点O ，90BAD ∠=︒，BO DO =，那么添加下列一个条件后，仍不能判定四边形ABCD 是矩形的是( )A ．90ABC ∠=︒B ．90BCD ∠=︒C ．AB CD = D ．//AB CD15．（2019•浦东新区二模）已知在四边形ABCD 中，//AD BC ，对角线AC 与BD 相交于点O ，AO CO =，如果添加下列一个条件后，就能判定这个四边形是菱形的是( )A ．BO DO =B ．AB BC = C ．AB CD = D ．//AB CD16．（2019•普陀区二模）如图，ABCD 的对角线AC 、BD 交于点O ，顺次连接ABCD 各边中点得到一个新的四边形，如果添加下列四个条件中的一个条件：①AC BD ⊥；②ABO CBO C C ∆∆=；③DAO CBO ∠=∠；④DAO BAO ∠=∠，可以使这个新的四边形成为矩形，那么这样的条件个数是( )A ．1个B ．2个C ．3个D ．4个17．（2019•徐汇区二模）在四边形ABCD 中，//AB CD ，AB AD =，添加下列条件不能推得四边形ABCD 为菱形的是( )A ．AB CD = B ．//AD BC C ．BC CD = D ．AB BC =18．（2018•闵行区二模）已知四边形ABCD 是平行四边形，下列结论中不正确的是( )A ．当AB BC =时，四边形ABCD 是菱形B ．当AC BD ⊥时，四边形ABCD 是菱形C ．当90ABC ∠=︒时，四边形ABCD 是矩形D ．当AC BD =时，四边形ABCD 是正方形19．（2019春•金山区期末）已知矩形ABCD ，下列条件中不能判定这个矩形是正方形的是( )A ．AC BD ⊥B ．AC BD = C ．AC 平分BAD ∠ D ．ADB ABD ∠=∠ 20．（2019春•浦东新区期中）如图，正方形ABCD 的面积为5，正方形BEFG 面积为3，那么GCE ∆的面积是．21．（2019•松江区二模）如图，已知ABCD 中，AB AC =，CO AD ⊥，垂足为点O ，延长CO 、BA 交于点E ，联结DE ．（1）求证：四边形ACDE 是菱形；（2）联结OB ，交AC 于点F ，如果OF OC =，求证：22AB BF BO =．22．（2019•奉贤区二模）已知：如图，正方形ABCD ，点E 在边AD 上，AF BE ⊥，垂足为点F ，点G 在线段BF 上，BG AF =．（1）求证：CG BE ⊥；（2）如果点E是AD的中点，联结CF，求证：CF CB=．23．（2019•金山区二模）已知：如图，菱形ABCD的对角线AC与BD相交于点O，若CAD DBC∠=∠．（1）求证：四边形ABCD是正方形．（2）E是OB上一点，DH CE=．⊥，垂足为H，DH与OC相交于点F，求证：OE OF24．（2018•浦东新区二模）已知：如图，在正方形ABCD中，点E为边AB的中点，联结DE，点F在DE 上CF CD⊥交AD于点G．=，过点F作FG FC（1）求证：GF GD=；（2）联结AF，求证：AF DE⊥．25．（2018•金山区二模）如图，已知AD是ABCAE BC，CM的∆的中线，M是AD的中点，过A点作//延长线与AE相交于点E，与AB相交于点F．（1）求证：四边形AEBD是平行四边形；（2）如果3AC AF =，求证四边形AEBD 是矩形．26．（2018•金山区二模）如果梯形的中位线长为6，一条底边长为8，那么另一条底边长等于．27．（2019秋•松江区期末）如图，梯形ABCD 中，//AD BC ，AF BC ⊥于F ，M 是CD 中点，AM 的延长线交BC 的延长线于E ，AE AB ⊥，60B ∠=︒，AF =，则梯形的面积是．28．（2019春•金山区期末）梯形ABCD 中，//AD BC ，6AB AD DC ===，BD DC ⊥，那么BD = ．29．（2019春•徐汇区校级期中）如果一个直角梯形的一条底边长为7厘米，两腰长分别为8厘米和10厘米，那么这个梯形的中位线是厘米．30．（2019春•浦东新区期末）如图，在梯形ABCD 中，//AB CD ，AD BC =，对角线AC BD ⊥，且AC =则梯形ABCD 的中位线的长为．31．（2018春•青浦区校级月考）等腰梯形的周长为30cm ，中位线长为8cm ，则腰长为_____cm ．32．（2018春•闵行区期末）在梯形ABCD 中，//AD BC ，如果4AD =，10BC =，E 、F 分别是边AB 、CD 的中点，那么EF = ．33．（2019春•长宁区期末）已知：如图，AM 是ABC ∆的中线，D 是线段AM 的中点，AM AC =，//AE BC ．求证：四边形EBCA 是等腰梯形．34．（2019春•金山区期末）梯形ABCD中，//=，E、F分别是腰AB、CD的中点，过AD BC，AB CD点F作//FG AB，交BC于点G．（1）求证：四边形AEGF为平行四边形；（2）联结DG，如果DGE B∠=∠，求证：四边形AEGF是矩形．35．（2019春•浦东新区期末）如图，在梯形ABCD中，//∠=︒，AC=，30DBCAD BC，AC DB⊥，5（1）求对角线BD的长度；（2）求梯形ABCD的面积．36．（2018春•浦东新区期末）如图，已知在梯形ABCD中，//AD BC，P是下底BC上一动点（点P与点B不重合），10B︒<∠<︒，设BP x=，四边形APCD的面积为∠=︒，4590CAB AD==，24BC=，45y．（1）求y关于x的函数解析式，并写出它的定义域；（2）联结PD，当APD∆是以AD为腰的等腰三角形时，求四边形APCD的面积．37．（2018春•青浦区期末）已知：如图，在梯形ABCD中，//∠=︒．CDB∠，30=，BD平分ABCDC AB，AD BC求：（1）求A∠的度数；（2）当4AD=时，求梯形ABCD的面积．38．（2018•杨浦区二模）已知：如图，在梯形ABCD中，//A∠=︒．=，BD平分ABC∠，60DC B，AD BC求：（1）求CDB∠的度数；（2）当2AD=时，求对角线BD的长和梯形ABCD的面积．。