新九年级数学下册第三章圆3-9弧长及扇形的面积同步练习新版北师大版
北师大版九年级数学下册3.9: 弧长及扇形的面积 同步测试

3.9 弧长及扇形的面积同步测试一、选择题1.如图,半径为1cm 、圆心角为90°的扇形OAB 中,分别以OA 、OB 为直径作半圆,则图中阴影部分的面积为( )A.πcm2B.32πcm2C.21cm2D.32cm22.一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( )A..5π B .4π C .3π D .2π3.如图,在△ABC 中,∠A=90°,AB=AC=2,以BC 的中点O 为圆心的圆弧分别与AB 、AC 相切于点D 、E ,则图中阴影部分的面积是( )A. B. C. D.4.如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶状”阴影图案的面积为( )A .4π-2B .2π-2C .4π-4D .2π-45.如图,直径AB 为6的半圆,绕A 点逆时针旋转60°,此时 点B 到了点B ’,则图中阴影部分的面积是( )A. B. C. D.6.如图,已知一块圆心角为270°的扇形铁皮,用它做一个圆锥形的烟囱帽(接缝忽略不计),圆锥底面圆的直径是60cm,则这块扇形铁皮的半径是()A.40cm B.50cm C.60cm D.80cm7.如图,在Rt△ABC中,∠C=90°,∠A=30°,AB=2.将△ABC绕顶点A顺时针方向旋转至△AB′C′的位置,点B,A,C′在同一条直线上,则线段BC扫过的区域面积为()A. B. C. D.8.如图,Rt△ABC中,∠ACB=90°∠A=30°,BC=2,O、H分别为AB、AC的中点,将△ABC顺时针旋转120°到△A1BC1的位置,则整个旋转过程中线段OH所扫过的面积为()A. B.C. D.9.如图所示,扇形AOB的圆心角120°,半径为2,则图中阴影部分的面积为()A. B. C. D.10.如图,在Rt △ABC 中,∠ABC =90°,AB ==2,以AB 的中点O 为圆心,OA 的长为半径作半圆交AC 于点D,则图中阴影部分的面积为( )2π 2π C.π- D.2π-二、填空题11.已知扇形的圆心角为60°,半径为1,则扇形的弧长为 .12.一个扇形的半径为8cm ,弧长为 cm ,则扇形的圆心角为 .13.如图,四边形ABCD 是⊙O 的内接四边形,⊙O 的半径为4,∠B=135°,则弧AC 的长为_________.14.)如图,在边长为4的正方形ABCD 中,以点B 为圆心,AB 为半径画弧,交对角线BD与点E,则图中阴影部分的面积是 (结果保留π)15.如图,在边长为4的正方形ABCD 中,先以点A 为圆心,AD 的长为半径画弧,再以AB 边的中点为圆心,AB 长的一半为半径画弧,则阴影部分面积是________(结果保留π).16.如图,在△ABC 中,CA =CB ,∠ACB =90°,AB =2,点D 为AB 的中点,以点D 为圆心作圆心角为90°的扇形DEF ,点C 恰在弧EF 上,则图中阴影部分的面积为________.三、综合题17.如图,⊙O的半径为6cm,直线AB是⊙O的切线,切点为点B,弦BC∥AO.若∠A =30°,求劣弧BC的长。
北师大版九年级数学下册第三章 3.9 弧长及扇形的面积 同步测试

北师大版九年级数学下册第三章 3.9 弧长及扇形的面积同步测试一.选择题1.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则劣弧的长是()A.πB.C.D.2.若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动(如图),则直尺上的10cm刻度线对应量角器上的度数约为()A.90°B.115°C.125°D.180°3. 如图,已知□ABCD的对角线BD=4cm,将▱ABCD绕其对称中心O旋转180°,则点D所转过的路径长为()A.4π cm B.3π cm C.2π cm D.π cm4.如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则的长为()5.如图,已知扇形AOB 的半径为2,圆心角为90°,连接AB ,则图中阴影部分的面积是( )A .π-2B .π-4C .4π-2D .4π-46.如图,等边三角形ABC 中,将边AC 逐渐变成以BA 为半径的AB ,其他两边的长度不变,则∠ABC 的度数大小由60变为( ) A.180π B. 120π C. 90π D. 60π7.如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )A .2B .2π C .12 D .18.如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A ,C ,B 三点的圆弧与AE 交于H ,则弧AH 的弧长为( )9.如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4,4)则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为()A.8πB.πC.2πD.48π10.如图,AB是⊙O的直径,且AB=4,C是⊙O上一点,将弧AC沿直线AC翻折,若翻折后的圆弧恰好经过点O,π≈3.14,≈1.41,≈1.73,那么由线段AB、AC和弧BC所围成的曲边三角形的面积与下列四个数值最接近的是()A.3.2 B.3.6 C.3.8 D.4.211.如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,OA =OB=OC=2,则这朵三叶花的面积为()A.3π﹣3 B.3π﹣6 C.6π﹣3 D.6π﹣612.如图,在圆O上依次有A.B,C三点,BO的延长线交圆O于E,=,点C作CD∥AB交BE的延长线于D,AD交圆O于点F,连接OA,OF,若∠AOF=3∠FOE,且AF=2,劣弧CF的长是()A.πB.πC.πD.π二.填空题13.若扇形的半径为3,圆心角120°,为则此扇形的弧长是.14.已知扇形的圆心角为120°,弧长为2π,则它的半径为15.如图,正方形ABCD的四个顶点分别在扇形OEF的半径OE,OF和上,且点A是线段OB的中点,若的长为π,则OD长为.17.如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为18.如图,在矩形ABCD中,AD=2,以点A为圆心,AD长为半径画弧,交BC边于点E,若E恰为BC的中点,则图中阴影部分的面积为.三.解答题19.如图,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.(1)求点P经过的弧长;(结果保留π)(2)写出点Q的坐标是.20.如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,∠CDB=30°,CD=,求图中阴影部分的面积.21.如图,长方形ABCD的周长为28,且AB:BC=3:4,求:(1)弧BE的长度;(2)图中阴影部分的面积.22.如图,已知AB是⊙O的直径,点C在⊙O上,延长BC至点D,使得DC=BC,直线DA与⊙O的另一个交点为E,连结AC,CE.(1)求证:CD=CE;(2)若AC=2,∠E=30°,求阴影部分(弓形)面积.23.如图,点A,B,C在直径为2的⊙O上,∠BAC=45°,求图中阴影部分的面积.(结果中保留π)24.如图,已知Rt△ABC中,∠A=90°,将斜边BC绕点B顺时针方向旋转至BD,使BD∥AC,过点D作DE⊥BC于点E.(1)求证:△ABC≌△EDB;(2)若CD=BD,AC=3,求在上述旋转过程中,线段BC扫过的面积.北师大版九年级数学下册第三章 3.9 弧长及扇形的面积同步测试(解析版) 一.选择题1.如图,在⊙O中,弦BC=1,点A是圆上一点,且∠BAC=30°,则劣弧的长是()A.πB.C.D.解:连接OB,OC.∵∠BOC=2∠BAC=60°,∵OB=OC,∴△OBC是等边三角形,∴OB=OC=BC=1,∴劣弧的长==,故选:B.2.若将直尺的0cm刻度线与半径为5cm的量角器的0°线对齐,并让量角器沿直尺的边缘无滑动地滚动(如图),则直尺上的10cm刻度线对应量角器上的度数约为()A .90°B .115°C .125°D .180° 解:本题中弧长应该是10cm ,根据半径为5cm ,那么5×π×n ÷180=10,那么圆心角n ≈115°.故选:B .3. 如图,已知□ABCD 的对角线BD=4cm ,将▱ABCD 绕其对称中心O 旋转180°,则点D 所转过的路径长为( )A .4π cmB .3π cmC .2π cmD .π cm解: 将▱ABCD 绕其对称中心O 旋转180°,点D 所转过的路径为以BD 为直径的422r ππ=2πcm 4.如图,AB 是⊙O 的直径,CD 是弦,点C ,D 在直径AB 的两侧.若∠AOC :∠AOD :∠DOB =2:7:11,CD =4,则的长为( )A .2πB .4πC .D .π 解:∵∠AOC :∠AOD :∠DOB =2:7:11,∠AOD+∠DOB =180°,∴∠AOD =×180°=70°,∠DOB =110°,∠COA =20°,∴∠COD =∠COA+∠AOD =90°, ∵OD =OC ,CD =4,∴2OD 2=42,∴OD =2, ∴的长是==, 故选:D .5.如图,已知扇形AOB 的半径为2,圆心角为90°,连接AB ,则图中阴影部分的面积是( )A .π-2B .π-4C .4π-2D .4π-4413602π×2×-2 故选:A . 6.如图,等边三角形ABC 中,将边AC 逐渐变成以BA 为半径的AB ,其他两边的长度不变,则∠ABC 的度数大小由60变为( )A.180π B. 120π C. 90π D. 60π180AB π,由180π ,.7.如图,在边长为2的正方形内部,以各边为直径画四个半圆,则图中阴影部分的面积是( )A .2B .2C .12D .1解: 如图所示,S 阴影=S △AOB =14S 正方形=14×2×2=1. 故选D .8.如图,5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A ,C ,B 三点的圆弧与AE 交于H ,则弧AH 的弧长为( )A .πB .πC .πD .π 解:连接EB ,BH ,AB ,∵BE =AB ==,AE ==, ∴BE 2+AB 2=AE 2,∴∠ABE =90°,∴△ABE是等腰直角三角形,∵∠ACB=90°,∴AB是圆的直径,∴∠AHB=90°,∴BH⊥AH,∴∠ABH=∠BAH=45°,∴弧AH所对的圆心角为90°,∴的长==.故选:B.9.如图,△OAC按顺时针方向旋转,点O在坐标原点上,OA边在x轴上,OA=8,AC=4,把△OAC绕点A按顺时针方向转到△O′AC′,使得点O′的坐标是(4,4)则在这次旋转过程中线段OC扫过部分(阴影部分)的面积为()A.8πB.πC.2πD.48π解:过O′作O′M⊥OA于M,则∠O′MA=90°,∵点O′的坐标是(4,4),∴O′M=4,OM=4,∵AO=8,∴AM=8﹣4=4,∴tan∠O′AM==,∴∠O′AM=60°,即旋转角为60°,∴∠CAC′=∠OAO′=60°,∵把△OAC绕点A按顺时针方向旋转到△O′AC′,∴S△OAC =S△O′AC′,∴阴影部分的面积S=S扇形OAO′+S△O′AC′﹣S△OAC﹣S扇形CAC′=S扇形OAO′﹣S扇形CAC′=﹣=8π,故选:A.10.如图,AB是⊙O的直径,且AB=4,C是⊙O上一点,将弧AC沿直线AC翻折,若翻折后的圆弧恰好经过点O,π≈3.14,≈1.41,≈1.73,那么由线段AB、AC和弧BC所围成的曲边三角形的面积与下列四个数值最接近的是()A.3.2 B.3.6 C.3.8 D.4.2解:作OE⊥AC交⊙O于F,交AC于E.连接OB,BC.由折叠的性质可知,EF=OE=OF,∴OE=OA,在Rt△AOE中,OE=OA,∴∠CAB=30°,∵AB是直径,∴∠ACB =90°,∠BOC =2∠BAC =60°,∵AB =4,∴BC =AB =2,AC =BC =2,∴线段AB 、AC 和弧BC 所围成的曲边三角形的面积=•AC •BC+S 扇形OBC ﹣S △OBC =××2+﹣×22=+π≈3.8,故选:C .11.如图,由六段相等的圆弧组成的三叶花,每段圆弧都是四分之一圆周,OA =OB =OC =2,则这朵三叶花的面积为( )A .3π﹣3B .3π﹣6C .6π﹣3D .6π﹣6 解:如图所示:弧OA 是⊙M 上满足条件的一段弧,连接AM 、MO ,由题意知:∠AMO =90°,AM =OM∵AO =2,∴AM =.∵S 扇形AMO =×π×MA 2=. S △AMO =AM •MO =1,∴S 弓形AO =﹣1,∴S 三叶花=6×(﹣1) =3π﹣6.故选:B .12.如图,在圆O上依次有A.B,C三点,BO的延长线交圆O于E,=,点C作CD∥AB交BE的延长线于D,AD交圆O于点F,连接OA,OF,若∠AOF=3∠FOE,且AF=2,劣弧CF的长是()A.πB.πC.πD.π解:∵=,∴∠CBD=∠ABD,∵CD∥AB,∴∠ABD=∠CDB,∴∠CBD=∠CDB,∴CB=CD,∵BE是⊙O的直径,∴=,∴AB=BC=CD,∵CD∥AB,∴四边形ABCD是菱形,∴BC∥AD,∵∠AOF=3∠FOE,设∠FOE=x,则∠AOF=3x,∠AOD=∠FOE+∠AOF=4x,∵OA =OF ,∴∠OAF =∠OFA =(180﹣3x )°,∵OA =OB ,∴∠OAB =∠OBA =2x ,∴∠ABC =4x ,∵BC ∥AD ,∴∠ABC+∠BAD =180°,∴4x+2x+(180﹣3x )=180,解得:x =20°,∴∠AOF =3x =60°,∠AOE =80°,∴∠COF =80°×2﹣60°=100°,∵OA =OF ,∴△AOF 是等边三角形,∴OF =AF =2,∴的长==π,故选:C .二.填空题13.若扇形的半径为3,圆心角120°,为则此扇形的弧长是 2π . 解:∵扇形的半径为3,圆心角为120°,∴此扇形的弧长==2π.故答案为:2π14.已知扇形的圆心角为120°,弧长为2π,则它的半径为 解:∵l=180n R π , ∴R=1802120ππ=3. 15.如图,正方形ABCD 的四个顶点分别在扇形OEF 的半径OE ,OF 和上,且点A 是线段OB 的中点,若的长为π,则OD 长为 4 .解:∵四边形ABCD是正方形,∴AD=AB,∠DAB=90°,∴点A是线段OB的中点,∴OA=AB,∴OA=AD,∵∠OAD=∠DAB=90°,∴∠EOF=45°,∵的长为π,∴=π,∴OF=4,连接OC,∴OC=OF=4,设OA=BC=x,∴OB=2x,∴OC=x=4,∴x=4,∴OA=AD=4,∴OD=4,故答案为:4.16.圆心角为120°,半径为6的弧的弧长是4π.解:∵圆心角为120°,半径为6的弧,∴弧长是:=4π.故答案为:4π.17.如图,⊙O的半径为4,PC切⊙O于点C,交直径AB延长线于点P,若CP长为4,则阴影部分的面积为解:连接CO,∵PC切⊙O于点C,∴OC⊥PC,∵⊙O的半径为4,CP长为4,∴CO=CP,∴∠COP=∠CPO=45°,∴阴影部分的面积为:S△COP -S扇形COB=12×4×4-2454360=8-2π.故答案为:8-2π.18.如图,在矩形ABCD中,AD=2,以点A为圆心,AD长为半径画弧,交BC边于点E,若E恰为BC的中点,则图中阴影部分的面积为.解:连接AE,∵四边形ABCD是矩形,∴∠B=∠DAB=90°,AD=BC=AB=2=AE,∵E恰为BC的中点,∴BE=1,∴∠BAE=30°,∴∠EAD=90°﹣30°=60°,在Rt△ABE中,由勾股定理得:AB==,∴阴影部分的面积S=S矩形ABCD ﹣S△ABE﹣S扇形EAD=﹣﹣=﹣π,故答案为:﹣π.三.解答题19.如图,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.(1)求点P经过的弧长;(结果保留π)(2)写出点Q的坐标是(﹣3,1).解:(1)如图,过P作PA⊥x轴于A,∵P (1,3),∴,∴点P 经过的弧长为; (2)把点P 绕坐标原点O 逆时针旋转90°后得到点Q ,过点P 作x 轴的垂线,垂足是B ,∴OQ =PO ,∠POQ =90°,∴∠POA+∠QOB =90°,∠QOB =∠OPA ,△QOB ≌△OPA (AAS ),∴OB =PA =3,BQ =AO =1,则点Q 的坐标是(﹣3,1).故答案是:(﹣3,1).20.如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,∠CDB=30°,CD= ,求图中阴影部分的面积.解: ∵AB 是⊙O 的直径,弦CD ⊥AB ,∴CE= DE .∵∠CDB=30°,∴∠COE=60°,在Rt △OEC 中,OC=60°sin OE =2, ∵CE=DE ,∠COE=∠DBE=60°∴Rt△COE≌Rt△DBE,∴S阴影=S扇形OBC=16π×OC2=16π×4=2321.如图,长方形ABCD的周长为28,且AB:BC=3:4,求:(1)弧BE的长度;(2)图中阴影部分的面积.解:(1)由题意AB=28÷2×=6,BC=28÷2×=8,∴==3π.(2)由(1)知,AB=6,BC=8,∵四边形ABCD是长方形,∴∠A=∠C=90°,AD=BC=8,∴DE=AD﹣AE=2,S=S扇形BCF ﹣S△EDF﹣(S长方形ABCD﹣S扇形ABE)=S扇形BCF +S扇形ABE﹣S△EDF﹣S长方形ABCD=+﹣﹣6×8=25π﹣50.22.如图,已知AB是⊙O的直径,点C在⊙O上,延长BC至点D,使得DC=BC,直线DA与⊙O的另一个交点为E,连结AC,CE.(1)求证:CD=CE;(2)若AC=2,∠E=30°,求阴影部分(弓形)面积.(1)证明:∵AB是直径,∴∠ACB=90°,∵DC=BC,∴AD=AB,∴∠D=∠ABC,∵∠E=∠ABC,∴∠E=∠D,∴CD=CE.(2)解:由(1)可知:∠ABC=∠E=30°,∠ACB=90°,∴∠CAB=60°,AB=2AC=4,在Rt△ABC中,由勾股定理得到BC=2,连接OC,则∠COB=120°,∴S阴=S扇形OBC﹣S△OBC=﹣×××2=﹣.23.如图,点A,B,C在直径为2的⊙O上,∠BAC=45°,求图中阴影部分的面积.(结果中保留π)解:连接OB、OC,过O作OD⊥BC于D,∵∠BAC=45°,∴∠BOC=2∠BAC=90°,∵OB=OC,OD⊥BC,∴∠OBC=∠OCB=45°,BD=DC,∴BD=OD,∵OB==1,∴OD=BD=CD=OB×sin45°=,即BC=BD+CD=,∴阴影部分的面积S=S扇形BOC ﹣S△BOC=﹣=π﹣.24.如图,已知Rt△ABC中,∠A=90°,将斜边BC绕点B顺时针方向旋转至BD,使BD∥AC,过点D作DE⊥BC于点E.(1)求证:△ABC≌△EDB;(2)若CD=BD,AC=3,求在上述旋转过程中,线段BC扫过的面积.解:(1)∵DE⊥BC,∴∠DEB=90°,∵AC∥BD,∴∠A=∠ABD=∠DEB=90°,∵∠ABC+∠CBD=90°,∴∠CBD+∠BDE=90°,∴∠ABC=∠BDE,∵BC=BD,∴△ABC≌△EDB(AAS).(2)∵CD=BD=BC,∴△BCD为等边三角形,∴∠CBD=60°,∠ABC=90°﹣∠CBD=30°,∵AC=3,∴BC=2AC=6,∴线段BC扫过的面积=6π.。
2022-2023学年北师大版九年级数学下册《3-9弧长及扇形面积》同步达标测试题(附答案)
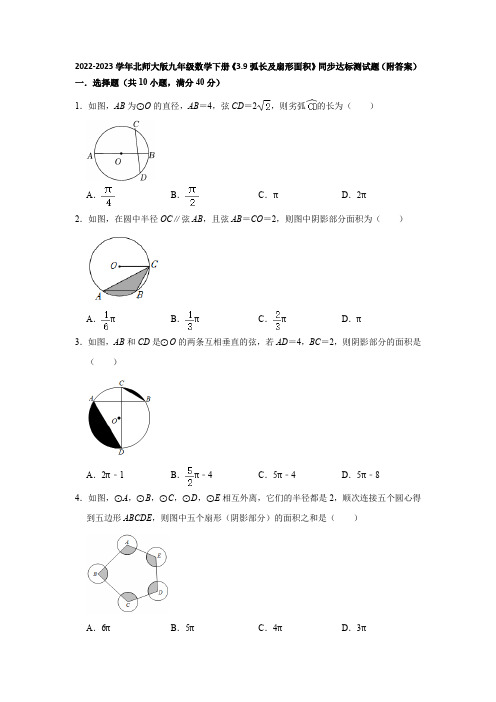
2022-2023学年北师大版九年级数学下册《3.9弧长及扇形面积》同步达标测试题(附答案)一.选择题(共10小题,满分40分)1.如图,AB为⊙O的直径,AB=4,弦CD=2,则劣弧的长为()A.B.C.πD.2π2.如图,在圆中半径OC∥弦AB,且弦AB=CO=2,则图中阴影部分面积为()A.πB.πC.πD.π3.如图,AB和CD是⊙O的两条互相垂直的弦,若AD=4,BC=2,则阴影部分的面积是()A.2π﹣1B.π﹣4C.5π﹣4D.5π﹣84.如图,⊙A,⊙B,⊙C,⊙D,⊙E相互外离,它们的半径都是2,顺次连接五个圆心得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是()A.6πB.5πC.4πD.3π5.一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若∠ACB=60°,则劣弧AB的长是()A.8πcm B.16πcm C.32πcm D.192πcm6.如图,在Rt△ABC中,∠ACB=90°,分别以AB,BC,CA为直径作半圆围成两月牙形,过点C作DF∥AB分别交三个半圆于点D,E,F.若=,AC+BC=15,则阴影部分的面积为()A.16B.20C.25D.307.如图,点A、B、C在⊙O上,若∠BAC=45°,OC=2,则图中阴影部分的面积是()A.π﹣2B.π﹣4C.D.8.如图,在⊙O中,OA=2,∠C=45°,则图中阴影部分的面积为()A.﹣B.π﹣C.﹣2D.π﹣29.如图,已知⊙P与坐标轴交于点A,O,B,点C在⊙P上,且∠ACO=60°,若点B的坐标为(0,3),则劣弧OA的长为()A.2πB.3πC.D.10.如图1是一块弘扬“社会主义核心价值观”的扇面宣传展板,该展板的部分示意图如图2所示,它是以O为圆心,OA,OB长分别为半径,圆心角∠O=120°形成的扇面,若OA=3m,OB=1.5m,则阴影部分的面积为()A.4.25πm2B.3.25πm2C.3πm2D.2.25πm2二.填空题(共8小题,满分32分)11.一个扇形的圆心角是135°,半径为4,则这个扇形的面积为.(保留π)12.如图,在扇形OAB中,已知∠AOB=90°,OA=2,过的中点C作CD⊥OA,CE ⊥OB,垂足分别为D、E,则图中阴影部分的面积为.13.如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π).14.如图,在Rt△ABC中,AB=2,BC=1.将边BA绕点B顺时针旋转90°得线段BD,再将边CA绕点C顺时针旋转90°得线段CE,连接DE,则图中阴影部分的面积是.15.如图,在扇形AOB中,∠AOB=120°,半径OC交弦AB于点D,且OC⊥AO,若OA =6,则阴影部分的面积为.16.如图,半径为10的扇形AOB中,∠AOB=90°,C为上一点,CD⊥OA,CE⊥OB,垂足分别为D、E.若∠CDE=36°,则图中阴影部分的面积为.17.如图,在Rt△ABC中,∠B=90°,AD平分∠BAC交BC于点D,点E在AC上,以AE为直径的⨀O经过点D.若∠C=30°,且CD=3,则阴影部分的面积是.18.如图,以A为圆心AB为半径作扇形ABC,线段AC交以AB为直径的半圆弧的中点D,若AB=4,则阴影部分图形的面积是(结果保留π).三.解答题(共6小题,满分48分)19.如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,点E是BC的中点,连结并延长OE交圆于点D.(1)求证:OD∥AC.(2)若DE=2,BE=2,求阴影部分的面积.20.如图,在⊙O中,AC为⊙O的直径,AB为⊙O的弦,点E是的中点,过点E作AB 的垂线,交AB于点M,交⊙O于点N,分别连接EB,CN.(1)EM与BE的数量关系是;(2)求证:=;(3)若AM=,MB=1,求阴影部分图形的面积.21.如图,在Rt△ABC中,∠ACB=90°,以直角边BC为直径的⊙O交斜边AB于点D.点E为边AC的中点,连接DE并延长交BC的延长线于点F.(1)求证:直线DE是⊙O的切线;(2)若∠B=30°,AC=4,求阴影部分的面积.22.如图,AB是⊙O的直径,点C为半径OA的中点,CD⊥AB交⊙O于点D和点E,DF∥AB交⊙O于F,连接AF,AD.(1)求∠DAF的度数;(2)若AB=10,求弦AD,AF和所围成的图形的面积.(结果保留π)23.如图,C,D是以AB为直径的半圆上的两点,∠CAB=∠DBA,连结BC,CD.(1)求证:CD∥AB.(2)若AB=4,∠ACD=30°,求阴影部分的面积.24.如图,△ABC内接于⊙O,AD∥BC交⊙O于点D,DF∥AB交BC于点E,交⊙O于点F,连接AF,CF.(1)求证:AC=AF;(2)若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).参考答案一.选择题(共10小题,满分40分)1.解:连接OC,OD.∵OC=ODD=2,CD=2,∴OC2+OD2=CD2,∴∠COD=90°,∴的长==π,故选:C.2.解:连接OA,OB,∵OC∥AB,AB=AB,∴△OAB的面积=△CAB的面积(等底等高的三角形的面积相等),∵AB=OC=2,∴OA=OB=AB=2,∴△OAB是等边三角形,∴∠AOB=60°,∴阴影部分的面积S=S扇形AOB==π,故选:C.3.解:连接AC,连接AO并延长,交⊙O于E点,连接DE ∵AB⊥CD,∴∠CAB+∠ACD=90°,∵AE是直径,∴∠ADE=90°,∴∠AED+∠EAD=90°,又∵∠ACD=∠AED,∴∠CAB=∠EAD,∴CB=DE=2,AE==2,将弓形BC旋转到弓形DE的位置两块阴影部分面积之和为半圆面积减去△ADE的面积,即S=﹣=﹣4.故选:B.4.解:由图可得,5个扇形的圆心角之和为:(5﹣2)×180°=540°,则五个阴影部分的面积之和==6π.故选:A.5.解:由题意得:CA和CB分别与⊙O相切于点A和点B,∴OA⊥CA,OB⊥CB,∴∠OAC=∠OBC=90°,∵∠ACB=60°,∴∠AOB=120°,∴=16π(cm),故选:B.6.解:连接AF、BE,∵AC是直径,∴∠AFC=90°.∵BC是直径,∴∠CDB=90°.∵DF∥AB,∴四边形ABDF是矩形,∴AB=DF,取AB的中的O,作OG⊥CE.∵,设DF=10k,CE=6k,∵CG=CE=3k,OC=OA=5k,∴OG=4K,∴AF=BD=4K,CF=DE=2K,∴AC=.∵AC+BC=15,∴2k+4k=15,∴k=,∴AC=5,BC=10,S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC﹣直径为AB的半圆的面积=π()2+π()2+AC×BC﹣π()2=π(AC)2+π(BC)2﹣π(AB)2+AC×BC=π(AC2+BC2﹣AB2)+AC×BC=AC×BC=×5×10=25.故选:C.7.解:∵∠BOC=2∠BAC=90°,∴S阴=S扇形OBC﹣S△OBC=﹣×2×2=π﹣2,故选:A.8.解:∵∠C=45°,∴∠AOB=90°,∴S阴影=S扇形AOB﹣S△AOB=﹣=π﹣2.故选:D.9.解:连接AB、OP,∵∠AOB=90°,∴AB为⊙P的直径,∵∠ACO=60°,∴∠APO=120°,∠ABO=60°,∴∠BAO=30°,∵OB=3,∴AB=2OB=6,∴的长=2π,故选:A.10.解:S阴=S扇形DOA﹣S扇形BOC=﹣=2.25πm2.故选:D.二.填空题(共8小题,满分32分)11.解:扇形的面积==6π,故答案为:6π.12.解:连接OC,∵OA=2,∴OC=0A=2,∵∠AOB=90°,C为的中点,∴∠AOC=∠BOC=45°,∵CD⊥OA,CE⊥OB,∴∠CDO=∠CEO=90°,∴∠DCO=∠AOC=∠ECO=∠COE=45°,∴CD=OD,CE=OE,∴2CD2=22,2OE2=22,即CD=OD=OE=CE=,∴阴影部分的面积S=S扇形AOB﹣S△CDO﹣S△CEO=﹣﹣=π﹣2,故答案为:π﹣2.13.解:连接AD,OD,∵等腰直角△ABC中,∴∠ABD=45°.∵AB是圆的直径,∴∠ADB=90°,∴△ABD也是等腰直角三角形,∴=.∵AB=8,∴AD=BD=4,∴S阴影=S△ABC﹣S△ABD﹣S弓形AD=S△ABC﹣S△ABD﹣(S扇形AOD﹣S△ABD)=×8×8﹣×4×4﹣+××4×4=16﹣4π+8=24﹣4π.故答案为:24﹣4π.14.解:作EF⊥CD于F,由旋转变换的性质可知,EF=BC=1,CD=CB+BD=3,由勾股定理得,CA==,则图中阴影部分的面积=△ABC的面积+扇形ABD的面积+△ECD的面积﹣扇形ACE的面积=×1×2++×3×1﹣=﹣,故答案为:﹣.15.解:∵∠AOB=120°,OA=OB,∴∠A=∠OBA=30°,∵OC⊥AO,∴∠AOD=90°,∴∠BOD=30°,∴DO=DB,在Rt△AOD中,OD=OA=,OD=AD,∴BD=AD,∵S△AOD=×6×=6,∴S△BOD=S△AOD=3,∴阴影部分的面积=S△AOD+S扇形BOC﹣S△BOD=6+﹣3=3+3π.故答案为3+3π.16.解:连接OC,∵∠AOB=90°,CD⊥OA,CE⊥OB,∴四边形CDOE是矩形,∴CD∥OE,∴∠DEO=∠CDE=36°,由矩形CDOE易得到△DOE≌△CEO,∴∠COB=∠DEO=36°∴图中阴影部分的面积=扇形OBC的面积,∵S扇形OBC==10π∴图中阴影部分的面积=10π,故答案为10π.17.解:连接OD,连接DE、OD、DF、OF,设圆的半径为R,∵AD是∠BAC的平分线,∴∠DAB=∠DAO,∵OD=OA,∴∠DAO=∠ODA,则∠DAB=∠ODA,∴DO∥AB,而∠B=90°,∴∠ODB=90°,∵∠C=30°,CD=3,∴OD=CD•tan30°=3×=3,∵∠DAB=∠DAE=30°,∴=,∵∠DOE=60°,∴∠DOF=60°,∴∠FOA=60°,∴△OFD、△OF A是等边三角形,∴DF∥AC,∴S阴影=S扇形DFO==.故答案为:.18.解:连接DO,∵线段AC交以AB为直径的半圆弧的中点D,AB=4,∴∠DAO=45°,∠DOA=90°,DO=AO=2,∴阴影部分的面积是:()+()=2π﹣4,故答案为:2π﹣4.三.解答题(共6小题,满分48分)19.(1)证明:∵AB是⊙O的直径,∴∠C=90°,∵点E是BC的中点,∴BE=CE,∴OD⊥BC,∴∠BEO=90°,∴∠C=∠BEO,∴OD∥AC;(2)解:连接OC,设OB=OD=r,∵DE=2,∴OE=r﹣2,∵BE2+OE2=BO2,∴(2)2+(r﹣2)2=r2,解得:r=4,∴OB=OD=4,∴OE=2,∴OE=OB,∴∠B=30°,∴∠AOC=60°,∴阴影部分的面积=S扇形AOC﹣S△AOC=﹣×4×2=π﹣4.20.解:(1)∵AC为⊙O的直径,点E是的中点,∴∠ABE=45°,∵AB⊥EN,∴△BME是等腰直角三角形,∴BE=EM,故答案为BE=EM;(2)连接EO,∵AC是⊙O的直径,E是的中点,∴∠AOE=90°,∴∠ABE=∠AOE=45°,∵EN⊥AB,垂足为点M,∴∠EMB=90°∴∠ABE=∠BEN=45°,∴=,∵点E是的中点,∴=,∴=,∴﹣=﹣,∴=;(3)连接AE,OB,ON,∵EN⊥AB,垂足为点M,∴∠AME=∠EMB=90°,∵BM=1,由(2)得∠ABE=∠BEN=45°,∴EM=BM=1,又∵BE=EM,∴BE=,∵在Rt△AEM中,EM=1,AM=,∴tan∠EAB==,∴∠EAB=30°,∵∠EAB=∠EOB,∴∠EOB=60°,又∵OE=OB,∴△EOB是等边三角形,∴OE=BE=,又∵=,∴BE=CN,∴△OEB≌△OCN(SSS),∴CN=BE=又∵S扇形OCN==,S△OCN=CN×CN=×=,∴S阴影=S扇形OCN﹣S△OCN=﹣.21.(1)证明:连接OD、CD,∵OC=OD,∴∠OCD=∠ODC,又∵BC是⊙O的直径,∴∠BDC=90°,∴△ACD是直角三角形,又∵点E是斜边AC的中点,∴EC=ED,∴∠ECD=∠EDC又∵∠ECD+∠OCD=∠ACB=90度,∴∠EDC+∠ODC=∠ODE=90°,∴直线DE是⊙O的切线;(2)解:由(1)已证:∠ODF=90°,∵∠B=30°,∴∠DOF=60°,∴∠F=30°,在Rt△ABC中,AC=4,∴BC===4,∴,在Rt△ODF中,,∴阴影部分的面积为:=.22.解:(1)∵DF∥AB,CD⊥AB,∴∠EDF=∠ECB=90°,∴EF为⊙O的直径,∵点C为半径OA的中点,∴OC=,∴∠E=30°,∴∠DAF=∠E=30°;(2)连接OD,则∠DOF=2∠E=60°,∵DF∥AB,∴S△ADF=S△DOF,∴S阴影=S扇形,∵OD=AB=5,∴弦AD,AF和所围成的图形的面积==π.23.(1)证明:∵=,∴∠ACD=∠DBA,又∵∠CAB=∠DBA,∴∠CAB=∠ACD,∴CD∥AB.(2)如图,连结OD,过点D作DE⊥AB,垂足为E.∵∠ACD=30°,∴∠ACD=∠CAB=30°,∴∠AOD=60°,∴∠BOD=180°﹣∠AOD=120°,∴S扇形BOD=.在Rt△ODE中,∵DE=sin60°•OD==,∴S△BOD===,∴S阴影=S扇形BOD﹣S△BOD,=.∴S阴影=.24.证明:(1)∵AD∥BC,DF∥AB,∴四边形ABED为平行四边形,∴∠B=∠D,∵∠AFC=∠B,∠ACF=∠D,∴∠AFC=∠ACF,∴AC=AF.(2)连接AO,CO,如图,由(1)得∠AFC=∠ACF,∵∠AFC==75°,∴∠AOC=2∠AFC=150°,∴的长l==.。
【北师大版】数学九(下)弧长及扇形的面积同步练习本(课件版)

第三章 圆
第13课 弧长及扇形的面积
目录
温故知新
新课学习 重难易错 三级检测
温故知新
1. 圆的周长 C = 2πR
.
2. 圆的面积 S = πR2
.
3.(1)若圆的直径为 4,则圆的周长 = 4π
Байду номын сангаас
;
(2)若圆的周长为 8π,则圆的半径 = 4
.
4.(1)若圆的半径为 3,则圆的面积 =
9π
A. 10π
3
C. 5 π
18
B. 5π
9
D. 10π
9
9. 如图,AB的长为 12π,圆心角∠AOB=120°,则
此弧所在圆的半径=
18
.
10. (例 2)扇形的圆心角是 30°. 它的半径是 6, 则扇形的面积是 3π (结果保留 π).
11. 已知扇形 OAB 的半径是 5,圆心角是 72°,则此
扇形的面积是
5π
.
12. 如图,五个半径为 2 的圆,圆心分别是点 A,B, C,D,E,则图中阴影部分的面积和是多少?
解:由图可得, 5 个扇形的圆心角之和为(5 - 2) × 180° = 540°. ∴五个阴影部分的面积之和 = 540π×22 = 6π.
360
重难易错
13. 如图,AB的长为 20π,圆心角∠AOB = 120°,求 此弧所在圆的半径.
解:外边的较长的弧长为(360−120)×20π = 80π(cm),
180
3
里边的弧长为(360−120)×10π = 40π(cm),
180
3
AC = BD = 20 - 10 = 10(cm).
北师大九年级数学下册--第三单元(含答案)3.9《弧长及扇形的面积》同步练习

一、填空题:
1.半径为9cm的圆中,长为12 cm 的一条弧所对的圆心角的度数为______;60°的圆心角所对的弦的长为________.毛
2.弯制管道时,先按中心线计算其“展直长度”,再下料. 根据如图1所示的图形可算得管道的展直长度为__ _____.(单位:mm,精确到1mm).
A.115° B.60° C.57° D.29°
10.一个扇形的弧长是20 cm,面积是240 cm2,那么扇形的圆心角是( )
A.120° B.150° C.210° D.240°
三、解答题:
13.已知,一条弧长为 cm,它所对的圆心角为120°,求这条弧所对的弦长.
14.如图是一把绸扇,线段AD、BC所在的直线相交于点O, 与 是以点O为圆心、半径 分别为10cm,20cm的圆弧,且∠AOB=150°,这把绸扇的绸布部分ADCB的面积是多少?(不考虑绸布的折皱,结果用含 的式子表示)
8.如图5的五个半圆,邻近的两半圆相切,两只上虫同时出发,以相同的速度从 A点到B点,甲虫沿 、 、 、 、路线爬行,乙虫沿 路线爬 行, 则下列结论正确的是( )
A.甲先到B点 B.乙先到B点; C.甲、乙同时到B点 D.无 法确定
9.一个滑轮起重装 置如图6所示,滑轮的半径是10cm,当重物上升10cm时, 滑轮的一条半径OA绕轴心O按逆时针方向旋转的角度约为(假设绳索与滑轮之间没有滑动, 取3.14,结果精确到1°)( )
6.如图4,扇形AOB的圆心角为60°,半径为6cm,C、D分别是 的三等分点, 则阴影部分的面积是________.
(4) (5) (6)
二、选择题:
7.秋千拉绳长3米,静止时踩板离地面0.5米,一小朋友荡该秋千时, 秋 千最高处踩板离地面2米(左,右对称),则该秋千所荡过的圆弧长为( )
2021-2022学年北师大版九年级数学下册《3-9弧长及扇形面积》同步练习题(附答案)
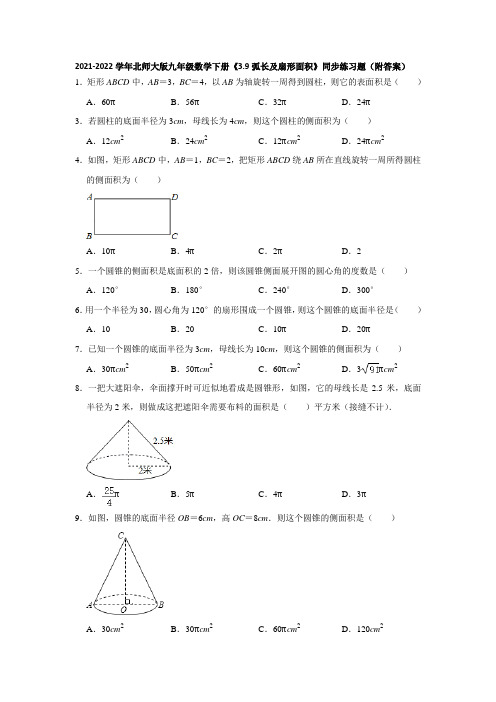
2021-2022学年北师大版九年级数学下册《3.9弧长及扇形面积》同步练习题(附答案)1.矩形ABCD中,AB=3,BC=4,以AB为轴旋转一周得到圆柱,则它的表面积是()A.60πB.56πC.32πD.24π3.若圆柱的底面半径为3cm,母线长为4cm,则这个圆柱的侧面积为()A.12cm2B.24cm2C.12πcm2D.24πcm24.如图,矩形ABCD中,AB=1,BC=2,把矩形ABCD绕AB所在直线旋转一周所得圆柱的侧面积为()A.10πB.4πC.2πD.25.一个圆锥的侧面积是底面积的2倍,则该圆锥侧面展开图的圆心角的度数是()A.120°B.180°C.240°D.300°6.用一个半径为30,圆心角为120°的扇形围成一个圆锥,则这个圆锥的底面半径是()A.10B.20C.10πD.20π7.已知一个圆锥的底面半径为3cm,母线长为10cm,则这个圆锥的侧面积为()A.30πcm2B.50πcm2C.60πcm2D.3πcm28.一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2.5米,底面半径为2米,则做成这把遮阳伞需要布料的面积是()平方米(接缝不计).A.πB.5πC.4πD.3π9.如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是()A.30cm2B.30πcm2C.60πcm2D.120cm210.工人师傅用一张半径为24cm,圆心角为150°的扇形铁皮做成一个圆锥的侧面,则这个圆锥的高为()cm.A.B.2C.4D.11.若一个圆锥的侧面积是18π,侧面展开图是半圆,则该圆锥的底面圆半径是()A.6B.3C.D.1212.已知圆柱的底面半径为3cm,母线长为5cm,则圆柱的侧面积是cm2.13.已知圆柱的侧面积是20πcm2,高为5cm,则圆柱的底面半径为.14.已知圆柱体的底面圆周长是6πcm,母线长为5cm,则该圆柱体的全面积为cm2.15.如图,已知AB是⊙O的直径,C,D是⊙O上的点,OC∥BD,交AD于点E,连接BC.(1)求证:AE=ED;(2)若AB=10,∠CBD=36°,求的长.16.如图,AB是⊙O的直径,点D在⊙O上,∠DAB=45°,BC∥AD,CD∥AB.若⊙O 的半径为1,求图中阴影部分的面积(结果保留π).17.如果从半径为5cm的圆形纸片上剪去圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),求这个圆锥的高.18.如图,圆锥的底面半径为6cm,高为8cm,求这个圆锥的侧面积和表面积.19.如图,点C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,作DE⊥AB,垂足为E,DE交AC于点F.(1)求证:AF=DF.(2)求阴影部分的面积(结果保留π和根号).20.如图,O为半圆的圆心,直径AB=12,C是半圆上一点,OD⊥AC于点D,OD=3.(1)求AC的长;(2)求图中阴影部分的面积.21.如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EO、FO,若DE=4,∠DP A=45°(1)求⊙O的半径.(2)若图中扇形OEF围成一个圆锥侧面,试求这个圆锥的底面圆的半径.22.如图,已知⊙O半径为10cm,弦AB垂直平分半径OC,并交OC于点D.(1)求弦AB的长;(2)求弧AB的长,并求出图中阴影部分面积.23.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,延长AD,BC交于点E,且CE=CD.(1)求证:AB=AE;(2)若∠BAE=40°,AB=4,求劣弧的长.24.如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.(1)求直径AB的长.(2)求阴影部分的面积(结果保留π).25.如图,一个圆锥形工艺品,它的高为3cm,侧面展开图是半圆.求:(1)圆锥的母线长与底面半径之比;(2)圆锥的侧面积.26.已知:如图,点P是正方形ABCD内一点,连接P A、PB、PC.(1)将△P AB绕点B顺时针旋转90°得到△P'CB,若AB=m,PB=n(n<m).求△P AB 旋转过程中边P A扫过区域(阴影部分)的面积;(2)若P A=,PB=2,∠APB=135°,求PC的长.27.如图,已知四边形ABCD内接于圆O,连接BD,∠BAD=100°,∠DBC=80°.(1)求证:BD=CD;(2)若圆O的半径为9,求的长(结果保留π).28.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2cm,扇形的圆心角θ=120°.(1)求该圆锥的母线长l;(2)求该圆锥的侧面积.29.已知Rt△ABC的斜边AB=13cm,一条直角边AC=5cm,以直线AB为轴旋转一周得一个几何体.求这个几何体的表面积.30.如图,△ABC中,AB=AC,E在AC上,经过A、B、E三点的⊙O交BC于点D,且.(1)求证:AB为⊙O的直径;(2)若AB=8,∠BAC=45°,求阴影部分的面积.31.如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.(1)求弧BC的长;(2)求弦BD的长.32.如图,弦CD垂直于⊙O的直径AB,垂足为H,且CD=6,BD=6.(1)求AB的长.(2)求弓形CBD的面积.参考答案1.解:∵以直线AB为轴旋转一周得到的圆柱体,得出底面半径为4cm,母线长为3cm,∴圆柱侧面积=2π•AB•BC=2π•3×4=24π(cm2),∴底面积=π•BC2=π•42=16π(cm2),∴圆柱的表面积=24π+2×16π=56π(cm2).故选:B.3.解:根据侧面积公式可得:π×2×3×4=24πcm2,故选:D.4.解:圆柱的侧面面积=π×2×2×1=4π.故选:B.5.解:设母线长为R,底面半径为r,∴底面周长=2πr,底面面积=πr2,侧面面积=πrR,∵侧面积是底面积的2倍,∴2πr2=πrR,∴R=2r,设圆心角为n,则=2πr=πR,解得,n=180°,故选:B.6.解:设圆锥的底面圆半径为r,依题意,得2πr=,解得r=10.故小圆锥的底面半径为10.故选:A.7.解:圆锥的侧面积=2π×3×10÷2=30π.故选:A.8.解:圆锥的底面周长=2πr=2π×2=4π,∵圆锥的底面周长等于圆锥的侧面展开扇形的弧长,∴圆锥的侧面积=lr=×4π×2.5=5π,故选:B.9.解:∵它的底面半径OB=6cm,高OC=8cm.∴BC==10(cm),∴这个圆锥漏斗的侧面积是:πrl=π×6×10=60π(cm2).故选:C.10.解:由题意可得圆锥的母线长为:24cm,设圆锥底面圆的半径为:r,则2πr=,解得:r=10,故这个圆锥的高为:(cm).故选:B.11.解:设圆锥的母线长为R,π×R2÷2=18π,解得:R=6,∴圆锥侧面展开图的弧长为:6π,∴圆锥的底面圆半径是6π÷2π=3.故选:B.12.解:π×2×3×5=30πcm2,故答案为30π.13.解:设圆柱底面圆的半径为r,那么侧面积为2πr×5=20πr=2cm.故答案为2cm.14.解:因为圆柱底面周长为6πcm,所以圆柱的底面半径为3cm,圆柱体的全面积为:18π+5×6π=48π.故答案为:48π.15.证明:(1)∵AB是⊙O的直径,∴∠ADB=90°,∵OC∥BD,∴∠AEO=∠ADB=90°,即OC⊥AD,∴AE=ED;(2)∵OC⊥AD,∴,∴∠ABC=∠CBD=36°,∴∠AOC=2∠ABC=2×36°=72°,∴.16.解:连接OD,∵OA=OD,∠A=45°,∴∠A=∠ADO=45°,∴∠DOB=90°,即OD⊥AB,∵BC∥AD,CD∥AB,∴四边形ABCD是平行四边形,∴CD=AB=2∴S梯形OBCD===,∴图中阴影部分的面积S=S梯形OBCD﹣S扇形OBD=﹣=﹣.17.解:∵从半径为5cm的圆形纸片上剪去圆周的一个扇形,∴留下的扇形的弧长==8π,根据底面圆的周长等于扇形弧长,∴圆锥的底面半径r==4cm,∴圆锥的高为=3(cm).18.解:∵圆锥的底面半径为6cm,高为8cm,∴圆锥的母线长为10cm,∴S侧=π×6×10=60πcm2;∵圆锥的底面积=π×62=36π,∴S表=60π+36π=96πcm2.19.(1)证明:连接OD,OC,∵C、D是半圆O上的三等分点,∴==,度数都是60°,∴∠AOD=∠DOC=∠COB=60°,∴∠DAC=30°,∠CAB=30°,∵DE⊥AB,∴∠AEF=90°,∴∠ADE=180°﹣90°﹣30°﹣30°=30°,∴∠DAC=∠ADE=30°,∴AF=DF;(2)解:由(1)知,∠AOD=60°,∵OA=OD,AB=4,∴△AOD是等边三角形,OA=2,∵DE⊥AO,∴DE=,∴S阴影=S扇形AOD﹣S△AOD=﹣×2×=π﹣.20.解:(1)∵OD⊥AC,∴AD=DC,∵AO=OB,∴BC=2OD=6,∵AB是直径,∴∠ACB=90°,∴AC===6.(2)连接OC,∵OC=OB=BC=6,∴∠BOC=60°,∴∠AOC=120°,∴S阴=S扇形OAC﹣S△AOC=﹣•6•3=12π﹣9.21.解:(1)∵弦DE垂直平分半径OA,∴CE=DC=DE=2,OC=OE,∴∠OEC=30°,∴OC==2,∴OE=2OC=4,即⊙O的半径为4;(2)∵∠DP A=45°,∴∠D=45°,∴∠EOF=2∠D=90°,设这个圆锥的底面圆的半径为r,∴2πr=,解得r=1,即这个圆锥的底面圆的半径为1.22.解:(1)如图,⊙O半径为10cm,∴OB=OC=10,∵弦AB垂直平分半径OC,∴AB=2BD,∠ODB=90°,OD=OC=5,在Rt△BOD中,根据勾股定理得,BD==5,∴AB=2BD=10cm;(2)由(1)知,OD=5,在Rt△BOD中,cos∠BOD==,∴∠BOD=60°,∵OC⊥AB,∴∠AOB=2∠BOD=120°,∴===cm,S阴影=S扇形AOB﹣S△AOB=﹣AB×OD=﹣×=﹣25(cm2).23.解:(1)∵CE=CD,∴∠E=∠CDE,∵∠CDE=∠B,∴∠B=∠E,∴AB=AE;(2)连接OC,OD,∵∠BAE=40°,AB=AE,∴∠B=∠E=70°,在等腰三角形OBC中,得出∠BOC=40°,在等腰三角形OAD中,∠AOD=100°,∴∠COD=40°,∴劣弧的长为:=π.24.解:(1)∵AB为⊙O的直径,∴∠ACB=90°,∵∠B=30°,∴AB=2AC,∵AB2=AC2+BC2,∴AB2=AB2+62,∴AB=4.(2)连接OD.∵AB=4,∴OA=OD=2,∵CD平分∠ACB,∠ACB=90°,∴∠ACD=45°,∴∠AOD=2∠ACD=90°,∴S△AOD=OA•OD=•2•2=6,∴S扇形△AOD=•π•OD2=•π•(2)2=3π,∴阴影部分的面积=S扇形△AOD﹣S△AOD=3π﹣6.25.解:(1)设圆锥底面半径为rcm,母线为ℓcm,由题知2πr=πℓ解得ℓ:r=2:1答:圆锥母线与底面半径之比为2:1.(2)由题知把ℓ=2r代入,解得r1=﹣3(舍去),r2=3∴ℓ=6∴圆锥的侧面积=πrℓ=18π(cm2)26.解:(1)由旋转的性质可知,S△ABP=S△CBP′,∴△P AB旋转过程中边P A扫过区域面积=﹣=(m2﹣n2);(2)连接PP′,由旋转的性质可知,∠BP′C=∠APB=135°,∠PBP′=90°,BP′=BP=2,P′C=P A=,∴PP′==4,∠PP′C=90°,∴PC==3.27.(1)证明:∵四边形ABCD内接于圆O,∴∠DCB+∠BAD=180°,∵∠BAD=100°,∴∠DCB=180°﹣100°=80°,∵∠DBC=80°,∴∠DCB=∠DBC=80°,∴BD=CD;(2)解:∵∠DCB=∠DBC=80°,∴∠BDC=20°,由圆周角定理,得,的度数为:40°,故的长==2π,答:的长为2π.28.解:(1)由题意,得2πr=.∴l=3r=6(cm).(2)S侧==12π(cm2).29.解:∵Rt△ABC的斜边AB=13cm,直角边AC=5cm,∴另一直角边BC=12cm,以斜边AB为轴旋转一周,得到由两个圆锥组成的几何体,直角三角形的斜边上的高OC==cm,则以cm为半径的圆的周长=πcm,几何体的表面积=×π×(5+12)=π(cm2).30.(1)证明:连接AD,∵,∴∠BAD=∠CAD,又AB=AC,∴AD⊥BC,∴∠ADB=90°,∴AB为⊙O的直径;(2)∵AB为⊙O的直径,∴点O在AB上,连接OE,由圆周角定理得,∠AOE=∠BOE=90°,∴阴影部分的面积=×4×4+=8+4π.31.解:(1)如图,连接OC,OD,,∵AB是⊙O的直径,∴∠ACB=∠ADB=90°,在Rt△ABC中,∵cos∠BAC===,∴∠BAC=60°,∴∠BOC=2∠BAC=2×60°=120°,∴的长==π.(2)∵CD平分∠ACB,∴∠ACD=∠BCD,∴∠AOD=∠BOD,∴AD=BD,∴∠ABD=∠BAD=45°,在Rt△ABD中,BD=AB×sin45°=10×=5.32.解:(1)连接OD.由垂径定理得HD=CD=×=3,由勾股定理得HB===3,设⊙O的半径为r,在Rt△ODH中,OH=r﹣1,则r2=(3)2+(r﹣1)2,由此得2r=12,所以AB=12;(2)连接OC,在Rt△ODH中,OD=6,OH=3,∴∠ODH=30°,∴∠DOH=60°,∴∠COD=120°,∴S弓形CBD=S扇形OCD﹣S△COD=﹣××3=12π﹣9.。
2021-2022学年北师大版九年级数学下册《3-9弧长及扇形面积》同步练习题(附答案)
2021-2022学年北师大版九年级数学下册《3-9弧长及扇形面积》同步练习题(附答案)1.已知圆心角度数为60°,半径为30,则这个圆心角所对的弧长为()A.20πB.15πC.10πD.5π2.已知扇形半径是9cm,弧长为4πcm,则扇形的圆心角为()A.20°B.40°C.60°D.80°3.如图,圆锥的底面半径OB=6cm,高OC=8cm.则这个圆锥的侧面积是()A.30cm2B.30πcm2C.60πcm2D.120cm24.如图,在纸上剪下一个圆形和一个扇形的纸片,使之恰好能围成一个圆锥模型,若圆的半径为r,扇形的圆心角等于120°,则围成的圆锥模型的高为()A.r B.2r C.r D.3r5.如图,P A切⊙O于点A,PB切⊙O于点B,如果∠APB=60°,⊙O半径是3,则劣弧AB的长为()A.B.πC.2πD.4π6.如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2,则阴影部分图形的面积为()A.4πB.2πC.πD.7.如图平面直角坐标系中,已知⊙D经过原点O,与x轴、y轴分别交于A、B两点,B点坐标为(0,2),OC与⊙D相交于点C,∠OCA=30°,则图中阴影部分的面积为()A.2π﹣2B.4π﹣C.4π﹣2D.2π﹣8.如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为()A.()°B.()°C.()°D.()°9.如图,在矩形ABCD中,AB=3,BC=2,以点A为圆心,AD长为半径画弧交边BC 于点E,连接AE,则的长为()A.πB.πC.πD.π10.已知圆心角为120°的扇形的面积为12π,则扇形的半径为()A.4B.6C.4D.611.如图,扇形AOB的圆心角是45°,正方形CDEF的顶点分别在OA,OB和弧AB上.若OD=2,则图中阴影部分的面积为()A.B.C.D.12.如图,⊙O的半径为2,∠AOB=90°,则图中阴影部分的面积为()A.B.πC.2πD.4π13.在半径为12的圆中,60°圆心角所对的弧长是.14.已知圆弧的度数为80°,弧长为16π,则圆弧的半径为.15.如图,在⊙O中,直径AB=4,C是⊙O上一点,∠CAB=30°,则的长为.16.已知扇形的弧长为6π,半径为3,则这个扇形的面积为17.如图,点A、B、C均在⊙O上,若∠A=60°,OB=2,则阴影部分的面积为.18.一个扇形的圆心角是135°,半径为4,则这个扇形的面积为.(保留π)19.如图,已知AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC 交于点E,∠D=65°.(1)求∠CAD的度数;(2)若AB=4,求的长.20.如图,的半径OA=2,OC⊥AB于点C,∠AOC=60°.(1)求弦AB的长.(2)求的长.21.如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.(1)求直径AB的长.(2)求阴影部分的面积(结果保留π).22.如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,求图中阴影部分的面积.(结果保留π)参考答案1.解:圆心角是60°,半径为30的扇形的弧长是=10π,故选:C.2.解:根据弧长公式==4π,解得:n=80,故选:D.3.解:∵它的底面半径OB=6cm,高OC=8cm.∴BC==10(cm),∴这个圆锥漏斗的侧面积是:πrl=π×6×10=60π(cm2).故选:C.4.解:∵圆的半径为r,则扇形的弧长等于底面圆的周长,设圆锥的母线长为R,则=2πr,解得:R=3r.根据勾股定理得圆锥的高为2r,故选:B.5.解:连接OA,OB.则OA⊥P A,OB⊥PB∵∠APB=60°∴∠AOB=120°∴劣弧AB的长是:=2π.故选:C.6.解:如图,假设线段CD、AB交于点E,∵AB是⊙O的直径,弦CD⊥AB,∴CE=ED=,又∵∠CDB=30°,∴∠COE=2∠CDB=60°,∠OCE=30°,∴OE=CE•cot60°=×=1,OC=2OE=2,∴S阴影=S扇形OCB﹣S△COE+S△BED=﹣OE×EC+BE•ED=﹣+=.解法二:连接OD,BC,证明OD∥BC,可以证明S阴影=S扇形OCB=.故选:D.7.解:∵∠AOB=90°,∴AB是直径,连接AB,根据同弧对的圆周角相等得∠OBA=∠C=30°,由题意知,OB=2,∴OA=OB tan∠ABO=OB tan30°=2×=2,AB=AO÷sin30°=4即圆的半径为2,∴阴影部分的面积等于半圆的面积减去△ABO的面积,S阴=S半﹣S△=﹣×2×2=2π﹣2.故选:A.8.设∠ABC的度数大小由60变为n,则AC=,由AC=AB,解得n=,故选:D.9.解:由题意可知:AE=AD=BC=2,在Rt△ABE中,sin∠AEB===,∴∠AEB=60°,∵AD∥BC,∴∠AEB=∠DAE=60°,l===,故A、B、D错误,故选:C.10.解:设该扇形的半径是r,则12π=,解得r=6.故选:B.11.解:∵∠O=45°,四边形CDEF是正方形,∴∠CDO=90°,△COD是等腰直角三角形,∴DE=EF=OD=2,连接OF,Rt△EOF中,OE=4,EF=2,∴OF==2.∴扇形AOB的面积是=,正方形CDEF的面积是2×2=4,等腰三角形COD的面积是×2×2=2,∴阴影部分的面积是﹣4﹣2=﹣6.故选:B.12.解:∵∠AOB=90°,OA=OB=2,∴S扇形==π,故选:B.13.解:在半径为12的⊙O中,60°圆心角所对的弧长是:=4π,故答案为:4π.14.解:设圆弧的半径为r,∵圆弧的度数为80°,∴圆弧所对的圆心角的度数是80°,∵弧长为16π,∴=16π,解得:r=36,即圆弧的半径是36,故答案为:36.15.解:连接OC,∵OA=OC,∠CAB=30°,∴∠ACO=∠CAB=30°,∴∠COB=∠ACO+∠CAB=30°+30°=60°,∵直径AB=4,∴OB=2,∴的长==,故答案为:.16.解:由题意,S=×6π×3=9π,故答案为:9π.17.解:∵∠A=60°,∴∠BOC=2∠A=120°,∴阴影部分的面积==,故答案为:;18.解:扇形的面积==6π,故答案为:6π.19.解:(1)如图,连接OC,∵OA=OD,∴∠OAD=∠ODA=65°,∴∠AOD=180°﹣65°﹣65°=50°,∵OD∥BC,OB=OC,∴∠AOD=∠OBC=∠OCB=∠COD=50°,∴∠CAD=∠COD=25°;(2)由AB=4可得半径为2,∠BOC=180°﹣50°﹣50°=80°,因此的长为=.20.解:(1)∵的半径OA=2,OC⊥AB于点C,∠AOC=60°,∴AC=OA•sin60°=2×=,∴AB=2AC=2;(2)∵OC⊥AB,∠AOC=60°,∴∠AOB=120°,∵OA=2,∴的长是:=.21.解:(1)∵AB为⊙O的直径,∴∠ACB=90°,∵∠B=30°,∴AB=2AC,∵AB2=AC2+BC2,∴AB2=AB2+62,∴AB=4.(2)连接OD.∵AB=4,∴OA=OD=2,∵CD平分∠ACB,∠ACB=90°,∴∠ACD=45°,∴∠AOD=2∠ACD=90°,∴S△AOD=OA•OD=•2•2=6,∴S扇形△AOD=•π•OD2=•π•(2)2=3π,∴阴影部分的面积=S扇形△AOD﹣S△AOD=3π﹣6.22.解:连接OC,∵AB与圆O相切,∴OC⊥AB,∵OA=OB,∴∠AOC=∠BOC,∠A=∠B=30°,在Rt△AOC中,∠A=30°,OA=4,∴OC=OA=2,∠AOC=60°,∴∠AOB=120°,AC==2,即AB=2AC=4,则S阴影=S△AOB﹣S扇形=×4×2﹣=4﹣.故图中阴影部分的面积为4﹣.。
_九级数学下册第三章圆3.9弧长及扇形的面积同步练习新版北师大版10311125
课时作业 ( 二十九 )[ 第三章9弧长及扇形的面积]一、选择题1.2017·武汉期末如图 K- 29-1,等边三角形ABC的边长为 4,D,E,F分别为边AB,BC, AC的中点,分别以 A,B,C三点为圆心,以 AD长为半径作三条圆弧,则图中三条圆弧的弧长之和是 ()图 K-29-1A.π B . 2π C . 4π D . 6π2.2018 ·福州二模如图K- 29- 2,AD是半圆O的直径,AD= 12,B,C是半圆O上两点.若︵︵︵AB= BC= CD,则图中暗影部分的面积是()链接听课例 3概括总结图 K-29-2A. 6π B . 12π C . 18π D . 24π二、填空题3.2017·长春如图K- 29- 3,在△ABC中,∠BAC=100°,AB=AC= 4,以点B为圆心,︵AB长为半径作圆弧,交BC于点 D,则 AD的长为________.(结果保存π)链接听课例 2概括总结图 K-29-34.如图 K- 29- 4,在边长为4 的正方形ABCD中,先以点 A 为圆心, AD长为半径画弧,再以AB 边的中点为圆心,AB 长的一半为半径画弧,则两弧之间的暗影部分的面积是________.( 结果保存π )链接听课例 4概括总结图 K-29-4︵︵5.如图 K- 29- 5,△ABC是正三角形,曲线CDEF叫正三角形的渐开线,此中CD, DE,︵EF的圆心挨次是A, B, C,假如 AB=1,那么曲线CDEF的长是________.图 K-29-56.如图 K- 29- 6,在 Rt △ABC中,∠ACB=90°,AC= 23,以点C为圆心,CB长为半径画弧,与边交于点,将︵D 旋转 180°后点B与点A恰巧重合,则图中暗影部绕点AB D BD分的面积为 ________.图 K-29-6三、解答题7.如图 K- 29- 7,在扇形OAB中,∠AOB= 90°,半径OA= 6. 将扇形OAB沿过点B 的直线折叠,点 O恰巧落在扇形上的点 D处,折痕交 OA于点 C,求整个暗影部分的周长和面积.图 K-29-78.2018·椒江区模拟如图K- 29-8,是⊙的直径,C 是圆上一点,连结,,AB O CA CB过点O 作弦的垂线,交︵,连结.于点BC BC D AD(1) 求证:∠CAD=∠BAD;︵(2)若⊙ O的半径为1,∠ B=50°,求 AC的长.图 K-29-89.2017·如东县一模如图K- 29- 9,在△ABC中,∠ACB= 130°,∠BAC= 20°,BC =4,以点C为圆心,BC长为半径的圆交AB于点D,交AC于点E.(1)求 BD的长;(2)求暗影部分的面积.图 K-29-910.2017·贵阳如图K-29- 10,C,D是半圆O上的三平分点,直径AB=4,连结 AD,AC, DE⊥ AB,垂足为 E, DE交 AC于点 F.(1)求∠ AFE的度数;(3) 求暗影部分的面积( 结果保存π和根号).链接听课例 4概括总结图 K- 29-1011.如图 K- 29- 11,把 Rt △ABC的斜边上转动两次,使它转到△ A″B″ C″的地点,设地点时,(1)求点 A 所经过的路线长;AB放在直线 l 上,按顺时针方向将△ ABC在 l BC=1, AC=3,则极点 A 运动到点 A″的(2)点 A 所经过的路线与 l 围成的图形的面积是多少?图 K- 29-11研究型在学习扇形的面积公式时,同学们推得SnπR2扇形=360 ,并经过比较扇形面积公式与弧长公式lnπ RS1. 接着老师让同学们解决两个问=,得出扇形面积的另一种计算方法扇形=1802lR题:问题Ⅰ:求弧长为 4π,圆心角为 120°的扇形面积.问题Ⅱ:某小区设计的花坛形状如图K-29- 12 中的暗影部分,已知弧AB和弧CD所在圆的圆心都是点,弧的长为l1,弧的长为l2,==,求花坛的面积.O AB CD AC BD d(1)请你解答问题Ⅰ .(2) 在解完问题Ⅱ后的全班沟通中,闻名同学发现扇形面积公式扇形=1近似于三S2lR1角形面积公式;类比梯形面积公式,他猜想花坛的面积S=2( l1+l2 ) d. 他的猜想正确吗?如果正确,写出推导过程;假如不正确,请说明原因.图 K- 29-12详解详析【课时作业】[ 讲堂达标 ]11.[ 分析]B60π×2× 4依题意知:图中三条圆弧的弧长之和=× 3= 2π. 应选 B.1802.[ 分析]A︵︵︵∵ AB= BC=CD,∴∠ AOB=∠ BOC=∠ COD=60°,60π× 62∴暗影部分的面积== 6π. 应选 A.3608π3.[ 答案 ]9[ 分析 ]∵在△ ABC中,∠ BAC=100°,AB=AC,1∴∠ B=∠ C=(180°-100°)=40°.2︵40π× 4 8π∵ AB=4,∴AD的长为180=9 .4.[ 答案]2π5.[ 答案]4π[分析]︵120π× 12π的长是=,CD1803︵120π× 2 4π︵120π× 3DE的长是180=3, EF的长是180= 2π,2π4π则曲线 CDEF的长是 3 +3+2π=4π.故答案为 4π .2π6.[ 答案]23-3[分析]依题意,有=. 又∠= 90°,因此==,即△为等边三角形,AD BD ACB CB CD BD BCD∴∠=∠ =60°,∠ =∠=30°. 由= 23,求得= 2,=4,BCD B A ACD AC BC AB弓形 BD=S60π× 222△ACD-S弓形 AD=3扇形 BCD-△ BCD=-3=π- 3,故暗影部分的面积为S S3603S-( 2π- 3) = 23-2π.337.解:如图,连结OD.依据折叠的性质,得CD=CO, BD=BO,∠ DBC=∠ OBC,∴OB=OD= BD,即△ OBD 是等边三角形,1∴∠ DBO = 60°,∴∠ CBO = 2∠ DBO =30° .∵∠ AOB = 90°,∴ = ·tan ∠= 6×3= 2 3,OC OBCBO31 1∴ S △BDC = S △OBC =2· OB · OC = 2× 6× 23=63.902︵ 90∵ S 扇形 OAB =360π× 6 =9π, lAB = 180π× 6= 3π,∴整个暗影部分的周长为︵ ︵ ︵ AC + CD + BD + lAB = AC + OC + OB + lAB = OA + OB + lAB = 6+ 6 +3π= 12+ 3π,整个暗影部分的面积为S 扇形 OAB △ BDC △ OBC3- 6 3= 9π- 123.- S - S = 9π- 68.解: (1) 证明:∵点O 是圆心, OD ⊥ BC ,︵ ︵∴ CD =BD ,∴∠ CAD =∠ BAD .(2) 连结 CO ,∵∠ B = 50°, OB = OC , ∴∠ OCB =∠ B =50°, ∴∠ AOC = 100°,∴ ︵的长为 100π× 1 = 5π.AC 18099.解: (1) 如图,过点 C 作 CH ⊥ AB 于点 H .在△ ABC 中,∠ B = 180°-∠ A -∠ ACB = 180°- 20°- 130°= 30° . 在 Rt △ BCH 中,∵∠ CHB = 90°,∠ B = 30°, BC = 4,1∴ CH = 2BC = 2, BH =3CH = 2 3. ∵ CH ⊥BD ,∴ DH = BH ,∴ BD = 2BH = 43.(2) 连结 CD .∵ BC =DC ,∴∠ CDB =∠ B = 30°,∴∠ BCD = 120°,∴暗影部分的面积=扇形CBD 的面积-△ CBD 的面积=120π× 421360 - 216×43 ×2= π-4 3.10.解: (1) 连结 OD , OC ,︵ ︵ ︵∵ C ,D 是半圆 O 上的三平分点,∴ AD = CD =BC ,∴∠ AOD =∠ DOC =∠ COB = 60°,∴∠ CAB =30° .∵ DE ⊥AB ,∴∠ AEF = 90°, ∴∠ AFE = 90°- 30°= 60° .(2) 由 (1) 知∠ AOD = 60° .又∵ OA = OD ,∴△ AOD 是等边三角形.∵ AB =4,∴ OA = AD = 2.∵ DE ⊥AO ,∴ DE = 3,∴ S 暗影= S 扇形 AOD △ AOD60·π× 22 12 - S = 360 - 2× 2×3= 3π- 3. 11.解: (1) 在 Rt △ ABC 中, BC =1, AC = 3,1∴ AB =2,∴ cos ∠ ABC =2,∴∠ ABC = 60°, 则∠ ABA ′= 120°,∠ A ′ C ″ A ″= 90°,︵ 120π× 2 4π︵ 90π×33∴ lAA ′ =180= 3 , lA ′ A ″=180= 2 π,∴点 A 所经过的路线长为4π 33 + 2 π . (2) S 1 ︵ 1 4π 4π=′ · = × × 2= ,扇形 BAA ′1 ︵1 3π 3 S 扇形 C ″ A ′ A ″ = lA ′ A ″· C ″ A ′= ×2× 3= π,224△A ′ B ′C ′= 1× 1×3= 3, S22∴点 A 所经过的路线与43 3 253l 围成的图形的面积是 π+ π+= π+ .3 4 2122[ 修养提高 ][分析]依据扇形面积公式、弧长公式之间的关系,联合已知条件推出结果.解:(1) 依据弧长公式 l=n π R,弧长为 4π,圆心角为 120°,可得 = 6,∴ S扇形=1180R 2lR1= × 4π× 6= 12π .2(2) 他的猜想正确.n πR设大扇形的半径为,小扇形的半径为 r ,圆心角的度数为n °,则由l =,得 =R R180l,r=180l,12nπnπ∴花坛的面积为112l 1R-2l 2r1l 1·180l11180l2=·nπ-·l 2·nπ229022=nπ( l1-l 2)90=nπ( l1+l2)( l1-l2)1 180nπnπ=2·nπ ( l1+l2)( 180R-180r ) 11=2( l1+l2)( R-r ) =2( l1+l2) d.故他的猜想正确.。
最新北师大版数学九年级下同步练习 3.9 弧长及扇形的面积
ABC OA 'B 'C '3.9 弧长及扇形的面积1.在半径为4π的圆中,45°的圆心角所对的弧长等于 .2. 已知扇形的弧长为6πcm ,圆心角为60°,则扇形的面积为_________. 3.母线长为2,底面圆的半径为1的圆锥的侧面积为__________.4.一个圆锥的侧面展开图是半径为4,圆心角为90°的扇形,则此圆锥的底面半径为 . 5.一圆锥的侧面展开图是半径为2的半圆,则该圆锥的全面积是( )A..5π B .4π C .3π D .2π6、如图,有一直径为4的圆形铁皮,要从中剪出一个最大圆心角为60°的扇形ABC.那么剪下的扇形ABC (阴影部分)的面积为 ; 用此剪下的扇形铁皮围成一个圆锥,该圆锥的底面圆的半径r= .7.如图(2),将ABC △绕点B 逆时针旋转到A BC ''△使A 、B 、C’在同一直线上,若90BCA ∠=°,304cm BAC AB ∠==°,,则图中阴影部分面积为 cm 2.8、如图,菱形OABC 中,120A =o∠,1OA =,将菱形OABC 绕点O 按顺时针方向旋转90o ,则图中由¼BB',B A '',¼A C ',CB 围成的阴影部分的面积是 .′9、如图,将半径为1、圆心角为︒60的扇形纸片AOB ,在直线l 上向右作无滑动的滚动至扇形B O A '''处,则顶点O 经过的路线总长为10、如图,半圆的直径AB=10,P 为AB 上一点,点C\D 为半圆的三等分点,求得阴影部分的面积为11、如图,AC 是汽车挡风玻璃前的刮雨刷.如果AO=65,CO=15,当AC 绕点O 旋转90°时,则刮雨刷AC 扫过的面积为cm 2.12、如图,王虎使一长为4cm ,宽为3cm 的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A 位置变化为12A A A →→,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A 翻滚到A 2位置时共走过的路径长为_________cm.13.图1是某学校存放学生自行车的车棚的示意图(尺寸如图所示),车棚顶部是圆柱侧面的一A O′C A ′AB部分,其展开图是矩形.图2是车棚顶部截面的示意图,»AB 所在圆的圆心为O .车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积14、一位小朋友在粗糙不打滑的“Z ”字形平面轨道上滚动一个半径为10cm 的圆盘,如图所示,AB 与C D 是水平的,BC 与水平面的夹角为600,其中AB=60cm ,CD=40cm ,BC=40cm ,请你作出该小朋友将园盘从A 点滚动到D 点其圆心所经过的路线的示意图,并求出此路线的长度。
2022-2023学年北师大版九年级数学下册《3-9弧长及扇形面积》假期同步提升练习题(附答案)
2022-2023学年北师大版九年级数学下册《3.9弧长及扇形面积》假期同步提升练习题(附答案)一.选择题1.半径为6,圆心角为60°的弧长为()A.6B.3πC.2πD.4π2.如图,已知⊙O的半径为6,AB,BC是⊙O的弦,若∠ABC=50°,则的长是()A.B.10πC.D.12π3.如图,在△ABC中,AC=2,将△ABC绕点A顺时针旋转90°后得到△ADE,则C点运行痕迹长为()A.B.C.πD.2π4.一个扇形的弧长是10πcm,其圆心角是150°,此扇形的面积为()A.30πcm2B.60πcm2C.120πcm2D.180πcm25.已知扇形的面积为12πcm2,圆心角为120°,则扇形的弧长为()A.4 cm B.2cm C.4πcm D.2πcm6.已知一个圆锥的母线长为是30,底面半径为10,则这个圆锥的侧面展开图的圆心角等于()A.90°B.100°C.120°D.150°7.圆锥的底面半径为3,侧面积为12π,则圆锥的母线长为()A.4B.5C.5D.二.填空题8.已知扇形的弧长是π,圆心角120°,则这个扇形的半径是.9.如图,从一个腰长为60cm,顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,则此扇形的弧长为cm.10.如图,已知⊙O的半径为2,AB是⊙O的弦.若AB=2,则劣弧的长为.11.一扇形的圆心角是40°,弧长是2π,则此扇形的面积是.12.已知直角三角形ABC的一条直角边AB=12cm,斜边AC=13cm,则以AB为轴旋转一周,所得到的圆锥的侧面积是.13.若一个圆锥的母线长为5cm,它的半径为3cm,则这个圆锥的全面积为cm2.14.如图,若圆锥的母线长为6,底面半径为2,则其侧面展开图的圆心角为.三.解答题15.如图,已知扇形AOB的圆心角为120°,半径OA为6cm.求扇形AOB的弧长和面积.16.如图所示,扇形OAB的面积为4πcm2,∠AOB=90°,用这个扇形围成一个圆锥的侧面.求这个圆锥的底面圆的半径.17.已知:如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上一动点且不与点A,C重合,AG,DC的延长线交于点F,连结BC.CD=4,BE=2.(1)求半径长;(2)求扇形DOC的面积.18.如图所示,菱形ABCD,∠B=120°,AD=1,扇形BEF的半径为1,圆心角为60°,求图中阴影部分的面积.19.如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.(1)由AB,BD,围成的阴影部分的面积是;(2)求线段DE的长.20.如图,AB是⊙O的直径,弦DE垂直平分半径OA,C为垂足,弦DF与半径OB相交于点P,连接EO、FO,若DE=4,∠DP A=45°(1)求⊙O的半径.(2)若图中扇形OEF围成一个圆锥侧面,试求这个圆锥的底面圆的半径.参考答案一.选择题1.解:半径为6,圆心角为60°的弧长为=2π,故选:C.2.解:如图,连接OA,OC,∵∠ABC=50°,∴∠AOC=2∠ABC=100°,∴弧AC的长为:=,故选:C.3.解:由题意得,AC=AE=2,∠CAE=90°,由弧长的计算方法可得,的长为=π,故选:C.4.解:根据题意可得,设扇形的半径为rcm,则l=,即10π=,解得:r=12,∴S===60π(cm2).故选:B.5.解:令扇形的半径和弧长分别为R和l,则∵S==12π,∴R=6cm,∴l==4πcm.∴扇形的弧长为4πcm.故选:C.6.解:设这个圆锥的侧面展开图的圆心角为n°,根据题意得2π×10=,解得n=120,即这个圆锥的侧面展开图的圆心角等于120°.故选:C.7.解:设圆锥的母线长为l,根据题意得×2π×3×l=12π,解得l=4,即圆锥的母线长为4.故选:A.二.填空题8.解:根据弧长的公式l=,得到:π=,解得r=2,故答案为:2.9.解:过O作OE⊥AB于E,当扇形的半径为OE时扇形OCD最大,∵OA=OB=60cm,∠AOB=120°,∴∠A=∠B=30°,∴OE=OA=30cm,∴弧CD的长==20πcm,故答案为:20π.10.解:∵⊙O的半径为2,∴AO=BO=2,∵AB=2,∴AO2+BO2=22+22==AB2,∴△AOB是等腰直角三角形,∴∠AOB=90°,∴的长==π.故答案为:π.11.解:设该扇形的半径为r,∵扇形的圆心角是40°,扇形的弧长是2π,∴2π=,解得:r=9,∴该扇形的面积为2π×9=9π,故选:9π.12.解:∵直角三角形ABC的一条直角边AB=12cm、斜边AC=13cm,∴BC==5cm,∴圆锥的侧面积=•2π•13•5=65π(cm2).,故答案为:65πcm2.13.解:底面圆的半径为3cm,则底面周长=6πcm,侧面面积=×6π×5=15π(cm2);底面积为=9π(cm2);全面积为:15π+9π=24π(cm2).故答案为24π.14.解:设圆锥的侧面展开图的圆心角为n°,根据题意得2π×2=,解得n=120,所以侧面展开图的圆心角为120°.故答案为:120°.三.解答题15.解:扇形AOB的弧长==4π(cm);扇形AOB的扇形面积==12π(cm2).16.解:设扇形的半径为Rcm,根据题意得=4π,解得R=4(负值舍去),设这个圆锥的底面圆的半径为rcm,则×2πr×4=4π,解得r=1,所以这个圆锥的底面圆的半径为1cm.17.解:(1)连接OD.设OD=OB=r.∵AB是直径,AB⊥CD,∴DE=EC=2,在Rt△ODE中,则有r2=(2)2+(r﹣2)2,∴r=4,∴⊙O的半径为4;(2)连接OC.∵tan∠DOE===,∴∠DOE=60°,∵OD=OC,OE⊥CD,∴∠COE=∠DOE=60°,∴∠DOC=120°,∴扇形DOC的面积==.18.解:如图,延长弧EF交半径BC于点C,连接BD,∠EBD+∠DBF=60°,∠DBF+∠FBC=60°,∴∠EBD=∠FBC,∠DBC=60°,∴原来阴影部分的面积等于弧DFC所对应部分的面积,S原来阴影部分的面积=S扇形BDFC﹣S△BDC=•1﹣•1•=﹣.19.解:(1)连接OD,∵⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,∴∠ADB=90°,AD=BD,∴∠OBD=∠ODB=45°,∴OB=OD=6,∴由AB,BD,围成的阴影部分的面积是:=9π+18,故答案为:9π+18;(2)作AF⊥DE于点F,则AF=OD=6,∵AB∥DE,∠OAB=45°,∴∠ADF=∠OAB=45°,∴DF=AF=6,∵∠ACB=90°,AC=6,AB=12,∴∠CBA=30°,∴∠CAB=60°,∵AB∥DE,∴∠E=∠CAB=60°,∵AF=6,∠AFE=90°,2,∴EF=3∴DE=EF+DF=2+6.20.解:(1)∵弦DE垂直平分半径OA,∴CE=DC=DE=2,OC=OE,∴∠OEC=30°,∴OC==2,∴OE=2OC=4,即⊙O的半径为4;(2)∵∠DP A=45°,∴∠D=45°,∴∠EOF=2∠D=90°,设这个圆锥的底面圆的半径为r,∴2πr=,解得r=1,即这个圆锥的底面圆的半径为1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新九年级数学下册第三章圆3-9弧长及扇形的面积同步练习新版北师大版(二十九)[第三章 9 弧长及扇形的面积]一、选择题1.2017·武汉期末如图K -29-1,等边三角形ABC 的边长为4,D ,E ,F 分别为边AB ,BC ,AC 的中点,分别以A ,B ,C 三点为圆心,以AD 长为半径作三条圆弧,则图中三条圆弧的弧长之和是( )图K -29-1A .πB .2πC .4πD .6π 2.2018·福州二模如图K -29-2,AD 是半圆O 的直径,AD =12,B ,C 是半圆O 上两点.若AB ︵=BC ︵=CD ︵,则图中阴影部分的面积是( )链接听课例3归纳总结图K -29-2A .6πB .12πC .18πD .24π 二、填空题3.2017·长春如图K -29-3,在△ABC 中,∠BAC =100°,AB =AC =4,以点B 为圆心,AB 长为半径作圆弧,交BC 于点D ,则AD ︵的长为________.(结果保留π)链接听课例2归纳总结图K -29-34.如图K -29-4,在边长为4的正方形ABCD 中,先以点A 为圆心,AD 长为半径画弧,再以AB 边的中点为圆心,AB 长的一半为半径画弧,则两弧之间的阴影部分的面积是________.(结果保留π)链接听课例4归纳总结图K -29-45.如图K -29-5,△ABC 是正三角形,曲线CDEF 叫正三角形的渐开线,其中CD ︵,DE ︵,EF ︵的圆心依次是A ,B ,C ,如果AB =1,那么曲线CDEF 的长是________.图K -29-56.如图K -29-6,在Rt △ABC 中,∠ACB =90°,AC =2 3,以点C 为圆心,CB 长为半径画弧,与AB 边交于点D ,将BD ︵绕点D 旋转180°后点B 与点A 恰好重合,则图中阴影部分的面积为________.图K -29-6三、解答题7.如图K -29-7,在扇形OAB 中,∠AOB =90°,半径OA =6.将扇形OAB 沿过点B 的直线折叠,点O 恰好落在扇形上的点D 处,折痕交OA 于点C ,求整个阴影部分的周长和面积.图K -29-78.2018·模拟如图K -29-8,AB 是⊙O 的直径,C 是圆上一点,连接CA ,CB ,过点O 作弦BC 的垂线,交BC ︵于点D ,连接AD .(1)求证:∠CAD =∠BAD ;(2)若⊙O 的半径为1,∠B =50°,求AC ︵的长.图K -29-89.2017·一模如图K -29-9,在△ABC 中,∠ACB =130°,∠BAC =20°,BC =4,以点C 为圆心,BC 长为半径的圆交AB 于点D ,交AC 于点E .(1)求BD的长;(2)求阴影部分的面积.图K-29-910.2017·贵阳如图K-29-10,C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,DE⊥AB,垂足为E,DE交AC于点F.(1)求∠AFE的度数;(3)求阴影部分的面积(结果保留π和根号).链接听课例4归纳总结图K-29-1011.如图K-29-11,把Rt△ABC的斜边AB放在直线l上,按顺时针方向将△ABC在l 上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=3,则顶点A运动到点A″的位置时,(1)求点A所经过的路线长;(2)点A所经过的路线与l围成的图形的面积是多少?图K -29-11研究型在学习扇形的面积公式时,同学们推得S 扇形=n πR 2360,并通过比较扇形面积公式与弧长公式l =n πR180,得出扇形面积的另一种计算方法S 扇形=12lR .接着老师让同学们解决两个问题:问题 Ⅰ:求弧长为4π,圆心角为120°的扇形面积. 问题Ⅱ:某小区设计的花坛形状如图K -29-12中的阴影部分,已知弧AB 和弧CD 所在圆的圆心都是点O ,弧AB 的长为l 1,弧CD 的长为l 2,AC =BD =d ,求花坛的面积.(1)请你解答问题Ⅰ.(2)在解完问题 Ⅱ 后的全班交流中,有名同学发现扇形面积公式S扇形=12lR 类似于三角形面积公式;类比梯形面积公式,他猜想花坛的面积S =12(l 1+l 2)d .他的猜想正确吗?如果正确,写出推导过程;如果不正确,请说明理由.图K -29-12详解详析【课时作业】 [课堂达标]1.[解析] B 依题意知:图中三条圆弧的弧长之和=60π×12×4180×3=2π.故选B.2.[解析] A ∵AB ︵=BC ︵=CD ︵, ∴∠AOB =∠BOC =∠COD =60°,∴阴影部分的面积=60π×62360=6π.故选A.3.[答案] 8π9[解析] ∵在△ABC 中,∠BAC =100°,AB =AC , ∴∠B =∠C =12(180°-100°)=40°.∵AB =4,∴AD ︵的长为40π×4180=8π9.4.[答案] 2π5.[答案] 4π[解析] CD ︵的长是120π×1180=2π3,DE ︵的长是120π×2180=4π3,EF ︵的长是120π×3180=2π, 则曲线CDEF 的长是2π3+4π3+2π=4π.故答案为4π. 6.[答案] 2 3-2π3[解析] 依题意,有AD =BD .又∠ACB =90°,所以CB =CD =BD ,即△BCD 为等边三角形,∴∠BCD =∠B =60°,∠A =∠ACD =30°.由AC =2 3,求得BC =2,AB =4,S 弓形BD =S 扇形BCD -S △BCD =60π×22360-3=23π-3,故阴影部分的面积为S △ACD -S 弓形AD =3-(2π3-3)=2 3-2π3.7.解:如图,连接OD .根据折叠的性质,得CD =CO ,BD =BO ,∠DBC =∠OBC , ∴OB =OD =BD ,即△OBD 是等边三角形,∴∠DBO =60°,∴∠CBO =12∠DBO =30°.∵∠AOB =90°, ∴OC =OB ·tan∠CBO =6×33=2 3, ∴S △BDC =S △OBC =12·OB ·OC =12×6×2 3=6 3.∵S 扇形OAB =90360π×62=9π,lAB ︵=90180π×6=3π,∴整个阴影部分的周长为AC +CD +BD +lAB ︵=AC +OC +OB +lAB ︵=OA +OB +lAB ︵=6+6+3π=12+3π,整个阴影部分的面积为S 扇形OAB -S △BDC -S △OBC =9π-6 3-6 3=9π-12 3. 8.解:(1)证明:∵点O 是圆心,OD ⊥BC , ∴CD ︵=BD ︵,∴∠CAD =∠BAD .(2)连接CO ,∵∠B =50°,OB =OC , ∴∠OCB =∠B =50°, ∴∠AOC =100°, ∴AC ︵的长为100π×1180=5π9.9.解:(1)如图,过点C 作CH ⊥AB 于点H .在△ABC 中,∠B =180°-∠A -∠ACB =180°-20°-130°=30°. 在Rt △BCH 中,∵∠CHB =90°,∠B =30°,BC =4, ∴CH =12BC =2,BH =3CH =2 3.∵CH ⊥BD ,∴DH =BH ,∴BD =2BH =4 3. (2)连接CD .∵BC =DC ,∴∠CDB =∠B =30°,∴∠BCD =120°,∴阴影部分的面积=扇形CBD 的面积-△CBD 的面积=120π×42360-12×4 3×2=163π-4 3.10.解:(1)连接OD ,OC ,∵C ,D 是半圆O 上的三等分点,∴AD ︵=CD ︵=BC ︵, ∴∠AOD =∠DOC =∠COB =60°,∴∠CAB =30°. ∵DE ⊥AB ,∴∠AEF =90°, ∴∠AFE =90°-30°=60°. (2)由(1)知∠AOD =60°.又∵OA =OD ,∴△AOD 是等边三角形. ∵AB =4,∴OA =AD =2.∵DE ⊥AO ,∴DE =3,∴S 阴影=S 扇形AOD -S △AOD =60·π×22360-12×2×3=23π- 3.11.解:(1)在Rt △ABC 中,BC =1,AC =3, ∴AB =2,∴cos ∠ABC =12,∴∠ABC =60°,则∠ABA ′=120°,∠A ′C ″A ″=90°,∴lAA ′︵=120π×2180=4π3,lA ′A ″︵=90π×3180=32π,∴点A 所经过的路线长为4π3+32π.(2)S 扇形BAA ′=12lAA ′︵·AB =12×4π3×2=4π3,S 扇形C ″A ′A ″=12lA ′A ″︵·C ″A ′=12×3π2×3=34π,S △A ′B ′C ′=12×1×3=32, ∴点A 所经过的路线与l 围成的图形的面积是43π+34π+32=2512π+32.[素养提升][解析] 根据扇形面积公式、弧长公式之间的关系,结合已知条件推出结果. 解:(1)根据弧长公式l =n πR180,弧长为4π,圆心角为120°,可得R =6,∴S 扇形=12lR =12×4π×6=12π. (2)他的猜想正确.设大扇形的半径为R ,小扇形的半径为r ,圆心角的度数为n °,则由l =n πR180,得R =180l 1n π,r =180l 2n π, ∴花坛的面积为 12l 1R -12l 2r =12·l 1·180l 1n π-12·l 2·180l 2n π =90n π()l 12-l 22 =90n π(l 1+l 2)(l 1-l 2) =12·180n π(l 1+l 2)(n π180R -n π180r ) =12(l 1+l 2)(R -r )=12(l 1+l 2)d . 故他的猜想正确.。
