复数转极坐标形式
复数的两种表示形式

复数的两种表示形式
复数是数学中的一个重要概念,指的是大于1的整数。
它有两种常见的表示形式,分别是直角坐标形式和极坐标形式。
直角坐标形式是指用实部和虚部表示复数,通常写作a+bi的形式。
其中,a是实部,b是虚部,i是虚数单位,满足i^2=-1。
实部和虚部都可以是实数,也可以是负数。
例如,3+4i就是一个复数,其中实部为3,虚部为4。
极坐标形式是指用模长和辐角表示复数,通常写作|z|∠θ的形式。
其中,|z|是复数的模长,表示复数到原点的距离;∠θ是复数的辐角,表示复数与正实轴之间的夹角。
模长是一个非负实数,辐角是一个有无数个值的实数。
例如,5∠π/6就是一个复数,模长为5,辐角为π/6。
复数的两种表示形式可以相互转换。
对于给定的直角坐标形式的复数a+bi,可以通过如下公式计算得到它的模长和辐角:
|z|=√(a^2+b^2)
θ=atan2(b,a)
同样地,对于给定的极坐标形式的复数|z|∠θ,可以通过如下公式计算得到它的实部和虚部:
a=|z|*cos(θ)
b=|z|*sin(θ)
复数的两种表示形式在数学和工程领域中都有广泛应用。
在电路分析、信号处理等领域,直角坐标形式的复数常用于表达信号的振幅和相位,而极坐标形式的复数常用于表示信号的频率和幅度。
总而言之,复数的两种表示形式,即直角坐标形式和极坐标形式,分别以实部和虚部、模长和辐角来表达。
它们可以相互转换,有着广泛的应用领域。
对于求解复数相关问题,我们需要根据具体情况选择合适的形式进行计算和分析。
复数与根的运算知识点总结

复数与根的运算知识点总结复数与根的运算是数学中的重要部分,对于学习代数和数学分析等学科具有重要意义。
本文将对复数与根的运算进行知识点总结,以帮助读者更好地理解和掌握相关知识。
一、复数的基本概念复数是由实数和虚数构成的数,一般形式为a+bi,其中a为实部,bi为虚部,i为虚数单位,满足i²=-1。
复数的加法、减法、乘法和除法规则与实数相似。
二、复数的运算1. 加法和减法:复数a+bi与c+di的加法为:(a+c)+(b+d)i。
复数a+bi与c+di的减法为:(a-c)+(b-d)i。
2. 乘法:复数a+bi与c+di的乘法为:(ac-bd)+(ad+bc)i。
3. 除法:复数a+bi与c+di的除法为:[(ac+bd)/(c²+d²)]+[(bc-ad)/(c²+d²)]i。
三、复数的模和共轭1. 模:复数z=a+bi的模为|z|=√(a²+b²)。
模表示复数与原点之间的距离,也可用于求复数的绝对值。
2. 共轭:复数z=a+bi的共轭复数为z*=a-bi。
共轭复数的实部相同,虚部符号相反。
四、复数的表示方式与极坐标形式1. 代数形式:复数可用代数形式表示,即复数的实部和虚部以加号相连,例如3+4i。
2. 极坐标形式:复数可用极坐标形式表示,即复数的模和辐角以乘号相连,形如r(cosθ+isinθ),其中r和θ分别为复数的模和辐角。
复数的辐角θ满足-π<θ≤π。
五、复数的乘方与开方1. 乘方:将复数z=a+bi进行乘方运算,可以将其转化为极坐标形式z=r(cosθ+isinθ),则z^n=r^n(cos(nθ)+isin(nθ))。
2. 开方:对于复数z=a+bi,可以进行开方运算,即求解方程w^n=z的解w,其中n为正整数。
设z的模为r,辐角为θ,则复数的开方公式为w_k=∛r(cos((θ+2kπ)/n)+isin((θ+2kπ)/n)),k=0,1,2,...,n-1。
复数的8种运算规则专题讲解

复数的8种运算规则专题讲解1. 加法运算规则:复数的加法规则是将实部相加,虚部相加。
例如,对于两个复数a+bi和c+di,它们的和为(a+c)+(b+d)i。
2. 减法运算规则:复数的减法规则是将实部相减,虚部相减。
例如,对于两个复数a+bi和c+di,它们的差为(a-c)+(b-d)i。
3. 乘法运算规则:复数的乘法规则是将实部与虚部相乘,并通过虚部的平方成为负数来计算。
例如,对于两个复数a+bi和c+di,它们的乘积为(ac-bd)+(ad+bc)i。
4. 除法运算规则:复数的除法规则是通过将被除数和除数同时乘以共轭复数的倒数来计算。
共轭复数是指将虚部取负的复数。
例如,对于两个复数a+bi和c+di的除法计算,可以使用公式[(a+bi)/(c+di)]*[(c-di)/(c-di)]来得到结果。
5. 模运算规则:复数的模运算规则是计算复数的绝对值,即复数的平方和的平方根。
例如,对于复数a+bi,它的模为√(a^2+b^2)。
6. 幂运算规则:复数的幂运算规则是通过将复数转换为极坐标形式,并使用欧拉公式计算。
欧拉公式可以表示为e^(iθ)=cosθ+isinθ。
例如,对于复数a+bi的幂运算a^b,可以使用欧拉公式来计算。
7. 开方运算规则:复数的开方运算规则是将复数转换为极坐标形式,并使用特定的公式来计算。
例如,对于复数a+bi的开方运算,可以使用公式√(r*[cos(θ/n)+isin(θ/n)])来计算。
8. 对数运算规则:复数的对数运算规则是将复数转换为极坐标形式,并使用特定的公式来计算。
例如,对于复数a+bi的对数运算,可以使用公式ln(r)+i[θ+(2nπ)]来计算。
这些是复数的8种基本运算规则,了解和掌握这些规则将有助于在复数运算中进行准确的计算操作。
初中数学复习复数的极坐标与指数形式

初中数学复习复数的极坐标与指数形式复中数学复习:复数的极坐标与指数形式复数是数学中一种重要的数系统,它包含了实数和虚数。
在复数的表示方法中,极坐标和指数形式都是常见且实用的。
本文将介绍复数的极坐标表示和指数形式的相关概念及其应用。
一、复数的极坐标表示复数可以用一个实部和一个虚部组成,通常用a+bi的形式表示,其中a为实部,b为虚部,i为虚数单位。
在复平面中,我们可以将复数a+bi看作是在横轴上表示实部a,在纵轴上表示虚部bi。
为了更方便地表示复数在复平面中的位置,我们引入了极坐标系统。
在极坐标系统中,每一个复数都可以用它的模和幅角来表示。
复数z的模即为它到原点的距离,用|r|表示。
复数z的幅角即为它对应的向量与正实轴的夹角,用θ表示。
根据三角函数的定义,我们可以得到复数的极坐标表示:z = |r|(cosθ + i*sinθ)其中,|r|为复数的模,θ为复数的幅角。
复数的极坐标形式提供了一种高效简明的表示方法,特别是在进行复数的乘除运算时,它相较于直角坐标形式更加方便和直观。
二、复数的指数形式复数的指数形式是基于欧拉公式而得出的一种特殊表示方法。
欧拉公式是数学中的重要公式之一,它将虚数单位i的幂次方与三角函数的关系进行了联系。
欧拉公式的表达式为:e^(iθ) = cosθ + i*sinθ其中,e为自然对数的底,i为虚数单位,θ为实数。
通过欧拉公式,复数的指数形式可以表示为:z = |r| * e^(iθ)其中,|r|为复数的模,θ为复数的幅角。
复数的指数形式在求解复数的乘方和开方运算时非常有用,它简化了运算过程,提高了计算的效率。
三、复数的转换与应用复数的极坐标表示和指数形式表示之间可以相互转换。
下面以一个具体的例子来说明:假设有一个复数z = 3 + 4i,我们可以将其转换为极坐标形式。
首先计算其模:|z| = √(3^2 + 4^2) = 5然后计算其幅角,可以利用反三角函数来求解:cosθ = 3 / 5sinθ = 4 / 5θ = arccos(3 / 5)因此,复数z在极坐标表示下为:z = 5 (cos(arccos(3 / 5)) + i*sin(arccos(3 / 5)))同样地,我们也可以将复数z转换为指数形式。
复数极坐标形式加减运算规则

复数极坐标形式加减运算规则1. 复数的入门知识说到复数,很多人可能会皱眉,觉得这东西就像是高深莫测的黑暗料理。
但是,放心吧,今天我们不搞复杂的公式,只聊聊复数的极坐标形式,轻松加减就行。
想象一下,你在逛超市,看到一个新奇的商品,心里想着:“哎呀,这东西我得试试!”复数也是如此,稍微用点心,就能让你领略到它的魅力。
复数其实就是一个由实部和虚部组成的数,比如说 ( z = a + bi )。
在这里,( a ) 是实部,( b ) 是虚部,而 ( i ) 则是那神秘的虚数单位,等于 (sqrt{1)。
不过,当我们把复数用极坐标的形式表达出来时,情况就有趣了:复数可以表示成 ( z = r(cos theta + i sin theta) ),其中 ( r ) 是模长,代表到原点的距离,而 ( theta ) 是角度,代表方向。
听起来是不是有点像在讲导航系统?没错,复数也有它的“方向感”呢!2. 复数的加法2.1 极坐标加法的概念说到加法,大家都知道这是一件简单的事。
但在复数的世界里,加法就像是调味品,得看你怎么用。
在极坐标形式下,如果我们要把两个复数相加,首先得找到它们的“模长”和“角度”。
比如说,有两个复数 ( z_1 = r_1(cos theta_1 + i sin theta_1) ) 和 ( z_2 =r_2(cos theta_2 + i sin theta_2) )。
这俩家伙就像是不同的乐器,要合作出一首动听的曲子。
2.2 加法的公式那么,加法怎么做呢?简单来说,我们需要把它们的模长和角度结合起来。
可以使用“矢量加法”这个概念,把这两个复数看作是在平面上的两个向量,然后用平行四边形法则来找出它们的和。
这就好比你和朋友在公园里一起散步,你向东走,朋友向北走,最后你们的目标就会是两个人的结合点。
其实在数学上,我们通过将两个复数的角度和模长进行转换,最后得到一个新的复数。
3. 复数的减法3.1 极坐标减法的技巧接下来,我们聊聊减法。
电工技术:复数的表示形式及复数的四则运算

一、复数的四种表示形式
虚数单位 j =
1.代数形式: 在复平面上表示 •
1
j2 = -1
A a jb
+j b
复数的模 复数的辐角
A r
a r cos ψ
b r sin ψ
r a2 b2 b ψ arctan a
O
a +1
2. 三角函数形式
A r cos ψ jr sin ψ r (cos ψ jsin ψ)
A 32 42 5
求它们的和、差、积、商。
B 82 62 10
4 A arctan 53o 3
6 B arctan 37 o 8B 10370A Nhomakorabea 5530
A B 51053 37 5090
A 5 53 37 0.516 B 10
A1 A1 1
A2 A2 2
A1 A1 1 2 A2 A2
二、复数的四则运算
例题:已知两个复数
解:
A B 3 8 j 4 6 11 j10
A 3 j4
B 8 j6
A B 3 8 j 4 6 5 j 2
二、复数的四则运算
2.复数的乘法运算 • 都转换为极坐标表达式或指数式,两复数的模相乘作为积的模,幅角相加作为积的模角。
A1 A1 1
A2 A2 2
3.复数的除法运算
A1 A2 A1 A2 1 2
• 都转换成极坐标式或指数式,将两复数的模相除作为商的模,幅角相减作为商的模角。
这两种表示形式适用于复数的加减运算。 简化画法
极坐标形式相乘

极坐标形式相乘引言极坐标是一种描述平面上点位置的坐标系统,它使用距离和角度来确定点的位置。
在数学中,我们经常遇到需要相乘的两个复数。
而将复数表示为极坐标形式,有时可以更方便地进行乘法运算。
本文将介绍极坐标形式相乘的概念和计算方法。
复数的极坐标形式复数由实部和虚部组成,可以表示为 a + bi 的形式,其中 a 和 b 分别为实部和虚部的值。
而极坐标形式表示复数的模和辐角(或幅角)。
对于复数 z,可以表示为模长 |z| 与辐角θ 的乘积形式z = |z| * e^(iθ),其中 e 是自然对数的底。
在极坐标形式中,模长 |z| 表示复数 z 到原点的距离,辐角θ 表示复数 z 与正实轴的夹角。
极坐标形式相乘的计算方法当我们将两个复数转换为极坐标形式后,可以很方便地进行相乘运算。
设两个复数分别为 z1 和 z2,它们的极坐标形式分别为 z1 = |z1| * e^(iθ1) 和 z2 = |z2| *e^(iθ2)。
根据乘法的定义,我们有:z1 * z2 = (|z1| * e^(iθ1)) * (|z2| * e^(iθ2))= |z1| * |z2| * e^(i(θ1 + θ2))上式表示两个复数的乘积,其中 |z1| * |z2| 是它们模长的乘积,e^(i(θ1 + θ2)) 是它们辐角之和的指数形式。
因此,我们只需要将模长相乘并将辐角相加,就可以得到它们相乘的结果。
示例假设我们要计算两个复数 z1 = 2 + i 和z2 = √3 * e^(iπ/6) 的乘积。
首先,我们将 z1 和 z2 转换为极坐标形式:z1 = √(2^2 + 1^2) * e^(i arctan(1/2)) = √5 * e^(i 0.4636)z2 = √3 * e^(i π/6)接下来,我们将模长相乘并将辐角相加:|z1| * |z2| = (√5 * √3) ≈ 2.7386θ1 + θ2 = 0.4636 + π/6 ≈ 0.8980最后,将两个结果代入相乘公式,得到它们的乘积:z1 * z2 ≈ 2.7386 * e^(i 0.8980)总结本文讨论了复数的极坐标形式以及如何通过极坐标形式相乘。
复数包括实部和虚部复数r可以用直角坐标或极坐标两种形...
复数复数包括实部和虚部。
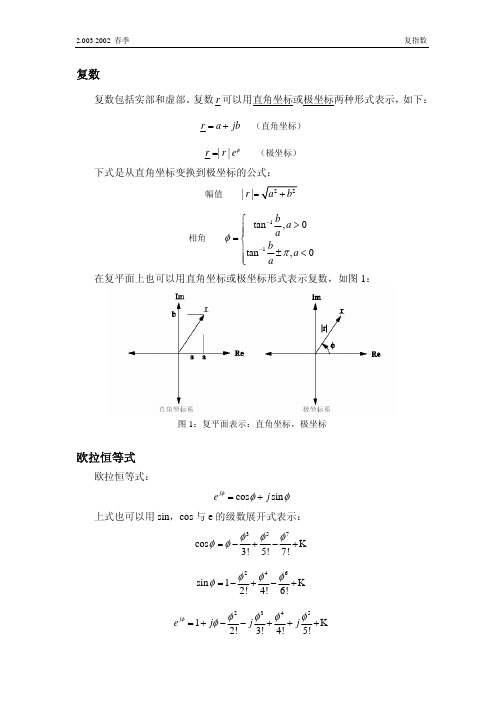
复数r 可以用直角坐标或极坐标两种形式表示,如下:r a jb =+ (直角坐标)||r r e φ= (极坐标)下式是从直角坐标变换到极坐标的公式:幅值||r =相角 11tan ,0tan ,0b a a b a a φπ−−⎧>⎪⎪=⎨⎪±<⎪⎩在复平面上也可以用直角坐标或极坐标形式表示复数,如图1:图1:复平面表示:直角坐标,极坐标欧拉恒等式欧拉恒等式:cos sin j e j φφφ=+上式也可以用sin ,cos 与e 的级数展开式表示:357cos 3!5!7!φφφφφ=−+−+K246sin 12!4!6!φφφφ=−+−+K234512!3!4!5!j e j j j φφφφφφ=+−−+++K代入:2345cos sin 12!3!4!5!j j j j j e φφφφφφφφ+=+−−+++=K复指数假设φ是以ω恒速增长的时间函数:()t t φω= 则()r t 变为:()j t r t e ω=如图2,()r t 在复平面上的轨迹是一个半径为1的圆。
画出()r t 实部与虚部随时间变化的曲线(图3),观察得:实部{}Re ()cos r t t ω=,对应的虚部{}Im ()sin r t t ω=。
·令变量()r t 用如下形式表示:()st r t e = 其中s 是复数:s j σω=+图2:()j t r t e ω=复平面图图3:()r t 实部,虚部随时间变化的曲线 ·()r t 在复平面上的路径是怎样的呢?假设:()()st j t t r t e e e e j t σωσ+ω===⋅可以将上式看作是一个随时间变化的量值(t e σ)乘上一个以ω速率在单位圆上旋转的点。
由j t e ω随时间变化的曲线图(图4),可以看出三个明显的区域:1.0σ>时,这种情况不稳定。
2.0σ=时,j t e ω的值为常量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
复数转极坐标形式
复数是数学中的一个概念,表示为a+bi的形式,其中a和b都是实数,i是虚数单位。
在复数中,实部a表示复数在实轴上的投影,虚部b表示复数在虚轴上的投影。
复数可以通过极坐标形式来表示,这种形式可以更直观地理解复数的特点和性质。
极坐标表示法使用长度和角度来表示复数的位置。
在极坐标表示中,复数可以表示为r(cosθ + isinθ)的形式,其中r是复数的模长(也称为绝对值或幅值),θ是与正实轴的夹角(也称为幅角或辐角)。
通过使用极坐标形式,复数的乘法和除法变得更容易。
将复数转换为极坐标形式的方法是使用勾股定理和三角函数。
具体步骤如下:
1.计算复数的模长:模长r等于复数的绝对值,也可以通过使用勾股定理计算得出。
假设复数表示为a+bi,那么模长r可以通过计算√(a^2 + b^2)来得到。
2.计算复数的幅角:幅角θ可以通过使用反三角函数来计算。
使用反正切函数可以得到复数在复平面上与正实轴的夹角。
3.将复数表示为r(cosθ + isinθ)的极坐标形式:将模长和幅角代入到极坐标形式中,得到复数的极坐标表示。
举个例子来说明。
假设有一个复数z = 3 + 4i,我们将其转换为
极坐标形式。
1.计算模长r:r = √(3^2 + 4^2) = √(9 + 16) = √25 = 5。
2.计算幅角θ:θ = atan(4/3) ≈ 0.93弧度(或约为
53.13°)。
3.将复数表示为极坐标形式:z = 5(cos0.93 + isin0.93)。
极坐标形式的优点之一是可以更方便地进行复数的乘法和除法运算。
对于两个复数w = r1(cosθ1 + isinθ1)和z = r2(cosθ2 +
isinθ2),它们的乘积可以通过将模长相乘,并将幅角相加来得到:
wz = (r1r2)(cos(θ1+θ2) + isin(θ1+θ2))。
同样地,两个复数的
商可以通过将模长相除,并将幅角相减来得到:w/z =
(r1/r2)(cos(θ1-θ2) + isin(θ1-θ2))。
极坐标形式还有其他一些有用的性质。
例如,使用欧拉公式,可
以将复数表示为指数形式:z = re^(iθ),其中e是自然对数的底数。
这种表示形式在复数的乘法和除法运算中尤为有用。
此外,尽管在直
角坐标形式中较为复杂,幂函数在极坐标形式中则变得容易计算,并
产生更简洁的结果。
总结起来,复数的极坐标形式提供了一种更直观和方便的表示法,可以更容易地进行复数的乘法和除法运算。
通过将模长和幅角代入到
极坐标形式中,可以更好地理解复数的特点和性质。
极坐标形式还可
以与欧拉公式结合使用,使复数运算变得更加简洁和方便。
