甘肃省定西市岷县第二中学2019-2020学年高二下学期期中考试(文)(解析版)
甘肃省定西市岷县第二中学2020-2021学年高二数学下学期期中试题 文(含解析)

甘肃省定西市岷县第二中学2020-2021学年高二数学下学期期中试题文(含解析)一、选择题 1.(1)(2)i i +-= A. 3i -- B. 3i -+ C. 3i - D. 3i +【答案】D 【解析】 【分析】由复数的乘法运算展开即可.【详解】解: ()()21i 2i 2i 2i 3i i +-=-+-=+故选D.【点睛】本题主要考查复数的四则运算,属于基础题. 2.以下哪种推理方法是类比推理( )A. ∵数列{}n a 中,11a =,23a =,35a =,∴()*21n a n n N =-∈B. ∵23x =,∴x =C. ∵平面内平行于同一直线的两直线平行,∴空间平行于同一平面的两个平面平行 D ∵()3f x x =+,∴()03f =【答案】C 【解析】 【分析】对于选项A ,是归纳推理;对于选项B ,是演绎推理;对于选项C ,是类比推理;对于选项D ,是演绎推理,即得解.【详解】对于选项A ,是归纳推理,所以该选项不是类比推理; 对于选项B ,是演绎推理,所以该选项不是类比推理; 对于选项C ,是类比推理,所以该选项是类比推理; 对于选项D ,是演绎推理,所以该选项不是类比推理. 故选:C.【点睛】本题主要考查合情推理和演绎推理,意在考查学生对这些知识的理解掌握水平. 3.执行如图所示的程序框图,输出的s值为( )A. 2B.32C.53D.85【答案】C【解析】试题分析:0k=时,03<成立,第一次进入循环:111,21k s+===;13<成立,第二次进入循环:2132,22k s+===;23<成立,第三次进入循环:31523,332k s+===,33<不成立,输出53s=,故选C【名师点睛】解决此类型问题时要注意:第一,要明确是当型循环结构,还是直到型循环结构,并根据各自的特点执行循环体;第二,要明确图中的累计变量,明确每一次执行循环体前和执行循环体后,变量的值发生的变化;第三,要明确循环体终止的条件是什么,会判断什么时候终止循环体,争取写出每一个循环,这样避免出错.4.在复平面内,O为原点,向量OA对应复数为12i--,若点A关于直线y x=-的对称点为B,则向量OB对应复数为()A. 2i-- B. 2i+ C. 12i+ D. 12i-+【答案】B【解析】【分析】由已知得到A的坐标,进一步得到A关于直线y x=-的对称点为B的坐标,则答案可求.【详解】解:向量OA 对应的复数为12i --,(1,2)A ∴--,则(1,2)A --关于y x =-的对称点为(2,1)B ,∴向量OB 对应的复数为2i +.故选:B .【点睛】本题考查复数的代数表示法及其几何意义,训练了点关于直线的对称点的求法,是基础题.5.对命题“正三角形的内切圆切于三边的中点”,可类比猜想出:正四面体的内切球切于四面各正三角形的什么位置( ) A. 各正三角形内的点 B. 各正三角形内的某高线上的点 C. 各正三角形的中心 D. 各正三角形外的某点【答案】C 【解析】 【分析】立体几何中的四面体,可以与平面几何中的三角形类比,四面体的面可以与三角形的边类比,因此可得结论【详解】解:四面体的面可以与三角形的边类比,因此三边的中点也就类比成各三角形的中心, 故选:C .【点睛】本题主要考查类比思想的运用,有平面到空间,应注意相类比的元素,属于基础题. 6.已知复数z 满足()20161i z i -=(其中i 为虚数单位),则z 的虚部为( )A.12B. 12-C.12i D. 12i -【答案】B 【解析】 【分析】 根据题意求出1122z i =+,即可得到z ,得出虚部. 【详解】20164504=⨯,201641i i ∴==.111122z i i ∴==+-,1122z i ∴=-,z ∴的虚部为12-.故选:B.【点睛】此题考查复数的运算和概念辨析,易错点在于没能弄清虚部的概念导致选错. 7.已知2()(1)()2f x f x f x +=+,(1)1f =(*x N ∈),猜想()f x 的表达式为( )A. 2()1f x x =+ B. 4()22x f x =+ C. 1()1f x x =+ D.2()21f x x =+ 【答案】A 【解析】 因为()()()212f x f x f x +=+,所以111(1)()2f x f x =++ ,因此11112(1)(1)()()(1)221x x f x f x f x =+-=+⇒=+,选A. 8.下列三句话按“三段论”模式排列顺序正确的是( )①cos ()y x x R =∈是周期函数;②三角函数是周期函数;③cos ()y x x R =∈是三角函数 A. ②③① B. ②①③ C. ①②③ D. ③②①【答案】A 【解析】 【分析】根据“三段论”的排列模式:“大前提”→“小前提”→“结论”,分析即可得到正确的顺序.【详解】根据“三段论”的排列模式:“大前提”→“小前提”→“结论”,可知: ①cos ()y x x R =∈是周期函数是“结论”; ②三角函数是周期函数是“大前提”; ③cos ()y x x R =∈是三角函数是“小前提”; 故“三段论”模式排列顺序为②③①. 故选:A【点睛】本题考查了演绎推理的模式,需理解演绎推理的概念,属于基础题. 9.某产品的广告费用x 与销售额y 的统计数据如下表:广告费用(万元) 4 2 3 5 销售额(万元)49263954根据上表可得回归方程ˆˆˆybx a =+中的ˆb 为9.4,据此模型预报广告费用为6万元时销售额为 A. 63.6万元 B. 65.5万元C. 67.7万元D. 72.0万元【答案】B 【解析】【详解】试题分析:4235492639543.5,4244x y ++++++====,∵数据的样本中心点在线性回归直线上,回归方程ˆˆˆybx a =+中的ˆb 为9.4, ∴42=9.4×3.5+a ,∴ˆa=9.1, ∴线性回归方程是y=9.4x+9.1,∴广告费用为6万元时销售额为9.4×6+9.1=65.5 考点:线性回归方程10.利用独立性检验来考虑两个分类变量X 和Y 是否有关系时,通过查阅下表来确定断言“X 和Y 有关系”的可信度.如果k>5.024,那么就有把握认为“X 和Y 有关系”的百分比为( ) P(k 2>k) 0.500.400.250.150.100.050.0250.0100.0050.001k 0.4550.7081.3232.0722.7063.845.0246.6357.87910.83A. 25%B. 75%C. 2.5%D. 97.5%【答案】D 【解析】【详解】试题分析:根据所给的观测值,与所给的临界值表中的数据进行比较,而在观测值表中对应于5.024的是0.025,有1﹣0.025的把握认为“X 和Y 有关系”,得到结果. 解:∵k>5.024,而在观测值表中对应于5.024的是0.025,∴有1﹣0.025=97.5%的把握认为“X 和Y 有关系”, 故选D .点评:本题考查独立性检验的应用,是一个基础题,这种题目出现的机会比较小,但是一旦出现,就是我们必得分的题目. 11.下列函数为奇函数的是( ) A. 32()3f x x x =+ B. ()22x xf x -=+ C. ()sin f x x x = D. 3()ln3xf x x+=- 【答案】D 【解析】 【分析】根据奇函数的定义逐项检验即可.【详解】A 选项中()()f x f x -≠-故不是奇函数,B 选项中()()f x f x -=故不是奇函数, C 选项中()()f x f x -=故不是奇函数, D 选项中33()ln ln ()33x xf x f x x x-+-==-=-+-,是奇函数,故选D.【点睛】本题主要考查了奇函数的判定,属于中档题. 12.已知函数()f x =的定义域为M ,()()ln 1g x x =-的定义域为N ,则() RMN =( )A. {}1x x >- B. {}1x x ≥ C. ∅D. {}11x x -<<【解析】 【分析】可以求出集合M ,N ,然后进行交集的运算即可. 【详解】解:因为()f x =的定义域为M ,所以{}11M x x =-<<,()()ln 1g x x =-的定义域为N 所以{}1N x x =<,所以{} 1RN x x =≥,所以(){} 1RM N x x ⋃=>-.故选:A【点睛】考查函数定义域的定义及求法,对数函数的定义域,以及交集的运算,描述法的定义,属于基础题. 二、填空题 13.由数列前四项:32,1,58,38,…,归纳出通项公式n a =______. 【答案】22nn + 【解析】 【分析】把数列前四项可变为:32,44,58,616,…,结合规律,即可求解. 【详解】由题意,该数列前四项可变为:32,44,58,616,…, 由此可归纳得到数列的通项公式为22n n n a +=. 故答案为:22nn + 【点睛】本题主要考查了根据数列的前几项归纳数列的通项公式,其中解答中找出数列前几项的规律是解答的关键,属于基础题14.已知等差数列{}n a 中,若()*,,,m n p q n n p q N +=+∈,则mn p q aa a a +=+,类比上述性质,在等比数列{}n a 中,则有______. 【答案】m n p q a a a a ⋅=⋅【分析】结合等差数列与等比数列具有类比性,且等差数列与和差有关,等比数列与积商有关即可得解.【详解】解:类比上述性质,在等比数列{}n a 中,则有若(m n p q m +=+,n ,p ,*)q N ∈,则m n p q a a a a =,故答案为: m n p q a a a a =.【点睛】本题主要考查等差数列类比到等比数列的类比推理,类比推理一般步骤:①找出等差数列、等比数列之间的相似性或者一致性.②用等差数列的性质去推测物等比数列的性质,得出一个明确的命题(或猜想).15.某程序框图如图所示,则该程序运行后输出的k 的值是________ .【答案】5 【解析】 【分析】由题意结合流程图运行程序,确定输出的数值即可. 【详解】由流程图可知,程序运行如下: 首先初始化数据,2k =,第一次循环,执行:13k k =+=,464k a ==,481b k ==,此时不满足a b >;第二次循环,执行:14k k =+=,4256k a ==,4256b k ==,此时不满足a b >; 第三次循环,执行:15k k =+=,41024k a ==,4625b k ==,此时满足a b >; 输出5k =. 故答案为5.【点睛】识别、运行程序框图和完善程序框图的思路: (1)要明确程序框图的顺序结构、条件结构和循环结构. (2)要识别、运行程序框图,理解框图所解决的实际问题. (3)按照题目的要求完成解答并验证.16.设复数1z i =+,则复数22z z+的共轭复数为______. 【答案】1i - 【解析】 【分析】直接利用复数的四则混合运算化简求解即可. 【详解】复数1z i =+,则复数2222(1)1z i z i+=+++2(1)2(1)(1)i i i i -=++- 1i =+.复数22z z+的共轭复数为:1i - 故答案为1i -.【点睛】本题考查复数的四则混合运算,是基础题,分式类型的复数计算注意分母实数化的方法. 三、解答题17.已知函数[](],0,2()4,2,4.x x f x x x ⎧∈⎪⎨∈⎪⎩,(Ⅰ)画出函数()f x 的大致图象;(Ⅱ)写出函数()f x 的最大值和单调递减区间【答案】(Ⅰ) 见解析(Ⅱ) ()f x 的最大值为2.其单调递减区间为[]24,或(]24,. 【解析】【详解】试题分析:(Ⅰ)利用描点法分别作出[]y ,0,2x x =∈与(]4y ,2,4x x=∈的图象,即可得到函数()f x 的大致图象;(Ⅱ)根据图象可得函数()f x 的最大值和单调递减区间. 试题解析:(Ⅰ)函数()f x 的大致图象如图所示.(Ⅱ)由函数()f x 的图象得出,()f x 的最大值为2.其单调递减区间为[]24,或(]24,. 18.已知复数241miz i+=-,(,m R i ∈是虚数单位). (1)若z 是纯虚数,求m 的值;(2)设z 是z 的共轭复数,复数2z z +在复平面上对应的点在第一象限,求m 的取值范围. 【答案】(1)12;(2)11,22⎛⎫- ⎪⎝⎭. 【解析】 【分析】(1)根据复数的运算,化简复数z ,根据其为纯虚数,即可列方程求得参数;(2)根据(1)中的化简结果,以及共轭复数的定义,求得2z z +,根据对应点所在象限,列出不等式,解不等式即可求得.【详解】(1)()()()()()241241221111mi i mi z m m i i i i +++===-++--+, ∵z 是纯虚数,∴120m -=,且210m +≠, 解得12m =. (2)∵z 是z 的共轭复数,所以()1221z m m i =--+, ∴()()2122121221z z m m i m m i +=--++-++⎡⎤⎣⎦()3621m m i =-++,复数2z z +在复平面上对应的点在第一象限,∴360210m m ->⎧⎨+>⎩,解得1122m -<<,即实数m 的取值范围为11,22⎛⎫- ⎪⎝⎭.【点睛】本题考查复数的运算,涉及共轭复数的求解,由复数对应点所在象限,求参数范围的问题,属综合基础题.19.某学校社团为调查学生课余学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图如图所示,将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.根据已知条件完成下面的22⨯列联表,并据此资料判断能不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关?附:()()()()()22n ad bcKa b c d a c b d-=++++,其中n a b c d=+++.【答案】列联表详见解析,不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关.【解析】【分析】列出二联表,计算2K观测值k,与3.841比较大小得出结论;【详解】解:由频率分布直方图可知,在抽取的100人中,“围棋迷”有1000.2525⨯=人,从而22⨯残联表如下所示:将22⨯残联表中的数据代入公式计算,得2K的观测值()210030101545100 3.0304555752533k ⨯⨯-⨯==≈⨯⨯⨯,因为3.030 3.841<,所以不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关.【点睛】本题考查了列联表与独立性检验问题,属于基础题.20.函数f (x )是R 上的偶函数,且当x >0时,函数的解析式为2()1f x x=- (1)用定义证明f (x )在(0,+∞)上是减函数; (2)求当x <0时,函数的解析式. 【答案】(1)见解析;(2)()21f x x=-- 【解析】 【分析】(1)用函数的单调性定义证明单调性的步骤:取值、作差、化简、下结论可得()f x 在()0,∞+上是减函数;(2)应用偶函数的性质()()f x f x -=,与0x >时()f x 的解析式,可以求出0x <时()f x 的解析式.【详解】(1)证明:∵()21f x x=-,任取()120x x ∈+∞,,,且12x x <; 则()()()2112121222211x x f x f x x x x x -⎛⎫⎛⎫-=---= ⎪ ⎪⎝⎭⎝⎭;∵120x x <<,∴210x x ->,120x x >; ∴()()120f x f x ->,即()()12f x f x >; ∴()f x 在()0,∞+上是减函数; (2)当0x <时,0x ->, ∵0x >时,()21f x x =-,∴()2211f x x x-=-=---, 又∵()f x 是R 上的偶函数,∴()()f x f x -= ∴()21f x x =--;即0x <时,()21f x x=--. 【点睛】本题主要考查了利用定义证明函数的单调性,利用奇偶性求函数在对称区间内的解析式,利用定义证明单调性的步骤:取值、作差、化简、下结论,最大的难点即为化简(因式分解)判断()()12f x f x -的符号,属于基础题.21.已知集合{|3A x x =≤-或2}x ≥,{|15}B x x =<<,{|12}=-≤≤C x m x m (1)求A B ,()R C A B ⋃;(2)若BC C =,求实数m 的取值范围.【答案】(1) {|25}A B x x =≤< (){|35}R C A B x x ⋃=-<< (2) 5(,1)(2,)2-∞-【解析】试题分析:(1)根据集合的交集的概念得到{|25}A B x x ⋂=≤<,{|32}R C A x x =-<<,进而得到结果;(2)∵B C C ⋂= ∴C B ⊆,分情况列出表达式即可. 解析:(1){|25}A B x x ⋂=≤<{|32}R C A x x =-<< (){|35}R C A B x x ⋃=-<<(2)∵B C C ⋂= ∴C B ⊆Ⅰ)当C =∅时,∴12m m ->即1m <-Ⅱ)当C ≠∅时,∴121125m mm m -≤⎧⎪->⎨⎪<⎩∴522m <<综上所述:m 的取值范围是()5,12,2⎛⎫-∞-⋃ ⎪⎝⎭22.已知sin α是sin θ、cos θ的等差中项,sin β是sin θ、cos θ的等比中项.求证:cos 44cos 43βα-=.【答案】证明见解析 【解析】 【分析】由题意,得到sin cos 2sin θθα+=,2sin cos sin θθβ⋅=,进而得到224sin 2sin 1αβ-=,再结合余弦的倍角公式,即可求解.【详解】由sin α是sin θ、cos θ的等差中项,可得sin cos 2sin θθα+=, ①由sin β是sin θ、cos θ的等比中项,可得2sin cos sin θθβ⋅=,②22-⨯①②得224sin 2sin 1αβ-=,③又21cos 2sin2αα-=,21cos 2sin 2ββ-=,代入③得,2cos 2cos 2αβ=,所以224cos 2cos 2αβ=.所以1cos 41cos 4422αβ++⋅=,所以cos 44cos 43βα-=. 【点睛】本题主要考查了三角恒等变换的应用,以及等差、等比中项公式的应用,其中解答中熟练应用余弦的倍角公式进行化简是解答的关键,着重考查推理与运算能力,属于基础题.。
甘肃省定西市岷县二中2020-2021学年高二数学下学期期中试题文(含解析)

甘肃省定西市岷县二中20212021学年高二数学下学期期中试题文(含解析)高二(文)·数学满分:150分时刻:120分钟一、选择题(每小题5分,共60分)1.1.已知全集U=Z,,则( )A. {-2,0}B. {2,0}C. {-1,1,2}D. {-2,0,2}【答案】C【解析】【分析】先解方程求出集合,再利用中的元素属于不属于,即可求出结论.【详解】,又中的元素属于不属于,,故选C.【点睛】研究集合问题,一定要抓住元素,看元素应满足的属性.研究两集合的关系时,关键是将两集合的关系转化为元素间的关系,本题实质求满足属于集合且不属于集合的元素的集合.2.2.若函数在区间内不是单调函数,则实数的取值范畴是( )A. B. C. D.【答案】C【解析】【分析】先求出二次函数的对称轴方程,然后依照二次函数在区间内不是单调函数,则对称轴在区间内,建立不等关系,解之即可.【详解】函数是一个开口向上的二次函数,对称轴为,函数在区间内不是单调函数,,即,实数的取值范畴是,故选C.【点睛】本题要紧考查二次函数的对称性以及二次函数的对称性,意在考查综合利用所学知识解答问题的能力,属于中档题.3.3.下列图形中能够表示以M=为定义域N=为值域的函数的图象是( )A. B. C. D.【答案】C【解析】【分析】依照函数图象,逐一判定选项中函数的定义域、值域即可得结果.【详解】关于选项,函数定义域为,值域不是;关于选项,函数定义域不是,值域为;关于选项,函数定义域是,值域为,符合题意;关于选项,集合中存在与集合中的两个对应,不构成映射关系,故也不构成函数关系,故选C.【点睛】本题要紧考查函数的表示方法,函数的定义域、值域,意在考查对差不多概念把握的熟练程度,属于中档题.4.4.异面直线是指 ( )A. 空间中两条不相交的直线B. 分别位于两个不同平面内的两条直线C. 平面内的一条直线与平面外的一条直线D. 不同在任何一个平面内的两条直线【答案】D【解析】A 不正确,因为空间中两条不相交的直线可能平行;B 不正确,因为分别位于两个不同平面内的两条直线可能平行,也可能相交;C不正确,因为平面内的一条直线与平面外的一条直线可能平行,也可能相交;D 正确,这确实是异面直线的定义,故选 D.5.5.在下列区间中,函数的零点所在的区间为A. B.C. D.【答案】C【解析】因为,因此零点所在的区间为,故选C.6.6.已知函数,若有最小值-2, 则的最大值为( )A. -1B. 0C. 1D. 2【答案】C【解析】【分析】将二次函数配方,确定函数在单调递增,进而可求函数的最值.【详解】函数,,函数在单调递增,当时,有最小值,当时,有最大值,故选C.【点睛】本题要紧考查二次函数的单调性以及利用单调性求最值,意在考查函数与方程思想,数形结合思想的应用,属于中档题.7.7.如图,直三棱柱中,若,,则异面直线与所成的角为( )...........................A. B. C. D.【答案】A【解析】【分析】延长到,依照异面直线所成角的定义可知确实是异面直线与所成的角,利用三角形为等边三角形,可求得此角.【详解】延长到,使得,则为平行四边形,确实是异面直线与所成的角,直三棱柱中,,三角形为等边三角形,,故选A.【点睛】求异面直线所成的角要紧方法有两种:一是向量法,依照几何体的专门性质建立空间直角坐标系后,分别求出两直线的方向向量,再利用空间向量夹角的余弦公式求解;二是传统法,利用平行四边形、三角形中位线等方法找出两直线成的角,再利用平面几何性质求解.8.8.设函数,则 ( )A. B. C. D.【答案】D【解析】【分析】先求出,从而,由此能求出结果.【详解】函数,且.,,故选D.【点睛】本题要紧考查分段函数的解析式,属于中档题.关于分段函数解析式的考查是命题的动向之一,这类问题的特点是综合性强,对抽象思维能力要求高,因此解决这类题一定要层次清晰,思路清晰.9.9.若的弦AB的中点,则直线AB的方程是( )A. B.C. D.【答案】A【解析】试题分析:圆的圆心C(1,0),点P(2,-1)为弦AB的中点,PC的斜率为,∴直线AB的斜率为1,点斜式写出直线AB的方程y+1=1×(x-2),即x-y-3=0考点:直线与圆的位置关系10.10.设是直线,是两个不同的平面( ).A. 若 ,则B. 若,则C. 若,则D. 若,则【答案】B【解析】【分析】依照线面平行的性质判定不正确,正确;由面面垂直及线面垂直的性质可判定不正确;由面面垂直及线面平行的性质判定不正确.【详解】若,则或相交,故不正确;依照线面平行的性质可得:若,通过的直线与的交线为,则,,依照平面与平面垂直的判定定理,可得,故正确;若,则或,故不正确;作出正方体,设平面为为,则,观看正方体,得到:且,且,且与相交,面及直线满足:,则一定有或或与相交,故不正确,故选B.【点睛】本题要紧考查线面平行的判定与性质、面面垂直的性质及线面垂直的判定,属于难题.空间直线、平面平行或垂直等位置关系命题的真假判定,常采纳画图(专门是画长方体)、现实实物判定法(如墙角、桌面等)、排除选择法等;另外,若原命题不太容易判定真假,能够考虑它的逆否命题,判定它的逆否命题真假,原命题与逆否命题等价.11.11.直线与平行,则的值为( )A. B. 或 C. D.【答案】A【解析】【分析】由直线与平行,得,解出值后,验证两条直线是否重合,可得结论.【详解】若直线与平行,则,解得或,又时,直线与表示同一条直线,故,故选A.【点睛】本题要紧考查直线的方程,两条直线平行与斜率的关系,属于简单题. 对直线位置关系的考查是热点命题方向之一,这类问题以简单题为主,要紧考查两直线垂直与两直线平行两种专门关系:在斜率存在的前提下,(1);(2),这类问题尽管简单却容易出错,专门是容易遗忘斜率不存在的情形,这一点一定不能掉以轻心.12.12.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为A. B. C. D.【答案】B【解析】由题意,该几何体是由高为6的圆柱截取一半后的图形加上高为4的圆柱,故其体积为,故选B.点睛:(1)解答此类题目的关键是由多面体的三视图想象出空间几何体的形状并画出其直观图.(2)三视图中“正侧一样高、正俯一样长、俯侧一样宽”,因此,能够依照三视图的形状及相关数据推断出原几何图形中的点、线、面之间的位置关系及相关数据.二、填空题(每空5分,共计20分)13.13.函数的定义域是____.【答案】【解析】【分析】欲求函数的定义域,只需找到使函数解析式有意义的的取值范畴,函数中有对数,真数大于零,函数中有二次根式,被开方数大于等于零,解不等式即可.【详解】要使函数有意义,需满足,解得,函数的定义域为,故答案为.【点睛】求函数定义域的注意点:①不要对解析式进行化简变形,以免定义域变化;②当一个函数由有限个差不多初等函数的和、差、积、商的形式构成时,定义域一样是各个差不多初等函数定义域的交集;③定义域是一个集合,要用集合或区间表示,若用区间表示,不能用“或”连接,而应该用并集符号“∪”连接.14.14.设偶函数的定义域为,当时, 是增函数,则,,按从小到大的顺序排列是___________.【答案】【解析】【分析】由偶函数的性质知,若时,是增函数,则时,是减函数,因此函数的自变量的绝对值越小函数值越小,从而可得结果.【详解】由偶函数与单调性的关系知,若时,是增函数,则时,是减函数,故其函数的自变量的绝对值越小,则其函数值越小,,,故答案为.【点睛】本题要紧考查函数奇偶性的应用以及函数单调性的应用,意在考查综合利用所学知识解决问题的能力,属于中档题.15.15.在空间直角坐标系中,设点是点关于坐标平面的对称点,则线段的长度等于 .【答案】10【解析】试题分析:点关于坐标平面的对称点,故线段.考点:空间中的距离.16.16.如图,三棱锥,平面平面,若,则△的形状为__________.【答案】直角三角形【解析】【分析】依照面面垂直的性质即可得到面,依照线面垂直的性质可得到,从而可得结果.【详解】平面平面,平面平面平面,面,,为直角三角形,故答案为直角三角形.【点睛】解答空间几何体中垂直关系时,一样要依照已知条件把空间中的线线、线面、面面之间垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;证明直线和平面垂直的常用方法有:(1)利用判定定理;(2)利用判定定理的推论;(3)利用面面平行的性质;(4)利用面面垂直的性质,当两个平面垂直时,在一个平面内垂直于交线的直线垂直于另一个平面.三、解答题(共计70分)17.17.解下列不等式:.【答案】见解析【解析】【分析】当时,原不等式等价于,当时,原不等式等价于,由此能求出结果.【详解】当时,原不等式等价于解得.当时,原不等式等价于解得.综上所述,当时,原不等式的解集为;当时,原不等式的解集为.【点睛】本题要紧考查对数函数定义域以及对数函数单调性的应用,以及分类讨论思想的应用,属于简单题.解简单的对数不等式要注意两点:(1)依照底数讨论单调性;(2)一定要注意函数的定义域.18.18.已知函数.(1)当,求函数的最大值和最小值;(2)函数在区间上是单调函数,求的取值范畴.【答案】(1)是的最小值,是的最大值;(2).【解析】试题分析:(1)是二次函数,它在闭区间上的最值问题,第一看对称轴,本题函数对称轴为,,因此函数在顶点处取得最小值,在离对称轴较远的端点处取得最大值;(2)二次函数被对称轴分为两个单调区间,因此只要对称轴不在某区间内,则函数在此区间上一定是单调的.试题解析:(1),,∴是的最小值,是的最大值.(2)的对称轴为;∵在区间上是单调函数,∴或,∴或,∴实数的范畴为.考点:二次函数的最值与单调性.【名师点睛】二次函数的单调性:时,在上单调递减,在上单调递增;时,在上单调递增,在上单调递减.从而时,在区间上离对称轴距离越远的端点处的函数值越大;时,在区间上离对称轴距离越远的端点处的函数值越小.求二次函数在闭区间的最值要按对称轴与区间的关系分类讨论.19.19.如图所示,在正方体中, 分别为棱和的中点,求异面直线与所成角的正弦值.【答案】【解析】【分析】设棱长为,取中点,连接,与相交于,可判定,故与所成角即为异面直线与所成的角,利用余弦定理以及平方关系即可得结果.【详解】设棱长为,取中点,连接,可判定与相交于,,故与所成角即为所求,在中, ,.∴,∴【点睛】本题要紧考查异面直线所成的角,属于中档题题.求异面直线所成的角的角先要利用三角形中位线定理以及平行四边形找到,异面直线所成的角,然后利用直角三角形的性质及余弦定理求解,假如利用余弦定理求余弦,因为异面直线所成的角是直角或锐角,因此最后结果一定要取绝对值.20.20.如图,四棱锥中,为的中点.求证:平面.【答案】证明见解析【解析】试题分析:方法一,取PA的中点H,连接EH、DH。
高考语文满分作文范例及解析--中国精神永传承

阅读下面的材料,根据要求写作。
什么是中国精神?每个人的看法不尽相同。
下面一组画面或许能给我们一些启示:86岁的他,穿着跨栏背心编程的镜头上了央视。
这个不起眼的小老头,用一辈子的隐姓埋名和不服输的劲头,给中国的尖端武器装上了“眼睛”,让我们的武器做到了指哪儿打哪儿。
(我国激光陀螺研究领域泰斗、工程院院士、已故国防科技大学教授高伯龙)追梦“北斗”卫星导航十九年,攻克卫星导航关键技术20多项。
功成名就的她,放弃部队相对轻松的安排,奔走于大江南北,到“北斗”最大的用户——交通运输行业做推广应用。
(“北斗”重要奠基人、交通运输信息化专家王淑芳)装上智能义肢的她,和钢琴大师郎朗“四手”联弹的《乘着歌声的翅膀》,让人沉醉,让人动容。
而这背后,是她承受着常人难以想象的痛苦,与义肢无数次的磨合“交流”。
(自幼喜爱音乐,因意外失去右手,却笑对未来的圆梦女孩林安露)你心中的中国精神是什么?当代社会最需要怎样的中国精神?请结合材料含意,在阐释其具体内涵的基础上,联系自己的认知、理解和感悟,完成一篇作文。
要求:选好角度,确定立意,明确文体,不要套作,不得抄袭,不得泄露个人信息;不少于800字。
【试题来源】甘肃省定西市岷县第二中学2019-2020学年高二下学期期中考试语文试题【答案解析】中国精神永传承中华文明,上下五千年,亦延绵不息,源远流长。
在这片华夏大地,炎黄子孙世代传承着一种伟大坚强精神,这种精神使我们的民族跨越了五千年不曾中断,使我们的民族历经磨难而更加顽强。
它就是中国精神,浩浩的中华魂。
滚滚黄河,浩浩荡荡,向东奔腾。
五千年前它在奔腾,五千年后它仍不停歇。
它,孕育着五千年的中华文明,它,凝聚了五千年的民族精神。
曾记否,从三皇五帝到夏商周,从千古一帝到开皇、贞观、开元,再到腐败懦弱的清王朝,再到新中国成立。
中华民族从繁荣昌盛到落后挨打,从辉煌的古代文明到水深火热的近代磨难,再到中华民族的伟大复兴。
曾记否,屈原吟着《离骚》饮恨汨罗江。
【数学】甘肃省定西市岷县第二中学2019-2020学年高二下学期期中考试(文)(解析版)
甘肃省定西市岷县第二中学2019-2020学年高二下学期期中考试(文)一、选择题(每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的. 请将答案写在答题卡上) 1.(1+i)(2-i)=()A .-3-iB .-3+iC .3-iD .3+i 2.以下哪种推理方法是类比推理()A .∵数列{a n }中,a 1=1,a 2=3,a 3=5, ∴a n =2n -1(n ∈N *)B .∵x 2=3,∴x =±3C .∵平面内平行于同一直线的两直线平行, ∴空间平行于同一平面的两个平面平行D .∵f (x )=x +3,∴f (0)=33.执行如图1所示的程序框图,输出的s 值为() A .2 B.32 C.53 D.854.在复平面内,O 为原点,向量OA →对应复数为-1-2i ,若点A 关于直线y =-x 的对称点为B ,则向量OB →对应复数为()A .-2-iB .2+iC .1+2iD .-1+2i5.对命题“正三角形的内切圆切于三边的中点”,可类比猜想出:正四面体的内切球切于四面各正三角形的什么位置()A .各正三角形内的点B .各正三角形内的某高线上的点C .各正三角形的中心D .各正三角形外的某点 6.已知复数z 满足()20161i i z -= (其中i 为虚数单位),则z 的虚部为( )A.12B .12-C.1i 2D .1i 2-7.已知f (x +1)=2f (x )f (x )+2,f (1)=1(x ∈N *),猜想f (x )的表达式为()A .f (x )=42x+2 B .f (x )=2x +1 C .f (x )=1x +1 D .f (x )=22x +18.下列三句话按“三段论”模式排列顺序正确的是() ①y =cos x (x ∈R)是三角函数;②三角函数是周期函数; ③y =cos x (x ∈R)是周期函数.A .①②③B .③②①C .②③①D .②①③ 9.某产品的广告费用x 与销售额y 的统计数据如下表:根据上表可得回归方程y =b x +a 中的b 为9.4,据此模型预报广告费用为6万元时销售额为()A .63.6万元B .65.5万元C .67.7万元D .72.0万元10.利用独立性检验来考虑两个分类变量X 和Y 是否有关系时,通过查阅下表来确定断言“X 和Y 有关系”的可信度.如果k >5.024,那么就有把握认为“X 和Y 有关系”的百分比为()A.25%B .75%C .2.5%D .97.5%11.下列函数为奇函数的是( )A.()323f x x x =+B.()22x xf x -=+C.()sin f x x x =D.()3ln3xf x x+=-二、填空题(每题5分,共20分, 请将答案写在答题卡上)13.由数列的前四项:32,1,58,38,…,归纳出通项公式a n =________.14.已知等差数列{a n }中,若m +n =p +q (m ,n ,p ,q ∈N *),则a m +a n =a p +a q ,类比上述性质,在等比数列{a n }中,则有____________15.若某程序框图如图2所示,则该程序运行后输出的k 的值是________.12.16.设复数1i z =+,则复数22z z+的共轭复数为______. 三、解答题(17题10分 ,其余每题12分, 共70分,请将答案写在答题卡上) 17.(本小题满分10分)已知函数f (x )=⎩⎪⎨⎪⎧x ,x ∈[0,2],4x ,x ∈(2,4].(1)在图中画出函数f (x )的大致图象;(2)写出函数f (x )的最大值和单调递减区间.18.(本小题满分12分)已知复数 (m R ∈,i 是虚数单位).=1-i(1)若z 是纯虚数,求m 的值; (2)设z 是z 的共轭复数,复数2z z +在复平面上对应的点在第一象限,求m 的取值范围.19.(本小题满分12分)某学校社团为调查学生课余学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图如图所示,将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.根据已知条件完成下面的2×2列联表,并据此资料判断能不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关?附:()()()()()22n ad bc K a b c d a c b d =++++-,其中n a b c d =+++.20.(本小题满分12分)函数f (x )是R 上的偶函数,且当x >0时,函数的解析式为f (x )=2x -1.(1)用定义证明f(x)在(0,+∞)上是减函数;(2)求当x<0时,函数的解析式.21.(本小题满分12分)已知集合A={x|x≤-3或x≥2},B={x|1<x<5},C={x|m-1≤x≤2m}.(1)求A∩B,(∁R A)∪B;(2)若B∩C=C,求实数m的取值范围.22.(本小题满分12分)已知sinα是sinθ、cosθ的等差中项,sinβ是sinθ、cosθ的等比中项.求证:cos4β-4cos4α=3.参考答案二、选择题(每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的.请将答案写在答题卡上)1.(1+i)(2-i)=()A .-3-iB .-3+iC .3-iD .3+i 解析:(1+i)(2-i)=2-i +2i -i 2=3+i. 答案:D2.以下哪种推理方法是类比推理()A .∵数列{a n }中,a 1=1,a 2=3,a 3=5, ∴a n =2n -1(n ∈N *)B .∵x 2=3,∴x =±3C .∵平面内平行于同一直线的两直线平行, ∴空间平行于同一平面的两个平面平行D .∵f (x )=x +3,∴f (0)=3答案:C3.执行如图1所示的程序框图,输出的s 值为() A .2 B.32 C.53 D.85解析:运行该程序,k =0,s =1,k <3; k =0+1=1,s =1+11=2,k <3; k =1+1=2,s =2+12=32,k <3;k =1+2=3,s =32+132=53,k =3.输出的s 值为53.故选C.答案:C4.在复平面内,O 为原点,向量OA →对应复数为-1-2i ,若点A 关于直线y =-x 的对称点为B ,则向量OB →对应复数为()A .-2-iB .2+iC .1+2iD .-1+2i答案:B5.对命题“正三角形的内切圆切于三边的中点”,可类比猜想出:正四面体的内切球切于四面各正三角形的什么位置()A .各正三角形内的点B .各正三角形内的某高线上的点C .各正三角形的中心D .各正三角形外的某点 答案:C6.已知复数z 满足()20161i iz -= (其中i 为虚数单位),则z 的虚部为( )图1A.12B .12-C.1i 2 D .1i 2-6答案及解析:答案:B 解析:∵()()504201641i i i 1z -===∴()()211i 1i 11i 1i 1i 1i 1i 22z ++====+--+- ∴11i 22z =-∴z 的虚部为12- 7.已知f (x +1)=2f (x )f (x )+2,f (1)=1(x ∈N *),猜想f (x )的表达式为()A .f (x )=42x+2 B .f (x )=2x +1 C .f (x )=1x +1 D .f (x )=22x +1解析:由f (1)=1, 排除C 、D ,再由f (2)=2f (1)f (1)+2=23,f (3)=2f (2)f (2)+2=12, 排除A.答案:B8.下列三句话按“三段论”模式排列顺序正确的是() ①y =cos x (x ∈R)是三角函数; ②三角函数是周期函数; ③y =cos x (x ∈R)是周期函数.A .①②③B .③②①C .②③①D .②①③ 解析:显然②是大前提,①是小前提,③是结论.答案:D 9.某产品的广告费用x 与销售额y 的统计数据如下表:根据上表可得回归方程y =b x +a 中的b 为9.4,据此模型预报广告费用为6万元时销售额为()A .63.6万元B .65.5万元C .67.7万元D .72.0万元 解析:由统计数据计算得:x =3.5,y =42.将x =3.5,y =42代入方程得:42=9.4×3.5+a ^∴a ^=9.1. ∴当x =6时,y ^=9.4×6+9.1=65.5(万元),故选B.答案:B 10.利用独立性检验来考虑两个分类变量X 和Y 是否有关系时,通过查阅下表来确定断言“X 和Y 有关系”的可信度.如果k >5.024,那么就有把握认为“X 和Y 有关系”的百分比为()A.25% B .75% C .2.5% D .97.5%答案:D11.下列函数为奇函数的是( )A.()323f x x x =+B.()22x xf x -=+C.()sin f x x x =D.()3ln3xf x x+=- 11答案及解析: 答案:D解析:若函数为奇函数,则在定义域内()00f =且()()f x f x -=-.A 中,()()323f x x x f x -=-+≠-,故不正确;B 中,()000222f =+=,故不正确;C 中,()()()sin ?sin f x x x x f x -=--==,故不正确; D 中,x 应满足303xx+>-,解得33x -<<, 则函数()f x 的定义域为(33)-,,()0ln10f ==,()()33ln ln 33x xf x f x x x-+-==-=-+-,故正确.故选D.三、填空题(每题5分,共20分, 请将答案写在答题卡上)13.由数列的前四项:32,1,58,38,…,归纳出通项公式a n =________.解析:该数列前四项可变为:32,44,58,616,…, 由此猜想a n =n +22n .12. 12.答案:n +22n14.已知等差数列{a n }中,若m +n =p +q (m ,n ,p ,q ∈N *),则a m +a n =a p +a q ,类比上述性质,在等比数列{a n }中,则有____________答案:a m ·a n =a p ·a q 15.若某程序框图如图2所示,则该程序运行后输出的k 的值是________.解析:按程序框图的运算次序一步步写出来, 便知k =5.答案:5 16.设复数1i z =+,则复数22z z+的共轭复数为______. z 三、解答题(17题10分 ,其余每题12分, 共70分,请将答案写在答题卡上) 17.(本小题满分10分)已知函数f (x )=⎩⎪⎨⎪⎧x ,x ∈[0,2],4x ,x ∈(2,4].(1)在图中画出函数f (x )的大致图象;(2)写出函数f (x )的最大值和单调递减区间. 解:(1)函数f (x )的大致图象如图所示.=1-i(2)由函数f (x )的图象得出,f (x )的最大值为2,函数的单调递减区间为[2,4]. (m R ∈,i 是虚数单位).18.(本小题满分12分)已知复数 (1)若z 是纯虚数,求m 的值; (2)设z 是z 的共轭复数,复数2z z +在复平面上对应的点在第一象限,求m 的取值范围.18答案及解析: 答案:(1)()()()()()241241221111mi i mi z m m i i i i +++===-++--+ 因为z 是纯虚数,所以120m -=且210m ≠+, 解得12m =. (2)因为z 是z 的共轭复数,所以()1221z m m i =--+.所以()()()212212[1221]3621z z m m i m m i m m i +=--++-++=-++. 因为复数2z z +在复平面上对应的点在第一象限, 所以360,210,m m ->⎧⎨+>⎩解得1122m -<<,即实数m 的取值范围为()11,22-.19.(本小题满分12分)某学校社团为调查学生课余学习围棋的情况,随机抽取了100名学生进行调查.根据调查结果绘制的学生日均学习围棋时间的频率分布直方图如图所示,将日均学习围棋时间不低于40分钟的学生称为“围棋迷”.根据已知条件完成下面的2×2列联表,并据此资料判断能不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关?附:()()()()()22n ad bc K a b c d a c b d =++++-,其中n a b c d =+++.19答案及解析: 答案:不能解析:由频率分布直方图可知,在抽取的100人中,“围棋迷”有1000.2525⨯=人, 从而22⨯列联表如下所示:将22⨯列联表中的数据代入公式计算,得2K 的观测值210030101545100 3.030455575()2533k ⨯⨯-⨯==≈⨯⨯⨯,因为3.030 3.841<,所以不能在犯错误的概率不超过0.05的前提下认为“围棋迷”与性别有关.20.(本小题满分12分)函数f (x )是R 上的偶函数,且当x >0时,函数的解析式为f (x )=2x -1. (1)用定义证明f (x )在(0,+∞)上是减函数; (2)求当x <0时,函数的解析式. 解析:(1)设0<x 1<x 2,则f (x 1)-f (x 2)=⎝⎛⎭⎫2x 1-1-⎝⎛⎭⎫2x 2-1=2x 2-x 1x 1x 2, ∵0<x 1<x 2,∴x 1x 2>0,x 2-x 1>0, ∴f (x 1)-f (x 2)>0, 即f (x 1)>f (x 2),∴f (x )在(0,+∞)上是减函数. (2)设x <0,则-x >0, ∴f (-x )=-2x -1, 又f (x )为偶函数, ∴f (-x )=f (x )=-2x -1, 即f (x )=-2x -1(x <0). 21.(本小题满分12分)已知集合A ={x |x ≤-3或x ≥2},B ={x |1<x <5},C ={x |m -1≤x ≤2m }.(1)求A ∩B ,(∁R A )∪B ;(2)若B ∩C =C ,求实数m 的取值范围. 解:(1)∵A ={x |x ≤-3或x ≥2}, B ={x |1<x <5}, ∴A ∩B ={x |2≤x <5}, ∁R A ={x |-3<x <2}, ∴(∁R A )∪B ={x |-3<x <5}. (2)∵B ∩C =C ,∴C ⊆B .①当C =∅时,∴m -1>2m ,∴m <-1; ②当C ≠∅时,∴⎩⎪⎨⎪⎧m -1≤2m ,m -1>1,2m <5,解得2<m <52.( )综上m 的取值范围m <-1或2<m <52. 22.(本小题满分12分)已知sin α是sin θ、cos θ的等差中项,sin β是sin θ、cos θ的等比中项. 求证:cos4β-4cos4α=3.证明:由已知sin θ+cos θ=2sin α,① sin θ·cos θ=sin 2β,②①2-2×②得4sin 2α-2sin 2β=1.③又sin 2α=1-cos2α2,sin 2β=1-cos2β2,代入③得, 2cos2α=cos2β,∴4cos 22α=cos 22β. ∴4·1+cos4α2=1+cos4β2. ∴cos4β-4cos4α=3.。
甘肃省定西市岷县第二中学2019_2020学年高二地理下学期期中试题(含解析)

甘肃省定西市岷县第二中学2019-2020学年高二地理下学期期中试题(含解析)第Ⅰ卷(选择题共60分)一、单项选择题(本题共20个小题,每小题3分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)我国人口众多,生活垃圾产生量巨大,迫切需要对垃圾进行无害化、资源化处理。
近些年,某企业开发了厨余垃圾自动处理系统,并在全国很多城市推广。
下图示意该厨余垃圾自动处理系统的主要工艺流程。
据此完成下面小题。
1. 厨余垃圾自动处理系统所取得的社会效益是A. 实现废弃物零排放B. 促进经济发展C. 提高资源利用率D. 增加就业机会2. 厨余垃圾自动处理系统在全国很多城市得到推广,将有利于实现我国的A. 人口战略B. 环境战略C. 能源战略D. 经济战略【答案】1. D 2. B【解析】【1题详解】厨余垃圾自动处理不可能实现废弃物零排放,A错误;促进经济发展属于经济效益,B错误;提高资源利用率属于生态效益,C错误;厨余垃圾自动处理系统所取得的社会效益是增加就业机会,D正确。
故选D。
【2题详解】厨余垃圾自动处理系统在全国很多城市得到推广,可以减少垃圾的排放,改善生态环境,有利于实现我国的环境战略,B正确;厨余垃圾自动处理系统对实现人口战略、能源战略、经济战略帮助不大,ACD错误。
故选B。
2019年7月1日在上海实行的垃极分类处罚方法《条例》规定,产生生活垃圾的单位和个人应当将生活垃圾分别投放至相应的收集容器,不得随意丢弃垃圾。
此次(条例)将垃级明确为“四分法”,包括可回收物,有害垃圾,湿垃圾和干垃圾4种,其中“湿垃圾”指易腐的生物质生活废弃物。
该(条例)还规定:如果混合投放垃圾,最高可罚200元。
这标志着上海垃圾分类将步入强制时代。
据此完成下面小题。
3. 适合“湿垃圾”的处理方式是()A. 焚烧B. 填埋C. 露天推放D. 堆肥4 上海垃圾分类将步入强制时代,说明了()A. 社会公众素质低B. 垃圾处理资金较短缺C. 环境管理在加强D. 人们环境意识在提高【答案】3. D 4. C【解析】【分析】本题组主要考查固体废弃物的处理措施等相关知识【3题详解】根据材料“湿垃圾是指易腐的生物质生活废弃物”,主要是指厨余垃圾,如剩菜剩饭、食材废料、过期食品等,有机质含量较高,适合堆肥,D正确;该类垃圾焚烧发电热值低,A错;湿垃圾含水量较大,填埋产生的滤液污染土壤和地下水,B错;露天堆放易腐败腐烂产生恶臭,滋生蚊蝇,并易传播疾病,C错误,故选D。
2019高二第二学期期中考试语文试卷及答案精品教育.doc

2019高二第二学期期中考试语文试卷及答案【2019高二第二学期期中考试语文试卷及答案】一、语言文字运用(15分)1.下列词语中,加点字的读音全都正确的一项是(3分)A.胚胎(pēi) 框架(kuàng ) 脖颈(gěng) 着手成春(zhuó)B.龟裂(jūn) 慰藉(jiè) 挣揣(chuài) 解甲归田(xiè)C.轮廓(kuò) 销行(háng) 骄横(hèng) 数见不鲜(shuò)D.氛围(fèn) 攒射(cuán) 缂丝(kè) 日薄西山(bó)2.下列词语字形全都正确的一项是(3分)A.绚烂爆发力无所是从凤毛麟角B.青睐电线杆劳燕纷飞平心而论C.文身协奏曲桀骜不驯抑扬顿错D.膨胀蒸汽机其貌不扬殒身不恤3.下列各句中,没有语病的一句是(3分)A.《深化普通高中课程改革方案》要求推进普通高中多样化和特色化发展,为每个学生提供适合的教育,以满足不同潜质学生的发展。
B.在“宁做凤尾不做鸡头”的职业取向下,基层和中小企业一方面急需人才,却难以寻觅;另一方面大量毕业生又聚集大城市,僧多粥少。
C.《美的历程》是中国美学的经典之作,作者李泽厚先生将他多年的研究付诸于笔端,把中国人古往今来对美的感觉玲珑剔透地展现在大家眼前,感性而亲切。
D.人生苦乐并非纯粹由物质条件决定,百万富翁很可能不如身无分文的流浪汉生活得幸福,原因就在于感受生活的乐趣还需要艺术的眼光与悠闲的心境。
4. 请补写出空缺的语句,与前两句构成排比,使语段意思连贯,风格统一。
(2分)作一次心灵旅行,就以那一本本零落的古卷残页为车票,感受着穿越时空的欣喜。
我与李白共攀蜀道,与辛弃疾拍遍栏杆,,。
无论是漠北黄沙,还是江南水乡,我都一一留下足迹。
5.阅读下面的材料,根据要求回答问题。
(4分)英国哲学家培根认为,做学问有三种方式:一是像蜘蛛一样,整天忙于从自己肚子里吐丝织网;二是像蚂蚁一样,整天忙于把食物从外面搬回自己的窝里;三是像蜜蜂一样,忙于采花粉,酿造成蜂蜜。
甘肃省岷县二中2020学年高二数学下学期期中试题 文
岷县二中2020学年度第二学期期中考试试卷高二(文)·数学满分:150分 时间:120分钟一、选择题(每小题5分,共60分) 1、已知全集,,,则( )A.{-2,0}B.{2,0}C.{-1,1,2}D.{-2,0,2} 2、若函数在区间内不是单调函数,则实数的取值范围是( ) A.B.C.D.3、下列图形中可以表示以为定义域,为值域的函数的图象是( )A. B. C. D.4、异面直线是指( ) A.空间中两条不相交的直线B.分别位于两个不同平面内的两条直线C.平面内的一条直线与平面外的一条直线D.不同在任何一个平面内的两条直线5、在下列区间中,函数()43xf x e x =+-的零点所在的区间为( ) A. 1,04⎛⎫-⎪⎝⎭ B. 10,4⎛⎫ ⎪⎝⎭ C. 11,42⎛⎫ ⎪⎝⎭ D. 13,24⎛⎫⎪⎝⎭6、已知函数()24f x x x a =-++,[]0,1x ∈若()f x 有最小值-2, 则()f x 的最大值为( )A.-1B.0C.1D.27、如图,直三棱柱111ABC A B C -中,若90BAC ∠=o ,1AB AC AA ==,则异面直线1BA 与1AC 所成的角为()A. 60oB. 90oC. 120oD. 150o8、设函数()()2112()1x x x xf x ⎧+≤>⎪=⎨⎪⎩,则()3f f =⎡⎤⎣⎦ ( )A.15 B. 3 C. 49 D. 1399、若()2,1P -为圆()22125x y -+=的弦AB 的中点,则直线AB 的方程是( ) A. 30x y --= B. 230x y +-= C. 10x y +-= D. 250x y --= 10、设是直线,,是两个不同的平面( ). A.若,则 B.若,则 C.若,则D.若,则11、.直线210x ay +-=与()110a x ay --+=平行,则a 的值为( ) A.12 B. 12或0 C. 0 D. 2- 12、如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A. 90πB.63πC.42πD.36π 二、填空题(每空5分,共计20分) 13、函数的定义域是 .14. 设偶函数()f x 的定义域为R ,当[)0,x ∈+∞时, ()f x 是增函数,则(2)f -,()f π,(3)f -按从小到大的顺序排列是___________.15、在空间直角坐标系中,设点是关于坐标平面的对称点,则.16、如图,三棱锥P ABC -,平面PAB ⊥平面PBC ,若PB BC ⊥,则△ABC 的形状为__________.三、解答题(共计70分)17、(10分)解下列不等式:()()log 25log 1a a x x ->-. 18、(12分)已知函数()222,[5,5]f x x ax x =++∈-.(1)当1a =-时,求函数的最大值和最小值;(2)函数()y f x =在区间[]5,5-上是单调函数,求实数a 的取值范围.19、(12分)如图所示,在正方体1111ABCD A B C D -中, ,M N 分别为棱1A A 和1B B 的中点,求异面直线CM 与1D N 所成角的正弦值.20、(12分)如图,四棱锥P ABCD -中, //AB CD ,2AB CD =,E 为PB 的中点.求证://CE 平面PAD .21、(12分)ABC ∆中, (0,1)A , AB 边上的高CD 所在直线的方程为240x y +-=,AC 边上的中线BE 所在直线的方程为 230x y +-=.(1)求直线AB 的方程; (2)求直线BC 的方程; 22、(12分)已知圆:与圆:相交于、两点,(1)求公共弦所在的直线方程; (2)求圆心在直线上,且经过、两点的圆的方程.岷县二中2020学年度第二学期期中考试高二(文)·数学答案一、选择题(每空5分,共计60分) 1 2 3 4 5 6 7 8 9 10 11 12 CCCDCCADABAB13、14、()()()23f f f π-<-<15、 1016、直角三角形 三、解答题(共计70分)17、解析:当1a >时,原不等式等价于250,{10,251,x x x x ->->->-解得4x >.当01a <<时,原不等式等价于250,{10,251,x x x x ->->-<-解得542x <<.综上所述,当1a >时,原不等式的解集为{}|4x x >; 当01a <<时,原不等式的解集为5|42x x ⎧⎫<<⎨⎬⎩⎭. 18、解析:(1)当1a =-时, ()222f x x x =-+,则函数()f x 图像的对称轴为直线1x =,可知, ()()()()min max 11,537f x f f x f ===-=. (2)由已知得,函数()f x 图像的顶点横坐标为a -, 要使()f x 在区间[]5,5-上是单调函数, 需有5a -≤-或5a -≥,即5a ≥或5a ≤-.19、解析:设棱长为a ,取1DD 中点E ,连接BE ,可判断CM 与BE 相交于O ,1//BE D N , 故CM 与1D N 所成角即为所求。
甘肃省定西市岷县第二中学2019-2020学年高二第二学期期末考试数学(文)试卷
高二 • 数学(文)答案满分:150分 时间:120分钟一、选择题(每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的. 请将答案写在答题卡上)1.设集合A ={1,2,4},B ={x |x 2-4x +m =0}.若A ∩B ={1},则B =( ) A .{1,-3} B.{1,0} C .{1,3} D.{1,5}[解析] ∵A ∩B ={1},∴1∈B .∴1-4+m =0,即m =3.∴B ={x |x 2-4x +3=0}={1,3}.故选C.2.设(1+2i)(a +i)的实部与虚部相等,其中a 为实数,则a =( ) A .-3 B.-2 C .2 D.3[解析] (1+2i)(a +i)=(a -2)+(2a +1)i ,由已知条件,得a -2=2a +1,解得a =-3.故选A.3.执行如图所示的程序框图,输出的 s 值为( )A. 12B. 56C. 76D. 712[解析] 初始化数值1,1k s ==循环结果执行如下:第一次: 1111(1),2,2322s k k =+-⋅===≥不成立;第二次: 2151(1),3,3336s k k =+-⋅===≥成立,循环结束,输出56s =,故选B.4.在△ABC 中,“A =B ”是“tan A =tan B ”的( )A .充分不必要条件 B.必要不充分条件 C .充要条件 D.既不充分也不必要条件 答案:C5.一枚均匀的正方体玩具的各个面上分别标有数字1,2,3,4,5,6.将这个玩具向上抛掷1次,设事件A 表示向上的一面出现奇数,事件B 表示向上的一面出现的数字不超过3,事件C 表示向上的一面出现的数字不小于4,则( )A .A 与B 是互斥而非对立事件 B .A 与B 是对立事件C .B 与C 是互斥而非对立事件D .B 与C 是对立事件[解析] 根据互斥事件与对立事件的意义作答,A ∩B ={出现数字1或3},事件A ,B 不互斥也不对立;B ∩C =∅,B ∪C =Ω,故事件B ,C 是对立事件.故选D. 6.已知正项等比数列{a n }的前n 项和为S n ,且a 1a 6=2a 3,a 4与2a 6的等差中项为32,则S 5=( )A .36 B.33 C .32 D.31解析:设{a n }的公比为q (q >0),因为a 1a 6=2a 3,而a 1a 6=a 3a 4,所以a 3a 4=2a 3,所以a 4=2.又a 4+2a 6=3,所以a 6=12,所以q =12,a 1=16,所以S 5=16⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫1251-12=31.故选D.答案:D7.已知非零向量a ,b 满足|b|=4|a|,且a ⊥(2a +b )则a 与b 的夹角为( ) A.π3 B.π2 C.2π3 D.5π6解析:由已知可得a ·(2a +b )=0⇒2a 2+a ·b =0,设a 与b 的夹角为θ,则有2|a|2+|a|·|b|cos θ=0⇒cos θ=-2|a|24|a|2=-12,又因为θ∈[0,π],所以θ=2π3,故选C. 答案:C8.已知函数y =f (x )的图象关于x =1对称,且在(1,+∞)上单调递增, 设a =f ⎝ ⎛⎭⎪⎫-12,b =f (2),c =f (3),则a ,b ,c 的大小关系为( )A .c <b <a B.b <a <c C .b <c <a D.a <b <c [解析] 法一 由题意知f (x )=f (2-x ),则f ⎝ ⎛⎭⎪⎫-12=f ⎝ ⎛⎭⎪⎫2+12=f ⎝ ⎛⎭⎪⎫52,又f (x )在(1,+∞)上单调递增,所以f (2)<f ⎝ ⎛⎭⎪⎫52<f (3),即b <a <c .法二 由对称性及单调性得其图象草图如图所示.结合图象得f (2)<f ⎝ ⎛⎭⎪⎫-12<f (3),即b <a <c .[答案] B9.f (x )是R 上的奇函数,当x ≥0时,f (x )=x 3+ln(1+x ),则当x <0时, f (x )=( )A.-x 3-ln(1-x ) B.x 3+ln(1-x ) C.x 3-ln(1-x ) D.-x 3+ln(1-x ) 答案:C10.函数f (x )=2|x -1|的图象大致是( )[解析]f (x )=⎩⎪⎨⎪⎧2x -1,x ≥1,⎝ ⎛⎭⎪⎫12x-1,x <1,故选B.11. 函数f (x )=cos 2x +2cos x 的最大值与最小值的和是( ) A .-2 B.0 C.32 D.-12[解析] f (x )=2cos 2x +2cos x -1=2⎝⎛⎭⎪⎫cos x +122-32,设t =cos x ∈[-1,1],∴f (x )max =3,f (x )min =-32.∴f (x )max +f (x )min =3-32=32.[答案] C 12.如图,一个简单空间几何体的三视图其主视图与侧视图都是 边长为2的正三角形,俯视图轮廓为正方形,则此几何体的表面积是( )A .443+B .12C .43D .8 答案:B二、填空题(每题5分,共20分, 请将答案写在答题卡上)13.若x ,y 满足约束条件⎩⎨⎧x -y +1≥0,x +y -3≥0,x -3≤0,则z =x -2y的最小值为________.[解析] 作出可行域,如图中阴影部分所示,由z =x -2y ,得y =12x -12z ,作直线y =12x 并平移,观察可知,当直线经过点A (3,4)时,z min =3-2×4=-5.[答案] -514.设双曲线x 2a 2-y 29=1(a >0)的渐近线方程为3x ±2y =0,则a 的值为________.[答案] 215.如图所示,某住宅小区内有一个正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的23。
甘肃省定西市岷县第二中学2019-2020学年高二数学下学期期中试题理【含答案】
甘肃省定西市岷县第二中学2019-2020学年高二数学下学期期中试题 理本卷分第Ⅰ卷(选择题)和第Ⅱ卷(解答题)两部分。
考试结束,只需交上答题卡。
一、选择题(每小题5分,共12道,总共60分,只有一个选项符合题意)1、设y=2x -x ,则x ∈[0,1]上的最大值是( )A 0B -41C 21D 412、若质点P 的运动方程为S(t)=2t 2+t (S 的单位为米,t 的单位为秒),则当t=1时的瞬时速度为( )A 2米/秒B 3米/秒C 4米/秒D 5米/秒3、曲线y=-313x -2在点(-1,35-)处切线的倾斜角为( )A30ºB45ºC135ºD150º4、已知a>0,函数y=3x -a x在[1,+∞)上是单调增函数,则a 的最大值为()A 0B 1C 2D 35、已知)(x f =23x -62x +m (m 为常数),在[-2,2]上有最大值3,则此函数在[-2,2]上的最小值为()A -37B -29C -5D -116、曲线3x y =在点)1,1(处的切线与x 轴、直线2=x 所围成的三角形的面积为( )(A )38 (B )37 (C )35 (D )347、设ai b bi a ++,,1是一等比数列的连续三项,则b a ,的值分别为( )(A )21,23±=±=b a (B )23,21=-=b a (C )21,23=±=b a (D )23,21-=-=b a 8、方程)(04)4(2R a ai x i x ∈=++++有实根b ,且bi a z +=,则=z ( )(A )i 22- (B )i 22+ (C )i 22+- (D )i22--9、已知三角形的三边分别为c b a ,,,内切圆的半径为r ,则三角形的面积为a s (21=r c b )++;四面体的四个面的面积分别为4321,,,s s s s ,内切球的半径为R 。
甘肃省岷县第二中学2020学年高二语文下学期第一次月考试题(含解析)
岷县二中2020学年度第二学期月考试卷高二语文阅读下面的文字,完成小题。
从赵本山的《不差钱》说起王蒙事实上,赵本山已经成了近年央视春晚的台柱子之一。
他以大众化、尤其是农民化的语言、做派、幽默与“狡黠”,表现当代生活,铺陈笑料,营造喜乐,鞭挞不正之风,追求诚实纯朴与人心深处的古道热肠,引起观众的普遍欢迎。
2020年春节晚会上他带着两个徒弟表演的小品《不差钱》,更凸现了年轻演员的才艺功夫,弘扬了东北地区“二人转”不拘一格的表演特色,含蓄地表达了来自基层所谓“土得掉渣”的文艺走上主流媒体,进入主流文艺生活、进入城市舞台的酸甜苦辣,以及相互整合交流的大趋势。
尽管我知道在知识精英中不无对于小品与大众文艺的白眼,但人们已经无法不正视这个赵本山“现象”的意味深长,即以地道的东北土腔土调攀登央视文艺殿堂的连续成功。
赵本山将本来在某些人包括我本人心目中未必能登大雅之堂的喜剧小品提高到了骄人的水准。
正像金庸为武侠小说、张艺谋为大制作的奥运会开幕式文艺展演树立了后来人难以企及的标杆一样。
同时我们并不满足,我们有更高的与更多方面的期待。
我们需要的不仅是文化的普及、热闹与和谐,我们还需要文化的巅峰、文化的巨人、文化的前瞻。
我们期待的是中华民族的智慧新果实。
我们不但需要有模仿秀的天才,更需要提供原型、新型的创造者、发明者,开一代风气之先的文化宗师。
我们希望得到笑料,更希望笑的背后有洞见式的深邃。
我们追求群众的喜闻乐见,我们还期盼对于群众的振聋发聩或者春风化雨或者洗涤启迪。
我们需要思想、需要艺术、需要想象力,需要应对挑战的勇气与本领,需要全面小康的、有中国特色社会主义的、独树一帜的也是汲取了一切精神营养的哲学、伦理学、人文科学与社会科学的苗头与思考,需要正视历史也正视现实,能够为今天的、乃至于明天的读者观众解惑释疑、能够带领读者观众探索真理消化真理的作家艺术家学者。
我们需要大众化,也需要化大众,就是说,我们期待全面的文化的繁荣与振兴,期待人民文化素质的全面提高,我们期待文化艺术巨匠的新人辈出,我们期待今天的文化艺术发展能够无愧于前人,同样也不会害怕后人的审视。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
甘肃省定西市岷县第二中学2019-2020学年
高二下学期期中考试(文)
一、选择题(每小题5分,共60分,在每小题给出的四个选项中,有且只有一项是符合题目要求的. 请将答案写在答题卡上)
1.(1+i)(2-i)=()
A .-3-i
B .-3+i
C .3-i
D .3+i
2.以下哪种推理方法是类比推理()
A .∵数列{a n }中,a 1=1,a 2=3,a 3=5, ∴a n =2n -1(n ∈N *)
B .∵x 2=3,∴x =± 3
C .∵平面内平行于同一直线的两直线平行,
∴空间平行于同一平面的两个平面平行
D .∵f (x )=x +3,∴f (0)=3
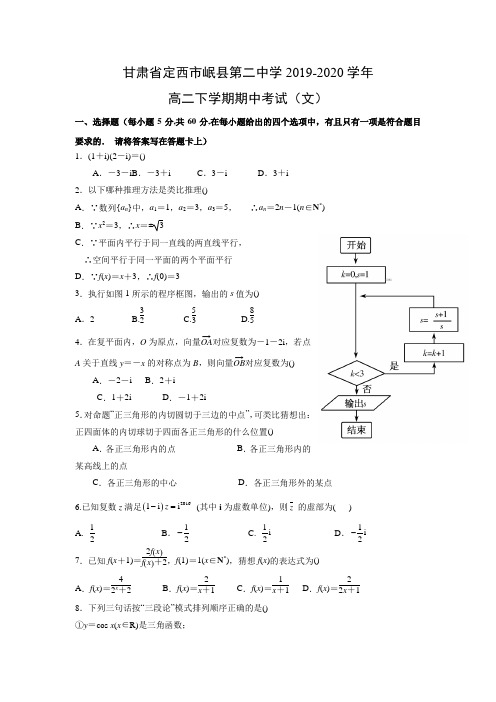
3.执行如图1所示的程序框图,输出的s 值为()
A .2 B.32 C.53 D.8
5
4.在复平面内,O 为原点,向量OA →
对应复数为-1-2i ,若点A 关于直线y =-x 的对称
点为B,则向量OB→对应复数为()
A.-2-i B.2+i
C.1+2i D.-1+2i
5.对命题“正三角形的内切圆切于三边的中点”,可类比猜想出:正四面体的内切球切于四面各正三角形的什么位置()
A.各正三角形内的点B.各正三角形内的某高线上的点
C.各正三角形的中心D.各正三角形外的某点
6.已知复数z满足()2016
1i i
z
-=(其中i为虚数单位),则z的虚部为( )
A. 1
2B.1
2
- C.
1
i
2
D.1i
2
-
7.已知f(x+1)=2f(x)
f(x)+2,f(1)=1(x∈N*),猜想f(x)的表达式为()
A.f(x)=4
2x+2B.f(x)=2
x+1C.f(x)=1
x+1D.f(x)=2
2x+1
8.下列三句话按“三段论”模式排列顺序正确的是()
①y=cos x(x∈R)是三角函数;
②三角函数是周期函数;
③y=cos x(x∈R)是周期函数.
2
3
A .①②③
B .③②①
C .②③①
D .②①③
9.某产品的广告费用x 与销售额y 的统计数据如下表:
根据上表可得回归方程y =b x +a 中的b 为9.4,据此模型预报广告费用为6万元时销售额为()
A .63.6万元
B .65.5万元
C .67.7万元
D .72.0万元
10.利用独立性检验来考虑两个分类变量X 和Y 是否有关系时,通过查阅下表来确定断言“X 和Y 有关系”的可信度.如果k >5.024,那么就有把握认为“X 和Y 有关系”的百分比为()
A.25% B .75% C .2.5% D .97.5%
11.下列函数为奇函数的是( )
A.()32
3f x x x =+
B.()22x x
f x -=+
C.()sin f x x x =
D.()3ln
3x
f x x
+=-
4
二、填空题(每题5分,共20分, 请将答案写在答题卡上)
13.由数列的前四项:32,1,58,3
8,…,归纳出通项公式a n =________.
14.已知等差数列{a n }中,若m +n =p +q (m ,n ,p ,q ∈N *),则a m +a n =a p +a q ,类比上述性质,在等比数列{a n }中,则有____________
15.若某程序框图如图2所示,则该程序运行后输出的k 的值是________.
12.
5
16.设复数1i z =+,则复数2
2z z
+的共轭复数为______.
三、解答题(17题10分 ,其余每题12分, 共70分,请将答案写在答题卡上)
17.(本小题满分10分)已知函数f (x )=⎩⎪⎨⎪
⎧x ,x ∈[0,2],4x ,x ∈(2,4].
(1)在图中画出函数f (x )的大致图象;
=1-i。
