北大随机过程课件:第 6 章 第 1 讲 最小均方误差线性估计
合集下载
随机过程第六章

T
T
X (t )dt
<x(t)>是随机过程的样本函数按不同时刻取平均,它随样本不同而不同, 是个随机变量。 对于一个确定的样本
X (t ) lim 1 T 2T
T
T
X (t )dt 常数
时间平均
集合平均
20
定义6.10 设{X(t),-∞<t<∞}是均方连续的平稳过程,若
n
lim E[| X n X |2 ] 0
成立,则称{Xn}均方收敛于X,记作
Xn X
m. s
l.i.m X
n
n
X
称二阶矩随机序列{Xn}依分布收敛于二阶矩随机变量X,若{Xn}相应的分 布函数列{Fn(x)},在X的分布函数F(x)的每一个连续点处,有
n
lim Fn ( x) F ( x)
t
a
X ( ) d
在均方意义下存在,且随机过程{Y(t), t∈T}在区间[a,b]上均方可微,且有 Y’(t)=X(t)。
18
推论:设X (t )均方可微,且X (t )均方连续,则 X (t ) X (a) X (t )dt.
a t
及
X (b) X (a) X (t )dt.
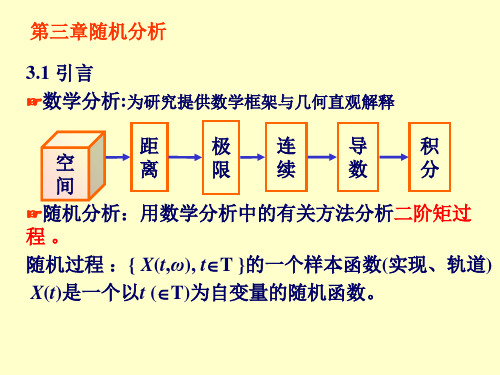
第六章:平稳随机过程
严平稳过程的定义 宽平稳过程的定义 平稳过程的数字特征 平稳过程自相关函数的性质 时间平均和集合平均的概念 平稳过程遍历性定义 遍历性判定定理 遍历性应用举例
1
严平稳过程的定义
设{X(t),t∈T}是随机过程,如果对任意常数τ和正整数n, t1,t2, …,tn∈T,t1+τ,t2+τ, …,tn+τ ∈T, (X(t1),X(t2), …,X(tn))与(X(t1+τ),X(t2+τ), …,X(tn+τ))有 相同的联合分布,则称{X(t),t∈T}为严平稳过程或侠义 平稳过程。
随机过程的统计特性中小学PPT教学课件

FX ( x1, x2; t1, t2 ) P{X (t1) x1, X (t2 ) x2}
称为随机过程X(t)的二维概率分布函数。
若 FX ( x1, x2;t1, t2 ) 对x1,x2的偏导数 存在,则定义
fX
(x1, x2;t1, t2 )
2 FX
(x1, x2;t1, t2 ) x1x2
国;
•我国的杂交水稻更是举世闻名; •我国水稻的栽培技术也是突出的。
2021/2/12
42
2、分布与区划
Ⅰ.华南双季稻作带(区):本区位于南岭以南。双季稻为主,品种 有早、中、晚籼稻。
Ⅱ.华中单双季稻作区:本区位于南岭以北,秦岭淮河以南。双季稻 为主,品种早、中籼。
Ⅲ.西南高原单双季稻作区:本区位于云贵高原和青藏高原。稻麦 (蚕豆)两熟,双季稻或单季稻、低地多籼稻,高地多粳稻。
nX ( n
,
t)
| 0
相关函数与二维特征函数之间的关系为:
RX
(t1, t2 )
2X
(1,2 ; t1, t2 ) 12
|12 0
主 讲 内 容 : 6学时
●概述
●生长发育
●种稻的土肥水条件
●栽培技术
2021/2/12
34
●概 述 ▲水稻生产在国民经济中的地位
▲水稻的分布与生产概况
▲栽培稻的起源和类型
e j1x1 j2x2
f X ( x1, x2;t1, t2 )dx1dx2
定义为随机过程X(t)的二维特征函数。
fX (x1, x2;t1,t2 )
1
4 2
X
(1,2;t1, t2 )e j1x1 j2x2d1d2
随机过程的特征函数与矩函数之间的 关系为:
称为随机过程X(t)的二维概率分布函数。
若 FX ( x1, x2;t1, t2 ) 对x1,x2的偏导数 存在,则定义
fX
(x1, x2;t1, t2 )
2 FX
(x1, x2;t1, t2 ) x1x2
国;
•我国的杂交水稻更是举世闻名; •我国水稻的栽培技术也是突出的。
2021/2/12
42
2、分布与区划
Ⅰ.华南双季稻作带(区):本区位于南岭以南。双季稻为主,品种 有早、中、晚籼稻。
Ⅱ.华中单双季稻作区:本区位于南岭以北,秦岭淮河以南。双季稻 为主,品种早、中籼。
Ⅲ.西南高原单双季稻作区:本区位于云贵高原和青藏高原。稻麦 (蚕豆)两熟,双季稻或单季稻、低地多籼稻,高地多粳稻。
nX ( n
,
t)
| 0
相关函数与二维特征函数之间的关系为:
RX
(t1, t2 )
2X
(1,2 ; t1, t2 ) 12
|12 0
主 讲 内 容 : 6学时
●概述
●生长发育
●种稻的土肥水条件
●栽培技术
2021/2/12
34
●概 述 ▲水稻生产在国民经济中的地位
▲水稻的分布与生产概况
▲栽培稻的起源和类型
e j1x1 j2x2
f X ( x1, x2;t1, t2 )dx1dx2
定义为随机过程X(t)的二维特征函数。
fX (x1, x2;t1,t2 )
1
4 2
X
(1,2;t1, t2 )e j1x1 j2x2d1d2
随机过程的特征函数与矩函数之间的 关系为:
随机过程及其统计描述ppt课件.ppt

任意时刻下,观测目的是X取什么值;全程的情况下, 观测目的是X(t)的函数形式.
7
12.1 随机过程的概念
随机相位正弦波
随机过程举例
考虑: X (t) a cos(t ), t (,)
式中 a,是正常数,是 (0, 2 ) 上服从均匀分布的随机变量。
当 在(0, 2 ) 内随机的取一个值 i ,可得样本函数:
2
0 cos(t1 ) cos(t2 ) f ( )d
a2
2
2
0 cos(t1 ) cos(t2 )d
a2
4
2
0 {cos[(t1 t2 ) 2 ] cos(t1 t2 )}d
a2 2
cos (t1
t2 )
方差函数
2 X
(t)
RX
(t , t )
2 X
(t)
a2 2
18
12.2 随机过程的统计描述
随机过程举例
抛掷一枚硬币的试验,样本空间是S={H,T}, 现借此定义随机过程:
cos t,
X (t) t,
当出现H, 当出现T,
t (, )
可将此随机过程改写为
X (t) Y cost (1Y )t ,
其中
Y
1, 0,
出现H 出现T
,
t (, )
X对Y和t的依赖,决定了X是一个随机过程. 确定了 Y之后,即可确定任意时刻和全程的观测结果.
集平均(统计平均)
X (t)是随机过程的所有样本函数在时刻 t 的函数值的平均值,通常称
这种平均为集平均或统计平均。
12
12.2 随机过程的统计描述
(二) 随机过程的数字特征
均方值函数
Ψ
北大随机过程课件:第 6 章 第 1 讲 最小均方误差线性估计汇编

sˆ(t) = ax(t) ,且
a = E{s(t )x(t)}/ E{x(t) x(t)} = Rss (0) /[Rss (0) + Rnn (0)]
{ } { } 相应的最小均方误差是, E⎩⎨⎧ξ − ξˆ 2 ⎭⎬⎫ = E ξ 2 − E ξξˆ*
{ } E s(t) − sˆ(t) 2 = E{[s(t) − ax(t)]s(t)}
为了使均方误差最小,
应使 K = E{ξ/η },即:ξˆ(η= Y) = E{ξ/η= Y}
定理
设随机矢量 ξ = (ξ 1,ξ 2,"ξ n) 和 η = (η 1,η 2,"η m) 的联合概率密度函数是,
fξ η (x1, x2 ,", xn ; y1, y2 ," ym ) 且 fη ( y1, y2 ," ym ) ≠ 0 ,则ξ关于η的最小均方误
讨论 2:在上述条件下,估计误差正交于 s(u), u < t
E{[s(t + λ ) − as(t )]⋅ s(u)} = Rs s (t + λ − u) − aRs s (t − u)
σ σ σ σ =
e2 −α (t+λ −u) − a e2 −α (t−u) =
e − e e 2 −α (t+λ −u)
其中一个重要的问题就是确定估值参数 估值的评估:分析估值误差
均方误差最小的最佳线性估计
估值问题
设ξ和η是两个随机矢量,两者存在联合分布,其中η是观察矢量,通过η对ξ进 行估值,得到符合某种准则的最佳估值ξ。
1 均方误差最小的估值问题
均方误差最小的估值问题
设ξ和η是两个随机矢量,两者存在联合分布,设η是观察矢量,通过η对ξ进行 估值,求均方误差最小的估值ξ。
a = E{s(t )x(t)}/ E{x(t) x(t)} = Rss (0) /[Rss (0) + Rnn (0)]
{ } { } 相应的最小均方误差是, E⎩⎨⎧ξ − ξˆ 2 ⎭⎬⎫ = E ξ 2 − E ξξˆ*
{ } E s(t) − sˆ(t) 2 = E{[s(t) − ax(t)]s(t)}
为了使均方误差最小,
应使 K = E{ξ/η },即:ξˆ(η= Y) = E{ξ/η= Y}
定理
设随机矢量 ξ = (ξ 1,ξ 2,"ξ n) 和 η = (η 1,η 2,"η m) 的联合概率密度函数是,
fξ η (x1, x2 ,", xn ; y1, y2 ," ym ) 且 fη ( y1, y2 ," ym ) ≠ 0 ,则ξ关于η的最小均方误
讨论 2:在上述条件下,估计误差正交于 s(u), u < t
E{[s(t + λ ) − as(t )]⋅ s(u)} = Rs s (t + λ − u) − aRs s (t − u)
σ σ σ σ =
e2 −α (t+λ −u) − a e2 −α (t−u) =
e − e e 2 −α (t+λ −u)
其中一个重要的问题就是确定估值参数 估值的评估:分析估值误差
均方误差最小的最佳线性估计
估值问题
设ξ和η是两个随机矢量,两者存在联合分布,其中η是观察矢量,通过η对ξ进 行估值,得到符合某种准则的最佳估值ξ。
1 均方误差最小的估值问题
均方误差最小的估值问题
设ξ和η是两个随机矢量,两者存在联合分布,设η是观察矢量,通过η对ξ进行 估值,求均方误差最小的估值ξ。
随机过程课件

1
m X (t1 )][ x2 m X (t 2 )] f ( x1 x2 ; t1 , t 2 )dx1dx 2 f ( x1, x2 ; t1 , t 2 )dx1dx 2
x x
1 2
X(t) 协方差与相关函数的关系为 当 mx (t ) 0 时 C X (t 1 , t 2 ) R X (t 1 , t 2 ) 在协方差定义中取t1=t2=t,就有
为XT 的均值函数或数学期望。其中F(x,t)是过程 的一维分布函数。 若是连续型随机变量,有 mX (t) xf(x,t)dx 其中f(x,t)是一维分布密度。 12
2.随机过程的方差 若 DX (t) 2 (t) E[X(t) mX (t)]2 存在,t∈T, X 称为X(t)的方差。 x (t) Dx (t) 称为X(t)的标准差。 它们描绘过程的样本曲线在各个t时刻对均 值 m X ( t ) 的离散程度, 对每个t1∈T, EX (t1 ) 反映t1状态取值的概率平均。 DX (t1 ) 反映t1状态取值与 EX (t1 ) 离散程度。 在工程中随机过程的均方值具有物理意义,比 较有用。均方值定义为: E[ X 2 (t )] X (t ) DX (t ) E( X 2 (t )) E 2 ( X (t )) 有关系式: 13 Dx (t ) x (t ) [mx (t )]2 即
第一章. 随机过程的基本概念
§1.1 随机过程及其概率分布
在实际问题中,有时需要对随机现象的变化进 行研究,这时就必须考虑无穷个随机变量或一族 随机变量, 我们就称这种随机变量族为随机过程。 例1: 生物群体的增长问题。在描述群体的发展 或演变过程中, 以 Xt 表示在时刻 t 群体的个数, 则 对每一个 t ,Xt 是随机变量。假设我们从 t =0 开 始每隔24小时对群体的个数观测一次, 则{Xt , t =0, 1, 2, ...}是一个随机过程。 例2: 电话呼唤问题。某电话总机在[0,t]时间 内收到的呼唤次数用 Xt 来表示, 则对于固定的 t , 1 Xt 是随机变量。于是{Xt , t ∈[0, ∞)}是随机过程。
随机过程的基本概念ppt课件

求X(t)的均值、均方值和方差。
.
2.3 平稳随机过程
三、相关系数及相关时间
也称为归一化协方差函 数或标准协方差函数。
相关系数: rX()KXX 2 ()RX()X 2mX 2
相关时间:
0
0 rX()d
rX ( )
1
rX(0) 0.05
0
0
相关时间示意图
.
2.3 平稳随机过程
三、相关系数及相关时间
为随机过程X(t)的二维概率分布。定义
fX(x1,x2,t1,t2)2FX(xx11,xx22,t1,t2)
为随机过程X(t)的二维概率密度。 注意:X(t1)及X(t2)为同一随机过程上的随机变量。
.
2.2 随机过程的统计描述
2、二维概率分布
例2、设随机相位信号
X (n )co s( n/1 0 )
.
2.2 随机过程的统计描述
二、随机过程的数字特征(连续)
• 协方差函数
K X ( t 1 , t 2 ) E { [ X ( t 1 ) m X ( t 1 ) ] [ X ( t 2 ) m X ( t 2 ) ] } (1)如果 KX(t1,t2)0,则称 X (t1 )和 X (t2 )是不相关的。
.
2.3 平稳随机过程
一、定义
(1)严格平稳随机过程
f X ( x 1 , ,x n ,t 1 , ,t n ) f X ( x 1 , ,x n ,t 1 , ,t n )
一维概率密度: fX(x,t)fX(x)
二维概率密度: fX (x 1 ,x 2 ,t1 ,t2 ) fX (x 1 ,x 2 ,) t1 t2
接收机噪声
5
x1(t) 0
.
2.3 平稳随机过程
三、相关系数及相关时间
也称为归一化协方差函 数或标准协方差函数。
相关系数: rX()KXX 2 ()RX()X 2mX 2
相关时间:
0
0 rX()d
rX ( )
1
rX(0) 0.05
0
0
相关时间示意图
.
2.3 平稳随机过程
三、相关系数及相关时间
为随机过程X(t)的二维概率分布。定义
fX(x1,x2,t1,t2)2FX(xx11,xx22,t1,t2)
为随机过程X(t)的二维概率密度。 注意:X(t1)及X(t2)为同一随机过程上的随机变量。
.
2.2 随机过程的统计描述
2、二维概率分布
例2、设随机相位信号
X (n )co s( n/1 0 )
.
2.2 随机过程的统计描述
二、随机过程的数字特征(连续)
• 协方差函数
K X ( t 1 , t 2 ) E { [ X ( t 1 ) m X ( t 1 ) ] [ X ( t 2 ) m X ( t 2 ) ] } (1)如果 KX(t1,t2)0,则称 X (t1 )和 X (t2 )是不相关的。
.
2.3 平稳随机过程
一、定义
(1)严格平稳随机过程
f X ( x 1 , ,x n ,t 1 , ,t n ) f X ( x 1 , ,x n ,t 1 , ,t n )
一维概率密度: fX(x,t)fX(x)
二维概率密度: fX (x 1 ,x 2 ,t1 ,t2 ) fX (x 1 ,x 2 ,) t1 t2
接收机噪声
5
x1(t) 0
随机过程课件1

2
3 4 5
P( A B) = P( A) P( B) P( AB)
P( Ac ) = 1 P( A) Ac为E的余集.
设 E1,E2, ,En 两两互不相容 ,则
P ( Ei ) = P ( Ei )
i =1 i =1 n n
6 7
P( Ai ) P( Ai )
xk
的概率:
则称上式为X的概率分布或分布率 .且满足
pk 0
k =1
pk = 1
3.分布密度
连续型 随机变量 如果对于随机变量X的分布函数为F(x), 存在非负的函数 f(x),使对任意的实数x有
F ( x) =
x
f (t )dt
则称X为连续型随机变量,f(x)称为X的概率密度, 且满足
lim P ( E n ) = P ( lim E n )
n n
四、独立性 1.定义
两个
如果事件A,B满足
P(AB) P(A)P(B) =
则称事件A,B相互独立。
n个
设 A1,A2, ,An 是n个事件,如果对于任意
s ( 2 s n) 和 1 i1 i2 is n
概率论
probability theory
数理统计
Mathematical statistics
随机过程
stochastic process
随机现象 偶然性
内在规律 必然性
随机过程的起源及发展
Brown运动: 1827 年,Brown在显微镜下发现花粉的无 规则运动, 将此奇怪现象公诸于世, 无人能解释原因. 1900年,法国数学家Bachelier给出 一维Brown运 动粗略模型, 其博士论文为《投机的理论》, 研究证券价格 的涨落,开创近代金融数学的先河,但他的结果几十年之 后才得到认可. 1905年,Einstein 首次进行量化分析, 认是花粉运 动源自分子无规则热运动, 每秒碰撞 1019 1021 次. Wiener 1918年发表系列论文, 成功解决这一问题, 故称Wiener—Einstein过程.
《数学随机过程》PPT课件
所以X与Y不相关。 故 (X,Y )=0 X与Y不相关
几何直观意义
3.3 随机分析初步
附注C—关于赋范线性空间概念的回顾
设V是一个线性空间,若 V,存在一个实数|| ||与
之对应,且具有下列性质:
(1) || ||0 , 且|| ||=0 =0 ; (2) ||c· ||= |c|·|| || , 特别 ||- ||= || ||; c R (3) || + || || ||+ || ||; V 则称|| || 为V中元素 的范数(norm)(模、长度),此时线
CXX (t1, t2 ) cov{ X (t1), X (t2 )} E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} | CXX (t1, t2 ) |2 | cov{ X (t1), X (t2 )} |2 | E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} |2 {E | [ X (t1) mX (t1)][ X (t2 ) mX (t2 )] |}2 E | X (t1) mX (t1) |2 E | X (t2 ) mX (t2 ) |2 D[ X (t1)]D[ X (t2 )]
3.3 随机分析初步
附注A—关于线性空间概念的回顾
设V是一个非空的集合,K是一个数域,又设
(a)在V中定义加法: , V : + V ; (b)在V中定义数乘: V, k K: k · V ; 且 , , V , k,l K , 满足 (1) k ,l K, , V : (2) +( +)= ( + )+ ; (3) + = + ; (4)0V, V: +0= ; (5) V, V: +=0 (6) 1 K: 1· = ; (7) k ,l K, V: (kl)· =k·(l) ; (8)k ,l K, V: (k+l) = k +l ; (9) k K, , V : k( + )= k + k .
几何直观意义
3.3 随机分析初步
附注C—关于赋范线性空间概念的回顾
设V是一个线性空间,若 V,存在一个实数|| ||与
之对应,且具有下列性质:
(1) || ||0 , 且|| ||=0 =0 ; (2) ||c· ||= |c|·|| || , 特别 ||- ||= || ||; c R (3) || + || || ||+ || ||; V 则称|| || 为V中元素 的范数(norm)(模、长度),此时线
CXX (t1, t2 ) cov{ X (t1), X (t2 )} E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} | CXX (t1, t2 ) |2 | cov{ X (t1), X (t2 )} |2 | E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} |2 {E | [ X (t1) mX (t1)][ X (t2 ) mX (t2 )] |}2 E | X (t1) mX (t1) |2 E | X (t2 ) mX (t2 ) |2 D[ X (t1)]D[ X (t2 )]
3.3 随机分析初步
附注A—关于线性空间概念的回顾
设V是一个非空的集合,K是一个数域,又设
(a)在V中定义加法: , V : + V ; (b)在V中定义数乘: V, k K: k · V ; 且 , , V , k,l K , 满足 (1) k ,l K, , V : (2) +( +)= ( + )+ ; (3) + = + ; (4)0V, V: +0= ; (5) V, V: +=0 (6) 1 K: 1· = ; (7) k ,l K, V: (kl)· =k·(l) ; (8)k ,l K, V: (k+l) = k +l ; (9) k K, , V : k( + )= k + k .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为了使均方误差最小,
应使 K = E{ξ/η },即:ξˆ(η= Y) = E{ξ/η= Y}
定理
设随机矢量 ξ = (ξ 1,ξ 2,"ξ n) 和 η = (η 1,η 2,"η m) 的联合概率密度函数是,
fξ η (x1, x2 ,", xn ; y1, y2 ," ym ) 且 fη ( y1, y2 ," ym ) ≠ 0 ,则ξ关于η的最小均方误
= E{s(t) s(t)}− aE{x(t ) s(t)}
= Rss (0) − aRss (0)
=
Rss
(0)
−
Rss
Rss (0) (0) + Rnn
(0)
Rss
(0)
=
Rss
(0)
Rss
Rnn (0) (0) + Rnn
(0)
例3
设有零均值实平稳随机过程的信号 s(t),试根据 s(0)及 s(T)对 s(t)进行估值。
{ } + E [ξ− E{ξ/η}]⋅[E{ξ/η}− K]/ η= Y { } + E [ξ− E{ξ/η}]⋅[E{ξ/η}− K]/ η= Y
{ } + E ξ− E{ξ/η} 2 / η= Y { } { } = E E{ξ/η}− K 2 / η= Y + E ξ− E{ξ/η} 2 / η= Y
它们是统计独立的随机过程,实际测到的是 x(t)=s(t)+n(t),试根据 x(t)对 s(t)进行估值。 例 3,设有零均值实平稳随机过程的信号 s(t),试根据 s(0)及 s(T)对 s(t)进行估值。 例 4,利用 t 时刻随机过程 s(t)的观察值和它的导数 s’(t)观察值,对未来的 s(t+λ),
值,这时 ξˆ(η) = Aη+ b 称作为最佳线性估值。其中ξ是 n×1 的矢量,η是 m×1 的
矢量,A 是 n×m 的矩阵,b 是 n×1 的矢量。
问题:
确定 A、b
结论:
bj = Eξ j− A j Eη
( )( ) A j = C[ξjη]
−1
C[ηη ]
即,
ξˆj = Eξ j − C[ξ j η]C[ηη]−1Eη + C[ξ j η]C[ηη]−1η
解:
G 利用最佳线性估值原理,ξˆ = aTη= [Cξ η ]T [Cηη ]−1 ⋅η
s(t)
=
(Rss
(t)
Rss
(T
−
t))⎜⎜⎝⎛
Rss Rss
(0) (T )
Rss Rss
(T ) (0)
⎟⎟⎠⎞
−1
⎜⎜⎝⎛
s(0) s(T )
⎟⎟⎠⎞
= as(0) + bs(T )
其中,
a = Rss (t)Rss (0) − Rss (T − t)Rss (T ) [Rss (0)]2 − [Rss (T )]2
其中一个重要的问题就是确定估值参数 估值的评估:分析估值误差
均方误差最小的最佳线性估计
估值问题
设ξ和η是两个随机矢量,两者存在联合分布,其中η是观察矢量,通过η对ξ进 行估值,得到符合某种准则的最佳估值ξ。
1 均方误差最小的估值问题
均方误差最小的估值问题
设ξ和η是两个随机矢量,两者存在联合分布,设η是观察矢量,通过η对ξ进行 估值,求均方误差最小的估值ξ。
{ } { } 相应的最小均方误差是, E⎩⎨⎧ξ − ξˆ 2 ⎭⎬⎫ = E ξ 2 − E ξξˆ*
{ } E s(t + λ ) − sˆ(t + λ ) 2 = E{[s(t + λ ) − as(t)]s(t + λ )}
= E{s(t + λ ) s(t + λ )}− aE{s(t ) s(t + λ )}
= Rss (0) − aRss (λ ) = Rss (0) − [Rss (λ )]2 / Rss (0)
讨论 1:如果随机过程的相关函数是 Rss (τ ) = σ 2e−α τ
a = Rss (λ ) / Rss (0) = e−α λ
{ } ( ) E s(t + λ ) − sˆ(t + λ ) 2 = σ 2 1 − e−2α λ
估值准则的选取:有实际意义,有用;并且是能够得到简单解的。
“估计的均方误差最小”的估计准则是应用最广的一种估计思想,简称 MS 估计, 相应的估计误差简称 MMSE。
“输出信噪比最大”是雷达系统中最佳接收的工作原理。
在一定的估计准则下,有不同的解决具体估值问题的方法:
9 非线性估值 9 线性估值 9 维纳滤波 9 匹配滤波 9 递归线性均方估值
{ } { } 差估计为 ξˆ(η) = E{ξ /η },它满足 E ξ− ξˆ(η) 2 = min E ξ− g(η) 2 。
例:
设ξ和η服从二元高斯分布,求最佳估值 ξˆ(η )
解:
( ) fξ /η (x /η = y) =
2π
1 1− r2
σ
2 ξ
⎛ exp ⎜ −
⎜⎝
1 2(1− r2 )σ
计复随机变量ξ,其估计误差 e = ξ − ξˆ 。若 e 和η1,η2,…,ηm 正交,则此估计是
最小均方误差线性估计。
{ } { } 利用 E e ⋅η j = E [ξ − (a1η 1+ a2η 2+ a3η 3+" + amη m)]⋅η j = 0
注意:两种方法得到的结论一致,正交性原理的推导证明中,先假设
E {ξ} = E {η} = 0 ,进一步的论述中说明了 E {ξ} ≠ 0, E {η} ≠ 0 时,满足正交性原理
的线性估计仍然是最小均方误差估计。
最佳线性估计的均方误差
根据正交性原理,均方误差最小的最佳线性估计的误差与观察量正交,从而与估计值正 交:
{ } { } E e ⋅ η j = E (ξ− ξˆ)η j = 0
减少量是[Cξ η ][Cηη ]−1[Cξ η ]T 。
推论 3
如果复随机变量η1,η2,η3,…,ηm 彼此之间相互正交,有
( ) aj =
Cξ η ⋅ Cηη −1
= C C j j
ξ η j η jη j
推论 4
增加新的数据可以改善原有的估值,但是如果增加用来估值的数据η1+m,η2+m,…
= ( ρσ ξ )2
2 均方误差最小的线性估计
对于正态分布的随机变量,ξ关于的η最小均方误差估计ξˆ(η) = E(ξ /η ) 是一个线性 估计,对于非正态分布的随机变量,估计ξˆ(η) = E(ξ /η ) 一般不是线性的。这时需要找到
一个关于η的线性函数作为最佳估计。
定义:
{ } ξ关于的η估计 ξˆ(η) = Aη+ b ,使得 到最小
2. 估值的应用
最基本的问题是利用对一个随机变量的观测对另一个随机变量进行估计
根据当前取值来预测下一个时刻取值的预测编码; 根据接收的信号序列来估计发送序列某个时刻发送值的均衡问题; 根据信号和噪声之和的序列来估计信号的噪声抑制问题;
3. 估值问题的研究内容与方法
估值研究的是统计意义上的估计问题。由于是对一个不确定量的估计,一定存在估 计误差,关键在于利用某种原则、方法选择估计值,使估计误差在某种意义下是最小的。
ξˆ = Eξ− CξηCηη −1Eη + CξηCηη −1η
如果ξ, η = (η 1 η 2 "η m )T 均值为零,则有
ξˆ j
η = C C −1 [ξ j η] [η η]
方法: 1)极值分析法
求估值的均方误差
{ } ( ) ( ) E
⎡⎣ξ j− ξˆ j ⎤⎦2 /η
= Dξ j+ A jC[ηη ]A j H − A j
讨论 2:在上述条件下,估计误差正交于 s(u), u < t
E{[s(t + λ ) − as(t )]⋅ s(u)} = Rs s (t + λ − u) − aRs s (t − u)
σ σ σ σ =
e2 −α (t+λ −u) − a e2 −α (t−u) =
e − e e 2 −α (t+λ −u)
佳估计就是ξˆ(η) = 0 。
推论 2
如果复随机变量ξ和复随机变量η1,η2,η3,…,ηm 有相关性,进行估计,相 应的均方误差就减少了,
{ } { } E e 2 = E⎩⎨⎧ξ − ξˆ 2 ⎭⎬⎫ = E (ξ− ξˆ)(ξ− ξˆ) 。
= Cξ ξ − [Cξ η ][Cηη ]−1[Cξ η ]T
则:
{ } E (ξ− ξˆ)ξˆ = 0
因此:
{ } { } { } E ξ− ξˆ 2 = E ξ 2 − E ξˆ 2 ,
{ } E ξ− ξˆ 2 = Cξξ − [Cξη ][Cηη ]−1[Cηξ ] 。
推论 1
如果复随机变量ξ和复随机变量η1,η2,η3,…,ηm 不相关,即相互正交,此 时无法用复随机变量η1,η2,η3,…,ηm 对复随机变量ξ进行估计。此时的最
1. 估值的意义
估值概述
随机变量的分布函数完全确定了它的统计特性,但是,基于这种统计特性的描述, 我们依然无法预测某一次试验的观察结果确定地是什么。
如果想用某一个确定的值去作为观察结果的估计值,可以利用概率分布函数去选择 一个合理的值。
数学期望:统计平均值,无条件估值,统计误差为方差
估值:利用已有的观测量的信息,估计估计量的取值,减小关于估计量的不确定性。
C[ξ j η ]
应使 K = E{ξ/η },即:ξˆ(η= Y) = E{ξ/η= Y}
定理
设随机矢量 ξ = (ξ 1,ξ 2,"ξ n) 和 η = (η 1,η 2,"η m) 的联合概率密度函数是,
fξ η (x1, x2 ,", xn ; y1, y2 ," ym ) 且 fη ( y1, y2 ," ym ) ≠ 0 ,则ξ关于η的最小均方误
= E{s(t) s(t)}− aE{x(t ) s(t)}
= Rss (0) − aRss (0)
=
Rss
(0)
−
Rss
Rss (0) (0) + Rnn
(0)
Rss
(0)
=
Rss
(0)
Rss
Rnn (0) (0) + Rnn
(0)
例3
设有零均值实平稳随机过程的信号 s(t),试根据 s(0)及 s(T)对 s(t)进行估值。
{ } + E [ξ− E{ξ/η}]⋅[E{ξ/η}− K]/ η= Y { } + E [ξ− E{ξ/η}]⋅[E{ξ/η}− K]/ η= Y
{ } + E ξ− E{ξ/η} 2 / η= Y { } { } = E E{ξ/η}− K 2 / η= Y + E ξ− E{ξ/η} 2 / η= Y
它们是统计独立的随机过程,实际测到的是 x(t)=s(t)+n(t),试根据 x(t)对 s(t)进行估值。 例 3,设有零均值实平稳随机过程的信号 s(t),试根据 s(0)及 s(T)对 s(t)进行估值。 例 4,利用 t 时刻随机过程 s(t)的观察值和它的导数 s’(t)观察值,对未来的 s(t+λ),
值,这时 ξˆ(η) = Aη+ b 称作为最佳线性估值。其中ξ是 n×1 的矢量,η是 m×1 的
矢量,A 是 n×m 的矩阵,b 是 n×1 的矢量。
问题:
确定 A、b
结论:
bj = Eξ j− A j Eη
( )( ) A j = C[ξjη]
−1
C[ηη ]
即,
ξˆj = Eξ j − C[ξ j η]C[ηη]−1Eη + C[ξ j η]C[ηη]−1η
解:
G 利用最佳线性估值原理,ξˆ = aTη= [Cξ η ]T [Cηη ]−1 ⋅η
s(t)
=
(Rss
(t)
Rss
(T
−
t))⎜⎜⎝⎛
Rss Rss
(0) (T )
Rss Rss
(T ) (0)
⎟⎟⎠⎞
−1
⎜⎜⎝⎛
s(0) s(T )
⎟⎟⎠⎞
= as(0) + bs(T )
其中,
a = Rss (t)Rss (0) − Rss (T − t)Rss (T ) [Rss (0)]2 − [Rss (T )]2
其中一个重要的问题就是确定估值参数 估值的评估:分析估值误差
均方误差最小的最佳线性估计
估值问题
设ξ和η是两个随机矢量,两者存在联合分布,其中η是观察矢量,通过η对ξ进 行估值,得到符合某种准则的最佳估值ξ。
1 均方误差最小的估值问题
均方误差最小的估值问题
设ξ和η是两个随机矢量,两者存在联合分布,设η是观察矢量,通过η对ξ进行 估值,求均方误差最小的估值ξ。
{ } { } 相应的最小均方误差是, E⎩⎨⎧ξ − ξˆ 2 ⎭⎬⎫ = E ξ 2 − E ξξˆ*
{ } E s(t + λ ) − sˆ(t + λ ) 2 = E{[s(t + λ ) − as(t)]s(t + λ )}
= E{s(t + λ ) s(t + λ )}− aE{s(t ) s(t + λ )}
= Rss (0) − aRss (λ ) = Rss (0) − [Rss (λ )]2 / Rss (0)
讨论 1:如果随机过程的相关函数是 Rss (τ ) = σ 2e−α τ
a = Rss (λ ) / Rss (0) = e−α λ
{ } ( ) E s(t + λ ) − sˆ(t + λ ) 2 = σ 2 1 − e−2α λ
估值准则的选取:有实际意义,有用;并且是能够得到简单解的。
“估计的均方误差最小”的估计准则是应用最广的一种估计思想,简称 MS 估计, 相应的估计误差简称 MMSE。
“输出信噪比最大”是雷达系统中最佳接收的工作原理。
在一定的估计准则下,有不同的解决具体估值问题的方法:
9 非线性估值 9 线性估值 9 维纳滤波 9 匹配滤波 9 递归线性均方估值
{ } { } 差估计为 ξˆ(η) = E{ξ /η },它满足 E ξ− ξˆ(η) 2 = min E ξ− g(η) 2 。
例:
设ξ和η服从二元高斯分布,求最佳估值 ξˆ(η )
解:
( ) fξ /η (x /η = y) =
2π
1 1− r2
σ
2 ξ
⎛ exp ⎜ −
⎜⎝
1 2(1− r2 )σ
计复随机变量ξ,其估计误差 e = ξ − ξˆ 。若 e 和η1,η2,…,ηm 正交,则此估计是
最小均方误差线性估计。
{ } { } 利用 E e ⋅η j = E [ξ − (a1η 1+ a2η 2+ a3η 3+" + amη m)]⋅η j = 0
注意:两种方法得到的结论一致,正交性原理的推导证明中,先假设
E {ξ} = E {η} = 0 ,进一步的论述中说明了 E {ξ} ≠ 0, E {η} ≠ 0 时,满足正交性原理
的线性估计仍然是最小均方误差估计。
最佳线性估计的均方误差
根据正交性原理,均方误差最小的最佳线性估计的误差与观察量正交,从而与估计值正 交:
{ } { } E e ⋅ η j = E (ξ− ξˆ)η j = 0
减少量是[Cξ η ][Cηη ]−1[Cξ η ]T 。
推论 3
如果复随机变量η1,η2,η3,…,ηm 彼此之间相互正交,有
( ) aj =
Cξ η ⋅ Cηη −1
= C C j j
ξ η j η jη j
推论 4
增加新的数据可以改善原有的估值,但是如果增加用来估值的数据η1+m,η2+m,…
= ( ρσ ξ )2
2 均方误差最小的线性估计
对于正态分布的随机变量,ξ关于的η最小均方误差估计ξˆ(η) = E(ξ /η ) 是一个线性 估计,对于非正态分布的随机变量,估计ξˆ(η) = E(ξ /η ) 一般不是线性的。这时需要找到
一个关于η的线性函数作为最佳估计。
定义:
{ } ξ关于的η估计 ξˆ(η) = Aη+ b ,使得 到最小
2. 估值的应用
最基本的问题是利用对一个随机变量的观测对另一个随机变量进行估计
根据当前取值来预测下一个时刻取值的预测编码; 根据接收的信号序列来估计发送序列某个时刻发送值的均衡问题; 根据信号和噪声之和的序列来估计信号的噪声抑制问题;
3. 估值问题的研究内容与方法
估值研究的是统计意义上的估计问题。由于是对一个不确定量的估计,一定存在估 计误差,关键在于利用某种原则、方法选择估计值,使估计误差在某种意义下是最小的。
ξˆ = Eξ− CξηCηη −1Eη + CξηCηη −1η
如果ξ, η = (η 1 η 2 "η m )T 均值为零,则有
ξˆ j
η = C C −1 [ξ j η] [η η]
方法: 1)极值分析法
求估值的均方误差
{ } ( ) ( ) E
⎡⎣ξ j− ξˆ j ⎤⎦2 /η
= Dξ j+ A jC[ηη ]A j H − A j
讨论 2:在上述条件下,估计误差正交于 s(u), u < t
E{[s(t + λ ) − as(t )]⋅ s(u)} = Rs s (t + λ − u) − aRs s (t − u)
σ σ σ σ =
e2 −α (t+λ −u) − a e2 −α (t−u) =
e − e e 2 −α (t+λ −u)
佳估计就是ξˆ(η) = 0 。
推论 2
如果复随机变量ξ和复随机变量η1,η2,η3,…,ηm 有相关性,进行估计,相 应的均方误差就减少了,
{ } { } E e 2 = E⎩⎨⎧ξ − ξˆ 2 ⎭⎬⎫ = E (ξ− ξˆ)(ξ− ξˆ) 。
= Cξ ξ − [Cξ η ][Cηη ]−1[Cξ η ]T
则:
{ } E (ξ− ξˆ)ξˆ = 0
因此:
{ } { } { } E ξ− ξˆ 2 = E ξ 2 − E ξˆ 2 ,
{ } E ξ− ξˆ 2 = Cξξ − [Cξη ][Cηη ]−1[Cηξ ] 。
推论 1
如果复随机变量ξ和复随机变量η1,η2,η3,…,ηm 不相关,即相互正交,此 时无法用复随机变量η1,η2,η3,…,ηm 对复随机变量ξ进行估计。此时的最
1. 估值的意义
估值概述
随机变量的分布函数完全确定了它的统计特性,但是,基于这种统计特性的描述, 我们依然无法预测某一次试验的观察结果确定地是什么。
如果想用某一个确定的值去作为观察结果的估计值,可以利用概率分布函数去选择 一个合理的值。
数学期望:统计平均值,无条件估值,统计误差为方差
估值:利用已有的观测量的信息,估计估计量的取值,减小关于估计量的不确定性。
C[ξ j η ]
