北大随机过程课件:第_3_章_第_5_讲_更新过程
随机过程课件打印版

当An An 1 , n 1
9
A1 A2
连续性定理
A1 A2
则称P为(Ω,F)上的概率,(Ω,F,P)称 为概率空间,P(A)为事件A的概率。
An Ai 新事件:lim n i 1
lim An Ai
n i 1
3 对于R n中的任意区域, a1 , b1; a2 , b2 ;;a n , bn ,其中 ai bi , i 1,, n
F b1 , b2 ,, bn F b1 ,, bi 1 , ai , bi 1 ,bn F b1 ,, bi 1 , ai , bi 1 ,, b j 1 , a j , b j 1 ,, bn ,
d P({e : g( X ) y, e X }) dy
如果上式右端概率的导数对于y处处存在,那么这 个导数就给出了随机变量Y的概率密度
fY ( y)
19
20
n维联合分布函数F x1 , x 2 , x n 具有下列性质 :
三、边缘分布
若二维联合分布函数中有一个变元趋于无 穷,则其极限函数便是一维分布函数,对于这 种特殊性质,我们称其为边缘分布。 对于任意两个随机变量X,Y,其联合分布函数为: F ( x, y ) 则: FX ( x ) P ( X x ) P ( X x , Y ) F ( x , )
P( X x,Y y) P((X x) (Y y)) P( X x)P(Y y)kFra biblioteknpkq
nk
, k 0 ,1 , 2 n
p
P(X k)
k
k!
北大随机过程课件:第章第讲高斯随机变量(PDF)

高斯分布随机变量及其性质¾ 中心极限定理 ¾ 高斯分布的随机变量¾ N 维高斯随机变量的统计独立特性 ¾ 高斯随机变量的线性变换¾高斯分布的随机变量的条件分布和边缘分布1.引言.中心极限定理给定n 个独立的随机变量,1,2,i x i ="n ,它们的和为:12n x x x x =+++",x 的均值为12n ηηηη=+++",方差为222212n σσσσ=+++",在一定的条件下,当n 趋于无穷时,x 的概率密度函数f(x)趋向于具有相同均值和方差的高斯(正态)分布:22()2()x f x ησ−−≈中心极限定理逼近的性质以及对一个给定误差所需的随机变量的数目n 依赖于概率密度函数()i f x 。
2高斯分布的随机变量典型高斯分布的随机变量的概率密度与特征函数的描述。
()f x ξ,{}()()ju jux u E e e f x dx ξξξ∞−∞Φ==∫2.1一元高斯随机变量一元高斯随机变量N(0,1),均值为零、方差为1,其概率密度和特征函数:2221)(x ex f −=πξ22)(u eu −=Φξ一元高斯随机变量N(μ,σ2),均值为μ、方差为σ2,其概率密度和特征函数:222)(221)(σμξπσ−−=x ex f222)(u u j eu σμξ−=Φ2.2二元高斯随机变量二元高斯随机变量21,ξξ,均值为零、协方差矩阵为:⎟⎟⎠⎞⎜⎜⎝⎛=11r r B ,121111r B r r −−⎛⎞=⎜⎟−−⎝⎠,21B r =− 其二元概率密度和特征函数为:⎟⎟⎠⎞⎜⎜⎝⎛+−−−−=]2[)1(21exp 121),(222121222121x x rx x r r x x f πξξ ⎟⎠⎞⎜⎝⎛++−=Φ]2[21exp ),(2221212121u u u r u u u ξξ二元高斯随机变量21,ξξ,其均值、协方差矩阵为,μμμξξ=⎟⎟⎠⎞⎜⎜⎝⎛=⎟⎟⎠⎞⎜⎜⎝⎛2121E , ⎟⎟⎠⎞⎜⎜⎝⎛=22212121σσσσσσr r B , ()222121B r σσ=− ()()22121222212121211222122111111r B r r r r r σσσσσσσσσσσσσσ−⎛⎞−=⎜⎟⎜⎟−−⎝⎠⎛⎞−=⎜⎟⎜⎟−−⎝⎠其二元概率密度和特征函数为1221122(,exp f x ξξ⎛⎞⎤⎜⎟⎥⎜⎟⎢⎥⎝⎠⎝⎠⎝⎠⎝⎠⎣⎦⎝⎠()⎟⎠⎞⎜⎝⎛++−+=Φ]2[21exp ),(222221212121221121u u u r u u u j u u σσσσμμηξ 2.3 n 元高斯随机变量n 元高斯随机变量ξ,其均值、协方差矩阵(正定的)为,⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛=⎟⎟⎟⎟⎟⎠⎞⎜⎜⎜⎜⎜⎝⎛=nn n n n n n b b b b b b b b b B "###""#21222121121121,μμμμ 其n 元概率密度和特征函数为()[]()()⎟⎠⎞⎜⎝⎛−−−=−μx μx x 12/121exp 21)(B B f Tnπξ⎟⎠⎞⎜⎝⎛−=Φu u u μT T B j U 21exp )(ξ其中,()Tn x x x "21=x ,()Tn u u u "21=u考虑到矩阵是B 正定对称的,则存在一个非奇异矩阵L ,使得B=LL T ,作线性变换L ,)(1X L μx y −=−,X L μy x +=,111111)()()(−−−−−−=⋅==L L L L LL B t t tyy μx μx μx μx μx μx T X T X X t T X X T X L L L L B =−−=−⋅−=−−−−−−−)]([)]([)()()()()(11111对应这个变换的雅可比行列式是2/1B L ==∂∂yx ()[]()[]⎟⎠⎞⎜⎝⎛−=⋅⎟⎠⎞⎜⎝⎛−−−=−y y μx μx T n X T X nB B B Y f 21exp 21)()(21exp 21)(2/12/112/1ππη()[]⎟⎠⎞⎜⎝⎛−=∑=N n n n y 122/121exp 21π显然有1)()()(21===∫∫∫∫∫∫∞∞−∞∞−∞∞−∞∞−∞∞−∞∞−N dy dy dy Y f dYY f dX X f """"ηηξ2.4 n 元高斯随机变量的特征函数的计算考虑以下的矩阵运算XTTX T T X T T j jS j L j L j j μu y μu y u μy u x u +=+=+=)(其中:u u T T T L S L S==,2/2/)()(2/2/)()(211S S jS jS j jS j j B j T T X T T T X T T X T X T −−−−=−+=−=−−−−y y μu y y y μu y y x u μx μx x u TN 元高斯随机变量的特征函数是:{}()()()()()()()11/211/21/2()exp()exp()()11exp()exp 2211exp 221exp[/2]2exp[()(TTT TnT T nT T X n T E j j f d j B d B j B d B j S S jS j ξξπππ∞∞−∞−∞∞∞−−∞−∞∞∞−−∞−∞∞∞−∞−∞Φ==⎛⎞=−−−⎜⎟⎝⎠⎡⎤⎣⎦⎛⎞=−−−⎜⎟⎝⎠⎡⎤⎣⎦=−⎡⎤⎣⎦−−−∫∫∫∫∫∫∫∫u u x u x x x u x x μx μx u x x μx μxu μy y """")/2]exp[/2]exp[/2]exp[/2]T T X T T T X T T X S d j S S j LL j B =−=−=−yu μu μu u u μu u⎟⎠⎞⎜⎝⎛−=Φu u μu u B j T X T 21exp )(ξ当协方差矩阵是非负定的,可以证明若它的秩为r<n ,它的概率分布集中在r 维子空间上,这种分布是退化正态分布,或奇异正态分布。
随机过程的基本概念ppt课件

.
2.3 平稳随机过程
三、相关系数及相关时间
也称为归一化协方差函 数或标准协方差函数。
相关系数: rX()KXX 2 ()RX()X 2mX 2
相关时间:
0
0 rX()d
rX ( )
1
rX(0) 0.05
0
0
相关时间示意图
.
2.3 平稳随机过程
三、相关系数及相关时间
为随机过程X(t)的二维概率分布。定义
fX(x1,x2,t1,t2)2FX(xx11,xx22,t1,t2)
为随机过程X(t)的二维概率密度。 注意:X(t1)及X(t2)为同一随机过程上的随机变量。
.
2.2 随机过程的统计描述
2、二维概率分布
例2、设随机相位信号
X (n )co s( n/1 0 )
.
2.2 随机过程的统计描述
二、随机过程的数字特征(连续)
• 协方差函数
K X ( t 1 , t 2 ) E { [ X ( t 1 ) m X ( t 1 ) ] [ X ( t 2 ) m X ( t 2 ) ] } (1)如果 KX(t1,t2)0,则称 X (t1 )和 X (t2 )是不相关的。
.
2.3 平稳随机过程
一、定义
(1)严格平稳随机过程
f X ( x 1 , ,x n ,t 1 , ,t n ) f X ( x 1 , ,x n ,t 1 , ,t n )
一维概率密度: fX(x,t)fX(x)
二维概率密度: fX (x 1 ,x 2 ,t1 ,t2 ) fX (x 1 ,x 2 ,) t1 t2
接收机噪声
5
x1(t) 0
随机过程课件PPT资料(正式版)

☞随机事件:样本空间的子集,常记为 A ,B ,…它是满足某些条件的样本点所组成的集合.
排队和服务系统 ◙A∩勤B 奋⇔、A刻B :苦A、与合➢B作的、积探事索件;; 更新过程 为从事科学研究打下坚实的基础;
☞抽取的是精装中➢文版数学书 ⇒
➢ 时间序列分析
➢ 鞅过程
绪论
《随机过程》基础
概率(或然率或几率) ——随机事件出现的可能 性的量度;
概率论其起源与博弈、 、天气预报等问题有 关
⊕16世纪意大利学者开始研究掷骰子等赌博 中的一些问题;
⊕17世纪中叶,「现有两个赌徒相约赌若干 局,谁先赢S局就算赢了,当赌徒A赢K局(K<S), 而赌徒B赢L局(L<S)时,赌博中止,赌资应怎 样分才合理呢?」
随机过程课件
《随机过程》
➢ 教材: ◙ 张卓奎,陈慧婵,随机过程.西安电子科技大 学.2003.
➢ 主要参考文献: ◙ 胡奇英编著,随机过程.西安电子科技大学.1998. ◙ 周荫清 ,随机过程习题集. 清华大学出版社, 2004. ◙ 林元纟金烈 ,应用随机过程. 清华大学出版社, 2002.
……
➢ 随机过程理论在社会科学中例如在社会统计, 学、经 济、金融工程、管理中也得到极其广泛的应用。
➢ 为从事科学研究打下坚实的基础;
绪论
教学目标
➢ 充分理解、熟练掌握教材的内容 ◙ 熟练掌握基本的数学概念和定理;
◙ 熟练掌握随机过程研究对象的数学描述;
Hale Waihona Puke ➢ 通过学习和练习,具备一定的分析、解决本专业具体 问题的能力;
☞拉普拉斯曾说:“生活中最重要的问题,其中 绝大多数在实质上只是概率的问题”。
☞概率论是研究随机现象数量规律的数学分支。 在实际中,人们往往还需要研究在时间推进中某 一特定随机现象的演变情况,描述这种演变的就 是概率论中的随机过程。
北大随机过程课件:第3章第5讲更新过程

2.更新过程分析
2.1 计算 N(t)的概率分布
对于更新过程,当给定事件间隔 xn (n ≥ 1) 的概率分布函数 F(t),或概率密度函数
f(t) 时,计算 N(t)的概率分布。
设 Sn 的分布函数是 Fn (t) , Fn (t) 是 F (t) 的 n 次卷积;
设{N(t), t>0}是一个计数过程, xn (n ≥ 1) 表示第 n-1 次事件和第 n 次事件的时间间隔,
再设 {x1, x2 ,"} 为非负、独立、同分布的随机变量序列,则称计数过程{N(t), t>0}为更新过
程。 特点:根据事件间隔的特征(独立、同分布)定义; 举例: 假设灯泡的寿命是统计独立、同分布的随机变量,若每次使用一个灯泡,当灯泡损 坏后立刻更换新的,则在时间 t 内损害的灯泡数是一个更新过程{N(t), t>0},其中 N(t)是在时间 t 内损坏的灯泡数。
0
给定了更新过程强度 λ(t)后,更新过程间隔概率密度函数 f(t)可由上述积分方程求
解。
2.4 更新过程的极限,平均更新时间与更新速率
在有限的时间内更新的次数是有限的、当时间 t 趋于无穷时,更新的次数趋于无穷, 考虑到,
Sn 是第 n 次更新事件发生的时刻,
N(t)是直到时刻 t 发生更新事件的次数,
P{N (t) = n} = Fn (t) − Fn+1 (t) 。
2.2 计算更新过程的期望
∞
m(t) = E{N (t)} = ∑ nP{N (t) = n}
n=1
∞n
∞∞
随机过程_课件---第三章

随机过程_课件---第三章第三章随机过程3.1 随机过程的基本概念1、随机过程定义3-1 设(),,F P Ω是给定的概率空间,T 为一指标集,对于任意t T ∈,都存在定义在(),,F P Ω上,取值于E 的随机变量()(),X t ωω∈Ω与它相对应,则称依赖于t 的一族随机变量(){},:X t t T ω∈为随机过程,简记(){}tX ω,{}tX 或(){}X t 。
注:随机过程(){,:,}X t t T ωω∈Ω∈是时间参数t 和样本点ω的二元函数,对于给定的时间是()00,,t T X t ω∈是概率空间(),,F P Ω上的随机变量;对于给定样本点()00,,X t ωω∈Ω是定义在T 上的实函数,此时称它为随机过程对应于0ω的一个样本函数,也成为样本轨道或实现。
E 称为随机过程的相空间,也成为状态空间,通常用""t X x =表示t X 处于状态x 。
2、随机过程分类:随机过程t X 按照时间和状态是连续还是离散可以分为四类:连续型随机过程、离散型随机过程、连续随机序列、离散随机序列。
3、有穷维分布函数定义3-2 设随机过程{}t X ,在任意n 个时刻1,,n t t 的取值1,,nt tX X 构成n 维随机向量()1,,n t t XX ,其n 维联合分布函数为:()()11,,11,,,,nnt t nt t nF x x P X x Xx ≤≤其n 维联合密度函数记为()1,,1,,n t tn f x x 。
我们称(){}1,,11,,:1,,,nt t n n Fx x n t t T ≥∈ 为随机过程{}t X 的有穷维分布函数。
3.2 随机过程的数字特征1、数学期望对于任何一个时间t T ∈,随机过程{}t X 的数学期望定义为()()tX t t E X xdF x μ+∞-∞==?()t E X 是时间t 的函数。
2、方差与矩随机过程{}t X 的二阶中心矩22()[(())],tX t t t Var X E X E X t T σ==-∈称为随机过程{}t X 的方差。
《数学随机过程》PPT课件
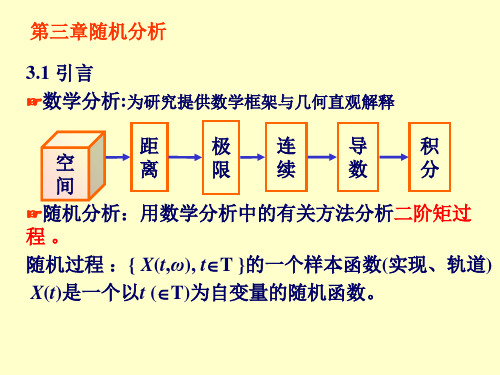
几何直观意义
3.3 随机分析初步
附注C—关于赋范线性空间概念的回顾
设V是一个线性空间,若 V,存在一个实数|| ||与
之对应,且具有下列性质:
(1) || ||0 , 且|| ||=0 =0 ; (2) ||c· ||= |c|·|| || , 特别 ||- ||= || ||; c R (3) || + || || ||+ || ||; V 则称|| || 为V中元素 的范数(norm)(模、长度),此时线
CXX (t1, t2 ) cov{ X (t1), X (t2 )} E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} | CXX (t1, t2 ) |2 | cov{ X (t1), X (t2 )} |2 | E{[ X (t1) mX (t1)][ X (t2 ) mX (t2 )]} |2 {E | [ X (t1) mX (t1)][ X (t2 ) mX (t2 )] |}2 E | X (t1) mX (t1) |2 E | X (t2 ) mX (t2 ) |2 D[ X (t1)]D[ X (t2 )]
3.3 随机分析初步
附注A—关于线性空间概念的回顾
设V是一个非空的集合,K是一个数域,又设
(a)在V中定义加法: , V : + V ; (b)在V中定义数乘: V, k K: k · V ; 且 , , V , k,l K , 满足 (1) k ,l K, , V : (2) +( +)= ( + )+ ; (3) + = + ; (4)0V, V: +0= ; (5) V, V: +=0 (6) 1 K: 1· = ; (7) k ,l K, V: (kl)· =k·(l) ; (8)k ,l K, V: (k+l) = k +l ; (9) k K, , V : k( + )= k + k .
随机过程 北京理工课件

π
2 2
2
3 2 2
P
π F (x; ) = 4
1 3
0, 1 , 3 2 , 3 1,
1 3
x < 2 2
1 3
∴
2 ≤ x < 2 2 ≤ x < x ≥ 3 2 2 3
2 2 2
X(
π
2
) = A cos π
∴
0, π F ( x, ) = 2 1,
4
随机过程 的有限维分布族
对任意固定的t∈ , 是一维随机变量, 对任意固定的 ∈T,X(t)是一维随机变量 其分 是一维随机变量 布函数是P{X(t)≤x}, 记为 记为F(x; t), 即 布函数是 F(x; t)= P{X(t)≤x}, 为随机过程X(t)的一维分布函数。 的一维分布函数。 称F(x; t)为随机过程 为随机过程 的一维分布函数 如对任意两个固定t 是二个随 如对任意两个固定 1 , t2∈T , X(t1) , X(t2)是二个随 机变量, 机变量,称 F(x1, x2 ; t1, t2) = P{X(t1)≤x1, X(t2) ≤x2} 为随机过程X(t) 的二维分布函数; 的二维分布函数; 为随机过程 一般地,对任意固定的t 一般地,对任意固定的 1, t2, … , tn∈T。X(t1), 。 个随机变量, X(t2) , … , X(tn)是n个随机变量,称 是 个随机变量 F(x1, …, xn ; t1, …, tn) = P{X(t1)≤x1, …, X(tn)≤xn} 5 为随机过程X(t) 的n 维分布函数 维分布函数. 为随机过程
= 0 取值仅一个0,且知 P ( X ( ) = 0) = 1 取值仅一个0 2 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Λ( s) =
φ (s) Λ( s) , φ ( s) = 1 + Λ(s) 1 − φ (s)
φ ( s) = Λ( s) − Λ( s )φ ( s)
对上式做拉氏反变换得到:
f (t ) = λ (t ) − ∫ λ (t − u ) f (u )du
0
t
给定了更新过程强度 λ(t)后,更新过程间隔概率密度函数 f(t)可由上述积分方程求 解。
定义
Λ ( s ) = ∫ λ (t )e − st dt , φ ( s ) = ∫ f (t )e − st dt , [φ ( s )] n = ∫ f n (t )e − st dt
0
0
∞
∞
∞
0
等式右端有,
∞ φ (s) = ∑ [φ ( s )] n , 1 − φ ( s ) n =1
更新强度拉氏变换的结果是:
其中 ( N (t ) + 1) N (t ) 随着 t 趋于无穷趋于 1, 上述不等式两端随着 t 趋于无穷,都趋于μ, 因此有,
N (t ) = 1/ μ t t lim =μ t →∞ N (t )
lim
t →∞
1/μ称为更新过程的速率:单位时间内的更新次数; μ称为更新过程的平均更新时间:平均的更新间隔。
更新。
S n (n ≥ 1) 是由 n 个相互独立的 x m (m = 1,2, " n) 组成。S n =k 由 k 个时间间隔构
成,表示经过 k 个时间间隔发生了 n 次更新事件(结束工作的事件)。k 个时间间隔 的最后一个时间间隔对应概率为 p 的结束工作的 1 个时间间隔,在它之前,总共 有 (k − 1) 个时间间隔,其中有 (n − 1) 个概率为 p 的结束工作事件的时间间隔,
λt
1!
e − λt
n −1
从0
( λ t ) e − λt 时间开始,到 t 时刻发生第 n 次事件的概率密度是 λ ⋅ ( n − 1)!
泊松过程中事件之间的时间间隔是呈负指数分布 泊松过程是更新时间间隔呈负指数分布的更新过程 事件间隔 x 呈负指数分布: f (t ) = λe
− λt
= f1 (t )
P{N (t ) = k } = Fk (t ) − Fk +1 (t )
i k ⎡ k −1 ( λt )i − λt ⎤ ⎡ λt ) − λt ⎤ (λt )k −λt ( e e ⎥ − ⎢1 − ∑ e ⎥= = ⎢1 − ∑ k ! ! ! i i i =0 i =0 ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ ⎣ ⎦
泊松过程作为更新过程的均值过程
⎡ n −1 ( λt )i − λt ⎤ m ( t ) = ∑ Fn (t ) = ∑ ⎢1 − ∑ e ⎥ i ! n =1 n =1 ⎢ i =0 ⎥ ⎣ ⎦ i i ∞ ⎡ ∞ ( λt ) e− λt − n−1 ( λt ) e− λt ⎤ = ∑ ⎢∑ ⎥ ∑ i i ! ! n =1 ⎢ i = 0 i =0 ⎥ ⎣ ⎦
1.2 更新过程的基本参数及其关系
N(t):[0,t)内发生的事件数,更新次数;
x n :第 n 次事件的更新间隔;
S n :第 n 次事件的更新时刻;
S n 与 x n 的关系:
S n = ∑ xi , S 0 = 0 表示过程的起始时刻;
i =1
n
若给定事件间隔 x n (n ≥ 1) 的概率分布函数 F(t),或概率密度函数 f(t) 时,设更新 概率密度函数是 f n (t ) , 因为 S n = 时刻 S n 的分布函数是 Fn (t ) 、
n
应用数学归纳法可以证明
更新时刻的概率密度函数:
F1 (t ) = ∫ f (t )dt = ∫ λe −λt dt = 1 − e −λt
t t 0 0
F2 (t ) = ∫ f 2 (t )dt = ∫ λ ⋅ λte −λt = 1 − e −λt − λte −λt
0 0
t
t
"
Fn (t ) = ∫ λ
λ (t ) =
∞ ∞ d d ∞ d m(t ) = ∑ Fn (t ) = ∑ Fn (t ) = ∑ f n (t ) dt dt n =1 n =1 dt n =1
对上式两端作拉氏变换,有
∞ − st − st ∫ λ (t )e dt = ∑ ∫ f n (t )e dt 0 n =1 0 ∞ ∞
2.2 计算更新过程的期望
m(t ) = E{N (t )} = ∑ nP{N (t ) = n}
n =1 ∞
= ∑∑ P{N (t ) = n} = ∑∑ P{N (t ) = n}
n =1 k =1 ∞ k =1 n = k
∞
n
∞
∞
= ∑ P{N (t ) ≥ k } = ∑ P{N (t ) ≥ n}
f (t ) = f1 (t ) ⊗ f 2 (t ) = ∫ λ e − λ (t − μ ) ⋅ λ e − λμ d μ
0 t
= ∫ e − λt ⋅ λ 2 d μ
0
t
= λ ⋅ λ te − λt
Sn
( λt )n −1 −λt = ∑ xi ,表示过程的第 n 次更新时刻; f n (t ) = λ ⋅ e (n − 1)! i =1
其中
<
S N ( t ) +1 t ≤ N (t ) N (t )
S N (t ) N (t ) S N (t ) N (t )
=
∑x
i =0
N(t)
i
N (t ) 是 t 时间内 N(t)个同分布独立随机变量的平均值,
<
S N ( t ) +1 N (t ) + 1 t ≤ ⋅ N (t ) N (t ) + 1 N (t )
∑ x ,{x , x
i =1 i
1
n
2
, "} 为
非负、独立、同分布的随机变量序列,则 Fn (t ) 应是 F (t ) 的 n 次卷积, f n (t ) 应是 f (t ) 的 n 次卷积。 N(t)与 S n 的关系: 如果 S n < t ,则在时间 t 内,至少发生了 n 次更新,即
p{Sn < t} = p{N (t ) ≥ n}
k =1 ∞ n =1
∞
= ∑ P{S n < t} =∑ Fn (t )
n =1 n =1
∞
m(t)是更新过程的数学期望,或者是更新过程的均值,表示[0,t)内发生事件的 平均次数;
2.3 计算更新过程的强度(平均强度)
更新过程的强度记为 λ (t ) ,表示某时刻发生更新的强度;
λ (t ) dt 表示 [t,t+dt)内发生更新事件的次数。
3.从更新过程研究泊松过程
12.2.1 泊松过程和更新过程: 泊松过程的分布特性: 在(0,t)时间间隔内发生 n 个事件的概率是
(λt ) n − λt e , n!
− λt
从 0 时间开始,到 t 时刻发生第 1 次事件的概率密度是 λ e 从 0 时间开始,到 t 时刻发生第 2 次事件的概率密度是 λ ⋅
马尔可夫过程 更新过程
更新过程的基本概念 定义、更新过程的基本参数,参数间的关系 更新过程分析 计算 N(t)的概率分布 计算更新过程的期望 计算更新过程的强度 计算更新过程的速率 典型更新过程-泊松过程 泊松过程的分布特性 更新时间间隔呈负指数分布的更新过程 事件间隔、更新时刻、计数过程 N(t)、均值过程、更新过程的强度 更新过程举例: 例1、 给定一种更新间隔分布,计算更新过程 N(t)的概率分布 例 2、给定更新强度,计算更新间隔的概率分布 例 3、给定更新间隔分布,计算更新过程的速率 例 4、计算更新过程的速率 例 5、计算更新过程的速率 例6、事件间隔呈负指数分布的更新过程
k =n t ⎛ k − 1⎞ n k −n = ∑⎜ ⎟ p (1 − p ) n − 1 k =n ⎝ ⎠ t
则 N (t ) 的概率分布为:
P{N (t ) = n} = Fn (t ) − Fn +1 (t )
t t ⎛ k − 1⎞ n ⎛ k − 1⎞ n +1 k −n k − n −1 ⎟ ⎜ = ∑⎜ − − p ( 1 p ) ∑ ⎜ n − 1⎟ ⎜ n ⎟ ⎟ p (1 − p ) k =n ⎝ k = n +1 ⎝ ⎠ ⎠
∞ ∞
= ∑∑
n =1 i = n − λt
∞
∞
( λt ) e − λt =
i
i!
∑∑
i =1 n =1 ∞
∞
i
( λt ) e − λt
i
i!
=e
∑
i =1
∞
( λt ) i
i!
i
=e
i
− λt
( λt ) λt ∑ i =1 ( i − 1) !
i −1
= λt ⋅ e
− λt
∑
i =0
∞
( λt )
i!
= λt
泊松过程作为更新过程的强度
λ (t ) =
d m(t ) = λ dt
结论:泊松过程是更新强度是常数的更新过程。
4.更新过程举例
例 1、计算更新过程 N(t)的概率分布
设 更 新 过 程 的 更 新 间 隔 x n (n ≥ 1) 是 非 负 整 数 的 i −1 , i ≥ 1 ,求更新过程 N(t)的概率分布。
更新时刻的概率密度函数:
S 0 = 0 ,表示过程的起始时刻;
S1 = x1 ,表示过程的第一次更新时刻; S1 = x1 与事件间隔 x 的分布相同,呈负指数分布: f (t ) = λ e − λt = f1 (t ) , S 2 = x1 + x 2 ,表示过程第一次更新时刻,它的分布是; f 2 (t ) = λ ⋅ λ te − λt S 2 = x1 + x 2 ,
