时序逻辑电路应用举例1
时序逻辑电路cp脉冲信参与输出

时序逻辑电路cp脉冲信参与输出时序逻辑电路是一种特殊类型的数字电路,其输出状态不仅取决于当前输入信号,还取决于输入信号的先前状态。
时序逻辑电路能够用于实现计数器、寄存器、状态机等电路,广泛应用于数字逻辑系统中。
在时序逻辑电路中,时钟信号是非常重要的一个输入信号。
时钟信号通常以周期性的脉冲信号形式存在,它会定时触发电路中的各个逻辑门或触发器。
当时钟信号上升沿或下降沿到来时,电路中的计算、存储或状态转换等操作会被触发。
因此,时钟信号的频率和相位是时序逻辑电路设计中需要考虑的重要因素之一。
时序逻辑电路中的脉冲信号也是一种重要的参与输出的信号。
脉冲信号使时序逻辑电路能够在特定的时钟脉冲到来时,对输入信号进行处理并生成输出信号。
举例来说,假设我们设计了一个简单的4位二进制计数器。
计数器需要从0开始依次计数到15,然后再回到0重新计数。
在这个计数器电路中,时钟信号驱动计数器进行计数操作,而脉冲信号则用于检测计数值是否达到15,如果达到15,则产生一个输出脉冲信号来表示计数器已经溢出。
具体实现时,我们可以使用触发器来存储当前计数值。
在每个时钟脉冲到来时,计数器会根据当前计数值进行加1操作,并将加1后的结果存储回触发器中。
当计数值为15时,则产生一个脉冲信号来表示溢出。
在这个例子中,脉冲信号直接参与计数器的输出,用于表示计数器是否溢出。
这种设计方式非常常见,在许多应用中都能见到。
脉冲信号作为一种简洁、高效的输出形式,通常用于表示某些特定事件的发生或状态的改变。
除了计数器,时序逻辑电路中的脉冲信号还可以用于实现状态机。
状态机是一种能够根据输入信号的不同而切换不同状态的电路。
在状态机中,脉冲信号通常用于触发状态的转换。
当输入信号满足某些条件时,状态机会生成一个脉冲信号,该脉冲信号用于切换到下一个状态或执行某个特定的操作。
总的来说,时序逻辑电路中的脉冲信号是一种重要的参与输出的信号。
脉冲信号能够在特定的时钟脉冲到来时,实现一些特定的操作,如计数、状态转换等。
时序逻辑电路应用举例

时序逻辑电路应用举例1 时序逻辑电路应用举例1
设计串行比较器。串行比较器对两个位数 设计串行比较器。 相同的二进制数A 进行比较,如果A>B, 相同的二进制数A,B进行比较,如果A>B, 则输出Z1Z0=10,A<B则输出 则输出Z1Z0=01, 则输出Z1Z0=10,A<B则输出Z1Z0=01, A=B则输出 A=B则输出Z1Z0=00。 则输出Z1Z0=00。
《数字逻辑电路》 数字逻辑电路》
时序逻辑电路应用举例1 时序逻辑电路应用举例1
分析:根据题意, 分析:根据题意,电路的输入为两个位数相同的数 输出为Z1Z0,状态A>B用S1,A<B用S2, 据A,B;输出为Z1Z0,状态A>B用S1,A<B用S2, A=B用S0表示 画出状态转换图如下: A=B用S0表示。画出状态转换图如下: 表示。
AB=11 × × × ×
《数字逻辑电路》 数字逻辑电路》
时序逻辑电路应用举例4 时序逻辑电路应用举例4
设计售4分的邮票机。 设计售4分的邮票机。自动售邮票机能 出售一张4分邮票,并向顾客退回余款, 出售一张4分邮票,并向顾客退回余款,它 的投币口每次只能接受一个1 的投币口每次只能接受一个1分、2分、5分 的硬币。 的硬币。
00/00 11/10 S5 10/00 01,10/01 00,01, 10/00 S0 01,11/00 10/00 10,11/01 S4 00/00 01/00 S3 00/00 10,11/00 01/00 S2 00/00 X1X2/F1F2 00/00 11/00 S1
01,11/01
《数字逻辑电路》 数字逻辑电路》
时序逻辑电路应用举例3 时序逻辑电路应用举例3
时序逻辑电路典型例题分析

第六章时序逻辑电路典型例题分析第一部分:例题剖析触发器分析例1在教材图6.1所示的基本RS触发器电路中,若⎺R、⎺S 的波形如图P6.1(a)和(b),试分别画出对应的Q和⎺Q端的波形。
解:基本RS触发器,当⎺R、⎺S同时为0时,输出端Q、⎺Q均为1,当⎺R=0、⎺S=1时,输出端Q为0、⎺Q为1,当⎺R=⎺S=1时,输出保持原态不变,当⎺R=1、⎺S=0时,输出端Q为1、⎺Q为0,根据给定的输入波形,输出端对应波形分别见答图P6.1(a)和(b)。
需要注意的是,图(a)中,当⎺R、⎺S同时由0(见图中t1)变为1时,输出端的状态分析时不好确定(见图中t2),图中用虚线表示。
例2 在教材图6.2.3(a)所示的门控RS触发器电路中,若输入S 、R和E的波形如图P6.2(a)和(b),试分别画出对应的输出Q和⎺Q端的波形。
解:门控RS触发器,当E=1时,实现基本RS触发器功能,即:R=0(⎺R=1)、S=1(⎺S=0),输出端Q为1、⎺Q为0;R=1(⎺R=0)、S=0(⎺S=1)输出端Q为0、⎺Q为1;当E=0时,输出保持原态不变。
输出端波形见答图P6.2。
例3在教材图6.2.5所示的D锁存器电路中,若输入D、E的波形如图P6.3(a)和(b)所示,试分别对应地画出输出Q和Q端的波形。
解:D锁存器,当E=1时,实现D锁存器功能,即:Q n+1=D,当E=0时,输出保持原态不变。
输出端波形见答图P6.3。
例4在图P6.4(a)所示的四个边沿触发器中,若已知CP、A、B的波形如图(b)所示,试对应画出其输出Q端的波形。
设触发器的初始状态均为0。
解:图中各电路为具有异步控制信号的边沿触发器。
图(a)为边沿D触发器,CP上升沿触发,Q1n+1= A,异步控制端S D接信号C(R D=0),当C=1时,触发器被异步置位,输出Q n+1=1 ;图(b)为边沿JK触发器,CP上升沿触发,Q2n+1= A⎺Q2n +⎺BQ2n,异步控制端⎺R D接信号C(⎺S D =1),当C=0时,触发器被异步复位,输出Q n+1=0;图(c)为边沿D触发器,CP下降沿触发,Q3n+1= A,异步控制端⎺S D接信号C(⎺R D =1),当C=0时,触发器被异步置位,输出Q n+1=1;图(d)为边沿JK触发器,CP下降沿触发,Q4n+1= A⎺Q4n +⎺BQ4n,异步控制端R D接信号C(S D =0),当C=1时,触发器被异步复位,输出Q n+1=0。
MSI时序逻辑电路及其应用电路设计

1
1
1
0 保持
QD是最高位,QA是最低位。
CO是加计数进位输出端;
BO是减计数借位输出端。
2005-6-4
9
74LS192 引脚图
74LS192时序图
2005-6-4
10
30s计时器的设计
Q7 Q6 Q5 Q4
Q3 Q2 Q1 Q0
76 2 3
76 2 3
13 BO
Q3 Q2 Q1 Q0 4 CPD
7 CTP
D3 D2 D1 D0
2 6 543
+5V
84
10Hz 3
7
+5V 5.1k
555 6 2
4.7k
5
1
0.1F
10F
8
30s计时器的设计
74LS192 是双时钟加/减十进制 同步计数器,其功能表为:
UP DOWN LOAD CLR 操 作
X
X
X
1 清零
X
X
1
1
0
0 置数
1
0 加计数
1
0 减计数
➢ 可由555定时器或石英晶体振荡器构成
30s计时器的设计
➢ 由各种有递减计数功能的IC芯片构成 ➢ 由CPLD构成
译码显示器的设计 控制电路的设计(难点)
➢ 根据设计要求,用试凑法设计
2005-6-4
7
2005-6-4
秒脉冲发生器的设计
1 Hz
1
15
10 +5V
CO
CTT
CC40161
9 LD
2005-6-4
16
篮球竞赛 24s 定时器设计
参考框图
振分 荡频 器器
触发器和时序逻辑电路

(2) 第二位触发器 FF1 ,在 Q0 = 1 时再来一种时钟脉冲才翻转,故 J1 = K1 = Q0 ;
大家网:
(3) 第三位触发器 FF2 ,在 Q1= Q0 = 1 时再来一种时钟脉冲才翻转,故 J2 = K2 = Q1Q0 ;
大家网:
只有当初钟脉冲来到后,即 CP = 1 时,触发器才按 R 、S 端旳输入状态 来决 定其输出状态。
触发器置R和D0 或置是S1直D,接一置般0用和于直置接初置态1。端在,工就作是过不程经中过它时们钟处脉于冲1 旳态控。制能够对基本
可控 RS 触发器旳逻辑式
Q S CP Q ,
可分四种情况分析CP = 1 时触 发器旳状态转换和逻辑功能,如右 表所示。
转一次,即
,具有计数功能。
SD
S
Q
D
1D
CP
C1
Q
RD
R
Q Q n1
n
上升沿 D 触发 器图形符号
1D
Q
CP
C1
Q
D 触发器转换 为 T 触发器
大家网:
返回
14.2 寄存器
寄存器用来临时存储参加运算旳数据和运算成果。
14.2.1 数码寄存器
下图是由 D 触发器(上升沿触发)构成旳四位数码寄存器,这是并行输入/并行 输出旳寄存器。工作之初要先清零。
时序逻辑电路旳特点:它旳输出状态不但决定于当初旳输入状态,而且还与电 路旳原来状态有关,也就是时序逻辑电路具有记忆功能。
触发器是时序逻辑电路旳基本单元。
大家网:
14.1 双稳态触发器
14.1.1 RS 触发器
时序逻辑电路
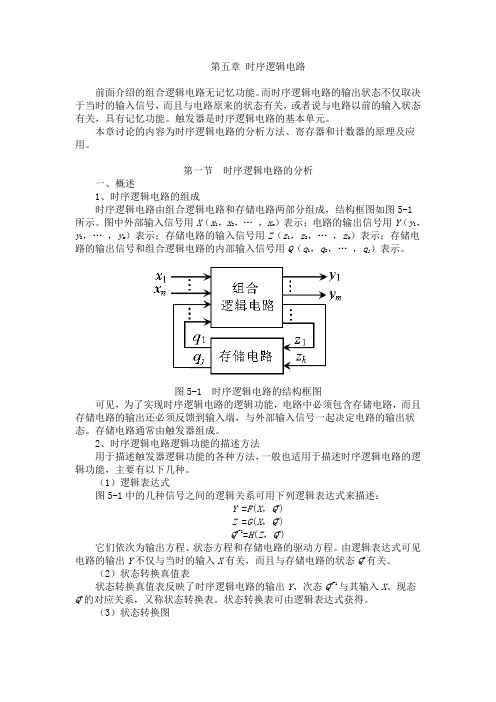
第五章时序逻辑电路前面介绍的组合逻辑电路无记忆功能。
而时序逻辑电路的输出状态不仅取决于当时的输入信号,而且与电路原来的状态有关,或者说与电路以前的输入状态有关,具有记忆功能。
触发器是时序逻辑电路的基本单元。
本章讨论的内容为时序逻辑电路的分析方法、寄存器和计数器的原理及应用。
第一节时序逻辑电路的分析一、概述1、时序逻辑电路的组成时序逻辑电路由组合逻辑电路和存储电路两部分组成,结构框图如图5-1所示。
图中外部输入信号用X(x1,x2,…,x n)表示;电路的输出信号用Y(y1,y,…,y m)表示;存储电路的输入信号用Z(z1,z2,…,z k)表示;存储电2路的输出信号和组合逻辑电路的内部输入信号用Q(q1,q2,…,q j)表示。
图5-1 时序逻辑电路的结构框图可见,为了实现时序逻辑电路的逻辑功能,电路中必须包含存储电路,而且存储电路的输出还必须反馈到输入端,与外部输入信号一起决定电路的输出状态。
存储电路通常由触发器组成。
2、时序逻辑电路逻辑功能的描述方法用于描述触发器逻辑功能的各种方法,一般也适用于描述时序逻辑电路的逻辑功能,主要有以下几种。
(1)逻辑表达式图5-1中的几种信号之间的逻辑关系可用下列逻辑表达式来描述:Y =F(X,Q n)Z =G(X,Q n)Q n+1=H(Z,Q n)它们依次为输出方程、状态方程和存储电路的驱动方程。
由逻辑表达式可见电路的输出Y不仅与当时的输入X有关,而且与存储电路的状态Q n有关。
(2)状态转换真值表状态转换真值表反映了时序逻辑电路的输出Y、次态Q n+1与其输入X、现态Q n的对应关系,又称状态转换表。
状态转换表可由逻辑表达式获得。
(3)状态转换图状态转换图又称状态图,是状态转换表的图形表示,它反映了时序逻辑电路状态的转换与输入、输出取值的规律。
(4)波形图波形图又称为时序图,是电路在时钟脉冲序列CP的作用下,电路的状态、输出随时间变化的波形。
应用波形图,便于通过实验的方法检查时序逻辑电路的逻辑功能。
若干典型的时序逻辑集成电路

FF0 FF1 FF2 FF3
0 00 0
Q0n+1=DSI Q1n+1 = Q0n Q2n+1 =Qn1 Q3n+1 =Qn2
1CP 后 1 2CP 后 1 3CP 后 0 4CP 后 1
10 0 0 1 10 0 0 11 0 1 01 1
1011 DSI CP
FF0 Q0 FF1 Q1 FF2 Q2 FF3
D1
1R R
D2 1S C1
D2
1R R
D3 1S C1
D3
1R R
CP
CR
Q0
Q1
Q2
Q3
74HCT194 的功能表
输入
输出
清 控制信 串行输
零号
入
时
并行输入
CR
S1
S0
右 移
左 移
钟 CP
DI0
DI1
DI2
DI3
Q
n1 0
Q1n1Q
2n1Q
n1 3
行
DSR DSL
L ×× × × × × × × × L L L L1
H LL×× H LHL × H LHH× HHL× L H HL × H H HH× ×
×
×
×
×
×
Q 0n
Q1n
Q
n 2
Q
n 3
2
↑ ↑
× ×
× ×
× ×
× ×
L H
Q
n 0
Q 0n
Q1n Q1n
Q
n 2
Q
n 2
3 4
↑
×
×
×
×
Q1n
Q
数电第六章时序逻辑电路

• 根据简化的状态转换图,对状态进行编码,画出编码形式 的状态图或状态表
• 选择触发器的类型和个数 • 求电路的输出方程及各触发器的驱动方程 • 画逻辑电路图,并检查电路的自启动能力 EWB
典型时序逻辑集成电路
• 寄存器和移位寄存器 – 寄存器 – 移位寄存器 –集成移位寄存器及其应用 • 计数器 – 计数器的定义和分类 – 常用集成计数器 • 74LVC161 • 74HC/HCT390 • 74HC/HCT4017 – 应用 • 计数器的级联 • 组成任意进制计数器 • 组成分频器 • 组成序列信号发生器和脉冲分配器
– 各触发器的特性方程组:Q n1 J Q n KQ n CP
2. 将驱动方程组代入相应触发器的特性方程,求出各触发器 的次态方程,即时序电路的状态方程组
n n FF0:Q0 1 Q 0 CP n n n FF1:Q1 1 A Q0 Q1 CP
同步时序逻辑电路分析举例(例6.2.2C)
分析时序逻辑电路的一般步骤
• 根据给定的时序电路图写方程式 – 各触发器的时钟信号CP的逻辑表达式(同步、异步之分) – 时序电路的输出方程组 – 各触发器的驱动(激励)方程组 • 将驱动方程组代入相应触发器的特性方程,求出各触发器 的次态方程,即时序电路的状态方程组 • 根据状态方程组和输出方程组,列出该时序电路的状态 表,画状态图或时序图 • 判断、总结该时序电路的逻辑功能
• 电路中存在反馈
驱动方程、激励方程: E F2 ( I , Q )
状态方程 : Q n1 F3 ( E , Q n ) • 电路状态由当前输入信号和前一时刻的状态共同决定
• 分为同步时序电路和异步时序电路两大类
什么是组合逻辑电路?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《数字逻辑电路》
时序逻辑电路应用举例2
y1y2 S0 S1 S2 S3 S4 S5 X1X2=00 S0/00 S1/00 S2/00 S3/00 S4/00 S5/00 y1n+1y2n+1/F1F2 X1X2=01 X1X2=11 S0/00 S0/00 S3/00 S4/00 S0/01 S0/01 S1/00 S0/00 S0/00 S0/01 S0/01 S0/10 X1X2=10 S0/00 S2/00 S0/00 S0/01 S5/00 S0/01
00,11/00 0 10/10
00,01,10,11/10 S1
00,01,10,11/01 S2
01/01 AB/Z1Z2
《数字逻辑电路》
时序逻辑电路应用举例1
y1n+1y0n+1/Z1Z0
y1y0 S0 S1 S2
AB=00 S0/00 S1/10 S2/01
AB=01 S2/00 S1/10 S2/01
《数字逻辑电路》
时序逻辑电路应用举例4
根据上述分析,得出状态转换图如下:
000/0000 S 001/1001 0 100/1000 010/1001 001/1100 000/0000 S3 010/1000 001/1011
100/0000 001/1010 S1 000/0000
010/0000
《数字逻辑电路》
时序逻辑电路应用举例4
解:设1分、2分、5分分别用x1、x2、x3表示,1 表示有输入,0表示无输入;给出邮票用y1表示,1 表示给出邮票;退回余款应有0分、1分、2分、3 分、4分四种情况,用y2y3y4的组合表示,如下表: y2y3y4 余款 000 0分 001 1分 010 2分 011 3分 100 4分
S0 S1 S2 S3
AB=00 S0/00 S1/00 S2/00 S3/00
AB=01 S0/11 S0/11 S0/11 S0/11
AB=10 S1/00 S2/00 S3/00 S0/10
AB=11 × × × ×
《数字逻辑电路》
时序逻辑电路应用举例4
设计售4分的邮票机。自动售邮票机能 出售一张4分邮票,并向顾客退回余款,它 的投币口每次只能接受一个1分、2分、5分 的硬币。
AB=11 S0/00 S1/10 S2/01
AB=10 S1/00 S1/10 S2/01
《数字逻辑电路》
时序逻辑电路应用举例2
设计一简易保密门。一个用两个按钮X1 X2 控制的保密门,仅当按以下次序操作时才 能打开:(1)同时按一下X1和X2;(2)先 按一下X1再按一下X2;(3)先按一下X2再 按一下X1;(4)同时按一下X1和X2。操作 时,如果有一项不符,必须从头启动才有可能 把门打开,而且在进行(3)和(4)操作时有 误,还要发出报警信号。
100/0000
010/0000 100/0000 x1x2x3/y1y2y3y4 S2 000/0000
《数字逻辑电路》
时序逻辑电路应用举例4
q1q2 S0 S1 S2 S3 000
S0 /0000 S1 /0000 S2 /0000 S3 /0000
001
S0 /1001 S0 /1010 S0 /1011 S0 /1100
q1n+1q2n+1/y1y2y3y4 010 011 100 101
S2 /0000 S3 /0000 S0 /1000 S0 /1001
110 111
× × × ×
S1 /0000 S2 /0000 S3 /0000 S0 /1000
× × × ×
× × × ×
× × × ×
《数字逻辑电路》
时序逻辑电路应用举例4
《数字逻辑电路》
时序逻辑电路应用举例3
根据上述分析,得出状态转换表和状态转换图如下0 10/00 S2 00/00 AB/XY
S0
S1
01/11 10/10 00/00 S3
10/00
《数字逻辑电路》
时序逻辑电路应用举例3
y1n+1y2n+1/XY y1y2
根据上述分析,得出状态转换图如下:
x3/1001 S0 x1/1000 x2/1001 x3/1100 S3 x2/1000 x3/1011 x2/0000 x1/0000 x1x2x3/y1y2y3y4 S2 x1/0000 x3/1010 S1
《数字逻辑电路》
时序逻辑电路应用举例1
设计串行比较器。串行比较器对两个 位数相同的二进制数A,B进行比较,如果 A>B,则输出Z1Z0=10,A<B则输出 Z1Z0=01,A=B则输出Z1Z0=00。
《数字逻辑电路》
时序逻辑电路应用举例1
分析:根据题意,电路的输入为两个位数相同的数 据A,B;输出为Z1Z0,状态A>B用S1,A<B用 S2,A=B用S0表示。画出状态转换图如下:
《数字逻辑电路》
时序逻辑电路应用举例2
解:设F1为开门信号,F2为报警信号; X1X2为两个按钮输入; S0为起始状态。 根据题意画出的状态转换图如下:
00/00 11/10 S5 10/00 01,10/01 01,11/01 10,11/01 S4 00/00 01/00 S3 00/00 10,11/00 01/00 S2 00/00 00,01, 10/00 S0 00/00 11/00 01,11/00 S1 10/00 X1X2/F1F2
《数字逻辑电路》
时序逻辑电路应用举例3
设计简易自动售铅笔机。它的投 币口每次只能投入一角或五角的硬币,投 入四个一角硬币机器给出一只铅笔;投入 一个五角硬币机器给出一只铅笔的同时找 回(并且只能找回)一个一角硬币。
《数字逻辑电路》
时序逻辑电路应用举例3
分析: 输入变量:投入硬币;投入一角硬币 A=1,未 投入A=0;投入五角硬币 B=1,未投入B=0; 输出变量:给出铅笔 X=1,否则X=0;给出一 角硬币 Y=1,否则Y=0。 设未投入硬币前的状态为S0,投入一个一角 硬币后状态为S1,投入两角后状态为S2,投入 三角后状态为S3在S3状态下再投入一角硬币, 则状态应返回S0的同时,使X=1。在任何状态下 投入五角硬币,状态返回S0的同时,使X=1, Y=1。所以电路应有4个不同的状态,2个输入变 量和2个输出变量。
