XRD-单晶
XRD(4-衍射仪法)

10
试样中包含了无数个取向不同 但结构一样的小晶粒。
当一束单色X光照射到样品上 时,对晶体的某一面网 (hkl),总有某些小晶粒的 (hkl)面能恰好满足布拉格 条件而产生衍射。
由于试样中小晶粒数量巨大,所以能够满足布拉格条件的面 很多,与入射线的方位角都是θ,因而它们的衍射线分布在 一个以入射线为轴、以衍射角2θ位半顶角的圆锥面上。
➢ 保证衍射强度值有很好的重复性和避免择优取向 ➢ 衍射峰宽化
粉末平板样品的制备
背压法
正压法
其它样品的制备
35
§4 X射线衍射方法
第一章 习题4
1、粉末或多晶体的衍射原理是什么? 2、衍射仪主要结构组成及其功能是什么? 3、什么是衍射仪圆,什么是聚焦圆? 4、为了满足聚焦几何条件,样品必须制成平板状,同时衍射
计数率仪等。
15
17
(1)测角仪
A、测品台 大转盘—X射线源S 、接收狭缝RS
衍射仪轴—大小转盘的共同轴线O 衍射仪圆—圆周上安装有X射线辐射探
测器D、固定的X光源入射点(焦点S)
平板状粉末多晶样品安放小转 盘正中间的样品台上,并保证 试样表面与O轴线严格重合。
B、衍射线强度 I 的确定
绝对强度:由定标器所测得的计数率,单位为cps, 即每秒多少个计数。
相对强度:以最强峰的强度作为100,然后将其它衍射峰 与最强峰强度进行对比。
衍射峰强度的测量方法主要有
峰高强度测量 积分强度测量
31
(a)峰高强度
以减去背景后的峰顶高度代表整个衍射峰的强度。
在一般的物相定性分析工作中,多采用峰高强度。
Rigaku D/max-1400型 X射线衍射仪
单晶XRD分析
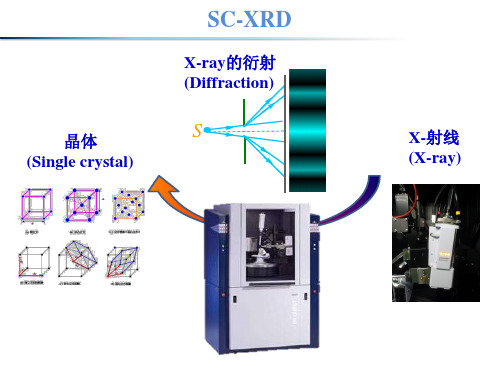
X-射线源
✓ Cu 光源的散射强度= 6-10 倍Mo光源 ✓ 所以 60秒Mo光源的数据收集 ≈ 10秒Cu光源数据收集 ✓ Cu光源对测试小或散射弱的晶体有很大的帮助
但是...
Cu光源的吸收效应 大于Mo光源
体样品。 ——请记住,常常小晶体的质量会更好。 ➢ 挑选面/角清晰的晶体;避免挑选有裂缝和表面有缺陷的晶体;从簇状或
薄片状晶体中分离出单颗晶体(小心处理以免损坏晶体)。 ➢ 将挑选好的晶体转移到合适的上样工具上—尽量少裹油、尽量减少样品转
移到衍射仪上的时间、尽量减少在转移过程中对晶体的损坏。 ➢ 对心—确认晶体处于低温气流中,并通过一幅衍射照片来快速评估晶体质
重金属 (Pt, Pb, Hg, Bi 等)将导致强的吸 收效应。所以,常 常使用Mo光源来测 试这类样品。
应用方向 无机晶体/有机金属配合物 大/超分子 绝对构型(有机晶体) 高压应用 小/衍射弱的晶体 蛋白质 电子密度 强吸收晶体 准晶 粉末
Mo Cu ✓
✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓ ✓✓
晶体
测试分析
更多仪器和测试操作将在上机演示中讲解
个人观点供参考,欢迎讨论
HK L ; I
-1 2 4 ; 3678 -2 0 2 ; 2354 1 2 -4 ; 3496
X-rays
衍射
晶体大小<0.5 mm
数据处理与结构精修
已收到的衍射点: HK L ; I -1 2 4 ; 3678 -2 0 2 ; 2354 1 2 -4 ; 3496
结构解析 Cycle 2 : R1 = 11.28% Cycle 3 : R1 = 8.49% Cycle 4 : R1 = 7.21% Cycle 5 : R1 = 5.73% (final refined structure)
单晶XRD分析2015 2

单晶XRD分析2015 2
浓度 C
当溶液浓度增加达到 过饱和状态时,溶质 将以固体的形式从溶 液中析出
固体溶液
固体析出涉及两个过程: ① 形成晶核; ② 晶核进一步长大;
产生大量微晶; 微晶易团聚; 粉末状; 沉淀过程
晶体内部易产生缺陷; 容易包裹母液;
二者速率合适方可
单晶培养条件 需要摸索; 细心调控条件; 具有很强经验性
单晶XRD分析2015 2
小分子
三维结构
精确的键长 120° 键角数据
活性位点的形 状和化学结构
蛋白质的三维结构/ 折叠
蛋白质晶体结构
单晶XRD分析2015 2
化学晶体学 Chemical Crystallography
➢ 确定分子立体结构 • 确定新的无机和金属有机化合物结构的主要技术 • 广泛应用于有机物的结构尤其是立体结构的确定 • 有机物/天然产物/药物分子的绝对构型确定 ➢ 确定分子结构参数 • 键长 +/- 0.001 Å • 键角 better than 0.1 度 • 扭曲角 0.1 度 ➢ 研究化学键性质 ➢ 理解固体化合物性质 • 建立构效关系 • 变温/变压实验理解相变/热膨胀和其他物理性质的分子基础
2
Solve the structure
研究对象:一切可以结晶的物质
+
chemistry judgement
单晶XRD分析2015 2
X射线源-产生X射线
测角仪-晶体定位平台
检测器(CCD, CMOS) -特殊设计的数码 相机 - 拍摄X射线照片
单晶XRD分析2015 2
Converts To
Green light
单晶XRD分析2015 2
XRD晶体结构分析

布拉格方程的提出
1913-1914年,英国物理学家Bragg父子利用X-射线成功测 定了NaCl晶体的结构并提出了Bragg方程,共同获得1915 年的诺贝尔物理学奖。
n2dsin
Bragg 父子
NaCl晶体及模型
DNA双螺旋结构的发现
1953年,英国科学家沃森等利用X-射线衍射技术成功揭示 了DNA分子具有双螺旋结构,获得了1962年诺贝尔医学奖。
Bragg方程
n为1,2,3…等整数 θ为相应某一n值的衍射角 n则称衍射级数
X-射线晶体学中最基本的方程之一
据此,每当我们观测到一束衍射线,就能立即想象出产生这个衍射的面网 的取向,并且由衍射角θ便可依据Bragg方程计算出这组面网的面网间距
(X-射线波长已知)
Bragg方程
Bragg方程: 2dhklsinθ = nλ
电子衍射
1954 化学
鲍林Linus Carl Panling
化学键的本质
1962 化学
肯德鲁John Charles Kendrew 帕鲁兹Max Ferdinand Perutz
蛋白质的结构测定
1962
生理医学
Francis Maurice
H.C.Crick、JAMES h.f.Wilkins
d.Watson、
Christian
William
Nicolaus Steno
Haüy
Samuel Weiss Hallowes Miller
(1638-1686) (1743-1822) (1780-1856)
(1801-1880)
Auguste Bravais (1811-1863)
晶体结构中的平移重复规律只有14种
XRD

X射线衍射分析(X-ray diffraction,简称XRD),是利用晶体形成的X射线衍射,对物质进行内部原子在空间分布状况的结构分析方法。
将具有一定波长的X射线照射到结晶性物质上时,X射线因在结晶内遇到规则排列的原子或离子而发生散射,散射的X射线在某些方向上相位得到加强,从而显示与结晶结构相对应的特有的衍射现象。
X射线衍射方法具有不损伤样品、无污染、快捷、测量精度高、能得到有关晶体完整性的大量信息等。
X射线衍射分析-样品要求1、金属样品如块状、板状、圆拄状要求磨成一个平面,面积不小于10X10毫米,如果面积太小可以用几块粘贴一起。
2、对于片状、圆拄状样品会存在严重的择优取向,衍射强度异常。
因此要求测试时合理选择响应的方向平面。
3、对于测量金属样品的微观应力(晶格畸变),测量残余奥氏体,要求样品不能简单粗磨,要求制备成金相样品,并进行普通抛光或电解抛光,消除表面应变层。
4、粉末样品要求磨成320目的粒度,约40微米。
粒度粗大衍射强度底,峰形不好,分辨率低。
要了解样品的物理化学性质,如是否易燃,易潮解,易腐蚀、有毒、易挥发。
5、粉末样品要求在3克左右,如果太少也需5毫克。
6、样品可以是金属、非金属、有机、无机材料粉末。
用途1、物相分析衍射图晶体的X射线衍射图像实质上是晶体微观结构的一种精细复杂的变换,每种晶体的结构与其X射线衍射图之间都有着一一对应的关系,其特征X射线衍射图谱不会因为它种物质混聚在一起而产生变化,这就是X射线衍射物相分析方法的依据。
制备各种标准单相物质的衍射花样并使之规范化,将待分析物质的衍射花样与之对照,从而确定物质的组成相,就成为物相定性分析的基本方法。
鉴定出各个相后,根据各相花样的强度正比于改组分存在的量(需要做吸收校正者除外),就可对各种组分进行定量分析。
目前常用衍射仪法得到衍射图谱,用“粉末衍射标准联合会(JCPDS)”负责编辑出版的“粉末衍射卡片(PDF卡片)”进行物相分析。
催化剂结构表征的方法

结构表征:1. 晶相:XRD(多晶,单晶)——确定样品晶体类型(2θ-d 晶面间距,T强度);TEM(透射电镜)。
2. 化学环境,配位状态:IR,UV,UV-Ramon,XPS,NMR,EPS,Mossbour。
组成表征:XRF,ICP(准确),XPS,AEM(分析电镜)。
宏观物性表征:1. 粒度(密度,强度):SEM(扫描电镜),TEM,XRD,激光衍射和光散射(统计结果)2. 形貌:TEM+SEM3. 多孔性:氮气吸附,压汞法,烃分子探针4. 稳定性:TG-DTA,XRD酸性及酸强度表征:1. 酸性:NH3-IR,吡啶(Py)-FT-IR,FT-IR,MAS-NMR(31Al,1H)。
2. 酸强度:NH3-TPD,Hammett指示剂,吸附量热。
3. 内外表面酸的识别:探针分子反应法。
金属性表征:1. 分散度:H2吸附,HOT,TEM,XPS。
2. 还原性:TPR。
3. 氧化还原态:XPS。
4. 表面吸附物种:IR。
金属与载体/助剂相互作用:TPR,XPS,DTA。
再生:TG-DTA,TPO。
1 什么是XRF?一台典型的X射线荧光(XRF)仪器由激发源(X射线管)和探测系统构成。
X射线管产生入射X射线(一次X射线),激发被测样品。
受激发的样品中的每一种元素会放射出二次X射线,并且不同的元素所放射出的二次X射线具有特定的能量特性或波长特性。
探测系统测量这些放射出来的二次X射线的能量及数量。
然后,仪器软件将探测系统所收集到的信息转换成样品中各种元素的种类及含量。
利用X射线荧光原理,理论上可以测量元素周期表中的每一种元素。
在实际应用中,有效的元素测量范围为11号元素(Na)到92号元素(U)。
2 X射线荧光的物理意义:X射线是电磁波谱中的某特定波长范围内的电磁波,其特性通常用能量(单位:千电子伏特,keV)和波长(单位:nm)描述。
X射线荧光是原子内产生变化所致的现象。
一个稳定的原子结构由原子核及核外电子组成。
XRD数据计算晶粒尺寸
XRD数据计算晶粒尺寸)公式计算晶粒尺寸(XRDScherrer公式计算晶粒尺寸(Scherrer公式计算晶粒尺寸(XRD数据计算晶粒尺寸)根据X射线衍射理论,在晶粒尺寸小于100nm时,随晶粒尺寸的变小衍射峰宽化变得显著,考虑样品的吸收效应及结构对衍射线型的影响,样品晶粒尺寸可以用Debye-Scherrer公式计算。
Scherrer公式:Dhkl=kλ/βcosθ其中,Dhkl为沿垂直于晶面(hkl)方向的晶粒直径,k为Scherrer常数(通常为0.89),λ为入射X射线波长(Cuka波长为0.15406nm,Cuka1波长为0.15418nm。
),θ为布拉格衍射角(°),β为衍射峰的半高峰宽(rad)。
但是在实际操作中如何从一张普通的XRD图谱中获得上述的参数来计算晶粒尺寸还存在以下问题:1)首先,用XRD计算晶粒尺寸必须扣除仪器宽化和应力宽化影响。
如何扣除仪器宽化和应力宽化影响?在什么情况下,可以简化这一步骤?答:在晶粒尺寸小于100nm时,应力引起的宽化与晶粒尺度引起的宽化相比,可以忽略。
此时,Scherrer公式适用。
但晶粒尺寸大到一定程度时,应力引起的宽化比较显著,此时必须考虑引力引起的宽化,Scherrer公式不再适用。
2)通常获得的XRD数据是由Kα线计算得到的。
此时,需要K α1和Kα2必须扣除一个,如果没扣除,肯定不准确。
3)扫描速度也有影响,要尽可能慢。
一般2°/min。
4)一个样品可能有很多衍射峰,是计算每个衍射峰对应晶粒尺寸后平均?还是有其它处理原则?答:通常应当计算每个衍射峰晶粒尺寸后进行平均。
当然只有一两峰的时候,就没有必要强求了!5)有的XRD数据中给出了width值,是不是半高宽度的值?能不能直接代入上面公式吗?如果不能,如何根据XRD图谱获得半峰宽?β为衍射峰的半高峰宽时,k=0.89β为衍射峰的积分宽度时,k=1.0。
其中积分宽度=衍射峰面积积分/峰高如何获得单色Kα1:1)硬件滤掉Kβ:K系射线又可以细分为Kα(L层电子填充)和Kβ(M层电子填充)两种波长略有差异的两种射线。
X射线单晶体衍射仪原理简介
X射线单晶体衍射仪原理简介X射线单晶体衍射仪原理简介X射线单晶体衍射仪一.引言X射线单晶体衍射仪的英文名称是X-ray single crystal diffractometer,简写为XRD。
本仪器分析的对象是一粒单晶体,如一粒砂糖或一粒盐。
在一粒单晶体中原子或原子团均是周期排列的。
将X射线〔如Cu的Kα辐射〕射到一粒单晶体上会发生衍射,由对衍射线的分析可以解析出原子在晶体中的排列规律,也即解出晶体的结构[1]。
物质或由其构成的材料的性能是与晶体的结构密切相关的,如金刚石和石墨都是由纯的碳构成的,由于它们的晶体结构不同就有着截然不同的性质。
二.X射线单晶体衍射仪测定晶体结构的原理和仪器构造[2,3].〔一〕晶体衍射的根本公式由于晶体中原子是周期排列的,其周期性可用点阵表示。
而一个三维点阵可简单地用一个由八个相邻点构成的平行六面体〔称晶胞〕在三维方向重复得到。
一个晶胞形状由它的三个边〔a,b,c〕及它们间的夹角〔γ,α,β〕所规定,这六个参数称点阵参数或晶胞参数,见图1。
这样一个三维点阵也可以看成是许多相同的平面点阵平行等距排列而成的,这样一族平面点阵称为一个平面点阵族,常用符号HKL〔HKL为整数〕来表示。
一个三维空间点阵划分为平面点阵族的方式是很多的,其平面点阵的构造和面间距d可以是不同的,见图1。
晶体结构的周期性就可以由这一组dHKL来表示。
图1 代表结晶体周期性的点阵一个小晶体衍射X射线,其衍射方向是与晶体的周期性〔d〕有关的。
一个衍射总可找到一个晶面族HKL,使它与入射线在此面族上符合反射关系,就以此面族的符号HKL作为此衍射之指数。
其间关系用布拉格方程〔式1〕来表示。
2dHKLsinθHKL=nλ〔1〕式中,θHKL为入射线或反射线与晶面族之间的夹角(见图2),λ为入射X射线波长,n为反射级数。
图2 布拉格反射示意图衍射线的强度是与被重复排列的原子团的结构,也即和原子在晶胞中的分布装况〔坐标〕有关,其间的关系由方程式〔2〕表示〔2〕式中, E称为累积能量,I0为入射线强度,e, m为电子的电荷与质量,c为光速,λ为X射线波长,Vu为晶胞体积,称洛仑兹偏振〔LP〕因子,|F|为结构振幅,e-2MT为温度因子,A为吸收因子,V为小单晶体的体积,ω为样品的转速,其中结构因子=|FHKL|eiαHKL 〔3〕式中, fj, xj,yj,zj 分别为第j个原子的原子散射因子及它在晶胞中的分数坐标〔以晶胞边长为1〕。
XRD衍射仪法测定晶体
四 X射线衍射方法的实际应用
(一)X射线物相分析
• 材料或物质的组成包括两部分: 一是确定材料的组成元素及其含量; 二是确定这些元素的存在状态,即是什么物相。
• 材料由哪些元素组成的分析工作可以通过化学分析、 光谱分析、X射线荧光分析等方法来实现,这些工作 称之成份分析。
• 材料由哪些物相构成可以通过X射线衍射分析加以确 定,这些工作称之物相分析或结构分析。
X射线物相定性分析原理
• X射线物相分析是以晶体结构为基础,通过比较晶体 衍射花样来进行分析的。
• 对于晶体物质中来说,各种物质都有自己特定的结 构参数(点阵类型、晶胞大小、晶胞中原子或分子 的数目、位置等),结构参数不同则X射线衍射花样 也就各不相同,所以通过比较X射线衍射花样可区分 出不同的物质。
粉末衍射卡的组成
• 粉末衍射卡(简称ASTM或PDF卡)卡片的形式如图所示
粉末衍射卡的组成
• 1栏:卡片序号。 • 2栏: 1a、1b、1c是最强、次强、再次强三强线 的面间距。 2a、2b、2c、2d分别列出上述各线条 以最强线强度(I1)为100时的相对强度I/I1。 • 3栏: 1d是试样的最大面间距和相对强度I/I1 。 • 4栏:物质的化学式及英文名称 • 5栏:测样时的实验条件。 • 6栏:物质的晶体学数据。 • 7栏:光学性质数据。 • 8栏:试样来源、制备方式、测样温度等数据 • 9栏:面间距、相对强度及密勒指数。
举例:
a. 鉴别结晶性化合物
将样品的XRD谱图与标准谱图PDF对照
物相鉴别更多应用于非聚合物材料中(金属,陶 瓷,化合物)
b.区别同种结晶性化合物的不同晶型
例:等规聚丙烯IPP α (单斜晶系) β (六方晶系) 刚性增加,冲击强度下降 拉伸强度和拉伸模型下降, 而韧性增加
XRD单晶定向新装置的应用
中图分类 号: 7 2 02 文献标 识码 : A di1 .9 9ji n 17 - 3 5 2 1 .6 0 0 o:0 36 /. s.6 2 40 .0 10 .3 s
Ap l a in o e e up n d tr n h p i yo fn w q ime tt eemie t e c o o in ain o ige cy tlb re tt fsn l r sa y XRD o
灵验 了。
让晶体绕端面法线 自转 , 而完成大块单 晶的直接 从
测试。
在 固定 安 装 电机支 撑 架 时 , 保 持 电机 轴 垂直 要
0 轴半 圆切面。作实验时 , 将可拆卸的夹具 放在桌 面上 , 样品用胶泥 固定在夹具上 , 使样品表面和活动
夹 具 园盘表 面处 于 同一平 面 。当给 电机吸盘 上安装
( 西安交通大学 电子陶瓷与器件教育部重点 实验室,陕西 西安 704 ) 109
摘 要 :介绍 了一种对 “ 单晶”类样 品进行鉴定评价 和定 向切割 的新方 法、新装 置。以往解决此类 问题需要
专用仪器 ,资源紧缺 。现在从衍射基本原理出发提 出了一条新 的测试路线 ,通过 X D自转条件下 的 0扫描蝴 R 蝶 图能对 “ 单晶”类 型进行鉴定 。它直接测 出的就是 晶向偏离角 ,再慢速点 动捕捉到它 的方位 ,从 而指导定 向切割 ,能三维定 向,还能进一步作 出 X D摇摆 曲线 ,对单 晶品质进行评价 。新装置为定 向切 割和各 向异性 R 研究提供 了简便手段 ,任何 x衍射仪都可安装 。 关键词 :单 晶;取 向性晶体 ;X射线衍射
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、衍射分析技术的发展
• 与X射线及晶体衍射有关的部分诺贝尔奖获得者名单
年 份 学 科 1901 物理 1914 物理 1915 1917 1924 1937 1954 1962 1962 1964 1985 1986 1994 得奖者 伦琴Wilhelm Conral Rontgen 劳埃Max von Laue 亨利.布拉格Henry Bragg 物理 劳伦斯.布拉格Lawrence Bragg. 物理 巴克拉Charles Glover Barkla 物理 卡尔.西格班Karl Manne Georg Siegbahn 戴维森Clinton Joseph Davisson 物理 汤姆孙George Paget Thomson 化学 鲍林Linus Carl Panling 肯德鲁John Charles Kendrew 化学 帕鲁兹Max Ferdinand Perutz Francis H.C.Crick、JAMES d.Watson、 生理医学 Maurice h.f.Wilkins 化学 Dorothy Crowfoot Hodgkin 霍普特曼Herbert Hauptman 化学 卡尔Jerome Karle 鲁斯卡E.Ruska 物理 宾尼希G.Binnig 罗雷尔H.Rohrer 布罗克豪斯 B.N.Brockhouse 物理 沙尔 C.G.Shull 内 容 X射线的发现 晶体的X射线衍射 晶体结构的X射线分析 元素的特征X射线 X射线光谱学 电子衍射 化学键的本质 蛋白质的结构测定 脱氧核糖核酸DNA测定 青霉素、B12生物晶体测定 直接法解析结构 电子显微镜 扫描隧道显微镜 中子谱学 中子衍射
(1)
晶体结构与空间格子-B
• 等同点与结点
•格子类型
•格子的对称—点群、劳埃群、 衍射群、空间群
(1)晶体结构与空间格子-C
The 14 possible BRAVAIS LATTICES {note that spheres in this picture represent lattice points, not atoms!}
2、 衍射分析的基本概念及基本理论晶体 (1)结构与空间格子-A
• 晶体(crystal) It is solid.The arrangement of atoms in the crystal is periodic. • 格子(Lattice) An infinite array of points in space, in which each point has identical surroundings to all others. • 晶体结构(Crystal Structure) It can be described by associating each lattice point with a group of atoms called the MOTIF (BASIS) • 单位晶胞(Unit Cell) The smallest component of the crystal, which when stacked together with pure translational repetition reproduces the whole crystal • 晶胞参数Unit Cell Dimensions a, b and c are the unit cell edge lengths. a, b and g are the angles (a between b and c, b between c and a , g between a and b c .)
晶胞中有一原子坐标为 xj 、 yj 、 zj ,必有坐标为 1/2+xj、 1/2+yj、 1/2+zj 的相同原子存在, 它们对结构因子的贡献为 Fhkl=fjei2п (hxj+kyj+lzj) +fjei2п (hxj+kyj+lzj+1/2(h+k+l)) = fjei2п (hxj+kyj+lzj) (1+eiп ((h+k+l ) ) 根据欧拉公式: eiп ((h+k+l )=cosп (h+k+l)+isinп (h+k+l) 由于h+k+l为整数,所以: isin (h+k+l)=0 因此1+eiп ((h+k+l )=1+cosп (h+k+l) Fhkl=fjei2 п (hxj+kyj+lzj) +fjei2 п (hxj+kyj+lzj+1/2(h+k+l)) = fjei2 п (hxj+kyj+lzj) (1+ei п ((h+k+l ) ) =(1+cos п (h+k+l))fjei2 (hxj+kyj+lzj) 对于晶胞中所有的原子而言 Fhkl =(1+cosп (h+k+l))∑fj ei2 (hxj+kyj+lzj) 由前面的系数项,可以看出,当h+k+l=2n+1时,该系数为0, Fhkl =0 , 那么结构振幅也为0,得不到相应的衍射强度。h+k+l=2n+1这就是体心格子的 消光条件,也称h+k+l=2n为体心格子的衍射条件。
•结构因子Fhkl-衍射强度的条件--与晶胞中原子的种类及分布的关系
衍射强度:实验数据,积分强度 结构因子: Fhkl=∑fjeiα j=∑fjei2(hxj+kyj+lzj) 结构振幅:[Fhkl] 结构振幅与衍射强度的关系:Ihkl∝[Fhkl]2
•系统消光-结构因子Fhkl--空间群的关系A 格子类型的作用--体心格子消光条件的推导
《X射线晶体学》 简介
中国地质大学(北京)晶体结构实验室
主要内容
一、衍射分析方法的发展及基本理论 二、 衍射仪基本结构及发展 三、粉晶衍射原理、衍射图的特征及应用 四、单晶样品制备 五、单晶衍射分析及应用 六、晶体结构测定及晶体学参数
一、衍射分析方法的发展及基本理论
• • • • • 1、 衍射分析的历史及发展 2、 衍射分析的基本概念及基本理论 晶体结构与空间格子 衍射的概念、劳埃方程、结构因子、 3、倒易点阵及衍射仪设计原理
1 2d sin = hkl = 1/ 2d hkl
dhkl
A θhkl θhkl
O
O1
1/λ
λ =2dhklsinθ
s in = d OP = hkl = AO 2 2d hkl
λ =2dhklsinθ
二、 衍射仪基本结构及发展
-SMART APEX-CCD衍射仪 基本结构及新型的面探技术 Smart CCD Overview SMART APEX-CCD探测器
a*
c*
b
b*
c*=a×b/V
a
倒易点阵的性质:
•倒 易 向 量 Hhkl 的 方 向 是 正 点 阵 (hkl)面网的法线方向;
•倒易向量Hhkl的长度是正点阵面网 间距dhkl的倒数Hhkl =1/ dhkl;
•倒易点阵(Reciprocal Space)及衍射仪设计原理 -反射球及晶体的衍射方向 (衍射仪的设计原理)
•系统消光-结构因子Fhkl-空间群的关系B
螺旋轴的作用--螺旋轴消光条件的推导
设晶体在b方向由一平移量为1/2的螺旋轴21处于X=0、Z=0处, 晶胞中由它联系的每对原子的坐标为: xj 、 yj 、 zj ;- xj 、 1/2+yj、-zj,它们对结构因子的贡献为: Fhkl=fjei2п
(hxj+kyj+lzj)
应用领域:矿 物学、岩石学、 材料合成研究、 药物合成研究、 材料性能研究 (如配合低温、 高温物台的使 用可研究不同 环境下晶格的 变化)。
四、单晶样品制备
1、单晶的概念及识别(晶体结构特征、几何外 型特征、光学性质特征
2、单晶分析样品的要求、选择和安装
上机的样品尽可能选择呈球形(粒状)的单晶体 或晶体碎片,直径大小在0.1-0.7mm,无解理、无 裂纹 •确保用于单晶衍射的样品代表要鉴定的物相,从 晶体的形状、颜色、解理和其他的分析方法给予 保证。
+fjei2п
( hxj+kyj+-lzj+k/2)
= fjei2п
kyj
(ei2п
(hxj+lzj)+eiп ((hxj+lyj+k/2 )
)
当h, l都为零时: F0k0=fjei2п
kyj
(1+eiп
k/2 )
)
对于晶胞内所有原子: Fhkl = ( 1 + eiп ∑fjei2п kyj
k/2
One fourfold axis
P I
Orthorhomb ic
a≠b≠c a=b =g=90
Three twofold axes or mirror plane
P I F A(B or C)
Hexagona
A=b≠c a=g=90
b=120
One threefold axis
P
Trigonal
A=b≠c a=g=90
) ∑ fjei2п
kyj=
( 1 + cosп k )
k=2n+1时,系数为0,这就是21轴平行b轴的消光条件,即在b 方向存在21螺旋轴时,oko的衍射中,k为奇数的衍射点都不存 在。
3、倒易点阵(Reciprocal Space)及衍射仪设计原理 c -倒易点阵概念及性质
倒易点阵的定义:
