(完整)全等三角形动点问题提高题
(完整)初二全等三角形提高习题精选

全等三角形提高练习1. 如图所示,△AB C ≌△ADE ,BC 的延长线过点E ,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,求∠DEF 的度数。
2. 如图,△AOB 中,∠B=30°,将△AOB 绕点O 顺时针旋转52°,得到△A ′OB ′,边A ′B ′与边OB 交于点C (A ′不在OB 上),则∠A ′CO3. 如图所示,在△ABC 中,∠A=90°,D 、E 分别是AC、BC EDC ,则∠C 的度数是多少?4.如图所示,把△ABC 绕点C 顺时针旋转35°,得到△A ′B ′C ,A′B ′交AC 于点D ,若∠A ′DC=90°,则∠A=5. 已知,如图所示,AB=AC ,A D ⊥BC 于D ,且AB+AC+BC=50cm,而AB+BD+AD=40cm ,则AD是多少?6. 如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B 、C 作过点A 的垂线BC 、CE ,垂足分别为D 、E ,若BD=3,CE=2,则DE= 7. 如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,连接EF ,交AD于G ,AD 与EF 垂直吗?证明你的结论。
8. 如图所示,在△ABC 中,AD 为∠BAC 的角平分线,D E ⊥AB 于E ,DF ⊥AC 于F ,△ABC的面积是28cm 2,AB=20cm ,AC=8cm ,求DE 的长。
A B'C A B9. 已知,如图:AB=AE ,∠B=∠E ,∠BAC=∠EAD ,∠CAF=∠DAF ,求证:AF10. 如图,AD=BD ,A D ⊥BC 于D ,BE ⊥AC 于E ,AD 与BE 相交于点H ,则BH 与AC 相等吗?为什么?11. 如图所示,已知,AD 为△ABC 的高,E 为AC 上一点,BE 交AD 于F,且有BF=AC ,FD=CD ,求证:B E ⊥AC12. △DAC 、△EBC 均是等边三角形,AF 、BD 分别与CD 、CE 交于点M 、N ,求证:(1)AE=BD(2)CM=CN (3)△CMN 为等边三角形 (4)MN13. 已知:如图1,点C 为线段AB 上一点,△ACM 、△CBN 都是等边三角形,AN 交MC 于点E ,BM 交CN 于点F (1) 求证:AN=BM(2) 求证:△CEF 为等边三角形14. 如图所示,已知△ABC 和△BDE 都是等边三角形,下列结论:①AE=CD ;②BF=BG ;③BH平分∠AHD ;④∠AHC=60°;⑤△BFG 是等边三角形;⑥FG ∥AD ,其中正确的有( ) A .3个 B. 4个 C. 5个 D. 6个15. 已知:BD 、CE 是△ABC 的高,点F 在BD 上,BF=AC ,点G 在CE 的延长线上,CG=AB ,求证:A G ⊥AFC B B A A B16. 如图:在△ABC 中,BE 、CF 分别是AC 、AB 两边上的高,在BE 上截取BD=AC ,在CF 的延长线上截取CG=AB ,连结AD 、AG求证:(1)AD=AG (2)AD 与AG 的位置关系如何17.如图,已知E 是正方形ABCD 的边CD 的中点,点F 在BC 上,且∠DAE=∠FAE求证:AF=AD-CF18.如图所示,已知△ABC 中,AB=AC ,D 是CB 延长线上一点,∠ADB=60°,E 是AD 上一点,且DE=DB ,求证:AC=BE+BC19.如图所示,已知在△AEC 中,∠E=90°,AD 平分∠EAC ,DF ⊥AC ,垂足为F ,DB=DC ,求证:BE=CF20.已知如图:AB=DE ,直线AE 、BD 相交于C ,∠B+∠D=180°,AF ∥DE ,交BD 于F ,求证:CF=CD21.如图,OC 是∠AOB 的平分线,P 是OC 上一点,PD ⊥OA 于D ,PE ⊥OB 于E ,F 是OC 上一点,连接DF 和EF ,求证:DF=EF22.已知:如图,BF ⊥AC 于点F ,CE ⊥AB 于点E ,且BD=CD ,求证:(1)△BDE ≌△CDF (2) 点D 在∠A 的平分线上BDB23.如图,已知AB ∥CD ,O 是∠ACD 与∠BAC 的平分线的交点,OE ⊥AC 于E ,且OE=2,则AB 与CD 之间的距离是多少?24.如图,过线段AB 的两个端点作射线AM 、BN ,使AM ∥BN ,按下列要求画图并回答: 画∠MAB 、∠NBA 的平分线交于E (1)∠AEB 是什么角?(2)过点E 作一直线交AM 于D ,交BN 于C ,观察线段DE 、CE ,你有何发现?(3)无论DC 的两端点在AM 、BN 如何移动,只要DC 经过点E ,①AD+BC=AB ;②AD+BC=CD谁成立?并说明理由。
八年级数学全等三角形中的动点问题专题强化训练

八年级数学全等三角形中的动点问题专题强化训练1、在等腰三角形ABC中,AC=BC=5,AB=8,D为底边AB上一动点(不与点A,B重合),DE⊥AC,DF⊥BC,垂足分别为E,F,则DE+DF=10.2、在边长为2cm的正方形ABCD中,点Q为BC边的中点,点P为对角线AC上一动点,连接PB、PQ,则△PBQ周长的最小值为8cm。
3、将边长为1的等边三角形OAP按图示方式,沿x轴正方向连续翻转2019次,点P依次落在点P1,P2,P3,P4,…,P2007的位置。
P1的坐标为(1,0),P3的坐标为(-1,0),P50的坐标为(0,-1),P2019的坐标为(1,0)。
4、在等腰直角三角形ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE。
连接DE、DF、EF。
1)证明△ADF≌△CEF。
首先,AD=CE,AF=BF,因此△ADF≌△BDF,△CEF≌△XXX。
又因为BF=EF,所以△BDF≌△XXX。
因此,△ADF≌△CEF。
2)证明△DFE是等腰直角三角形。
因为AD=CE,所以DE=DF。
又因为AF=BF,所以EF=2DF。
因此,△DFE是等腰直角三角形。
5、在等边三角形ABC的顶点A、C处各有一只蜗牛,它们同时出发,分别以每分钟1个单位的速度沿AB向B和沿CA向A爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t分钟后,它们分别爬行到D、E处。
1)在爬行过程中,CD和BE始终相等。
2)若蜗牛沿着AB和CA的延长线爬行,EB与CD交于点Q,其他条件不变,如图所示,蜗牛爬行过程中∠CQE的大小条件不变,证明∠CQE=60°。
3)如果将原题中“沿着CA向A爬行”改为“沿着BC的延长线爬行,连接DE交AC于F”,其他条件不变,则爬行过程中,DF始终等于EF。
6、如图1,若△ABC和△ADE为等边三角形,M、N分别为BC、CD的中点,易证:CD=BE,△AMN是等边三角形。
全等三角形动点问题(人教版)(含答案)

全等三角形动点问题(人教版)一、单选题(共8道,每道12分)1.已知:如图,在长方形ABCD中,AB=6厘米,BC=9厘米,点P从点A出发,沿AB边向终点B以1厘米/秒的速度移动,同时点Q从点B出发沿BC边向终点C以2厘米/秒的速度移动,如果P,Q两点同时出发,当其中一点到达终点后停止运动,另一点也随之停止运动,设点P的运动时间为t秒,连接PQ,DQ.若△DCQ≌△QBP,则t的值为( )A.1B.2C. D.3答案:D解题思路:试题难度:三颗星知识点:动点问题2.已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AD=12,BC=24,动点P从点A出发沿AD向点D以每秒1个单位的速度运动,动点Q从点C出发沿CB向点B以每秒2个单位的速度运动,P,Q同时出发,当点P停止运动时,点Q也随之停止,连接PQ,DQ.设点P的运动时间为t秒,当t为( )时,△PDQ≌△CQD.A.12B.8C.6D.4答案:D解题思路:试题难度:三颗星知识点:动点问题3.已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE.动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t 秒.当t的值为( )时,△ABP和△DEC全等.A.1B.1或3C.1或7D.3或7答案:C解题思路:试题难度:三颗星知识点:动点问题4.已知:如图,在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.点P在线段BC上以每秒2cm的速度由点B向点C运动,同时点Q在线段CA上由点C向点A运动.设点P 运动时间为t秒,当t的值为( )时,△BPD与△CQP全等.A. B.3C.或2D.或3答案:C解题思路:试题难度:三颗星知识点:动点问题5.已知:如图,在矩形ABCD中,AB=4cm,BC=6cm,点E为AB中点,如果点P在线段BC 上以每秒2cm的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.设点P的运动时间为t秒,若某一时刻△BPE与△CQP全等,则点Q的运动速度是( )A.cm/sB.2cm/sC.2cm/s或4cm/sD.cm/s或2cm/s答案:D解题思路:1.思路分析首先判断这是一道动点问题,对于动点问题,我们的解决套路是:①研究基本图形,动点的运动状态;②分析状态转折点,分段;③画出符合题意的图形,表达线段长,建等式.2.解题过程试题难度:三颗星知识点:动点问题6.如图,在矩形ABCD中,AB=6m,BC=8m,AC=10m,动点P以2m/s的速度从点A出发,沿AC方向向点C移动,同时动点Q以1m/s的速度从点C出发,沿CB方向向点B移动,当P,Q两点中其中一点到达终点时则停止运动.设运动时间为t秒,则当t为( )时,△PQC 是以PQ为底的等腰三角形.A.5B.C.4D.答案:D解题思路:试题难度:三颗星知识点:动点问题7.如图,在矩形ABCD中,AB=20cm,BC=4cm,动点P以3cm/s的速度从B点出发,沿BA 方向向点A移动,同时动点Q以1cm/s的速度,沿CD方向向点D移动,当其中一点到达终点时,另一点也随之停止运动,设运动时间为t(s),则当t为( )时,线段PQ恰好平分矩形ABCD的面积.A.3B.4C.5D.6答案:C解题思路:试题难度:三颗星知识点:动点问题8.已知:如图,等边△ABC的边长为6,动点P从点A出发沿AB-BC-CA方向以每秒2个单位的速度运动,再次回到点A时停止运动.连接BP,CP,设点P运动的时间为t秒.若△BCP的面积是△ABC面积的,则t的值为( )A.2或7B.4或14C.2或14D.4或7答案:A解题思路:1.思路分析首先判断这是一道动点问题,对于动点问题,我们的解决套路是:①研究基本图形,动点的运动状态;②分析状态转折点,分段;③画出符合题意的图形,表达线段长,建等式.2.解题过程试题难度:三颗星知识点:动点问题。
2024年人教版八年级上册数学第十二章全等三角形专题四 全等三角形中的动点问题

第十二章 全等三角形
专题四 全等三角形中的动点问题
专题四
全等三角形中的动点问题
类型1 以 U 型框为背景的动点问题
1. [2024雅安月考]如图,做一个“U”字形框架
PABQ ,其中 AB =42 cm, AP , BQ 足够长, PA ⊥
AB , QB ⊥ AB ,点 M 从点 B 出发,向点 A 运动,
10厘米, BC =8厘米, CD =12厘米,∠ B =∠ C ,点 E
为 AB 的中点.如果点 P 在线段 BC 上以3厘米/秒的速度由
B 点向 C 点运动,同时,点 Q 在线段 CD 上由 C 点向 D 点
运动.(1)ຫໍສະໝຸດ 点 Q 的运动速度与点 P 的运动速度相等,经过1秒
后,△ BPE 与△ CQP 是否全等?请说明理由.
∴ BE =5厘米,∴ BE = PC ,
=,
在△ BPE 和△ CQP 中,ቐ∠=∠,
=,
∴△ BPE ≌△ CQP (SAS).
1
2
3
4
专题四
全等三角形中的动点问题
(2)当点 Q 的运动速度为多少时,能够使△ BPE 与△ CQP
全等?
【解】∵△ BPE 与△ CQP 全等,
∵∠ A =∠ B =90°,
∴使△ ACM 与△ BMN 全等,可分两种情况:
情况一:当 BM = AC , BN = AM 时,
∵ BN = AM , AB =42 cm,
∴4 t +3 t =42,解得 t =6,
∴ AC = BM =3×6=18(cm);
1
2
3
4
专题四
全等三角形中的动点问题
全等三角形经典动点问题
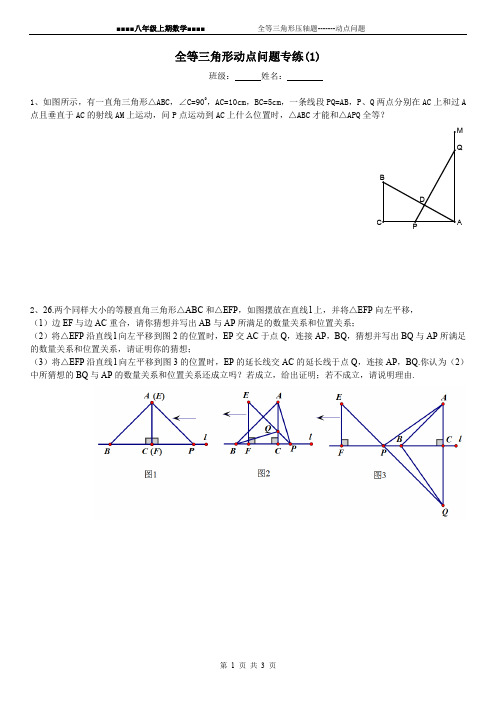
全等三角形动点问题专练(1)班级: 姓名:1、如图所示,有一直角三角形△ABC ,∠C=900,AC=10cm ,BC=5cm ,一条线段PQ=AB ,P 、Q 两点分别在AC 上和过A 点且垂直于AC 的射线AM 上运动,问P 点运动到AC 上什么位置时,△ABC 才能和△APQ 全等?2、26.两个同样大小的等腰直角三角形△ABC 和△EFP ,如图摆放在直线l 上,并将△EFP 向左平移, (1)边EF 与边AC 重合,请你猜想并写出AB 与AP 所满足的数量关系和位置关系;(2)将△EFP 沿直线l 向左平移到图2的位置时,EP 交AC 于点Q ,连接AP ,BQ ,猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;(3)将△EFP 沿直线l 向左平移到图3的位置时,EP 的延长线交AC的延长线于点Q ,连接AP ,BQ.你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.3.如图1,在△ABC 中,点P 为BC 边中点,直线a 绕顶点A 旋转,若点B P 、在直线a 的异侧,BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,连接.PM PN 、 (1)延长MP 交CN 于点E (如图2),①求证:BPM CPE △≌△;②求证:PM PN =;(2)若直线a 绕点A 旋转到图3的位置时,点B P 、在直线a 的同侧,其它条件不变.此时PM PN =还成立吗?若成立,请给予证明;若不成立,请说明理由;(3)若直线a 绕点A 旋转到与BC 边平行的位置时,其它条件不变,请直接判断PM PN =还成立吗?不必说明理由.4.在等边△ABC 的顶点A 、C 处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A 向B 和由C 向A 爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t 分钟后,它们分别爬行到D 、E 处,请问: (1)如图1,在爬行过程中,CD 和BE 始终相等吗? (2)如果将原题中的“由A 向B 和由C 向A 爬行”,改为“沿着AB 和CA 的延长线爬行”,EB 与CD 交于点Q ,其他条件不变,蜗牛爬行过程中∠CQE 的大小保持不变,请利用图2说明:∠CQE=60°; (3)如果将原题中“由C 向A 爬行”改为“沿着BC 的延长线爬行,连接DE 交AC 于F ”,其他条件不变,如图3,则爬行过程中,DF 始终等于EF 是否正确?C图1 图2 图3 图1 图2 图35.如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.(1)如果点P在线段BC上以3厘米/秒得速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?(2)若点Q以(1)②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?。
专题全等三角形中的动点运动问题(30题)(原卷版)

(苏科版)八年级上册数学《第1章全等三角形》专题全等三角形中的动点运动问题(30题)1.(2023春•横山区期末)如图,AB=8cm,∠A=∠B,AC=BD=6cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上以xcm/s的速度由点B向点D运动.它们运动的时间为t (s).当△ACP与△BPQ全等时,x的值为.2.(2022春•普宁市期末)如图,∠A=∠B=90°,AB=60,E,F分别为线段AB和射线BD上的一点,若点E从点B出发向点A运动,同时点F从点B出发向点D运动,二者速度之比为3:7,运动到某时刻同时停止,在射线AC上取一点G,使△AEG与△BEF全等,则AG的长为.1、全等三角形中的动点运动问题,通过点的运动,用代数式表示线段的大小,从而寻找线段间的等量关系,建立方程,进而快速解题.2、解题策略:①明晰点的运动方向和速度;②根据已知和求证的目标,寻找线段或角之间的数量关系,进而解决问题;③有时要用到分类讨论的思想.典型题训练3.(2022秋•攸县期末)如图,在四边形ABCD中,∠DAB=∠ABC,AB=5cm,AD=BC=3cm,点E在线段AB上以1cm/s的速度由点A向点B运动,同时,点F在线段BC上由点B向点C运动.设运动时间为t(s),当△ADE与以B,E,F为顶点的三角形全等时,则点F的运动速度为cm/s.4.(2023春•吴江区期末)如图,已知长方形ABCD中,AB=8cm,AD=12cm,点E在AB边上,BE=3cm,点F在线段BC上以3cm/s的速度由B点向C点运动,到达点C后马上折返,向点B运动,点G在线段CD上以vcm/s的速度由C点向D点运动.点F,G同时出发,当一个点到达终点停止运动时,另一个点也随之停止运动,设运动的时间为t秒.若以E,B,F为顶点的三角形和以F,C,G为顶点的三角形全等,则t=秒.5.如图,△ABC中,AB=AC=24cm,BC=16cm,AD=BD.如果点P在线段BC上以2cm/s的速度由B 点向C点运动,同时,点Q在线段CA上以vcm/s的速度由C点向A点运动,那么当△BPD与△CQP 全等时,v=()A.3B.4C.2或4D.2或36.(2022秋•高邑县期中)如图,在Rt△ABC中,AC=6,BC=8,AB=10.点P从点A出发,以每秒2个单位长度的速度沿折线A﹣C﹣B向终点B运动,同时点Q从点B出发,以每秒3个单位长度的速度沿折线B﹣C﹣A向终点A运动,点P,Q都运动到各自的终点时停止.设运动时间为t(秒),直线l经过点C,且l∥AB,过点P,Q分别作直线l的垂线段,垂足为E,F.当△CPE与△CQF全等时,t的值不可能是()A.2B.2.8C.3D.67.(2022秋•浠水县校级期中)如图,在△ABC中,AB=AC,∠BAC=90°,BC=6cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒2cm的速度运动,动点E也同时从点C开始在直线CM上以每秒1cm的速度运动,连接AD、AE,设运动时间为t秒.当△ABD≌△ACE时,t的值为()A.2B.4C.6D.2或68.(2023春•和平区校级期中)如图,已知Rt△ABC中,∠ACB=90°,满足AC=7,BC=12,点P从A 点出发沿A→C→B路径向终点B运动:点Q从B出发沿B→C→A路径向终点A运动;点P,Q的速度分别以每秒1个单位长度和每秒3个单位长度的速度同时开始运动,两个点都要到达相应的终点时才能停止运动,分别过P,Q作PE⊥l于E,QF⊥l于F.设运动时间为t秒,当以P,E,C为顶点的三角形与以Q,F,C为顶点的三角形全等时,t的值为(不考虑两三角形重合的情况).9.如图,在△ABC中,BC=8cm,AG∥BC,AG=8cm,点F从点B出发,沿线段BC以4cm/s的速度连续做往返运动,点E从点A出发沿线段AG以2cm/s的速度运动至点G,E、F两点同时出发,当点E到达点G时,E、F两点同时停止运动,EF与直线AC交于点D,设点E的运动时间为t(秒)(1)分别写出当0<t<2和2<t<4时段BF的长度(用含t的代数式表示)(2)当BF=AE时,求t的值;(3)当△ADE≌△CDF时,直接写出所有满足条件的t值.10.在Rt△ABC中,∠C=90°,AC=10cm,BC=5cm,P,Q两点分别在AC上和过点A且垂直于AC的射线AM上运动,且PQ=AB,问P点运动到AC上什么位置时△ABC才能和△QP A全等.11.(2022秋•昭阳区期中)如图,已知在△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点,如果点P在线段BC上以3cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.(1)若点Q与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等?请说明理由;(2)若点Q与点P的运动速度不相等,当点Q的运动速度为多少时,能使△BPD与△CQP全等?12.如图,△ABC中,∠ACB=90°,AC=12,BC=16.点P从A点出发沿A﹣C﹣B路径向终点运动,终点为B点;点Q从B点出发沿B﹣C﹣A路径向终点运动,终点为A点.点P和Q分别以2和6的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.13.(2022秋•苍溪县期末)如图,AE与BD相交于点C,AC=EC,BC=DC,AB=8cm,点P从点出发,沿A→B→A方向以2cm/s的速度运动,点Q从点D出发,沿D→E方向以lcm/s的速度运动,P、Q两点同时出发,当点P到达点A时,P、Q两点同时停止运动,设点P的运动时间为t(s).(1)求证:AB∥DE.(2)写出线段AP的长(用含t的式子表示).(3)连接PQ,当线段PQ经过点C时,求t的值.14.如图,在等腰△ABC中,AB=AC=6cm,BC=10cm,点P从点B出发,以2cm/s的速度沿BC向点C 运动,设点P的运动时间为ts.(1)PC=cm.(用t的代数式表示)(2)当点P从点B开始运动,同时,点Q从点C出发,以vcm/s的速度沿CA向点A运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.15.如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.(1)如果点P在线段BC上以1cm/s的速度由点B向C运动,同时,点Q在线段CA上由点C向A运动,①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等?请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?(2)若点Q以(1)②中的运动速度从点C出发,点P以1cm/s的运动速度从B同时出发,都逆时针沿△ABC三边运动,则经过秒后,点P与点Q第一次在△ABC上相遇.(在横线上直接写出答案,不必书写解题过程)16.(2022秋•南召县期末)如图,在四边形ABCD中,∠B=∠C,AB=20cm,BC=15cm,E为AB的中点,若点P在线段BC上以5cm/s的速度由点B向点C运动,同时,点Q在线段CD上由点C向点D运动.(1)若点Q运动的速度是5cm/s,经过1秒后,△BPE与△CQP是否全等,请说明理由;(2)若点Q的运动速度与点P的运动速度不相等,当△BPE与△CQP全等时,求出点Q的运动速度.17.(2022春•二七区校级期中)如图,点E在线段CD上,EA,EB分别平分∠DAB和∠CBA,点F在线段AB上运动,AD=4cm,BC=3cm,且AD∥BC.(1)当点F运动到离点A多少厘米时,△ADE和△AFE全等?为什么?(2)在(1)的情况下,此时BF=BC吗?为什么?求出AB的长.18.如图,在长方形ABCD中,AD=6cm,AB=4cm,点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BC上由点B向点C运动.(注:长方形中,∠A=∠B=∠C=∠D=90°,AB=CD,AD=BC)(1)若点Q的运动速度与点P的运动速度相等:①经过1秒后,△AEP与△BPQ是否全等,请说明理由,并判断此时线段PE和线段PQ的位置关系;②设运动时间为t秒时,△PEQ的面积为Scm2,请用t的代数式表示S.(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为cm/s时,能够使△AEP与△BPQ全等.19.(2023春•碑林区校级期末)如图,△ABC的两条高AD与BE交于点O,AD=BD,AC=6.(1)求BO的长;(2)F是射线BC上一点,且CF=AO,动点P从点O出发,沿线段OB以每秒1个单位长度的速度向终点B运动,同时动点Q从点A出发,沿射线AC以每秒4个单位长度的速度运动,当点P到达点B时,P,Q两点同时停止运动,设运动时间为t秒,当△AOP与△FCQ全等时,求t的值.20.如图1,长方形ABCD中,AB=CD=7cm,AD=BC=5cm,∠A=∠B=∠C=∠D=90°,点E在线段AB上以1cm/s的速度由点A向点B运动,与此同时点F在线段BC上由点B向点C运动,设运动的时间均为ts.(1)若点F的运动速度与点E的运动速度相等,当t=2时:①判断△BEF与△ADE是否全等?并说明理由;②求∠EDF的度数.(2)如图2,将图1中的“长方形ABCD”改为“梯形ABCD”,且∠A=∠B=70°,AB=7cm,AD=BC=5cm,其他条件不变.设点F的运动速度为xcm/s.是否存在x的值,使得△BEF与△ADE全等?若存在,直接写出相应的x及t的值;若不存在,请说明理由.21.在Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,点D在AC上,且AD=6cm,过点A作射线AE⊥AC(AE与BC在AC同侧),若动点P从点A出发,沿射线AE匀速运动,运动速度为1cm/s,设点P运动时间为t秒.连接PD、BD.(1)如图①,当PD⊥BD时,求证:△PDA≌△DBC;(2)如图②,当PD⊥AB于点F时,求此时t的值.22.如图,在四边形ABCD中,AD=BC=10,AB=CD,BD=14,点E从点D出发,以每秒2个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒5个单位的速度,沿C→B→C做匀速移动,点G 从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒,G点的移动距离为y.(1)请用含t的代数式表示以下线段:ED=,当0<t≤2时,BF=,当2<t≤4时,BF=;(2)请猜想AD与BC的位置关系,并说明理由;(3)在移动过程中,请你探究当t取何值时,△DEG与△BFG全等?并求出此时G点的移动距离y.23.(2023春•渭滨区期末)如图①,在Rt△ABC中,∠C=90°,BC=9cm,AC=12cm,AB=15cm,现有一动点P,从点A出发,沿着三角形的边AC→CB→BA运动,回到点A停止,速度为3cm/s,设运动时间为ts.(1)如图(1),当t=时,△APC的面积等于△ABC面积的一半;(2)如图(2),在△DEF中,∠E=90°,DE=4cm,DF=5cm,∠D=∠A.在△ABC的边上,若另外有一个动点Q,与点P同时从点A出发,沿着边AB→BC→CA运动,回到点A停止.在两点运动过程中的某一时刻,恰好△APQ≌△DEF,求点Q的运动速度.24.(2022春•华容县期中)如图,已知正方形ABCD的边长为10cm,点E在AB边上,BE=6cm.(1)如果点P在线段BC上以4cm/s的速度由B点向C点运动,同时,点Q在线段CD上由C点向D 点运动.①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等.请说明理由.②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?相遇点在何处?25.(2022秋•红花岗区期中)如图1,直线AM⊥AN,AB平分∠MAN,过点B作BC⊥BA交AN于点C;动点E、D同时从A点出发,其中动点E以2cm/s的速度沿射线AN方向运动,动点D以1cm/s的速度运动;已知AC=6cm,设动点D,E的运动时间为t.(1)当点D在射线AM上运动时满足S△ADB:S△BEC=2:1,试求点D,E的运动时间t的值;(2)当动点D在直线AM上运动,E在射线AN运动过程中,是否存在某个时间t,使得△ADB与△BEC 全等?若存在,请求出时间t的值;若不存在,请说出理由.26.如图,AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在射线AB上以1cm/s的速度由点A出发沿射线AB方向运动,同时,点Q在射线DB上由点D出发沿射线DB方向运动.它们运动的时间为t (s).(1)若点Q的运动速度是点P的运动速度的2倍,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;(2)设点Q的运动速度为xcm/s(x≠2),是否存在实数x,使△ACP与△BPQ全等?若存在,请画出示意图,将全等的三角形用符号表示出来,并直接写出相应的x,t的值;若不存在,请说明理由.27.(2022秋•沭阳县校级月考)如图①,线段BC=6,过点B、C分别作垂线,在其同侧取AB=4,另一条垂线上任取一点D.动点P从点B出发,以每秒2个单位的速度沿BC向终点C运动;同时动点Q从点C出发,以每秒a个单位的速度沿射线CD运动,当点P停止时,点Q也随之停止运动.设点P的运动的时间为t(s).(1)当t=1,CP=,用含a的代数式表示CQ的长为;(2)当a=2,t=1时,①求证:△ABP≌△PCQ;②求证:AP⊥PQ;(3)如图②,将“过点B、C分别作垂线”改为“在线段BC的同侧作∠ABC=∠DCB”,其它条件不变.若△ABP与△PCQ全等,直接写出对应的a的值.28.在直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,①如图1,分别过点A和B作AD⊥直线l于点D,BE⊥直线l于点E.求证:△ACD≌△CBE;②如图2,过点A作AD⊥直线l于点D,点B与点F关于直线l对称,连接BF交直线l于E,连接CF.求证:DE=AD+EF.(2)当AC=8cm,BC=6cm时,如图3,点B与点F关于直线l对称,连接BF、CF.点M从A点出发,以每秒1cm的速度沿A→C路径运动,终点为C,点N以每秒3cm的速度沿F→C→B→C→F路径运动,终点为F,分别过点M、N作MD⊥直线l于点D,NE⊥直线l于点E,点M、N同时开始运动,各自达到相应的终点时停止运动,设运动时间为t秒.当△MDC与△CEN全等时,求t的值.29.(2022秋•浠水县期中)已知,在△ABC中,AB=AC,D,A,E三点都在直线m上,且DE=9cm,∠BDA=∠AEC=∠BAC(1)如图①,若AB⊥AC,则BD与AE的数量关系为,CE与AD的数量关系为;(2)如图②,判断并说明线段BD,CE与DE的数量关系;(3)如图③,若只保持∠BDA=∠AEC,BD=EF=7cm,点A在线段DE上以2cm/s的速度由点D向点E运动,同时,点C在线段EF上以xcm/s的速度由点E向点F运动,它们运动的时间为t(s).是否存在x,使得△ABD与△EAC全等?若存在,求出相应的t的值;若不存在,请说明理由.30.(2022秋•原平市校级期中)如图,在△ABC中,BC=5,高AD、BE相交于点O,BD=23CD,且AE=BE.(1)求线段AO的长;(2)动点P从点O出发,沿线段OA以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,△POQ的面积为S,请用含t的式子表示S;(3)在(2)的条件下,点F是直线AC上的一点且CF=BO.是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在,请直接写出符合条件的t值,若不存在,请说明理由.。
初中数学全等三角形中的动态问题(知识点例题解析)

初中数学全等三角形中的动态问题(知识点+例题解析)初中数学中,动点问题是学习的重、难点,在三角形、矩形等一些几何图形上,设计一个或多个动点,探究全等三角形存在性问题,该类题目具有较强的综合性。
解决动点问题常见的答题思路是:1.注意分类讨论;2.仔细探究全等三角形对应边与对应角的变化;3.利用时间表示出相应线段或边的长度,列出方程求解.【典例解析】【例1-1】(2020·周口市月考)如图,CA⊥AB,垂足为点A,AB=8,AC=4,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E离开点A后,运动______秒时,△DEB与△BCA全等.【例1-2】(2020·江阴市月考)已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为t秒,当t的值为_____秒时,△ABP和△DCE全等.A.1B.1或3C.1或7D.3或7【变式1-1】(2020·无锡市月考)如图,在△ABC中,∠ACB=90°,AC=7cm,BC=3cm,CD为AB边上的高.点E从点B出发沿直线BC以2cm/s的速度移动,过点E作BC的垂线交直线CD于点F.(1)试说明:∠A=∠BCD;(2)当点E运动多长时间时,CF=AB.请说明理由.【变式1-2】(2020·河北灵寿期末)如图,在平面直角坐标系中,O为坐标原点,A、B两点的坐标分别为A(0,m)、B(n,0),且|m﹣n﹣0,点P从A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.(1)求OA、OB的长;(2)连接PB,设△POB的面积为S,用t的式子表示S;(3)过点P作直线AB的垂线,垂足为D,直线PD与x轴交于点E,在点P运动的过程中,是否存在这样的点P,使△EOP≌△AOB?若存在,请求出t的值;若不存在,请说明理由.【例2】(2020·惠州市月考)如图,点C在线段BD上,AB⊥BD于B,ED⊥BD于D.∠ACE=90°,且AC =5cm,CE=6cm,点P以2cm/s的速度沿A→C→E向终点E运动,同时点Q以3cm/s的速度从E开始,在线段EC上往返运动(即沿E→C→E→C→…运动),当点P到达终点时,P,Q同时停止运动.过P,Q分别作BD的垂线,垂足为M,N.设运动时间为ts,当以P,C,M为顶点的三角形与△QCN全等时,t的值为_____.【变式2-1】(2020·江阴市月考)如图,在四边形ABCD中,AD=BC=4,AB=CD,BD=6,点E从D 点出发,以每秒1个单位的速度沿DA向点A匀速移动,点F从点C出发,以每秒3个单位的速度沿C→B→C 作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动.(1)试证明:AD∥BC.(2)在移动过程中,小芹发现当点G的运动速度取某个值时,有△DEG与△BFG全等的情况出现,请你探究当点G的运动速度取哪些值时,△DEG与△BFG全等.【变式2-2】(2020·重庆巴南月考)如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在cm s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它线段AB上以1/们运动的时间为t(s).(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的cm s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若运动速度为x/不存在,请说明理由.【变式2-3】(2020·江苏兴化月考)如图,在△ABC中,∠ACB=90°,AC=6,BC=8.点P从点A出发,沿折线AC—CB以每秒1个单位长度的速度向终点B运动,点Q从点B出发沿折线BC—CA以每秒3个单位长度的速度向终点A运动,P、Q两点同时出发.分别过P、Q两点作PE⊥l于E,QF⊥l于F.设点P的运动时间为t(秒):(1)当P、Q两点相遇时,求t的值;(2)在整个运动过程中,求CP的长(用含t的代数式表示);(3)当△PEC与△QFC全等时,直接写出所有满足条件的CQ的长.【例3】(2020·惠州市月考)如图,在△ABC中,AB=AC=18cm,BC=10cm,∠B=∠C,AD=2BD.如果点P在线段BC上以2cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.(1)若点Q的运动速度与点P的运动速度相等,经过2s后,△BPD与△CQP是否全等,请说明理由;(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP 全等?(3)若点Q以(2)中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC 三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?【变式3-1】(2019·山西太原月考)如图1,在长方形ABCD中,AB=CD=5cm,BC=12cm,点P从点B 出发,以2cm/s的速度沿BC向点C运动,设点P的运动时间为ts.(1)PC=___cm;(用含t的式子表示)(2)当t为何值时,△ABP≌△DCP?.(3)如图2,当点P从点B开始运动,此时点Q从点C出发,以vcm/s的速度沿CD向点D运动,是否存在这样的v值,使得某时刻△ABP与以P,Q,C为顶点的直角三角形全等?若存在,请求出v的值;若不存在,请说明理由.【变式3-2】(2020·四川成都)如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为_____厘米/秒时,能够使△BPE与以C、P、Q 三点所构成的三角形全等.【习题精练】=,BC6=,线段PQ=AB,1.(2020·江苏东台月考)如图,有一个直角三角形ABC,∠C=90°,AC10点Q在过点A且垂直于AC的射线AX上来回运动,点P从C点出发,沿射线CA以2cm/s的速度运动,问>,才能使△ABC≌△QPA全等.P点运动___________秒时(t0)2.(2020·江苏泰州月考)如图,AB =12,CA ⊥AB 于A ,DB ⊥AB 于B ,且AC =4m ,P 点从B 向A 运动,每分钟走1m ,Q 点从B 向D 运动,每分钟走2m ,P 、Q 两点同时出发,运动_______分钟后△CAP 与△PQB 全等.3.(2020·常州市月考)如图, ADC 中.∠C =90°,AC =10cm ,BC =5cm .AD ⊥AC ,AB =PQ ,P 、Q 两点分别在AC 、AD 上运动,当AQ =_____时,△ABC 才能和△APQ 全等.4.(2020·江西新余期末)如图,ABC ∆中,90ACB ∠=︒,8cm AC =,15cm BC =,点M 从A 点出发沿A C B →→路径向终点运动,终点为B 点,点N 从B 点出发沿B C A →→路径向终点运动,终点为A 点,点M 和N 分别以每秒2cm 和3cm 的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M 和N 作ME l ⊥于E ,NF l ⊥于F .设运动时间为t 秒,要使以点M ,E ,C 为顶点的三角形与以点N ,F ,C 为顶点的三角形全等,则t 的值为______.5.(2020·武城县月考)如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为多少时,能够使△BPE与以C、P、Q三点所构成的三角形全等?6.(2020·盐城市盐都区月考)如图,有一个直角△ABC,∠C=90°,AC=6,BC=3,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问:当AP=________时,才能使以点P、A、Q 为顶点的三角形与△ABC全等.7.(2020·四川青羊期中)如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4cm,BC=8cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD=cm,CE=cm;(2)当t为多少时,△ABD的面积为12cm2?(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.8.(2020·郑州市月考)如图,在平面直角坐标系中,O 为坐标原点A 、B 两点的坐标分别A (m ,0),B(0,n ),且|m -n -3|=0,点P 从A 出发,以每秒1个单位的速度沿射线AO 匀速运动,设点P 运动时间为t 秒.(1)求OA 、OB 的长;(2)连接PB ,若△POB 的面积不大于3且不等于0,求t 的范围;(3)过P 作直线AB 的垂线,垂足为D ,直线PD 与y 轴交于点E ,在点P 运动的过程中,是否存在这样的点P ,使△EOP ≌△AOB ?若存在,请求出t 的值;若不存在,请说明理由.9.(2020·宜兴市月考)如图,在△ABC 中,∠BAD =∠DAC ,DF ⊥AB ,DM ⊥AC ,AF =10cm ,AC =14cm ,动点E 以2cm /s 的速度从A 点向F 点运动,动点G 以1cm /s 的速度从C 点向A 点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t .(1)求证:AF =AM ;(2)当t 取何值时,△DFE 与△DMG 全等;(3)求证:在运动过程中,不管t 取何值,都有2AED DGC S S =△△.10.(2020·江苏工业园区期末)如图①,将长方形纸片沿对角线剪成两个全等的直角三角形ABC、EDF,其中AB=8cm,BC=6cm,AC=10cm.现将△ABC和△EDF按如图②的方式摆放(点A与点D、点B与点E 分别重合).动点P从点A出发,沿AC以2cm/s的速度向点C匀速移动;同时,动点Q从点E出发,沿射线ED以acm/s(0<a<3)的速度匀速移动,连接PQ、CQ、FQ,设移动时间为ts(0≤t≤5).=3S△BQC,则a=;(1)当t=2时,S△AQF(2)当以P、C、Q为顶点的三角形与△BQC全等时,求a的值;(3)如图③,在动点P、Q出发的同时,△ABC也以3cm/s的速度沿射线ED匀速移动,当以A、P、Q为顶点的三角形与△EFQ全等时,求a与t的值.11.(2019·江苏期末)如图①,在ABC ∆中,12AB =cm ,20BC =cm ,过点C 作射线//CD AB .点M 从点B 出发,以3cm /s 的速度沿BC 匀速移动;点N 从点C 出发,以a cm /s 的速度沿CD 匀速移动.点M 、N 同时出发,当点M 到达点C 时,点M 、N 同时停止移动.连接AM 、MN ,设移动时间为t (s ).(1)点M 、N 从移动开始到停止,所用时间为s ;(2)当ABM ∆与MCN ∆全等时,①若点M 、N 的移动速度相同,求t 的值;②若点M 、N 的移动速度不同,求a 的值;(3)如图②,当点M 、N 开始移动时,点P 同时从点A 出发,以2cm /s 的速度沿AB 向点B 匀速移动,到达点B 后立刻以原速度沿BA 返回.当点M 到达点C 时,点M 、N 、P 同时停止移动.在移动的过程中,是否存在PBM ∆与MCN ∆全等的情形?若存在,求出t 的值;若不存在,说明理由.图①图②12.如图,ABC 中,90ACB ∠=︒,8AC cm =,15BC cm =,点M 从A 点出发沿A →C →B 路径向终点运动,终点为B 点,点N 从B 点出发沿B →C →A 路径向终点运动,终点为A 点,点M 和N 分别以每秒2cm 和3cm 的运动速度同时开始运动,两点都要到达相应的终点时才能停止运动,分别过M 和N 作ME l ⊥于E ,NF l ⊥于F 设运动时间为t 秒,要使以点M ,E ,C 为顶点的三角形与以点N ,F ,C 为顶点的三角形全等,则t 的值为________.13.(2019·湖北襄州)在平面直角坐标系中,点A(0,5),B(12,0),在y轴负半轴上取点E,使OA=EO,作∠CEF=∠AEB,直线CO交BA的延长线于点D.(1)根据题意,可求得OE=;(2)求证:△ADO≌△ECO;(3)动点P从E出发沿E﹣O﹣B路线运动速度为每秒1个单位,到B点处停止运动;动点Q从B出发沿B﹣O﹣E运动速度为每秒3个单位,到E点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PM⊥CD于点M,QN⊥CD于点N.问两动点运动多长时间△OPM与△OQN全等?14.(2019·福建省惠安期中)如图,在△ABC中,BC=8cm,AG∥BC,AG=8cm,点F从点B出发,沿线段BC以4cm/s的速度连续做往返运动,同时点E从点A出发沿线段AG以2cm/s的速度向终点G运动,当点E到达点G时,E、F两点同时停止运动,EF与AC交于点D,设点E的运动时间为t(秒)(1)分别写出当0≤t≤2和2<t≤4时线段BF的长度(用含t的代数式表示);(2)当BF=AE时,求t的值;(3)若△ADE≌△CDF,求所有满足条件的t值.15.(2020·无锡市月考)△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P 在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q 的运动速度为_____厘米/秒,△BPD与△CQP全等.16.(2020·广东龙岗期末)直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图①,分别过点A、B作AD⊥l于点D,BE⊥l于点E.求证:△ACD≌△CBE.(2)当AC=8,BC=6时,如图②,点B与点F关于直线l对称,连接BF,CF,动点M从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿F→C→B→C→F向终点F运动,点M、N到达相应的终点时停止运动,过点M作MD⊥l于点D,过点N 作NE⊥l于点E,设运动时间为t秒.①CM=,当N在F→C路径上时,CN=.(用含t的代数式表示)②直接写出当△MDC与△CEN全等时t的值.17.(2020·青岛市黄岛区月考)如图1,直线AM AN ⊥,AB 平分MAN ∠,过点B 作BC BA ⊥交AN 于点C ;动点E 、D 同时从A 点出发,其中动点E 以2/m s 的速度沿射线AN 方向运动,动点D 以1/m s 的速度运动;已知6AC cm =,设动点D ,E 的运动时间为t .图1备用图(1)试求∠ACB 的度数;(2)当点D 在射线AM 上运动时满足ADB S :2BEC S = :3,试求点D ,E 的运动时间t 的值;(3)当动点D 在直线AM 上运动,E 在射线AN 运动过程中,是否存在某个时间t ,使得ADB 与BEC 全等?若存在,请求出时间t 的值;若不存在,请说出理由.参考答案及解析初中数学中,动点问题是学习的重、难点,在三角形、矩形等一些几何图形上,设计一个或多个动点,探究全等三角形存在性问题,该类题目具有较强的综合性。
第-4讲---全等三角形动点提高题

第4讲全等三角形动点提高题动点型问题是最近几年中考的一个热点题型,所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.从变换的角度和运动变化来研究三角形、四边形,在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
典型例题例1、如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD 与△CQP全等(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇[【分析】(1)①根据时间和速度分别求得两个三角形中的边的长,根据SAS判定两个三角形全等.②根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;(2)根据题意结合图形分析发现:由于点Q的速度快,且在点P的前边,所以要想第一次相遇,则应该比点P多走等腰三角形的两个腰长.解:(1)①∵t=1s,∴BP=CQ=3×1=3cm,∵AB=10cm,点D为AB的中点,∴BD=5cm.又∵PC=BC﹣BP,BC=8cm,∴PC=8﹣3=5cm,》∴PC=BD.又∵AB=AC,∴∠B=∠C,在△BPD和△CQP中,∴△BPD≌△CQP(SAS).②∵v P≠v Q,∴BP≠CQ,若△BPD≌△CPQ,∠B=∠C,则BP=PC=4cm,CQ=BD=5cm,、∴点P,点Q运动的时间s,∴cm/s;(2)设经过x秒后点P与点Q第一次相遇,由题意,得x=3x+2×10,解得.∴点P共运动了×3=80cm.△ABC周长为:10+10+8=28cm,若是运动了三圈即为:28×3=84cm,∵84﹣80=4cm<AB的长度,∴点P、点Q在AB边上相遇,、∴经过s点P与点Q第一次在边AB上相遇.例2、如图,△ABC中,∠ACB=90°,AC=6BC=8.点P从点出发沿A-C-B路径向终点运动,终点为B点;点Q从B点出发沿B-C-A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,一点到相应的终点停止运动,某时刻,分别过P和Q作PE ⊥L于E,QF⊥L于F.问:点P运动多少时间时,△PEC与QFC全等请说明理由.解:设运动时间为t秒时,△PEC≌△QFC,∵△PEC≌△QFC,∴斜边CP=CQ,有四种情况:①P在AC上,Q在BC上,CP=6-t,CQ=8-3t,∴6-t=8-3t,∴t=1;②P、Q都在AC上,此时P、Q重合,∴CP=6-t=3t-8,∴t=;③P 在BC 上,Q 在AC 时,此时不存在;理由是:8÷3×1<6,Q 到AC 上时,P 应也在AC 上;④当Q 到A 点(和A 重合),P 在BC 上时,∵CQ=CP ,CQ=AC=6,CP=t-6,∴t-6=6∴t=12∵t <14∴t=12符合题意故点P 运动1或或12秒时,△PEC 与△QFC 全等.例3、(1)如图,在四边形ABCD 中,AB =AD ,∠B =∠D =90︒,E 、F 分别是边BC 、CD 上的点,且∠EAF=12∠BAD .求证:EF =BE +FD; FEDC B A(2) 如图,在四边形ABCD 中,AB =AD ,∠B+∠D =180︒,E 、F 分别是边BC 、CD上的点,且∠EAF=12∠BAD , (1)中的结论是否仍然成立不用证明. FEDC BA 证明:延长EB 到G ,使BG=DF ,联结AG .∵∠ABG =∠ABC=∠D =90︒, AB =AD , *∴ABG ADF ∆∆≌.∴AG =AF , 12∠=∠. ∴113232EAF BAD ∠+∠=∠+∠=∠=∠. ∴∠GAE=∠EAF .又AE =AE , ∴AEG AEF ∆∆≌.∴EG =EF . ∵EG=BE+BG .∴EF= BE +FD(2) (1)中的结论EF BE FD =+仍然成立.考点训练一.选择题!1.如图,△ACB ≌△A ′CB ′,∠BCB ′=30°,则∠ACA ′的度数为( )A .20°B .30°C .35°D .40°【分析】本题根据全等三角形的性质并找清全等三角形的对应角即可.解:∵△ACB ≌△A ′CB ′,∴∠ACB=∠A ′CB ′,即∠ACA ′+∠A ′CB=∠B ′CB+∠A ′CB ,∴∠ACA ′=∠B ′CB ,又∠B ′CB=30°∴∠ACA ′=30°.!故选:B .2.如图,AD 是△ABC 中∠BAC 的角平分线,DE ⊥AB 于点E ,S △ABC =7,DE=2,AB=4,则AC 长是( )A .3B .4C .6D .5【分析】过点D 作DF ⊥AC 于F ,根据角平分线上的点到角的两边距离相等可得DE=DF ,再根据S △ABC =S △ABD +S △ACD 列出方程求解即可.解:如图,过点D 作DF ⊥AC 于F ,∵AD 是△ABC 中∠BAC 的角平分线,DE ⊥AB ,∴DE=DF ,由图可知,S △ABC =S △ABD +S △ACD ,∴×4×2+×AC ×2=7,~解得AC=3.故选:A .3.如图,在△ABC 和△DEC 中,已知AB=DE ,还需添加两个条件才能使△ABC ≌△DEC ,不能添加的一组条件是()A.BC=EC,∠B=∠E B.BC=EC,AC=DC C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D【分析】根据全等三角形的判定方法分别进行判定即可.解:A、已知AB=DE,再加上条件BC=EC,∠B=∠E可利用SAS证明△ABC≌△DEC,故此选项不合题意;B、已知AB=DE,再加上条件BC=EC,AC=DC可利用SSS证明△ABC≌△DEC,故此选项不合题意;C、已知AB=DE,再加上条件BC=DC,∠A=∠D不能证明△ABC≌△DEC,故此选项符合题意;【D、已知AB=DE,再加上条件∠B=∠E,∠A=∠D可利用ASA证明△ABC≌△DEC,故此选项不合题意;故选:C.4.如图,△ABC的三边AB,BC,CA长分别是20,30,40,其三条角平分线将△ABC分为三个三角形,则S△ABO:S△BCO:S△CAO等于()A.1:1:1 B.1:2:3 C.2:3:4 D.3:4:5【分析】利用角平分线上的一点到角两边的距离相等的性质,可知三个三角形高相等,底分别是20,30,40,所以面积之比就是2:3:4.解:利用同高不同底的三角形的面积之比就是底之比可知选C.故选C.二.填空题1.如图,已知AB∥CF,E为DF的中点,若AB=9cm,CF=5cm,则BD=4cm.~【分析】先根据平行线的性质求出∠ADE=∠EFC,再由ASA可求出△ADE≌△CFE,根据全等三角形的性质即可求出AD的长,再由AB=9cm即可求出BD的长.解:∵AB∥CF,∴∠ADE=∠EFC,∵∠AED=∠FEC,E为DF的中点,∴△ADE≌△CFE,∴AD=CF=5cm,∵AB=9cm,∴BD=9﹣5=4cm.故填4.*2.在数学活动课上,小明提出这样一个问题:∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,如图,则∠EAB是多少度大家一起热烈地讨论交流,小英第一个得出正确答案,是35度.【分析】过点E作EF⊥AD,证明△ABE≌△AFE,再求得∠CDE=90°﹣35°=55°,即可求得∠EAB的度数.解:过点E作EF⊥AD,∵DE平分∠ADC,且E是BC的中点,∴CE=EB=EF,又∠B=90°,且AE=AE,∴△ABE≌△AFE,∴∠EAB=∠EAF.又∵∠CED=35°,∠C=90°,∴∠CDE=90°﹣35°=55°,(即∠CDA=110°,∠DAB=70°,∴∠EAB=35°.3.如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为4.【分析】根据垂线段最短,当DP垂直于BC的时候,DP的长度最小,则结合已知条件,利用三角形的内角和定理推出∠ABD=∠CBD,由角平分线性质即可得AD=DP,由AD的长可得DP的长.解:根据垂线段最短,当DP⊥BC的时候,DP的长度最小,∵BD⊥CD,即∠BDC=90°,又∠A=90°,∴∠A=∠BDC,又∠ADB=∠C,∴∠ABD=∠CBD,又DA⊥BA,BD⊥DC,∴AD=DP,又AD=4,%∴DP=4.故答案为:4.4.如图,△ABC中,∠C=90°,CA=CB,点M在线段AB上,∠GMB=∠A,BG⊥MG,垂足为G,MG与BC相交于点H.若MH=8cm,则BG=4cm.【分析】如图,作MD⊥BC于D,延长DE交BG的延长线于E,构建等腰△BDM、全等三角形△BED和△MHD,利用等腰三角形的性质和全等三角形的对应边相等得到:BE=MH,所以BG=MH=4.解:如图,作MD⊥BC于D,延长MD交BG的延长线于E,∵△ABC中,∠C=90°,CA=CB,∴∠ABC=∠A=45°,∵∠GMB=∠A,∴∠GMB=∠A=°,^∵BG⊥MG,∴∠BGM=90°,∴∠GBM=90°﹣°=°,∴∠GBH=∠EBM﹣∠ABC=°.∵MD∥AC,∴∠BMD=∠A=45°,∴△BDM为等腰直角三角形∴BD=DM,而∠GBH=°,∴GM平分∠BMD,'而BG⊥MG,∴BG=EG,即BG=BE,∵∠MHD+∠HMD=∠E+∠HMD=90°,∴∠MHD=∠E,∵∠GBD=90°﹣∠E,∠HMD=90°﹣∠E,∴∠GBD=∠HMD,∴在△BED和△MHD中,,∴△BED≌△MHD(AAS),∴BE=MH,\∴BG=MH=4.故答案是:4.三.解答题1.(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=150°,∠XBC+∠XCB= 90°.(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.【分析】本题考查的是三角形内角和定理.已知∠A=30°易求∠ABC+∠ACB的度数.又因为∠X为90°,所以易求∠XBC+∠XCB.解:(1)∵∠A=30°,∴∠ABC+∠ACB=150°,∵∠X=90°,~∴∠XBC+∠XCB=90°,∴∠ABC+∠ACB=150°;∠XBC+∠XCB=90°.(2)不变化.∵∠A=30°,∴∠ABC+∠ACB=150°,∵∠X=90°,∴∠XBC+∠XCB=90°,∴∠ABX+∠ACX=(∠ABC﹣∠XBC)+(∠ACB﹣∠XCB)=(∠ABC+∠ACB)﹣(∠XBC+∠XCB)=150°﹣90°=60°.^2.已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.(1)如图1,若AB∥ON,则①∠ABO的度数是20°;②当∠BAD=∠ABD时,x=120°;当∠BAD=∠BDA时,x=60°.(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角若存在,求出x的值;若不存在,说明理由.【分析】利用角平分线的性质求出∠ABO的度数是关键,分类讨论的思想.解:(1)①∵∠MON=40°,OE平分∠MON∴∠AOB=∠BON=20°∵AB∥ON∴∠ABO=20°②∵∠BAD=∠ABD∴∠BAD=20°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=120°-∵∠BAD=∠BDA,∠ABO=20°∴∠BAD=80°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=60°故答案为:①20 ②120,60(2)①当点D在线段OB上时,∵OE是∠MON的角平分线,∴∠AOB=∠MON=20°,∵AB⊥OM,∴∠AOB+∠ABO=90°,∴∠ABO=70°,若∠BAD=∠ABD=70°,则x=20-若∠BAD=∠BDA=(180°﹣70°)=55°,则x=35若∠ADB=∠ABD=70°,则∠BAD=180°﹣2×70°=40°,∴x=50②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,所以只有∠BAD=∠BDA,此时x=125.综上可知,存在这样的x的值,使得△ADB中有两个相等的角,且x=20、35、50、125.3.平面内的两条直线有相交和平行两种位置关系(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD,又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B﹣∠D.将点P移到AB、CD内部,如图b,以上结论是否成立若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系(不需证明)·(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.【分析】(1)延长BP交CD于E,根据两直线平行,内错角相等,求出∠PED=∠B,再利用三角形的一个外角等于和它不相邻的两个内角的和即可说明不成立,应为∠BPD=∠B+∠D;(2)作射线QP,根据三角形的外角性质可得;(3)根据三角形的外角性质,把角转化到四边形中再求解.解:(1)不成立.结论是∠BPD=∠B+∠D延长BP交CD于点E,∵AB∥CD∴∠B=∠BED又∵∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D.¥(2)结论:∠BPD=∠BQD+∠B+∠D.(3)连接EG并延长,根据三角形的外角性质,∠AGB=∠A+∠B+∠E,又∵∠AGB=∠CGF,在四边形CDFG中,∠CGF+∠C+∠D+∠F=360°,∴∠A+∠B+∠C+∠D+∠E+∠F=360°.4.如下几个图形是五角星和它的变形.$(1)图(1)中是一个五角星,求∠A+∠B+∠C+∠D+∠E.(2)图(2)中的点A向下移到BE上时,五个角的和(即∠CAD+∠B+∠C+∠D+∠E)有无变化说明你的结论的正确性.(3)把图(2)中的点C向上移到BD上时(1)如图(3)所示,五个角的和(即∠CAD+∠B+∠ACE+∠D+∠E)有无变化说明你的结论的正确性.【分析】(1)如图,连接CD,把五个角和转化为同一个三角形内角和.根据三角形中一个外角等于与它不相邻的两个内角和,再根据三角形内角和定理可得.(2)、(3)五个角转化为一个平角.解:(1)如图,连接CD.在△ACD中,根据三角形内角和定理,得出∠A+∠2+∠3+∠ACE+∠ADB=180°.∵∠1=∠B+∠E=∠2+∠3,"∴∠A+∠B+∠ACE+∠ADB+∠E=∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠2+∠3+∠ACE+∠ADB=180°;(2)无变化.根据平角的定义,得出∠BAC+∠CAD+∠DAE=180°.∵∠BAC=∠C+∠E,∠EAD=∠B+∠D,∴∠CAD+∠B+∠C+∠D+∠E=∠BAC+∠CAD+∠DAE=180°;(3)无变化.∵∠ACB=∠CAD+∠D,∠ECD=∠B+∠E,∴∠CAD+∠B+∠ACE+∠D+∠E=∠ACB+∠ACE+∠ECD=180°.13.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.》【分析】连接BE,由三角形内角和外角的关系可知∠C+∠D=∠CBE+∠DEB,由四边形内角和是360°,即可求∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.解:如图连接BE.∵∠1=∠C+∠D,∠1=∠CBE+∠DEB,∴∠C+∠D=∠CBE+∠DEB,∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=∠A+∠ABC+∠CBE+∠DEB+∠DEF+∠F=∠A+∠ABE+∠BEF+∠F.又∵∠A+∠ABE+∠BEF+∠F=360°,∴∠A+∠ABC+∠C+∠D+∠DEF+∠F=360°.&14.将纸片△ABC沿DE折叠使点A落在A′处的位置.(1)如果A′落在四边形BCDE的内部(如图1),∠A′与∠1+∠2之间存在怎样的数量关系并说明理由.(2)如果A′落在四边形BCDE的BE边上,这时图1中的∠1变为0°角,则∠A′与∠2之间的关系是2∠A=∠2.(3)如果A′落在四边形BCDE的外部(如图2),这时∠A′与∠1、∠2之间又存在怎样的数量关系并说明理由.【分析】(1)根据折叠性质得出∠AED=∠A′ED,∠ADE=∠A′DE,根据三角形内角和定理得出∠AED+∠ADE=180°﹣∠A,代入∠1+∠2=180°+180°﹣2(∠AED+∠ADE)求出即可;(2)根据三角形外角性质得出∠DME=∠A′+∠1,∠2=∠A+∠DME,代入即可求出答案;(3)根据三角形外角性质得出∠DME=∠A′+∠1,∠2=∠A+∠DME,推出∠2=∠A+∠A′+∠1,即可得出答案.解:(1)图1中,2∠A=∠1+∠2,理由是:∵延DE折叠A和A′重合,.∴∠AED=∠A′ED,∠ADE=∠A′DE,∵∠AED+∠ADE=180°﹣∠A,∠1+∠2=180°+180°﹣2(∠AED+∠ADE),∴∠1+∠2=360°﹣2(180°﹣∠A)=2∠A;(2)2∠A=∠2,如图∠2=∠A+∠EA′D=2∠A,故答案为:2∠A=∠2;(3)如图2,2∠A=∠2﹣∠1,理由是:∵延DE折叠A和A′重合,[∴∠A=∠A′,∵∠DME=∠A′+∠1,∠2=∠A+∠DME,∴∠2=∠A+∠A′+∠1,即2∠A=∠2﹣∠1.△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.(1)若点P在线段AB上,如图(1)所示,且∠α=50°,则∠1+∠2=140°;(2)若点P在边AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为:∠1+∠2=90°+α;{(3)若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系猜想并说明理由.(4)若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间的关系为:∠2=90°+∠1﹣α.【分析】(1)根据四边形内角和定理以及邻补角的定义得出∠1+∠2=∠C+∠α,进而得出即可;(2)利用(1)中所求得出答案即可;(3)利用三角外角的性质得出∠1=∠C+∠2+α=90°+∠2+α;(4)利用三角形内角和定理以及邻补角的性质可得出.解:(1)∵∠1+∠2+∠CDP+∠CEP=360°,∠C+∠α+∠CDP+∠CEP=360°,∴∠1+∠2=∠C+∠α,∵∠C=90°,∠α=50°,:∴∠1+∠2=140°;故答案为:140°; (2)由(1)得出: ∠α+∠C=∠1+∠2, ∴∠1+∠2=90°+α故答案为:∠1+∠2=90°+α;(3)∠1=90°+∠2+α,理由:∵∠2+∠α=∠DME ,∠DME+∠C=∠1, #∴∠1=∠C+∠2+α=90°+∠2+α.(4)∵∠PFD=∠EFC ,∴180°﹣∠PFD=180°﹣∠EFC ,∴∠α+180°﹣∠1=∠C+180°﹣∠2, ∴∠2=90°+∠1﹣α.故答案为:∠2=90°+∠1﹣α.1、 如图(1),已知线段AB 的长为2a ,点P 是AB 上的动点(P 不与A ,B 重合),分别以AP 、PB 为边向线段AB 的同一侧作正△APC 和正△PBD .(1)当△APC 与△PBD 的面积之和取最小值时,AP=___________;(直接写结果) (2)连结AD 、BC ,相交于点Q ,设∠AQC=α,那么α的大小是否会随点P 的移动而变化请说明理由; ](3)如图(2),若点P 固定,将△PBD 绕点P 按顺时针方向旋转(旋转角小于180°),此时α的大小是否发生变化(只需直接写出你的猜想,不必证明)【思路】设AP 为x , 则PB 为a -x ,△APC 的面积为243x ,△BPD 的面积为2)2(43x a ,列出两三角形面积和的二次函数解析式,通过二次函数求极值得出面积和最小时AP 的值;通过△APD ≌△CPB, 得到∠PAD=∠PCB,由等量代换得到∠QCP+∠QAC+∠ACP=1200, 所以∠AQC=1800-1200 =600.图(2)图(1)【答案】(1)a;(2)α的大小不会随点P的移动而变化,理由:∵△APC是等边三角形,∴PA=PC, ∠APC=600,∵△BDP是等边三角形,∴PB=PD, ∠BPD=600, ∴∠APC=∠BPD,∴∠APD=∠CPB, ∴△APD≌△CPB, ∴∠PAD=∠PCB,∵∠QAP+∠QAC+∠ACP=1200,∴∠QCP+∠QAC+∠ACP=1200, ∴∠AQC=1800-1200 =600;|(3) 此时α的大小不会发生改变,始终等于600.2、在△ABC中,∠A=90°,AB=AC,D为BC的中点.(1)如图1,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形;(2)如图2,若E,F分别是AB,CA延长线上的点,仍有BE=AF,其他条件不变,•那么△DEF是否仍为等腰直角三角形证明你的结论.图1 图2解析(1)连结AD.∵AB=AC,∠BAC=90°,D为BC的中点,∴AD⊥BC,BD=AD,∴∠B=∠DAC=45°.又BE=AF,∴△BDE≌△ADF(SAS),∴ED=FD,∠BDE=∠ADF,∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°.∴△DEF为等腰直角三角形.…(2)连结AD.∵AB=AC,∠BAC=90°,D为BC的中点,∴AD=BD,AD⊥BC.∴∠DAC=∠ABD=45°,∴∠DAF=∠DBE=135°.又AF=BE,∴△DAF≌△DBE(SAS),∴FD=ED,∠FDA=∠EDB,∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°.∴△DEF仍为等腰直角三角形.试题分析:(1)连接AD,由AD是等腰直角三角形ABC底边上的中线,可得∠CAD=∠BAD=45°,AD=BD=CD,而即可得到∠B=∠DAF,再有BE=AF,AD=BD,即可证得△BED≌△AFD,从而得出DE=DF,∠BDE=∠ADF,从而得出∠EDF=90°,即可证得结论;(2)先由∠DBE=180°-45°=135°,∠DAF=90°+45°=135°,可得∠DAF=∠DBE,再结合两组对边对应相等,即可证得△BED≌△AFD从而证得结论.证明:①连结AD,∵,∠BAC=90°,为BC的中点∴AD⊥BC,BD=AD∴∠B=∠DAC=45°又∵BE=AF∴△BDE≌△ADF(SAS)∴ED=FD,∠BDE=∠ADF∴∠EDF=∠EDA+∠ADF=∠EDA+∠BDE=∠BDA=90°∴△DEF为等腰直角三角形;②若E,F分别是AB,CA延长线上的点,如图所示,连结AD∵AB=AC,∠BAC=90°,D为BC的中点∴AD=BD,AD⊥BC∴∠DAC=∠ABD=45°∴∠DAF=∠DBE=135°又AF=BE∴△DAF≌△DBE(SAS)∴FD=ED,∠FDA=∠EDB∴∠EDF=∠EDB+∠FDB=∠FDA+∠FDB=∠ADB=90°∴△DEF仍为等腰直角三角形.3.如图l,已知正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连结EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.(1)求证:OE=OF;(2)如图2,若点E在AC的延长线上,AM⊥BE于点M,交DB的延长线于点F,其它条件不变,则结论“OE=OF”还成立吗如果成立,请给出证明;如果不成立,请说明理由.图1F M O CDBAE图2FMOCDBAE\答案:(1)证明:∵四边形ABCD 是正方形. ∴∠BOE=∠AOF =90︒.OB =OA又∵AM ⊥BE ,∴∠MEA+∠MAE =90︒=∠AFO+∠MAE ∴∠MEA =∠AFO ∴Rt △BOE ≌Rt △AOF ∴OE=OF(2)OE =OF 成立证明:∵四边形ABCD 是正方形, ∴∠BOE=∠AOF =90︒.OB =OA又∵AM ⊥BE ,∴∠F+∠MBF =90︒=∠E+∠OBE—又∵∠MBF =∠OBE ∴∠F =∠E∴R t △BOE ≌Rt △AOF ∴OE=OF4.如图1,点P 、Q 分别是边长为4cm 的等边∆ABC 边AB 、BC 上的动点,点P 从顶点A ,点Q 从顶点B 同时出发,且它们的速度都为1cm/s ,(1)连接AQ 、CP 交于点M ,则在P 、Q 运动的过程中,∠CMQ 变化吗若变化,则说明理由,若不变,则求出它的度数; (2)何时∆PBQ 是直角三角形(3)如图2,若点P 、Q 在运动到终点后继续在射线AB 、BC 上运动,直线AQ 、CP 交点为M ,则∠CMQ 变化吗若变化,则说明理由,若不变,则求出它的度数;A P】CM第4题图1A&PBQCM第4题图2…答案:(1)060=∠CMQ 不变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形动点问题提高题
1.如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.
(1)如果点P在线段BC上以3厘米/秒得速度由B点向C点运动,同时点Q在线段CA 上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BP D≌△CQP?
(2)若点Q以(1)②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
2.如图,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.
(1)请你通过观察,测量,猜想并写出AB与AP所满足的数量关系和位置关系;
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ,猜想并写出BQ与AP所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(2)中所猜想的BQ与AP的数量关系和位置关系还成立吗?若成立,给
出证明;若不成立,请说明理由.
3.如图,在△ABC中,∠CAB=70°. 在同一平面内, 将△ABC绕点A旋转到△AB′C′的位置, 使得CC′∥AB, 则∠B′AB = _________
4. 已知如图(1),△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B、C在AE 的两侧,BD⊥AE于D,CE⊥AE于E,求证:(1)BD=DE+CE;(2)若直线AE绕A点旋转到(2)位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予证明.(3)若直线AE绕A点旋转到图(3)位置时,(BD>CE),其余条件不变,问BD与DE、CE的关系如何?请直接写出结果,不须证明.(4)归纳(1)、(2)、(3),请用简捷语言表述BD、DE、CE 的关系.
5.在图中,直线MN与线段AB相交于点O,∠1 = ∠2 = 45°.
(1)如图,若AO = OB,请写出AO与BD 的数量关系和位置关系;
(2)将图中的MN绕点O顺时针旋转得到下图,其中AO = OB.求证:AC = BD,AC ⊥BD;
6.如图,A、B、C、D在同一直线上,AB=CD,DE∥AF,且DE=AF,
(1)求证:△AFC≌△DEB.
(2)如果将BD沿着AD边的方向平行移动,如图,B点与C点重合时,如图,B点在C 点右侧时,其余条件不变,结论是否仍成立,如果成立,请予证明;如果不成立,请说明理由.
7.如图,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点,若AB=CD,AF= CE,BD交AC于M点,(1)求证:MB=MD,ME=MF(2)当E、F两点移到至如图所示的置时,其它条件不变,上述结论能否成立?若成立,请说明你的理由。
8.如图,宽为50cm 的长方形图案由20个全等的直角三角形拼成,其中一个直角三角形的面积为______.
9.如图,△ABC 中,∠C =90°,AD 平分∠BAC ,AB =5,CD =2,则△ABD 的面积是______.
10.如图,在△ABC 中,∠CAB=70°. 在同一平面内, 将△ABC 绕点A 旋转到△AB ′C ′ 的位置, 使得 CC ′∥AB, 则∠B′AB = _________
11.如图,在△ABC 中,AB =AC ,AD 是ABC △的角平分线,DE AB DF AC ⊥⊥,,垂足分别为E ,F .则下列四个结论:①AD 上任意一点到点C ,B 的距离相等;②AD 上任意一点到边AB ,AC 的距离相等;③BD =CD ,AD ⊥BC ;④∠BDE =∠CDF .其中,正确的个数为 ( )
A .1个
B .2个
C .3个
D .4个
A
D
E C
B
F A
D
C
B
12.在等边△ABC 的顶点A 、C 处各有一只蜗牛,它们同时出发,分别以每分钟1米的速度由A 向B 和由C 向A 爬行,其中一只蜗牛爬到终点时,另一只也停止运动,经过t 分钟后,它们分别爬行到D 、E 处,请问:
(1)如图1,在爬行过程中,CD 和BE 始终相等吗?
(2)如果将原题中的“由A 向B 和由C 向A 爬行”,改为“沿着AB 和CA 的延长线爬行”,EB 与CD 交于点Q ,其他条件不变,蜗牛爬行过程中∠CQE 的大小保持不变,请利用图2说明:∠CQE=60°;
(3)如果将原题中“由C 向A 爬行”改为“沿着BC 的延长线爬行,连接DE 交AC 于F”,其他条件不变,如图3,则爬行过程中,DF 始终等于EF 是否正确?
直线l 上,AC ⊥BC ,且AC=
13.如图,△ABC 的边BC 在
BC ;△EFP 的边FP 也在直线l 上,边EF 与边AC 重合,且EF=FP.
(1)请你通过观察,测量,猜想并写出AB 与AP 所满足的数量关系和位置关系;
(2)将△EFP 沿直线l 向左平移到图2的位置时,EP 交AC 于点Q ,连接AP ,BQ ,猜想并写出BQ 与AP 所满足的数量关系和位置关系,请证明你的猜想;
(3)将△EFP 沿直线l 向左平移到图3的位置时,EP 的延长线交AC 的延长线于点Q ,连接AP ,BQ.你认为(2)中所猜想的BQ 与AP 的数量关系和位置关系还成立吗?若成立,给出证明;若不成立,请说明理由.
D
E
A
Q
E
A
B
C
F
D
A
C
14.等边△ABC ,点D 是直线BC 上一点,以AD 为边在AD 的右侧作等边△ADE ,连接CE .
(1)如图1,若点D 在线段BC 上,求证:CE+CD=AB ;
(2)如图2,若点D 在CB 的延长线上,线段CE ,CD ,AB 的数量有怎样的数量关系?请加以证明.
15.如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .
经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,则AM =EC ,易证
AME ECF △≌△,所以AE EF =.
在此基础上,同学们作了进一步的研究:
(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
A
D
F
C G E B
图1
A
D
F
C G E B 图2
A
D
F
C G
E B
图3
16.如图所示,有一直角三角形△ABC ,∠C=900,AC=10cm ,BC=5cm ,一条线段PQ=AB ,P 、Q 两点分别在AC 上和过A 点且垂直于AC 的射线AM 上运动,问P 点运动到AC 上什么位置时,△ABC 才能和△APQ 全等?
17.在△ABC 中,AB=AC ,P 是△ABC 内任意一点,将AP 绕点A 顺时针旋转至AQ ,使∠QAP=∠BAC ,连接BQ ,CP ; (1)如图1,试说明BQ=CP ;
(2)若将点P 在△ABC 外,如图2,其它条件不变,结论依然成立吗?试说明理由。
18.如图1,在△ABC 中,点P 为BC 边中点,直线a 绕顶点A 旋转,若点B P 、在直线a 的异侧,BM ⊥直线a 于点M ,CN ⊥直线a 于点N ,连接.PM PN 、 (1)延长MP 交CN 于点E (如图2),①求证:BPM CPE △≌△;②求证:PM PN =;
(2)若直线a 绕点A 旋转到图3的位置时,点B P 、在直线a 的同侧,其它条件不变.此时PM PN =还成立吗?若成立,请给予证明;若不成立,请说明理由; (3)若直线a 绕点A 旋转到与BC 边平行的位置时,其它条件不变,请直接判断PM PN =还成立吗?不必说明理由.
Q
B C
P
A
Q
B C
P
A
D
B
C
P
A
Q
M
图1 图2 图3
19.如图所示,有一块塑料模板ABCD,长为10㎝,宽为4㎝,将你手中足够大的直角三角板PHF的直角顶点P落在AD边上(不与A、D重合)并在AD上平行移动:
(1)能否使你的三角板两直角边分别通过点B与点C?若能,请你求出这时AP的长;若不能,请说明理由.
(2)再次移动三角板位置,使三角板顶点P在AD上移动,直角边PH始终通过点B,另一直角边PF与DC的延长线交于点Q,与BC交于点E,能否使CE=2㎝?若能,请你求出这时AP的长;若不能,请说明理由.。
