稍复杂的方程解决问题
第5单元----⑦稍复杂的方程解决问题2

答:这辆汽车平均每小时行驶80千米。
例2
天津到济南的铁路长 357 千米。 一列快车从 天津开出,同时有一列慢车从济南开出,两车相向而 行,经过3小时相遇,快车平均每小时行 79千米,慢 车平均每小时多少千米?(方程解)
快车 天津每小时79千米每小时?千米 慢车 济南
357千米
P80第2.3.4
3.甲乙两地相距400千米,一辆汽车用甲地开 往乙地,行驶了4.5小时后离乙地还有40千 米。这辆汽车平均每小时行驶多少千米?
4.5小时行的路程+剩下的路程40千米=总路程400千米 解:设这辆汽车平均每小时行驶x千米。
4.5x+40=400
4.5x=400-40 4.5x=360 x=360÷4.5 x=80
1.妈妈买了2千克苹果和3千克梨,共付13.2元钱, 梨每千克2.8元,苹果每千克多少元?(方程解)
2千克苹果的总价+3千克梨的总价=总钱数13.2元 解:设苹果每千克x元.
2x+2.8×3=13.2 2x+8.4=13.2 2x=13.2-8.4 2x=4.8 x=4.8÷2 x=2.4 答:苹果每千克2.4元。
2、李师傅买来72米布,正好做20件大人衣服和16 件儿童衣服。每件大人衣服用布2.4米,每件儿童 衣服用布多少米?(方程)
20件大人衣服用料+16件儿童衣服用料=总数72米 解:设每件儿童衣服用布x米。
2.4×20+16x=72 48+16x=72 16x=72-48 16x=24 x=24÷16 x=1.5 答:每件儿童衣服用布1.5米。
稍复杂方程解决问题(二)
复习 1.苹果每千克2.6元,买a千克苹果要( 2.6a )元。 香蕉每千克3.5元,买b千克香蕉要 3.5b)元。一共要付(2.6a+3.5b ( )元。 2.一只 鸡有( 2 )条腿,那么x只鸡有 ( 2x )条腿,一只兔子( 4 )条腿,那么y只 兔子( 4y )条腿。 3.汽车每小时行80千米,x小时行( 80x ) 千米 4.做一件衣服要4.5米布,做x件衣服要(4.5x )米。
列方程解决稍复杂的问题(教学设计)- 四年级下册数学 青岛版(五四制)

列方程解决稍复杂的问题(教学设计)- 四年级下册数学青岛版(五四制)一、教学背景本次教学设计是面向四年级下册数学教学工作的,教材采用的是青岛版(五四制)。
在进入四年级数学学习后,学生们已经掌握了基本四则运算和简单的代数法则,获得了初步的方程解题能力。
而本次教学通过列方程解决稍复杂的问题,要求学生们在方程中运用各种数学知识,提高他们的思维能力和解决问题的能力。
二、教学目标1.学生能够理解方程的概念和列方程的方法。
2.学生能够用方程解决稍复杂的实际问题。
3.学生能够掌握在列方程中用到的各种数学知识。
三、教学步骤1. 导入新知识,引出方程的概念要求学生事先预习教材,了解方程的概念和形式,并介绍方程解决实际问题的作用。
2. 认识及列方程在复习小班教学中,教师会采取多种形式的讲解,让学生进一步认识和领会方程列式的概念:(1)通过解决实际问题,理解方程的概念1.引导学生挖掘更多的实际问题。
2.让学生掌握如何将实际问题转化为方程。
(2)列方程的方法及其步骤1.教师介绍方程的解题方法,并将其列入黑板。
2.学生可以多次演习,便于每个学生彻底理解。
3. 解决实际问题(1)基础应用练习1.教师可以提供逐渐升级的基础应用题目。
2.学生在教师的指导下,进行理解、列方程、解题等方面的练习。
(2)助手系数之类的题型1.针对这种题型进行专门的讲解。
2.老师可以提供一些经典的案例,帮助学生加深理解。
4. 总结通过以上内容的讲解和训练,让学生加深对方程的认识和应用,并复习了之前的关键点。
通过教师总结本课的知识内容和难点,为学生今后进行解决问题方面的实践打下坚实基础。
四、教学反思本课程在梳理课程情境和详细规划教学步骤的时候,深入思考了学生的不同层次,在基础应用练习以及助手系数之类题型方面都有良好的帮助。
在课堂上顺利完成整个严密设计的课程,英语老师和语文老师的加入,促进了整个课程的严谨和连续性,也展示出了二十一个世纪教育对学生的高度关注,为整个课程奠定了良好的基础。
小学解方程复杂练习题

小学解方程复杂练习题解方程是数学中重要的概念之一,也是小学学习数学的基础内容之一。
通过解方程,学生可以培养逻辑思维能力和应用数学知识解决实际问题的能力。
本文将给出一些小学解方程的复杂练习题,以帮助小学生更好地掌握解方程的方法和技巧。
题目一:小明有15支铅笔,小华有8支铅笔,他们一共有多少支铅笔?解:设小明和小华一共有x支铅笔。
根据题意可以得到方程15 + 8 = x。
计算得x = 23。
所以小明和小华一共有23支铅笔。
题目二:小红和小黄的年龄加起来是30岁,小红比小黄大5岁,他们的年龄分别是多少?解:设小红的年龄为x岁,则小黄的年龄为x-5岁。
根据题意可以得到方程x + (x-5) = 30。
计算得x = 17。
所以小红的年龄为17岁,小黄的年龄为12岁。
题目三:小明爸爸今年32岁,比小明大28岁,小明今年几岁?解:设小明今年x岁,则小明爸爸今年为32 + x岁。
根据题意可以得到方程32 + x = x + 28。
计算得x = -4。
由于年龄不能为负数,所以这个方程无解,题目不满足实际情况。
题目四:一只小鸟和一只小猫一起跳舞,小鸟跳了7次,小猫跳了3次,他们一共跳了多少次?解:设小鸟和小猫一共跳了x次。
根据题意可以得到方程7 + 3 = x。
计算得x = 10。
所以小鸟和小猫一共跳了10次。
题目五:某数的三倍减去7得到25,这个数是多少?解:设这个数为x。
根据题意可以得到方程3x - 7 = 25。
计算得x = 10。
所以这个数是10。
通过以上几个复杂练习题,我们可以看到解方程的方法和思路。
解方程的关键是根据题目的条件设置合适的未知数,列出方程,并通过计算求解出未知数的值。
通过这种方法,我们可以解决很多实际问题,提高数学运算能力和逻辑思维能力。
总结起来,解方程是小学数学学习中重要的内容之一。
通过不断练习解方程的方法和技巧,学生可以更好地理解数学知识,提高解决实际问题的能力。
希望以上提供的复杂练习题对小学生解方程的学习有所帮助。
列方程解决稍复杂的实际问题

1. 从题目中你找到了什么样的等量关系?
2. 根据等量关系式列出方程解决这个问题
三、巩固新知 拓展应用
每筒网球的个数×筒数+3=网球总数 解:设一共装了x筒。 5x+3=1428 5x+3-3=1428-3 5x=1425 5x÷5=1425÷5 x=285 答:一共装了285筒。
三、巩固新知 拓展应用
解:设共有x块黑色皮。解:设共有x块黑色皮。 2x-20=4 2x=20+4
黑色皮块数×2-4=白色皮块数
解:设共有x块黑色皮。 2x- 4 =20
总结提升
列方程解决实际问题有哪些步骤?
(1)找出未知数,用字母x表示;
(2)分析问题,找出等量关系,再 列方程; (3)解方程。 (4)检验并作答。
三、巩固新知 拓展应用 1.共有1428个网球,每5个装一筒,装 完后还剩3个。一共装了多少筒?
简易方程
列方程解决稍复杂的问题(一)
操场上有8人在打乒乓球,踢足球的人数比打乒乓球的人 数的2倍多2人,请大家算算有多少人在踢足球。
8人 打乒乓球的人数:
踢足球的人数: ?人
多 2人
8×2+2=18
答:有18在人在踢足球。
一、看情境图,获取数学信息
你能找出哪些信息反映出白色皮块数 和黑色皮的关系呢?
2.一些网球,每5个装一筒,共装了285筒,结果还 剩3个。这些网球一共有多少个?
同学们想一想这道题还需要列方程吗?
四、反思
1. 回顾一下,今天这节课你有哪些收获?
五、布置作业
作业:第75页练习十六,第6题。
ቤተ መጻሕፍቲ ባይዱ
第76页练习十六,第7题、第11题。
二、合作交流 探究新知 ?块 黑色皮: 20块 白色皮:
较复杂的解方程练习题

较复杂的解方程练习题解方程是数学中的一项重要内容,也是数学思维和解决问题的关键能力之一。
较复杂的解方程练习题是测试学生对解方程方法的掌握程度和灵活运用能力的一种方式。
本文将通过一些具有挑战性的解方程练习题,帮助读者巩固和提升解方程的技巧和能力。
1、练习题一:三角方程已知√3sinx + cosx = 2,求x的解。
解答:将√3sinx + cosx = 2进行整理√3sinx = 2 - cosx3sin^2x = 4 - 4cosx + cos^2x3(1 - cos^2x) = 4 - 4cosx + cos^2x3 - 3cos^2x =4 - 4cosx + cos^2x4cos^2x - cosx - 1 = 0解这个方程可以利用韦达定理。
令cosx = t,则方程化为4t^2 - t - 1 = 0解这个二次方程,得到两个解t1 = (1+√17)/8, t2 = (1-√17)/8由cosx = t,可以解得x1 = arccos((1+√17)/8), x2 = arccos((1-√17)/8)2、练习题二:含参数方程求方程组x^2 + y^2 = a^2和y = kx的解。
解答:将y = kx代入第一个方程,得到x^2 + (kx)^2 = a^2整理后得到方程(1+k^2)x^2 = a^2解这个方程有两种情况:情况一:当1+k^2 ≠ 0时,方程有两个实数解。
解为x = ±(a/√(1+k^2)),y = ±(ka/√(1+k^2))情况二:当1+k^2 = 0时,方程无实数解。
3、练习题三:含绝对值的方程求方程|2x - 3| = 5的解。
解答:要解这个方程,可以将方程拆解为两个方程:1) 2x - 3 = 5,解得x = 42) -(2x - 3) = 5,解得x = -1综合以上两种情况,方程的解为x = 4或x = -1。
4、练习题四:含分式方程求方程(2x+1)/(x-1) + 2/(x+2) = 1的解。
(小学数学五年级上册第四单元)稍复杂的方程(精选3篇)

(小学数学五年级上册第四单元)稍复杂的方程(精选3篇)(小学数学五年级上册第四单元)稍复杂的方程篇1教学内容:教科书第70页的例3教学目标:1、解决实际问题中的有关和、差、倍的数量关系。
2、初步学会设计一个未知数,列方程解答含有两个未知数的实际问题。
3、培养学生学会比较、分析、并能应用已学知识解决实际问题的能力。
教学过程:一、复习1、4x+5=54 3×2.1+2x=13.4 0.3x÷2=9 4(x+8)=202、学校科技小组的男生是女生人数的4倍,设女生有x人,男生有()人,男女生共()人。
3、学校图书组有女生x人,男生为女生的2.5倍,男生有()人,男女同学共()人。
4、果园里有桃树45棵,杏树的棵数是桃树的3倍,两种树一共有多少棵?二、新授课教学教科书第70页的例3。
1、分析题目的已知条件和问题。
2、分析本题的数量关系。
请学生说出数量关系,教师板书。
陆地面积+ 海洋面积= 地球表面积教师:这道题目中有两个未知数,而这两个未知数之间存在着倍数关系。
我们在解题时,只要设其中的一个未知数为x,而另一个未知数就可以用这个未知数来表示,为了解方程方便,通常情况下,设一倍数为x。
3、列方程解应用题。
解:设陆地面积为x亿平方千米,海洋面积就为2.4x亿平方千米x + 2.4x = 5.1(1 + 2.4)x = 5.13.4x = 5.13.4x÷3.4 = 5.1÷3.4x=1.5提问:1.5表示什么?(1.5表示陆地面积是1.5亿平方千米)那海洋面积该怎样求呢?一种:5.1-1.5=3.6(亿平方千米)另一种:2.4 x=2.4×1.5=3.6(亿平方千米)答:陆地面积是1.5亿平方千米,海洋面积是3.6亿平方千米。
引导学生进行检验。
三、巩固练习1、甲乙两堆货物共重60吨,乙的重量甲的3倍,甲乙两堆货物各种多少吨?2、苹果重量是梨子重量的4倍,梨子比苹果少600千克,梨子和苹果各重多少千克?3、练习13 (4、6、7题用方程解)学生独立完成,教师评讲小结:今天你学了什么?有什么收获?(小组同学相互交流)四、作业:练习十三(5 —10题)(小学数学五年级上册第四单元)稍复杂的方程篇2教学内容:教科书69页例2教学目标:1、是学生感受数学与现实生活的联系。
四年级复杂解方程练习题

四年级复杂解方程练习题解方程是数学中一项基础且重要的技能,它涉及到代数运算和逻辑推理。
通过解方程可以找到未知数的值,从而解决各种数学问题。
在四年级学习阶段,我们将继续深入学习解方程的方法和技巧。
下面是一些复杂的解方程练习题,帮助你巩固相关知识。
1. 解方程:2x + 5 = 13解:首先,我们需要将方程中的未知数与常数分开。
将5移到等号右边,得到2x = 13 - 5,即2x = 8。
然后,我们将方程中的2移到等号右边,并将其除以2,得到x = 8 ÷ 2,即x = 4。
2. 解方程:4(x + 3) = 32解:首先,我们需要将括号内的式子进行运算。
这里可以使用分配律,将4乘以括号内的每一项。
得到4x + 12 = 32。
然后,将12移到等号右边,得到4x = 32 - 12,即4x = 20。
最后,将方程中的4移到等号右边,并将其除以4,得到x = 20 ÷ 4,即x = 5。
3. 解方程:3(x - 2) + 4 = 19解:首先,我们需要将括号内的式子进行运算,得到3x - 6 + 4 = 19,即3x - 2 = 19。
然后,将-2移到等号右边,得到3x = 19 + 2,即3x = 21。
最后,将方程中的3移到等号右边,并将其除以3,得到x = 21 ÷ 3,即x = 7。
4. 解方程:2(x + 5) - 3(x - 2) = 1解:首先,我们需要将括号内的式子进行运算。
先计算2(x + 5)和3(x - 2),得到2x + 10 - 3x + 6 = 1。
然后,将等号两边的项合并,得到-1x + 16 = 1。
将16移到等号右边,得到-1x = 1 - 16,即-1x = -15。
最后,我们将方程中的-1移到等号右边,并将其除以-1,得到x = -15 ÷ -1,即x = 15。
5. 解方程:2x - 3 = 2(x + 4)解:首先,我们需要将方程中的括号内的式子进行运算,得到2x - 3 =2x + 8。
2014人教版解稍复杂的方程例4例5
方法2:
解: 2 x-32=8
2x-32+32=8+32 2x=40
2x÷2=40÷2 x=20
问题:你能说说他们的想法吗?他们分别把什么看做一个整体? 分几大步解决?运用了什么运算定律?
(三)反思检验
2(x-16)=8 别忘了检验! 方程左边=2(x-16)
=2×(20-16) =2×4 =8 =方程右边 所以,x=20是方程的解。
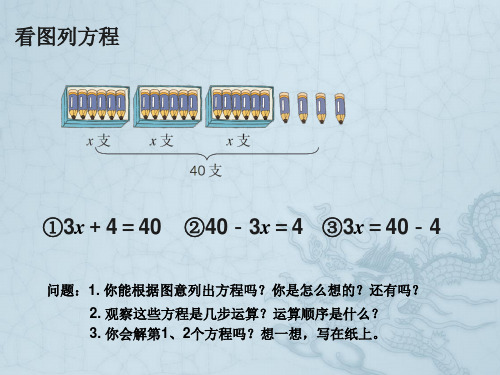
问题:1. 你能根据图意列出方程吗? 2. 这个方程有几步运算?怎样解?把过程写下来。
3. 请你检验一下x=49是不是方程的解。
作业:第71页练习十五,第9题。
一、复习
解方程。 4x÷3=1.44
解: 4x÷3×3=1.44×3 4x=4.32
4x÷4=4.32÷4 x=1.08
问题:在解方程过程中你分几大步进行?每步的目的是什么?
检验:
方程左边=(100-3x)÷2 =(100-3×28)÷2 =16÷2 =8 =方程右边
所以, x=28是方程的解。
问题:1. 你能说说他们的想法吗?分几大步解决?分别把什么看做
一个整体?依据是什么? 2. 请你检验一下。 小结:在解两步、三步方程时,你有什么感悟?和大家分享一下。
2. 看图列方程并求解。
问题: x=20是不是方程的解?请你检验一下。
三、巩固练习,提升认识
1. 解方程。 (5x-12)×8=24 (100-3x)÷2=8
问题:1. 观察这个方程有几步运算?可以先把什么看做一个整体? 2. 请你独立思考,并在纸上完成。
1. 解方程。
(5x-12)×8=24 解: (5x-12)×8÷8=24÷8
三、巩固练习,提升认识
