锥齿轮画法
机械制图入门到精通,齿轮画法基础知识讲解

机械制图入门到精通,齿轮画法基础知识讲解
齿轮是指轮缘上有齿轮连续啮合传递运动和动力的机械元件。
齿轮在传动中的应用很早就出现了。
19世纪末,展成切齿法的原理及利用此原理切齿的专用机床与刀具的相继出现,随着生产的发展,齿轮运转的平稳性受到重视。
一、齿轮
二、齿轮相关参数计算
三、圆柱齿轮的画法
四、锥齿轮、蜗杆与蜗轮的画法
锥齿轮用来传递两相交轴之间的运动和动力,在一般机械中,锥齿轮两轴之间的交角等于90°(但也可以不等于90°)。
与圆柱齿轮类似,锥齿轮有分度圆锥、齿顶圆锥、齿根圆锥和基圆锥。
圆锥体有大端和小端,其对应大端的圆分别称为分度圆(其半径为r)、齿顶圆、齿根圆和基圆。
一对锥齿轮的运动相当于一对节圆锥作纯滚动。
锥齿轮画法
锥齿轮啮合画法
2、涡轮蜗杆传动
蜗杆传动:用来传递相互垂直的两轴之间的运动。
特点:降速比大,结构凑,自锁性,传动平稳,噪音小等优点。
缺点传动效率低,发热大,需要良好的润滑。
涡轮蜗杆画法
涡轮蜗杆啮合画法。
锥齿轮画法
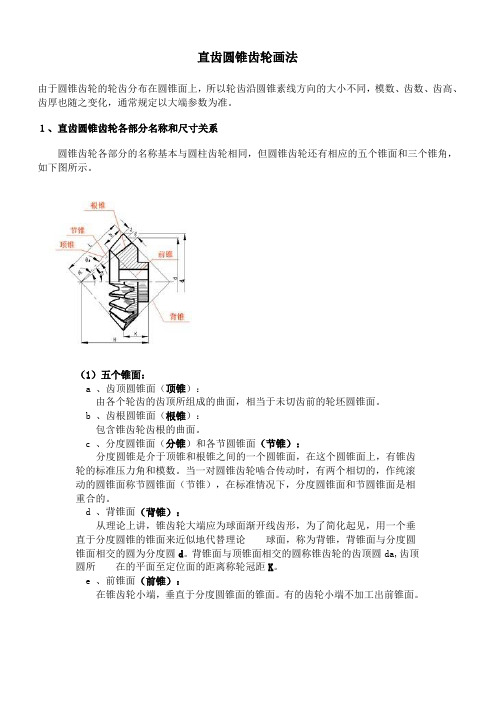
直齿圆锥齿轮画法由于圆锥齿轮的轮齿分布在圆锥面上,所以轮齿沿圆锥素线方向的大小不同,模数、齿数、齿高、齿厚也随之变化,通常规定以大端参数为准。
1、直齿圆锥齿轮各部分名称和尺寸关系圆锥齿轮各部分的名称基本与圆柱齿轮相同,但圆锥齿轮还有相应的五个锥面和三个锥角,如下图所示。
(1)五个锥面:a 、齿顶圆锥面(顶锥):由各个轮齿的齿顶所组成的曲面,相当于未切齿前的轮坯圆锥面。
b 、齿根圆锥面(根锥):包含锥齿轮齿根的曲面。
c 、分度圆锥面(分锥)和各节圆锥面(节锥):分度圆锥是介于顶锥和根锥之间的一个圆锥面,在这个圆锥面上,有锥齿轮的标准压力角和模数。
当一对圆锥齿轮啮合传动时,有两个相切的,作纯滚动的圆锥面称节圆锥面(节锥),在标准情况下,分度圆锥面和节圆锥面是相重合的。
d 、背锥面(背锥):从理论上讲,锥齿轮大端应为球面渐开线齿形,为了简化起见,用一个垂直于分度圆锥的锥面来近似地代替理论球面,称为背锥,背锥面与分度圆锥面相交的圆为分度圆d。
背锥面与顶锥面相交的圆称锥齿轮的齿顶圆da,齿顶圆所在的平面至定位面的距离称轮冠距K。
e 、前锥面(前锥):在锥齿轮小端,垂直于分度圆锥面的锥面。
有的齿轮小端不加工出前锥面。
2、锥齿轮的规定画法(1)单个锥齿轮的画法及其画图步骤锥齿轮一般用二个视图或用一个视图、一个局部视图表示,轴线放成水平,主视图可采用剖视,剖切平面通过齿轮轴线时,轮齿按不剖处理。
在平行锥齿轮轴线的投影面的视图中,用粗实线画出齿顶线及齿根线,用点划线画出分度线,在垂直于锥齿轮轴线的投影面的视图中,规定用点划线画出大端分度圆,用粗实线画出大端齿顶圆和小端齿顶圆。
齿根圆省略不画,如下图所示。
知识准备(三):子项目三直齿圆锥齿轮圆锥齿轮简称锥齿轮,其轮齿有直齿、斜齿和曲线齿(圆弧齿、摆线齿)等多种形式。
直齿圆锥齿轮的设计、制造和安装均较简单,故在一般机械传动中得到了广泛的应用。
但是在汽车拖拉机等高速重载机械中,为提高传动的平稳性和承载能力,减少噪音,多用曲线齿圆锥齿轮。
锥齿轮的画法

更多资源请访问空间/413802742/infocenter第一步:输入如下参数:名称,类型,值,指定,访问,源,说明,受限制的,单位ZC,实数,24.000000,No,完全,用户定义的,齿数,,M,实数,2.500000,No,完全,用户定义的,模数,,ZD,实数,45.000000,No,完全,用户定义的,大齿轮齿数,, ALPHA,实数,20.000000,No,完全,用户定义的,压力角,, B,实数,20.000000,No,完全,用户定义的,齿宽,,HAX,实数,1.000000,No,完全,用户定义的,齿顶高系数,, HA,实数,2.500000,No,锁定,关系,齿顶高,,CX,实数,0.250000,No,完全,用户定义的,顶隙系数,, HF,实数,0,No,锁定,关系,齿根高,,H,实数,0,No,锁定,关系,全齿高,,D,实数,0,No,锁定,关系,分度圆直径,,DB,实数,0,No,锁定,关系,基圆直径,,DA,实数,0,No,锁定,关系,齿顶圆直径,,DF,实数,0,No,锁定,关系,齿根圆直径,,DELTA,实数,0,No,锁定,关系,分锥角,,DELTA_A,实数,0,No,锁定,关系,顶锥角,,DELTA_B,实数,0,No,锁定,关系,基锥角,,DELTA_F,实数,0,No,锁定,关系,根锥角,,HB,实数,0,No,锁定,关系,齿基高,,RX,实数,0,No,锁定,关系,锥距,,THETA_A,实数,0,No,锁定,关系,齿顶角,,THETA_B,实数,0,No,锁定,关系,齿基角,,THETA_F,实数,0,No,锁定,关系,齿根角,,BA,实数,0,No,锁定,关系,齿顶宽,,BB,实数,0,No,锁定,关系,齿基宽,,BF,实数,0,No,锁定,关系,齿根宽,,X,实数,0,No,完全,用户定义的,变位系数,,第二步:在front平面上建立如下草图并添加关系为sd12=90sd6=df/2sd8=db/2sd9=d/2sd10=da/2sd11=bsd13=delta第三步:绘制如下图所示的四个同心圆,添加关系为sd6=d/cos(delta)sd9=da/cos(delta)sd10=db/cos(delta)sd11=df/cos(delta)第四步:同第三部,其中关系式为sd4=(df-2*bf*sin(delta_f))/cos(delta) sd9=(db-2*bb*sin(delta_b))/cos(delta) sd10=(d-2*b*sin(delta))/cos(delta)sd11=(da-2*ba*sin(delta_a))/cos(delta)第五步:建立如图所示的新坐标系,其中x轴向上,y轴水平。
proe锥齿轮画法教程

锥齿轮的绘制所要绘制的锥齿轮模型如下1. 设置参数M=4,Z=30 模数与齿数Z_ASM=60 与之啮合的齿轮的齿数B=20,Alpha=20 齿宽与压力角 HAX=1 齿顶高系数CX=0.25 顶隙系数pro/E 的模型树绘制步骤X=0 变位系数2.添加关系HA=(HAX+X)*MHF=(HAX+CX-X)*MH=(2*HAX+CX)*MDELTA=ATAN(Z0/Z1)D=M*Z0DB=D*COS(ALPHA)DA=D+2*HA*COS(DELTA)DF=D-2*HF*COS(DELTA)DDA=(DA/2)*COS(DELTA)DD=(D/2)*COS(DELTA)DDF=(DF/2)*COS(DELTA) DDB=(DB/2)*COS(DELTA)3.草绘14.回转中心线角度尺寸:90-D elta四个直线尺寸从大到小依次为:dda, dd, ddb, ddf(d da处是直角约束)5.法向剖平面Front面沿上图中红色线段旋转90度后得到的平面Front 和Top 两基准面的相交线6.基准点0-1 (PNT0, PNT1)草绘1 中的线段与Top 基准平面的交点7.草绘28.渐开线坐标系CS0为以后用方程绘制渐开线齿廓做准备9.渐开线轮廓基准曲线1输入以下渐开线参数方程:r = db/2 theta=t*45x=r*cos(theta)+r*sin(theta)*theta* (pi/180) y=r*sin(theta)-r*cos(theta)*theta*(pi/180)z=010.啮合点分度圆与渐开线齿廓的交点13.镜像得到的渐开线轮廓2使用镜像基准平面11. 过啮合点的平面12. 镜像基准平面15. 齿槽为(14. 轮体用“扫描混合 / 切口”实现。
16.齿槽阵列。
锥齿轮画法

锥齿轮画法ha=(hax+x)*mhf=(hax+cx-x)*M h=(2*hax+cx)*M delta=atan(z/z_asm)d=m*zdb=d*cos(alpha) da=d+2*ha*cos(delta) df=d-2*ha*cos(delta) rx=d/(2*sin(delta)) theta_a=atan(ha/rx) theta_b=atan(hb/rx) theta_f=atan(hf/rx) delta_a=delta+theta_a delta_b=delta-theta_b delta_f=delta-theta_f ba=b/cos(theta_a) bb=b/cos(theta_b) bf=b/cos(theta_f)sd16=deltasd8=90sd21=bsd15=df/2sd14=db/2sd13=d/2sd7=da/2sd0=d/cos(delta)sd1=da/cos(delta)sd2=db/cos(delta)sd3=df/cos(delta)sd0=(d-2*b*sin(delta))/cos(delta)sd1=(da-2*ba*sin(delta_a))/cos(delta) sd2=(db-2*bb*sin(delta_b))/cos(delta) sd3=(df-2*bf*sin(delta_f))/cos(delta)r=db/cos(delta)/2theta=t*60x=r*cos(theta)+r*sin(theta)*theta*pi/180 y=r*sin(theta)-r*cos(theta)*theta*pi/180z=0r=(db-2*bb*sin(delta_b))/cos(delta)/2theta=t*60x=r*cos(theta)+r*sin(theta)*theta*pi/180 y=r*sin(theta)-r*cos(theta)*theta*pi/180z=01.打开参数添加2.3.编辑-再生1)创建基准平面。
Pro-E格利森螺旋锥齿轮的画法

3.6格利森螺旋锥齿轮的创建3.6.1格利森螺旋锥齿轮简介锥齿轮在机械行业有着广泛的应用,目前,国际上主要以美国的格里森和德国的克林根贝尔格两大锥齿轮技术为主。
格利森公司的创始人威廉·格里森先生在1874年发明了第一台圆锥齿轮刨齿机,开创了圆锥齿轮的新领域。
格里森锥齿轮于上世纪50年代引入我国,70年代,格里森圆锥齿轮技术和机床又开始引入中国市场,近来我国又引进了最新的凤凰Ⅱ型数控机床,从而使这种锥齿轮在我国有了很大的发展和广泛的应用。
Gleason锥齿轮包括弧齿锥齿轮和准双曲面齿轮。
弧齿锥齿轮用来传递相交轴之间的动力和运动。
准双曲面齿轮用于传递交叉轴之间的动力和运动。
它们一般采用收缩齿,具有较好的强度性能。
目前,广泛应用于冶金、航空、汽车、矿山、石油等行业。
3.6.2格利森螺旋锥齿轮的建模分析建模分析(如图3-243所示):(1)创建基本曲线、齿轮基本圆(2)创建齿廓曲线(3)创建齿根圆(4)创建截面与扫引轨迹(5)扫描混合生成第一个轮齿(6)阵列创建轮齿图3-243建模分析3.6.3格利森螺旋锥齿轮的建模过程1.创建基本曲线(1)单击,在新建对话框中输入文件名gleason_gear,然后单击;(2)创建基准平面“DTM1”。
在工具栏内单击按钮,系统弹出“基准平面”对话框,按如图3-244的设置创建基准平面;图3-244“基准平面”对话框(3)草绘曲线1。
在工具栏内单击按钮,系统弹出“草绘”对话框,选择“FRONT”面作为草绘平面,选取“RIGHT”面作为参考平面,参考方向为向“右”,如图3-245所示。
单击【草绘】进入草绘环境;图3-245“草绘”对话框(4)绘制如图3-246所示的二维草图,在工具栏内单击按钮,完成草图的绘制;曲线图3-246绘制二维草图2.创建齿轮基本圆(1)创建基准平面“DTM2”。
在工具栏内单击按钮,系统弹出“基准平面”对话框,单击选取“FRONT”面法向作为参照,单击选取如图3-246所示的“曲线1”作为参照,完成后的“基准平面”对话框如图3-247所示,图3-247“基准平面”对话框完成后的基准平面如图3-248所示;基准平面DTM2图3-248创建基准平面(2)创建基准点。
圆锥齿轮的画法

圆锥齿轮的画法 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】圆锥齿轮的画法[文本]圆锥齿轮通常用于交角90°的两轴之间的传动,其各部分结构如图所示。
齿顶圆所在的锥面称为顶锥面、大端端面所在的锥面称为背锥,小端端面所在的锥面称为前锥,分度圆所在的锥面称为分度圆锥,该锥顶角的半角称为分锥角,用δ表示。
圆锥齿轮的轮齿是在圆锥面上加工出来的,在齿的长度方向上模数、齿数、齿厚均不相同,大端尺寸最大,其它部分向锥顶方向缩小。
为了计算、制造方便,规定以大端的模数为准计算圆锥齿轮各部分的尺寸,计算公式见下表。
其实与圆柱齿轮区别也不大,只是圆锥齿轮的计算参数都是打断的参数,齿根高是倍的模数,比同模数的标准圆柱齿轮的齿顶高要小,另外尺高的方向垂直于分度圆圆锥的母线,不是州县的平行方向。
单个圆锥齿轮的画法规则同标准圆柱齿轮一样,在投影为非圆的视图中常用剖视图表示,轮齿按不剖处理,用粗实线画出齿顶线、齿根线,用点画线画出分度线。
在投影为非圆的视图中,只用粗实线画出大端和小端的齿顶圆,用点画线画出大端的分度圆,齿根圆不画。
[文本]注意:圆锥齿轮计算的模数为大端的模数,所有计算的数据都是大端的参数,根据大端的分度圆直径,分锥角画出分度线细点画线,量出齿顶高、齿根高,即可画出齿顶和齿根线,根据齿宽,画出齿形部分,其余部分根据需要进行设计。
单个齿轮的画法同圆柱齿轮的规定完全相同。
应当根据分锥角,画出分度圆锥的分度线,根据分度圆半径量出大端的位置,根据齿顶高、齿根高找出大端齿顶和齿根的位置,向分度锥顶连线,就是顶锥(齿顶圆锥)和根锥(齿根圆锥),根据齿宽量出分度圆上小端的位置,做分度圆线的垂直线,其他的次要结构根据需要设计即可。
[文本]锥齿轮的啮合画法同圆柱齿轮相同,如图所示。
弧齿锥齿轮的传动设计(弧齿锥齿轮的传动设计弧齿锥齿轮的基本概念锥齿轮的节锥对于相交轴之间的齿轮传动,一般采用锥齿轮。
proe圆锥齿轮全参数化画法

锥齿轮在机械工业中有着广泛的应用,它用来实现两相交轴之间的传动,两轴的相交角一般采用90度。
锥齿轮的轮齿排列在截圆锥体上,轮齿由齿轮的大端到小端逐渐收缩变小,本节将介绍参数化设计锥齿轮的过程。
与本章先前介绍的齿轮的建模过程相比拟,锥齿轮的建模更为复杂。
参数化设计锥齿轮的过程中应用了大量的参数与关系式。
锥齿轮建模分析〔如图3-122所示〕:〔1〕输入关系式、绘制创建锥齿轮所需的根本曲线〔2〕创建渐开线〔3〕创建齿根圆锥〔4〕创建第一个轮齿〔5〕阵列轮齿图3-122锥齿轮建模分析1.输入根本参数和关系式〔1〕单击,在新建对话框中输入文件名conic_gear,然后单击;〔2)在主菜单上单击“工具〞→“参数〞,系统弹出“参数〞对话框,如图3-123所示;图3-123 “参数〞对话框〔3〕在“参数〞对话框内单击按钮,可以看到“参数〞对话框增加了一行,依次输入新参数的名称、值、和说明等。
需要输入的参数如表3-3所示;名称值说明名称值说明M 模数DELTA ___ 分锥角Z 24 齿数DELTA_A ___ 顶锥角Z_D 45 大齿轮齿数DELTA_B ___ 基锥角ALPHA 20 压力角DELTA_F ___ 根锥角B 20 齿宽HB ___ 齿基高HAX 1 齿顶高系数RX ___ 锥距CX 顶隙系数THETA_A ___ 齿顶角HA ___ 齿顶高THETA_B ___ 齿基角HF ___ 齿根高THETA_F ___ 齿根角H ___ 全齿高BA ___ 齿顶宽D ___ 分度圆直径BB ___ 齿基宽DB ___ 基圆直径BF ___ 齿根宽DA ___ 齿顶圆直径X 0 变位系数DF ___ 齿根圆直径表3-3 创建齿轮参数注意:表3-3中未填的参数值,表示是由系统通过关系式将自动生成的尺寸,用户无需指定。
〔4〕在主菜单上依次单击“工具〞→“关系〞,系统弹出“关系〞对话框;〔5〕在“关系〞对话框内输入齿轮的根本关系式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.3锥齿轮的创建锥齿轮在机械工业中有着广泛的应用,它用来实现两相交轴之间的传动,两轴的相交角一般采用90度。
锥齿轮的轮齿排列在截圆锥体上,轮齿由齿轮的大端到小端逐渐收缩变小,本节将介绍参数化设计锥齿轮的过程。
3.3.1锥齿轮的建模分析与本章先前介绍的齿轮的建模过程相比较,锥齿轮的建模更为复杂。
参数化设计锥齿轮的过程中应用了大量的参数与关系式。
锥齿轮建模分析(如图3-122所示):(1)输入关系式、绘制创建锥齿轮所需的基本曲线(2)创建渐开线(3)创建齿根圆锥(4)创建第一个轮齿(5)数组轮齿图3-122锥齿轮建模分析3.3.2锥齿轮的建模过程1.输入基本参数和关系式(1)单击,在新建对话框中输入文件名conic_gear,然后单击;(2)在主菜单上单击“工具”→“参数”,系统弹出“参数”对话框,如图3-123所示;图3-123 “参数”对话框(3)在“参数”对话框内单击按钮,可以看到“参数”对话框增加了一行,依次输入新参数的名称、值、和说明等。
需要输入的参数如表3-3所示;名称值说明名称值说明注意:表3-3中未填的参数值,表示是由系统通过关系式将自动生成的尺寸,用户无需指定。
(4)在主菜单上依次单击“工具”→“关系”,系统弹出“关系”对话框;(5)在“关系”对话框内输入齿轮的基本关系式。
由这些关系式,系统便会自动生成表3-4所示的未指定参数的值,完成后的“关系”对话框如图3-124所示;图3-124“关系”对话框2.创建基本曲线(1)创建基准平面。
在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“平面”。
系统弹出“基准平面”对话框,按如图3-125的设置创建基准平面“DTM1”;图3-125“基准平面”对话框(2)在“基准平面”对话框的偏移项内输入偏移距离为“d/(2*tan(delta))”,单击【确定】完成。
(3)将偏移距离添加到“关系”对话框,在主菜单上依次单击“工具”→“关系”,在弹出的“关系”对话框内添加关系式,如图3-126所示;图3-126“关系”对话框(4)创建基准轴。
在工具栏内单击按钮,创建通过“FRONT”面与“RIGHT”面的基准轴“A_1”,如图3-127所示;图3-127“基准轴”对话框(5)草绘曲线。
在工具栏内单击按钮,选择“FRONT”面作为草绘平面,选取“RIGHT”面作为参考平面,参考方向为向“顶”,如图3-128所示。
单击【草绘】进入草绘环境;图3-128“草绘”对话框(6)绘制如图3-129所示的二维草图,标注如图示的尺寸,尺寸大小任意,保证图形的基本外形;图3-129绘制二维草图(7)将尺寸代号添加到“关系”对话框中,在主菜单上依次单击“工具”→“关系”,系统弹出“关系”对话框,添加如图3-130所示的关系式;图3-130“关系”对话框3.创建大端齿轮基本圆(1)创建基准平面。
在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“平面”。
系统弹出“基准平面”对话框,按如图3-131的设置创建基准平面“DTM2”。
平面与“FRONT”面为法向关系,并且穿过图3-132所示的“参照曲线1”;图3-131“基准平面”对话框(2)创建基准点。
在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“点”→“点”。
系统弹出“基准点”对话框,创建经过如图3-132所示两条曲线的基准点“PNT1”。
参照曲线1参照曲线2图3-132创建基准点完成后的“基准点”对话框如图3-133所示;图3-133“基准点”对话框(3)草绘曲线。
在工具栏内单击按钮,选择“DTM2”面作为草绘平面,选取“FRONT”面作为参考平面,参考方向为向“顶”,如图3-134所示。
单击【草绘】进入草绘环境;图3-134草绘”对话框(4)绘制如图3-135所示的二维草图,标注如图示的尺寸,尺寸大小任意,保证图形的基本外形。
直线图3-135绘制二维草图注意绘制一条直线,目的是为了在下面的步骤中创建坐标系的方便;(5)添加关系式。
将大端齿轮基本圆的关系式添加到“关系”对话框中,在主菜单上依次单击“工具”→“关系”,在弹出的“关系”对话框内添加关系式,如图3-136所示;图3-136“关系”对话框4.创建小端齿轮基本圆(1)创建基准平面。
在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“平面”。
系统弹出“基准平面”对话框,按如图3-137的设置创建基准平面“DTM3”。
平面与“FRONT”面为法向关系,并且穿过图3-138所示的“参照曲线1”;图3-137“基准平面”对话框(2)创建基准点。
在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“点”→“点”。
系统弹出“基准点”对话框,创建经过如图3-138所示两条曲线的基准点“PNT2”。
图3-138 创建基准点完成后的“基准点”对话框如图3-139所示;图3-139“基准点”对话框(3)草绘曲线。
在工具栏内单击按钮,选择“DTM3”面作为草绘平面,选取“FRONT ”面作为参考平面,参考方向为向“左”,如图3-140所示。
单击【草绘】进入草绘环境;图3-140“草绘”对话框 (4)绘制如图3-141所示的二维草图,标注如图示的尺寸,尺寸大小任意,保证图形的基本外形。
参照曲线1参照曲线2直线图3-141绘制二维草图注意绘制一条直线,目的是为了在下面的步骤中创建坐标系的方便;(5)添加关系式。
将小端齿轮基本圆的关系式添加到“关系”对话框中,在主菜单上依次单击“工具”→“关系”,在弹出的“关系”对话框内添加关系式,如图3-142所示;图3-142“关系”对话框5.创建渐开线(1)创建坐标系CS0。
在工具栏内单击按钮,系统弹出“坐标系”对话框,在“原始”选项卡里,单击选取“PNT1”点作为参照。
在“坐标系”对话框内打开“定向”选项卡,选取图3-143所示的“曲线1”为y轴的负向参照,“曲线2”为x轴正向参照。
曲线2曲线1图3-143创建坐标系完成后的“坐标系”对话框如图3-144所示,单击【确定】完成坐标系CS0 的创建;图3-144“坐标系”对话框(2)创建坐标系CS1。
在工具栏内单击按钮,系统弹出“坐标系”对话框,在“原始”选项卡里,单击选取坐标系CS0作为参照。
在“坐标系”对话框内打开“定向”选项卡,进行如图3-145所示的设置,单击【确定】完成坐标系CS1的创建。
图3-145“坐标系”对话框(3)将坐标系CS1与CS0的关系式添加到“关系”对话框内。
在模型树内右键单击坐标系CS1,在弹出的快捷菜单内单击“编辑”。
在主菜单上依次单击“工具”→“关系”,系统弹出“关系”对话框,单击如图3-146所示的尺寸。
单击尺寸d38z图3-146添加尺寸关系添加关系式为“D38=360*cos(delta)/(4*z)+180*tan(alpha)/pi-alpha”,完成后的“关系”对话框如图3-147所示;图3-147“关系”对话框(4)创建渐开线。
依次在主菜单上单击“插入”→“模型基准”→“曲线”,或者在工具栏上单击按钮,系统弹出“曲线选项”菜单管理器,如图3-148所示;图3-148 “曲线选项”菜单管理器(5)在“曲线选项”菜单管理器上依次单击“从方程”→“完成”,弹出“得到坐标系”菜单管理器,如图3-149所示;图3-149“得到坐标系”菜单管理器(6)在绘图区单击选取坐标系CS1作为参照,弹出“设置坐标类型”菜单管理器,如图3-150所示;图3-150“设置坐标系类型”菜单管理器(7)在“设置坐标类型”菜单管理器中单击“笛卡尔”,系统弹出一个记事本窗口;(8)在弹出的记事本窗口中输入曲线的方程,如下:r=db/cos(delta)/2theta=t*60x=r*cos(theta)+r*sin(theta)*theta*pi/180y=r*sin(theta)-r*cos(theta)*theta*pi/180z=0(9)保存资料,退出记事本,单击如图3-151所示“曲线:从方程”对话框中的【确定】,完成后的曲线如图3-152所示;图3-151 “曲线:从方程”对话框图3-152 完成后的渐开线(10)创建齿轮小端上的渐开线。
为了视觉上的清晰,可以先将齿轮大端的基本圆曲线隐藏。
用相同的方法,创建坐标系CS2,选取如图3-153所示的点“PNT2”作为坐标系CS2的放置参照。
在“坐标系”对话框内打开“定向”选项卡,选取图3-153所示的“曲线1”作为y轴的负向参照,“曲线2”为x轴正向参照。
曲线2曲线1图3-153创建坐标系完成后的“坐标系”对话框如图3-154所示,单击【确定】完成坐标系CS2的创建;图3-154“坐标系”对话框(11)创建坐标系CS3。
在工具栏内单击按钮,系统弹出“坐标系”对话框,在“原始”选项卡里,单击选取坐标系CS2作为参照。
在“坐标系”对话框内打开“定向”选项卡,进行如图3-155所示的设置,单击【确定】完成坐标系CS3的创建。
图3-155“坐标系”对话框(12)将坐标系CS3与CS2的关系式添加到“关系”对话框内。
在模型树内右键单击坐标系CS3,在弹出的快捷菜单内单击“编辑”。
在主菜单上依次单击“工具”→“关系”,系统弹出“关系”对话框,单击如图3-156所示的尺寸。
单击尺寸d44z图3-156添加尺寸关系添加关系式为“D44=360*cos(delta)/(4*z)+180*tan(alpha)/pi-alpha”,完成后的“关系”对话框如图3-157所示;图3-157“关系”对话框(13)用相同的方法创建齿轮小端的渐开线。
选取坐标系CS3作为参照,坐标系类型为“笛卡尔”,渐开线方程为:r=(db-2*bb*sin(delta_b))/cos(delta)/2theta=t*60x=r*cos(theta)+r*sin(theta)*theta*pi/180y=r*sin(theta)-r*cos(theta)*theta*pi/180z=0完成后的渐开线如图3-158所示;图3-158完成后的渐开线6.镜像渐开线(1)创建基准点“PNT3”。
在工具栏内单击按钮,或者依次在主菜单上单击 “插入”→ “模型基准”→ “点”→ “点”,系统弹出“基准点”对话框,如图3-159所示。
在绘图区选取齿轮大端的渐开线和分度圆曲线作为参照,如图3-160。
图3-159“基准点”对话框图3-160创建基准点完成后的“基准点”对话框如图3-161所示,单击【确定】,完成基准点“PNT3”的创建;分度圆曲线 渐开线图3-161“基准点”对话框(2)创建基准平面“DTM4”。
在工具栏内单击按钮,或者依次在主菜单上单击“插入”→“模型基准”→“平面”,系统弹出“基准平面”对话框;(3)创建经过“A_1”轴与基准点“PNT3”的基准平面,完成后的“基准平面”对话框如图3-162所示;图3-162“基准平面”对话框(4)创建基准平面“DTM5”。
