理想气体计算专题
理想气体状态方程计算题 半张

接着根很细的弹簧,已知活塞的横截面积S=0.01m,大气压强P=1.0×10Pa。
当缸内气体温度为27℃时弹簧的长度为30cm,汽缸内气体压强为缸外大气压的1.2倍,当缸内气体温度升高到327℃时,弹簧的长度为36cm。
不计活塞与缸壁的摩擦且两个过程弹簧都处于拉伸状态,求(1)此时汽缸内气体的压强P2(2)此过程中缸内气体对外做的功2.如图所示,一个内壁光滑的圆柱形汽缸竖直放在水平地面上,缸内部横截面积S=10cm2,用质量m=l0kg的活塞在汽缸内封闭一定质量的气体,活塞可以在缸内无摩擦地滑动,外界大气压p0=1.0×105pa。
当气体温度T1=300K时,封闭气柱长h=40cm,活塞保持静止,重力加速度g=10m/s2,则:(1)在活塞上再放一质量为M=20kg的物块,活塞将向下移动,使活塞停在一个新的位置保持静止,若变化过程中温度不变,求活塞移动的距离△h。
(2)欲使活塞再回到原来的位置,需要使温度升高到T2,求T2。
12p0=76cmHg,气体初始温度t1=57℃。
(i)将气体温度缓慢升高至多少K时,所有水银会全部挤入细管内?(ii)求温度升高至T3=492K时,液柱下端距离玻璃管底部的高度h。
接着根很细的弹簧,已知活塞的横截面积S=0.01m,大气压强P=1.0×10Pa。
当缸内气体温度为27℃时弹簧的长度为30cm,汽缸内气体压强为缸外大气压的1.2倍,当缸内气体温度升高到327℃时,弹簧的长度为36cm。
不计活塞与缸壁的摩擦且两个过程弹簧都处于拉伸状态,求(1)此时汽缸内气体的压强P2(2)此过程中缸内气体对外做的功2.如图所示,一个内壁光滑的圆柱形汽缸竖直放在水平地面上,缸内部横截面积S=10cm2,用质量m=l0kg的活塞在汽缸内封闭一定质量的气体,活塞可以在缸内无摩擦地滑动,外界大气压p0=1.0×105pa。
当气体温度T1=300K时,封闭气柱长h=40cm,活塞保持静止,重力加速度g=10m/s2,则:(1)在活塞上再放一质量为M=20kg的物块,活塞将向下移动,使活塞停在一个新的位置保持静止,若变化过程中温度不变,求活塞移动的距离△h。
(完整版)理想气体状态方程专题训练
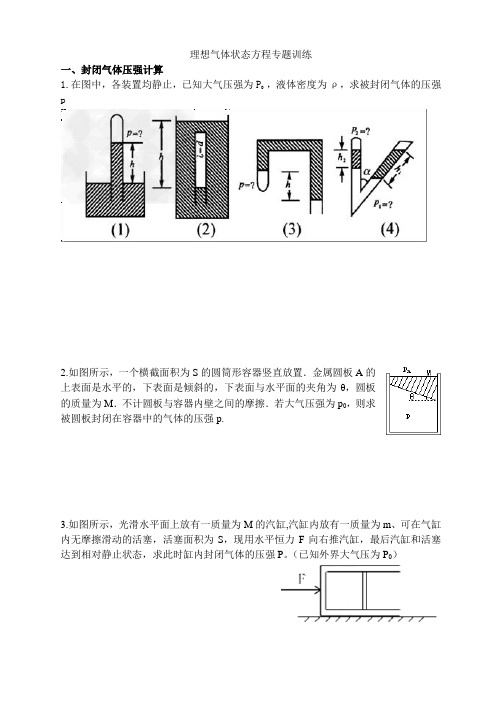
理想气体状态方程专题训练一、封闭气体压强计算1.在图中,各装置均静止,已知大气压强为P0 ,液体密度为ρ,求被封闭气体的压强p2.如图所示,一个横截面积为S的圆筒形容器竖直放置.金属圆板A的上表面是水平的,下表面是倾斜的,下表面与水平面的夹角为θ,圆板的质量为M.不计圆板与容器内壁之间的摩擦.若大气压强为p0,则求被圆板封闭在容器中的气体的压强p.3.如图所示,光滑水平面上放有一质量为M的汽缸,汽缸内放有一质量为m、可在气缸内无摩擦滑动的活塞,活塞面积为S,现用水平恒力F向右推汽缸,最后汽缸和活塞达到相对静止状态,求此时缸内封闭气体的压强P。
(已知外界大气压为P0)二、理想气体状态方程的基础应用4.一定质量的理想气体由状态A经过状态B变为状态C,其有关数据如p-T图象甲所示.若气体在状态A的温度为-73.15℃,在状态C的体积为0.6m3.求:(1)状态A的热力学温度;(2)说出A至C过程中气体的变化情形,并根据图象提供的信息,计算图中V A的值;(3)在图乙坐标系中,作出由状态A经过状态B变为状态C的V-T图象,并在图线相应位置上标出字母A、B、C.如果需要计算才能确定坐标值,请写出计算过程.三、单一封闭气体问题5.一足够长的粗细均匀的玻璃管开口向上竖直放置,管内由15cm长的水银柱封闭着50cm长的空气柱.若将管口向下竖直放置,空气柱长变为多少cm?(设外界大气压强为75cmHg,环境温度不变)6.在如图所示的气缸中封闭着温度为400K的空气,一重物用绳索经滑轮与缸中活塞相连接,重物和活塞均处于平衡状态,这时活塞离缸底的高度为10cm,如果缸内空气变为300K,问:(1)重物是上升还是下降?(2)这时重物将从原处移动多少厘米?(设活塞与气缸壁间无摩擦)7.如图所示,固定的绝热气缸内有一质量为m的“T”型绝热活塞(体积可忽略),距气缸底部h0处连接一U形管(管内气体的体积忽略不计).初始时,封闭气体温度为T0,活塞距离气缸底部为1.5h0,两边水银柱存在高度差.已知水银的密度为ρ,大气压强为p0,气缸横截面积为s,活塞竖直部分长为1.2h0,重力加速度为g.试问:(1)初始时,水银柱两液面高度差多大?(2)缓慢降低气缸内封闭气体的温度,当U形管两水银面相平时封闭气体的温度是多少?8.一汽缸竖直放在水平地面上,缸体质量M= 10kg,活塞质量M=4kg,活塞横截面积S=2×10-3 m2,活塞上面的汽缸内封闭了一定质量的理想气体,下面有气孔O与外界相通,大气压强p0=1.0×105Pa.活塞下面与劲度系数k = 2×103 N/m 的轻弹簧相连.当汽缸内气体温度为127℃时弹簧为自然长度,此时缸内气柱长度L1=20 cm,g取10m/s2,缸体始终竖直,活塞不漏气且与缸壁无摩擦.①当缸内气柱长度L2=24cm时,缸内气体温度为多少K?②缸内气体温度上升到T0以上,气体将做等压膨胀,则T0为多少K?四、多个相互关联的封闭气体问题9.如图,绝热气缸A与导热气缸B均固定于地面,由刚性杆连接的绝热活塞与两气缸间均为摩擦。
热学如何计算理想气体的压力和体积

热学如何计算理想气体的压力和体积在热力学中,理想气体是一个简化模型,用来研究气体的性质和行为。
理想气体满足理想气体状态方程,即PV = nRT,其中P表示气体的压力,V表示气体的体积,n表示气体的物质量,R表示气体常数,T表示气体的绝对温度。
这个方程可以用来计算理想气体的压力和体积。
一、计算理想气体的压力根据理想气体状态方程PV = nRT,我们可以将等式改写为P = (nRT) / V,这样就可以用给定的参数计算理想气体的压力。
例如,如果我们知道气体的物质量n、温度T和体积V,我们可以将这些值代入方程P = (nRT) / V来计算压力P。
举个例子,假设有一个气体样本,它的物质量为2摩尔,温度为300K,体积为10升,气体常数R为0.0821 L·atm/(mol·K),那么我们可以根据上述方程计算气体的压力。
P = (2 mol * 0.0821 L·atm/(mol·K) * 300K) / 10 L= 4.924 atm所以,这个气体样本的压力为4.924 atm。
二、计算理想气体的体积同样地,根据理想气体状态方程PV = nRT,我们可以将等式改写为V = (nRT) / P,这样就可以用给定的参数计算理想气体的体积。
例如,如果我们知道气体的物质量n、温度T和压力P,我们可以将这些值代入方程V = (nRT) / P来计算体积V。
举个例子,假设有一个气体样本,它的物质量为0.5摩尔,温度为400K,压力为3 atm,气体常数R为0.0821 L·atm/(mol·K),那么我们可以根据上述方程计算气体的体积。
V = (0.5 mol * 0.0821 L·atm/(mol·K) * 400K) / 3 atm= 5.473 L所以,这个气体样本的体积为5.473升。
总结:根据理想气体状态方程PV = nRT,我们可以计算理想气体的压力和体积。
理想气体教案理想气体的状态方程和计算

理想气体教案理想气体的状态方程和计算理想气体教案:理想气体的状态方程和计算一、理想气体简介理想气体是指在一定温度和压力下,分子之间没有相互作用力,体积可以忽略不计的气体。
它是理想气体动力学理论的基础,广泛应用于不同领域的科学研究和工程实践中。
二、理想气体的状态方程理想气体的状态方程描述了气体的压力、体积和温度之间的关系。
根据实验观察和统计力学理论,我们可以得到两种常见的理想气体状态方程。
1. 玻意耳-马略特定律(Boyle-Mariotte定律)在恒温条件下,理想气体的压力与其体积成反比。
数学表达式为:P₁V₁ = P₂V₂其中P₁和V₁分别代表气体的初始压力和初始体积,P₂和V₂分别代表气体的最终压力和最终体积。
2. 查理定律(Charles定律)在恒压条件下,理想气体的体积与其绝对温度成正比。
数学表达式为:V₁/T₁ = V₂/T₂其中V₁和T₁分别代表气体的初始体积和初始温度,V₂和T₂分别代表气体的最终体积和最终温度。
三、理想气体计算基于理想气体的状态方程,我们可以进行一些常见的气体计算。
1. 气体的摩尔数计算根据理想气体方程(PV = nRT),我们可以通过已知气体的压力、体积和温度,来计算气体的摩尔数。
摩尔数公式为:n = PV / RT其中P代表气体的压力,V代表气体的体积,T代表气体的绝对温度,R为气体常数。
2. 气体的密度计算理想气体的密度可以通过气体的摩尔质量和气体的摩尔数来计算。
密度公式为:ρ = m / V其中ρ代表气体的密度,m代表气体的摩尔质量,V代表气体的体积。
3. 气体的物态方程计算理想气体方程可以转化为理想气体的物态方程:PV = nRT通过已知气体的压力、体积和温度,我们可以求解气体的摩尔数。
4. 混合气体的计算当混合不同气体时,我们可以利用Dalton定律进行计算。
Dalton定律认为,混合气体总压等于各组成气体分压的和。
数学表达式为:P_total = P₁ + P₂ + ...其中P_total为混合气体的总压,P₁、P₂为各组成气体的分压。
高中物理热学理想气体题举例

高中物理热学理想气体题举例热学是高中物理中的重要内容,而理想气体题是其中的一种常见题型。
在这篇文章中,我将通过举例,详细解析几道典型的理想气体题目,帮助高中学生更好地理解和应用相关知识。
例题一:一个理想气体的体积从V1变为V2,压强由P1变为P2,温度保持不变。
求气体的状态方程。
解析:根据理想气体状态方程PV=nRT,其中P为压强,V为体积,T为温度,n为物质的物质量,R为气体常数。
根据题目条件,温度保持不变,即T1=T2,那么根据状态方程可得:P1V1=nRT1P2V2=nRT2由于T1=T2,所以P1V1=P2V2,这就是气体的状态方程。
例题二:一个理想气体的体积从V1变为V2,温度由T1变为T2,压强保持不变。
求气体的状态方程。
解析:同样根据理想气体状态方程PV=nRT,根据题目条件,压强保持不变,即P1=P2,那么根据状态方程可得:P1V1=nRT1P2V2=nRT2由于P1=P2,所以V1/T1=V2/T2,这就是气体的状态方程。
通过以上两个例题,我们可以看到,理想气体的状态方程与压强、体积、温度三者之间的关系密切相关。
在解题时,我们需要根据题目给出的条件,灵活运用状态方程,推导出所需的结果。
例题三:一个理想气体的体积从V1变为V2,温度由T1变为T2,压强由P1变为P2。
求气体的状态方程。
解析:根据理想气体状态方程PV=nRT,根据题目条件,我们可以列出以下方程:P1V1=nRT1P2V2=nRT2将两个方程相除得到:(P1V1)/(P2V2)=(nRT1)/(nRT2)化简后可得:(V1/T1)/(V2/T2)=P1/P2由于P1/P2为常数,所以(V1/T1)/(V2/T2)也为常数,这就是气体的状态方程。
通过以上例题的分析,我们可以发现,理想气体的状态方程与压强、体积、温度三者之间的关系是密不可分的。
在解题时,我们需要根据题目给出的条件,灵活运用状态方程,推导出所需的结果。
总结起来,理想气体的题目常常涉及到状态方程的应用,需要我们根据题目给出的条件,灵活运用状态方程,推导出所需的结果。
理想气体相关试题及答案

理想气体相关试题及答案一、选择题1. 理想气体的内能仅与温度有关,不依赖于气体的体积或压力。
这种说法是否正确?A. 正确B. 错误答案:A2. 根据理想气体定律,当温度不变时,气体的体积与压力的关系是:A. 成正比B. 成反比C. 不相关D. 先正比后反比答案:B3. 理想气体定律的数学表达式是:A. PV = nRTB. PV = nTC. PV = nRT/VD. PV = nR答案:A二、填空题1. 理想气体定律中,P表示______,V表示______,n表示______,R表示______,T表示______。
答案:压力;体积;摩尔数;通用气体常数;绝对温度2. 根据理想气体定律,1摩尔气体在标准大气压下的体积是______升。
答案:22.4三、简答题1. 解释理想气体定律的微观意义。
答案:理想气体定律的微观意义在于描述了气体分子在无相互作用力和无体积的情况下,分子运动的宏观表现。
它表明了气体分子的动能与温度成正比,而分子的动能是其内能的唯一来源。
2. 为什么理想气体定律在实际应用中有时会出现偏差?答案:理想气体定律在实际应用中出现偏差是因为实际气体分子之间存在相互作用力,且分子本身也有一定的体积。
当气体压力较高或温度较低时,这些因素会影响气体的行为,使其偏离理想气体的行为。
四、计算题1. 已知1摩尔的氧气在标准大气压下的温度为300K,求其体积。
答案:根据理想气体定律 PV = nRT,其中P = 1 atm,R = 0.0821 L·atm/mol·K,T = 300 K,n = 1 mol。
代入公式计算得 V = 22.4 L。
2. 如果1摩尔的氮气在1.5 atm和298 K的条件下,其体积是多少?答案:同样使用理想气体定律 PV = nRT,其中P = 1.5 atm,R = 0.0821 L·atm/mol·K,T = 298 K,n = 1 mol。
专题---理想气体状态方程计算题带答案

Word 资料理想气体状态方程计算题 1、如图所示,竖直放置的粗细均匀的 U 形管,右端封闭有一段空气柱,两管内水 银面高度差为h = 19 cm ,封闭端空气柱长度为 L i = 40 cm.为了使左、右两管中的 水银面相平,(设外界大气压强 p o = 76 cmHg ,空气柱温度保持不 变)试问: ①需从左管的开口端再缓慢注入高度多少的水银柱?此时封 闭端空气柱的长度是多少?②注入水银过程中,外界对封闭空气做 ________ (填“正功” “负功” 或“不做功”),气体将 _____ (填“吸热”或“放热”). 始温度为T °= 200 K ,外界大气压恒定不变为 p 0= 76 cmHg 。
现将玻璃管开口圭寸闭, 将系统温度升至 T = 400 K ,结果发现管中水银柱上升了 2 cm ,若空气可以看作理想气体,试求:①升温后玻璃管内封闭的上下两部分空气的压强分别为多少cmHg?②玻璃管总长为多少?5、如图所示为一简易火灾报警装置。
其原理是:竖直放置的试管中装有水银,当 温度升高时,水银柱上升,使电路导通,蜂鸣器发出报警的响声。
27 C 时,空气柱长度L i 为20cm ,水银上表面与导线下端的距离 L ?为10cm ,管内水银柱的高度 h 为8cm ,大气压强为75cm 水银柱高。
2、如图所示,U 形管右管横截面积为左管横截面积的 2倍,在左管内用水银封闭 一段长为26 cm 、温度为280 K 的空气柱,左、右两管水银面高度 差为36 cm ,外界大气压为76 cmHg 。
若给左管的封闭气体加热, 使管内气柱长度变为 30 cm ,则此时左管内气体的温度为多少?r26 r rn36 cdJdt-Jr —— (1 )当温度达到多少C 时,报警器会报警?(2)如果要使该装置在 87 C 时报警,则应该再往玻璃管 内注入多少cm 高的水银柱? ( 3)如果大气压增大,则该报警器的报警温度会受到怎样的影响?3、如图所示为一可以测量较高温度的装置,左、右两壁等长的 U 形管内盛有温度为0 C 的水银,左管上端开口,水银恰到管口,在封闭的右管上方有空气, 空气柱高h = 24 cm ,现在给空气柱加热,空气膨胀,挤出部分水银,当空气又 冷却到0 C 时,左边开口管内水银面下降了 H =5 空气被加热到的最高温度。
热力学练习题理想气体状态方程和熵的计算

热力学练习题理想气体状态方程和熵的计算热力学练习题:理想气体状态方程和熵的计算在热力学中,理想气体状态方程和熵是两个重要的概念。
理解和运用这些概念对于热力学问题的解决至关重要。
本文将通过解答一些热力学练习题,探讨如何计算理想气体的状态方程和熵。
1. 根据理想气体状态方程PV = nRT,计算下列问题:问题1.1:如果一定量的气体在温度为300K下体积为2L,压强为3atm,计算气体的物质的摩尔数。
解答1.1:根据理想气体状态方程PV = nRT,将已知的数值代入计算得:(3atm)(2L) = n(0.0821atm·L/mol·K)(300K),解得n ≈ 0.37 mol。
问题1.2:一定质量的气体在温度为227°C下压强为1.5atm,体积为5L,计算气体的摩尔数。
解答 1.2:先将温度转换为开尔文温标,227°C + 273.15 = 500.15K。
然后将已知的数值代入理想气体状态方程PV = nRT,得到(1.5atm)(5L) = n(0.0821atm·L/mol·K)(500.15K),解得n ≈ 6.14 mol。
2. 计算上述问题中理想气体的熵变:问题2.1:根据理想气体的熵变计算公式ΔS = nRln(V₂/V₁),计算气体在体积从2L变为4L时的熵变。
解答2.1:已知初始体积V₁为2L,最终体积V₂为4L。
根据公式ΔS = nRln(V₂/V₁),将已知的数值代入得ΔS =(0.37mol)(0.0821atm·L/mol·K)ln(4L/2L),解得ΔS ≈ 0.31 J/K。
问题2.2:根据理想气体的熵变计算公式ΔS = nRln(T₂/T₁),计算气体在温度从300K变为400K时的熵变。
解答2.2:已知初始温度T₁为300K,最终温度T₂为400K。
根据公式ΔS = nRln(T₂/T₁),将已知的数值代入得ΔS =(0.37mol)(0.0821atm·L/mol·K)ln(400K/300K),解得ΔS ≈ 0.04 J/K。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理想气体计算专题
1、如图所示,竖直放置的汽缸,活塞横截面积为s=o.oim, 可在汽缸内无摩擦滑动。
汽缸侧壁有一个小孔与装有水银
的u形玻璃管相通,汽缸内封闭了一段高为80 cm的气柱(U形管内的气丁^^〒*
体体积不计)。
此时缸内气体温度为赵“pl
7C,U形管内水银面高度差h i=5cm 亠
已知大气压强p o=1.O x 105Pa,水银的
密度p =13.6 x 103kg/m3,重力加速度g取10m/s2。
①求活塞的质量m。
②若对汽缸缓慢加热的同时,在活塞上缓慢添加沙粒,可保持活塞的高度不变。
当缸内气体温度升高到37C时, 求U 形管内水银面的高度差为多少?
2、如图所示,一上端开口的圆筒形导热汽缸竖直静置于地面,汽缸由粗、细不同的两部分构成,粗筒的横截面积是细筒横截面积S(cm i)的2倍,且细筒足够长。
粗筒中一个质量和厚度都不计的活塞将一定量的理想气体封闭在粗筒内,活塞恰好在两筒连接处且与上壁无作用,此时活塞相对于汽缸底部的高度h=12cm,大气压强p°=75cmHg现把体积为17S(cm3)的水银缓缓地从上端倒在活塞上方,在整个过程中气体温度保持不变,不计活塞与汽缸壁间的摩擦。
求活
塞静止时下降的距离x
3、如图所示,有一圆柱形汽缸,上部有一固定挡板,汽缸
内壁的高度是2L, 一个很薄且质量不
计的活塞封闭一定质量的理想气体,开始时活塞处在离底部L高处,外界大气压为1.0 x 105Pa,温
1L
度为27C,现对气体加热,求:①当加热到
127°C时活塞离底部的高度
②当加热到427C时,气体的压强
4、(2015重庆理综10)北方某地的冬天室外气温很低,吹出的肥皂泡会很快冻结.若刚吹出时肥皂泡内气体温度为
T i,压强为p i,肥皂泡冻结后泡内气体温度降为T2. 整个过程中泡内气体视为理想气体,不计体积和质量变化,大气压强为P o.求冻结后肥皂膜内外气体的压强差.
5、(2015山东理综37)扣在水平桌面上的热杯盖有时会
发生被顶起的现象.如图1,截面积为S的热杯盖扣在水平桌面上,开始时内部封闭气体的温度为300 K,压
强为大气压强p o.当封闭气体温度上升至303 K时,杯盖恰好被整体顶起,放出少许气体后又落回桌面,其内部气体压强立刻减为P0,温度仍为303 K .再经过一段时间,内部气体温度恢复到300 K •整个过程中封闭气体均可视为理想气体•求:
图1
(i )当温度上升到303 K且尚未放气时,封闭气体的压强;
(ii )当温度恢复到300 K时,竖直向上提起杯盖所需的最小力.
6、如图所示,容器A的体积是B的体积的2倍用带阀门K的细管相连通,K关闭时A贮存100atm27o C 理想气体,B中贮存有3°C的同种气体,打开K,A中有4的气体
进入B中平衡后的温度为15°C,试求容器B 中原气体的压强。
7、某容积为20L的氧气瓶装有30atm的氧气,现把氧气分装到容积为5L的小说钢瓶中,使每个小钢瓶中氧气的压强为5atm,若每个钢瓶中原有氧气压强为1atm问能分装多少瓶?
8、用活塞气筒向一个容积为V的容器内打气,每次能把体积为V o、压强为P o的空气打入容器内。
若容器内原有空气的压强为P o,大气过程中温度不变,这打了n次后容器内的气体的压强为多少?
1、⑵①对活塞,有:p o S+mg=p i S p i =p o + pgh i ,解得: m= ph i S
代入数值得m=6.8kg ②活塞位置不变,汽缸
内气体做等容变化
丄 Pl P2
由厂=「,T i =280K,T 2=310K pgh 2,解得 h 2=13.4cm
答案:⑴D (2)①6.8kg ② 13.4cm
2、(2)以汽缸内封闭气体为研究对象
初态压强p 1=p °=75cmHg
初态体积 V 1=2hS 末态 17S-2xS 体积 V 2=2(h-x)S 末态压强 p 2=p 0+x+—
由玻意耳定律可知P 1V 1=P 2V 2 即 75 X2 X12S=(75+x+17-
2x) X2 冬12-x)S 化简得 x 2-104x+204=0
解得 x=2cm 或 x=102cm(舍)
答案:⑴A 、B (2)2 cm
由题意,可知: p 2=p o +
3、(2)开始加热活塞上升的过程封闭气体做等压变化 设汽缸横截面积为S,活塞恰上升到汽缸上部挡板处时气
V T
体温度为t °C,则对于封闭气体,由一=「,可解得
t=327 °C
①当加热到127 C 时,活塞没有上升到汽缸上部挡板处。
设此时活塞离底部高度为
h,对于封闭气体,初状态: T i =300K,V i =LS;末状态:T 2=400K,V 2=hS 。
由一=丄,可
hS 400 4 得三=二,解得h=:L 。
②设当加热到427 C 时气体的压强变为 p 3,在此之前活 塞已上升到汽缸上部挡板处, 对于封闭气体, 初状态:T i =300K,V i =LS,p i =1.0 X105Pa;
末状态:T 3=700K,V 3=2LS,p 3=?
4
答案:(i)B (2)①;L ②i.i7 xi05Pa
kJ
» T 2
Vi A
,代入数据得:
p 3=i.i7 xi05Pa
4、市-P0
解析对泡内气体由查理定律得p=半2①内外气体
I 1 I 2
的压强差为Ap= P2—p o②
联立①②式解得巾==P1 —p o
一…、201 _
5.( 1 )1.01 p o (11 )107o O P o S
解析(1 )以开始封闭的气体为研究对象,由题意可知,初状态温度T o= 300 K,压强为p o;末状态温度T1 = 303 K,压强设为"由查理定律得T o=*①
101
代入数据得P1 = 10o p o= 1.O1p o②
(ii )设杯盖的质量为m,刚好被顶起时,由平衡条件得
P1S= p o S+ mg③
放出少许气体后,以杯盖内的剩余气体为研究对象,由
题意可知,初状态温度T2= 303 K,压强p2= p o,末状态温度T3= 300 K,压强设为P3,由查理定律得T2 = T3④
设提起杯盖所需的最小力为F,由平衡条件得F + p j S= p o S+ mg⑤
201
联立②③④⑤式,代入数据得F = I。
IOQ P O S。
