导体和介质
电磁学02静电场中的导体与介质

A q -q
-q+q
UA
q'
4 0 R0
q ' 4 0R1
q q '
4 0 R2
0
可得 q ( q) 1(9略)
例4 接地导体球附近有一点电荷,如图所示。
求:导体上感应电荷的电量
R
解: 接地 即 U0
o
感应电荷分布在表面,
l
q
电量设为:Q’(分布不均匀!)
由导体等势,则内部任一点的电势为0
选择特殊点:球心o计算电势,有:
1) Dds
S
1 (
r
1) q0内
l i mq内
V0V
1 (
r
1) limq0内 V0V
1 (
r
1)0
00 0。 40
[例2] 一无限大各向同性均匀介质平板厚度为 d
表明:腔内的场与腔外(包括壳的外表面)
物理 内涵
的电荷及分布无关。
在腔内 E 腔 外表 E 腔 面外 0带
电 量 的电 体 的
二.腔内有带电体时
q
① 带电量: Q腔内 q (用高斯定理易证)
表面
23
② 腔内的电场: 不为零。
由空腔内状况决定,取决于:
*腔内电量q;
*腔内带电体及腔内壁的 几何因素、介质。
平行放置一无限大的不带电导体平板。
0 1 2 求:导体板两表面的面电荷密度。
E2 • E1 解: 设导体电荷密度为 1、 2 ,
E0 电荷守恒: 1 + 2 = 0
(1)
导体内场强为零:E0 +E1‐E2 = 0
0 1 2 0 20 20 20
(1)、(2)解得:
导体和介质
o
o
P dS
S
电位移矢量:
D oE P
C m 2
介质中的高斯定理: 在静电场中,通过任意封闭 曲面的电位移通量等于该曲面所包围的自由电荷的 代数和。
D dS qi
S
4. D、E、P 三矢量之间的关系
D E
P 0e E D 0E P 0E 0e E 0 (1 e ) E 0 r E E
S
q
0
有介质时,上述高斯定理中的Σ q 应理解为所有 电荷的代数和,既包括自由电荷,也包括极化电荷。
1 E d S q q i i
S
o
q
i
封闭曲面S所包围的自由电荷。
i
q
封闭曲面S所包围的极化电荷。
+ +
-
n
+
P
+
+ -
高斯面上的极化电荷为
+ +σ ´
r
ε r = 1 + e
——相对介电常数与电极化率的关系
E E0 0 E0 E0 r 0 1 E0 (1 ) r 0 0 1 (1 ) 0 r 0
0 (1
1
r
)
——极化电荷面密度与自 由电荷面密度的关系
0 r
——介电常数
D E 只适用于各向同性的均匀介质。
外电场: E0
极化电荷产生的电场:E 介质内的电场: E
E E
E Eo E
1
1
06 静电场中的导体和介质
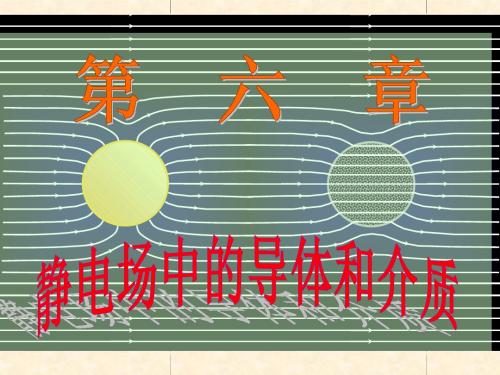
当 r R1 和 r R2 时:
r
q 2 S E dS E 4 r
E
q 4 0 r
2
0
q 4 0 r 2 (r R1 ) E 0( R1 r R2 ) 2 q 4 0 r (r R2 )
6-1
例1: 点电荷 q 处于导体球壳的中心,球壳不带电, 内、外半径分别为 R1 和 R2 ,求这一带电体系产生 的电场和电荷在空间的分布。 电荷只能分布于球壳的内、 外表面,在导体内作一同心 球面高斯面。
当 R1 r R2 和 r R2 时: 当 r R1 时:
E0
r
R2 q S D dS S ( DdS cos 0 ) S DdS D S dS 2 D 4 r q自 q 0( r R1 ) q D 0 r E E q 2 ( R1 r R2 ) 2 4 r 4 0 r r
q2
q q1 S E dS 0
R1 q1
q R2 q
q1 q
0
r
根据电荷守恒定律: q2
q
6-1
例 2: 点电荷 q 处于导体球壳的中心,球壳接地,内 外半径分别为 R1 和 R2 ,求这一带电体系产生的电 场和电荷在空间的分布。
解:电场方向:沿半径向外。 当 R1 r R2 时: E 当 r R1 时:
导体内电场强度 外电场强度 感应电荷电场强度
6-1
二. 导体处于静电平衡时的特征
2)导体内部没有电荷,电荷只能分布于导体 表面。
证明:假设导体内部某点有电荷,在导体内作一 极小高斯面包围该点,则
q S E dS 0
电介质分类

电介质分类
电介质是指电子元件中用来传导电流的物质,它可以是固体、液体或气体。
电介质的分类可以根据其物理性质和电学性质来划分。
一、根据物理性质分类
1、固体介质:固体介质是指以固体形式存在的电介质,它们的电阻率比液体和气体要高,常见的固体介质有金属、石英、玻璃、石墨等。
2、液体介质:液体介质是指以液体形式存在的电介质,它们的电阻率比固体要低,常见的液体介质有水、油、醇类等。
3、气体介质:气体介质是指以气体形式存在的电介质,它们的电阻率比液体和固体要低,常见的气体介质有氧气、氢气、氩气等。
二、根据电学性质分类
1、导体:导体是指具有良好的电导性的电介质,它们的电阻率比绝缘体要低,常见的导体有金属、水、油等。
2、绝缘体:绝缘体是指具有良好的绝缘性的电介质,它们的电阻率比导体要高,常见的绝缘体有石英、玻璃、石墨等。
三、根据电介质的用途分类
1、电气介质:电气介质是指用于传导电流的电介质,它们的电阻率比绝缘体要低,常见的电气介质有金属、水、油等。
2、电磁介质:电磁介质是指用于传导电磁波的电介质,它们的电阻率比电气介质要高,常见的电磁介质有空气、石英、玻璃等。
四、根据电介质的结构分类
1、单相介质:单相介质是指由一种电介质组成的电路,它们的电阻率比多相介质要低,常见的单相介质有金属、水、油等。
2、多相介质:多相介质是指由多种电介质组成的电路,它们的电阻率比单相介质要高,常见的多相介质有空气、石英、玻璃等。
电介质是电子元件中不可缺少的重要组成部分,它们的特性决定了电子元件的性能。
根据电介质的物理性质、电学性质、用途和结构,可以将电介质分为固体介质、液体介质、气体介质、导体、绝。
静电场中的导体与电介质

在静电场中平衡时: 1.内部电场强度不为零;2.电介质表面出现极化电荷
真空中的导体和电介质
P
pi
ΔV
P0eE
01
02
实验证
电 考 真空和P 偶 虑 中电c的介o 导质sS 极 一 P,体ln矩 电 pi, 0介 S 极 2质 l, 化 P 斜 0 . 极度定面 化:义V 圆 和 强:p 2i 电 柱 S 0 ,c荷 L So 体 明 各 性 介l0 : 向 质的 s密 在 同 中电co s度
此式对其它情况仍然适 用
D
义:电位移矢量D可, 得:D Dd0ESP S
q0
此既电介质中的高斯定理:通过电场中任意闭合曲面的电位移通量, 等于该闭合曲面所包围的自由电荷的代数和。
仿照电场线,用电位移线来描述电位移在空间的分布。但两者有 区别: 电场线起始于正电荷,终止于负电荷(包括极化电荷) 电位移线只起始于自由正电荷,终止于自由负电荷
在国际单位制中,D 的单位是: 库/米2(C/m2)
对各向同性电介质,因
所以 P0 eE
D 0EP 0 ( 1 ) E
式中 ε = ε0εr 叫电介质的介电常数, εr 称电介质的相对介电常数。
引入D,避免了求极化电荷的复杂问题,可使有电介质存在时解题简化。 只要有电介质,均应先求D 再求E 等。
E E0 E E0 与E 方 向 相 反 :
E
P
E0 // n
E
0 0
0
P cos
P
n
P
e 0E
E
E0
- E
10.4
E0 -
电介
质中0 静电E场0的-基本e
E
静电场中的导体和电介质

-
目录
静电场中的导体 和电介质
0
静电场中的导体和电介质
静电场中的导体和电介质
静电场是指在没有电流流动的情况下,电荷分布所产生的电场。在静电场中,导体和电介质 是两种不同的物质,它们的特性和作用也不同,本文将探讨导体和电介质在静电场中的性质 和应用 首先,我们需要了解导体和电介质的基本概念。导体是一种具有良好导电性能的物质,常见 的导体包括金属等。导体内的自由电子可以在外加电场的作用下移动,形成电流。而电介质 则是一种不良导电的物质,它的电导率远远低于导体。电介质在外加电场下无法形成连续的 电流,而是通过极化现象来响应电场的作用 在静电场中,导体和电介质的行为有很大的不同。对于导体来说,其特点是在静电平衡状态 下,内部电场为零。这是因为导体内的自由电子能够自由移动,它们会在外加电场的作用下 重新分布,直到达到平衡状态。这种现象被称为电荷运动的屏蔽效应。导体的另一个重要性 质是表面上的电荷分布是均匀的,这也是导体可以用来储存电荷的
与导体不同,电介质在静电场中的响应更加复杂。当外加电场作用于电介质时,电介 质分子会发生极化现象,即分子内部正、负电荷的分离。这种分离会导致电介质内部 产生电位移场,从而相应地改变电场分布。电介质的极化程度可以用极化强度来衡量 ,极化强度与外加电场的强度成正比。除了极化现象,电介质还可能发生击穿现象, 即在电场强度过高时,电介质内部的绝缘失效,导致电流的突然增加
0
静电场中的导体和电介质
导体在静电场中的一个重要应用 是电路中的导线。电路中的导线 由导体制成,它们能够有效地传 导电流。在电力系统中,导体连 接电源和电器设备,将电能传输 到目标地点。此外,在电子设备 制造中,导体用于制作电路板, 连接不同的电子元件,实现电信 号的传输和处理
导体和介质

导体和介质在我们的日常生活中,导体和介质无处不在。
比如说,电线和绝缘材料都是这个大千世界的组成部分。
你可能会想,导体和介质到底有什么不同呢?嘿,今天就让我们一起探讨这个有趣的话题。
一、导体的魅力1.1 导体是什么简单来说,导体就是那些可以很好地传导电流的材料。
比如铜、铝这些金属,都是导体的典型代表。
我们在家里的电器,几乎都少不了这些材料。
想象一下,当你打开灯,电流通过电线,灯泡亮起来,那一瞬间的光芒,就是导体在发挥作用。
1.2 导体的应用导体的应用非常广泛。
你知道吗?从手机到电脑,从家里的电器到工业设备,都离不开导体。
它们像是连接各种设备的桥梁。
没有导体,我们的生活将会变得暗淡无光。
就像缺少了盐的菜肴,怎么可能好吃呢?二、介质的世界2.1 介质是什么介质则是那些不能很好传导电流的材料。
塑料、玻璃和木头都是常见的介质。
它们的作用往往是隔绝电流,保护我们不被电击。
想象一下,当你触碰到电线时,如果电线没有被绝缘材料包裹,那后果可真不堪设想。
2.2 介质的特性介质的特性也各有千秋。
比如,某些介质在高频电场中表现得很好,而另一些在低频电场中则比较有效。
它们就像不同的运动员,在各自擅长的领域中大显身手。
绝缘材料能抵御电流,保护我们;而在某些特殊情况下,它们还可以存储电能。
2.3 介质的应用介质的应用同样不可小觑。
比如,在电力传输中,绝缘材料不仅保护导体,还能提高传输效率。
再看看我们的手机,里面也用到了许多绝缘材料,帮助提高信号质量。
想象一下,没有这些材料,手机的信号质量就会大打折扣,生活也会变得更加不便。
三、导体与介质的关系3.1 互为依存导体和介质的关系就像阴阳,缺一不可。
没有导体,电流就无法流动;没有介质,电流的流动就会带来危险。
它们就像两位舞者,在电力的舞台上相互依偎,共同演绎出美妙的乐章。
3.2 在科学中的应用在科学领域,导体和介质的研究同样重要。
科学家们不断探索更好的导体和介质材料,提升电力传输效率。
电介质和导体的物理特性

电介质和导体的物理特性电介质和导体是电学的基本概念,它们是电路中最重要的两种材料。
电介质和导体各自具有独特的物理特性,它们在电路中的作用也有所不同。
本文将介绍电介质和导体的物理特性及其在电路中的应用。
一、导体导体是一种能够传递电荷的物质。
通常情况下,所有金属都是导体,但并不是所有的导体都是金属。
导体材料最主要的特点是能够将电子传递给其他原子,使其处于高电势状态。
这些高电势原子又可以将电子传递给其他原子,从而使电子在导体内自由流动。
在导体中,电子的运动是自由的,它们可以自由地从一个原子跳跃到另一个原子。
这种自由运动的结果就是导体具有极低的电阻。
因为电子在导体内自由运动,所以导体可以被用作电线和电缆等电路元件。
导体在电路中的应用非常广泛。
电路中的铜线、铝线都是典型的导体。
导体具有良好的电导性,对电路的通电和电流传输起到了重要的作用。
此外,导体还可以作为各种电器设备的连接线路,如电子元器件、家电等。
二、电介质电介质是指那些不能很好地传导电荷的物质,比如空气、玻璃等。
电介质中的电子不能自由地在其中运动,这是由于电介质中的原子束缚电子的力比较大。
当电场通过电介质时,它会把原子拉伸并使电介质中的电子向一个方向暂时借助,从而形成一个致密电荷区,这个区域称为电介质中的电荷分布。
电介质在电路中的应用也有很多,它们主要是用于电容器、绝缘材料等。
电介质本身并不能导电,但在电场的作用下会形成电荷分布,进而形成电容器。
电容器的作用是能够储存电荷,在电路中用来过滤和平滑电压和电流。
电介质也常用作绝缘材料。
绝缘材料的主要作用是隔离电路中的导体,避免电流流失和短路。
电机、变压器、电缆、电线等电器中都需要使用大量绝缘材料。
这些材料不仅需要具备很好的绝缘性能,而且还需要耐高温、耐腐蚀和机械强度等特点,以保障电器设备的正常运行。
三、导体与电介质的对比导体和电介质是两种截然不同的材料,它们在电路中的作用也大相径庭。
导体具有优良的导电性能,它们能够传递电荷并将电压和电流传输到电路中的各个位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.静电平衡的条件
E内 0
或V c
2.基本性质方程
E
ds
i
qi
S
0
LE dl 0
3.电荷守恒定律
Qi const.
i
例1. 有一外半径R1,内半径为R2的金属球壳。在球壳中 放一半径为R3的金属球,球壳和球均带有电量q=10-8C 的正电荷。问:(1)两球电荷分布。(2)球心的电势。 (3)球壳电势。
E 外
+ + + + +
+ + +
加上外电场后
导体的静电感应过程
E 外
+ + + + + + + + +
加上外电场后
导体的静电感应过程
E 外
+ + + + + +
+ + + +
加上外电场后
导体的静电感应过程
E 外
+ + + + + +
+ + + +
加上外电场后
导体达到静平衡
+
+
+
+
+
E 感
E +
第六章
静电场中的导体和电介质
导体:
能够让电流通过的材料。
导体的分类:
根据导电性不同,可以分为超导体、导体、 半导体、及绝缘体。
• 超导体(superconductor):指可以在在特定温 度以下,呈现电阻为零的导体
• 导体(conductor):存在大量可以自由移动的 电荷
• 半导体(semiconductor):介于导体和绝缘体 之间
2.ห้องสมุดไป่ตู้表面场强垂直于导体表面。
用电势来描写: 1. 导体为一等势体; 2. 导体表面是一个等势面。
E
F
-
E0
金属球放入前电场为一均匀场
E
金属球放入后电力线发生弯曲 电场为一非均匀场
6-1-2 静电平衡时导体上的电荷分布
1. 在静电平衡下,导体所带的电荷只能分布在导 体的表面,导体内部没有净电荷。
越大,曲率越小的地方电荷密度也越小。
两个半径分别为 R 和 r 的球形导体(R> r), 用一根很长的细导线连接起来,使这个导体组带 电,电势为U,求两球表面电荷与曲率的关系?
解:由于两球由导线连接,两球电势相等:
U 1 Q 1 q
4 0 R 4 0 r
得:
QR
qr
可见,大球所带电量Q比小球q多。 两球的面电荷密度分别为:
解:电荷守恒: 1S 2S q1
3S 4S q2
由静电平衡条件,导体板内E = 0
q1
q2
EA
1 2 o
2 2 o
3 2 o
4 2 o
0
1 2 3 4
EB
1 2 O
1 2
2 2 O q1 S
3 4 0
2o 2o
3+ 4
q2 S
A
B
1
4
q1 q2 2S
2
3
q1 q2 2S
例3 设有一无限大不带电的接地导体平板,如图所示, 在离导体表面距离为a的左侧有一点电荷,求:导体平板 上的感应电荷面密度及导体表面上感应电荷总电量。
E 外
+
+
加上外电场后
导体的静电感应过程
E 外
+
+
+
加上外电场后
导体的静电感应过程
E 外
+ +
+
+ +
加上外电场后
导体的静电感应过程
E 外
+ +
+
+ +
加上外电场后
导体的静电感应过程
E 外
+ +
+
+ + +
加上外电场后
导体的静电感应过程
E 外
+ + +
+
+ + +
加上外电场后
导体的静电感应过程
解(:1)1、电荷+q分布在内球表面。
2、球壳内表面带电-q。
3、球壳外表面带电2q。
E3 E2
0
4
q
o
r
(r < R3 )
2 (R3 < R2
)
E1 0 2q(R2 < R1 )
E0 4or 2 (r > R1 )
Vo
E dl
0
R3
0
R2
R3
R1
R2
R1
Vo
E dS
1
S
o
qi
E 0 qi 0
结论:
导体内部没有净电荷,电荷只能分布在导体表面。
2. 处于静电平衡的导体,其表面上各点的电荷密度 与表面邻近处场强的大小成正比。
证明:由高斯定理:
dS
E • dS EdS
s
o
E
o
E
dS
3. 静电平衡下的孤立导体,其表面处电荷密度 与该
表面曲率有关,曲率(1/R)越大的地方电荷密度也
• 绝缘体(insulator):理论上认为没有自由移动 电荷,阻碍电流流动,又称电介质(dielectric)
§6-1 导体的静电平衡性质
6-1-1 导体的静电平衡条件
金属导体特征:存在大量的自由电子
无外电场时
导体的静电感应过程
E 外
加上外电场后
导体的静电感应过程
E 外
+
加上外电场后
导体的静电感应过程
6.1.3 空腔导体
1.腔内无带电体
1
E dS
S
o
qi
E 0 qi 0
结论:
2. 腔内有带电体
根据高斯定理:
E 0 qi 0
q q
结论: 在静电平衡下,电荷分布在导体内、外两个表
面,其中内表面的电荷是空腔内带电体的感应电 荷,与腔内带电体的电荷等量异号。
6-1-4 静电屏蔽
解:P点处的电场强度是由点电荷和导体平板上感应电荷
静电屏蔽: 一个接地的空腔导体可以隔离内外 电场的影响。
1、空腔导体,腔内没有电荷
空腔导体起到屏蔽外电场
E
的作用。
2、空腔导体,腔内存在电荷
接地的空腔导体可以屏
蔽内、外电场的影响。 空腔导体置入外电场后
4-4 静电屏蔽
不接地的导体腔
接地的导体腔
金属罩
静电屏蔽
仪器
有导体存在时静电场场量的计算原则
+
外
+
+
+
E 内
=
E外 +
E感
=
0
静电感应:
在外电场影响下,导体 表面不同部分出现正负电 荷的现象。
静电平衡: 导体内部和表面没有电
荷的宏观定向运动。
-
+
-
- E=0
-
- - - E
+
+ +
Eo
+
++
F-
感应电荷: 因静电感应而在导体两侧表面上出现 的电荷。
静电平衡时导体中的电场特性:
用场强来描写: 1. 导体内部场强处处为零;
R2 R3
E2dr
R1 Eodr
R2 qdr
R3 4or 2
2qdr
4or 2
q
4o
1 R3
1 R2
2q
4 o R1
q
4o
1 R3
1 R2
2 R1
(3)
2q
2q
V1 R1 4or 2 dr 4o R1
例2.两块大导体平板,面积为S,分别带电q1和q2,两极 板间距远小于平板的线度。求平板各表面的电荷密度。
R
Q
4R2
r
q
4r 2
所以:
R r
Qr2 qR2
r R
结论:两球电荷面密度与曲率半径成反比,即 与曲率成正比。
应用
避雷针:Lightning Mast或Lightning Rod
一个柱子或基础结构,由它的顶到地有 一垂直导体或它本身就是一到地的导体, 其 目的通过引导与疏导,把接闪的雷电 流释放到大地,栏截雷击使不落在其保护 范围内的物体上 ,保护建筑物免遭直接 雷击的破坏 。
