静电场中的导体与电介质作业
大学物理学 大作业参考解答

静电场中的导体和电介质
大作业参考解答
选择题1:当一个带电导体达到静电平衡时, (A)导体表面上电荷密度较大处电势较高; (B)导体表面曲率较大处电势较高; (C)导体内部的电势比导体表面的电势高; (D)导体内任一点与表面上任一点的电势差等于零。
NIZQ 第1页
大学物理学
静电场中的导体和电介质
d a
a
E dx
x
d a d ln ln 0 a 0 a
0 q 1 C U U A U B ln d a
NIZQ 第18页
大学物理学
静电场中的导体和电介质
计算题3:如图所示,在一不带电的金属球旁,有一点电荷 +q,金属球半径为R,点电荷+q与金属球球心的间距为d, 试求: (1)金属球上感应电荷在球心处产生的电场强度。 (2)若取无穷远处为电势零点,金属球的电势为多少?
-σ1 σ1 σ2 -σ2
d1 (A) d2 (C) 1
d2 (B) d1 d2 (D) 2 d1
2
d1
d2
1 2 d1 d2 0 0
NIZQ 第8页
大学物理学
静电场中的导体和电介质
填空题1:如图所示,两同心导体球壳,内球壳带 电量+q,外球壳带电量 -2q . 静电平衡时,外球壳 的内表面带电量为 ;外表面带电量 -q 为 。 -q
q CU r C 0U r q 0
U E E0 d
1 1 1q 2 W qU CU r E0 2 2 2C
NIZQ 第16页
2
计算题1:两块相互平行的导体板a和b ,板面积均为S,
大学物理学
静电场中的导体和电介质
静电场中的导体与电介质习题课

静电场中的导体和介质习题课
全部分布在外表面。 (2)连接后电荷 +q全部分布在外表面。 )连接后电荷Q+ 全部分布在外表面
Q+q U1 = U 2 = 4πε 0 R3
(3)内球接地,U1=0。内球带电 ´,外球壳内表面- q´, )内球接地, 。内球带电q´ 外球壳内表面- ´ 外表面Q+ ´ 外表面 + q´,
− q′ Q + q′ U1 = + + =0 4πε 0 R1 4πε 0 R2 4πε 0 R3 R1 R2Q q′ = R1 R2 + R3 ( R2 − R1 )
U 2 = −∫
R1 R2
q′
− q′( R2 − R1 ) Edr = ∫ dr = R2 4πε r 2 4πε 0 R1 R2 0
静电场中的导体和介质习题课
例:计算机键盘的键结构如图。按键连有一可移动的金属片。 计算机键盘的键结构如图。按键连有一可移动的金属片。 下面是一固定的金属片,中间是软的绝缘介质( )。两 下面是一固定的金属片,中间是软的绝缘介质(εr=2)。两 )。 块金属片就构成一个平板电容器。当键按下时, 块金属片就构成一个平板电容器。当键按下时,电容器的电容 发生变化,与之相连的电路就能检测出哪一个键被按下, 发生变化,与之相连的电路就能检测出哪一个键被按下,从而 给出相应的信号。设金属片面积为50mm2,两金属片间距 给出相应的信号。设金属片面积为 0.6mm。如果电路能检测出的电容的变化是 。如果电路能检测出的电容的变化是0.25pF,那么需要 , 将键按下多大的距离才能给出必要的信号? 将键按下多大的距离才能给出必要的信号? 解:按键前电容 C = ε r ε 0 S 1 d ε rε 0 S 按键后电容 C2 = d − ∆d
工科物理大作业06-静电场中的导体与电介质

图6-1(a)图6-1(b)0606 静电场中的导体与电介质班号 学号 姓名 成绩一、选择题(在下列各题中,均给出了4个~5个答案,其中有的只有1个是正确答案,有的则有几个是正确答案,请把正确答案的英文字母序号填在题后的括号内)1.如图6-1(a)所示,一个原来不带电的导体球壳,内半径为R 1,外半径为R 2,其圆心O 处放置一个点电荷q +。
现将q +由O 点移至P 点,则在下列说法中,正确的是:A .在1R r <的区域内,各点的电场强度要发生变化,而2R r >的区域电场强度不变;B .球壳内、外表面的感应电荷分布没有变化;C .球壳内表面的感应电荷不再均匀分布,外表面不受影响;D .球壳内、外表面的感应电荷不再均匀分布。
(A 、C )[知识点] 静电感应、感应电荷的分布。
[分析与解答] 导体球壳内放入点电荷+q ,球壳内表面要感应出-q ,外表面将感应出+q 的电荷。
由于点电荷+q 在球壳内由O 点移到P 点,球壳内表面距离点电荷+q (P 点)近的地方,感应电荷的密度大,距离点电荷+q (P 点)远处的地方,感应电荷的密度小,即球壳内表面-q 的分布将不均匀;而对于球壳外表面来说,其内部(指内表面和点电荷)有等量异号的电荷,由于屏蔽,其电场将完全不影响壳外电场,外表面又是球面,因此外表面感应电荷+q 分布均匀,如图6-1(b)所示。
由点电荷电场强度公式知,当点电荷+q 在O 点时,其电场为球对称分布,而移到P 点后,在1R r <区域内,距离P 点近的场点电场强度要大,远场点电场强度要小,在2R r >,由高斯定理知为球对称分布电场,与点电荷+q 放置在O 点时一致。
2.如图6-2所示,一金属球半径为R ,带电Q -,距球心为3R 处有一点电荷q -。
现将金属球接地,则金属球面上的电荷为:A .0;B .q Q +-;C .3q; D .q +。
(C )图6-2图6-3(a)图6-3(b)[知识点] 外壳接地后电势叠加为零。
第十章 静电场中的导体和电介质习题解答
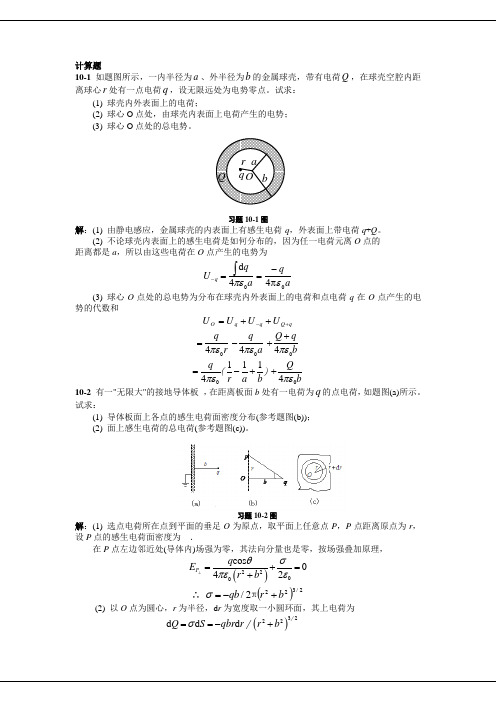
10-1 如题图所示,一内半径为a 、外半径为b 的金属球壳,带有电荷Q ,在球壳空腔内距离球心r 处有一点电荷q ,设无限远处为电势零点。
试求: (1) 球壳内外表面上的电荷;(2) 球心O 点处,由球壳内表面上电荷产生的电势;(3) 球心O 点处的总电势。
习题10-1图解:(1) 由静电感应,金属球壳的内表面上有感生电荷-q ,外表面上带电荷q +Q 。
(2) 不论球壳内表面上的感生电荷是如何分布的,因为任一电荷元离O 点的 距离都是a ,所以由这些电荷在O 点产生的电势为0d 4q qU aπε-=⎰aq04επ-=(3) 球心O 点处的总电势为分布在球壳内外表面上的电荷和点电荷q 在O 点产生的电势的代数和q Q q q O U U U U +-++=04qr πε=04qa πε-04Q qb πε++01114()q r a bπε=-+04Q bπε+ 10-2 有一"无限大"的接地导体板 ,在距离板面b 处有一电荷为q 的点电荷,如题图(a)所示。
试求:(1) 导体板面上各点的感生电荷面密度分布(参考题图(b)); (2) 面上感生电荷的总电荷(参考题图(c))。
习题10-2图解:(1) 选点电荷所在点到平面的垂足O 为原点,取平面上任意点P ,P 点距离原点为r ,设P 点的感生电荷面密度为.在P 点左边邻近处(导体内)场强为零,其法向分量也是零,按场强叠加原理,()220cos 024P q E r b θσεπε⊥=+=+ ∴ ()2/3222/b r qb +-=πσ (2) 以O 点为圆心,r 为半径,d r 为宽度取一小圆环面,其上电荷为 ()3222d d d //Q S qbr r r bσ==-+q Q a bO r()q brrr qb S Q S-=+-==⎰⎰∞2322d d /σ10-3 如题图所示,中性金属球A ,半径为R ,它离地球很远.在与球心O 相距分别为a 与b 的B 、C 两点,分别放上电荷为A q 和B q 的点电荷,达到静电平衡后,问: (1) 金属球A 内及其表面有电荷分布吗?(2) 金属球A 中的P 点处电势为多大?(选无穷远处为电势零点)B C R AP Oq A q Bba习题10-3图解:(1) 静电平衡后,金属球A 内无电荷,其表面有正、负电荷分布,净电荷为零. (2) 金属球为等势体,设金属球表面电荷面密度为. ()()000d 4=4////AP A B S U U S R q a q a σπεπε==⋅+⎰⎰∵d 0AS S σ⋅=⎰⎰∴ ()()04///P A B U q a q a πε=+10-4 三个电容器如题图联接,其中C 1 = 10×10-6 F ,C 2 = 5×10-6 F ,C 3 = 4×10-6 F ,当A 、B 间电压U =100 V 时,试求:(1) A 、B 之间的电容;(2) 当C 3被击穿时,在电容C 1上的电荷和电压各变为多少?ABC 1C 2 C 3U习题10-4图解:(1) =+++=321321)(C C C C C C C 3.16×10-6 F(2) C 1上电压升到U = 100 V ,电荷增加到==U C Q 111×10-3 C10-5 一个可变电容器,由于某种原因所有动片相对定片都产生了一个相对位移,使得两个相邻的极板间隔之比为2:1,问电容器的电容与原来的电容相比改变了多少?(a) (b)习题10-5图解:如图所示,设可变电容器的静片数为n ,定片数为1-n ,标准情况下,极板间的距离为d (图a ),极板相对面积为S 。
大学物理第7章静电场中的导体和电介质课后习题及答案

大学物理第7章静电场中的导体和电介质课后习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第7章 静电场中的导体和电介质 习题及答案1. 半径分别为R 和r 的两个导体球,相距甚远。
用细导线连接两球并使它带电,电荷面密度分别为1σ和2σ。
忽略两个导体球的静电相互作用和细导线上电荷对导体球上电荷分布的影响。
试证明:Rr=21σσ 。
证明:因为两球相距甚远,半径为R 的导体球在半径为r 的导体球上产生的电势忽略不计,半径为r 的导体球在半径为R 的导体球上产生的电势忽略不计,所以半径为R 的导体球的电势为R R V 0211π4επσ=14εσR= 半径为r 的导体球的电势为r r V 0222π4επσ=24εσr= 用细导线连接两球,有21V V =,所以R r =21σσ 2. 证明:对于两个无限大的平行平面带电导体板来说,(1)相向的两面上,电荷的面密度总是大小相等而符号相反;(2)相背的两面上,电荷的面密度总是大小相等而符号相同。
证明: 如图所示,设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ,2σ,3σ,4σ(1)取与平面垂直且底面分别在A 、B 内部的闭合圆柱面为高斯面,由高斯定理得S S d E S ∆+==⋅⎰)(10320σσε 故 +2σ03=σ上式说明相向两面上电荷面密度大小相等、符号相反。
(2)在A 内部任取一点P ,则其场强为零,并且它是由四个均匀带电平面产生的场强叠加而成的,即0222204030201=---εσεσεσεσ 又 +2σ03=σ 故 1σ4σ=3. 半径为R 的金属球离地面很远,并用导线与地相联,在与球心相距为R d 3=处有一点电荷+q ,试求:金属球上的感应电荷的电量。
解:如图所示,设金属球表面感应电荷为q ',金属球接地时电势0=V由电势叠加原理,球心电势为=O V R qdq R 3π4π4100εε+⎰03π4π400=+'=Rq R q εε故 -='q 3q 4.半径为1R 的导体球,带有电量q ,球外有内外半径分别为2R 、3R 的同心导体球壳,球壳带有电量Q 。
《大学物理学》习题解答(第12章 静电场中的导体和电介质)(1)

(2)两输电线的电势差为 U
xR
E dl
R
Ed x
d R ln 0 R
(3)输电线单位长度的电容 C
U
0 / ln
d R d 0 / ln 4.86 1012 F R R
【12.9】半径为 R1 的导体球被围在内半径为 R2 、外半径为 R3 、相对电容率为 r 的介质球壳内,它们是同 球心的。若导体带电为 Q ,则导体内球表面上的电势为多少? 【12.9 解】先求各区域电场 (1)
Q 4 0 R3
( R3 r )
B 球壳为等势体,其电势为
V
R3
E dr
Q 4 0
R3
r
dr
2
【12.2】一导体球半径为 R1,外罩一半径为 R2 的同心薄导体球壳,外球壳所带总电荷为 Q,而内球的电势为 V0.求此系统的电势和电场分布。 【12.2 解】已知内球电势为 V0 ,外球壳带电 Q 。 (1)先求各区域的电场强度:设内球带电荷 q 。由高斯定理,有
E
U
z
2R
( 1 )一根带电 的输电线在两线之间、距其轴心 x 处 p 点的场强为
x
dx
p
E i 2 0 x
另一根带电 的输电线在 p 点产生的电场强度为
x
E
2 0 ( d x )
i
p 点的总电场强度为
E E E
d R
1 1 ( )i 2 0 x d x
E1 0
(r R1 ) ( R1 r R2 ) 4 r 2 D Q , D 0 r E3
第十二章 静电场中的导体和电介质作业答案

B E dx
A
B A
q1 q2 S20
dx
q1 q2 20S
d
3. 有一接地的金属球,用一弹簧吊起,金属球原来不带电.若在它的下方放置一电荷
为q的点电荷,如图所示,则 C
(A) 只有当q 0时,金属球才下移.
(B) 只有当q 0时,金属球才下移.
(C) 无论q是正是负金属球都下移.
(D) 无论q是正是负金属球都不动.
0
Q球
1 2
q
二、填空题
1. 地球表面附近的电场强度约为100N/C,方向垂直地面向下,假设地球上的电荷都均
匀分布在地球表面上,则地面的电荷密度为______。
分析:地球是一个等势体,里边的场强为零,达到静电平衡,表面附近的场强
E
0
100
0 100 8. 85 1012 100 8. 85 1010 C2 m-2
q UAB
q
1
UAB
q
1
UAB 40RB外表面
1
q UAB
1 4 0 R B外表面
40RB外表面
q UAB
q UAB
4 0 R B外表面
q
1
UAB
q
1
UAB 40RB外表面
jintian 2. 在空气平行板电容器中,平行地插上一块各向同性均匀电介质板,如图所示,当电 容器充电后,若忽略边缘效应,则电介质中的场强E与空气中的场强E0相比较,应
q
分析:一带电量为q、半径为R的金属薄球壳,里边的场强为零,电介质不被极化,电介质
不产生附加电场,壳外是真空,壳外的场强就是电量q产生的场强。半径为R的金属薄球壳
是一个等势体,
E U壳
大物AI作业参考解答_No.08 静电场中的导体和电介质

《大学物理AI 》作业No.08静电场中的导体和电介质班级________学号________姓名_________成绩______--------------------------------------------------------------------------------------------------------------------****************************本章教学要求****************************1、理解静电平衡的条件,理解静电感应、静电屏蔽的原理;2、掌握静电平衡时导体表面感应电荷的分布和电场、电势的计算;3、了解电介质的极化现象和微观解释,理解电位移矢量D的定义,确切理解电介质中的高斯定理,并能利用它求解有电介质存在时具有一定对称性的电场问题;4、理解电容的定义,掌握电容器电容的计算方法;5、掌握电容器的储能公式,理解电场能量密度的概念,并能计算电荷系的静电能;6、理解电流强度和电流密度的概念,理解恒定电场的特点及电源电动势的概念。
--------------------------------------------------------------------------------------------------------------------一、选择题:1.把A ,B 两块不带电的导体放在一带正电导体的电场中,如图所示。
设无限远处为电势零点,A 的电势为U A ,B 的电势为U B ,则[D ](A)U B >U A ≠0(B)U B >U A =0(C)U B =U A (D)U B <U A解:电力线如图所示,电力线指向电势降低的方向,所以U B <U A 。
2.半径分别为R 和r 的两个金属球,相距很远。
用一根细长导线将两球连接在一起并使它们带电。
在忽略导线的影响下,两球表面的电荷面密度之比为[D ](A)R/r (B)R 2/r 2(C)r 2/R 2(D)r/R解:两个金属球用导线相接意味着它们的电势相等,设它们各自带电为21q q 、,选无穷远处为电势0点,那么有:rq Rq 020144,我们对这个等式变下形r R rr r q R R R q 21020144 ,即面电荷密度与半径成反比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静电场中的导体与电介质作业
1.题号:40743001 分值:10分
如图下所示,一半径为1R 的无限长导体,单位长度带电量为λ,外有一半径为2R ,
单位长度带电量为λ-的圆筒形导体,两导体同轴,内外圆柱面间充满相对电容率为
r ε的均匀电介质。
求:(1)该导体系统内外的电场分布;(2)两导体轴心处的电势(设
外圆筒面外任意一点P 的电势为零,P 点与中心轴的距离为P R );(3)电介质中的极化强度;(4)画出r E -曲线。
2.题号:40743002 分值:10分
半径为1R 的金属球带电荷量Q +,外罩一半径为2R 的同心金属球壳,球壳带电量
Q +,厚度不计,内外两球面间充满相对电容率为r ε的均匀电介
质。
求:(1)该球面系统内外的电场分布;(2)球心处的电势;(3)电介质中的极化强度;(4)画出r E -曲线。
3.题号:40743003 分值:10分
一个半径为R 电容率为ε的均匀电介质球的中心放有点电荷q ,求(1)电介质球内、外电位移的分布;(2)电介质球内、外电场强度和电势的分布;(3)球体表面极化电荷的密度。
4.题号:40743004
分值:10分
如图所示,带电量为Q 、半径为0R 的金属球置于介电常量为ε,半径为R 的均匀介质球内。
求(1)介质层内、
外的D 、E
的分布;(2)介质层内、外表面上的束缚电荷面密度。
5.题号:40843012 分值:10分
如下图所示,真空中的球形电容器的内、外球面的半径分别为1R 和2R ,所带电荷量为Q ±。
求:(1)该系统各区间的场强分布;(2)该系统各区间的电势分布;(3)该系统的电容。
6.题号:40842020 分值:10分
(1).一电荷面密度为σ “无限大”均匀带电平面,若以该平面处为电势零点,试求带电平面
x >0 空间的电势分布。
(2).如图所示,真空中的球形电容器的内、外半径分别为1R 和2R ,所带电荷量为Q ±。
求该电容器的电容。
静电场中的导体与电介质作业解答
1.题号:40743001 分值:10分 解答及评分标准:
(1)由高斯定理得出电场分布:0
2032
022
1
11
=>=
<<=<E R r r
E R r R E R r r επελ
(3分)
方向均沿径矢方向。
(1分)
(2)设外圆筒面外任意一点P 的电势为零,P 点与中心轴的距离为P R ,如图所示,则轴心处的电势为:(2分)
1
2
0003210ln 21
2
1
2
R R l d E l d E l d E l d E V P
P
R R R R R R r ⎰⎰⎰⎰=
⋅+⋅+⋅=⋅=επελ
(3)电介质中的极化强度为:
)(21
)1(2120R r R r
E P r r r <<-=-=λ
πεεεε(2分)
方向与电场强度同向。
(1分) (4)r E -曲线:(1分)
2.题号:40743002
分值:10分
解:(1)根据高斯定理,可得出整个系统的电场分布:
2
032
2
022*******r Q
E R r r Q E R r R E R r r πεεπε=
>=
<<=<(3分)
方向沿径矢方向。
(1分)
(2)球心处的电势:(2分) 2
0210
003210
1
42)11(
41
21
2
R Q R R Q l d E l d E l d E l d E V R R R R r
πεεπε+
-=
⋅+⋅+⋅=⋅=
⎰⎰⎰⎰∞
∞
(3)极化强度:2
2041)1(r
Q
E P r r r πεεεε-=
-=(2分) 方向与电场强度方向一相同。
(1分)
(4)r E -曲线:(1分)
3.题号:40743003
分值:10分
解:(1)由高斯定理 ⎰
=⋅S
q S d D
得
R r < 2
4r q D π=
R r > 2
4r
q D π= (2)由 E E D r
εεε==0 得
电场强度的分布 R r < 2
4r
q E πε=
R r > 2
04r q E πε=
由 ⎰∞
⋅=r l d E V
得
电势的分布 R r < )1
1(440R r q R q V -+=
πεεπ
R r > r
q V 04πε=
(3)球体表面极化电荷的密度: ε
πεε2
0)(0r 4)()1'R q
E εεP σR -=-==(
4.题号:40743004 分值:10分 解答及评分标准:
根据对称问题的性,D
的分布具有球对称性, 在介质层中取一半径为r 的高斯面。
⎰
=⋅s
r D S d D 2
4π ⎰=⋅s Q S d D
(2分)
求得介质内的电位移为:
2
14r
Q
D π=
)(0R r R <<(2分) 介质外的电位移为:
2
24r Q
D π=
)(R r >(2分) 根据E D ε=,得
2
14r Q
E πε=
)(0R r R <<(2 分) 2
24r
Q
E πε= )(R r >(2分)
5.题号:40843012 分值:10分
解答与评分标准:
(1)由高斯定理得电场分布:0
40
32
2
022
111=>=
<<=<E R r r
Q E R r R E R r πε (4分)
(2)电势分布:
⎰⎰⎰⎰⎰⎰⎰⎰∞∞∞∞∞=⋅=>-=⋅+⋅=⋅=<<-=⋅+⋅+⋅=⋅=<r
r R r R r R r R R R l d E U R r R r Q l d E l d E l d E U R r R R R Q l d E l d E l d E l d E U R r 0
)
1
1(4)
1
1(4322
02212
101122
1212
πεπε(4分) (3)两极板间的电势差:)1
1(42
1021
R R Q l d E U R R -=⋅=⎰πε (1分) 电容:1
22
104R R R R U Q C -==
πε (1分)
6.题号:40842020 分值:10分
(1).解答及评分标准:
2εσ
=
E (2分)
x dx l d E V p
a
x 0
0022εσ
εσ-==⋅=⎰⎰ (3分)
(2).解答及评分标准:
由高斯定理得电场分布:
40
32
2
022111=>=
<<=<E R r r Q E R r R E R r πε(2分)
两极板间的电势差:)11(42
102
1
R R Q l d E U R R -=⋅=
⎰
πε (2分)
电容:1
22
104R R R R U Q C -==
πε(1分)。
