第九章静电场中的导体与电介质
大学物理下 第九章 静电场中的导体和电介质5
2
ε0S C= d
四,静电场的能量 (1)电容器的能量 )
1 Q2 W = CU 2 = 2 2C
(2)静电场的能量 有电场的地方就有能量 )
1 ωe = D E 2
W = ∫ ωe dV
(3)静电场的能量与功的关系 )
A 静 = W
已知 ε r1 : ε r 2 = 1 : 2 ,问 W1 : W2 = ?
λ o d a
λ λ U = ∫ + dr 2πε0r 2πε0 (d r ) a -λ λ λ d a λ d = Ln ≈ Ln πε0 a πε0 a
λ λ πε 0 ∴ C0 = = = d d λ U Ln Ln a a πε 0
r
d a
P79 99 讨论
1)通电后维持电压不变插入电介质 ) 2)通电后断开再插入电介质 ) 讨论插入前后的 E,D,U,Q. , , , 令插入前为E , , , (令插入前为 0,D0,U0,Q0) 2) Q = Q 0
4a
UBA = UB∞
场具有球对称性
a
3a
解(1)a < r < 3a
∫∫ D dS = ∫∫ DdS = D4πr = QA
2 S S
Q
4a
a
QA D= 2 4πr
D QA E= = 2 ε0εr 4πε0εr r
3a
r > 4a ∫∫ D dS = D 4 πr = Q + Q A
2 S
Q + QA D= 2 4 πr
∫∫ D dS = Q0
S
E = E0 + E'
9-6,8 ,
E0
讨论 p79
-静电场的能量和能量密度

l
-+ - + R1 - + R2 -+
_
_ _ _
++ + _ + + _ + ++ _
_
R2 Eb R2 U max Eb R1 ln 9.10103 V R1 2 e
9 – 5 静电场的能量 能量密度
C, U, q, E 的变化。 ( 1 ) 充电后切断电源 (2)充电后不切断电源
9 – 静电场的能量 5 静电场的能量 能量密度 第九章静电场中的导体和电介质 例9-9 求半径为R 带电量为Q 的均匀带电球的静电能。 解一:计算定域在电场中的能量 球内 r 处电场
Qr E , 3 4 0 R (r R)
1 2 0 R Qr 2 4r dr W 0 E dV 0 3 2 2 4 0 R
第九章静电场中的导体和电介质
例 1.平行板电容器,其间充满介质 r , 求下列情况充入介质前后的
A
K 300V
E0
d
B
r
U Ed U0
(1)q不变 解 : 提示: (1)q不变
(2)U不变
C r C0 E
r
U (2)U不变 C r C0 E 不变 q CU r CU d S U 基本公式: C E d d q C C r C0 U
Q2 We 8π R1
(孤立导体球贮存的能量)
9 – 5 静电场的能量 能量密度
第九章静电场中的导体和电介质
例2 如图圆柱形电容器,中间是空气,空气的击 2 6 -1 穿场强是 Eb 310 V m,电容器外半径 R2 10 m. 在空气不被击穿的情况下,内半径 R1 ? 可使电容器 存储能量最多. ( 空气 r 1 )43; ++ _
第九章导体和电介质中的静电场

q3 0,
V1
1 4 0
( q1 R1
q2 R2
)
60(V ).
2.提示:未插金属板之前 E0
V d
,则选择题
2
可知两边场强,则所求金属
板的电势V
E
d 2
(E0
2 0
)
d 2
(V d
q )
2 0 S
d 2
V 2
qd 4 o S
。
3 . 提 示 :( 1 ) 据 有 介 质 时 的 高 斯 定 理 , 空 间 任 意 点 的
(1)系统静电能的改变。 (2)电场对电源作的功。 (3)外力对极板作的功。
参考答案 一、 选择题 1.(D) 2.(A) 3.(B) 4.(B) 5.(C) 6.(D) 7.(B) 8.(B) 9.(B) 10.(C)
二、填空题
1. 垂直于导体表面 0
q
2.
4 o R
3. r 一样
3.半径为 R0 的导体球带有电荷 Q,球外有一层均匀介质同心球壳,其内、外
半径分别为 R1, R2 ,相对介电常数为 r ,如图 18。求:
(1)介质内、外的电场 E 和电位移矢量 D。
(2)介质内的电板化强度 P 和表面上的极化电荷面密度 。
4.一平行板电容器极板面积为 S,间距为 d,接在电源上并保持电压为 V,若 将极板的距离拉开一倍,试求:
A
U
(Q2
Q1 )
U
2
(C2
C1 )
0S 2d
U
2
静电场中的导体与电介质

在静电场中平衡时: 1.内部电场强度不为零;2.电介质表面出现极化电荷
真空中的导体和电介质
P
pi
ΔV
P0eE
01
02
实验证
电 考 真空和P 偶 虑 中电c的介o 导质sS 极 一 P,体ln矩 电 pi, 0介 S 极 2质 l, 化 P 斜 0 . 极度定面 化:义V 圆 和 强:p 2i 电 柱 S 0 ,c荷 L So 体 明 各 性 介l0 : 向 质的 s密 在 同 中电co s度
此式对其它情况仍然适 用
D
义:电位移矢量D可, 得:D Dd0ESP S
q0
此既电介质中的高斯定理:通过电场中任意闭合曲面的电位移通量, 等于该闭合曲面所包围的自由电荷的代数和。
仿照电场线,用电位移线来描述电位移在空间的分布。但两者有 区别: 电场线起始于正电荷,终止于负电荷(包括极化电荷) 电位移线只起始于自由正电荷,终止于自由负电荷
在国际单位制中,D 的单位是: 库/米2(C/m2)
对各向同性电介质,因
所以 P0 eE
D 0EP 0 ( 1 ) E
式中 ε = ε0εr 叫电介质的介电常数, εr 称电介质的相对介电常数。
引入D,避免了求极化电荷的复杂问题,可使有电介质存在时解题简化。 只要有电介质,均应先求D 再求E 等。
E E0 E E0 与E 方 向 相 反 :
E
P
E0 // n
E
0 0
0
P cos
P
n
P
e 0E
E
E0
- E
10.4
E0 -
电介
质中0 静电E场0的-基本e
E
静电场中的导体和电介质

-
目录
静电场中的导体 和电介质
0
静电场中的导体和电介质
静电场中的导体和电介质
静电场是指在没有电流流动的情况下,电荷分布所产生的电场。在静电场中,导体和电介质 是两种不同的物质,它们的特性和作用也不同,本文将探讨导体和电介质在静电场中的性质 和应用 首先,我们需要了解导体和电介质的基本概念。导体是一种具有良好导电性能的物质,常见 的导体包括金属等。导体内的自由电子可以在外加电场的作用下移动,形成电流。而电介质 则是一种不良导电的物质,它的电导率远远低于导体。电介质在外加电场下无法形成连续的 电流,而是通过极化现象来响应电场的作用 在静电场中,导体和电介质的行为有很大的不同。对于导体来说,其特点是在静电平衡状态 下,内部电场为零。这是因为导体内的自由电子能够自由移动,它们会在外加电场的作用下 重新分布,直到达到平衡状态。这种现象被称为电荷运动的屏蔽效应。导体的另一个重要性 质是表面上的电荷分布是均匀的,这也是导体可以用来储存电荷的
与导体不同,电介质在静电场中的响应更加复杂。当外加电场作用于电介质时,电介 质分子会发生极化现象,即分子内部正、负电荷的分离。这种分离会导致电介质内部 产生电位移场,从而相应地改变电场分布。电介质的极化程度可以用极化强度来衡量 ,极化强度与外加电场的强度成正比。除了极化现象,电介质还可能发生击穿现象, 即在电场强度过高时,电介质内部的绝缘失效,导致电流的突然增加
0
静电场中的导体和电介质
导体在静电场中的一个重要应用 是电路中的导线。电路中的导线 由导体制成,它们能够有效地传 导电流。在电力系统中,导体连 接电源和电器设备,将电能传输 到目标地点。此外,在电子设备 制造中,导体用于制作电路板, 连接不同的电子元件,实现电信 号的传输和处理
9-(1-2)静电场中的导体

r
q
4 0 R1
q 4 0 r
(
1 R3
)
q
( R1 r R2 )
V2
1
4 0 R3
( ) 4 0 r R2 R3
q
1
q3
q2
q
R3
R2
第六章热力学基础 ( R2 r R3 )
V3 q 4 0 r
q 4 0 R3
R1 r
q 4 0 r
'
0
R1 R2 R2 R3 R1 R3
'
q2
'
R1 R3 R2 R3 R1 R2
q3 q q2
'
( R2 R3 R1 R3 )q R1 R3 R2 R3 R1 R2
q3 '
q2 '
q'
R1 r
第六章热力学基础 球壳内表面的电势:
V3
q1 4 0 r
第六章热力学基础 电压:在AB之间 1. 4产生的场强抵消,
2 . 3产生的场强相加,
(若 2 >0,电力线如图) 2 d 故:U AB Ed 0
a
d
a
X
若QA=-QB0
1 4
QA QB
QA QB 2S
0
2S
2 3
这时电场只集中在两板之间。
+++ ++
+
+
+++
< 避雷针 >
尖端放电现象的利用
2、空腔导体 1)腔内无带电体
静电场中的导体与电介质

§2 静电场中的导体和电介质§2-1 静电场中的导体1. 导体的静电平衡条件当电荷静止不动时,电场散布不随转变,该体系就达到了静电平衡。
在导体中存在自由电荷,它们在电场的作用下可以移动,从而改变电荷的散布……导体内自由电荷无宏观运动的状态。
导体的静电平衡的必要条件是其体内图2-1导体的静电平衡场强处处为零。
从静电平衡的条件动身可以取得以下几点推论:推论1)导体是等位体,导体表面是等位面:2)导体表面周围的场强处处与它的表面垂直:因为电力线处处与等位面正交,所以导体外的场强必与它的表面垂直。
(注意:本章所用的方式与第一章不同,而是假定这种平衡以达图2-2导体对等位面的控制作用到,以平衡条件动身结合静电场的普遍规律分析问题。
)2.电荷散布1) 体内无电荷,电荷只散布在导体的表面上:当带电导体处于静电平衡时,导体内部不存在净电荷(即电荷的体密度)电荷仅散布在导体的表面。
可以用高斯定理来证明:设导体内有净电荷,则可在导体内部作一闭合的曲面,将包围起来,依静电条件知S面上处处, 即由高斯定理必有q=02) 面电荷密度与场强的关系:当导体静电平衡时,导体表面周围空间的 与该处导体表面的面电荷密度 有如下关系:论证: 在电荷面密度为 的点取面元设 点为导体表面之外周围空间的点,面元。
充分小,可以为 上的面电荷密度 是均匀的,以为横截面作扁圆柱形高斯面(S ),上底面过P 点,把电荷q= 包围起来. 通太高斯面的电通量是:3) 表面曲率的影响、尖端放电导体电荷如何散布,定量分析研究较复杂,这不仅与这个导体的形状有关,还和它周围有何种带电体有关。
对孤立导体,电荷的散布有以下定性的规律:图2-3导体表面场强与电荷面密度曲率较大的地方(凸出而尖锐处),电荷密度e 较大;曲率较小的地方(较平坦处)电荷密度e 较小;曲率为负的地方(凹进去向)电荷密度e 更小。
1) 端放电的利和弊3 导体壳(腔内无带电体情况)大体性质:当导体壳内无带电体时,在静电平衡当导体壳内无 带电体时,在静电平衡下:导体壳内表面上处处无电荷,电荷仅散布在外 表面;空腔内无带电场,空腔内电位处处相等。
静电场中的导体和电介质教学教案

第九章 静电场中的导体和电介质1、D分析:带电导体达到静电平衡时0=内E ,导体为等势体,导体表面的电场强度垂直于导体表面;2、B分析:两金属球用细长导线相连成等势体,由于是细长导线,可视为两孤立的导体球,孤立导体球的电势)0(=∞U 242400=⇒=qQ r qr Qπεπε 3、C分析:因为金属球不带电,当在其下方放置一电量为q 的点电荷时,只有当金属球下方感应异号电荷后金属球内的电场强度才可能为零,必定可以看到金属秋下移的现象;4、B直接应用两等大的金属平板带电的分布规律: SQ Q S Q Q S Q Q B AB A B A 2,2,23241--=-=+==σσσσ 依据上式有:2,212σσσσ-==5、D 均匀带电球面的电场强度公式为:204R QE πε= m R E Q R 3689021********.11094--⨯=⇒⨯⨯⨯⨯==πε 6、C有介质时的高斯定理为:E D q S d D r S εε00,==⋅⎰∑选项A :E 是空间点和产生的,如果高斯面内没有自由电荷,但是外部可能有电荷,一般而言,E 不为零,故D 也不为零;选项B :两同心球壳上带等量异号电荷后,再做一个同心的大球面为高斯面,因为0=E 则高斯面上0=D ;选项C :从高斯定理可以解出高斯面的D 通量仅仅与面内的自由电荷有关;7、B依据等效电容的规律: 212121,111C C C C C C C C +=+=若中1C 插入r ε的电介质,则11'C C r ε=,且1>r ε,即1C 的电容增大;总电容: C C C C C C C C C C r>+=+=ε21212121'''8、B电容器充电后,断开电路,基板上的电荷量不变,然后充满电介质,有:0C C r ε=,电容增大;r U U ε0=,电压减小; ,2121022C q C q W r ε==能量减小; 9、B在q 不变的条件下,已知02021C q W =,充满电介质后,0C C r ε=, rr W C q C q W εε00222121=== 10、rE r D r επελπλ02,2== 应用有介质时的高斯定理:⎰∑=⋅s q S d D 0在两同轴圆柱之间取一半径为r 的单位长度同轴圆柱面为高斯面,λπ===⋅⎰⎰rD DdS S d D s 2侧面∴rE r D r επελπλ02,2== 11、)(21B A Q Q s q -==σ,d Q Q S U B A AB )(210-=ε 应用静电平衡的结果:S Q Q S Q Q S Q Q B A B A B A 2,2,23241--=-=+==σσσσ )(21,2B A B A Q Q s q S Q Q -==-=σσ A 、 B 间为均匀电场,场强为:)(2100B A Q Q SE -==εεσ 电势差:d Q Q S Ed U B A AB )(210-==ε12、SQ Q S Q Q S Q Q B AB A B A 2,2,23241--=-=+==σσσσ 应用电荷守恒原理:121Q s s =+σσ243Q s s =+σσ在AB 板内取一点p,该点的0=E , 0222204030201=---εσεσεσεσ 在CD 板内取一点o,该点的0=E , 0222204030201=-++εσεσεσεσ 由以上四个式子可以解出: SQ Q S Q Q S Q Q B AB A B A 2,2,23241--=-=+==σσσσ 13、CdF 2 ,CdF 2 两极板间的相互作用力为一个极板在另外一个极板上产生的电场强度求,该极板上的电量为q : d SC S q q qE F 0020,22εεεσ==⋅== CdF q CdF SF q 22202=⇒==ε CdF C q U 2==∆ 14、dsU 22120ε 依据能量公式:dsU CU C Q W 22121212022ε=== 15、41,161 16、c q c q 9291103.13',1067.6'--⨯=⨯= ,V 3100.6⨯分析:两个导体球相连后成为一个等势体,由于两球相距很远,可以看做孤立的导体球,导体球的电势为:r QU 04πε=,.0.2,0.1,100.111821cm r cm r c q q ==⨯==- 2021014'4'r q r q πεπε=, 2121''q q q q +=+ 解得:c q c q 9291103.13',1067.6'--⨯=⨯= V r q U 3101100.64'⨯==πε17、)()(122112r R R Q R Q R r q ++= 原来不带电的导体球与半径为1R 的导体球壳相连后,导体球带电为q,半径为1R 的导体球壳带电为q Q -1,根据电势相等的条件有: rq R Q R q Q 020*******πεπεπε=+- 化简得:rq R Q R q Q =+-2211 )()(122112r R R Q R Q R r q ++=18、RQ πε82R UQ C R QU πεπε4,4=== RQ C Q W πε82122== 应用积分法:422223221,4rQ E r Q E m επεωπε=== dr r Q dr r r Q dV dW m 2224228432πεπεπω=== R Q r dr Q dW W R πεπε88222===⎰⎰∞ 19、J J 16.0,32.0电容串联后的等效电容:F C C C C C μ322121=+= c CV q 4610810120032--⨯=⨯⨯== J C q W 32.010)108(2121624121=⨯⨯⨯==- J C q W 16.010)108(4121624222=⨯⨯⨯==- 20、1dq R q04πε 2R Q 028πε解:1当球上已带有电荷q 的条件下,外力将dq 从无穷远移动到球上时,外力做的功为: ∞→→∞=R R dW dW 电外)]()([R E E p p -∞-=)(R E p = )(R dqU = dq R q04πε= 2 R Q Q R dq q R dW W Q 022*********πεπεπε=⨯===⎰⎰外外21、利用电势相等来解; b Q a Q ba0044πεπε=Q Q Q b a =+由以上两式可以解得: ba bQ Qb a aQ Q b a +=+=, U Q U Q Q C b a=+=dq)(4414000b a Q b a Qa a a Q U a+=+==πεπεπε ∴)(40b a C +=πε。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 静电场中的导体与电介质 1第九章 静电场中的导体与电介质§9-1 导体和电介质【基本内容】一、导体周围的电场导体的电结构:导体内部存在可以自由移动的电荷,即自由电子。
静电平衡状态:导体表面和内部没有电荷定向移动的状态。
1、导体的静电平衡条件(1)导体内部场强处处为零0=内E; (2)导体表面的场强和导体表面垂直。
2、静电平衡推论(1) 静电平衡时,导体内部(宏观体积元内)无净电荷存在; (2) 静电平衡时,导体是一个等势体,其表面是一个等势面。
3、静电平衡时导体表面外侧附近的场强εσ=E4、静电平衡时导体上的电荷分布(1) 实心导体:电荷只分布在导体表面。
(2)空腔导体(腔内无电荷):内表面不带电,电荷只分布在导体外表面。
(3)空腔导体(腔内电荷代数和为q ):内表面带电q -,导体外表面的电荷由电荷的守恒定律决定。
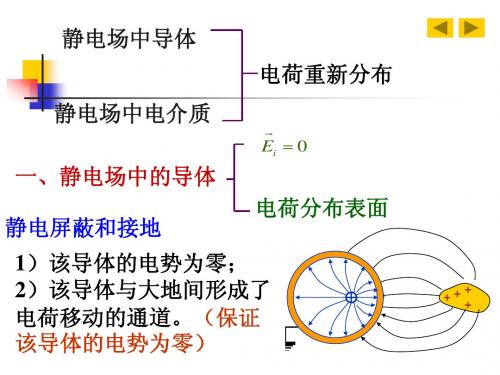
5、静电屏蔽导体上电荷分布的结果,使空腔内部电荷的运动不影响导体外部的电场;导体外部电荷的运动,不影响导体空腔内部的电场。
二、电介质与电场1、电介质的极化(1)电介质的极化:在外电场作用下,电介质表面和内部出现束缚电荷的现象。
(2)极化的微观机制电介质的分类:(1)无极分子电介质——分子的正、负电荷中心重合的电价质;(2)有极分子电介质——分子的正、负电荷中心不重合的电介质。
极化的微观机制:在外电场作用下,(1)无极分子正、负电荷中心发生相对位移,形成电偶极子,产生位移极化;(2)有极分子因有电偶矩沿外电场取向,形成取向极化。
2、电介质中的电场 (1)电位移矢量E Dε=其中ε——介电质的介电常数,0εεεr =,r ε——介电质的相对介电常数。
(2)有电解质时的高斯定理∑⎰=⋅0q S d D S,式中∑0q 指高斯面内自由电荷代数和。
【典型例题】【例9-1】三个平行金属板A 、B 和C ,面积都是200cm 2,A 、B 相距4.0mm ,A 、C 相距2.0mm ,B 、C 两板都接(1)求B (2【解】(1A 板的电位为U 即所以221212σσσ==d (3)将(3)式代入(1)式,得S Q /31=σ(4)由(4)式可求得B 板上的感应电荷为C Q S Q 7110.13/-⨯-=-=-=σ同理可得C 板上的感应电荷为C Q S Q 7220.23/2-⨯-=-=-=σ(3)由(2)式可求得A 板上的电位为V d SQd d E U A 310101111025.23⨯====εεσ 【讨论】导体接地的含义主要有两点:(1)导体接地后与地球同电势,一般定义为电势零点。
(2)带电导体接地,接地线提供了与地球交换电量的通道,至于电荷向哪流动,取决于导体接地前的电势是高于大地,还是低于大地。
当导体的电势高于大地时,接地后将有正电荷由导体流向大地,直到导体与大地电势相等为止。
【例9-2】 半径为R ,带电量为q 的金属球,浸于相对介电常为εr 的油中。
求: (1) 球外电场分布。
(2) 极化强度矢量。
(3)金属球表面油面上的束缚电荷和束缚电荷面密度。
【解】 (1)求电位移矢量 取半径为r 的球面为高斯面,则第九章 静电场中的导体与电介质 3(2由介质性质方程(3∧-=-=r r q E P r r r204)1()1(πεεεε(4)求束缚电荷及束缚面电荷密度2/4)1(cos rq P P n P r r πεεθσ--=-==⋅=q r dS r q S d r r q S d P q r S r r S r r )11(4)1(4)1(222'-=-=⋅--=⋅-=⎰⎰⎰∧επεεπεε 【讨论】电介质问题求解方法:所涉及的物理量:q P E D '',,,.,σ求解方法:(1)求电位移矢量∑⎰=⋅0q S d D S,(2)求电场强度E ED rεεε==0,(3)求极化强度矢量E P r )1(0-=εε,(4)求束缚电荷面密度θσcos /P n P =⋅= ,(5)求束缚电荷⎰⋅-='S d P q 。
【分类习题】【91】 大小为25C N /提示:将地球【9-2】 为0E 图7-2【9-3】 分别带电1Q 和2Q (1) 求A 、(2) 如【9-4】有两块面积均为S 的相同金属板,两板间距离为d ,S d <<2,其中一块金属板带电量为q ,另一块金属板带电量为q 2,求两板间的电势差。
【9-5】在半径为R 的金属球之外包有一层均匀介质层,介质层的外半径为/R 。
设电介质的相对介电常数为r ε,金属球带电为Q ,求: (1) 介质层内外的场强分布; (2) 介质层内外的电势分布。
§9-2 电容 电容器【基本内容】一、孤立导体的电容:表征导体容电能力的物理量。
Uq C =二、电容器及其电容实际孤立导体是不存在的,导体周围有其它物体时,其电势将发生变化,从而其电容随周围物体的性质而变化。
电容器的电容:BAU U q C -=电容器中一般充满电解质,电解质的作用有两个: (1) 增大电容;(2) 增强电容器的耐电压能力。
三、电容器的串联与并联串联:nC C C C111121++= 并联:n C C C C ++=21四、常见电容器的电容1、平行板电容器的电容 dS C r εε0=2、球形电容器的电容122104R R R R C r -=επε3、柱形电容器的电容 )/ln(2120R R L C r επε=五、电场的能量1、电容器的储能222121CU C Q W ==第九章 静电场中的导体与电介质 52、电场的能量、能量密度电场的能量密度:E D E e ⋅==21212εω 电场的能量:⎰=V e dV W ω【典型例题】【例9-3】平行板电容器(极板面积为S ,间距为d )中间有两层厚度各为1d 和2d 的均匀介质,介电常数分别为1ε和2ε,如图例7-3法一;按定义设极板带自由电荷Q ,大小SQD =别为S Q E 11ε=和E 1=势差为21212211d E d E U =+=按定义122121εεεεd d S U QC +==法二:按电容器的连接将整个电容器看成两个充满介质1ε和2ε的电容器的串联,两个电容器的电容分别为111d SC ε=,222d SC ε=由串联公式21111C C C += 可求得上面答案。
按定义求电容的方法:(1)设两极板分别带电+q 、-q ,(2)求两极间的电场,(3)求两极间的电势差,(4)求电容。
【例9-4】 求半径为R 。
、体电荷密度为ρ的均匀带电球体的静电能。
【解】 以半径为r 的球面为高斯面,则:24r E S d E Sπ⋅=⋅⎰⎰当r>R 时:∧==∑rr R E R q2033334ερρπ内当r<R 时:∧==∑rr E r q3334ερρπ内电场能量密度: 221E e εω=当r<R 时:02218ερωr =当r>R 时:406218r R ερω=电场能量5202462020220154418418R dr r r R dr r r dVdV dV W R RRR e ρεππερπερωωω=⋅+⋅=+==⎰⎰⎰⎰⎰∞∞0r(2)保持极间电压不变时221CU W =第九章 静电场中的导体与电介质 7抽出电介质前: 202112121U d S U C W r εε== 抽出电介质后: 202222121U dS U C W ε==电容器储能的改变量:0)1(22012<-=-=∆r dSU W W W εε电介质抽出后,极板电量改变:0)1(012<-=-=∆r dSUU C U C Q εε电源作功:0)1(20<-=∆=r dSU QU A εε电源由能量守恒定律:)1(20>-=-∆=⇒∆=+r dSU A W A W A A εε电源外电源外【分类习题】【9-6】平行板电容器电容pf C 100=,面积2100cm S =,两板间充满相对介电常数为=r ε6的云母片,将它接到V 50电源时,求:(1) 云母片中场强大小; (2) 导体板上自由电荷。
【9-7】来顿瓶是一内外贴有金属膜的圆柱形玻璃瓶。
设玻璃的相对介电常数为 5.0,击穿电场为m V /105.17⨯。
如玻璃瓶内径为cm 8,玻璃厚为mm 2,金属膜高为cm 40。
求:(1) 来顿瓶的电容。
(2)它最多能储存多少电量?(提示:内径处最先达到击穿电场)。
【9-8】两根无限长平行直导线相距为d ,半径均为R ()d R <<。
求该导体组单位长度的电容。
【9-9】分子的正负电荷中心重合的电介质叫做 电介质,在外电场的作用下,分子的正负电荷中心发生相对位移,形成 。
【9-10】当平行板电容器板间为真空时,其电容为0C ,板间场强为0E,电位移为0D 。
(1)如两板与一端电压相连,再充满相对介电常数为r ε的电介质,则电容为 ,场强为 ,电位移为 ;(2)如充电后将电源断开,再充满(1)中电介质,则电容 为,场强为 ,电位移为 。
【9-11】平行板电容器极板间充满相对介电常数为r ε的电介质,若极板上自由电荷面密度为σ,求电介质的电位移和场强。
【9-12】 电容器1和2串联后充电。
(1)保持连接电源,在电容器1中充满电介质,则电容器2上的电势差【9-22】 相距甚远的、半径均为cm 10的两导体球,分别充电至V 200和V 400,然后用一细导线连接使其电势相等。
求等势过程静电力的功。
【9-23】 空气平行板电容器,极板面积为S ,两极板间距为d ,如极板间电势差为U 。
求两极板间引力。
【9-24】 电容为C 的空气平行板电容器,极板间距为d ,充电后极板间作用力为F ,求: (1) 极板间电势差;(2)极板上电荷量。
分类习题答案【9-1】 (1)正电荷,210313/1085.8).2(,/104.4m C m C --⨯⨯【9-2】 00002,2εσεσ+-E E 图7-3Q1Q 2BDC图7-14图7-15(a )AB C第九章 静电场中的导体与电介质 9【9-3】0,,,0;2,2,2,21121122121SQ S Q S Q Q S Q Q S Q Q S Q Q -+--+【9-4】S qd02ε 【9-5】 (1))(0R r <,)(4/20R r R rQ r <<επε,)(4/20R r rQ >πε(2))(4)11(4/0/0R r R Q R R Q r<+-πεεπε,)(4)11(4//0/0R r R RQR r Q r <<+-πεεπε,)(4/0R r rQ >πε【9-6】 (1)m V /1042.93⨯ (2)C 9105-⨯【9-7】 F 91028.2-⨯,C 5107.6-⨯【9-8】 Rd ln 0πε【9-9】 无极,偶极子【9-10】 000,,D E C r r εε,000,/,D E C r r εε【9-11】 r εεσσ0,【9-12】 (1)增加,增加。
