四色定理证明(王)
四色定理数学证明过程

四色定理数学证明过程“四色定理”是指,由Kempe于1879年提出,即任意一个地图只需要四种颜色来涂色,就可以保证相邻区域颜色不同。
在过去的几十年中,数学家一直在努力寻找证明“四色定理”的正确方法。
在1976年,法国数学家A. Appel和W. Haken终于证明了“四色定理”的正确性。
本文将分享一下“四色定理数学证明”的过程。
证明“四色定理”的方法是“规约法”。
即将“涂色问题”转化为一些计算机可以处理的图论问题,然后通过算法求解。
步骤一:将“涂色问题”转化为图论问题首先要把“涂色问题”转化为一些计算机可以处理的图论问题。
通过数学家Halstead的研究,人们发现只需要涂四种颜色的是那些“好”的地图,将其进行编码,最终将地图还原成图。
这里的“好”的地图指的是那些没有的海岸线被其它地图穿过的地图。
步骤二:将“图论问题”转化为无矛盾的有限数学问题其次,将图论问题转化为有限的概率问题。
通过构建一个叫做“网格图”的数据结构,将图论问题通过计算概率,可以变成一个有限的数学问题。
然后通过数学的力量,我们可以证明这个数学问题是有解的。
这个证明过程中涉及到多项式定理、双射、图的对称性等。
步骤三:验证证明的正确性最后,通过计算机程序验证证明的正确性,确保其结果无误。
这个过程还涉及到超过1200页的论文撰写和审核,以及超过100万行的计算机程序代码,所有的证明过程都由计算机来完成。
总结作为一个数学难题,“四色定理”的证明让人们深入感受到数学的魅力。
它不仅仅让我们了解到了数学的应用价值,而且让人们更好地理解了数学这个学科本身的精或。
通过“规约法”,我们成功将这个看似无从下手的问题转化为计算机可处理的图论问题,最终证明了“四色定理”的正确性,为人类解决了一个具有重要实际意义的问题。
四色定理的初等证明

探索四色定理的数学证法一四色定理每幅㊣ (正规地图。
公认的定义见附图注)至多需要四种色能使相邻国着不同色。
它从1852年问世至今尚未获得数学证明。
二定理定义引理肯普定理:每幅㊣至少有一国有两、三、四或五个邻国,无每一国都大于五个邻国的情形。
按此,㊣可分为二构形、…、☆(五构形)四种情形。
定义:1-对各种构形,称邻国数最少的国家为构形国。
2-(可)约定㊣所有国家连成一片内部无空区域,则称内部和外部的界线(简单闭曲线)为㊣边界。
3-国B一段边界或一点在㊣边界上,则称B为边沿国。
4-一些国家包围了其它国家,则称这些国家形成的环为圈。
引理1:☆的国家数的集W={12,14,15,…,n,…}。
证:构造无穷多“四圈”☆。
类似图1的☆,内外圈各一国,中间两圈上取数列6,7,…,m,…(m≥6)⑴中的同一项,得国家数由大于12的偶数组成数列14,…,2(m+1),…⑵;虚线将P分成两国,得国家数由大于13的奇数组成数列15,…,2m+3,…⑶。
合并数列⑵⑶及12得到所有☆的国家数的集W={12,14,15,…,n,…}。
易验证1—13中仅12有☆。
除12外W中每个n所对应☆不同结构的个数复杂程度无论如何,皆视为由“四圈”☆演变而成。
引理2:任意☆中存在构形国不是边沿国。
证:假设命题不成立,则有一个☆G,使得构形国都是边沿国。
因平面地图与球面地图等价,故可使G的以边沿国形成的圈T在球面上并把球面分成对称的两部分。
令每部分被T包围的国家S对称地布满,示意如图2。
由此知T上每一国的邻国数(原来不一定都是五)都大于七,其余国家的邻国数都大于五,就得到一幅(STS)每一国的邻国数都大于五的㊣。
与肯普定理矛盾,故G不存在。
即任意☆中存在构形国不是边沿国。
引理3:在n≥15的☆中,若包围构形国Q的每个邻国与Q只有一条共同边界,Q 的邻国两两相邻的组数是五,这五个邻国中存在邻国数大于五的国家,则□(四色定理成立)。
证:若☆每一国的邻国数都是五,由欧拉公式知n=12。
四色定理的证明范文

四色定理的证明范文一、四色问题的简介根据网络上的一些内容,可知:四色猜想是说,任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。
也就是说,在不引起混淆的情况下,一张地图只需四种颜色来标记就行。
用数学语言来说就是,将平面任意地细分为不相重叠的区域,每一个区域总可以用1234这四个数字之一来标记而不会使相邻的两个区域得到相同的数字。
简单来说也就是,给平面或球面上的任意一张地图上色,使得相邻国家异色,那么至少需要预备几种颜料几种颜色?是否可以只预备四种颜色?在长期的论证过程中,人们发现,大量的试涂表明,四种颜色够用。
人们证明,三种颜色是不够用的,五种颜色肯定够用,四种颜色也够用(计算机证明)。
人们还证明,二维平面内无法构造五个或五个以上两两相邻区域。
在四色问题中假设相邻关系是指两个国家有一段或多段共同边界,是指有邻边,不是指有邻点。
假设没有公地,所有国家都直接接壤(分别相邻),或者间接接壤(分别相连)。
假设没有飞地,国土连通。
飞地相当于任意指定一些他国属于国,则四色肯定不够用了。
假设国家的面积都足够大,不是一丁点、一个点。
假设国家的数量有限,不是无限多。
假设国家的形状任意。
这可以是五花八门,变化莫测,花样繁多,譬如像麋鹿的剪影:在四色问题中需要考虑任意地带的上下方面的相邻情况,左右方面的相邻情况,内外方面的相邻情况,首尾衔接(例如圆周中)的相邻情况,跨越跳跃(例如国形状像拱桥、麋鹿、藤蔓、交际花,与诸多位置的国家们接壤)着的相邻情况,等等。
需要考虑各国的排序,需要考虑上色的顺序。
因为许多国家相邻相连,交织交错,来来往往,层层叠叠,那么从多个方向来上色的话,齐头并进来上色的话,就会互相遭遇、碰头,在交汇点上可能发生冲突,难以协调、确定国的颜色,使得问题复杂,影响证明的进行。
二、四色定理的证明一个平面或球面上的点是无限小、无限多,或者是足够小、非常多。
令这些点各自随机选择红黄蓝三色的一种,再做布朗运动。
四色定理的简短证明

四色定理的简短证明四色定理的简短证明虽然我们用计算机证明了四色定理,但正如汤米·R·延森和比雅尼·托夫特在《图染色问题》一书中问的:“是否存在四色定理的一个简短证明,……使得一个合格的数学家能在(比如说)两个星期里验证其正确性呢?”四色定理是一个著名的数学定理:如果在平面上划出一些邻接的有限区域,那么可以用四种颜色来给这些区域染色,使得每两个邻接区域染的颜色都不一样;另一个通俗的说法是:每个地图都可以用不多于四种颜色来染色,而且没有两个邻接的区域颜色相同。
进入20世纪以来,科学家们对四色猜想的证明基本上是按照肯普的想法在进行。
自从引入“构形”,“可约”概念后,逐步发展了检查构形以决定是否可约的一些标准方法,能够寻求可约构形的不可避免组,是证明“四色问题”的重要依据20世纪80-90年代中国曾邦哲从系统论观点(结构论)将其命题转换为“四色定理”等价于“互邻面最大的多面体是四面体”的问题,也就是点之间相互的联线超过3的是立体,而每增加一个点或表面时必然分割一条线或一个面,也就使分割开的不互邻面或联线可以重复使用一种颜色;因此,增加一个面同时也增加一次可重复使用同一种颜色。
拓扑学的概念来定义拓扑学拓扑学如果在平面上划出一些邻接的有限区域,那么可以用四种颜色来给这些区域染色,使得每两个邻接区域染的颜色都不一样;:每个地图都可以用不多于四种颜色来染色,而且没有两个邻接的区域颜色相同。
;x大于1为偶数的时候,y=2.四色定理成立的公式为,y定,表示所需的颜色总数,y表示任何一个国家与之接壤的国家个数x与需要颜色y的关系,y定=y+1.y最大值为3,所以y定最大值是4.以上如果正确,或许对于数学的进步也是一种阻碍。
以上的论证,我自己都感到过于简单,并且没有用到拓扑学,对于是否能够证明四色定理,欢迎大家的参与。
2013年12月31日16:59:41吴兴广参考文献:[1]四色定理百度百科【2】《数学公式1+1=1/2的成立》小马吃鱼。
四色定理的理论证明

个顶点看作一个顶点,得到与<b-ii>中讨论相
同的情形,因而这种情况下 G 是 4-可着色的。
因此我们剩下的问题是着相同颜色的二顶点
不挨着的情况。
不妨假设,按逆时针方向绕着 v 的顶点是
(图二)
v1 v2 v3 v4 v5,其中 v1 v3 着相同颜色 c1 ,v2 着 色 c2, v4 着色 c3,v5 着色 c4。(图二)
(3) 由图<4>知:v 1∈extC2,v 4∈intC2,圈 C2 由颜色 c2 c4 着其顶点(v 无 色除外)。因为 v1 v4 着色 c1 c 3,用 c1 c 3 着色的顶点产生子图 H9,所以 v1 v4 必然属于 H9 的不同分支。同样,v3∈intC2,v1 v3 属于 H9 的不同分支。 在 v1 所在的分支上交换颜色 c1 c3,而不影响 G-v 的正常着色。使 v1 着 色 c3。同样,v3∈extC1,v5∈intC1。用 c1 c4 着色的顶点产生子图 H10,H10 包含 v3 v5,因为圈 C1 由色 c2 c3 着其顶点(v 无色除外),所以 v3 v5 属于 H10 的不同分支,在 v3 所在的分支上交换色 c1 c4,而不影响 G-v 的正常 着色,使 v3 着色 c4。这样,我们使 v1 v4 着色 c3,v2 着色 c2,v3 v5 着色 c4, 余下的色 c1 给 v 着色。这样,对于情形<4>我们再次得到 G 的一个 4-着 色法。
着色,我们来证明存在 4-着色法,使得 G 可 4-着色。
a). 如果和 v 邻接的顶点上所使用的颜色少于 4 种,那么只要用余下的任一
种颜色给 v 着色,便可以得到 G 的一个 4-可着色法。
b). 与 v 邻接的顶点着满 4 种颜色,因为有 deg(v) ≤5,所以存在与 v 邻接
四色定理的简单证明
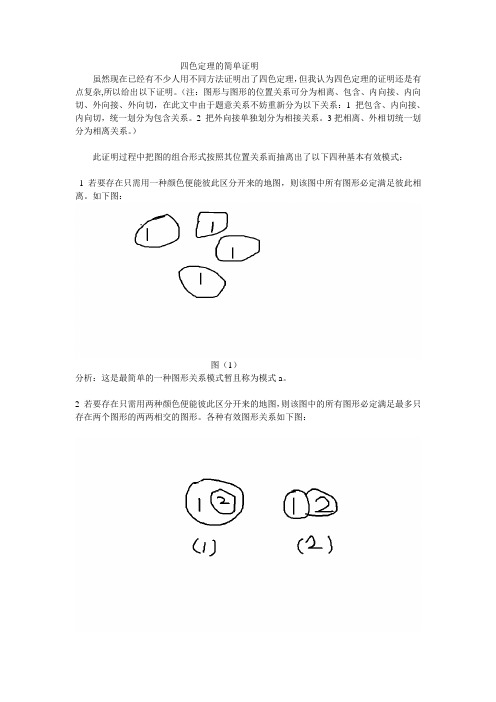
四色定理的简单证明虽然现在已经有不少人用不同方法证明出了四色定理,但我认为四色定理的证明还是有点复杂,所以给出以下证明。
(注:图形与图形的位置关系可分为相离、包含、内向接、内向切、外向接、外向切,在此文中由于题意关系不妨重新分为以下关系:1 把包含、内向接、内向切,统一划分为包含关系。
2 把外向接单独划分为相接关系。
3把相离、外相切统一划分为相离关系。
)此证明过程中把图的组合形式按照其位置关系而抽离出了以下四种基本有效模式:1 若要存在只需用一种颜色便能彼此区分开来的地图,则该图中所有图形必定满足彼此相离。
如下图:图(1)分析:这是最简单的一种图形关系模式暂且称为模式a。
2 若要存在只需用两种颜色便能彼此区分开来的地图,则该图中的所有图形必定满足最多只存在两个图形的两两相交的图形。
各种有效图形关系如下图:图(2)分析:两个图形的两两相交的所有图形关系均可变形而得出等价的以上两种图形关系模式之一。
由于图(1)存在包含关系,被包含的图形是对外部无影响的,所以图(1)仍属于模式a。
所以两个图形的两两相交只有图(2)的相交关系模式的图形有效的,我们暂且称之为模式b。
3 若要存在只需用三种颜色便能彼此区分开来的地图,则给图中所有图形必定满足最多只存在三个图形的两两相交图形。
各种有效图形关系如下图:图(3)分析:三个图形的两两相交的所有图形关系均可变形而得出等价的以上两种图形关系模式之一。
由于图(2)属于存在包含关系,同理整体回归于模式a。
所以三个图形的两两相交只有图(1)的相接关系模式的图形是有效图形模式,我们暂且称之为模式c。
4 若要存在只需用四种颜色便能彼此区分开来的地图,则给图中所有图形必定满足最多只存在四个图形的两两相交图形。
各种有效图形关系如下图:图(4)分析:四个图形的两两相交的所有图形关系均可变形而得出等价的以上两种图形关系。
由于图(2)属于存在包含关系,同理可得出整体也就回归于图形模式a。
四色猜想的证明

四色猜想的证明四色猜想的内容是:如果把地图上有共同边界的国家涂成不同颜色,那么只需要4种颜色就足够了。
要证明四色猜想,首先需要定义一些新的概念:1、国家的表示法——点由于该猜想的内容中不涉及与国家形状有关的问题,而只涉及国与国之间的相邻关系,因此任何一个国家都用点来表示。
2、相邻与不相邻在叙述时,用符号“=”表示相邻,用“#”表示不相邻,如果用图示法表示相邻与不相邻则要复杂一些,先看下图:(a)(b) (c)图1在图1(a)与(b)中,分别用了直线和曲线连接两个国家A和B,表示国家A与B相邻,为了简便起见,这里只用直线表示相邻,图1(c)中是已知A与B相邻,叫你判断C 与D能否相邻,连接CD、CD与AB相交,相交是否就是不相邻呢?我们先看一组图:图2图2是把图进行等分后的结果,从三等分开始,如果每一份代表一个国家,这表示等分后的所有国家相聚于一点,从四等分后的国家A 、B、C、D可知,如果国家之间点的接触算是相邻,则A与B,C与D都为相邻,显然这时的A与B,C与D是交叉相邻,与图1(c)中的情况相同,此时A与B,C与D的交点表示接触点。
若点的接触不算相邻,那么连接A与B的直线可以看作一道墙,在这中间不能有任何直线通过。
因此,由于C与D的连线与AB相交,据此判断出C与D不能相邻。
但是当相邻用曲线进行表示,C与D却能够相邻,这是否说明用直线表示相邻有问题呢?当然不是,仔细分析就可以发现,用曲线表示相邻同样不能有相交的情况出现,因此,用直线表示相邻时,适当移动C或D的位置就可以使C与D相邻。
3、完全相邻这是一个关键问题,可以这么说,没有这一概念的证明都是伪证明,现在给出完全相邻的定义:在一个面上(可以是平面也可以是曲面)给定N个国家,如果这N个国家两相邻,那么我们就称这N个国家完全相邻。
由于1个国家没有相邻关系,因此上面的N要求要大于1。
如果是3个国家完全相邻,它们的相邻关系为:(这三个国家分别设为1、2、3)1=2,1=3,2=3有了以上这些概念之后,就有了证明四色猜想的基础。
四色定理证明

四色定理证明
四色定理的内容是:在平面内任意分割区块,只用四种颜色就能保证所有相邻的区块不同色。
证明:
设有五种不同的颜色,把它们看作5个点,连实线代表两颜色相邻,连虚线代表两颜色不相邻,所以不可能有两个实线交叉。
如果这五个点两两连实线并且无交叉(总假设),则四色定理不成立。
下面来证明这种情况不可能发生:
方法/步骤
1
我们先看三个点的情况:
2
此时,添加第四个点D有两个情况:三角里面或三角外面。
观察发现,两个图的本质是一样的。
3
再添加第五个点E,也是大三角形内外两种情况,但发现无论如何会有一条虚线,
所以,总假设不成立,即四色定理成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
王若仲 (王洪)
贵州省务川自治县实验学校 贵州 564300
摘要:1852 年,毕业于伦敦大学的格斯里(FrancisGuthrie)来到一家科研单位搞地 图着色工作时,发现每幅地图都可以只用四种颜色着色。这个现象能不能从数学上加以严格 证明呢?1872 年,英国当时最著名的数学家凯利正式向伦敦数学学会提出了这个问题,于 是四色猜想成了世界数学界关注的问题,世界上许多一流的数学家都纷纷参加了四色猜想的 大会战。电子计算机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了 对四色猜想证明的进程。1976 年 6 月,由美国数学家阿佩尔(Kenneth Apprl)和哈肯 (Wolfgang Haken)在美国伊利诺斯大学的两台不同的电子计算机上,用了 1200 个小时, 作了 100 亿次判断,结果没有一张地图是需要五色的,最终证明了四色定理。我发现“四色 定理”还有一种简捷的证明方法,就是利用球面几何的知识来证明“四色定理”。也就是要 证明在球面上不能设计出这样的组合图形:五个独立封闭图形 A、B、C、D、E,任意两两独 立封闭图形均有公共边界,并且组合图形中不会出现有独立封闭图形与独立封闭图形重合或 者出现独立封闭图形与独立封闭图形部分重叠的情形。证明的方法就是把球面上的点看作是 独立封闭图形,球面上点与点之间的连线段看作是独立封闭图形与独立封闭图形的公共边 界。什么是独立封闭图形?就是指平面上或球面上一个封闭图形,如果这个封闭图形内没有 其它的封闭图形,我们则称这个封闭图形为独立封闭图形。什么是直接连接?就是指平面上 或球面上点与点之间的连线段,除了连线段的两边端点外,中间不经过其它的已知点,中间 不与其它的连线段相交。
(二)我们按照一定的次序总可以在球面上先直接连接 EA,直接连接 EB, 直接连接 EC,直接连接 ED;接下来还可以直接连接 AB,直接连接 BC,直接连接 CD,直接连接 DA;再可以直接连接 AC;最后连接 B 点和 D 点的时候,我们还是 要求直接连接,但是从前面得到的球面组合图形中不难得出这样的结论:最后连 接 B 点和 D 点,要求中间不能经过其它已知点,那么连接 BD 使终要经过一个封 闭的图形,所以按照此要求不管怎样连接,必定会多出一个交点。所以按照要求 直接连接 EA,直接连接 EB,直接连接 EC,直接连接 ED,直接连接 AB,直接连 接 AC,直接连接 AD,直接连接 BC,直接连接 BD,直接连接 CD 是不可能实现的 情形。也就是说,对于球面上任意两两互不重合的 A、B、C、D、E 五点,任意两 点之间不可能均可作一条连线段直接连接。同时也说明对于球面上任意两两互不 重合的 A、B、C、D、E 五点,如果任意两点之间作一条连线段,并且要求任一条 连线段中间不能经过其它已知点,按照此要求不管怎样连接,最终得到的图形中 至少会多出一个交点不在 A、B、C、D、E 这五点上。
定理 3:球面上 A、B 两点不呈现为球体中心平面轴对称时,那么球面上连接 A、B 两点的所有弧线段中,有一条弧线段最短。
证明:因为球面上 A、B 两点不呈现为球体中心平面轴对称,假定球面上连 接 A,B 两点的所有弧线段中,没有一条弧线段最短;虽然 OA=OB,现在以 OA 或 OB 为半径,以点 O 为圆心,从 A 点到 B 点作弧;显然作的弧不是半圆,那么以 连接 A,B 两点的直线为轴,以作的弧,不可能完全绕球面旋转一周,这样就产 生矛盾;故定理 3 成立。
3
定理 5:球面上任意两两互不重合的 A、B、C、D、E 五点,如果任意两点之 间作一条连线段连接,其中任一连线段(除端点外)中间不能经过其它已知点, 那么球面上一定不会出现这样的图形:连线段的交点只是 A、B、C、D、E 五点。
证明:因为 A、B、C、D、E 为球面上任意两两互不重合的五点,任意两点之 间如果作一条连线段连接,那么在球面上进行设计,可以按照下列程序操作:
高速数字计算机的发明,促使更多数学家对“四色问题”的研究。电子计算 机问世以后,由于演算速度迅速提高,加之人机对话的出现,大大加快了对四色 猜想证明的进程。就在 1976 年 6 月,由美国数学家阿佩尔(Kenneth Apprl)和 哈肯(Wolfgang Haken)在美国伊利诺斯大学的两台不同的电子计算机上,用了
关键词:四色定理;球面几何;线段;相交 中图分类号:0156
引言
1852 年,毕业于伦敦大学的格斯里(FrancisGuthrie)来到一家科研单位搞 地图着色工作时,发现每幅地图都可以只用四种颜色着色。这个现象能不能从数 学上加以严格证明呢?他和他正在读大学的弟弟决心试一试,但是稿纸已经堆了 一大叠,研究工作却是没有任何进展。1872 年,英国当时最著名的数学家凯利 正式向伦敦数学学会提出了这个问题,于是四色猜想成了世界数学界关注的问 题。
2
定义 6:球面上一条连线段与另一条连线段有交点,则称这两条连线段相交; 球面上一条连线段与另一条连线段没有交点,则称这两条连线段不相交。
定义 7:如果整个球面上是由一些封闭图形组合而成的球面图形,我们则称 这个球面为球面组合图形。
定义 8:平面上或球面上一个封闭图形,如果这个封闭图形内没有其它的封 闭图形,我们则称这个封闭图形为独立的封闭图形。
1
1200 个小时,作了 100 亿次判断,结果没有一张地图是需要五色的,最终证明 了四色定理。
尽管随着计算机的普及,绝大多数数学家对四色定理的证明没有疑问,但某 些数学家对经由电脑辅助的证明方式仍旧不够满意,希望能找到一个完全“人 工”的证明。
“四色定理”证明 定义 1:平面上或球面上任意 A、B 两点之间有一条连线连接,我们则称这条 连线为 A、B 两点之间的连线段。 定义 2:球面上任意 A、B 两点之间有这样的一条线连接,即以球体中心点 O 为中心点,以 OA 或 OB 为半径,从 A 点到 B 点或从 B 点到 A 点作一扇形,这样球 面上就得到从 A 点到 B 点或从 B 点到 A 点的一条线连接,这样的一条线称为球面 上 A、B 两点之间的弧线段。或者存在一中心点 O′,使得 O′A=O′B,以 O′为 中心点,以 O′A 或 O′B 为半径,从 A 点到 B 点或从 B 点到 A 点作一扇形,这样 球面上就得到从 A 点到 B 点或从 B 点到 A 点的一条线连接,这样的一条连线也称 为球面上 A、B 两点之间的弧线段。 定理 1:球面上任意 A、B 两点之间可以作无数条弧线段连接。 证明:因为球体内存在无数个中心点 O1,O2,O3,…,On;使得 O1A=O1B,O2A=O2B, O3A=O3B,…,OnA=OnB。由定义 2 可知,定理 1 成立。 定义 3:平面上或球面上任意两点之间有一条连线段,那么连线段两边最边 端的点,称为平面上或球面上任意两点之间连线段的端点。例如:平面上或球面 上任意 A、B 两点之间有一条连线段,A 和 B 就是端点。 定义 4:平面上或球面上任意 A、B 两点之间作一条线连接,而连接 A、B 两 点的连线段(除 A、B 两个端点外)中间不经过其它的已知点以及连接 A、B 两点 的连线段(除 A、B 两个端点外)中间不与其它的连线段相交,则称 A、B 两点为 直接连接。 定义 5:平面上或球面上任意 A、B 两点之间作一条线连接,而连接 A、B 两 点的连线段(除 A、B 两个端点外)中间经过了其它的已知点或者连接 A、B 两点 的连线段(除 A、B 两个端点外)中间与其它的连线段相交,则称 A、B 两点为间 接连接。
4
综上所述,故定理 5 成立。 定理 6:球面上任意两两互不重合的 A、B、C、D、E 五点,如果任意两点之 间作一条连线段连接,其中任一连线段(除端点外)中间不能经过其它已知点, 那么球面上一定不会出现这样的组合图形:球面上的组合图形只由五个独立封闭 图形组成。 证明:由定理 5 可知,定理 6 成立。 定理 7:平面上能够设计出满足某一特征的组合图形,那么在球面上也能设 计出满足该特征的组合图形。 证明:在平面上和球面上设计均要满足某一特征的组合图形,因为在球面上 设计可以从三维空间考虑设计,而在平面上设计只能从二维空间考虑设计,显然 三维空间要好设计一些。故定理 7 成立。 定理 8:设有独立封闭图形 A、B、C、D,则平面上或球面上可以设计出独立 封闭图形 A、B、C、D 的如下组合图形:独立封闭图形 A、B、C、D 中任意两两独 立封闭图形均有公共边界;并且组合图形中不会出现有独立封闭图形与独立封闭 图形重合或者出现独立封闭图形与独立封闭图形部分重叠的情形。 证明:我们在球面上设置任意两两互不重合的 E、F、G、H 四点,由定理 4 可知,球面上任意两两互不重合的 E、F、G、H 四点,任意两点之间均可以作一 条连线段直接连接,那么球面上必定会设计出这样的图形:连线段与连线段的交 点只是 E、F、G、H 四点。这样球面上就出现了由四块独立封闭图形组合成的球 面图形,其中四块独立封闭图形的组合图形中任意两块独立封闭图形均有公共边 界,并且任意两块独立封闭图形不重合以及任意两块独立封闭图形不部分重叠。 所以,说明球面上可以设计出独立封闭图形 A、B、C、D 中任意两两独立封闭图 形均有公共边界的组合图形,并且不会出现有独立封闭图形与独立封闭图形重合 或出现独立封闭图形与独立封闭图形部分重叠的情形。 或者我们总可以把两两互不重合的 E、F、G、H 四点,拓扑变换为四块独立 封闭图形,任意两点之间的连线段直接连接拓扑变换为公共边界,这样就可以得 到独立封闭图形 A、B、C、D 中任意两两独立封闭图形均有公共边界;并且组合 图形中不会出现有独立封闭图形与独立封闭图形重合或者出现独立封闭图形与 独立封闭图形部分重叠的情形。
(一)我们按照一定的次序总可以把 A、B、C、D 这四点设计为一个三棱锥 形的四个顶点,这样的话,球面上 A、B、C、D 四点中,任意两点之间可以作一 条连线段直接连接,那么球面上必定会是这样的图形:连线段与连线段的交点只 是 A、B、C、D 四点。这样的话,我们就可以从前面得到的球面组合图形中不难 得出结论:即这 A、B、C、D 四点中的其中任何一点相对于其它三点,这一点则 在一个封闭的图形内。如果我们再按要求直接连接 EA、EB、EC、ED,不管这样 连接,其中至少有一个连接使终要经过一个封闭的图形,所以其中至少有一个连 接不能进行直接连接。也就是说对于球面上任意两两互不重合的 A、B、C、D、E 五点,如果任意两点之间作一条连线段,并且要求任一条连线段中间不能经过其 它已知点,按照此要求不管怎样连接,最终得到的图形中至少会多出一个交点不 在 A、B、C、D、E 这五点上。
