初三数学月考模拟1
山西初三初中数学月考试卷带答案解析

山西初三初中数学月考试卷班级:___________ 姓名:___________ 分数:___________一、选择题1.如果a为任意实数,下列根式一定有意义的是()A.B.C.D.2.下列各式中属于最简二次根式的是()A.B.C.D.3.下列方程属于一元二次方程的是()A.B.C.D.4.下列图形中,是中心对称图形但不是轴对称图形的是()5.用配方法解方程,则配方正确的是()A.B.C.D.6.下列计算正确的是A.B.C.D.7.某中学标准化建设规划在校园内的一块长36米,宽20米的矩形场地ABCD上修建三条同样宽的人行道,使其中两条与AB平行,另一条与AD平行,其余部分种草(如图所示),若使每一块草坪的面积都为96平方米.设人行道的宽为x米,下列方程:①(36-2x)(20-x)=96×6;②2×20x+(36-2x)x=36×20-96×6;③(18-x)(10-)=×96×6,其中正确的个数为()A.0个B.1个C.2个D.3个8.如图是某座天桥的设计图,设计数据如图所示,桥拱是圆弧形,则桥拱的半径为()A.13m B.15m C.20 m D.26m9.若关于的一元二次方程有两个不相等的实数根,则的取值范围是()A.B.且C.D.且10.若方程的两根为、,则的值为( )A.3B.-3C.D.11.已知三角形两边的长分别是4和6,第三边的长是一元二次方程的一个实数根,则该三角形的周长是()A.20B.20或16C.16D.18或2112.如图,矩形的长为6,宽为3,O为其对称中心,过点O任画一条直线,将矩形分成两部分,则图中阴影部分的面积为()A.9B.18C.12D.15二、填空题1.若方程是关于x的一元二次方程,则m= .2.若关于的一元二次方程的一个根是,则另一个根是______.3.若成立,则x的取值范围是.4.若两个最简二次根式与可以合并,则x= .5.已知方程x2-7x+12=0的两根恰好是Rt△ABC的两条边的长,则Rt△ABC•的第三边长为.6.如图,R的直角边OA在y轴上,点B在第一象限内,OA=2,AB=1,若将△OAB绕点O按顺时针方向t△OAB旋转90°,则点B的对应点的坐标是。
初三月考数学试卷 (一) 答案 2013.03.28

初三月考数学试卷参考答案与试题解析一.选择题(共10小题,每题3分,共计30分)1.C2.C3.A4.A5.D6. C7.A8.B9.C 10.C二.填空题(共10小题,每题3分,共计30分)11.m=﹣2.12.x=2.13.m2+n2= 514.+ =115.m的取值范围是m>1.16.则列出关于x的方程为2(1+x)2=317.∠BMD为85度.18.∠BDE=∠BAC,(只需添加一个即可)19.a的值是900.20. 50或130度.三.解答题(共10小题,共计60分)21.(1)(2012•重庆)计算:.解:原式=2+1﹣5+1+9=8.(2)(2012•上海).解:原式===3.22、化简求值:,其中x=﹣.解:•=•=(或);当x=﹣时,原式=23、大庆市开始实施农村义务教育学校营养计划﹣﹣“蛋奶工程”.该地农村小学每份营养餐的标准是质量为300克,蛋白质含量为8%,包括一盒牛奶、一包饼干和一个鸡蛋.已知牛奶的蛋白质含量为5%,饼干的蛋白质含量为12.5%,鸡蛋的蛋白质含量为15%,一个鸡蛋的质量为60克.(1)一个鸡蛋中含蛋白质的质量为多少克?(2)每份营养餐中牛奶和饼干的质量分别为多少克?解:(1)由题意得:60×15%=9(克).(2)设每份营养餐中牛奶的质量为x克,则饼干的质量为(300﹣60﹣x)克,由题意得:5%x+12.5%(300﹣60﹣x)+60×15%=300×8%解得:x=200.故饼干的质量为:300﹣60﹣x=40.答:每份营养餐中牛奶和饼干的质量分别为200克和40克.24、(2011•扬州)古运河是扬州的母亲河.为打造古运河风光带,现有一段长为180米的河道整治任务由A、B两工程队先后接力完成.A工程队每天整治12米,B工程队每天整治8米,共用时20天.(1)根据题意,甲、乙两名同学分别列出尚不完整的方程组如下:甲:;乙:根据甲、乙两名问学所列的方程组,请你分别指出未知数x、y表示的意义,然后在方框中补全甲、乙两名同学所列的方程组:甲:x表示A工程队用的时间,y表示B工程队用的时间;乙:x表示A工程队整治河道的米数,y表示B工程队整治河道的米数.(2)求A、B两工程队分别整治河道多少米.(写出完整的解答过程)解:(1)故答依次为:20,180,180,20,A工程队用的时间,B工程队用的时间,A工程队整治河道的米数,B 工程队整治河道的米数;(2)选甲同学所列方程组解答如下:,②﹣①×8得4x=20,解得x=5,把x=5代入①得y=15,所以方程组的解为,A工程队整治河道的米数为:12x=60,B工程队整治河道的米数为:8y=120;(1)答:A工程队整治河道60米,B工程队整治河道120米.25、如图,△ABC中,AD⊥BC,点F在AC的垂直平分线上,且BD=DE.(1)如果∠BAE=40°,那么∠C=°,∠B=°;(2)如果△ABC的周长为13cm,AC=6cm,那么△ABE的周长=cm;(3)你发现线段AB与BD的和等于图中哪条线段的长,并证明你的结论.解:(1)∵点E在AC的垂直平分线上,∴AE=EC.∵BD=DE,AD⊥BC,∴AB=AE.∴∠ABE=∠AEB=2∠C=(180°﹣40°)÷2=140°÷2=70°,∠C=35°.(2)∵△ABC的周长为13cm,AC=6cm,∴AB+BC=13﹣6=7,∴△ABE的周长=AB+BC=7cm.(3)AB+BD=DC.证明:由(1)可知,AB=AE=CE,BD=DE,∴AB+BD=EC+DE=DC.26、(1)解方程:(x﹣3)2+4x(x﹣3)=0.解:原式可化为:(x﹣3)(x﹣3+4x)=0∴x﹣3=0或5x﹣3=0解得(2)解方程:3x2﹣6x+1=0;即x1=,x2=;27、(2010•内江)如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,AE交CD于点F,BD分别交CE、AE于点G、H.试猜测线段AE和BD的数量和位置关系,并说明理由.解:猜测AE=BD,AE⊥BD;(2分)理由如下:∵∠ACD=∠BCE=90°,∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB,(3分)∵△ACD和△BCE都是等腰直角三角形,∴AC=CD,CE=CB,(4分)在△ACE与△DCB中,∴△ACE≌△DCB(SAS),(5分)∴AE=BD,(6分)∠CAE=∠CDB;(7分)∵∠AFC=∠DFH,∠FAC+∠AFC=90°,∴∠DHF=∠ACD=90°,(8分)∴AE⊥BD.(9分)故线段AE和BD的数量相等,位置是垂直关系.28、(2010•南京)某批发商以每件50元的价格购进800件T恤,第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓是单价为40元,设第二个月单价降低x元.(1)填表:(不需化简)时间第一个月第二个月清仓时单价(元)80 40销售量(件)200(2)如果批发商希望通过销售这批T恤获利9000元,那么第二个月的单价应是多少元?解:(1)80﹣x,200+10x,800﹣200﹣(200+10x)(3分)时间第一个月第二个月清仓时单价(元)80 80﹣x 40销售量(件)200 200+10x 800﹣200﹣(200+10x)(2)根据题意,得80×200+(80﹣x)(200+10x)+40[800﹣200﹣(200+10x)]﹣50×800=9000(6分)整理得10x2﹣200x+1000=0,即x2﹣20x+100=0,解这个方程,得x1=x2=10当x=10时,80﹣x=70>50答:第二个月的单价应是70元.(8分)。
初三年级第一次月考数学试卷

初三年级第一次月考数学试卷〔2022 10 15〕班级 姓名 学号 得分 一、填空题、〔每题3分,共30分〕 1、当x 时, 42-x 是二次根式.2、关于x 的方程〔m+1〕x |m|+1+2x-3=0 , 当m 时,它是关于x 的一元二次方程, 当m 时,它是关于x 的一元一次方程. 3、关于x 的一元二次方程:x 2=p 中,常数项是 . 4、计算 :3312- = 5、 xy 〉0 ,化简:________x2=-yx 6、计算 20062005)23()23(-+ = 7a 的大小如下图化简: |a-2|+=+-962a a8、方程 x 2-x-2=0配成方程〔x+a 〕2=b 的形式,那么 a+b= 9、关于x 的方程:x 2+mx-6=0有一根为2,那么m=10、写出一个根为3的一元二次方程〔二次项系数为1〕 二、选择题:〔每题3分,共18分〕 11、如图在数轴上表示数3的点是〔 〕 A 、 A 点 B 、 B 点 C 、 C 点 D 、 D 点 12、以下一定是关于x 的一元二次方程的是〔 〕A 、 x 2-x+3 B 、ax 2+bx+c=0 C 、x 2=0 D 、x 2+x=x113、以下根式中,最简的二次根式是〔 〕 A 、21B 、21C 、2xD 、12+x14、二次根式 4 20 50 21中化简后与2被开方数相同的个数为( )A 1个B 、 2个C 、3个D 、4个 15、以下各式中,计算正确的选项是〔 〕 A 、8)4()2(64)16()4(=-⨯-=-⨯-=-⨯- B 、a a 482= 〔a>0〕 C 、2243+=3+4=7D 、224041-=1940414041⨯=-•+=916一元二次方程的两根为x 1=2 , x 2=-3 那么这个方程是〔 〕 A 、〔x-2〕(x+3)=0 B 、〔x+2〕(x-3)=0 C 、〔x+2〕(x+3)=0 D 、〔x-2〕(x-3)=0 17、以下一元二次方程中、两个根之积等于2的是〔 〕 A 、x 2-x-2=0 B 、x 2+3x+2=0-2 -12 13-1-22135C 、2 x 2-x+2=0D 、x 2+x+2=018、某中学2022年上高中的人数为100人,由于中学狠抓质量和师生不断努力,上高中的人数逐渐上升,三年来上高中的人数到达331人,假设设这两年〔2022年和2022年〕高中人数的平均增长率为x,那么可列方程〔 〕 A 、100+100〔1+x 〕+100〔1+x 〕2=331 B 、100〔1+x 〕2=331C 、100〔1+x 〕+100〔1+x 〕2=331 D 、100〔1-x 〕2=331三、计算题〔每题4分,共12分〕19、0)12(8122+--- 20、27)64148(÷+21 、 xxx x 1246932-+四、解方程〔每题4分,共8分〕22、x 2-4x-12=0 23、 x 2-x-1=0五、解做题:〔第24、25小题每题6分,第26、27每题7分〕 24、251-=a 251+=b 求a 2b+ab 2的值25、关于x 的一元二次方程〔k+1〕x 2-2kx+k-2=0〔1〕、当k 为何值时,方程有两个不相等的实数根?〔2〕、选取一个你喜欢的且能使方程有两个不相等的实数根的整数k 代人方程,并且解出此方程.26、养鸡场的王叔叔想用篱笆围一个面积为108平方米的矩形鸡舍为了节省材料,使鸡舍的一面靠墙,三面用篱笆围成〔如下图〕墙为15米,所用的篱笆为30米.请你帮王叔叔设计一个合理的方案27、某种新产品的进价是120元,在试销阶段发现每件销售价〔元〕与产品的日销量〔件〕始终存在下表的数量关系:〔1〕、请根据上表所给的数据表述出每件售价提升的数量〔元〕与日销量减少的数量〔件〕之间的关系?〔2〕、在不变上述关系的情况下,请你帮助商场经理筹划每件商品定价为多少元时,每日的盈利可到达1600元?。
初三数学第一次月考模拟试卷.doc
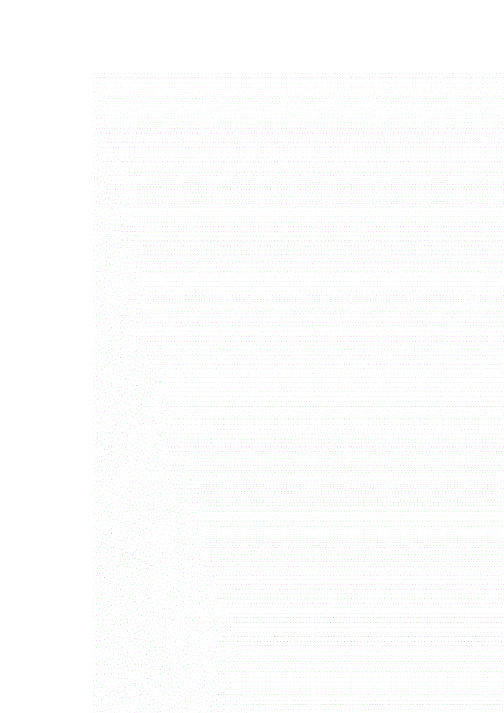
初三数学第一次月考模拟试卷阜宁县吴滩初级中学陈海霞一:选择题1、在统计中,样本的标准差可以反映这组数据的()A.平均状态B.分布规律C.离散程度D.数值大小2、要使二次根式『I有意义,字母x的取值范围必须满足的条件是()A.汶1B. xWlC. x>lD. x<l3、样本方差的计算式S2=£[(Xi-30)2 + (X2-30)2 + •••+(Xn-30)2]中,数字 90和30分别表示样本中的()A.众数、中位数B.样本中数据的个数、平均数C.方差、标准差D.样本中数据的个数、中位数4、对甲、乙两同学100米短跑进行5次测试,通过计算,他们成绩的平均数相等,方差S%=0. 025, S「=0. 246,下列说法正确的是()A.甲短跑成绩比乙好B,乙短跑成绩比甲好C.甲比乙短跑成绩稳定D,乙比甲短跑成绩稳定5、顺次连结等腰梯形各边中点所得的四边形是()A.矩形B.菱形C.正方形D.平行四边形B6、如图所示,ZA0P=ZB0P=15° , PC〃0A, /PD±0A,若 PC=4,则 PD 等于()A. 4B. 3C. 2D. 1 o --------A7、如图1,有一个数值转换器:当输入的x为64时,输出的y是............. ()A. 8B. 2^2C. 2^3D. 3^28、如图2,在数轴上表示实数应的点可能是()A.点户B.点 QC.点 MD.点、N输入r >取算术平方正无理笔输出' 0 12 3 4 I 是有理毕 | 图; 9、实数a 、b 在数轴上的b 0 a位置如图所示,那么化简la-bl-77的结果是( )A. 2a~bB. bC. ~bD. ~2a+b10、如图,将一个长为10cm,宽为8cm 的矩形纸片对折两次后,沿所得 矩形两邻边中点的连线(虚线)剪下,再打开,得到的菱形的面积为( )C 9 D. 4⑤ J/ — 2x + 2、4. 10cm 2 B. 20cm 2 C. 40cm 2 D. 80cm 211、如图,矩形纸片ABCD 中,AB=4, AD=3,折叠纸片使AD 边与对 角线BD 重合,折痕为DG,则AG 的长为( )4 3A. 1B. 3 c. 2 D . 2 12如图a, ABCD 是一矩形纸片,AB = 6cm,AD = 8cm, E 是AD 上一点,且AE = 6cm 。
北京市德胜中学2024-2025十月月考数学试卷

德胜中学初三数学练习-1行政班级:_________ 数学班级:________ 姓名:_________一.选择题(共8小题)1.随着人们健康生活理念的提高,环保意识也不断增强,以下是回收、绿色包装、节水、低碳四个标志,其中是中心对称图形的是( )A .B .C .D .2.已知O 中最长的弦为8,则O 的半径是( ) A .4B .8C .12D .163.将一元二次方程28100x x −+=通过配方转化为2()x a b +=的形式,下列结果中正确的是( )A .2(4)6x −=B .2(8)6x −=C .2(4)6x −=−D .2(8)54x −=4.如图,点A 、B 、C 在O 上,OAB ∆为等边三角形,则ACB ∠的度数是( )A .60︒B .50︒C .40︒D .30︒一、选择题题号 1 2 3 4 5 6 7 8 选项二、填空题9. _____________________ 10. ____________________ 11. ____________________ 12. ____________________ 13. ____________________ 14. ____________________ 15. ____________________ 16. ____________________5.生活垃圾无害化处理可以降低垃圾及其衍生物对环境的影响.据统计,2017年全国生活垃圾无害化处理能力约为2.5亿吨,随着设施的增加和技术的发展,2019年提升到约3.2亿吨.如果设这两年全国生活垃圾无害化处理能力的年平均增长率为x ,那么根据题意可以列方程为( ) A .2.5(1) 3.2x += B .2.5(12) 3.2x += C .22.5(1) 3.2x +=D .22.5(1) 3.2x −=6.如图,在O 中,AB 是直径,BC CD DE ==,60AOE ∠=︒,则BOC ∠的度数为( ) A .35︒B .40︒C .45︒D .60︒7.如图,在O 中,满足2AB CD =,则下列对弦AB 与弦CD 大小关系表述正确的是( ) A .2AB CD > B .2AB CD <C .2AB CD =D .无法确定8.抛物线2y ax bx c =++的顶点为(2,)A m ,且经过点(5,0)B ,其部分图象如图所示.对于此抛物线有如下四个结论:①0ac <;②0a b c −+>;③90m a +=;④若此抛物线经过点(,)C t n ,则4t −一定是方程2ax bx c n ++=的一个根.其中所有正确结论的序号是( ) A .①② B .①③C .①③④D .①④二.填空题(共8小题)9.关于x 的一元二次方程240x mx ++=有一个根为1,则m 的值为 . 10.若关于x 的方程220x x k −+=有两个不相等的实数根,则k 的取值范围为 . 11.已知抛物线2(0)y ax bx c a =++≠上部分点的横坐标x ,纵坐标y 的对应值如表:x⋯ 2− 1− 0123 ⋯ y⋯5 03−4−3−⋯那么该抛物线的顶点坐标是 .12.若点1(1,)A y −,2(2,)B y 在二次函数2y a x =+的图象上,则1y ,2y 的大小关系为:1y 2y (填“>”,“ =”或“<” ).13.如图所示,COD ∆是AOB ∆绕点O 顺时针方向旋转35︒后所得的图形,点C 恰好在AB 上,90AOD ∠=︒,则BOC ∠的度数是 .14.如图所示,ABC ∆绕点P 顺时针旋转得到DEF ∆,则旋转的角度是 .15.如图,在平面直角坐标系xOy 中,点A ,B ,C 的横、纵坐标都为整数,过这三个点作一条圆弧,则此圆弧的圆心坐标为 .16.平面直角坐标系中,C (0,6),K (4,0),A 为x 轴上一动点,连接AC ,将AC 绕A 点顺时针旋转90°得到AB ,当点A 在x 轴上运动,BK 取最小值时,点B 的坐标为 .三.解答题17.解方程:(1)2620x x ++=. (2)2450x x −−=18.已知二次函数243y x x =++.(1)求此函数图象的对称轴和顶点坐标;(2)画出此函数的图象;(3)若点1(0,)A y 和2(,)B m y 都在此函数的图象上,且12y y <,结合函数图象,直接写出m 的取值范围_________.19.已知关于x 的一元二次方程2(5)620x k x k −+++=. (1)求证:此方程总有两个实数根;(2)若此方程恰有一个根小于1−,求k 的取值范围.20.如图,在正方形ABCD 中,射线AE 与边CD 交于点E ,将射线AE 绕点A 顺时针旋转,与CB 的延长线交于点F ,BF DE =,连接FE . (1)求证:AF AE =;(2)若30DAE ∠=︒,2DE =,直接写出AEF ∆的面积.21.如图,AB 是O 的直径,CD 是O 的弦,CD AB ⊥于点E ,点F 在O 上且CF CA =,连接AF .求证:AF CD =;22.某校举办了“冰雪运动进校园”活动,计划在校园一块矩形的空地上铺设两块完全相同的矩形冰场,如图所示,已知空地长27m,宽12m,矩形冰场的长与宽的比为4:3,如果要使,并且预留的上、下通道的宽度相等,左、中、右通道的宽度冰场的面积是原空地面积的23相等,那么预留的上、下通道的宽度和左、中、右通道的宽度分别是多少米?23.如图,在ABC∆中,AB AC=,以AB为直径的O分别交AC、BC于点D、E.(1)求证:点E是BC的中点;(2)若70∠的度数.∠=︒,求BODC24.某篮球队员的一次投篮命中,篮球从出手到命中行进的轨迹可以近似看作抛物线的一部分,表示篮球距地面的高度y(单位:)m与行进的水平距离x(单位:)m之间关系的图象如图所示.已知篮球出手位置A与篮筐的水平距离为4.5m,篮筐距地面的高度为3.05m;当篮球行进的水平距离为3m时,篮球距地面的高度达到最大为3.3m.(1)图中点B表示篮筐,其坐标为,篮球行进的最高点C的坐标为;(2)求篮球出手时距地面的高度.25.在平面直角坐标系xOy 中,1(P x ,1)y ,2(Q x ,2)y 是抛物线2222y x mx m =−+−上任意两点. (1)求抛物线的顶点坐标(用含m 的式子表示); (2)若113x <,总有12y y ≥:① 当221m x m −<+<时,m 的取值范围是:_________. ② 当23x m =时,求m 的取值范围.26.如图1,在ABC ∆中,90ACB ∠=︒,CA CB =,点D ,E 分别在边CA ,CB 上,CD CE =,连接DE ,AE ,BD .点F 在线段BD 上,连接CF 交AE 于点H . (1)若CF AE ⊥,求证:2AE CF =;(2)如图2,将图1中的CDE ∆绕点C 顺时针旋转α(90180)α︒︒<<. 若点F 为BD 的中点,判断2AE CF =是否仍然成立.如果成立,请证明;如果不成立,请说明理由.图1图2BA(3) 将图1中CDE ∆绕点C 旋转一周,F 为BD的中点,若CA =CD =,则当,,A E D三点共线时,CF 的长为_____________.图327.在平面直角坐标系xOy中,对于点A,点B和直线l,点A关于l的对称点为点A',点B是直线l上一点.将线段A B'绕点A'顺时针旋转90︒得到A C',如果线段A C'与直线l有交点,称点C是点A关于直线l和点B的“轴旋点”.(1)若点A的坐标为(2,4),在点1(4,1)C,2(6,0)C,3(6,1)C−,4(6,1)C中是点A关于x轴和点B的“轴旋点”的是;(2)若点B的坐标是(0,4),点A、C都在直线4y x=−−上,点C是点A关于y轴和点B的“轴旋点”,点A的坐标为_________;(3)点A在以(0,)t为对角线交点,边长为2的正方形M(正方形的边与坐标轴平行)上,直线:1l y x=−+,若正方形M上存在点C是点A关于直线l和点B的“轴旋点”,直接写出t的取值范围_________.。
初三月考数学试题(一)
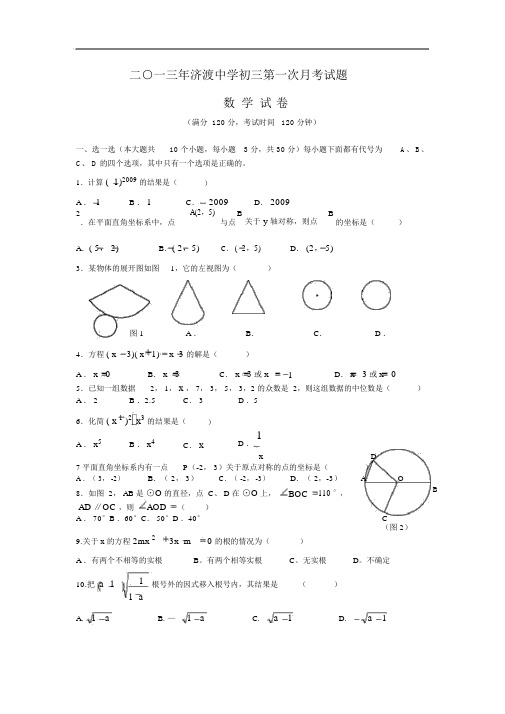
二○一三年济渡中学初三第一次月考试题数学试卷(满分 120 分,考试时间120 分钟)一、选一选(本大题共10 个小题,每小题 3 分,共 30 分)每小题下面都有代号为A、 B、C、 D 的四个选项,其中只有一个选项是正确的。
1.计算( 1)2009的结果是()A .1B .1C.2009D.20092A(2,5)与点B关于 y 轴对称,则点B的坐标是().在平面直角坐标系中,点A.( 5,2)B.( 2,5)C.( 2,5)D.(2,5)3.某物体的展开图如图1,它的左视图为()图 1 A .B.C. D .4.方程( x3)( x1)x 3 的解是()A .x 0B.x 3C.x 3或x1D.x 3或x 05.已知一组数据2, 1,x, 7, 3, 5, 3,2 的众数是 2,则这组数据的中位数是()A . 2B .2.5C. 3 D .56.化简( x1)2x3的结果是()A .x5B .x4C.x D .1x D7 平面直角坐标系内有一点P(-2, 3)关于原点对称的点的坐标是()A .( 3, -2)B.( 2, 3)C.( -2, -3)D.( 2,-3)A O8.如图 2, AB 是⊙O的直径,点 C、 D 在⊙O上,BOC110 °,B AD ∥OC ,则AOD()A . 70°B .60°C. 50°D .40°C(图 2)9.关于 x 的方程2mx23x m0 的根的情况为()A .有两个不相等的实根B。
有两个相等实根C。
无实根D。
不确定10.把a 11根号外的因式移入根号内,其结果是()1 aA. 1 aB. — 1 aC. a 1D.a1二、填一填(本大题共 6 个小题,每小题 3 分,共 18 分).11.不等式5( x1)3x 1的解集是.12.不透明的箱子里有7 个除颜色外完全相同的球, 3 黄 4 白,“摸出黄球”的概率是。
初三数学第一次月考试卷

初三数学第一次月考试卷姓名 班级 学号一、填空题(每小题2分,共20分) 1、一元二次方程012=-x 的根为 .2、若方程mx 2+3x -4=3x 2是关于x 的一元二次方程,则m 的取值范围是 .3、若m +10是整数,则正整数m 的最小值是4、已知2<x<5, 化简22)5()2(-+-x x =___________.5、直线l 过正方形ABCD 的顶点B ,点A 与C 到l 的距离 分别是2和3,则正方形ABCD 的面积是 平方单位。
6、已知a+a 1=10,则a -a 1= 7、=⨯8328 、在实数范围内分解因式:16x 2-7=9、菱形ABCD 的一条对角线长为6,边AB 的长是方程01272=+-x x 的一个根,则菱形ABCD 的周长为 .10、观察下列数据:0,,23,15,32,3,6,3……寻找规律得第10个数是 二、选择题(每题3分,共30分)11、用配方法解下列方程时,配方有错误的是 ( ) A. x 2-2x -99=0化为(x -1)2=100 B. x 2+8x +9=0化为(x +4)2=25 C. 2t 2-7t -4=0化为1681)47(2=-t D. 3y 2-4y -2=0化为910)32(2=-y 12.下列计算正确的是( )(A)=1=(C)(21==13.211+与1-2的关系是( )A .相等B 、互为倒数C 、互为相反数D 、以上都不对 14、若x <0化简xx x2+的结果是( )A 、0B 、-2C 、0或-2D 、2 15、下列四个结论中,正确的是 ( ) A. 32<52<52 B. 54<52<32 C. 32<52<2 D. 1<52<5416、若关于的x 方程022=++k x x 有实根,则k 值为( ) A 、k < 0 B 、k ≤0 C 、k ≤1 D 、k ≥-117、若方程02=++n mx x 中有一根为0,另一个根不等于0,则m 、n 的值是( ) A 、m=0,n=0 B 、m ≠0,n=0 C. m=0,n ≠0 D. mn ≠0 18、在33,98,,,2422yx ba-中最简二次根式的个数是( ) A 、1个 B 、2个 C 、3个 D 、4个 19、下列选项正确的是( ) A 、a a=2B 、)(2a a = C 、32321+=- D 、b aba 4284=20、如图,在长30m ,宽20m 的矩形场地上修筑两条同样宽且互相垂直的道路,余下部分为耕地,要使耕地面积为500m 2,设路宽为xm,可得方程 是( ) A 、(30-x)(20-2x)=500 B. (30-x)(20-x)=500 C. (30-x)(20-x)+x 2=500 D. (30-x)(20-x)-x 2=500三、解答题(共24分) 21、计算:(每题4分,共8分) (1)36316122+- (2)(5155)53÷+22.按要求解方程:(每小题5分,共10分)(1)、3x 2+5(2x+1)=0(用公式法) (2)、3(x -5)2=2(5-x ) (用因式分解法)23.化简求值:221211221++--÷++-x x x x x x ,其中22-=x (6分)四、(共26分)24、先阅读,再填空并解答:(8分)X 2+3x+2=0的解是x 1,x 2,x 1=-2,x 2=-1,则x 1+x 2=-3, x 1x 2=2 X 2-4x-5=0的解是x 1,x 2,x 1=5,x 2=-1,则x 1+x 2=4, x 1x 2=-5X 2+7x+10=0的解是x 1,x 2,x 1= ,x 2= ,则x 1+x 2= , x 1x 2=(1)由上面你能发现什么规律?试写出x 2+px+q=0的两根x 1,x 2的和与积和p,q 之间的关系。
初三数学月考试题及答案

第 1 页 共 3 页D.C.B.A.122212122212大庆六十九中学初三数学第一次月考试题一、单项选择题(每小题3分,共36分)1.若分解因式x 2-mx-15=(x-3)(x+5), 则m 的值为 ( ) A 、-2 B 、2 C 、-5 D 、52.本次“保护湿地”知识竞赛中共20道题,对于每一道题,答对了得10分,答错了或 不答扣5分,选手至少要答对几道题,其得分才会不少于80分?( ) A 、14 B 、13 C 、12 D 、113.一次函数323+-=x y 的图象如图所示, 当-3≤y <3时,x 的取值范围是( )A 、x >4B 、0<x <2C 、0≤x <4D 、0<x ≤44. 下列各式能用完全平方公式分解因式的是( ) A.4x 2+1 B.x 2-2x+4C.x 2+xy +y 2D.x 2-4x +45. 下列多项式,不能运用平方差公式分解的是( )A 、42+-mB 、22y x --C 、122-y xD 、()()22a m a m +--6.若不等式组⎩⎨⎧>-≤111x m x 无解,则m 的取值范围是( )A 、m <-11B 、m >-10C 、m ≤-11D 、m ≥-107.下列各式是因式分解的是( )A 、(a +3)(a -3)=a 2-9B 、x 2+x -5=(x -2)(x +3)+1C 、a 2b +ab 2=ab(a +b)D 、x 2+1=x (x +x1)8. 在平面直角坐标系内,P (2x -6,x -5)在第四象限,则x 的取值范围为( )A 、3<x <5B 、-3<x <5C 、-5<x <3D 、-5<x <-3 9. 若不等式组⎩⎨⎧-<<-1312a x x 的解集是x<2,则a 的取值范围是( )A .3<aB .3≤aC .3≥aD .无法确定10. 已知a 、b 、c 是△ABC 的三边长,且满足a 3+ab 2+bc 2=b 3+a 2b+ac 2,则△ABC 的形状是( )A.等腰三角形B.直角三角形C.等腰三角形或直角三角形D.等腰直角三角形 11.下列数学表达式:①2x -1<0 ②x -7=0 ③ y ≠4 ④x -2>x -1 ⑤4<0 ⑥ a 2b+ab 2其中是不等式的有( )A .2个B .3 个C .4个D .5个 12.不等式组212x x <⎧⎪⎨≥⎪⎩ 的解集在数轴上应表示为( )二、填空题: (每小题3分,共27分) 13. 若8m n +=,12m n =,则49212122-+mnn m 的值为 .14.若不等式组⎩⎨⎧--3212b >x a <x 的解集为11<x<-,那么)1)(1(++b a 的值等于 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三月考数学试卷
考生注意:
1.全卷满分150,全卷共三大题,31小题,考试时间120分钟 2.答题规范,讲究格式,书写工整,_必须将答案写在答卷纸上 3.诚实守信,独立思考,展露真才 敢于动手,相信你能成功!!!! 一. 选择(3×15=45)
1点A (-3,2)关于Y轴对称的点的坐标是
A(0,2) B(3,2) C(3,-2)D(2,-3)
2.为了鼓励节约用水,按以下规定收取水费:(1)每户每月用水量不超过20
立方米,则每立方米水费1.2元,;(2)每户每月用水量超过20立方米,则超过部分每立方米水费2元,设某户一个月所交水费为y (元),用水量为x (立方米),则y 与x 的函数关系用图像表示为( )
3.将抛物线22x y =平移可得到抛物线()1422
--=x y ( )
(A )向左平移4个单位,再向上平移1个单位 (B )向左平移4个单位,再向下平移1个单位 (C )向右平移4个单位,再向上平移1个单位 (D )向右平移4个单位,再向下平移1个单位
4.如图,是用杠杆撬石头的示意图,C 是支点,当用力压杠杆的端点A 时,杠
A B C D
杆绕C 点转动,另一端点B 向上翘起,石头就被撬动.现有一块石头,要使其滚动,杠杆的B 端必须向上翘起10cm ,已知杠杆的动力臂AC 与阻力臂BC 之比
为5︰1,则要使这块石头滚动,至少要将杠杆的端点A 向下压( )
A 、100cm
B 、60cm
C 、50cm
D 、10cm
5.直线b kx y +=经过一、二、四象限,则直线k bx y -=的图像只能是( ).
o
A B C D 6、如图,A ,C 是函数x
y 1
=
的图像上任意过A 作y 轴的垂线, 垂足为B ,过C 作x 轴的垂线,垂足为D , 记AOB Rt ∆的面积为S 1,COD Rt ∆的面积为S 2,则( ).
A 、 S 1 >S 2
B 、 S 1 <S 2
C 、 S 1=S 2
D 、 S 1和2
S 的大小关系不能确定
7使用直角钢尺检查某一工件是否恰好是半圆形的凹面,成半圆形的为合格,
O
x
y o
x
y
o
x
y o
x
y
O
B A
D x C
y
第10题图
D
P
O
C B
A 如图所示的四种情况中合格的是 ( )
8.如图,ABCD 为圆内接四边形,E 是AD 延长线上一点,如果∠B=60 那么∠EDC 等于( )
A.120°
B.60°
C.40°
D.30°
9.若点(-5,y 1)、(-3,y 2)、(3,y 3)都在反比例函数y= -3
x 的图像上,则( )
A .y 1>y 2>y 3
B .y 2>y 1>y 3
C .y 3>y 1>y 2
D .y 1>y 3>y 2 10.如图,在⊙O 中,P 是弦AB 的中点,CD 是过点P 的直径, 则下列结论中不正确的是(
A 、A
B ⊥CD B 、∠AOB =4∠ACD
C 、⋂
⋂
=BD AD D 、PO =PD
11.关于x 的方程x 2-2mx -m -1=0的根的情况是( )
A.有两个不相等的实数根
B.有两个相等的实数根
C.没有实数根
D.不能确定
12如果以y 轴为对称轴的抛物线y=ax 2+bx+c 的图象如图所示, 那么代数式b+c -a 与零的关系是( )
A.b+c -a=0
B.b+c -a >0
C.b+c -a <0
D.不能确定
13、如图,⊙O 中弧AB 的度数为60°,AC 是⊙O 的直径, 那么∠BOC 等于( )
A 、150°
B 、130°
C 、120°
D 、60°
14.已知抛物线3)4(3
1
2--=x y 的部分图像
(如图所示),图像再次与x 轴相交时的坐标是 ( ) A 、(5,0) B 、(6,0) C 、(7,0) D 、(8,0)
15.如图,若A 、B 、C 、P 、Q 、甲、乙、丙、丁都是方格纸中的格点,为使△ABC ∽△PQR ,则点R 应是甲、乙、丙、丁四点中的 A. 甲
B. 乙
C. 丙
D. 丁
二填空题(4×8=24)
16.在圆内接四边形ABCD 中,∠A ∶∠B ∶∠C=5∶2:1,则∠D= 。
17.已知⊙O 的半径为5,点A 到圆心O 的距离为3,则过点A 的所有弦中,最短弦的长为_________
18.若⊙O 所在平面内一点P 到⊙O 上的点的最大 距离为8,最小距离为4(a >b ),则此圆的半径为____
姓名_______ 考号______ 命题校对:徐超凡
以 内 不 准 答 题
19如图的围棋盘放在某个平面直角坐标系内,白棋② 的坐标为(7,4)--,白棋④的坐标为(6,8)--那么 黑棋①的坐标应该是 .
20.请写出一个开口向上,对称轴为直线x=2,且与y 轴的交点坐标为 (0,3)的抛物线的解析式 。
21.已知Rt △ABC 中,∠C=90°,AC=
为圆心,CB 为半径的圆交AB 于点22.周角的度数为 .
23.起租费:5元;基价里程:3等时费:每等5分钟加收1租 价:每公里1.20元.
火车站接一朋友回家.如图,表示该 则该同学最少应付车费 元.
答 卷 纸
一选择题(3×15=45)
二填空题(4×8=32)
16_________ 17_________ 18_______ 19___________ 20_________ 21_________ 22_______ 23__________
三解答题
24.(本题7分)已知5
42z
y x ==,且2x+y-z=9,求x+y+z的值
25.(本题8分)已知: 在⊙O 中,CD 平分∠ACB ,弦AB 、CD 相交于点E , 连结AD 、BD
(1) 写出图中3对相似的三角形; (2) 找出图中相等的线段,并说出理由.
26(本题10分). 已知平面直角坐标系中三点A (2,0),B (0,2), P (x ,0)()x <0,连结BP ,过P 点作PC PB ⊥交过点A 的直线a 于
点C(2,y),(1)求y与x之间的函数关系式;
(2)当x取最大整数时,求BC与PA的交点Q的坐标。
27(本题8分)小明代表班级参加校运会的铅球项目,他想:“怎样才能将铅球推得更远呢?”于是找来小刚做了如下的探索:小明手掷铅球在控制每次推出时用力相同的条件下,分别沿与水平线成300、450、600方向推了三次。
铅球推出后沿抛物线形运动。
如图,小明推铅球时的出手点距地面2m,以铅球出手点所在竖直方向为y轴、地平线为x轴建立直角坐标系,分别得到的有关数据如下
最
高点的坐标
铅球落点到
小明站
9.5m ___________m 7.3m
立处的水平
距离
⑴请你求出表格中两横线上的数据,写出计算过程,并将结果填入表格中的横线上;⑵请根据以上数据,对如何将铅球推得更远提出你的建议。
28.(本题8分)有一个拱桥是圆弧形,他的跨度为60m,拱高为18m,当洪水泛滥跨度小于30m时,要采取紧急措施。
若拱顶离水面只有4m时,问是否要采取紧急措施?
29(本题10分)如图所示:一次函数b kx y +=的图象与反比例函数x
m y =的 图象交于A 、B 两点,
(1)利用图中的条件,求一次函数与反比例函数的解析式;
(2)根据图象写出使一次函数的值大于反比例函数的值的x 的取值范围;
x
30(本题10分)如图⊙O 半径为2,弦BD =32,A 为弧BD 的中点,E 为弦AC 的中点,且在BD 上。
求:四边形ABCD 的面积。
31(本题12分)为了顺应市场要求,连云港花炮厂技术部研制开发一种新产品,年初上市后,公司经历了从亏损到盈利的过程.下面的二次函数图象(部分)刻
B
画了该厂年初以来累积利润s(万元)与销售时间t(月)之间的关系(即前t 个月的利润总和s和t之间的关系).根据图象提供的信息,解答下列问题:(1)由已知图象上的三点坐标,求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末花炮厂累积利润可达到30万元?
(3)求第8个月公司所获利润是多少万元?。
