初一数学下册经典题型集锦
初一下学期数学经典题型集锦

初一下册数学经典题型集锦1、某地区的民用电,按白天时段和晚间时段规定了不同的单价。
某户8月份白天时段用电量比晚间时段多50%,9月份白天时段用电量比8月份白天时段用电量少60%,结果9月份的用电量虽比8月份的用电量多20%,但9月份的电费却比8月份的电费少10%,求该地区晚间时段民用电的单价比白天时段的单价低的百分数(1)解:设白天电价为a,晚上电价为b;8月份白天电量为x,则8月晚上用电量为x×2/3,8月总电量为x+x×2/3;9月份白天用电量为(1-60%)x,9月份总电量为(1+20%)×(x+x×2/3);9月份晚上用电量为(1+20%)×(x+x×2/3)-(1-60%)x;则有:8月份电费:x×a+x×2/3×b;9月份电费:(1-60%)x×a+【(1+20%)×(x+x×2/3)-(1-60%)x】×b;根据题意,:(1-60%)x×a+【(1+20%)×(x+x×2/3)-(1-60%)x】×b=(1-10%)×【x×a+x×2/3×b】整理得b=0.5a,晚上的电价比白天低50%。
(2)解设8月用电为1,晚上比白天低x[3/5+2/5*(1-x)]*(1-10%)=3/5*(1-60)+[120%-3/5(1-60)](1-x)(3)设8月份晚间用电量为X则8月份白天用电量为(1+50%)X9月份白天用电量为(1—60%)(1+50%)X=0.6X8月份用电总量为(1+1+50%)X=2.5X9月份用电总量为(1+1+50%)X(1+20%)=3X9月晚间用电量为3X-0.6X=2.4X(4)解:设该地区白天时段的用电单价为a,晚间时段单价为b .把8月份晚间看作单位“1”。
七年级下册数学期末考试几何大题证明必考题精选
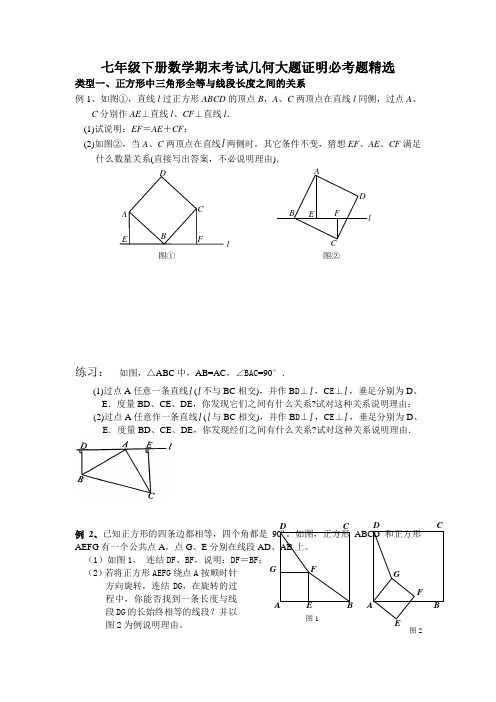
图①DA EC B Fl图②ABEF C lD 七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
(1)如图1, 连结DF 、BF ,说明:DF =BF ;(2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线段DG 的长始终相等的线段?并以图2为例说明理由。
A EB 图1D CG FA BD C GFE 图2练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上(1)BD 与CE 相等吗?请说明理由.(2)你能求出BD 与CE 的夹角∠BFC 的度数吗?(3)若将已知条件改为:四边形ABCD 与四边形AEFG 都是正方形,例3、正方形四边条边都相等,四个角都是90.如图,已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,点E 是直线MN 上一点,以AE 为边在直线MN 的上方作正方形AEFG .(1)如图1,当点E 在线段BC 上(不与点B 、C 重合)时: ①判断△ADG 与△ABE 是否全等,并说明理由;②过点F 作FH ⊥MN ,垂足为点H ,观察并猜测线段BE 与线段CH 的数量关系,并说明理由;(2)如图2,当点E 在射线CN 上(不与点C 重合)时: ①判断△ADG 与△ABE 是否全等,不需说明理由;F B②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度α,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C图 2FG D A 图 1F D A外.(1)请探究:图(2)--(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论. (4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o , R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为: ;图(4)与图(6)中的等式有何关系?练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中, 点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21A B C D EP A B C DE P M(3) A B C D EP M (2) A B C D EM (P ) (1) A B C D E P M(5)C B APDEFC B E 又因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中,h 1、h 2、h 3、h 之间的关系;⑵ ⑶ ⑷ ⑸ (2)说明图(2)所得结论为什么是正确的;例2、已知△ABC 是等边三角形,将一块含30角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存在,请指出这条线段,并证明;如果不存在,请说明理由.(B)CE F图1ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P ) (1)练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.(1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是 。
人教版七年级(下)-实数题型大全

七年级(下)学科教师辅导讲义高频考点专题(1):实数的分类:(2011--2012年真题1题)有限小数无限循环小数小数无限小数无限不循环小数正有理数有理数零有限小数和无限循环小数实数负有理数正无理数无理数无限不循环小数负无理数整数包括正整数、零、负整数。
正整数又叫自然数。
正整数、零、负整数、正分数、负分数统称为有理数。
1. 有理数的定义:任何有限小数或无限循环小数也都是有理数。
2. 无理数的定义:无限不循环小数叫无理数(2011--2012年真题2题)(2011--2012年真题11题)(2010--2011年真题2题)【例题选登】1. 9的算术平方根是( )A .-3B .3C .±3D .81 2、 64的平方根是( )3、4的平方的倒数的算术平方根是( ) A .4 B .18C .-14D .144、25的平方根是( )A 、5B 、5-C 、5±D 、5± 5.36的平方根是( )A 、6B 、6±C 、 6D 、 6±6.2)5(-的平方根是( )A 、 5±B 、 5C 、5-D 、5±7.1681的平方根是_______;9的平方根是_____8.若一个数的平方根是8±,则这个数的立方根是( ).A .2B .±2C .4D .±4 9.27-的立方根与81的平方根之和是( ).A .0B .6C .-12或6D .0或-6 10、144的算术平方根是 ,16的平方根是 ; 11、、327= , 64-的立方根是 ;12.3729--的平方根是( )A .9B .3C .3±D .9±C..A.A.1 AC(1)233221-+-+-(2)2224421816x x x x x x +++++--+例4.已知b a ,是实数,且有0)2(132=+++-b a ,求b a ,的值.例5 若|2x+1|与x y 481+互为相反数,则-xy 的平方根的值是多少?高频考点专题(8):求未知数x1、9x 2-256=02、4(2x-1)2=253、(2x+1)2 -16=0(1)(2x-1)2-169=0; (2)4(3x+1)2-1=0; (3)274x 3-2=0; (4)12(x+3)3=4. (2) 125-8x3=0高频考点专题(9):计算解答题 (2011--2012年真题20题)(2010--2011年真题13题)(2010--2011年真题20题)计算:40083321633⨯--- 36662101010++-22120123-914420045243⨯⨯⨯ 83122)10(973.0123+--⨯- 4×25 ; (2) 3064.0- (3)22513-15.(2010年重庆)计算:102010)51()5(97)1(-+-⨯+---π.16.(2010年四川省眉山)计算:1021()(52)18(2)23---+--⋅17.(2010浙江省喜嘉兴市)计算:|-2|+(2)0;18.(2010年浙江台州市)(1)计算:)1()2010(40---+;19(2010年浙江省东阳县)计算: 00145tan )21(4)31(--++--20.(2010江苏泰州,19⑴,8分)计算:(1)12)21(30tan 3)21(01+-+︒---;21.(2010年浙江省绍兴市)(1)计算: |2-|o 2o 12sin30(3)(tan 45)-+--+; 22.(2010年四川省眉山市)计算:1021()(52)18(2)23---+--⋅23.(2010年浙江省东阳市)(6分)计算: 00145tan )21(4)31(--++--24. (2010年兰州市)(1)(本小题满分4分)60tan 2-—0)14.3(-π+2)21(--1221+高频考点专题(10):数轴比较大小问题数a 、b 在数轴上的位置如图所示:化简:222)()1()1(b a b a ---++如图,数轴上表示1,的对应点分别为A ,B ,点B 关于点A 的对称点为C ,则点C 表示的数是( ).A .-1B .1-C .2-D .-2已知实数、、在数轴上的位置如图所示:化简高频考点专题(11):整数部分与分数部分2、 已知a 是7的整数部分,b 是7的小数部分,求(b -7)a 的值2、设实数的整数部分为a ,小数部分为b ,求的值。
七年级下册数学一元一次方程应用题归类集锦(经典)

七年级下册数学一元一次方程应用题归类集锦(经典)一元一次方程应用题归类汇集一、列方程解应用题的一般步骤(解题思路)(1)审—审题:认真审题,弄清题意,找出能够表示本题含义的相等关系(找出等量关系).(2)设—设出未知数:根据提问,巧设未知数.(3)列—列出方程:设出未知数后,表示出有关的含字母的式子,然后利用已找出的等量关系列出方程.(4)解——解方程:解所列的方程,求出未知数的值.(5)答—检验,写答案:检验所求出的未知数的值是否是方程的解,是否符合实际,检验后写出答案.(注意带上单位)二、各类题型解法分析一元一次方程应用题归类汇集:行程问题,工程问题,和差倍分问题(生产、做工等各类问题),等积变形问题,调配问题,分配问题,配套问题,增长率问题,数字问题,方案设计与成本分析,古典数学,浓度问题等。
(一)和、差、倍、分问题——读题分析法这类问题主要应搞清各量之间的关系,注意关键词语。
仔细读题,找出表示相等关系的关键字,例如:“大,小,多,少,是,共,合,为,完成,增加,减少,配套”,利用这些关键字列出文字等式,并且据题意设出未知数,最后利用题目中的量与量的关系填入代数式,得到方程.1、倍数关系:通过关键词语“是几倍,增加几倍,增加到几倍,增加百分之几,增长率”来体现。
2、多少关系:通过关键词语“多、少、和、差、不足、剩余”来体现。
增长量=原有量某增长率现在量=原有量+增长量例1.某单位今年为灾区捐款2万5千元,比去年的2倍还多1000元,去年该单位为灾区捐款多少元?例2.旅行社的一辆汽车在第一次旅程中用去油箱里汽油的25%,第二次旅程中用去剩余汽油的40%,这样油箱中剩的汽油比两次所用的汽油少1公斤,求油箱里原有汽油多少公斤?(二)等积变形问题等积变形是以形状改变而体积不变为前提。
常用等量关系为:原料体积=成品体积。
常见几何图形的面积、体积、周长计算公式,依据形虽变,但体积不变.2①圆柱体的体积公式V=底面积某高=S·h=rh②长方体的体积V=长某宽某高=abc③正方体(正六面体)的体积V=棱长3=a3例3.现有直径为0.8米的圆柱形钢坯30米,可足够锻造直径为0.4米,长为3米的圆柱形机轴多少根?练习:将一个装满水的内部长、宽、高分别为300毫米,300毫米和80毫米的长方体铁盒中的水,倒入一个内径为200毫米的圆柱形水桶中,正好倒满,求圆柱形水桶的高(精确到0.1毫米,≈3.14).(三)数字问题1.要搞清楚数的表示方法:一个三位数,一般可设百位数字为a,十位数字是b,个位数字为c(其中a、b、c均为整数,且1≤a≤9,0≤b≤9,0≤c≤9),则这个三位数表示为:100a+10b+c.2.数字问题中一些表示:两个连续整数之间的关系,较大的比较小的大1;偶数用2n表示,连续的偶数用2n+2或2n-2表示;奇数用2n+1或2n—1表示。
初一下数学典型题型

初一数学典型题型第一章整式的乘除一、化为同底1.已知x-2y+1=0,则2x÷4y×8=________。
变形:若4×2m×16×9×18×3n=29×36 ,则m=______,n=________。
2.若3x=4,9y=7,则3x-2y 的值为________。
二、化为同幂1.试比较2100 与375 的大小。
2.(—0.125)8(8)9=__________。
三、配项1.若a2-b2=1/4,a-b=1/2,则a+b=_______。
变形:已知a+b=8,ab=3,求(a-b)2的值。
2.计算:6(7+1)(72+1)(74+1)(78+1)+1变形:(n+1)(n2+1)(n4+1)(n8+1);(n-m)(n2-m)(n4-m)(n8-m)3.20152-2014×2016=;4.若a-b=1,则代数式a2-b2-2b的值为_______。
5.二次三项式x2-kx+9是一个完全平方式,则k的值是________。
6.3012=___________。
四、整体代入1.若a3b2=15,求-5a6b4 的值。
2.已知a+b=5,ab=—6,求下列各式的值:a2 +b2 ;;3.已知(m-n)2=8,(m+n)2=2,则m2+n2=__________。
4.已知x2-2=y,则x(x-3y)+y(3x-1)-2的值是_________。
五、平方差、完全平方公式整体运用1.(2x+3y)2—(2x-3y)2六、多项式求待定系数1.若代数式x 2+3x+2可以表示为(x-1)2+a(x-1)+b 的形式,则a+b=________。
第二章 相交线与平行线一、添加辅助线1.已知∠BCD=∠B+∠D ,试判断直线AB 与直线DE 是否平行。
二、方程思想1.若一个角的余角比它的补角的1/2少20。
,求这个角的度数。
2023-2024学年七年级数学下册 实数 压轴题(十大题型)(原卷版)

(1)如图1,当2n =时,拼成的大正方形ABCD 的边长为
如图2,当5n =时,拼成的大正方形1111D C B A 的边长为
如图3,当10n =时,拼成的大正方形2222A B C D 的边长为
(2)小李想沿着正方形纸片1111D C B A 边的方向能否裁出一块面积为()22.42dm
的长方形纸片,使它的长宽之比
为21:?他能裁出吗?请说明理由.
(1)仿照康康上述的方法,探究7
(2)继续仿照上述方法,在(1)中得到的
确,精确到0.001(画出示意图,标明数据,并写出求解过程)
(3)综合上述具体探究,已知非负整数
的估算值.
(1)有44⨯的网格,每个方格的边长为1,把正方形ABCD画在网格中,要求顶点在格点上.
(2)如图,把正方形ABCD放到数轴上,使得点A与数1-重合,边
为________.
任务:
(1)在图3中画图确定表示10的点M.
(2)把5个小正方形按图中位置摆放,并将其进行裁剪,拼成一个大正方形.请在图中画出裁剪线,并在图中画出所拼得的大正方形的示意图.
(3)小丽想用一块面积为36cm
它的长是宽的2倍.小丽能用这块纸片裁出符合要求的纸片吗?请你通过计算说明理由.
(4)在图6中的数轴上分别标出表示数。
七年级数学下册典型题习题

数学典型题汇总一、选择题1.等腰三角形的一个角为100°,则它的底角为 ( ) A 、100° B 、40° C 、100°或40° D 、不能确定2.已知方程组⎩⎨⎧=+=+22y 3x 6y 4x ,则x - y 的值是 ( ) A 、0 B 、-2 C 、2 D 、4 3.下列四组线段中,能组成三角形的是( ) A 、2 cm ,3 cm ,4 cm B 、3 cm ,4 cm ,7 cm C 、4 cm ,6 cm ,2 cm D 、7 cm ,10 cm ,2 cm 4.已知、互余,比大.设、的度数分别为、,下列方程组中符合题意的是( ) A 、B 、C 、D 、5.用一个10倍的放大镜去观察一个三角形,下列说法中正确的是( )① 三角形的每个角都扩大10倍;② 三角形的每条边都扩大10倍; ③ 三角形的面积扩大10倍; ④ 三角形的周长扩大10倍; A 、① ② B 、① ③ C 、② ④ D 、② ③ 6.如图,已知△ABC 为直角三角形,∠C=90°, 若沿图中虚线剪去∠C , 则∠1+∠2等于( ) A. 90° B. 135° C. 270° D. 315°7.三角形的两边长分别是3和5,第三边a 的取值范围是( ) A. 2≤a <8 B. 2<a ≤8 C. 2<a <8 D.2≤a ≤88.三角形一个外角小于与它相邻的内角,这个三角形是( )A .直角三角形B .锐角三角形C .钝角三角形D .属于哪一类不能确定 9.等腰三角形的两边分别为3和6,则这个三角形的周长是 ( ). A.12 B. 15 C .9 D .12或1510.如图,已知直线a 、b 被直线c 所截,a ∥b ,∠1=130°,则 ∠2=( )A. 130°B. 50°C.40°D.60°11.如图,直线AB 与CD 交于点O,OE ⊥AB 于O,图∠1与∠2的关系是( )A.对顶角B.互余C.互补 D 相等 二、填空题B DE 13A CF 2 1. 已知(2x+3y-18)2 +|4x+5y-32|=0,则4x-3y=_______________.2. 已知四边形四个内角的度数的比是1:2:3:4,则这个四边形最大内角=________.3. 将一个正方形剪开后按如图7所示的方法拼接起来,则ABC =_______.4. 如图8所示,在△ABC 中,外角∠DCA=100°,∠A=40°,则∠B=________, ∠ACB=_________.5.在△ABC 中,若∠A =∠B ,∠C =50°,则∠A = 度。
七年级下学期数学期末复习经典题型总结

七年级下学期数学期末复习一、相交线与平行线1、角度计算问题1.如图,已知、、相交于点O,⊥,平分∠,∠=28°,求∠、∠、∠的度数.2.已知∥∥,A是上一点,∠=70°,∠=50°,平分∠,求:⑴∠的大小;⑵∠的大小.3、如图:已知:,求∠4的度数4、如图,∥,∠B =1350,∠670,则求∠1的度数.2.证明问题1. 已知⊥,⊥,垂足分别为D 、G ,且∠1=∠2,猜想∠与∠C 有怎样的大小关系?试说明理由.2. 如图,已知直线l 1∥l 2,直线l 3和直线l 1、l 2交于点C 和D ,在C 、D 之间有一点P ,如果P 点在C 、D 之间运动时,问∠,∠,∠之间的关系是否发生变化.若点P 在C 、D 两点的外侧运动时(P 点与点C 、D 不重合),试探索∠,∠,∠之间的关系又是如何?3.如图,已知∠ +∠ = 180°,∠1 =∠2,求证:∠F =∠G.l 1 l CB DP l 2 A1 2 A C BF G ED4.如图,∠和∠的平分线交于E ,交于点F ,∠1 +∠2 = 90°.求证:(1)∥; (2)∠2 +∠3 = 90°.3、三线八角问题1.若三条直线交于一点,则共有对顶角(平角除外)( )C1 2 3A B DFA.六对B.五对C.四对D.三对2.如图所示,∠1的邻补角是( )A.∠B.∠和∠C.∠D.∠和∠3.如图所示,内错角共有( )对对对对4、如图,由已知条件推出的结论,正确的是().A.由,可推出 B.由,可推出C.由,可推出D.由,可推出二、实数1、基本概念1、代数式,,,,中一定是正数的有()。
A、1个B、2个C、3个D、4个2、若有意义,则x的取值范围是()。
A、x>B、x≥C、x>D、x≥3、下列说法中,错误的是()。
A、4的算术平方根是2B、的平方根是±3C、8的立方根是±2 D、立方根等于-1的实数是-14、下列命题中,正确的是()。
