绝对值考点专题讲解(新)
《绝对值》考点专题讲解(完整资料).doc
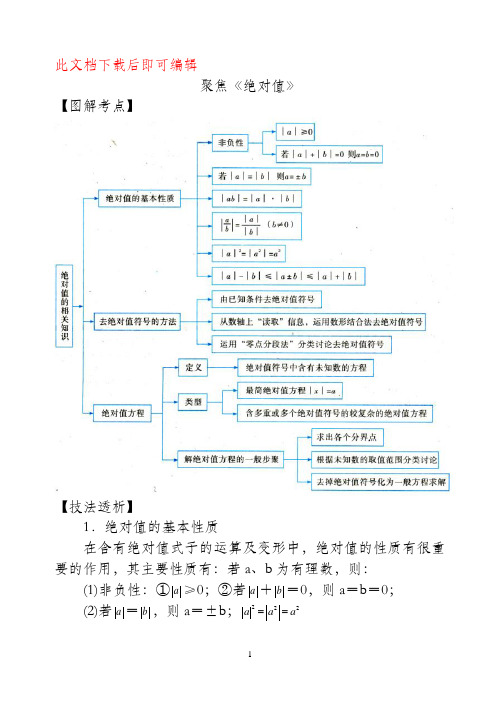
此文档下载后即可编辑聚焦《绝对值》【图解考点】【技法透析】1.绝对值的基本性质在含有绝对值式子的运算及变形中,绝对值的性质有很重要的作用,其主要性质有:若a、b为有理数,则:(1)非负性:①a≥0;②若a+b=0,则a=b=0;(2)若a=b,则a=±b;222==a a a(3)ab a b =•;a a b b =(b ≠0); ④a b a b a b -≤±≤+.特别关注:若干个非负数之和为0,则这几个非负数必须同时为0,即:a +b +…+n =0,则a =b =…=n =0.2.去绝对值符号的方法去掉绝对值符号是绝对值化简的关键,而绝对值符号内的数(或式)的正负性的判断是化简的关键,在实际运用中常见的去绝对值符号的方法有:(1)由已知条件去绝对值.(2)从数轴上“读取”相关信息,运用数形结合去绝对值.(3)运用“零点分段法”分类讨论去绝对值,特别关注:对于多个绝对值问题,其解题思路为:求零点、分区间、定性质、去符号,即令各绝对值代数式为零,得若干个绝对值为零的点,这些点把数轴分成若干个区间,再在各区间内化简求值即可.3.绝对值方程(1)最简单的绝对值方程为x =a ,它的解法情况如下: ①当a>0时,方程有两解:x =a 或x =-a ,②当a =0时,方程有一解:x =0,③当a<0时,方程无解.(2)解绝对值方程的一般步骤①求出各个零界点.②根据未知数的取值范围分类讨论.③去绝对值符号,化为一般方程求解,在转化过程中,经常荽用到分类讨论,数形结合等方法.在解题过程中,要充分利用绝对值的意义和性质,善于观察,发掘题目中的隐含条件,从而简化解题过程.特别关注:对于解绝对值方程,零点分段法是一种非常重要的方法.4.绝对值的几何意义在生活中的应用在实际生活中经常要通过借助数轴模型使复杂的数量关系形象化,简单化,同时又使实际问题数学化,从而运用绝对倌的几何定义求解.一般地,设a 1,a 2,a 3,…a n 是数轴上依次排列的点表示的有理数,对于12n x a x a x a -+-+-L ,则:(1)当n 为奇数时,此式在x =12n a +时取最小值;(2)当n 为偶数时,此式在2n a ≤x ≤12n a +时取最小值. 【名题精讲】赛点1 绝对值的化简例 1 1111111111201720162016201520152014322-+-+-++-+-L =_______.【切题技巧】 脱去绝对值符号是绝对值化简的切入点,而对绝对值符号中的正负性的判断是化简的关键,本例若直接化简会很繁锁,应从a 的性质入手,由题中条件可知,每一绝对值符号内均为负数,于是有当a<0时a =-a .【规范解答】 原式=1111111-----12017201620162015201520142----L ()()()()=12016-+120172017= 【借题发挥】 绝对值化简关键是要去掉绝对值符号,而要去掉绝对值符号,先要对绝对值符号中的数(或式)的正负性进行判断.去掉绝对值符号有三种方法,本例可以由已知条件直接判断各个绝对值符号内均为负数,于是可以利用1a 1的性质顺利达到去掉绝对值符号的目的.【同类拓展】1.有理数a ,b 的大小关系如图,则1212a b a b a b a b -++-+-++的值是( D )。
初一数学绝对值知识点、考点及例题梳理

初一数学绝对值知识点、考点及例题梳理绝对值是初一上册数学的重难点之一,很多同学绝对值的学习中都存在着一些问题,所有问题的根源大都是对绝对值的概念理解不透彻,没有建立起完整的知识体系,在此梳理下在绝对值学习中需要注意的一些要点。
在绝对值的学习中,首先需要去理解和掌握的就是绝对值的概念,什么是绝对值呢?在数轴上,一个数所对应的点与原点之间的距离。
在概念的理解中需要注意,绝对值这个概念是从数轴引出的,它表示的是距离,绝对值本质上是数轴上两点之间的距离,哪两点之间的距离呢?表示某个数的点和原点。
那么由绝对值的定义,我们可以得到有关绝对值的那些性质呢?因为绝对值表示的是距离,从日常经验可知,距离最小为0,不可能为负数,所以就得出了绝对值最重要的一条性质:绝对值具有非负性。
从绝对值的定义出发,结合绝对值的非负性,可以得到绝对值的代数意义,也看成是绝对值性质的推广:正数的绝对值等于它本身;0的绝对值是0;负数的绝对值等于它的相反数。
以上三条需要牢记。
这是求绝对值和简化绝对值的方法基础。
除过绝对值的定义和性质之外,在绝对值的学习中还需要注意以下细节和要点:任何数都有绝对值,只有一个,而且是非负的。
但是有两个数的绝对值等于正数,而且是相反的。
很多同学容易漏掉其中的一个,比较容易出错。
在有关绝对值的运算,在解含有绝对值的方程中,经常需要运用到分类讨论思路。
绝对值的概念来源于数轴,代表数轴上两点之间的距离。
绝对值与数轴有着密切的关系,在绝对值相关题目的分析和求解中,一定要注意数形结合思想的应用。
特别是在绝对值的几何意义的理解和应用上,需要结合数轴来分析和解决。
绝对值等于它本身的数是正数和0,绝对值等于它的相反数的数是负数和0.1.解决问题的关键是理解绝对值的定义和性质,把握其非负性。
2、求一个数的绝对值,先判定这个数是正数、负数还是0,再根据绝对值的性质确定最终的结果。
3、利用绝对值比较两个负数的大小:两个负数比较大小,绝对值大的反而小。
1.4 绝 对 值 考点梳理与突破(课件)华东师大版(2024)数学七年级上册

C.- |-5|=-5,故 C 项错误;
D.-[-(+8)]=8,故 D 项错误.
[答案]B
返回目录
1.4 绝 对 值
重 ■题型一 绝对值非负性的应用
难
例 1 已知 |a-3| 与 |2b-4| 互为相反数.
题
型
(1)求 a 与 b 的值;
突
破
(2)若|x|=2a+4b,求 x 的相反数.
1.4 绝 对 值
返回目录
变式衍生 数轴上点 A 表示的数的绝对值是 3,且在
重
难
题 原点的左侧,B,C 两点表示的数互为相反数,且点 B 到
型 点 A 的距离是 2,则点 C 表示的数应该是________.
5或1
突
破
1.4 绝 对 值
返回目录
解题通法 在数轴上表示互为相反数的两个点在原点的
重
返回目录
1.4 绝 对 值
重
难
题
型
突
破
返回目录
[答案] 解:(1)因为|a-3|与 |2b-4|互为相反数,
所以 |a-3|+ |2b-4| =0,所以 a-3=0,2b-4=0,
解得 a=3,b=2;
(2)因为 a=3,b=2,
所以 |x| =2a+4b=2×3+4×2=6+8=14,
所以 x=±14,所以 x 的相反数为-14 或 14.
析
[答案] C
[易错] D
[错因]|a| = |b| ,忽略了 a=-b 这种情况.
1.4 绝 对 值
返回目录
易错警示 两个数的绝对值相等时,这两个数可能相等
1-2-3绝对值定值、最值探讨.讲义教师版

内容 基本要求略高要求较高要求绝对值 借助数轴理解绝对值的意义,会求实数的绝对值会利用绝对值的知识解决简单的化简问题板块一:绝对值几何意义当x a =时,0x a -=,此时a 是x a -的零点值.零点分段讨论的一般步骤:找零点、分区间、定符号、去绝对值符号.即先令各绝对值式子为零,求得若干个绝对值为零的点,在数轴上把这些点标出来,这些点把数轴分成若干部分,再在各部分内化简求值. a 的几何意义:在数轴上,表示这个数的点离开原点的距离.a b -的几何意义:在数轴上,表示数a 、b 对应数轴上两点间的距离.一、绝对值定值探讨【例1】 若1232008x x x x -+-+-++- 的值为常数,试求x 的取值范围. 【考点】绝对值定值探讨 【难度】4星 【题型】解答 【关键词】【解析】要使式子的值为常数,x 得相消完,当10041005x ≤≤时,满足题意. 【解答】10041005x ≤≤【巩固】 若24513a a a +-+-的值是一个定值,求a 的取值范围. 【考点】绝对值定值探讨 【难度】4星 【题型】解答 【关键词】【解析】要想使24513a a a +-+-的值是一个定值,就必须使得450a -≥,且130a -≤,原式245(13)3a a a =+---=,即1435a ≤≤时,原式的值永远为3.【解答】1435a ≤≤例题精讲中考要求绝对值定值、最值探讨【巩固】 如果对于某一给定范围内的x 值,13p x x =++-为定值,则此定值为 .【考点】绝对值定值探讨 【难度】3星 【题型】填空【关键词】第17届希望杯培训试题【解析】利用绝对值的几何意义解答.零点1-、3把数轴分成分成3段,容易发现当13x -≤≤这个区间时13p x x =++-为定值4,当1x <-或3x >时,有134p x x =++->.【解答】当1x <-或3x >时【例2】 已知112x x ++-=,化简421x -+-. 【考点】绝对值定值探讨 【难度】4星 【题型】解答【关键词】第16届希望杯培训试题【解析】由112x x ++-=的几何意义,我们容易判断出11x -≤≤.所以421x -+-421434311x x x x x =-+-=--=-+=+=+.【解答】1x +【例3】 已知代数式374x x -+-=,则下列三条线段一定能构成三角形的是( ).A . 1,x ,5B . 2,x ,5C . 3,x ,5D . 3,x ,4【考点】绝对值定值探讨 【难度】3星 【题型】【关键词】第18届希望杯培训试题【解析】根据374x x -+-=可得37x ≤≤,所以选择C . 【解答】C【例4】 是否存在有理数x ,使132x x ++-=?【考点】绝对值定值探讨 【难度】4星 【题型】解答【关键词】分类讨论 【解析】略 【解答】不存在【巩固】 是否存在整数x ,使433414x x x x -+-++++=?如果存在,求出所有整数x ,如果不存在,请说明理由【考点】绝对值定值探讨 【难度】4星 【题型】解答 【关键词】 【解析】略【解答】3210x x x x =±=±=±=,,,【例5】 将200个数1~200任意分为两组(每组100个),将一组从小到大排列,设为12100a a a <<< ,另一组从大到小排列,设为12100b b b >>> ,求代数式1122100100a b a b a b -+-++- 的值.【考点】绝对值定值探讨 【难度】6星 【题型】 【关键词】【解析】设k 是1~100中任意一个数,如果100k a ≤且100k b ≤,那么在第一组中不大于100的数至少有1a 、2a 、…、k a 这k 个数,在第二组中不大于100的数至少有k b 、1k b +、…、100b 这(101)k -个数,则不大于100的数至少有101101k k -+=个,这不可能.因此k a 与k b 这两个数当中较大的一个一定大于100,所以代数式1122100100a b a b a b -+-++-(101102200)(12100)(1011)(1022)(200100)10010010000=+++-+++=-+-++-=⨯=【解答】10000二、绝对值最值探讨【例6】 设2020y x b x x b =-+-+--,其中020,20b b x <<≤≤,求y 的最小值. 【考点】绝对值最值探讨 【难度】3星 【题型】解答【关键词】2006年,七台河市中考题【解析】2020(20)(20)40y x b x x b x b x x b x =-+-+--=------=-, 则20x =时,y 有最小值为20.【解答】20【巩固】 已知2x ≤,求32x x --+的最大值与最小值.【考点】绝对值最值探讨 【难度】3星 【题型】解答【关键词】北京市中考题【解析】法1:根据几何意义可以得到,当2x ≤-时,取最大值为5;当2x =时,取最小值为3-.法2:找到零点3、2-,结合2x ≤可以分为以下两段进行分析:当22x -≤≤时,323212x x x x x --+=---=-,有最值3-和5; 当2x <-时,32325x x x x --+=-++=;综上可得最小值为3-,最大值为5. 【解答】最小值为3-,最大值为5.【例7】 已知04a ≤≤,那么23a a -+-的最大值等于 .【考点】绝对值最值探讨 【难度】4星 【题型】填空【关键词】第10届希望杯2试 【解析】(法1):我们可以利用零点,将a 的范围分为3段,分类讨论(先将此分类讨论的方法,而后讲几何意义的方法,让学生体会几何方法的优越性)(1)当02a ≤≤时,2352a a a -+-=-,当0a =时达到最大值5;(2)当23a <≤时,231a a -+-=(3)当34a <≤时,2325a a a -+-=-,当4a =时,达到最大值3 综合可知,在04a ≤≤上,23a a -+-的最大值为5(法2):我们可以利用零点,将a 的范围分为3段,利用绝对值得几何意义分类讨论,很 容易发现答案:当0a =时达到最大值5.【解答】5【巩固】 如果122y x x x =+-+-,且12x -≤≤,求y 的最大值和最小值 【考点】绝对值最值探讨 【难度】3星 【题型】解答 【关键词】【解析】当10x -<≤时,有12223y x x x x =+-+-=+,所以13y <≤;当02x ≤≤时,有12232y x x x x =+-+-=-,所以13y -≤≤综上所述,y 的最大值为3,最小值为1-【解答】y 的最大值为3,最小值为1-【巩固】 已知759x -≤≤,求x 取何值时13x x --+的最大值与最小值.【考点】绝对值最值探讨 【难度】3星 【题型】解答【关键词】2001年,大同市中考题【解析】法1:13x x --+表示x 到点1和3-的距离差,画出数轴我们会发现当,79x =时两者的距离 差最小为329-,即()m i n 32139x x --+=-;当53x -≤≤-时,两者的距离差最大为4,即m a x (13)4x x --+=. 法2:分类讨论:先找零点,根据范围分段,当53x -≤<-时,134x x --+=;当739x -≤≤时,1322x x x --+=--,当79x =有最小值329-;当3x =-有最大值4.综上所得,当53x --≤≤时,最大值为4;当79x =时,最小值为329-.【解答】当53x --≤≤时,最大值为4;当79x =时,最小值为329-.【例8】 已知11x y ≤,≤,设1124M x y y x =++++--,求M 的最大值和最小值【考点】绝对值最值探讨【难度】4星 【题型】解答 【关键词】【解析】由已知首先讨论绝对值符号内的代数式的符号因为1x ≤,所以11x -≤≤,所以012x +≤≤,同理可得012y +≤≤因为1y ≤,所以11y -≤≤,所以222y -≤≤⑴因为1x ≤,所以11x -≤≤,所以11x --≤≤,所以14414x -----≤≤即543x ----≤≤⑵⑴与⑵同向相加得7241y x ----≤≤ 化简M 的表达式:26M x y =-+ 求M 的取值范围:因为11y -≤≤,所以222x -≤≤ 因为11y -≤≤,所以11y --≤≤ 所以323x y --≤≤ 所以3269x y -+≤≤当11x y ==-,时,M 最大值为9 当11x y =-=,时,M 最小值为3 【解答】M 最大值为9;M 最小值为3【巩固】 已知m 是实数,求12m m m +-+-的最小值【考点】绝对值最值探讨 【难度】4星 【题型】解答【关键词】数形结合【解析】根据绝对值的几何意义,这个问题可以转化为在数轴上找一点m ,使点m 到点0,点1和点2的距离之和最小,显然当1m =时,原式的最小值为2 【解答】2【巩固】 已知m 是实数,求2468m m m m -+-+-+-的最小值 【考点】绝对值最值探讨 【难度】4星 【题型】解答【关键词】数形结合【解析】根据绝对值的几何意义,这个问题可以转化为在数轴上找一点m ,使m 到点2,点4,点6和点8的距离和最小,显然当点m 在点4和点6之间(包括点4和点6)时,原式的值最小为8 【解答】8【例9】 设123...n a a a a ,,,是常数(n 是大于1的整数),且123...n a a a a <<<<,m 是任意实数,试探索求123...n m a m a m a m a -+-+-++-的最小值的一般方法【考点】绝对值最值探讨【难度】4星 【题型】解答【关键词】数形结合【解析】根据题意,结合数轴,不难得到:⑴当n 为奇数时,即当21n k =+(k 为正整数)时,点m 应取在点1k a +处,原式的值最小,最小值为()()()211222...k k k k a a a a a a ++-+-++-⑵当n 为偶数2k (k 是正整数)时,m 应取点k a 和点1k a +之间的任意位置,原式的值最小,最小值为()()()212121...k k k k a a a a a a -+-+-++-【答案】根据题意,结合数轴,不难得到:⑴当n 为奇数时,即当21n k =+(k 为正整数)时,点m 应取在点1k a +处,原式的值最小,最小值为()()()211222...k k k k a a a a a a ++-+-++-⑵当n 为偶数2k (k 是正整数)时,m 应取点k a 和点1k a +之间的任意位置,原式的值最小,最小值为()()()212121...k k k k a a a a a a -+-+-++-【巩固】 122009x x x -+-++- 的最小值为 .【考点】绝对值最值探讨 【难度】4星 【题型】填空【关键词】数形结合【解析】当1005x =时,122009x x x -+-++- 取到最小值:122009x x x -+-++- 100511005210052009=-+-++- 1004100310110031004=++++++++ (10041)10041009020=+⨯=点评:若1221n a a a +<<< ,当1n x a +=时,1221n x a x a x a +-+-++- 取得最小值. 若122n a a a <<< ,当x 满足1n n a x a +≤≤时,122n x a x a x a -+-++- 取得最小值.【解答】【巩固】 试求123...2005x x x x -+-+-++-的最小值【考点】绝对值最值探讨 【难度】4星 【题型】解答【关键词】数形结合【解析】联想到绝对值的几何意义:n x x -即表示数轴上数x 的对应点与数n x 的对应点的距离,把这些绝对值转化为同一数轴上若干条线段之和来研究,发现12x x -+-,当12x ≤≤时,它有最小值1,对于123x x x -+-+-,当2x =时,最小值为2,…猜想当1003x =时,原式有最小值最小值为123...2005x x x x =-+-+-++-100311003210033...10032005=-+-+-++-100210011000...21012...1002=++++++++++()10021002122⨯+=⨯1005006= 【解答】1005006【例10】 设a b c <<,求当x 取何值时x a x b x c -+-+-的最小值.【考点】绝对值最值探讨 【难度】4星 【题型】解答【关键词】2000年,郑州市中考题【解析】x a x b x c -+-+-实际表示x 到a b c ,,三点的距离和,画图可知当x b =时,原式有最小值为c a -. 【解答】c a -【例11】 正数a 使得关于x 的代数式162x x x a ++-+-的最小值是8,那么a 的值为 . 【考点】绝对值最值探讨 【难度】4星 【题型】填空【关键词】数形结合【解析】如果6a ≤,那么当x a =时,16216(1)(6)7x x x a a a a a ++-+-=++-=++-=,小于8与已知条件矛盾.所以6a >,那么算式162x x x a ++-+-的几何意义是点x 到1-、6、a 、a 的4个距离之和,当6x a ≤≤时取最小值,因此令6x =可得7268a +-=,解得132a =. 【解答】132【例12】 若1x 、2x 、3x 、4x 、5x 、6x 是6个不同的正整数,取值于1,2,3,4,5,6,记122334455661||||||||||S x x x x x x x x x x x x =-+-+-+-+-+-,则S 的最小值是 .【考点】绝对值最值探讨 【难度】5星 【题型】填空【关键词】2009年,全国初中数学联赛四川初赛试卷【解析】利用此题我们充分展示一下数形结合的优越性:利用绝对值的几何意义122334455661||||||||||x x x x x x x x x x x x -+-+-+-+-+-在数轴上表示出来,从1x 开始又回到1x ,我们可以看成是一个圈,故最小值为10,如下图所示,即使重叠路程最少.【解答】10【例13】 在数轴上把坐标为123...2006,,,,的点称为标点,一只青蛙从点1出发,经过2006次跳动,且回到出发点,那么该青蛙所跳过的全部路径的最大长度是多少?请说明理由【考点】绝对值最值探讨 【难度】5星 【题型】【关键词】2006年,山东竞赛试题【解析】设青蛙依次到达的点为12320061...x x x x x ,,,,,,整个跳过的路径长度为 12233420061...S x x x x x x x x =-+-+-++-()()2210041005...20062123..100321003+++-++++=⨯≤故青蛙跳过的路径的最大长度为221003⨯【解答】221003⨯【例14】 如图所示,在一条笔直的公路上有7个村庄,其中A 、B 、C 、D 、E 、F 到城市的距离分别为4、10、15、17、19、20千米,而村庄G 正好是AF 的中点.现要在某个村庄建一个活动中心,使各村到活动中心的路程之和最短,则活动中心应建在什么位置?【考点】绝对值最值探讨 【难度】4星 【题型】解答 【关键词】【解析】因为村庄G 是AF 的中点,所以村庄G 到城市的距离为12千米,即村庄G 在村庄B C 、之间,7 个村庄依次排列为A B G C D E F 、、、、、、.设活动中心到城市的距离为x 千米,各村到活动中心的距离之和为y 千米,则:4101215171920y x x x x x x x =-+-+-+-+-+-+-因为4101215171920<<<<<<,所以当15x =时y 有最小值,所以活动中心应当建在C 处.【解答】C 处【例15】 如图,在一条数轴上有依次排列的5台机床在工作,现要设置一个零件供应站P ,使这5台机床到供应站P 的距离总和最小,点P 建在哪?最小值为多少?【考点】绝对值最值探讨 【难度】4星【题型】解答 【关键词】【解析】设供应站P 在数轴上所对应的数x ,则5台机床到供应站P 的距离总和为(1)1248x x x x x --+-+-+-+-,当2x =时,原式值最小为12.即供应站P 建在点C 处,这5台机床到供应站P 的距离总和最小为12.【解答】12【例16】 (6级)如图所示为一个工厂区的地图,一条公路(粗线)通过这个地区,7个工厂1A ,2A ,…,7A 分布在公路的两侧,由一些小路(细线)与公路相连.现在要在公路上设一个长途汽车站,车站到各工厂(沿公路、小路走)的距离总和越小越好,那么这个车站设在什么地方最好?如果在P 点又建立了一个工厂,并且沿着图上的虚线修了一条小路,那么这时车站设在什么地方好?FEDCBPA 7A 6A 5A 4A 3A 2A 1【考点】绝对值最值探讨 【难度】5星 【题型】解答 【关键词】【解析】每一条小路都是工厂到车站的必经之路,和其他工厂无关.但在公路上,有些路段将是一些工厂重复经过的,应使重复路线越短越好.要使各工厂到车站的距离之和最小,只要各工厂经小路进入公路的入口处(B C D E F 、、、、)到车站的距离之和最小即可,各路段的弯曲程度是无关紧要的,因此可以把公路看成一条直线,即车站设在D 点最好.若在P 处再建一个工厂,则车站建在D 处、E 处或它们之间的任何地方都是最佳的.【解答】车站建在D 处、E 处或它们之间的任何地方都是最佳的.【例17】 先阅读下面的材料,然后回答问题:在一条直线上有依次排列的()1n n >台机床在工作,我们要设置一个零件供应站P ,使这n 台机床到供应站P 的距离总和最小,要解决这个问题,先“退”到比较简单的情形:如图甲,如果直线上有2台机床时,很明显设在1A 和2A 之间的任何地方都行,因为甲和乙所走的距离之和等于1A 到2A 的距离。
(新)绝对值不等式精编版

因。
谁和谁分离?
等位基因分离
什么时候分离? 在减数第一次分裂时分离
它们怎样分离? 等位基因随着同源染色体的分开而分离
为什么能够分离? 等位基因彼此独立
11.孟德尔的遗传学实验——假说—演绎法 P96
P96
假说—演绎法
•观察实验→分析现象,提出问题
•提出(解释问题的)假说。
•根据假说进行演绎推理;
⑶水毛茛叶的两种形态说明什么?
P11
表现型是基因型与环境共同作用的结果! 表现型 = 基因型+环境
13.一对同源染色体相同位置上的基因一定是等位 基因吗? 不一定,可能是Aa 也可能是AA、aa, 14.一对同源染色体上只有一对等位基因吗? NO! 15.在F1进行减数分裂的时产生的配子中只含有成 对基因中的一个吗? YES! P7 16. 雌配子和雄配子的比例接近于1:1吗? NO!
解:|x-1|+|x+2|=5的解为x=-3或x=2
-3 -2
12
所以原不等式的解为 x x ≥2或x ≤3
解不等式|x-1|+|x+2|≥5
方法二:利用|x-1|=0,|x+2|=0的零点,把数轴分为三段, 然后分段考虑把原不等式转化为不含绝对值符号的不等
式求解(零点分段讨论法).(体现了分类讨论的思想)
{__x__x____32__且__x_.2}
考点2. x a x b c和 x a x b c型 不等式的解法
怎么解不等式|x-1|+|x+2|≥5 呢?
解绝对值不等式关键是去绝对值符号, 你有什么方法解决这个问题呢?
解不等式|x -1|+|x +2|≥5
方法一:利用绝对值的几何意义(体现了数形结 合的思想).
初中数学绝对值知识点

初中数学绝对值知识点一、绝对值的定义。
1. 几何定义。
- 在数轴上,表示数a的点与原点的距离叫做数a的绝对值,记作| a|。
例如,在数轴上表示5的点到原点的距离是5,所以|5| = 5;表示-3的点到原点的距离是3,所以| - 3|=3。
2. 代数定义。
- 一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0。
即当a>0时,| a|=a;当a = 0时,| a|=0;当a<0时,| a|=-a。
例如,|7| = 7,| -2|=-(-2)=2。
二、绝对值的性质。
1. 非负性。
- 任何数的绝对值都是非负数,即| a|≥slant0。
例如,| - 5| = 5≥slant0,|0| = 0。
2. 互为相反数的两个数绝对值相等。
- 若a与b互为相反数,即a=-b,那么| a|=| b|。
例如,3与-3互为相反数,|3|=| - 3| = 3。
3. 绝对值相等的两个数可能相等或互为相反数。
- 若| a|=| b|,则a = b或a=-b。
例如,若| x| = 5,则x = 5或x=-5。
三、绝对值的运算。
1. 简单的绝对值计算。
- 根据绝对值的定义进行计算。
例如:- 计算| - 8|,因为-8<0,根据代数定义| - 8|=-(-8)=8。
- 计算|3 - π|,因为π≈3.14>3,即3-π<0,所以|3 - π|=π - 3。
2. 含有绝对值的方程。
- 例如| x| = 2,根据绝对值的性质可知x = 2或x=-2。
- 对于方程|2x - 1| = 3,则2x - 1 = 3或2x - 1=-3。
- 当2x - 1 = 3时,2x=4,解得x = 2。
- 当2x - 1=-3时,2x=-2,解得x=-1。
3. 含有绝对值的不等式。
- 对于不等式| x|<3,根据绝对值的几何定义,它表示在数轴上到原点的距离小于3的点对应的数,所以-3 < x < 3。
绝对值-【寒假预习】六年级数学核心考点+重难点讲练与测试(沪教版)(解析版)

第03讲绝对值目录考点一:利用数轴比较有理数的大小考点二:绝对值的意义考点三:求一个数的绝对值考点四:化简绝对值考点五:绝对值非负性的应用考点六:有理数大小比较考点七:有理数大小比较的实际应用【基础知识】一.绝对值(1)概念:数轴上某个数与原点的距离叫做这个数的绝对值.①互为相反数的两个数绝对值相等;②绝对值等于一个正数的数有两个,绝对值等于0的数有一个,没有绝对值等于负数的数.③有理数的绝对值都是非负数.(2)如果用字母a表示有理数,则数a绝对值要由字母a本身的取值来确定:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数﹣a;③当a是零时,a的绝对值是零.即|a|={a(a>0)0(a=0)﹣a(a<0)二.有理数大小比较(1)有理数的大小比较比较有理数的大小可以利用数轴,他们从右到左的顺序,即从大到小的顺序(在数轴上表示的两个有理数,右边的数总比左边的数大);也可以利用数的性质比较异号两数及0的大小,利用绝对值比较两个负数的大小.(2)有理数大小比较的法则:①正数都大于0;②负数都小于0;③正数大于一切负数;④两个负数,绝对值大的其值反而小.【规律方法】有理数大小比较的三种方法1.法则比较:正数都大于0,负数都小于0,正数大于一切负数.两个负数比较大小,绝对值大的反而小.2.数轴比较:在数轴上右边的点表示的数大于左边的点表示的数.3.作差比较:若a﹣b>0,则a>b;若a﹣b<0,则a<b;若a﹣b=0,则a=b.【考点剖析】考点一:利用数轴比较有理数的大小一、单选题1.(2022·上海理工大学附属初级中学期中)下列说法正确的是()A.有理数都可以化成有限小数a b+=,则a与b互为相反数B.若0C.在数轴上表示数的点离原点越远,这个数越大D.两个数中,较大的那个数的绝对值较大【答案】B【分析】根据数轴的定义性质、相反数的定义、绝对值,有理数定义解决该题.【详解】A、∵有理数是有限小数或无限循环小数,所以此选项错误;B、∵a+b=0,∴a与b互为相反数,所以此选项正确;C、数轴上原点的右边,离原点越远的点表示的数越大;数轴上原点的左边,离原点越远的点表示的数越小,所以此选项错误;D、两个数中,较大的那个数的绝对值不一定大,例如,|-3|>|2|,但-3<2.所以此项错误,故选:B.【点睛】本题考查了有理数,相反数、数轴、绝对值,解决本题的关键是熟记有理数,相反数、数轴、绝对值的定义.2.(2021·上海市民办新复兴初级中学期中)已知有理数a、b在数轴上的位置如图所示,下列结论正确的是().A .a b ->B .a b -<-C .a b>-D .a a>-二、填空题3.(2022·上海市罗南中学阶段练习)数轴上到原点的距离小于132个单位长度的点中,表示整数的点共有______个.三、解答题4.(2022·上海奉贤·期中)(1)在数轴上画出分数34,43,125所对应的点A 、B 、C ;(2)点D 表示的点在A 左边0.25个单位,点E 表示的数是点D 的倒数,点F 表示的数是134的整数部分,求点D 、E 、F 表示的数并在数轴上作出对应的点,并将A 、B 、C 、D 、E 、F 所表示的数用“>”连接35;(2) 点D表示的点在A左边0.25个单位,点∴点D表示的数是331210.2544442-=-==,点F表示的数是3,∴将数12,2,3所对应的点D、E、F表示在数轴上,如图所示:再由(1)中各数,将A、B、C、D、E∵在数轴上从左到右,数逐步增大,12431325342∴>>>>>.【点睛】本题考查了有理数大小比较以及数轴,理解每个分数表示的意义,然后正确在数轴上表示出各个数是解决本题的关键.5.(2022·上海普陀·期中)在数轴上分别用A、B表示出225,3这两个分数对应的点,并写出数轴上的点C、D所表示的数,点C表示的数是;点D表示的数是.再将这几个数用“<”连接起来:.由图可知,C点表示的数是253,D点表示的数是4.5.左到右用“<”连接为1222 4.55 353 <<<.故答案为:图见解析;253;4.5;1222 4.55353<<<【点睛】本题考查了数轴,以及有理数的大小比较,牢固掌握数轴的性质是解题的关键.6.(2022·上海嘉定·期中)在数轴上分别画出点A、B、C、D,并将点A、B、C、D所表示的数用“<”连接:点A表示数32;点B表示数54;点C表示数223;点D表示数2.5327.(2022·上海·位育中学期中)在数轴上分别画出数1、23、1.5和5所对应的点A、B、C和D,并用“<”连接这几个数.将点A、B、C和D所表示的数用“<”连接__________.8.(2022·上海市闵行区莘松中学期中)在数轴上分别画出点A、B、C、D,点A表示数3,点B表示数1 2,点C表示数2-,点D表示数324;并将点A、B、C、D所表示的数用“>”连接.9.(2022·上海普陀·期末)写出数轴上点A、B表示的数,并且在数轴上画出点C,最后将点A、B、C所表示的数用“<”连接.点C表示的数为31 4.解:点A表示的百分数为,点B表示的假分数为.<<.10.(2022·上海黄浦·期中)(1)填空:写出数轴上的点A、点B所表示的数.点A表示的数是,点B表示的数是.(2)已知点C表示的数是325,点D表示的数是1.5,请在(1)中的数轴上分别画出点C和点D,并标明相应字母;(3)将A、B、C、D四个点所表示的数按从大到小的顺序排列,用“>”连接.11.(2021·上海·青教院附中期中)在数轴上分别画出数0.875、2、14和12所对应的点A、B、C和D,用“>”连接这几个数.将点A、B、C和D所表示的数用“>”连接:______.根据数轴上右边的数总比左边的大得:2>314>0.875>12.故答案为:2>314>0.875>12.【点睛】本题主要考查了数轴,数轴上的点与实数是一一对应的关系,要注意数轴上的点比较大小的方法是左边的数总是小于右边的数.把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.考点二:绝对值的意义一、单选题1.(2022·上海宝山·期中)数轴上有四个点分别表示65、56、34和43,这四个点中离表示1的点最远的是()A.表示65的点B.表示56的点C.表示34的点D.表示43的点【点睛】本题考查了数轴上两点距离,分数的减法运算,绝对值的意义,掌握以上知识是解题的关键.2.(2022·上海·位育中学期中)下列说法不正确的是()A.0既不是正数,也不是负数B.1是绝对值最小的有理数C.一个有理数不是整数就是分数D.0的绝对值是0【答案】B【分析】分别根据绝对值、0的特殊性,和有理数的分类进行逐个判断即可.【详解】解:A.0既不是正负,也不是负数,正确,不符合题意;B.绝对值最小的数是0,所以B选项错误,符合题意;C.整数和分数统称有理数,所以一个有理数不是整数就是分数,所以C选项正确,不符合题意;D.0的绝对值是0,所以D选项正确,不符合题意.故选:B.【点睛】本题主要考查绝对值、有理数的分类及0的特殊性,注意0既不是正数也不是负数.二、填空题3.(2022·上海民办民一中学期中)有理数a在数轴上的对应点的位置如图所示,若有理数b满足b a<,所有满足条件的b的值之和是____________.x=则x=________.4.(2022·上海杨浦·期中)若3【分析】根据绝对值的意义可直接进行求解.【详解】解:绝对值是3的数是3±,∴3x=±,故答案为:3±.【点睛】本题主要考查了绝对值的定义,正确理解其定义是解题的关键.a=,则=a__________.5.(2022·上海·位育中学期中)若||2±【答案】2【详解】解:∵|a|=2,∴a=±2.故答案为±2.考点三:求一个数的绝对值一、填空题1.(2022·上海市罗星中学模拟预测)有理数5-的绝对值为_______.2.(2022·上海市罗南中学阶段练习)在下列数﹣3,0,14,﹣|4|,﹣(﹣4)中,非负数是_____.3.(2022·上海理工大学附属初级中学期末)数轴上的点A表示0.3,点B表示﹣3,这两点中离原点距离较近的点是点______.【答案】A【分析】离原点较近的点是绝对值较小的数,据此解答即可.4.(2022·上海静安·二模)计算:|﹣2|=___.【答案】2【分析】根据一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0,即可求解【详解】∵﹣2<0,∴|﹣2|=2故答案为:2考点四:化简绝对值一、单选题1.(2022·上海杨浦·期中)若a ,b 各表示一个有理数,且0ab ≠,则算式a b a b-的可能值有()A .1个B .2个C .3个D .4个二、填空题2.(2022·上海理工大学附属初级中学期中)如图,根据数轴上表示的三个数的位置,化简:b c a b a c ---++=______.【答案】2c-3.(2022·上海民办民一中学期中)有理数a ,b ,c 在数轴上表示的点如图所示,则化简22b c a b c a +----=______.【答案】4a-b【分析】根据数轴可以判断a 、b 、c 的正负和它们的绝对值的大小,从而可以化简题目中的式子.【详解】解:由数轴可得,a <b <c ,|b |<|c |<|a |,∴|b +c |﹣2|a ﹣b |﹣|c ﹣2a |=b +c ﹣2(b ﹣a )﹣(c ﹣2a )=b +c ﹣2b +2a ﹣c +2a =4a-b .【点睛】本题考查数轴、绝对值,解答本题的关键是明确题意,利用数形结合的思想解答.三、解答题4.(2022·上海·七年级专题练习)已知,,a b c 在数轴上的对应点如图所示,且a b =;(1)根据数轴判断:a b +_________0,c b -__________0.(填>,<,=)(2)1c a c b a b c ---+++-.)考点五:绝对值非负性的应用一、单选题1.(2021·上海市第四中学期末)若0a b +=,则a 与b 的大小关系是()A .a 与b 不相等B .a 与b 互为相反数C .a 与b 互为倒数D .0a b ==故选:D .【点睛】题目主要考查绝对值的非负性,理解绝对值的非负性是解题关键.二、填空题2.(2021·上海·期末)已知||x y y x -=-,||2x =,||3y =,则x y +=_______.【答案】5或1##1或5【分析】根据绝对值的性质。
第03讲 绝对值与相反数(解析版)

第3讲 绝对值与相反数1.借助数轴理解绝对值和相反数的概念;2.知道|a|的绝对值的含义以及互为相反数的两个数在数轴上的位置关系; 3.会求一个数的绝对值和相反数,并会用绝对值比较两个负有理数的大小; 4.通过应用绝对值解决实际问题,体会绝对值的意义和作用.考点01:相反数1.定义:如果两个数只有符号不同,那么称其中一个数为另一个数的相反数.特别地,0的相反数是0. 要点诠释:(1)“只”字是说仅仅是符号不同,其它部分完全相同. (2)“0的相反数是0”是相反数定义的一部分,不能漏掉. (3)相反数是成对出现的,单独一个数不能说是相反数. (4)求一个数的相反数,只要在它的前面添上“-”号即可. 2.性质:(1)互为相反数的两数的点分别位于原点的两旁,且与原点的距离相等(这两个点关于原点对称).(2)互为相反数的两数和为0.考法01:20161-的相反数是( ) A .2016 B .﹣2016 C .20161 D .20161-【思路】解决这类问题的关键是抓住互为相反数的特征“只有符号不同”,所以只要将原数的符号变为相反的符号,即可求出其相反数. 【答案】C【解析】解:∵20161-与20161只有符号不同, ∴﹣20161的相反数是20161.故选:C .【总结】求一个数的相反数,只改变这个数的符号,其他部分都不变.考点02:多重符号的化简多重符号的化简,由数字前面“-”号的个数来确定,若有偶数个时,化简结果为正,如-{-[-(-4)]}=4 ;若有奇数个时,化简结果为负,如-{+[-(-4)]}=-4 . 要点诠释:(1)在一个数的前面添上一个“+”,仍然与原数相同,如+5=5,+(-5)=-5. (2)在一个数的前面添上一个“-”,就成为原数的相反数.如-(-3)就是-3的相反数,因此,-(-3)=3.考法02:(本溪校级月考)化简:(1)﹣{+[﹣(+3)]}; (2)﹣{﹣[﹣(﹣|﹣3|)]}. 【答案】解:(1)原式=﹣{+[﹣3]}=﹣{﹣3}=3;(2)原式=﹣{﹣[﹣(﹣3)]}=﹣{﹣[+3]}=﹣{﹣3}=3.【总结】运用多重符号化简的规律解决这类问题较为简单.即数一下数字前面有多少个负号.若有偶数个,则结果为正;若有奇数个,则结果为负.考点03:绝对值1.定义:在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值,例如+2的绝对值等于2,记作|+2|=2;-3的绝对值等于3,记作|-3|=3. 要点诠释:(1)绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.即对于任何有理数a 都有:(2)绝对值的几何意义:一个数的绝对值就是表示这个数的点到(0)||0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩原点的距离,离原点的距离越远,绝对值越大;离原点的距离越近,绝对值越小. (3)一个有理数是由符号和绝对值两个方面来确定的. 2.性质:(1)0除外,绝对值为一正数的数有两个,它们互为相反数. (2)互为相反数的两个数(0除外)的绝对值相等.(3)绝对值具有非负性,即任何一个数的绝对值总是正数或0.考法03:求下列各数的绝对值. 112-,-0.3,0,132⎛⎫-- ⎪⎝⎭【思路】112,-0.3,0,132⎛⎫-- ⎪⎝⎭在数轴上位置距原点有多少个单位长度,这个数字就是各数的绝对值.还可以用绝对值法则来求解. 【答案】 方法1:因为112-到原点距离是112个单位长度,所以111122-=. 因为-0.3到原点距离是0.3个单位长度,所以|-0.3|=0.3. 因为0到原点距离为0个单位长度,所以|0|=0. 因为132⎛⎫-- ⎪⎝⎭到原点的距离是132个单位长度,所以113322⎛⎫--= ⎪⎝⎭.方法2:因为1102-<,所以111111222⎛⎫-=--= ⎪⎝⎭. 因为-0.3<0,所以|-0.3|=-(-0.3)=0.3. 因为0的绝对值是它本身,所以|0|=0 因为1302⎛⎫--> ⎪⎝⎭,所以113322⎛⎫--= ⎪⎝⎭【总结】求一个数的绝对值有两种方法:一种是利用绝对值的几何意义求解(如方法1),一种是利用绝对值的代数意义求解(如方法2),后种方法的具体做法为:首先判断这个数是正数、负数还是零.再根据绝对值的意义,确定去掉绝对值符号的结果是它本身,是它的相反数,还是零.从而求出该数的绝对值.考点04:有理数的大小比较1.数轴法:在数轴上表示出这两个有理数,左边的数总比右边的数小. 如:a 与b 在数轴上的位置如图所示,则a <b . 2.法则比较法:两个数比较大小,按数的性质符号分类,情况如下:两数同号同为正号:绝对值大的数大同为负号:绝对值大的反而小两数异号 正数大于负数 -数为0正数与0:正数大于0负数与0:负数小于0要点诠释:利用绝对值比较两个负数的大小的步骤:(1)分别计算两数的绝对值;(2)比较绝对值的大小:(3)判定两数的大小.3. 作差法:设a 、b 为任意数,若a-b >0,则a >b ;若a-b =0,则a =b ;若a-b <0,a <b ;反之成立.4. 求商法:设a 、b 为任意正数,若1a b >,则a b >;若1a b =,则a b =;若1ab<,则a b <;反之也成立.若a 、b 为任意负数,则与上述结论相反.5. 倒数比较法:如果两个数都大于零,那么倒数大的反而小.考法04:比较下列有理数大小:(1)-1和0; (2)-2和|-3| ; (3)13⎛⎫-- ⎪⎝⎭和12- ; (4)1--______0.1-- 【答案】(1)0大于负数,即-1<0;(2)先化简|-3|=3,负数小于正数,所以-2<3,即-2<|-3|;(3)先化简1133⎛⎫--=⎪⎝⎭,1122-=,1123>,即1132⎛⎫--<- ⎪⎝⎭.(4)先化简11--=-,0.10.1--=-,这是两个负数比较大小:因为11-=,0.10.1-=,而10.1>,所以10.1-<-,即1--<0.1--【解析】(2)、(3)、(4)先化简,再运用有理数大小比较法则.【总结】在比较两个负数的大小时,可按下列步骤进行:先求两个负数的绝对值,再比较两个绝对值的大小,最后根据“两个负数,绝对值大的反而小”做出正确的判断.考向01:绝对值的非负性已知|2-m|+|n-3|=0,试求m-2n 的值.【思路】由|a |≥0即绝对值的非负性可知,|2-m |≥0,|n-3|≥0,而它们的和为0.所以|2-m |=0,|n-3|=0.因此,2-m =0,n-3=0,所以m =2,n =3. 【答案】解:因为|2-m|+|n-3|=0且|2-m|≥0,|n-3|≥0 所以|2-m|=0,|n-3|=0 即2-m =0,n-3=0 所以m =2,n =3 故m-2n =2-2×3=-4.【解析】由|a |≥0即绝对值的非负性可知,|2-m |≥0,|n-3|≥0,而它们的和为0.所以|2-m |=0,|n-3|=0.因此,2-m =0,n-3=0,所以m =2,n =3.【总结升华】若几个数的绝对值的和为0,则每个数都等于0,即|a|+|b|+…+|m|=0时,则a =b =…=m =0.考向02:绝对值的应用正式足球比赛对所用足球的质量有严格的规定,下面是6个足球的质量检测结果,用正数记超过规定质量的克数,用负数记不足规定质量的克数.检测结果(单位:克):-25,+10,-20,+30,+15,-40.裁判员应该选择哪个足球用于这场比赛呢?请说明理由.【答案】 因为|+10|<|+15|<|-20|<|-25|<|+30|<|-40|,所以检测结果为+10的足球的质量好一些.所以裁判员应该选第二个足球用于这场比赛.【解析】根据实际问题可知,哪个足球的质量偏离规定质量越小,则足球的质量越好.这个偏差可以用绝对值表示,即绝对值越小偏差也就越小,反之绝对值越大偏差也就越大. 【总结】绝对值越小,越接近标准.考向03:化简已知有理数a ,b ,c 在数轴上对应的点的位置如图所示:化简:【答案】由图所示,可得.∴ 30a c ->,,,∵.∴ 原式.【易错01】若|x ﹣2|与(y+3)2互为相反数,则x+y= . 【答案】-1.∵|x ﹣2|与(y+3)2互为相反数, ∴|x ﹣2|+(y+3)2=0, ∴x ﹣2=0,y+3=0, 解得x=2,y=﹣3, ∴x+y=2+(﹣3)=﹣1. 故答案为:﹣1. 【易错02】如果|x|=6,|y|=4,且x <y .试求x 、y 的值.四、考场失分防范【思路】6和-6的绝对值都等于6,4和-4的绝对值都等于4,所以要注意分类讨论.【答案】因为|x|=6,所以x=6或x=-6;因为|y|=4,所以y=4或y=-4;由于x<y,故x只能是-6,因此x=-6,y=±4.【总结】已知绝对值求原数的方法:(1)利用概念;(2)利用数形结合法在数轴上表示出来.无论哪种方法但要注意若一个数的绝对值是正数,则此数有两个,且互为相反数.此外,此题x=-6,y=±4,就是x=-6,y=4或x=-6,y=-4.【易错03】若﹣1<x<4,则|x+1|﹣|x﹣4|= .【思路】根据绝对值的性质:当a是正有理数时,a的绝对值是它本身a;当a是负有理数时,a的绝对值是它的相反数﹣a,可得|x+1|=x+1,|x﹣4|=﹣x+4,然后再合并同类项即可.【答案】2x﹣3.【解析】解:原式=x+1﹣(﹣x+4),=x+1+x﹣4,=2x﹣3.【总结】此题主要考查了绝对值,关键是掌握绝对值的性质,正确判断出x+1,x﹣4的正负性.【易错04】已知a、b为有理数,且满足:12,则a=_______,b=________.【答案】由,,,可得∴【总结】由于任何一个数的绝对值大于或等于0,要使这两个数的和为0,需要这两个数都为0.几个非负数的和为0,则每一个数均为0.五、考试真题探秘【真题01】一只可爱的小虫从点O 出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,小虫爬行的各段路程(单位:cm)依次记为:+5,-3,+10,-8,-6,+12,-10,在爬行过程中,如果小虫每爬行1cm 就奖励2粒芝麻,那么小虫一共可以得到多少粒芝麻?【思路】总路程应该为小虫爬行的距离和,和方向无关. 【答案】小虫爬行的总路程为:|+5|+|-3|+|+10|+|-8|+|-6|+|+12|+|-10|=5+3+10+8+6+12+10=54(cm) 小虫得到的芝麻数为54×2=108(粒) 答:小虫一共可以得到108粒芝麻.【总结】此题是绝对值的应用问题,当求爬行路程是即为各数的绝对值之和,如果求最后所在的位置时即为各数之和,最后看正负来决定方向.【真题02】已知|a|=2,|b|=2,|c|=3,且有理数a ,b ,c 在数轴上的位置如图所示,计算a+b+c 的值.【答案】解:由数轴上a 、b 、c 的位置知:b <0,0<a <c ; 又∵|a|=2,|b|=2,|c|=3, ∴a=2,b=﹣2,c=3; 故a+b+c=2﹣2+3=3.【真题03】已知有理数a ,b 满足ab 2<0,a +b >0,且|a |=2,|b |=3,求⎪⎪⎪⎪⎪⎪a -13+(b -1)2的值.【答案】解:由ab 2<0,知a <0.因为a +b >0,所以b >0.又因为|a |=2,|b |=3, 所以a =-2,b =3.所以⎪⎪⎪⎪⎪⎪a -13+(b -1)2=⎪⎪⎪⎪⎪⎪-2-13+(3-1)2=73+4 =613. 【真题04】如图,A ,B ,C 三点在数轴上,A 表示的数为-10,B 表示的数为14,点C 在点A 与点B 之间,且AC =BC .(1)求A ,B 两点间的距离; (2)求C 点对应的数;(3)甲、乙分别从A ,B 两点同时相向运动,甲的速度是1个单位长度/s ,乙的速度是2个单位长度/s ,求相遇点D 对应的数.【答案】解:(1)A ,B 两点间的距离为24. (2)C 点对应的数为2. (3)相遇点D 对应的数为-2.【真题05】已知|2-xy |+(1-y )2=0. (1)求y2 019+(-y )2 019的值;(2)求1xy +1(x +1)(y +1)+1(x +2)(y +2)+…+1(x +2 019)(y +2 019)的值.【答案】解:因为|2-xy |+(1-y )2=0,而|2-xy |≥0,(1-y )2≥0, 所以2-xy =0 ①,1-y =0 ②. 由②得y =1.把y =1代入①得2-x =0,故x =2. (1) y2 019+(-y )2 019=12 019+(-1)2 019=1+(-1)=0. (2)1xy +1(x +1)(y +1)+1(x +2)(y +2)+…+1(x +2 019)(y +2 019)=11×2+12×3+13×4+…+12 020×2 021=⎝ ⎛⎭⎪⎫1-12+⎝ ⎛⎭⎪⎫12-13+(13-14)+…+⎝ ⎛⎭⎪⎫12 020-12 021 =1-12+12-13+13-14+…+12 020-12 021=1+⎝ ⎛⎭⎪⎫-12+12+⎝ ⎛⎭⎪⎫-13+13+⎝ ⎛⎭⎪⎫-14+14+…+(-12 020+12 020)-12 021=1-12 021=2 0202 021.1.2021的相反数是( )A.2021B.-2021C. 20211-D.20211【答案】B2.如果0a b +=,那么,a b 两个数一定是( ).A .都等于0B .一正一负C .互为相反数D .互为倒数 【答案】C【解析】若0a b +=,则,a b 一定互为相反数;反之,若,a b 互为相反数,则0a b += 3.下列判断中,正确的是( ).A .如果两个数的绝对值相等,那么这两个数相等;B .如果两个数相等,那么这两个数的绝对值相等;C .任何数的绝对值都是正数;D .如果一个数的绝对值是它本身,那么这个数是正数. 【答案】B【解析】A 错误,因为两个数的绝对值相等,这两个数可能互为相反数;B 正确;C 错误,因为0的绝对值是0,而0不是正数;D 错误,因为一个数的绝对值是它本身的数除了正数还有0.4.已知点M 、N 、P 、Q 在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )A .MB .NC .PD .Q 【答案】D【解析】解:∵点Q 到原点的距离最远,∴点Q 的绝对值最大. 故选:D .5.下列各式中正确的是( ). A .103<- B .1134->- C .-3.7<-5.2 D .0>-2 【答案】D六、对点通关训练【解析】0大于负数.6.若两个有理数a 、b 在数轴上表示的点如图所示,则下列各式中正确的是( ).A .a >bB .|a|>|b|C .-a <-bD .-a <|b|【答案】B【解析】离原点越远的数的绝对值越大.7.如果a 与1互为相反数,则|a+2|等于________.【答案】1【解析】∵a 与1互为相反数,∴a=﹣1,把a=﹣1代入|a+2|得,|a+2|=|﹣1+2|=1.8. 化简下列各数: (1)23⎛⎫--= ⎪⎝⎭_ ;(2)45⎛⎫-+= ⎪⎝⎭ ;(3){[(3)]}-+-+=________. 【答案】24;;335- 【解析】多重符号的化简是由“-”的个数来定,若“-”个数为偶数个时,化简结果为正;若“-”个数为奇数个时,化简结果为负.9.已知|x|=2,|y|=5,且x >y ,则x =________,y =________.【答案】 ±2,-5【解析】| x |=2,则x=±2; | y |=5, y=±5.但由于x >y ,所以x=±2,y=-510.数a 在数轴上的位置如图所示.则|a-2|= .【答案】a-2【解析】由图可知:a ≥2,所以|a-2|=a-2.11.在数轴上,与-1表示的点距离为2的点对应的数是 .【答案】-3,112.已知4334x x -=-,则x 的取值范围是________.【答案】 34x ≤ 【解析】将43x -看成整体a ,即a a =-,则0a ≤,故430x -≤,34x ≤.13.绝对值大于2而小于6的所有整数的和是多少?(列式计算)【解析】解:根据题意画出数轴,如图所示:根据图形得:绝对值大于2而小于6的所有整数有:﹣3,﹣4,﹣5,3,4,5,这几个整数的和为:(﹣3)+(﹣4)+(﹣5)+3+4+5=[(﹣3)+3]+[(﹣4)+4]+[(﹣5)+5]=0.答:绝对值大于2而小于6的所有整数的和是0.14.化简下列各数,再用“<”连接.(1)-(-54) (2)-(+3.6) (3)53⎛⎫-+ ⎪⎝⎭(4)245⎛⎫--⎪⎝⎭【解析】 (1)-(-54)=54(2)-(+3.6)=-3.6(3)5533⎛⎫-+=- ⎪⎝⎭(4)224455⎛⎫--=⎪⎝⎭,按从小到大排列可得:52(+3.6)<(+)<(4)(54)35----<--15.已知:a是﹣(﹣5)的相反数,b比最小的正整数大4,c是最大的负整数.计算:3a+3b+c 的值是多少?【解析】解:∵a是﹣(﹣5)的相反数,∴a=﹣5,∵b比最小的正整数大4,∴b=1+4=5,∵c是最大的负整数,∴c=﹣1,∴3a+3b+c=3×(﹣5)+3×5﹣1,=﹣15+15﹣1=-11.(漳州)﹣13的相反数是()A . 13 B .-13 C .-3 D .3【答案】A2.在①+(+1)与-(-1);②-(+1)与+(-1);③+(+1)与-(+1);④+(-1)与-(-1)中,互为相反数的是().A.①② B.②③ C.③④ D.②④【答案】C【解析】先化简在判断,①+(+1)=1,-(-1)=1,不是相反数的关系;②-(+1)=-1,+(-1)=-1,不是相反数的关系;③+(+1)=1,-(+1)=-1,是相反数的关系;④+(-1)=-1,-(-1)=1,是相反数的关系,所以③④中的两个数是相反数的关系,所以答案为:C 3.满足|x|=-x的数有( ).A.1个 B.2个 C.3个 D.无数个【答案】D【解析】x为负数或零时都能满足|x|=-x,故有无数个.4.已知1|3|a=-,则a的值是( ).A.3 B.-3 C.13D.13+或13-【答案】D【解析】∵13a=,∴13a=±,∴13a=±5.a、b为有理数,且a>0、b<0,|b|>a,则a、b、-a、-b的大小顺序是( ). A.b<-a<a<-b B.-a<b<a<-b C.-b<a<-a<b D.-a<a<-b<b 【答案】A【解析】画数轴,数形结合.6.下列推理:①若a =b ,则|a|=|b|;②若|a|=|b|,则a =b ;③若a ≠b ,则|a|≠|b|;④若|a|≠|b|,则a ≠b .其中正确的个数为( ).A .4个B .3个C .2个D .1个【答案】C【解析】①正确;②错误,如|-2|=|2|,但是-2≠2;③错误,如-2≠2,但是|-2|=|2|;④正确.故选C .7.数轴上离原点的距离小于3.5的整数点的个数为m , 距离原点等于3.5的点的个数为n , 则3____m n -=.【答案】1【解析】由题意可知:7,2m n ==,所以27321m n -=-⨯=8.已知x 与y 互为相反数,y 与z 互为相反数,又2z =,则z x y -+= .【答案】-2【解析】因为,x z 均为y 的相反数,而一个数的相反数是唯一的,所以z x =,2z =,而y 为z 的相反数,所以y 为-2,综上可得:原式等于-2.9.1的相反数是 ; 的相反数是它本身.【答案】213-,0.10.绝对值不大于11的整数有 个.【答案】23【解析】要注意考虑负数.绝对值不大于11的数有:-11 、-10……0 、1 ……11共23个.11.如果m ,n 互为相反数,那么|m+n ﹣2021|= .【答案】2021.【解析】解:∵m ,n 互为相反数,∴m+n=0,∴|m+n ﹣2021|=|﹣2021|=2021;故答案为2021.12.若1a a =-,则a 0;若a a ≥,则a . 【答案】<;任意数.13.若有理数x 、y 满足|x|=5,|y|=2,且|x+y|=x+y ,求x ﹣y 的值.【解析】∵|x|=5,∴x=±5,又|y|=2,∴y=±2,又∵|x+y|=x+y ,∴x+y ≥0,∴x=5,y=±2,当x=5,y=2时,x ﹣y=5﹣2=3,当x=5,y=﹣2时,x ﹣y=5﹣(﹣2)=7.14.若|a+1.2|+|b ﹣1|=0,那么a+(﹣1)+(﹣1.8)+b 等于多少?【解析】解:∵|a+1.2|+|b ﹣1|=0,∴a+1.2=0,b ﹣1=0,∴a=﹣1.2,b=1,∴a+(﹣1)+(﹣1.8)+b=﹣3.15.阅读下面的材料:点A 、B 在数轴上分别表示实数a 、b ,A 、B 两点之间的距离表示为∣AB ∣,当A 、B 两点中有一点在原点时,不妨设点A 在原点,如图1-1-1,∣AB ∣=∣OB ∣=∣b ∣=∣a-b ∣;当A 、B 两点都不在原点时:①如图1-1-2,点A 、B 都在原点的右边:∣AB ∣=∣OB ∣-∣OA ∣=∣b ∣-∣a ∣=b-a=∣a-b ∣;②如图1-1-3,点A 、B 都在原点的左边:∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;③如图1-1-4,点A、B在原点的两边:∣AB∣=∣OA∣+∣OB∣=∣a∣+∣b∣=a+(-b)=∣a-b∣,综上,数轴上A、B两点之间的距离∣AB∣=∣a-b∣.回答下列问题:①数轴上表示2和5的两点之间的距离是_________,数轴上表示-2和-5的两点之间的距离是________,数轴上表示1和-3的两点之间的距离是___________;②数轴上表示x和-1的两点A和B之间的距离是________,如果∣AB∣=2,那么x为__________.③当代数式∣x+1∣+∣x-2∣取最小值时,相应的x的取值范围是______________.【解析】①∣2-5∣=3,∣-2-(-5)∣=3,∣1-(-3)∣=4.②∣AB∣=∣x-(-1)∣=∣x+1∣.∵∣AB∣=2,∴∣x+1∣=2,∴x+1=2或-2,∴x=1或-3.③令x+1=0,x-2=0,则x=-1,x=2.将-1、2在数轴上表示出来,如图1-1-5,则-1、2将数轴分为三部分x<-1、-1≤x≤2、x>2.当x<-1时,∣x+1∣+∣x-2∣=-(x+1)+〔-(x-2)〕=-2x+1>3;当-1≤x≤2时,∣x+1∣+∣x-2∣=x+1+2-x=3;当x>2时,∣x+1∣+∣x-2∣=x+1+x-2=2x-1>3.∴∣x+1∣+∣x-2∣的最小值是3,相应的x的取值范围是-1≤x≤2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
聚焦《绝对值》
【图解考点】
【技法透析】
1.绝对值的基本性质 在含有绝对值式子的运算及变形中,绝对值的性质有很重要的作用,其主要性质有:若a 、b 为有理数,则:
(1)非负性:①a ≥0;②若a +b =0,则a =b =0;
(2)若a =b ,则a =±b ;222a a a == (3)ab a b =•;a a b b
=(b ≠0);
④a b a b a b -≤±≤+.
特别关注:若干个非负数之和为0,则这几个非负数必须同时为0,即:a +b +…+n =0,则a =b =…=n =0.
2.去绝对值符号的方法
去掉绝对值符号是绝对值化简的关键,而绝对值符号内的数(或式)的正负性的判断是化简的关键,在实际运用中常见的去绝对值符号的方法有:
(1)由已知条件去绝对值.
(2)从数轴上“读取”相关信息,运用数形结合去绝对值.
(3)运用“零点分段法”分类讨论去绝对值,
特别关注:对于多个绝对值问题,其解题思路为:求零点、分区间、定性质、去符号,即令各绝对值代数式为零,得若干个绝对值为零的点,这些点把数轴分成若干个区间,再在各区间内化简求值即可.
3.绝对值方程
(1)最简单的绝对值方程为x =a ,它的解法情况如下:
①当a>0时,方程有两解:x =a 或x =-a ,
②当a =0时,方程有一解:x =0,
③当a<0时,方程无解.
(2)解绝对值方程的一般步骤
①求出各个零界点.
②根据未知数的取值范围分类讨论.
③去绝对值符号,化为一般方程求解,在转化过程中,经常荽用到分类讨论,数形结合等方法.在解题过程中,要充分利用绝对值的意义和性质,善于观察,发掘题目中的隐含条件,从而简化解题过程.
特别关注:对于解绝对值方程,零点分段法是一种非常重要的方法.
4.绝对值的几何意义在生活中的应用
在实际生活中经常要通过借助数轴模型使复杂的数量关系形象化,简单化,同时又使实际问题数学化,从而运用绝对倌的几何定义求解.一般地,设a 1,a 2,a 3,…a n 是数轴上依次排列的点表示的有理数,对于12n x a x a x a -+-+-,则:
(1)当n 为奇数时,此式在x =12n a +时取最小值;
(2)当n 为偶数时,此式在2n a ≤x ≤1
2n a +时取最小值.
【名题精讲】
赛点1 绝对值的化简
例1 1111111111201720162016201520152014322
-+-+-++-+-=_______. 【切题技巧】 脱去绝对值符号是绝对值化简的切入点,而对绝对值符号中的正负性的判断是化简的关键,本例若直接化简会很繁锁,应从a 的性质入手,由题中条件可知,每一绝对值符号内均为负数,于是有当a<0时a =-a .
【规范解答】 原式=
1111111-
----12017201620162015201520142----()()()()=12016-+120172017
= 【借题发挥】 绝对值化简关键是要去掉绝对值符号,而要去掉绝对值符号,先要对绝对值符号中的数(或式)的正负性进行判断.去掉绝对值符号有三种方法,本例可以由已知条件直接判断各个绝对值符号内均为负数,于是可以利用1a 1的性质顺利达到去掉绝对值符号的目的.
【同类拓展】1.有理数a ,b 的大小关系如图,则1212a b a b a b a b
-++-+-++的值是( D ) A .0 B .-1 C .-2 D .-3
赛点2 绝对值的分类讨论 例2 若abc<0,a +b +c>0,且x =a b c a b c
++,试求代数式(1-2x)2016-2016 x +2016的值.
【切题技巧】 解决本题的关键是对a 、b 、c 的符号的所有可能情况进行分类讨论,由abc<0可知a 、b 、c 中有一个或三个全为负数,又由a +b +c>0知a 、b 、c 不可能全为负数,所以a 、b 、c 中有一个负数,两个正数.
【规范解答】 由abc<0,可知a 、b 、c 中有一个负数或三个全为负数,又由a +b +c>0知a 、b 、c 不可能全为负数,所以可得a 、b 、c 中有一个负数,两个正数,依x 的轮换性,不妨设a>0、b>0、c<0.则:
1a b c x a b c
=
++=-.所以原代数式的值为:(1-2×1)2016-2016×1+2016=1-2016+2016=1.
【借题发挥】 解含绝对值符号的化简求值题的关键,在于善于运用已知条件去掉绝对值符号,而用分类讨论法是能达到去掉绝对值符号的常用方法.在分类讨论时,分类要全面、准确、不失一般性. 【同类拓展】 已知有理数x ,y ,z 满足xy<0,yz>0,且x =3,y =2,12z +=,求x +y +z 的值. -2
赛点3 求1232016x x x x -+-+-++-的最小值.
【规范解答】 由绝对值的几何意义知1x -a 1在数轴上表示数x 与数a 两点之间的距离,故求原式的最小值就是在数轴上找出表示x 的点,使它到1,2,3,…,2015,2016的点的距离和最小.
【规范解答】 由绝对值的几何意义可知:求原式的最小值,就是在数轴上找出表示x 的点,使它到1,2,3,…2016的点的距离之和最小,
可看出当1008≤x ≤1009时,原式的值最小,把x =1008代入原式中得: 原式=10081100821008310082016-+-+-++-
=1007+1006+1005+...+1+0+1+2+3+ (1008)
=2(1+2+3+…1007)+1008
【借题发挥】 (1)由绝对值的几何意义可知如图①当a ≤x ≤b 时,x a x b -+-的值最小,如图②当x =b 时,x a x b x c -+-+-的值最小.
(2)一般地,设a 1,a 2,a 3…a n 是数轴上依次排列的点表示的有理数,若n 为奇数,则当x =12n a +时,12n x a x a x a -+-+
+-的值最小;若n 为偶数,则当a 2n a ≤x ≤1
2n a +时, 12n x a x a x a -+-++-的值最小.
(3)在实际牛活中,有时需借助数轴模型,使实际问题数学化,从而运用绝对值的几何定义解决问题.
如某公共汽车运营线路AB 段上有A 、B 、C 、D 四个汽车站,如图所示,现在要在AB 段上修建一个加油站M ,为了使加油站选址合理,要求A 、B 、C 、D 四个汽车站到加油站M 的路程总和最小,试分析加油站M 在何处最好?求最小路程总和,即求M 到A 、
B 、
C 、
D 的距离和最小,不妨设A 、B 、C 、D 四点在数轴上且分别表示为数a ,b ,c ,d(a<c<d<b),点M 表示的数为工,则点M 到A 、B 、C 、D 四点距离和为x a x b x c x d -+-+-+-由绝对值几何定义可求解.
【同类拓展】 3.某城镇,沿环形路上依次排列有五所小学,它们顺次有电脑15台、7台、11台、3台、14台,为使各学校里电脑数相同,允许一些小学向相邻小学调出电脑,问怎样调配才能使调出的电脑总台数最少?并求出调出电脑的最少总台数.
一小向二小调3台,三小向四小调出1台,五小向四小调出6台,一小向五小调出2台,这样调出的电脑总数最小数目为12台.
赛点4 绝对值方程
例4 解方程22110x x -++=
【规范解答】 解含绝对值符号的方程的关键是去绝对值符号,这可采用“零点分段法”,即令x -2=0,2x +1=0,分别得到x =2,x =-12用2,-12
将数轴分成三段:
【规范解答】
【借题发挥】 对于含有多重绝对值符号的方程,可用零点分段法,从内向外逐个去掉绝对值符号,只是在分类讨论时要注意未知数的取值范围,以免出错,如解方程:21x x -+=3,解题时运用“零点分段法”从内向外,根据绝对值的代数定义、性质去简化方程.
【同类拓展】 4.已知21951x x y y ++-=----,求x +y 的最大值和最小值. -3.。
