【电动力学课件】4-4-5谐振腔-波导
中科大 电动力学 PPT

传播方向, 为衰减方向
《等离子体物理导论》
Copyright by Wandong LIU
复波矢求解
复波矢方程:
2 2 k k k 2i 2 0 i0
2
第八周
2 2 2 0 0
《等离子体物理导论》
电场的平行分量为零
平面边界电场垂直分量法向导数为零
E 0
1 H B
D E
nD
Copyright by Wandong LIU
矩形谐振腔电磁波模
直角坐标,电场(磁场)任一分量满足:
第九周
z
2u k 2u 0
E0 E0 2 0
1/ 2
第八周
H 0 0 0
1/ 2
E0
H 0 0 0
1/ 2
E0
H 0 0
1/ 2
ei / 4 E0
1/ 2
1 i E0 0
1/ 2 2
1 i 2 0 E0 1/ 2 E0 1 i 2 0
d X k x2 X 0 dx 2 2 d Y 2 2 k yY 0 dy d 2Z 2 k z2 Z 0 dz
2
k
2
2
L3
分离变量,令 u x, y, z X ( x)Y ( y ) Z ( z )
O
L1
y
k
《等离子体物理导论》
Copyright by Wandong LIU
矩形谐振腔驻波解
Ex x Ey Ez
电动力学课件 4.5 波导

Ex ( A sin k x x B cos k x x)(C sin k y y D cos k y y )ei ( kz z t ) i ( k z z t ) E ( A sin k x B cos k x )( C sin k y D cos k y ) e y x x y y i ( k z z t ) E ( A sin k x B cos k x )( C sin k y D cos k y ) e x x y y z
d 2Y 2 k yY 0 2 dy
X ( x) A sin k x x B cos k x x Y ( y ) C sin k y y D cos k y y
u ( x , y ) X ( x )Y ( y )
这里的 A、 B、C、 D、kx、ky都是待定常数。至此得到沿 z 轴方向传播的电磁波电场的三个分量为:
E
k
H
TE
k
z kz
TE波和 TM波是相对于叠加波的传播方向而言的
10
c) 截止频率
2 2
kx
m a
n m n 2 2 2 2 2 ky kz k k x k y kz k b a b 其中波数 k取决于波源的频率ω和波导内介质的性质,即
k
2 若电磁场的激发频率ω足够小,以致于 k 2 k x2 k y ,则 kz是
纯虚数, k z i ,显然由因子 e 能在该波导内传播。
i ( k z z t )
e z e i t 看到,这不再
是行波,而是场随着z的增加而指数衰减,所以此时电磁场不
2 2 2 2 ( 2 2 )u ( x , y ) ( k k z )u ( x , y ) 0 x y
电动力学 郭硕鸿 第三版 第21次课(4.5波导)

Ex = A1 cos kx x sin k y yei ( kz z −ωt ) Ey = A2 sin kx x cos k y yei ( kz z −ωt ) Ez = ( A′′ sin kx x + B′′ cos kx x)(C′′ sin k y y + D′′ cos k y y)ei ( kz z −ωt )
y
b
k x A + k y A2 − ik z A3 = 0 1
都确定的z 在y和x都确定的z向直线上 Ex = Ae
z
i (kz z−ωt )
a
x
= Acos(ωt − kz z)
Ex = A cos kx x sin ky yei(kz z−ωt ) 1 i (kz z−ωt ) Ey = A2 sin kx x cos ky ye Ez = A3 sin kx x sin ky yei(kz z−ωt )
nπ y = b, Ex = 0 k y = b v ∇⋅ E = 0
不能同时为零
b
Ex
Ey
z
a
x
kx A + k y A2 − ik z A3 = 0 1
电动力学-第4章-第4节-谐振腔

一、有界空间中的电磁波
这种有界空间中传播的电磁波有其本身的特点,而且广泛应二、理想导体边界条件
由于边界为理想导体,故认为导体内,只有面电流分布!略去角标表示介质一侧的场强,有边界条件:
3,理想导体为边界的边值问题在边界面上,若取轴沿法线方向,由
例:证明两平行无穷大的导体平面间可以传播一种偏振的
轴方向偏振,则此平面波满足导体板上
的边界条件,因此可以在导体板之间传播。
与导体面相切) 不满足
边界条件,因而不能在导体面间存在。
所以在两导
TEM平面波。
三、谐振腔
(10)
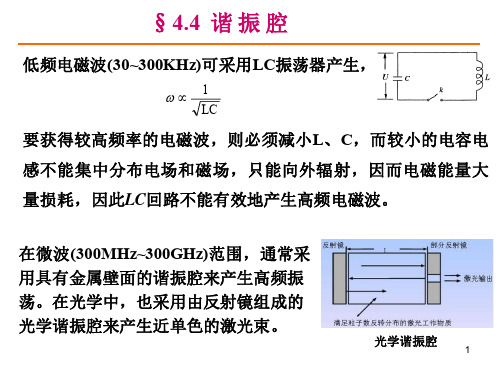
在光学中,采用由光学谐振腔来产生近单色的激光束。
反射镜(反射率100%)
反射镜(部分投射)
在微波范围,通常采用具有金属壁面的谐振腔来产生高频
2)设3)用可以得到三个方程:
4)用边界条件0
1≡⇒
D D C A =x
z
y
O
1
L 2
L 3
L 其中0同理可以求得
2,谐振波的讨论(2) 谐振腔的谐振频率(本征频率):(3) 最低频率的谐振波型。
《电动力学》第29讲§5.4波导管、谐振腔

山东大学物理学院 宗福建
17
1、有界空间中的电磁波 2、理想导体边界条件 3、谐振腔 4、高频电磁能量的传输 5、矩形波导中的电磁波 6、截止频率 7、TE10波的电磁场和管壁电流
山东大学物理学院 宗福建
18
§4.4 谐振腔、波导管
一、有界空间中的电磁波 第一节研究了在无界空间中,电磁波最基本的存在形式为
R
E
2
1
E
1
20
20
2
1
2
1 2
1
20
由上式可见,电导率愈高,则反射系数愈接近于1。
山东大学物理学院 宗福建
15
1、只要电磁波频率不太高,一般金属导体都可以看作良 导体。良导体内部没有自由电荷分布,电荷只能分布于导 体表面上。
2、导体中电磁波的表示式为
E ( x, t )
E e e αx i( βxt ) 0
波矢量k的实部β描述波的传播的相位关系,虚部α描述波 幅的衰减。β称为相位常数,α称为衰减常数。
山东大学物理学院 宗福建
16
3、对于高频电磁波,电磁场以及和它相互作用的高频电 流仅集中于表面很薄一层内,这种现象称为趋肤效应。
4、对于微波或无线电波,反射系数接近于1,只有很小一 部分电磁能量透入导体内部而被吸收掉,绝大部分能量被 反射出去。因此,在微波或无线电波情形下,往往可以把 金属近似地看作理想导体,其反射系数接近于1。
平面电磁波,这种波的电场和磁场都作横向振荡,称这种 类型的波为横电磁(TEM)波。 在有导体存在的电磁波情形中,由于电磁波与导体的相互 作用,电磁波主要是在导体以外的空间或绝缘介质内传播, 只有很小部分的电磁能量才能透人导体浅表层内。
山东大学物理学院 宗福建
电动力学课件 4.4 谐振腔
k B 0
B
k E
2.有界空间中的电磁波
金属一般为良导体,电磁波几乎全部被反射。因此,若空间中 的良导体构成电磁波存在的边界,金属边界制约管内电磁波的存 在形式。在这种情况下, Helmholtz方程的解不再是平面波解而 受到导体界面边界条件的束缚。
3
二.理想导体边界条件
实际导体虽然不是理想导体,但是象银或铜等金属导体,对无线 电波来说,透入其内而损耗的电磁能量一般很小,接近于理想导体。 在一定频率的电磁波情形,两不同介质(包括导体)界面上的 边值关系可以归结为
E z A 3 s in k x x s in k y y c o11 sk z z
表明 A1、 A2、 A3中只有两个是独立的
3.谐振波型
( 1)电场强度
E x , t E x e i t
E x E y E z m L1
m n A1 cos x sin y sin L1 L2 m n A2 sin x cos y sin L1 L2 m n A3 sin x sin y cos L1 L2 n p A1 A2 A3 0 L2 L3
0
C3 0
C
z
O
因此
E x A1 co s k x x sin k y y sin k z z
A1 C 1 D 2 D 3
L3
B
Ex
D
( 2)考虑 x L 1 E x 有 x L1 0 x
sin k x L 1 0
L2
A
k x A1 sin k x x sin k y y sin k z z
光学谐振腔
1
谐振腔是在微波频率下工作的谐振元件,它是一个任意形状的 由导电壁包围的,并能在其中形成电磁振荡的介质区域,它具 有储存电磁能及选择一定频率信号的特性. 根据不同用途,微波谐振腔的种类是多种多样的:矩形腔、圆 柱形腔、球形腔。
电动力学-第4章-第2节-电磁波在介质界面上的反射和折射
电磁波入射到介质界面发生反射和折射,其反射和折射的一、反射和折射定律在一定频率情形下,麦氏方程组不是完全独立的。
2,反射和折射定律的导出入射波、反射波和折射波的电场强度分别为:E E E ′′′,,(1) 角频率(2) 波矢分量间的关系:yy k ′′=′平面上,都在同一平面上,即分别代表入射角,反射角为电磁波在两介质中的相速度,则把波矢及它们的分量值代入它们之间的关系式,得这就是我们熟知的反射定律和折射定律!(3) 入射角、反射角和折射角的关系电磁波在介质界面上的反射和折射(9)211的相对折射率。
µ0,因此通常可认为就是两介质的相对折射率。
频率不同时,折射率亦不同,这是色散现象在折射问题中(4) 折射率电磁波在介质界面上的反射和折射(10)现应用边值关系式求入射、反射和折射波的振幅关系。
二、振幅和相位关系kr Hr k ′r k ′′r H ′′r H ′r E r E ′′r E ′r θθ′θ′′电磁波在介质界面上的反射和折射(11)1,E 入射面,如右图所示②①kr H r k ′r k ′′rH ′′r H ′r E r E ′′rE ′rθθ′θ′′xz nr利用已经推得的折射定律:2,E利用已经推得的折射定律得:(2a)(2b)三、全反射假设在情形下两介质中的电场形式上仍然不变,折射波电场:折射波磁场:电磁波在介质界面上的反射和折射(22)折射波平均能流密度:21θ分量,沿z 轴方向sin θ>n 21 情形下12122−n i θsin 则由菲涅耳公式可以求出反射波和折射波的振幅和相位。
例如在。
电动力学四五(波导)
用直角坐标分离变量, 设 u(x,y) 为 电磁场的任一直角分量。设
u x, y X x Y y
8
分解为两个方程
d X 2 k x X 0 2 dx 2 dY 2 k Y 0 y 2 dy
2
k k k k
2 x 2 y 2 z
c ,mn
m n a b
1 1 c ,10 2 2a
2
2
对 a>b,则TE10 波有最低截止频率
17
1 1 c ,10 2 2a
若管内为真空,最低截止频率为 c/2a ,相 应的截止波长为
c ,10 2a
E的解得出后,磁场 H为
i H E
13
对一定的 (m,n), 如果选一种波 模 具 有 Ez = 0 , 则 该 波 模 的 A1 / A2=ky / kx 就完全确定 , 因而另一种波模必须有Ez0。
14
i H E
对 Ez=0的波模,Hz0 。因此,在波导内 传播的波有如下特点:电场E和磁场H不能同 时为横波。通常选一种波模为 Ez = 0 的波, 称横电波(TE),另一种波模为Hz=0的波, 称横磁波( TM )。TE 波和TM 波又按( m , n)值的不同而分为TEmn和TMmn波 。 一般 情形下,在波导中可以存在这些波的叠加 。
3
在高频情况下,场的波动性显著,集中的电 容、电感等概念已不能适用,而且整个线路上的 电流不再是一个与位置x无关的量,而是和电磁场 相应地具有波动性质,此外,电压的概念亦失去 确切的意义。因此,在高频情况下,电路方程逐 渐失效,我们必须直接研究场和线路上的电荷电 流的相互作用,解出电磁场,然后才能解决电磁 能量传输问题.
电动力学第4章第2节电磁波在介质界面上的反射和折射
当改变入射角θ,致θ ” 变为90°时,折射波沿界面掠过。 这时的入射角θc 称为临界角,n21 = sinθc = ε 2 ε1
若入射角再增大,使 sinθ >n21,这时不能定义实数的折射 角,出现所谓的“虚角”,将有不同于一般反射折射的物 理现象。这时一般观察不到折射波,只有反射波,因而称 作全反射。现在我们研究这种情况下的电磁波解。
第二节 电磁波在介质界面上的反射和折射 (10)
二、振幅和相位关系 菲涅耳公式
的现由应于偏用对振边每波值一,关波它系矢们式在k求边有入界两射上个、的独反行立射和折射波的振θ幅E′′r关′′ 系krH。r′′′′
为不同,所以需要分别讨论 E ②
垂直于人射面和 E 平行于入射 面两种情形。
① Er θ θ ′ Er′
设 v1 和 v2 为电磁波在两介质中的相速度,则
k = k′ = ω v1 , k′′ = ω v2
把波矢及它们的分量值代入它们之间的关系式,得
sin θ = sin θ ′
sinθ sinθ ′′
=
k′′ k
θ =θ′ ,
sinθ sinθ ′′
=
v1 v2
这就是我们熟知的反射 定律和折射定律!
kr
z Er′′ kr′′
Hr ′′ θ ′′
θ θ′ Hr Hr ′
Er′x
kr′
Q
µ = µ0 , θ′ = θ , H =
εE µ
⇒ ε1 (E + E′) = ε2 E′′
第二节 电磁波在介质界面上的反射和折射 (15)
(2a) 菲涅耳公式 (对于E ⊥入射面)
E′ E
=
ε1 cosθ − ε1 cosθ +
电动力学-4-5几何光学的电磁学基础
常矢量
常矢量
真E空0中单er色ei时k0r谐, H球面0 波
r heik0r
变矢量
变矢量
场的更普遍形式
E0 er rr eik0Srr , H0
r h
rr
eik0Srr
“光程”,是位置的实标函数
代入麦克斯韦方程组
利用
矢量
H0
r
r
h
r
ikr0S
h
eik0S
r
H0 i E0 0
前两式消
去e或h
1
c
er S
=0
S er
S
2
cer
0
利用
c
a
b
c
b
a
c
ab
S 2 n2
n已知,可以获得S
S rr 常数
S x
2
S y
2
S z
2
n2
称为几何波面或几何波阵面
单色球面光波的光程函数为
S nr n x2 y2 z2 1 2
单色平面光波的光程函数为
光学长度[P1P2]等于光的真空速度和 光从P1传播到P2所需的时间之积
定义光学长度 P1P2
P2 P1
nds
S
P2
S
P1
由于平均能量密度是以速度v=c/n沿光线传播,因而
nds c ds cdt v
dt是能量沿光线行经距离ds所需的时间
P1P2
c P2 dt P1
4、电矢量和磁矢量在每一点都和光 线垂直
ds
ndsrrrdnsdrr
0
srds
用一过渡层代替突变面T,取一个面积元P1P2Q2Q1,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
注意:H是无散场,H场线闭合或延伸至无穷远。
另一种偏振的平面电
磁波(E与导体面相切)
不满足边界条件,因
而不能在导体面间存
在。所以在两导体板
之间只能传播一种偏
振的TEM平面波。
H E
8
三、谐振腔
实践上电磁波是用具有特定谐振频率的线路或元件激发。 低频无线电波采用LC回路产生振荡。在LC回路中,集中 分布于电容内部的电场和集中分布于电感线圈内部的磁 场交替激发,以一定频率振荡
就可以得到该边值问题的解。其中n×H=α反映介质中电磁 波的磁场强度与导体表面上高频电流的相互关系,其用途 主要是在解出介质中电磁波后,由它计算导体表面电流的 分布,以便计算第二级近似时求能量损耗,所以,真正制
约电磁波存在形式的是 n × E = 0,
∇2E + k2E = 0 ∇⋅E =0
n×E = 0
线由导体指向介质中。在理想导体情况下,导体内部没有
电磁场,因此,E1=H1=0。
略去角标2,以E和H表示介质一侧的场强,有边界条件:
n×E = 0
n×H = α
注意:E和H表示介质一侧的场强,n是从界面指向介质中。
4
在实际问题中,方程 ∇2 E + k 2 E = 0 ,再加上
∇ ⋅ E = 0, n × E = 0, n× H = α
对于理想导体(电导率σ→∞),电磁波全部被导体反射,穿
透深度趋于零,因此,导体表面自然构成电磁波存在的边界。
1
这种有界空间中传播的电磁波有其本身的特点,而且广泛应 用在许多无线电技术的实际问题中。 例如: 在微波技术中,常用波导来传输电磁能量。波导是中 空的金属管,电磁波在波导管内空间中传播,而金属管壁作 为电磁场存在的边界制约着管内电磁波的存在形式。 又如:在高频技术中常用谐振腔来产生一定频率的电磁振荡。 谐振腔是中空的金属腔,电磁波在腔内以某些特定频率振荡。
式中Ci,Di为任意常数。把u(x,y,z)具体化为E的各分 量时,考虑边界条件可得对这些常数的一些限制。
12
例如考虑Ex,通解为:
Ex (x, y, z) = (C1 cos kx x + D1 sin kx x)
(C2 cos ky y + D2 sin ky y)
(C3 cos kz z + D3 sin kz z)
1. 矩形谐振腔内的电磁振荡
如图,取金属壁的内表面分别为x =0和L1,y=0和 L2, z=0和L3面。 腔内电磁波的电场和磁场任一直角 分量都满足亥姆霍兹方程。
10
设u(x,y,z)为E或H 的任一直角分量,有
∇2u + k 2u = 0
用分离变量法,令
u(x, y, z) = X (x)Y ( y)Z (z)
ω = 1 2π LC
如果要提高谐振频率,必须减小L或C的值。 频率提高到一定限度后,具有很小的C和L值的电容和电 感不能再使电场和磁场集中分布于它们内部,这时向外 辐射的损耗随频率提高而增大。
9
另一方面由于趋肤效应,焦耳损耗亦增大。因此LC回路 不能有效地产生高频振荡。 在微波范围,通常采用具有金属壁面的谐振腔来产生高 频振荡。在光学中,也采用由反射镜组成的光学谐振腔 来产生近单色的激光束。
这类有界空间中的电磁波传播问题属于边值问题,在这类问 题中导体表面边界条件起着重要作用。因此下面先对导体界 面边界条件作一般讨论。
2
二、理想导体边界条件
实际导体虽然不是理想导体,但是对于大多数金属导体 而言,无线电波透入其内而损耗的电磁能量很小,接近于 理想导体。因此,分析实际问题时,在第一级近似下,把 金属看作理想导体,把问题解出来,然后在第二级近似下, 再考虑有限电导率引起的能量损失。 对于一定频率的电磁波,两不同介质(包括导体)界面上 的边值关系可以归结为:
∂E = 0 ∂n
综上所述,以理想导体为边界的电磁波,满足:
∇2E + k 2E = 0 k = ω µε
Et = 0 ∂En = 0 ∂n
6
例: 两无穷大的平面导体平行放置,则其间只能 传播y方向偏振的TEM电磁波。
证: 设两导体板与y轴垂 直。边界条件为: 在两导体平面上, Ex=Ez=0 , Hy=0 若沿z轴传播的平面 电磁波的电场沿y轴方向偏振,则此平面波满 足导体板上的边界条件,因此可以在导体板 之间传播。
对x=0壁面来说,Ex是法向分量,当 x=0时, ∂Ex/∂x =0
理想导体界面边界条件可以形象地表述为,在导体表面上, 电场线与界面正交,磁感应线与界面相切。
5
实际求解时,先看方程∇·E=0对边界电场的限制往往能 够带来方便。
在边界面上,若取x,y轴在切面上,z轴沿法线方向,由
于该处Ex=Ey=0,因此方程∇·E=0在靠近边界上为 ∂Ez/∂z
=0,即
∂En = 0 ∂n
n × (Eห้องสมุดไป่ตู้ − E1) = 0 n× (H2 − H1) = α
3
式中n为由介质1指向介质2的法线。这两等式成立后,另外
两个关于法向分量的关系:
n ⋅ (D2 − D1) = σ
自然能够满足。
n ⋅ (B2 − B1) = 0
导体表面边界条件:
取角标1代表理想导体,角标2代表真空或绝缘介质。取法
代入方程:∇2u + k 2u = 0
d2X dx 2
YZ
+
d 2Y dy 2
XZ
+
d2Z dz 2
XY
+ k 2 XYZ
=0
1 X
d2X dx 2
+1 Y
d 2Y dy 2
+
1 Z
d2Z dz 2
+k2
=0
11
可以得到三个方程
d2X dx 2
+
k
2 x
X
=
0,
d 2Y dy2
+ k y2Y
=
0,
§4.4 谐振腔
一、有界空间中的电磁波
第一节我们研究了无界空间中的电磁波。在无界空间中,电 磁波最基本的存在形式为平面电磁波,这种波的电场和磁场 都作横向振荡。这种类型的波称为横电磁(TEM)波。 从电磁波与导体的相互作用可知,电磁波主要是在导体以外 的空间或绝缘介质内传播的,只有很小部分电磁能量透入导 体表层内。
d2Z dz 2
+
k
2 z
Z
=
0
其中
k
2 x
+
k
2 y
+
k
2 z
=
ω 2µε
解出X,Y,Z后,便可得到u的通解。解得u(x,y,z)的通解为:
u(x, y, z) = (C1 cos kx x + D1 sin kx x) (C2 cos ky y + D2 sin ky y) (C3 cos kz z + D3 sin kz z)
