几种压缩感知算法
几种压缩感知算法
.1 压缩感知部分压缩感知算法主要可分为三类:贪婪迭代算法、凸凸优化(或最优化逼近方法)和基于贝叶斯框架提出的重构算法。
由于第三类方法注重信号的时间相关性,不适合图像处理问题,故目前的研究成果主要集中在前两类中。
目前已实现6中算法,分别为正交匹配追踪法(OMP)、迭代硬阈值法(IHT)、分段正交匹配追踪法(StOMP)、分段弱正交匹配追踪法(SwOMP)、广义正交匹配追踪(GOMP)、基追踪法(BP)。
1.1 正交匹配追踪法(OMP)在正交匹配追踪OMP中,残差是总与已经选择过的原子正交的。
这意味着一个原子不会被选择两次,结果会在有限的几步收敛。
OMP的算法如下(1)用x表示你的信号,初始化残差e0=x;(2)选择与e0内积绝对值最大的原子,表示为φ1;(3)将选择的原子作为列组成矩阵Φt,定义Φt列空间的正交投影算子为通过从e0减去其在Φt所张成空间上的正交投影得到残差e1;(4)对残差迭代执行(2)、(3)步;其中I为单位阵。
需要注意的是在迭代过程中Φt为所有被选择过的原子组成的矩阵,因此每次都是不同的,所以由它生成的正交投影算子矩阵P每次都是不同的。
(5)直到达到某个指定的停止准则后停止算法。
OMP减去的Pem是em在所有被选择过的原子组成的矩阵Φt所张成空间上的正交投影,而MP减去的Pem是em在本次被选择的原子φm所张成空间上的正交投影。
经OMP算法重构后的结果如下所示:算法的使用时间如下:1.2 迭代硬阈值法(IHT)目标函数为这里中的M应该指的是M-sparse,S应该指的是Surrogate。
这里要求:之后我们利用式对目标函数进行变形。
接着便是获得极值点:利用该式进行迭代可以得到极值点,我们需要的是最小值。
此时目标函数的最小值就得到了。
此时便得到我们需要的公式:我们要保证向量y的稀疏度不大于M,即,为了达到这一目标,要保留最大的M项(因为是平方,所以要取绝对值absolute value),剩余的置零(注意这里有个负号,所以要保留最大的M项)。
传感器网络中的数据传输与处理技术研究

传感器网络中的数据传输与处理技术研究传感器网络(Sensor Network)是一种将传感器进行有机组织、相互协作的网络系统,可以通过无线电波、红外线等信号进行信息传输和数据处理,广泛应用于环境监控、生态保护、智能交通等领域。
在传感器网络中,数据传输和处理技术是至关重要的一环。
一、数据传输技术在传感器网络中,数据传输技术的重点在于如何实现高效、稳定和低耗能的数据传输。
传统的数据传输方式包括基于有线的传输方式和基于无线的传输方式。
而对于传感器网络而言,无线传输方式成为了首选。
目前,常见的无线传输方式主要包括以下几种:1. ZigBee协议ZigBee协议是一种低功耗、低速率、短距离、低成本的无线通信协议。
它采用无线个人局域网(PAN)技术,能够实现传感器网络的无线连接和控制。
ZigBee协议的优点在于低成本、低功耗、数据传输实时和可靠,因此被广泛应用于家庭自动化、智能建筑和物联网等领域。
2. Wi-Fi协议Wi-Fi协议是一种常见的无线传输协议,其传输速率快且稳定。
但是,由于传输距离较短、功耗大,不适用于传感器网络的长期使用。
3. 4G网络传统的4G网络具有传输速率快、覆盖范围广等优势,被广泛应用于智能手机和物联网领域。
但由于传输距离、速率和功耗等方面的限制,4G网络并不太适用于传感器网络。
二、数据处理技术在传感器网络中,数据处理技术的重点在于如何实现更加智能和高效的数据处理。
传统的数据处理方式往往通过中心节点进行数据汇聚和处理,但这种方式存在单点故障,且数据重复性较高。
而在现代传感器网络中,采用分布式数据处理方式可以解决这些问题。
分布式数据处理利用数学、信息学等理论和方法,将数据处理分布在多个节点中,形成分布式网络结构。
其中,常用的分布式数据处理技术包括以下几种:1. 分布式压缩感知算法分布式压缩感知算法是通过数据压缩技术和稀疏表示技术来实现数据处理的一种算法,可以在不增加数据重复性的前提下,更加高效地进行数据处理和传输。
一种压缩感知重构算法

Blme s t 等 人 为 了 提 高 重 构 精 度 引 入 了共 轭 方 u n ah 向和 弱 阈值 原 子选择 策 略 ,提 出分段 弱 阈值共轭 梯
 ̄[] o rs d Snig S ,它突破了传统的 W' C mpe e es ,C ) 1( 2 s n 奈 奎 斯特 采 样定 理 ,实现 了采样 方 式 的转 变 即从信 号采 样转 变成信 息采 样 。CS 理论有 3 个核 心 问题 [. 3 】 信 号稀疏 变换 、观 测矩 阵设计和 恢 复重构 算法 。其 中恢 复重 构算 法直 接关 系 到重构 精度 的大 小 ,运算 时 间的长短 ,决定着 C 理 论是否 切实 可行 。一 些学 S 者 致 力 于 压 缩 感 知 的 恢 复 重 构 问 题 提 出 了 贝 叶 斯[ B S, 4 C )匹配追踪[MP , ] ( 5 )正交匹配追踪[ O ) 】 ( 6 MP 】 ( 和分段正交匹配追踪【 SO 7 T MP 算法 。为了提高运 】 f ) 算速 度 , 另 一些 学 者 另辟 蹊 径 提 出 了梯度 追 踪 算 法 【G ) 但 其 精 度 较 低 。在 G 8 P, J f P的 基 础 上 ,
apoiai ojgt G ai tP r i SWMC P a oi m i pooe hs a e. h l r h p rx t n C nuae rd n us t(t m o e u G ) l r h rp s i ti p pr T ia oi m g t s dn s g t
S 0M P— AR. t F
K yw rsC mpe e es g(S; i ci a p r i C nuae rdet e od: o rs dSni C )Dr t nl us t ojgt gai s n e o u; n
压缩感知重构算法

4.2.1 高斯白噪声影响
高斯白噪声均值为0,方差为0.01
图A 受高斯白噪声影响OMP算法重构
图B 受高斯白噪声影响信号CoSAMP算法重构
4.2.2 椒盐噪声影响
椒盐噪声噪声密度为0.05
图A 受椒盐噪声影响信号OMP算法重构
图B 受椒盐噪声影响信号IRLS算法重构
4.2.3 受噪声影响结果比较
4
2
0
SAMP
-2 -4
-6
0
50
100
150
200
250
300
2.7.2 各算法仿真实验分析
重构算法时间都较短,误差也都较小
2.7.2 各算法性能分析
随着稀疏度K的增加,到达一定的临界值以后,信号重构的概率逐步降低
3.1 改进算法
基于变步长的正则化回溯自适应追踪算法 2018年,王欣等人针对压缩感知重构过程中稀疏度 未知以及步长大小固定的情况,基于SAMP 算法 存在的而不足,提出一种基于变步长的正则化回
每次迭代时选择多列
2.4 压缩采样匹配追踪CoSaMP
每次迭代选择多个原子, 选择的原子在下次迭代中可能会被抛弃
2.5 压缩采样匹配追踪SP
后向追踪的方式,在每次迭代中将找出的错 误的原子剔出,再把新找的原子放入支撑集 中,最后进行逼近
2.6 压缩采样匹配追踪SAMP
稀疏度自适应匹配追踪算法(SAMP)解决了需己知稀疏度才能准确重 构信号的要求。该算法沿用SP算法的回溯思想,加入步长和分阶段选 择的思想,通过迭代次数的增加,支撑集增加,从而达到每次选择更 多的原子,更快的重构信号。但是,如何选择初始步长及固定步长对 该算法有一定影响。
3.3 迭代硬阈值算法IHT
压缩感知 稀疏贝叶斯算法

压缩感知稀疏贝叶斯算法
压缩感知是一种信号处理方式,其基本思想是通过采集少量的信号样本,然后通过某种算法重构出原始信号。
稀疏贝叶斯算法是压缩感知中的一种重要方法,它利用贝叶斯估计理论来恢复稀疏信号。
压缩感知的基本模型可描述为:y = Ax + v,其中y为观测到的信号,A为M×N的感知矩阵,x为N×1维的待求信号,v为M×1维的噪声向量。
稀疏贝叶斯学习则是在压缩感知的基础上引入了贝叶斯估计理论,用于恢复稀疏信号。
具体来说,稀疏贝叶斯学习将信号建模为一个稀疏的概率图模型,然后通过贝叶斯公式来求解最优的信号值。
然而,传统的稀疏贝叶斯算法在存在噪声的情况下,其恢复效果可能不佳。
为了解决这个问题,研究者们提出了结合自适应稀疏表示和稀疏贝叶斯学习的压缩感知图像重建方法。
此外,还有研究者提出基于块稀疏贝叶斯学习的多任务压缩感知重构算法,该算法利用块稀疏的单测量矢量模型求解多任务重构问题。
这些改进的方法都在一定程度上提高了压缩感知的性能。
压缩感知的重构算法

压缩感知的重构算法算法的重构是压缩感知中重要的一步,是压缩感知的关键之处。
因为重构算法关系着信号能否精确重建,国内外的研究学者致力于压缩感知的信号重建,并且取得了很大的进展,提出了很多的重构算法,每种算法都各有自己的优缺点,使用者可以根据自己的情况,选择适合自己的重构算法,大大增加了使用的灵活性,也为我们以后的研究提供了很大的方便。
压缩感知的重构算法主要分为三大类:1.组合算法2.贪婪算法3.凸松弛算法每种算法之中又包含几种算法,下面就把三类重构算法列举出来。
组合算法:先是对信号进行结构采样,然后再通过对采样的数据进行分组测试,最后完成信号的重构。
(1) 傅里叶采样(Fourier Representaion)(2) 链式追踪算法(Chaining Pursuit)(3) HHS追踪算法(Heavy Hitters On Steroids)贪婪算法:通过贪婪迭代的方式逐步逼近信号。
(1) 匹配追踪算法(Matching Pursuit MP)(2) 正交匹配追踪算法(Orthogonal Matching Pursuit OMP)(3) 分段正交匹配追踪算法(Stagewise Orthogonal Matching Pursuit StOMP)(4) 正则化正交匹配追踪算法(Regularized Orthogonal Matching Pursuit ROMP)(5) 稀疏自适应匹配追踪算法(Sparisty Adaptive Matching Pursuit SAMP)凸松弛算法:(1) 基追踪算法(Basis Pursuit BP)(2) 最小全变差算法(Total Variation TV)(3) 内点法(Interior-point Method)(4) 梯度投影算法(Gradient Projection)(5) 凸集交替投影算法(Projections Onto Convex Sets POCS)算法较多,但是并不是每一种算法都能够得到很好的应用,三类算法各有优缺点,组合算法需要观测的样本数目比较多但运算的效率最高,凸松弛算法计算量大但是需要观测的数量少重构的时候精度高,贪婪迭代算法对计算量和精度的要求居中,也是三种重构算法中应用最大的一种。
基于压缩感知的图像处理

基于压缩感知的图像处理基于压缩感知的图像处理一、压缩感知在过去的几十年里,人们获取数据的能力不断提高,需要处理的数据量也越来越大,因此信号的带宽也越来越大,所以对信号处理的速度和采样速率的要求也随之提高。
众所周知,奈奎斯特采样定理要求采样率不得低于信号带宽的两倍,这对目前的信号处理能力提出了巨大的挑战。
所以人们试图找到一种新的信号处理技术。
近年来提出了一种新的信号处理理论——压缩感知理论。
压缩感知理论表明:如果信号是稀疏的或者是可压缩的,就可以通过一个测量矩阵将其投影到一个低维的空间上,得到的低维信号成为测量信号,然后将这个测量信号进行传输,在接收端通过接收到的信号和已知的测量矩阵来重构出原始的信号。
理论上指出任何信号经过一定处理后都可以转化为稀疏信号,这也为压缩感知理论在各个领域的广泛使用提供了保障。
1、压缩感知理论传统的信号处理过程包括信号的采样、压缩、传输和重构四个部分,根据奈奎斯特采样定理,信号的采样速率不能低于信号最大带宽的两倍,只有以满足这一要求的采样速率进行采样,才能保证信息不丢失,但是在很多情况下,奈奎斯特采样速率显得很高,实现起来比较困难。
压缩感知是一种新的信号获取的方法,它突破了奈奎斯特采样定理的瓶颈,它将对信号的压缩和采样合并进行,使得测量数据量远远小于传统的采样方法所得的数据量。
压缩感知主要包括三个方面的内容:信号的稀疏表示、信号的压缩采样和信号的重构。
2、信号的稀疏表示前面提到,压缩感知理论只能直接应用于稀疏信号。
如果需要处理的信号是稀疏的,那就不需要稀疏表示这一部分,直接进行压缩采样就行了,但是就目前来看,我们所要处理的大多数信号都不是稀疏信号,这就需要将其转换为稀疏信号。
假设ψ=[ψ1, ψ2, ψ3, , ψN ]为R 空间上的一组基,Ψi (i=1,2,3…N)是N一个N*1的列向量,考虑x =[x 1, x 2, x 3, , x N ]T ,它是一个实值有限长的ψ线性表示:N x ∈R 一维离散信号,。
压缩感知介绍PPT-最终版

3
采样速率需达到信号带宽的两倍以上才能精确重构信号。这样的采样硬件成本昂贵,获取效率低下,对宽带信号处理的困难日益加剧。
1.1 传统采样理论介绍及问题提出
1 背景介绍
而现实生活中,随着信息技术的高速发展,信息量的需求增加,携带信息的信号所占带宽也越来越大
01
01
02
这就大大考验了数字化社会对信息处理的能力,包括:数据存储、传输和处理速度,基于Nyquist采样的理论遭到严峻的考验。
这是压缩感知理论的基础和前提,也是信号精确重构的保证。对稀疏表示研究的热点主要有两个方面: 1、基函数字典下的稀疏表示: 寻找一个正交基使得信号表示的稀疏系数尽可能的少。比较常用的稀疏基有:高斯矩阵、小波基、正(余)弦基、Curvelet基等。Candes和Tao经研究发现光滑信号的Fourier 系数、小波系数、有界变差函数的全变差范数、振荡信号的Gabor 系数及具有不连续边缘的图像信号的Curvelet 系数等都具有足够的稀疏性,可以通过压缩感知理论恢复信号。 2、超完备库下的稀疏表示: 用超完备的冗余函数库来取代基函数,称之为冗余字典,字典中的元素被称之为原子,目的是从冗余字典中找到具有最佳线性组合的K项原子来逼近表示一个信号,称作信号的稀疏逼近或高度非线性逼近。
背景介绍
01
传统采样理论介绍及问题提出
02
压缩感知理论的基本思想
03
传统的基于Nyquist采样定理指导下的信息的处理主要表现在两个方面:
1
2
在实际应用中,为了降低成本,人们常将采样的数据经压缩后以较少的比特数表示信号,而很多非重要的数据被抛弃,这种高速采样再压缩的方式浪费了大量的采样资源,另外一旦压缩数据中的某个或某几个丢失,可能将造成信号恢复的错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.1压缩感知部分
压缩感知算法主要可分为三类:贪婪迭代算法、凸凸优化(或最优化逼近方法)和基于贝叶斯框架提出的重构算法。
由于第三类方法注重信号的时间相关性,不适合图像处理问题,故目前的研究成果主要集中在前两类中。
目前已实现6中算法,分别为正交匹配追踪法()、迭代硬阈值法()、分段正交匹配追踪法()、分段弱正交匹配追踪法()、广义正交匹配追踪()、基追踪法()。
1.1 正交匹配追踪法()
在正交匹配追踪中,残差是总与已经选择过的原子正交的。
这意味着一个原子不会被选择两次,结果会在有限的几步收敛。
的算法如下
(1)用x表示你的信号,初始化残差e0;
(2)选择与e0内积绝对值最大的原子,表示为φ1;
(3)将选择的原子作为列组成矩阵Φt,定义Φt列空间的正交投影算子为
通过从e0减去其在Φt所张成空间上的正交投影得到残差e1;
(4)对残差迭代执行(2)、(3)步;
其中I为单位阵。
需要注意的是在迭代过程中Φt为所有被选择过的原子组成的矩阵,因此每次都是不同的,所以由它生成的正交投影算子矩阵P每次都是不同的。
(5)直到达到某个指定的停止准则后停止算法。
减去的是在所有被选择过的原子组成的矩阵Φt所张成空间上的正交投影,而减去的是在本次被选择的原子φm所张成空间上的正交投影。
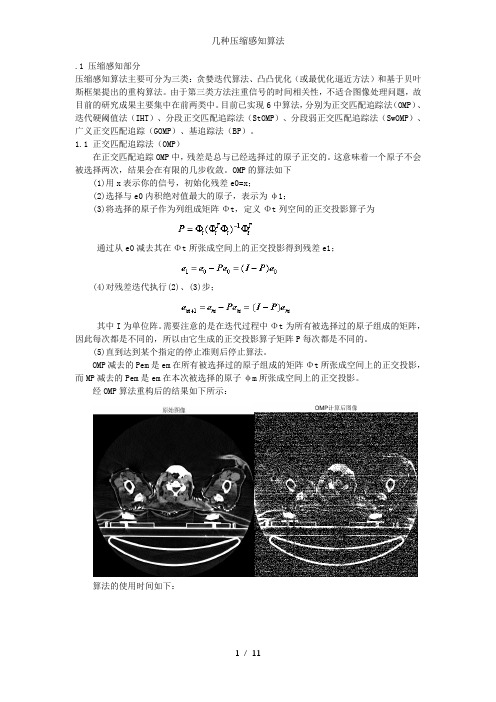
经算法重构后的结果如下所示:
算法的使用时间如下:
1.2 迭代硬阈值法()
目标函数为
这里中的M应该指的是,S应该指的是。
这里要求:
之后我们利用式
对目标函数进行变形。
接着便是获得极值点:
利用该式进行迭代可以得到极值点,我们需要的是最小值。
此时目标函数的最小值就得到了。
此时便得到我们需要的公式:
我们要保证向量y的稀疏度不大于M,即,为了达到这一目标,要保留最大的M项(因为是平方,所以要取绝对值),剩余的置零(注意这里有个负号,所以要保留最大的M项)。
算法结果:
算法使用时间如下:
1.3 分段正交匹配追踪法()
分段正交匹配追踪( )也是由改进而来的一种贪心算法,与、算法类似,不同之处在于、算法在迭代过程中选择的是与信号内积最大的2K或K个原子,而是通过门限阈值来确定原子。
此算法的输入参数中没有信号稀疏度K,因此相比于及有独到的优势。
的算法流程:
经算法重构后的结果如下所示:该算法的用时情况如下:
1.4 分段弱正交匹配追踪法()
分段弱正交匹配追踪( )可以说是的一种修改算法,它们的唯一不同是选择原子时的门限设置,这可以降低对测量矩阵的要求。
我们称这里的原子选择方式为"弱选择"(),的门限设置由残差决定,这对测量矩阵(原子选择)提出了要求,而的门限设置则对测量矩阵要求较低(原子选择相对简单、粗糙)。
的算法流程:
经算法重构后的结果如下所示:该算法的用时情况如下:
1.5 广义正交匹配追踪法()
广义正交匹配追踪( , )算法可以看作为算法的一种推广。
每次只选择与残差相关最大的一个,而则是简单地选择最大的S个。
之所以这里表述为"简单地选择"是相比于之类算法的,不进行任何其它处理,只是选择最大的S个而已。
算法流程如下:
经算法重构后的结果如下所示:该算法的用时情况如下:
1.6 基追踪法()
除匹配追踪类贪婪迭代算法之外,压缩感知重构算法另一大类就是凸优化算法或最优化逼近方法,这类方法通过将非凸问题转化为凸问题求解找到信号的逼近,其中最常用的方法就是基追踪( , ),该方法提出使用l1范数替代l0范数来解决最优化问题,以便使用线性规划方法来求解。
经算法重构后的结果如下所示:
该算法的用时情况如下:
2.推荐
压缩感知算法在上有很多介绍和资源,这里推荐一个大神的博客,基本包含了现在常用的所有的压缩感知算法的介绍,当然后很多是没有完整的代码资源的,不过初学者还是可以去学习一波。
这里还有我的几种算法的实现:。
