上海临港第一中学2020年期中单元测试
上海临港第一中学数学有理数单元测试卷附答案

一、初一数学有理数解答题压轴题精选(难)1.如图,点A、B都在数轴上,O为原点.(1)点B表示的数是________;(2)若点B以每秒2个单位长度的速度沿数轴向右运动,则2秒后点B表示的数是________;(3)若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动,而点O 不动,t秒后,A、B、O三个点中有一个点是另外两个点为端点的线段的中点,求t的值. 【答案】(1)-4(2)0(3)解:① 当点O是线段AB的中点时,OB=OA4-3t=2+tt=0.5② 当点B是线段OA的中点时, OA = 2 OB2+t=2(3t-4)t=2③ 当点A是线段OB的中点时, OB = 2 OA3t--4=2(2+t)t=8综上所述,符合条件的t的值是0.5,2或8.【解析】【解答】(1)点B表示的数是-4;(2)2秒后点B表示的数是 0 ;【分析】(1)根据数轴上所表示的数的特点即可直接得出答案;(2)用点B开始所表示的数+点B运动的路程=经过t秒后点B表示的数,即可得出结论;(3)找出t秒后点A、B表示的数,分①点O为线段AB的中点,②当点B是线段OA的中点,③点A是线段OB的中点,根据线段中点的数学语言列出方程,求解即可求出此时的t值,综上即可得出结论。
2.数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.(1)在数轴上标示出-4、-3、-2、4、(2)结合数轴与绝对值的知识回答下列问题:①数轴上表示4和-2的两点之间的距离是________,表示-2和-4两点之间的距离是________.一般地,数轴上表示数m和数n的两点之间的距离等于|m-n|.如果表示数a和-2的两点之间的距离是3,即那么a=________②若数轴上表示数a的点位于-3和2之间,则的值是________;③当a取________时,|a+4|+|a-1-|+|a-4|的值最小,最小值是________.【答案】(1)解:如图所示:(2)6;2;1或-5;5;1;8.【解析】【解答】解:(2)①数轴上表示4和−2的两点之间的距离是4−(−2)=6,表示−2和−4两点之间的距离是−2−(−4)=2;∵|a−(−2)|=3,∴a−(−2)=±3,解得a=−5或1;②因为|a+3|+|a−2|表示数轴上数a和−3,2之间距离的和,又因为数a位于−3与2之间,所以|a+3|+|a−2|=5;③根据|a+4|+|a−1|+|a−4|表示一点到−4,1,4三点的距离的和,所以当a=1时,式子的值最小,此时|a+4|+|a−1|+|a−4|的最小值是8.故答案为:6,2,−5或1;5;1,8.【分析】(1)数轴上原点表示正数,原点左边表示负数,原点右边表示正数,然后在数轴上找出表示各个数的点,用实心的小原点标记,并在实心小圆点上方写出该点所表示的数;(2)①根据数轴上任意两点的距离等于这两点所表示的数差的绝对值即可算出答案;解含绝对值的方程,根据绝对值的意义去掉绝对值符号,再解即可;②因为数a位于−3与2之间,故a+3>0,a−2<0,根据绝对值的意义去掉绝对值符号再合并他即可;③根据|a+4|+|a−1|+|a−4|表示一点到−4,1,4三点的距离的和,根据两点之间线段最短即可得出当a=1时,式子的值最小,从而将a=1代入即可算出答案。
2020-2021上海临港第一中学九年级数学上期中第一次模拟试卷(带答案)
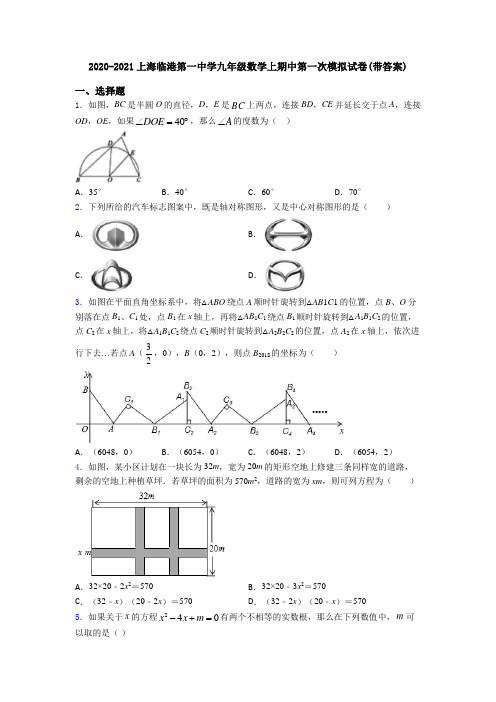
2020-2021上海临港第一中学九年级数学上期中第一次模拟试卷(带答案)一、选择题1.如图,BC 是半圆O 的直径,D ,E 是BC 上两点,连接BD ,CE 并延长交于点A ,连接OD ,OE ,如果40DOE ∠=︒,那么A ∠的度数为( )A .35°B .40°C .60°D .70°2.下列所给的汽车标志图案中,既是轴对称图形,又是中心对称图形的是( ) A . B .C .D .3.如图在平面直角坐标系中,将△ABO 绕点A 顺时针旋转到△AB 1C 1的位置,点B 、O 分别落在点B 1、C 1处,点B 1在x 轴上,再将△AB 1C 1绕点B 1顺时针旋转到△A 1B 1C 2的位置,点C 2在x 轴上,将△A 1B 1C 2绕点C 2顺时针旋转到△A 2B 2C 2的位置,点A 2在x 轴上,依次进行下去…若点A (32,0),B (0,2),则点B 2018的坐标为( )A .(6048,0)B .(6054,0)C .(6048,2)D .(6054,2)4.如图,某小区计划在一块长为32m ,宽为20m 的矩形空地上修建三条同样宽的道路,剩余的空地上种植草坪.若草坪的面积为570m 2,道路的宽为xm ,则可列方程为( )A .32×20﹣2x 2=570 B .32×20﹣3x 2=570 C .(32﹣x )(20﹣2x )=570D .(32﹣2x )(20﹣x )=570 5.如果关于x 的方程240x x m -+=有两个不相等的实数根,那么在下列数值中,m 可以取的是( )A .3B .5C .6D .8 6.用配方法解一元二次方程x 2﹣6x ﹣10=0时,下列变形正确的为( ) A .(x+3)2=1B .(x ﹣3)2=1C .(x+3)2=19D .(x ﹣3)2=19 7.若2245a a x -+-=,则不论取何值,一定有( ) A .5x >B .5x <-C .3x ≥-D .3x ≤- 8.已知()222226x y y x +-=+,则22x y +的值是( ) A .-2B .3C .-2或3D .-2且3 9.若关于x 的一元二次方程(m ﹣1)x 2+5x+m 2﹣5m+4=0有一个根为0,则m 的值等于( )A .1B .1或4C .4D .0 10.100个大小相同的球,用1至100编号,任意摸出一个球,则摸出的编号是质数的概率是 ( )A .120B .19100C .14D .以上都不对 11.函数y=x 2+bx+c 与y=x 的图象如图所示,有以下结论:①b 2﹣4c >0;②b+c+1=0;③3b+c+6=0;④当1<x <3时,x 2+(b ﹣1)x+c <0. 其中正确的个数为A .1B .2C .3D .412.公园有一块正方形的空地,后来从这块空地上划出部分区域栽种鲜花(如图),原空地一边减少了1m ,另一边减少了2m ,剩余空地的面积为18m 2,求原正方形空地的边长.设原正方形的空地的边长为xm ,则可列方程为( )A .(x+1)(x+2)=18B .x 2﹣3x+16=0C .(x ﹣1)(x ﹣2)=18 D .x 2+3x+16=0 二、填空题13.如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D.若AC=6,BD=52,则BC的长为_____.14.新园小区计划在一块长为20米,宽12米的矩形场地上修建三条互相垂直的长方形甬路(一条橫向、两条纵向,且横向、纵向的宽度比为3:2),其余部分种花草.若要使种花草的面积达到144米2.则横向的甬路宽为_____米.15.圆锥的底面半径为14cm,母线长为21cm,则该圆锥的侧面展开图的圆心角为_____度.16.关于x的方程的260-+=有两个相等的实数根,则m的值为________.x x m17.已知一个直角三角形的两条直角边长分别为3cm和4cm,则这个直角三角形的内切圆的半径为 cm18.如图,在平面直角坐标系xOy中,四边形OABC是正方形,点C(0,4),D是OA 中点,将△CDO以C为旋转中心逆时针旋转90°后,再将得到的三角形平移,使点C与点O重合,写出此时点D的对应点的坐标:_____.19.如图,已知△ABC内接于⊙O,∠C=45°,AB=4,则⊙O的半径为_____.20.如图,是一个长为30m,宽为20m的矩形花园,现要在花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为米.三、解答题21.“早黑宝”葡萄品种是我省农科院研制的优质新品种,在我省被广泛种植,邓州市某葡萄种植基地2017年种植“早黑宝”100亩,到2019年“卓黑宝”的种植面积达到196亩.(1)求该基地这两年“早黑宝”种植面积的平均增长率;(2)市场调查发现,当“早黑宝”的售价为20元/千克时,每天能售出200千克,售价每降价1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,同时减少库存,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1750元,则售价应降低多少元?22.某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣2x+80(20≤x≤40),设这种健身球每天的销售利润为w元.(1)求w与x之间的函数关系式;(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?23.已知关于x的方程x2+4x+3-a=0.(1)若此方程有两个不相等的实数根,求a的取值范围;(2)在(1)的条件下,当a取满足条件的最小整数,求此时方程的解.24.鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.(1)求出y与x的函数关系式,并写出自变量x的取值范围.(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?25.已知关于x的方程220++-=.x ax a(1)当该方程的一个根为1时,求a的值及该方程的另一根;(2)求证:不论a取何实数,该方程都有两个不相等的实数根.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【解析】【分析】连接CD,由圆周角定理得出∠BDC=90°,求出∠DCE=20°,再由直角三角形两锐角互余求解即可,【详解】解:连接CD,如图,∵BC是半圆O的直径,∴∠BDC=90°,∴∠ADC=90°,∵∠DOE=40°,∴∠DCE=20°,∴∠A=90°−∠DCE=70°,故选:D.【点睛】本题考查了圆周角定理、直角三角形的性质;熟练掌握圆周角定理是解题的关键.2.B解析:B【解析】分析:根据轴对称图形与中心对称图形的概念求解即可.详解:A.是轴对称图形,不是中心对称图形;B.是轴对称图形,也是中心对称图形;C.是轴对称图形,不是中心对称图形;D.是轴对称图形,不是中心对称图形.故选B.点睛:本题考查了中心对称图形和轴对称图形的知识,关键是掌握好中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,图形旋转180°后与原图重合.3.D解析:D【解析】【分析】首先根据已知求出三角形三边长度,然后通过旋转发现,B、B2、B4…每偶数之间的B相差6个单位长度,根据这个规律可以求得B2018的坐标.【详解】∵A(32,0),B(0,2),∴OA=32,OB=2,∴Rt△AOB中,AB52 =,∴OA+AB1+B1C2=32+2+52=6,∴B2的横坐标为:6,且B2C2=2,即B2(6,2),∴B4的横坐标为:2×6=12,∴点B2018的横坐标为:2018÷2×6=6054,点B2018的纵坐标为:2,即B2018的坐标是(6054,2).故选D.【点睛】此题考查了点的坐标规律变换以及勾股定理的运用,通过图形旋转,找到所有B点之间的关系是解决本题的关键.4.D解析:D【解析】【分析】六块矩形空地正好能拼成一个矩形,设道路的宽为xm,根据草坪的面积是570m2,即可列出方程.【详解】解:设道路的宽为xm,根据题意得:(32-2x)(20-x)=570,故选D.【点睛】本题考查的知识点是由实际问题抽象出一元二次方程,解题关键是利用平移把不规则的图形变为规则图形,进而即可列出方程.5.A解析:A【解析】【分析】根据根的判别式的意义得到16﹣4m>0,然后解不等式得到m<4,然后对各选项进行判断.【详解】根据题意得:△=16﹣4m>0,解得:m<4,所以m可以取3,不能取5、6、8.故选A.【点睛】本题考查了一元二次方程ax 2+bx +c =0(a ≠0)的根的判别式△=b 2﹣4ac :当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程没有实数根.6.D解析:D【解析】【分析】方程移项变形后,利用完全平方公式化简得到结果,即可做出判断.【详解】方程移项得:2610x x -=,配方得:26919x x -+=,即2(3)19x -=,故选D . 7.D解析:D【解析】【分析】由﹣2a 2+4a ﹣5=﹣2(a ﹣1)2﹣3可得:x ≤﹣3.【详解】∵x =﹣2a 2+4a ﹣5=﹣2(a ﹣1)2﹣3≤﹣3,∴不论a 取何值,x ≤﹣3.故选D .【点睛】本题考查了配方法的应用,熟练运用配方法解答本题的关键.8.B解析:B【解析】试题分析:根据题意,先移项得()2222260x y y x +---=,即()2222260x y x y ()+-+-=,然后根据“十字相乘法”可得2222(2)(3)0x y x y +++-= ,由此解得22x y +=-2(舍去)或223x y +=.故选B.点睛:此题主要考查了高次方程的解法,解题的关键是把其中的一部分看做一个整体,构造出简单的一元二次方程求解即可.9.C解析:C【解析】【分析】先把x =0代入方程求出m 的值,然后根据一元二次方程的定义确定满足条件的m 的值.【详解】解:把x =0代入方程得m²−5m +4=0,解得m ₁=4,m ₂=1,而a−1≠0,所以m =4.故选C .【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.注意一元二次方程的定义.10.C解析:C【解析】解答:在1到100这100个数中,是质数的是:2,3 ,5,7,11,13,17,19,23,29,31 ,37,41,43,47,53,59,61,67,71,73,79,83,89,97,共25个,所以摸出的编号是质数的概率是2511004=, 故选C . 点睛: 本题关键是清楚1到100这一范围内有几个质数,特别注意的是1既不是质数,又不是合数.11.B解析:B【解析】分析:∵函数y=x 2+bx+c 与x 轴无交点,∴b 2﹣4c <0;故①错误。
上海临港第一中学物理电功率单元测试卷附答案

上海临港第一中学物理电功率单元测试卷附答案 一、初三物理 电功率易错压轴题(难)1.(5)待测电阻与变阻器串联,当变阻器连入电路的电阻变小时,由欧姆定律I =U R可知,电路的电流变大,根据U =IR 得到待测电阻的电压变大,由串联电路电压的规律可知,变阻器两个的电压变小,根据绘制的如图丁所示的U -I 图象可知,电压表并联在变阻器的两端了;由图乙可知,当电流I 1=0.1A 时,变阻器两端的电压U 1=2V ,当电流I 2=0.2A 时,变阻器两端的电压U 2=1V ,设电源电压为U ,由串联电路电压的规律和欧姆定律可知,1212=U U U U R I I --=,即2V 1V =0.1A 0.2AU U --,U =3V ,待测电阻:113V 2V =0.1AU U R I --==10Ω.小明同学为了“测量小灯泡的电功率”,准备有如下器材:电源(电压6V ,保持不变),小灯泡(额定电压3.8V ,电阻约为20Ω),滑动变阻器A “10Ω 1A ”,滑动变阻器B “20Ω 1A ”,电压表(量程为0-3V 、0-15V)、电流表(量程为0-0.6A 、0~3A)各一个,开关一个,导线若干。
(1)要完成此实验应该选择滑动变阻器__________(填“A ”或“B ”)较为合适;(2)他在连线的过程中发现电压表的0-15V 量程已坏,要想测小灯泡的额定功率,请你补充完成图中的实验电路的设计;_________(3)他连接好电路后,闭合开关S ,移动滑动变阻器滑片时发现灯泡亮度较暗且不变,且两表示数也不变,出现此现象的原因是_____________。
【答案】B 滑动变阻器接的是两个下面的接线柱【解析】【分析】【详解】(1)[1]在实验中,小灯泡与变阻器是串联,当小灯泡正常发光时,变阻器两端的电压U 1=U -U L =6V-3.8V=2.2V据串联电路的特点有L1L1U UR R=,13.8V 2.2V20ΩR=此时,变阻器接入电路的阻值R1=11.5Ω所以应选择滑动变阻器B较为合适。
2020-2021上海临港第一中学小学三年级数学下期中第一次模拟试卷(带答案)

2020-2021上海临港第一中学小学三年级数学下期中第一次模拟试卷(带答案)一、选择题1.下列算式中,乘积小于1500的是()。
A. 48×29B. 31×52C. 43×412.某市体育馆的看台分16个区,每个区有15个座位。
它能同时容纳2500人观看比赛吗?()A. 能B. 不能C. 无法确定3.得数是三位数的有()。
①345÷3②126÷6③46×11④68×39A. ①③B. ①④C. ②③D. ②④4.一本《哈利·波特》的售价是29元,买21本大约要花()元。
A. 400B. 600C. 8005.6□2÷6,要使商的中间有0,且没有余数,那么□里最大应填()。
A. 2B. 5C. 46.下面算式的商最接近40的是()。
A. 802÷2B. 281÷7C. 340÷87.下面算式的商最接近80的是()。
A. 540÷6B. 430÷5C. 481÷68.小红放学回家朝东南走,学校在小红的()方。
A. 东北B. 西南C. 西北9.人民医院在第一实小的西北面,那么第一实小在人民医院的()面.A. 西南B. 东南C. 东北10.早上,小芳面对初升的太阳,这时她的左面是()方。
A. 西B. 南C. 北二、填空题11.16×39的积是________位数,25×40的积的末尾有________个0。
12.口算14×50时,可以先算14×5=________,再在积的后面加上一个________就是________。
13.用统计表表示的数量,还可以用________来表示。
14.9月份一共有________天,其中有________天不下雨。
15.□3÷6,要使商是一位数,□里最大可以填________;742÷□,要使商是两位数,□里最小可以填________。
2020-2021上海临港第一中学小学三年级数学上期中第一次模拟试卷(带答案)

2020-2021上海临港第一中学小学三年级数学上期中第一次模拟试卷(带答案)一、选择题1.水果店上午卖出橘子276个,下午卖出158个,那么这一天共卖出()个。
A. 424B. 434C. 3342.三位数加三位数,它的和()。
A. 一定是三位数B. 一定是四位数C. 可能是三位数也可能是四位数3.爸爸带了1000元钱买下边的两样物品,()。
A. 可以买回自行车和VCD。
B. 可以买回VCD和电饭锅。
C. 只能买回自行车和电饭锅。
4.400米+600米=()千米.A. 1B. 100C. 10005.一只老母鸡重3()。
A. 克B. 千克C. 吨6.如果一头大象重4吨,一头牛重500千克,那么一头大象的体重相当于()头牛的体重。
A. 6B. 7C. 8D. 97.小军把他的书放在书架的三个格子里,最少的一格放27本,最多的一格放34本,那么书架上的书总数大约是( )本.A. 180B. 150C. 120D. 908.估算398+389的得数与()最接近。
A. 800B. 600C. 7009.李莉家离学校500米,王强家离学校800米,李莉家和王强家相距()米。
A. 3000B. 1300C. 300或130010.1秒可以()A. 读一篇文章B. 眨(zhǎ)一次眼C. 吃一顿饭D. 跑100米11.小朋友每次刷牙大约用3()。
A. 分钟B. 秒C. 小时12.1时=()秒A. 60B. 120C. 3600二、填空题13.北京到沈阳飞机票700元,动车票220元。
从北京到沈阳,坐动车比坐飞机便宜________元。
14.1吨﹣700千克=________千克 400米+600米=________千米15.在横线上填上合适的单位。
一筐橘子重25________ 一个桃子重120________一只大象重3________ 一张桌子高76________16.“47+36”得数的十位上是________,“88-36”得数的十位上是________。
2020-2021上海临港第一中学小学四年级数学下期中第一次模拟试卷(带答案)

2020-2021上海临港第一中学小学四年级数学下期中第一次模拟试卷(带答案)一、选择题1.计算小数除法时,如果商要保留两位小数,商应除到小数部分的()A. 十分位B. 百分位C. 千分位2.去掉下面()中的“0”,这个数的大小不变。
A. 3.201B. 30.21C. 1.3203.下面算式中,正确运用乘法分配律的是()。
A. 25×(8+10)=25×8+10B. 25×(8+10)=25×8×10C. 25×(8+10)=25×8+25×10D. 25×(8+10)=25×8+10×84.在计算347-98时,下面的方法()正确。
A. 347-100-2B. 347-100+2C. 347-(100+2)5.101×76的简便算法是()。
A. 100×76+1B. 100×76+100C. 100×76+766.同样长的两根绳子,第一根剪去它的一半,第二根剪去0.5米,剩下的两根绳子()。
A. 第一根长B. 第二根长C. 同样长D. 不一定7.下面3个物体,从()看到的图形相同。
A. 上面B. 前面C. 左面8.这两幅茶杯图哪一幅是从“侧面“观察得到的?( )A. B.9.这两幅冰箱图中哪一幅是小朋友从“侧面偏上”观察得到的?()A. B.10.下列算式计算顺序正确的是()A. B. C.11.64×7÷64×7=( )。
A. 1B. 7C. 4912.4×(□-25)=56,□里应填( )。
A. 39B. 30C. 36D. 40二、填空题13.两个数相乘,交换两个因数的________,积不变,这叫做________,用字母表示是________。
14.25×108=25×100+25×8运用了乘法________。
2020-2021上海临港第一中学小学六年级数学上期中第一次模拟试卷(带答案)
2020-2021上海临港第一中学小学六年级数学上期中第一次模拟试卷(带答案)一、选择题1.把7:5的前项增加35,要使比值不变,后项应()。
A. 乘5B. 乘6C. 增加30D. 增加35 2.把750kg:1吨化简成最简单的整数比.下面答案错误的是()A. 3:4B.C. 0.753.六(1)班有48人,男女生人数比不可能是()。
A. 3:2B. 1:1C. 13:114.六(2)班有男生25人,女生20人,男生人数比女生人数多几分之几的列式是()。
A. (25-20)÷20B. (25-20)÷25C. 25÷205.下图中,小明家在学校的()处。
A. 南偏西300方向1.8千米B. 南偏东600方向1.8千米C. 南偏西600方向1.8千米6.以学校为观测点,贝贝家在学校的南偏西20 º方向,距离学校500米,那么以贝贝家为观测点,学校在贝贝家( )的方向。
A. 东偏北70 ºB. 北偏西70 ºC. 南偏北70 º7.B岛在灯塔的()。
A. 南偏西60°方向,距离是4千米B. 西偏南60°方向,距离是4千米C. 北偏东45°方向,距离是3千米D. 南偏西30°方向,距离是4千米8.哪幅图表示 × 的积?A. B. C.9.5千克的和1千克的相比较,结果是()。
A. 5千克的重B. 1千克的重C. 一样重D. 无法比较10.一件商品原价200元,涨价后再降价,现价()原价。
A. 高于B. 低于C. 等于11.把一根5m长的绳子,平均截成5段,每段长度是这根绳子总长度的()。
A. B. 1m C. m D. 112.吃了一包糖的后,剩下的是吃了的()。
A. B. C. 3倍 D. 2倍二、填空题13.甲数的和乙数的相等,甲数:乙数=________:________;已知甲、乙两数之差是9,甲数是________。
上海临港第一中学物理电流和电路单元测试卷附答案
上海临港第一中学物理电流和电路单元测试卷附答案一、初三物理电流和电路易错压轴题(难)1.在用电压表、电流表测量小灯泡电功率的实验中,灯泡上标有“2.5V”的字样.(1)测量小灯泡电功率的实验的原理是______________;小张根据电路图连接如图甲所示的实验电路,小王检查后发现有一根导线连接有错误,请你在这根导线上打“×”,并用笔画线代表导线,画出正确的连线。
___(2)电路改正后,小张闭合开关,发现灯泡不亮,电流表无示数,而电压表示数接近3V,取下灯泡,两表的示数仍然不变,出现故障的原因可能是____________________。
(3)故障排除后,开始进行实验,小王根据测出的数据,在图乙中画出了小灯泡的电流、电压变化的关系图像,由此可以判断,小灯泡的额定功率为______W。
此次实验中,使用滑动变阻器的目的是_________________。
(4)根据图乙还可以判断,小灯泡的电阻随电压的增大逐渐____________,原因是_____________________。
【答案】P=UI图略小灯泡断路0.75W改变(调节)灯泡两端的电压增大灯丝由金属制成,金属的电阻随温度的升高而增大【解析】(1)测量小灯泡电功率的实验的原理是P=UI;电路图连接如图:闭合开关,发现灯泡不亮,电流表无示数,说明电路中的开路的地方,而电压表示数接近3 V,取下灯泡,两表的示数仍不变,说明开路的地方在电灯处,即小灯泡断路;当电压为额定电压2.5V时,对应的电流值为0.3A,则电功率P=UI=2.5V×0.3A=0.75W;使用滑动变阻器的目的是改变(调节)灯泡两端的电压;(4)当小灯泡的电压升高时,实际功率也变大,温度升高,对于小灯泡的灯丝的电阻会变大2.如图所示的电路中,电源电压为U,闭合电键S,发现两电表指针的位置均不变,已知故障只发生在电阻R1、R2上,请根据相关信息写出电压表的示数及相应的故障.①如果电压表示数为_____;则可能存在的故障是_____.②如果电压表示数为_____;则可能存在的故障是_____.【答案】0 R1断路或R1、R2均断路或R1断路、R2短路 U R2断路或R2断路、R1短路【解析】【分析】【详解】如图所示,R1和R2串联在电路中,如果电压表示数为0,则可能存在的故障是R1断路或R1、R2均断路或R1断路、R2短路,如果电压表示数为U,则可能存在的故障是R2断路或R2断路、R1短路.【点睛】电路故障问题是电学测试中经常考查的问题.解决的一般步骤是将每种情况代入题目,根据应该出现的现象和题目中描述的现象进行对比,符合题意的即为正确答案.3.实验桌上有如下器材:满足实验要求的电源、电流表、电压表、开关、滑动变阻器各一个,若干个不同阻值的定值电阻和足够多的导线。
上海临港第一中学九年级上册期中试卷检测题
上海临港第一中学九年级上册期中试卷检测题一、初三数学 一元二次方程易错题压轴题(难)1.如图,直角坐标系xOy 中,一次函数y kx b =+的图象1l 分别与x 轴,y 轴交于A ,B两点,点A 坐标为()9,0,正比例函数12y x =的图象2l 与1l 交于点(),3C m ,点(),0N n 在x 轴上一个动点,过点N 作x 轴的垂线与直线1l 和2l 分别交于P 、Q 两点.(1)求m 的值及直线1l 所对应的一次函数表达式; (2)当03PQ <时,求n 的取值范围; (3)求出当n 为何值时,PQC ∆面积为12?【答案】(1)6m =;9y x =-+;(2)46n <或68n <;(3)2n =或10. 【解析】 【分析】(1)直接将点C 代入正比例函数,可求得m 的值,然后将点C 和点A 代入一次函数,可求得一次函数解析式;(2)用含n 的式子表示出PQ 的长,然后解不等式即可;(3)用含有n 的式子表示出△PQC 的底边长和高的长,然后求解算式即可得. 【详解】(1)将点C(m ,3)代入正比例函数12y x =得: 3=1m 2,解得:m=6 则点C(6,3) ∵A(9,0)将点A ,C 代入一次函数y kx b =+得:0936k bk b =+⎧⎨=+⎩解得:k=-1,b=9∴一次函数解析式为:y=-x+9 (2)∵N(n ,0) ∴P(n ,9-n),Q(n ,12n ) ∴PQ=192n n --∵要使03PQ < ∴0<1932n n --≤ 解得:46n <或68n <(3)在△PQC 中,以PQ 的长为底,则点C 到PQ 的距离为高,设为h 第(2)已知:PQ=139922n n n --=- 由图形可知,h=6n - ∵△PQC 的面积为12 ∴12=136922nn -- 情况一:当n <6是,则原式化简为:12=()136922n n ⎛⎫--⎪⎝⎭ 解得:n=2或n=10(舍)情况二:当n ≥6时,则原式化简为:12=()136922n n ⎛⎫-- ⎪⎝⎭解得:n=2(舍)或n=10 综上得:n=2或n=10. 【点睛】本题考查一次函数的综合,用到了解一元二次方程,求三角形面积等知识点,解题关键是用含n 的算式表示出PQ 的长度,注意需要添加绝对值符号.2.为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.(1)求这两年藏书的年均增长率;(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?【答案】(1)这两年藏书的年均增长率是20%;(2)到2018年底中外古典名著的册数占藏书总量的10%. 【解析】【分析】(1)根据题意可以列出相应的一元二次方程,从而可以得到这两年藏书的年均增长率; (2)根据题意可以求出这两年新增加的中外古典名著,从而可以求得到2018年底中外古典名著的册数占藏书总量的百分之几. 【详解】解:(1)设这两年藏书的年均增长率是x ,()2517.2x +=,解得,10.2x =,2 2.2x =-(舍去), 答:这两年藏书的年均增长率是20%;(2)在这两年新增加的图书中,中外古典名著有()7.2520%0.44-⨯=(万册), 到2018年底中外古典名著的册数占藏书总量的百分比是:5 5.6%0.44100%10%7.2⨯+⨯=,答:到2018年底中外古典名著的册数占藏书总量的10%. 【点睛】本题考查一元二次方程的应用,解答本题的关键是明确题意,列出相应的方程,利用方程的知识解答,这是一道典型的增长率问题.3.已知关于x 的一元二次方程()221210m x m x +-+=有两个不相等的实数根.(1)求实数m 的取值范围;(2)若原方程的两个实数根分别为1x ,2x ,且满足1212215x x x x +=-,求m 的值. 【答案】(1)14m <且0m ≠;(2)15m =- 【解析】 【分析】(1)根据一元二次方程的定义和判别式的意义得到:()22140m m ∴∆=-->且20m ≠,然后求出两个不等式解集的公共部分即可.(2)利用根与系数的关系得到12221m x x m -+=, 1221x x m =,加上14m <且0m ≠,则可判断10x <,20x <,所以1212215x x x x --=-,2221215m m m--=-,然后解方程求出m 即可得到满足条件的m 的值. 【详解】(1)因为方程()221210m x m x +-+=有两个不相等的实数根,()221240m m ∴∆=-->,解得14m <;又因为是一元二次方程,所以20m ≠,0m ∴≠.m ∴的取值范围是14m <且0m ≠. (2)1x ,2x 为原方程的两个实数根,12221m x x m -∴+=,1221x x m = 14m <且0m ≠,122210m x x m -∴+=<,12210x x m=>,10x ∴<,20x <. 1212215x x x x +=-,1212215x x x x --=-,2221215m m m -∴-=-,215210m m ∴--=,解得113m =,215m =-, 14m <且0m ≠,113m ∴=不合题意,舍去,15m ∴=-. 【点睛】 此题主要考查一元一次方程的定义和判别式的意义,正确理解概念和熟练运用根的判别式是解题的关键.4.已知关于x 的方程24832x nx n --=和()223220x n x n -+-+=,是否存在这样的n 值,使第一个方程的两个实数根的差的平方等于第二个方程的一整数根?若存在,请求出这样的n 值;若不存在,请说明理由?【答案】存在,n=0. 【解析】 【分析】在方程①中,由一元二次方程的根与系数的关系,用含n 的式子表示出两个实数根的差的平方,把方程②分解因式,建立方程求n ,要注意n 的值要使方程②的根是整数. 【详解】 若存在n 满足题意.设x1,x2是方程①的两个根,则x 1+x 2=2n ,x 1x 2=324n +-,所以(x 1-x 2)2=4n 2+3n+2, 由方程②得,(x+n-1)[x-2(n+1)]=0, ①若4n 2+3n+2=-n+1,解得n=-12,但1-n=32不是整数,舍. ②若4n 2+3n+2=2(n+2),解得n=0或n=-14(舍), 综上所述,n=0.5.(本题满分10分)如图,在平面直角坐标系中,直线AB 与x 轴、y 轴分别交于点A 、B ,直线CD 与x 轴、y 轴分别交于点C 、D ,AB 与CD 相交于点E ,线段OA 、OC 的长是一元二次方程-18x+72=0的两根(OA >OC ),BE=5,tan ∠ABO=.(1)求点A,C的坐标;(2)若反比例函数y=的图象经过点E,求k的值;(3)若点P在坐标轴上,在平面内是否存在一点Q,使以点C,E,P,Q为顶点的四边形是矩形?若存在,请写出满足条件的点Q的个数,并直接写出位于x轴下方的点Q的坐标;若不存在,请说明理由.【答案】(1)、A(12,0),C(﹣6,0);(2)、k=36;(3)、6个;Q1(10,﹣12),Q2(﹣3,6﹣3).【解析】试题分析:(1)、首先求出方程的解,根据OA>OC求出两点的坐标;(2)、根据∠ABO的正切值求出OB的长度,根据Rt△AOB得出AB的长度,作EM⊥x轴,根据三角形相似得出点E的坐标,然后求出k的值;(3)、分别以CE为矩形的边,在点C、E处设计直角,垂线与两坐标轴相交,得到点P,进而得到点Q;以CE为矩形对角线,则以CE的中点为圆心做圆,与两坐标轴相交,得到点P,再得点Q.试题解析:(1)由题意,解方程得:x1=6,x2=12.∵OA>OC,∴OA=12,OC=6.∴A(12,0),C(﹣6,0);(2)∵tan∠ABO=,∠AOB=90°∴∴OB=16.在Rt△AOB中,由勾股定理,得AB=20∵BE=5,∴AE=15.如图1,作EM⊥x轴于点M,∴EM∥OB.∴△AEM∽△ABO,∴,即:∴EM=12,AM=9,∴OM=12﹣9=3.∴E(3,12).∴k=36;(3)满足条件的点Q的个数是6,x轴的下方的Q1(10,﹣12),Q2(﹣3,6﹣3);方法:如下图①分别以CE为矩形的边,在点C、E处设计直角,垂线与两坐标轴相交,得到点P,进而得到点Q;(有三种)②以CE为矩形对角线,则以CE的中点为圆心做圆,与两坐标轴相交,得到点P,再得点Q;(有三种)如图①∵E(3,12),C(﹣6,0),∴CG=9,EG=12,∴EG2=CG•GP,∴GP=16,∵△CPE与△PCQ是中心对称,∴CH=GP=16,QH=FG=12,∵OC=6,∴OH=10,∴Q(10,﹣12),如图②作MN∥x轴,交EG于点N,EH⊥y轴于点H ∵E(3,12),C(﹣6,0),∴CG=9,EG=12,∴CE=15,∵MN=CG=,可以求得PH=3﹣6,同时可得PH=QR,HE=CR ∴Q(﹣3,6﹣3),考点:三角形相似的应用、三角函数、一元二次方程.二、初三数学 二次函数易错题压轴题(难)6.在平面直角坐标系中,O 为坐标原点,抛物线L :y =ax 2﹣4ax (a >0)与x 轴正半轴交于点A .抛物线L 的顶点为M ,对称轴与x 轴交于点D . (1)求抛物线L 的对称轴.(2)抛物线L :y =ax 2﹣4ax 关于x 轴对称的抛物线记为L ',抛物线L '的顶点为M ',若以O 、M 、A 、M '为顶点的四边形是正方形,求L '的表达式.(3)在(2)的条件下,点P 在抛物线L 上,且位于第四象限,点Q 在抛物线L '上,是否存在点P 、点Q 使得以O 、D 、P 、Q 为顶点的四边形是平行四边形,若存在,求出点P 坐标,若不存在,请说明理由.【答案】(1)2x =;(2)2122y x x =-+ ;(3)存在,P 点的坐标为(33,3或(33,3-或(13,3或(13,3+-或31,2⎛⎫- ⎪⎝⎭【解析】 【分析】(1)根据抛物线的对称轴公式计算即可.(2)利用正方形的性质求出点M ,M ′的坐标即可解决问题. (3)分OD 是平行四边形的边或对角线两种情形求解即可. 【详解】解:(1)∵抛物线L :y =ax 2﹣4ax (a >0), ∴抛物线的对称轴x =﹣42aa-=2. (2)如图1中,对于抛物线y=ax2﹣4ax,令y=0,得到ax2﹣4ax=0,解得x=0或4,∴A(4,0),∵四边形OMAM′是正方形,∴OD=DA=DM=DM′=2,∴M((2,﹣2),M′(2,2)把M(2,﹣2)代入y=ax2﹣4ax,可得﹣2=4a﹣8a,∴a=12,∴抛物线L′的解析式为y=﹣12(x﹣2)2+2=﹣12x2+2x.(3)如图3中,由题意OD=2.当OD为平行四边形的边时,PQ=OD=2,设P(m,12m2﹣2m),则Q[m﹣2,﹣12(m﹣2)2+2(m﹣2)]或[m+2,﹣12(m+2)2+2(m+2)],∵PQ∥OD,∴12m2﹣2m=﹣12(m﹣2)2+2(m﹣2)或12m2﹣2m=﹣12(m+2)2+2(m+2),解得m=3±3或1±3,∴P(3+3,3)或(3﹣3,﹣3)或(1﹣3,3)和(1+3,﹣3),当OD是平行四边形的对角线时,点P的横坐标为1,此时P(1,﹣32 ),综上所述,满足条件的点P的坐标为(3+3,3)或(3﹣3,﹣3)或(1﹣3,3)和(1+3,﹣3)或(1,﹣32 ).【点睛】本题属于二次函数综合题,考查了二次函数的性质,正方形的性质,平行四边形的判定和性质等知识,解题的关键是理解题意,学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题学会利用参数构建方程解决问题,学会用分类讨论的思想思考问题,属于中考压轴题7.如图,抛物线y=﹣x2+mx+n与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).(1)求抛物线的表达式;(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;(3)点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.【答案】(1)抛物线的解析式为:y=﹣x2+x+2(2)存在,P1(,4),P2(,),P3(,﹣)(3)当点E运动到(2,1)时,四边形CDBF的面积最大,S四边形CDBF的面积最大=.【解析】试题分析:(1)将点A、C的坐标分别代入可得二元一次方程组,解方程组即可得出m、n的值;(2)根据二次函数的解析式可得对称轴方程,由勾股定理求出CD的值,以点C为圆心,CD为半径作弧交对称轴于P1;以点D为圆心CD为半径作圆交对称轴于点P2,P3;作CH 垂直于对称轴与点H,由等腰三角形的性质及勾股定理就可以求出结论;(3)由二次函数的解析式可求出B点的坐标,从而可求出BC的解析式,从而可设设E点的坐标,进而可表示出F的坐标,由四边形CDBF的面积=S△BCD+S△CEF+S△BEF可求出S与a的关系式,由二次函数的性质就可以求出结论.试题解析:(1)∵抛物线y=﹣x2+mx+n经过A(﹣1,0),C(0,2).解得:,∴抛物线的解析式为:y=﹣x2+x+2;(2)∵y=﹣x2+x+2,∴y=﹣(x﹣)2+,∴抛物线的对称轴是x=.∴OD=.∵C(0,2),∴OC=2.在Rt△OCD中,由勾股定理,得CD=.∵△CDP是以CD为腰的等腰三角形,∴CP1=CP2=CP3=CD.作CH⊥x轴于H,∴HP1=HD=2,∴DP1=4.∴P1(,4),P2(,),P3(,﹣);(3)当y=0时,0=﹣x2+x+2∴x1=﹣1,x2=4,∴B(4,0).设直线BC的解析式为y=kx+b,由图象,得,解得:,∴直线BC的解析式为:y=﹣x+2.如图2,过点C作CM⊥EF于M,设E(a,﹣a+2),F(a,﹣a2+a+2),∴EF=﹣a2+a+2﹣(﹣a+2)=﹣a2+2a(0≤x≤4).∵S四边形CDBF=S△BCD+S△CEF+S△BEF=BD•OC+EF•CM+EF•BN,=+a(﹣a2+2a)+(4﹣a)(﹣a2+2a),=﹣a2+4a+(0≤x≤4).=﹣(a﹣2)2+∴a=2时,S四边形CDBF的面积最大=,∴E(2,1).考点:1、勾股定理;2、等腰三角形的性质;3、四边形的面积;4、二次函数的最值8.如图,已知抛物线y=ax2+bx+c(a≠0)的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A,B两点(点A在点B的右侧),点P是该抛物线上的一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.(1)求该抛物线的函数关系式;(2)当△ADP是直角三角形时,求点P的坐标;(3)在题(2)的结论下,若点E在x轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.【答案】(1) y=x2﹣4x+3;(2) P1(1,0),P2(2,﹣1);(3) F1(22,1),F2(22,1).【解析】【分析】(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点式,然后将函数图象经过的C点坐标代入上式中,即可求出抛物线的解析式;(2)由于PD∥y轴,所以∠ADP≠90°,若△ADP是直角三角形,可考虑两种情况:①以点P为直角顶点,此时AP⊥DP,此时P点位于x轴上(即与B点重合),由此可求出P点的坐标;②以点A为直角顶点,易知OA=OC,则∠OAC=45°,所以OA平分∠CAP,那么此时D、P关于x轴对称,可求出直线AC的解析式,然后设D、P的横坐标,根据抛物线和直线AC的解析式表示出D、P的纵坐标,由于两点关于x轴对称,则纵坐标互为相反数,可据此求出P 点的坐标;(3)很显然当P、B重合时,不能构成以A、P、E、F为顶点的四边形,因为点P、F都在抛物线上,且点P 为抛物线的顶点,所以PF 与x 轴不平行,所以只有(2)②的一种情况符合题意,由②知此时P 、Q 重合;假设存在符合条件的平行四边形,那么根据平行四边形的性质知:P 、F 的纵坐标互为相反数,可据此求出F 点的纵坐标,代入抛物线的解析式中即可求出F 点的坐标.【详解】(1)∵抛物线的顶点为Q (2,﹣1),∴设抛物线的解析式为y=a (x ﹣2)2﹣1,将C (0,3)代入上式,得:3=a (0﹣2)2﹣1,a=1;∴y=(x ﹣2)2﹣1,即y=x 2﹣4x+3;(2)分两种情况:①当点P 1为直角顶点时,点P 1与点B 重合;令y=0,得x 2﹣4x+3=0,解得x 1=1,x 2=3;∵点A 在点B 的右边,∴B (1,0),A (3,0);∴P 1(1,0);②当点A 为△AP 2D 2的直角顶点时;∵OA=OC ,∠AOC=90°,∴∠OAD 2=45°;当∠D 2AP 2=90°时,∠OAP 2=45°,∴AO 平分∠D 2AP 2;又∵P 2D 2∥y 轴,∴P 2D 2⊥AO ,∴P 2、D 2关于x 轴对称;设直线AC 的函数关系式为y=kx+b (k≠0).将A (3,0),C (0,3)代入上式得:303k b b +=⎧⎨=⎩, 解得13k b =-⎧⎨=⎩; ∴y=﹣x+3;设D 2(x ,﹣x+3),P 2(x ,x 2﹣4x+3),则有:(﹣x+3)+(x 2﹣4x+3)=0,即x 2﹣5x+6=0;解得x 1=2,x 2=3(舍去);∴当x=2时,y=x 2﹣4x+3=22﹣4×2+3=﹣1;∴P 2的坐标为P 2(2,﹣1)(即为抛物线顶点).∴P 点坐标为P 1(1,0),P 2(2,﹣1);(3)由(2)知,当P 点的坐标为P 1(1,0)时,不能构成平行四边形;当点P 的坐标为P 2(2,﹣1)(即顶点Q )时,平移直线AP 交x 轴于点E ,交抛物线于F ;∵P (2,﹣1),∴可设F (x ,1);∴x 2﹣4x+3=1,解得x 1=2﹣2,x 2=2+2;∴符合条件的F 点有两个,即F 1(2﹣2,1),F 2(2+2,1).【点睛】此题主要考查了二次函数的解析式的确定、直角三角形的判定、平行四边形的判定与性质等重要知识点,同时还考查了分类讨论的数学思想,能力要求较高,难度较大.9.定义:函数l 与l '的图象关于y 轴对称,点(),0P t 是x 轴上一点,将函数l '的图象位于直线x t =左侧的部分,以x 轴为对称轴翻折,得到新的函数w 的图象,我们称函数w 是函数l 的对称折函数,函数w 的图象记作1F ,函数l 的图象位于直线x t =上以及右侧的部分记作2F ,图象1F 和2F 合起来记作图象F .例如:如图,函数l 的解析式为1y x =+,当1t =时,它的对称折函数w 的解析式为()11y x x =-<.(1)函数l 的解析式为21y x =-,当2t =-时,它的对称折函数w 的解析式为_______; (2)函数l 的解析式为1²12y x x =--,当42x -≤≤且0t =时,求图象F 上点的纵坐标的最大值和最小值;(3)函数l 的解析式为()2230y ax ax a a =--≠.若1a =,直线1y t =-与图象F 有两个公共点,求t 的取值范围.【答案】(1)()212y x x =+<-;(2)F 的解析式为2211(0)211(0)2y x x x y x x x ⎧=--≥⎪⎪⎨⎪=--+<⎪⎩;图象F 上的点的纵坐标的最大值为32y =,最小值为3y =-;(3)当3t =-,31712t <≤,3175t +<<时,直线1y t =-与图象F 有两个公共点. 【解析】【分析】(1)根据对折函数的定义直接写出函数解析式即可;(2)先根据题意确定F 的解析式,然后根据二次函数的性质确定函数的最大值和最小值即可;(3)先求出当a=1时图像F 的解析式,然后分14t -=-、点(),1t t -落在223()y x x x t =--≥上和点(),1t t -落在()223y x x x t =--+<上三种情况解答,最后根据图像即可解答.【详解】解:(1)()212y x x =+<-(2)F 的解析式为2211(0)211(0)2y x x x y x x x ⎧=--≥⎪⎪⎨⎪=--+<⎪⎩当4x =-时,3y =-,当1x =-时,32y =, 当1x =时,32y =-,当2x =时,1y =, ∴图象F 上的点的纵坐标的最大值为32y =,最小值为3y =-. (3)当1a =时,图象F 的解析式为2223()23()y x x x t y x x x t ⎧=--≥⎨=--+<⎩∴该函数的最大值和最小值分别为4和-4;a :当14t -=-时,3t =-,∴当3t =-时直线1y t =-与图象F 有两个公共点;b :当点(),1t t -落在223()y x x x t =--≥上时,2123t t t -=--,解得1317t -=,2317t += c :当点(),1t t -落在()223y x x x t =--+<上时,2123t t t -=--+,解得34t =-(舍),41t =14t -=,∴55t =∴当3171t -<≤或3175t +<<时,直线1y t =-与图象F 有两个公共点; 综上所述:当3t =-,3171t -<≤,3175t +<<时,直线1y t =-与图象F 有两个公共点.【点睛】 本题属于二次函数综合题,考查了“称折函数”的定义、二次函数的性质、解二元一次方程等知识,弄清题意、灵活运用所学知识是解答本题的关键.10.如图,已知二次函数1L :()22311y mx mx m m =+-+≥和二次函数2L :()2341y m x m =--+-()1m ≥图象的顶点分别为M 、N ,与x 轴分别相交于A 、B 两点(点A 在点B 的左边)和C 、D 两点(点C 在点D 的左边),(1)函数()22311y mx mx m m =+-+≥的顶点坐标为______;当二次函数1L ,2L 的y值同时随着x 的增大而增大时,则x 的取值范围是_______;(2)判断四边形AMDN 的形状(直接写出,不必证明);(3)抛物线1L ,2L 均会分别经过某些定点;①求所有定点的坐标;②若抛物线1L 位置固定不变,通过平移抛物线2L 的位置使这些定点组成的图形为菱形,则抛物线2L 应平移的距离是多少?【答案】(1)()1,41m --+,13x ;(2)四边形AMDN 是矩形;(3)①所有定点的坐标,1L 经过定点()3,1-或()1,1,2L 经过定点()5,1-或()1,1-;②抛物线2L 应平移的距离是4+4-.【解析】【分析】(1)将已知抛物线解析式转化为顶点式,直接得到点M 的坐标;结合函数图象填空; (2)利用抛物线解析式与一元二次方程的关系求得点A 、D 、M 、N 的横坐标,可得AD 的中点为(1,0),MN 的中点为(1,0),则AD 与MN 互相平分,可证四边形AMDN 是矩形;(3)①分别将二次函数的表达式变形为1:(3)(1)1L y m x x =+-+和2:(1)(5)1L y m x x =----,通过表达式即可得出所过定点;②根据菱形的性质可得EH 1=EF=4即可,设平移的距离为x ,根据平移后图形为菱形,由勾股定理可得方程即可求解.【详解】解:(1)12b x a=-=-,顶点坐标M 为(1,41)m --+, 由图象得:当13x 时,二次函数1L ,2L 的y 值同时随着x 的增大而增大.故答案为:(1,41)m --+;13x; (2)结论:四边形AMDN 是矩形.由二次函数21:231(1)L y mx mx m m =+-+和二次函数22:(3)41(1)L y m x m m =--+-解析式可得:A 点坐标为(1-0),D 点坐标为(3+,0), 顶点M 坐标为(1,41)m --+,顶点N 坐标为(3,41)m -,AD ∴的中点为(1,0),MN 的中点为(1,0),AD ∴与MN 互相平分,∴四边形AMDN 是平行四边形,又AD MN =,∴□AMDN 是矩形;(3)①二次函数21:231(3)(1)1L y mx mx m m x x =+-+=+-+,故当3x =-或1x =时1y =,即二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点,二次函数22:(3)41(1)(5)1L y m x m m x x =--+-=----,故当1x =或5x =时1y =-,即二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点,②二次函数21:231L y mx mx m =+-+经过(3,1)-、(1,1)两点,二次函数22:(3)41L y m x m =--+-经过(1,1)-、(5,1)-两点,如图:四个定点分别为(3,1)E -、(1,1)F ,(1,1)H -、(5,1)G -,则组成四边形EFGH 为平行四边形,∴FH ⊥HG ,FH=2,HM=4-x ,设平移的距离为x ,根据平移后图形为菱形,则EH 1=EF=H 1M=4,由勾股定理可得:FH 2+HM 2=FM 2,即22242(4)x =+-,解得:423x =±,抛物线1L 位置固定不变,通过左右平移抛物线2L 的位置使这些定点组成的图形为菱形,则抛物线2L 应平移的距离是423+或423-.【点睛】本题考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.要会利用数形结合的思想把代数和几何图形结合来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.三、初三数学 旋转易错题压轴题(难)11.如图1,在Rt ABC △中,90A ∠=︒,AB AC =,点D ,E 分别在边AB ,AC 上,AD AE =,连接DC ,点M ,P ,N 分别为DE ,DC ,BC 的中点.(1)观察猜想:图1中,线段PM 与PN 的数量关系是_________,位置关系是_________;(2)探究证明:把ADE 绕点A 逆时针方向旋转到图2的位置,连接MN ,BD ,CE ,判断PMN 的形状,并说明理由;(3)拓展延伸:把ADE 绕点A 在平面内自由旋转,若4=AD ,10AB =,请直接写出PMN 面积的最大值.【答案】(1)PM PN =,PM PN ⊥;(2)等腰直角三角形,见解析;(3)492【解析】【分析】(1)由三角形中位线定理及平行的性质可得PN 与PM 等于DE 或CE 的一半,又△ABC 为等腰直角三角形,AD=AE ,所以得PN=PM ,且互相垂直;(2)由旋转可推出BAD CAE ∆∆≌,再利用PM 与PN 皆为中位线,得到PM=PN ,再利用角度间关系推导出垂直即可;(3)找到面积最大的位置作出图形,由(2)可知PM=PM ,且PM ⊥PN ,利用三角形面积公式求解即可.【详解】(1)PM PN =,PM PN ⊥;已知点M ,P ,N 分别为DE ,DC ,BC 的中点,根据三角形的中位线定理可得 12PM EC =,12PN BD =,//PM EC ,//PN BD 根据平行线性质可得DPM DCE ∠=∠,NPD ADC ∠=∠在Rt ABC ∆中,90A ∠=︒,AB AC =,AD AE =可得BD EC =,90DCE ADC ∠+∠=︒即得PM PN =,PM PN ⊥故答案为:PM PN =;PM PN ⊥.(2)等腰直角三角形,理由如下:由旋转可得BAD CAE ∠=∠,又AB AC =,AD AE =∴BAD CAE ∆∆≌∴BD CE =,ABD ACE ∠=∠,∵点M ,P 分别为DE ,DC 的中点∴PM 是DCE ∆的中位线∴12PM CE =,且//PM CE , 同理可证12PN BD =,且//PN BD ∴PM PN =,MPD ECD ∠=∠,PNC DBC ∠=∠,∴MPD ECD ACD ACE ACD ABD ∠=∠=∠+∠=∠+∠,DPN PNC PCN DBC PCN ∠=∠+∠=∠+∠,∴90MPN MPD DPN ACD ABD DBC PCN ABC ACB ∠=∠+∠=∠+∠+∠+∠=∠+∠=︒,即PMN ∆为等腰直角三角形.(3)把ADE ∆绕点A 旋转的如图的位置,此时1()72PN AD AB =+=,1()72PM AE AC =+= 且PN 、PM 的值最长,由(2)可知PM PN =,PM PN ⊥ 所以PMN ∆面积最大值为1497722⨯⨯=. 【点睛】本题主要考查三角形中位线的判定及性质、全等三角形的判定及性质、等腰直角三角形的判定及性质、旋转的性质等相关知识,解题关键在于找到图形中各角度之间的数量关系.12.如图,在边长为2的正方形ABCD 中,点P 、Q 分别是边AB 、BC 上的两个动点(与点A 、B 、C 不重合),且始终保持BP BQ =,AQ QE ⊥,QE 交正方形外角平分线CE 于点E ,AE 交CD 于点F ,连结PQ .(1)求证:APQ QCE ∆∆≌; (2)证明:DF BQ QF +=;(3)设BQ x =,当x 为何值时,//QF CE ,并求出此时AQF ∆的面积. 【答案】(1)证明见解析;(2)证明见解析;(3)当222x =-+//QF CE ;AQF S ∆442=-+.【解析】 【分析】(1)判断出△PBQ 是等腰直角三角形,然后求出∠APQ=∠QCE=135°,再根据同角的余角相等求出∠PAQ=∠CQE ,再求出AP=CQ ,然后利用“角边角”证明即可; (2)根据全等三角形对应边相等可得AQ=EQ ,判断出△AQE 是等腰直角三角形,将ADF ∆绕点A 顺时针旋转90︒得F AB '∆,再证明()F AQ FAQ SAS '∆∆≌;(3)连结AC ,设QFCE ,推出QCF ∆是等腰直角三角形°,再证明()ABQ ADF SAS ∆∆≌,根据全等三角形对应边相等可得QF=GF ,AQ AF =,22.5QAB DAF ∠=∠=︒,分别用x 表示出DF 、CF 、QF ,然后列出方程求出x ,再求出△AQF 的面积. 【详解】(1)∵四边形ABCD 是正方形,∴AB BC =,90B BCD DCM ∠=∠=∠=︒, ∵BP BQ =,∴PBQ ∆是等腰直角三角形,AP QC =, ∴45BPQ ∠=︒, ∴135APQ ∠=︒ ∵CE 平分DCM ∠, ∴45DCE ECM ∠=∠=︒, ∴135QCE ∠=︒,∴135APQ QCE ∠=∠=︒, ∵AQ QE ⊥,∴90AQB CQE ∠+∠=︒. ∵90AQB BAQ ∠+∠=︒. ∴BAQ CQE ∠=∠. ∴()APQ QCE ASA ∆≌. (2)由(1)知APQ QCE ∆∆≌. ∴QA QE =. ∵90AQE ∠=︒,∴AQE ∆是等腰直角三角形, ∴45QAE ∠=︒. ∴45DAF QAB ∠+∠=︒,如图4,将ADF ∆绕点A 顺时针旋转90︒得F AB '∆,其中点D 与点B 重合,且点F '在直线BQ 上,则45F AQ '∠=︒,F A FA '=,AQ AQ =, ∴()F AQ FAQ SAS '∆∆≌. ∴QF QF BQ DF '==+.(3)连结AC ,若QF CE ,则45FQC ECM ∠=∠=︒. ∴QCF ∆是等腰直角三角形, ∴2CF CQ x ==-, ∴DF BQ x ==.∵AB AD =,90B D ∠=∠=︒, ∴()ABQ ADF SAS ∆∆≌.∴AQ AF =,22.5QAB DAF ∠=∠=︒, ∴AC 垂直平分QF ,∴22.5QAC FAC QAB FAD ∠=∠=∠=∠=︒,2FQ QN =,∴22FQ BQ x ==.在Rt QCF ∆中,根据勾股定理,得222(2)(2)(2)x x x -+-=. 解这个方程,得1222x =-+, 2222x =--(舍去). 当222x =-+时,QFCE .此时,QCF QEF S S ∆∆=,∴212QCF AQF QEF AQF AQE S S S S S AQ ∆∆∆∆∆+=+==, ∴()2222111222AQF AQE QCF S S S AQ CQ AQ CQ ∆∆∆=-=-=- ()222112(2)4244222x x x x ⎡⎤=+--=⋅==-+⎣⎦ 【点睛】本题考查了正方形的性质,全等三角形的判定与性质,旋转的性质,等腰直角三角形的判定与性质,勾股定理的应用,难点在于(3)作辅助线构造成全等三角形并利用勾股定理列出方程.13.边长为2的正方形ABCD 的两顶点A 、C 分别在正方形EFGH 的两边DE 、DG 上(如图1),现将正方形ABCD 绕D 点顺时针旋转,当A 点第一次落在DF 上时停止旋转,旋转过程中, AB 边交DF 于点M ,BC 边交DG 于点N. (1)求边DA 在旋转过程中所扫过的面积;(2)旋转过程中,当MN 和AC 平行时(如图2),求正方形ABCD 旋转的度数; (3)如图3,设△MBN 的周长为p ,在旋转正方形ABCD 的过程中,p 值是否有变化?请证明你的结论.【答案】(1);(2);(3)不变化,证明见解析.【解析】试题分析:(1)将正方形ABCD 绕D 点顺时针旋转,当A 点第一次落在DF 上时停止旋转,旋转过程中,DA 旋转了,从而根据扇形面积公式可求DA 在旋转过程中所扫过的面积.(2)旋转过程中,当MN 和AC 平行时,根据平行的性质和全等三角形的判定和性质可求正方形ABCD 旋转的度数为.(3)延长BA 交DE 轴于H 点,通过证明和可得结论.(1)∵A 点第一次落在DF 上时停止旋转,∴DA 旋转了.∴DA 在旋转过程中所扫过的面积为.(2)∵MN ∥AC ,∴,.∴.∴.又∵,∴. 又∵,∴. ∴.∴.∴旋转过程中,当MN 和AC 平行时,正方形ABCD 旋转的度数为.(3)不变化,证明如下:如图, 延长BA 交DE 轴于H 点,则,,∴.又∵.∴. ∴.又∵, ,∴.∴.∴.∴. ∴在旋转正方形ABCD 的过程中,值无变化.考点:1.面动旋转问题;2.正方形的性质;3.扇形面积的计算;4.全等三角形的判定和性质.14.我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”。
上海临港第一中学初三化学上册期中测试化学试题(含答案)
上海临港第一中学上册期中测试化学试题(含答案)一、选择题(培优题较难)1.化学实验操作应严谨规范,下列操作符合要求的是A.看B.听C.闻D.吹2.下列实验操作正确的是A.塞紧橡皮塞B.加热液体C.取用液体D.读出液体的体积3.最近,我国科学家成功合成新型催化剂,将CO2高效转化为甲醇(CH3OH)。
这不仅可以缓解碳排放引起的温室效应,还将成为理想的能源补充形式。
该化学反应的微观过程如下图所示。
下列说法正确的是A.该反应中四种物质均为化合物B.反应前后H元素的化合价不变C.参加反应的甲、乙分子个数比为1:3D.反应前后原子数目发生改变4.下列加热高锰酸钾制取氧气的部分操作示意图中,正确的是A.检查装置气密性B.加热立即收集C .收满后移出集气瓶D .结束时停止加热5.下列有关氧气的说法,错误的是( )A .氧气能支持燃烧B .细铁丝在氧气中燃烧,生成氧化铁C .在通常状况下,氧气的密度比空气大D .氧气的化学性质比较活泼,能跟许多物质发生反应 6.下图表示某化学反应的微观示意图,依据图分析判断,下列说法正确的是A .甲物质由5个原子构成B .化学变化的后硅元素的化合价不变C .参加反应的乙的质量和生成的丁中氢元素的质量相等D .参加反应的甲、乙两种物质的分子个数比为l :17.下列关于空气的说法中,不正确的是( )A .工业上采用分离液态空气法获得氧气B .二氧化硫是空气污染物之一C .空气中氧气质量占空气质量的21%D .空气中的氧气来源于绿色植物的光合作用8.某纯净物3g 在氧气中完全燃烧,生成8.8g 二氧化碳和5.4g 水。
下列说法不正确的是 A .该纯净物中含有C 、H 元素,不含O 元素B .该反应中2O 和2CO 的质量比为14:11C .该反应中2O 和2H O 的分子数之比为7:6D .该纯净物中C 、H 原子的个数比为1:49.如图所示有关二氧化碳的实验中,只与二氧化碳物理性质有关的实验是( ) A . B . C . D .10.某有机物在9.6g 氧气中恰好完全燃烧,生成8.8gCO 2和5.4gH 2O ,下列说法正确的是()A.该有机物只含碳、氢两种元素B.该有机物中一定含有碳、氢元素,可能含有氧元素C.该有机物中一定含有碳、氢、氧三种元素D.无法确定11.过氧化钠(Na2O2)可作呼吸面具中氧气的来源,它与二氧化碳反应后的生成物为( ) A.Na2CO3和H2 B.Na2O和O2 C.NaOH和O2 D.Na2CO3和O212.正确记录实验数据是一项实验基本技能,某同学记录的实验数据错误的是A.用托盘天平称取2.9gNaCl固体B.用10mL量筒量取8.3mL蒸馏水C.在10mL试管中倒入约3mL蒸馏水进行加热D.用温度计测得水温为25.15C13.科学理论在传承中不断发展,科学家们传承前人的正确观点,纠正错误观点,形成科学理论,关于原子结构的学说有:①在球体内充斥正电荷,电子镶嵌其中②原子是可分的③原子呈球形④原子中有带负电的电子⑤原子中有带正电的原子核⑥原子核很小,但集中了原子的大部分质量其中经过卢瑟福传承和发展后形成的观点是()A.②③④⑤⑥B.①②③④C.④⑤⑥D.⑤⑥14.关于下列五种粒子结构示意图的说法中正确的是( )A.①④属于不同种元素B.②⑤属于金属元素C.④⑤均具有稳定结构D.①③两种粒子可以形成化合物MgCl215.用如图进行实验,下列说法中不正确的是()A.能证明分子在不断运动B.浓盐酸与浓氨水都具有挥发性C.氯化氢分子比氨分子运动得快D.实验过程中发生了化学变化16.化学实验是化学学习的重要方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上海临港第一中学2020年期中单元测试一、选择题1.近几年,在国家宏观政策调控下,我国房价上涨出现减缓趋势。
若将房价的“上涨”类比成“加速”,将房价的“下跌”类比成“减速”,据此,你认为“房价上涨出现减缓趋势”可类比成( ) A .速度增加,加速度减小 B .速度增加,加速度增大 C .速度减小,加速度增大 D .速度减小,加速度减小2.一物体在地面以速度为 v 向上竖直上抛,不计空气阻力,经过 t 时间到最高点,上升高度为 h ,则A .物体通过前半程和后半程所用时间之比为 1:(21 )B .物体通过2h 处的速度为 2v C .物体经过 2t 时的速度为2v D .物体经过前 2t和后 2t 的位移之比为 1:33.第19届亚洲运动会将于2022年9月10日~9月25日在中国杭州举行.杭州是中国第三个取得夏季亚运会主办权的城市,图中的“莲花碗”是田径的主赛场,下列关于亚运会田径项目的叙述正确的是( )A .研究短跑运动员终点撞线时可将运动员看成质点B .在田径比赛中跑步运动员的比赛成绩是一个时间间隔C .短跑运动员跑100m 和200m 都是指位移D .高水平运动员400m 比赛的平均速度有可能大于其他运动员200m 比赛的平均速度 4.鱼在水中沿直线水平向左减速游动过程中,水对鱼的作用力方向合理的是( )A .B .C.D.5.如图所示,此时表演者静止在弯曲倾斜的竹竿上,则下列说法正确的是()A.表演者对竹竿的弹力是由竹竿形变产生的B.表演者对竹竿的力竖直向下C.表演者对竹竿的摩擦力一定为零D.表演者对竹竿的力大于竹竿对表演者的力6.一辆汽车由静止开始做匀速直线运动,从开始运动到驶过第一个100m距离时,速度增加了10m/s,汽车驶过第二个100m时,速度的增加量是A.4.1m/s B.8.2m/s C.10m/s D.20m/s7.拿一个长约1.5m的玻璃筒,一端封闭,另一端有开关,把金属片和小羽毛放到玻璃筒里.把玻璃筒倒立过来,观察它们下落的情况,然后把玻璃筒里的空气抽出,再把玻璃筒倒立过来,再次观察它们下落的情况,下列说法正确的是A.玻璃筒充满空气时,金属片和小羽毛下落一样快B.玻璃筒充满空气时,金属片和小羽毛均做自由落体运动C.玻璃筒抽出空气后,金属片和小羽毛下落一样快D.玻璃筒抽出空气后,金属片比小羽毛下落快8.某同学绕操场一周跑了400m,用时65s,这两个物理量分别是A.路程、时刻B.位移、时刻C.路程、时间间隔D.位移、时间间隔9.在物理学的发展过程中,有一位科学家开创了以实验和逻辑推理相结合的科学研究方法,研究了落体运动的规律,这位科学家是()A.伽利略B.牛顿C.库伦D.焦耳10.一物体以一定的初速度在水平地面上匀减速滑动.若已知物体在第1秒内位移为8.0 m,在第3秒内位移为0.5 m.则下列说法正确的是A.物体的加速度一定为3.75 m/s2B.物体的加速度可能为3.75 m/s2C.物体在第0.5秒末速度一定为4.0 m/sD.物体在第2.5秒末速度一定为0.5 m/s11.物体沿一直线运动,下列说法中正确的是( )A.物体在第一秒末的速度是5 m/s,则物体在第一秒内的位移一定是5 mB.物体在第一秒内的平均速度是5 m/s,则物体在第一秒内的位移一定是5 mC.物体在某段时间内的平均速度是5 m/s,则物体在每一秒内的位移都是5 mD.物体在某段位移内的平均速度是5 m/s,则物体在经过这段位移中间时刻的速度一定是5 m/s12.大雪天车轮打滑,车辆难以前进,交警帮忙向前推车,如图所示,在推车的过程中,关于人和车之间的作用力,下列说法正确的一是()A.车对人有向后的力B.车对人没有作用力C.人对车的力大于车对人的力D.人对车的力小于车对人的力13.小洪同学乘出租车从校门口出发,到火车站接到同学后当即随车回校.出租车票如图所示,则以下说法正确的是( )A.位移为16.2kmB.路程为0C.11:48指的是时间D.11:05指的是时刻14.2018年8月26日,在雅加达亚运会男子田径100米决赛中,我国运动员苏炳添以9秒92打破亚运会记录夺冠。
这是由于他在这100米中A.平均速度大B.撞线时的瞬时速度大C.某时刻的瞬时速度大D.起跑时的加速度大15.关于重力加速度的说法中,不正确的是()A.在同一地点物体自由下落时的重力加速度与静止时的重力加速度大小一样B.在地面上不同的地方,重力加速度g的大小不同,但它们相差不是很大C.在地球上同一地点,一切物体在自由落体运动中的加速度都相同D.重力加速度g是标量,只有大小没有方向,通常计算中g取9.8m/s216.某质点向东运动12m,又向西运动20m,又向北运动6m,则它运动的路程和位移大小分别是A.2m,10m B.38m,10mC.14m,6m D.38m,6m17.(题文)重型自卸车利用液压装置使车厢缓慢倾斜到一定角度,车厢上的石块就会自动滑下,以下说法正确的是A.在石块下滑前后自卸车与石块整体的重心位置不变B.自卸车车厢倾角越大,石块与车厢的动摩擦因数越小C.自卸车车厢倾角越大,车厢与石块间的正压力减小D.石块开始下滑时,受到的摩擦力大于重力沿斜面方向的分力18.汽车以10 m/s的速度在马路上匀速行驶,驾驶员发现正前方15 m处的斑马线上有行人,于是刹车礼让,汽车恰好停在斑马线前。
假设驾驶员反应时间为0.5 s,汽车运动的v-t图象如图所示。
则汽车的加速度大小为()A.20 m/s2 B.6 m/s2C.5 m/s2 D.4 m/s219.下列速度表示平均速度的是()m sA.子弹射出枪口时的速度是800/km hB.汽车速度计某时刻的读数是90/m sC.运动员冲过终点时的速度是10/km h的速度向沿海海岸移动D.台风中心以25 /20.如图所示,球A在斜面上,被竖直挡板挡住而处于静止状态,关于球A所受的弹力,以下说法正确的是 ( )A .球A 仅受一个弹力作用,弹力的方向垂直斜面向上B .球A 受两个弹力作用,一个水平向左,一个垂直斜面向下C .球A 受两个弹力作用,一个水平向右,一个垂直斜面向上D .球A 受三个弹力作用,一个水平向右,一个垂直斜面向上,一个竖直向下.二、多选题21.如图所示,A 、B 、C 三个物体静止叠放在水平桌面上,物体A 的质量为2m ,B 和C 的质量都是m ,A 、B 间的动摩擦因数为μ,B 、C 间的动摩擦因数为4μ,B 和地面间的动摩擦因数为8μ.设最大静摩擦力等于滑动摩擦力,重力加速度为g .现对A 施加一水平向右的拉力F ,则下列判断正确的是A .若A 、B 、C 三个物体始终相对静止,则力F 不能超过32μmg B .当力F =μmg 时,A 、B 间的摩擦力为34mg μ C .无论力F 为何值,B 的加速度不会超过34μg D .当力F >72μmg 时,B 相对A 滑动 22.甲物体从离地面H 高空自由落下,而乙物体在地面以初速度v 0同时向上抛出,两物体在离地面34H 处相遇,如果g 、v 0为已知量,则( ) A .从自由下落到相遇,经过的时间为02v t g= B .甲物体落到地面时,乙物体仍在上升C .相遇时,甲乙两物体的速度大小相等,均为2v D .乙上升的最大高度就是H ,且202v H g=,而甲物体落地时的速度大小是v 023.如图所示,水平面上等腰三角形均匀框架顶角30BAC ∠=︒,一均匀圆球放在框架内,球与框架BC 、AC 两边接触但无挤压,现使框架以顶点A 为转轴在竖直平面内顺时针方向从AB 边水平缓慢转至AB 边竖直,则在转动过程中( )A.球对AB边的压力先增大后减小B.球对BC边的压力先增大后减小C.球对AC边的压力一直增大D.球的重心位置一直升高24.一辆客车以加速度a1由静止驶出车站并沿着平直的公路加速行驶,司机突然发现在车后方有一名乘客还没有上车,司机紧接着刹车,做匀减速的加速度大小为a2,停车时客车共行驶距离为s,则()A.加速行驶的距离为212asa a+B.客车的最大速度为122()s a a+C.加速时间为12122()saa a a+D.客车运动的总时间为12122()s a aa a+25.如图甲所示为倾斜的传送带,正以恒定的速度v沿顺时针方向转动,传送带的倾角为37,一物块以初速度0v从传送带的底部冲上传送带并沿传送带向上运动,物块到传送带頂端的速度恰好为零,其运动的v-t图象如乙所示,已知重力加速度为210/g m s=, 370.6,370.8sin cos==,则下列判断正确的是( )A.传送带的速度为4m/sB.传送带底端到顶端的距离为32mC.物块与传送带间的动摩擦因数为0.1D.物块所受摩擦力的方向一直与物块运动的方向相反三、实验题26.在“探究速度随时间变化规律”的实验中,装置如图1所示.从实验中挑选一条点迹清晰的纸带,每5个点取一个计数点,用刻度尺测量计数点间的距离如图2所示,已知打点计时器所用电的频率为50Hz.(1)从图2中所给的刻度尺上读出A、B两点间的距离1s=____________cm;V __________m/s(计算结果保留两位有效数字)(2)在打下D点时小车的瞬时速度D(3)实验中纸带的______________(填“左”或“右”)端与小车相连接.27.在做探究匀变速直线运动的实验中,给你以下器材:打点计时器与纸带(包括低压交流电)、复写纸、秒表、小车、钩码、细绳、导线一端带有定滑轮的长木板.(1)其中不需要的器材是______,还需要增加的器材是___________。
(2)下图是用纸带拖动小车用打点计时器测定匀变速运动的加速度打出的一条纸带A、B、C、D、E为我们在纸带上所选的计数点,相邻计数点间的时间间隔为0.1s。
求:打点计时器打下B点时小车的瞬时速度v B= __________ m/s;小车的加速度a=__m/s2(均保留2位有效数字)28.打点计时器是高中物理学中重要的物理实验仪器,在如图中甲、乙两种打点计时器是高物理实验中常用的,请回答下面的问题:(1)乙图是_____(填“电磁”或“电火花”)打点计时器,电源采用的是_____(填“交流4-6V”或“交流220V”)。
(2)在某次实验中,物体拖动纸带做匀加速直线运动,打点计时器所用的电源频率为50Hz,实验中得到的一条纸带如图所示,纸带上每相邻两个计数点之间都有4个点未画出,按时间顺序取0,1,2,3,4,5六个计数点,实验中用直尺量出各计数点到0点的距离。
①在计数点1所代表的时刻,纸带运动的瞬时速度为1v= ______m/s,加速度a=______m/s2(以上结果均保留两位有效数字)。
