大学物理 自感和互感.ppt
合集下载
电工学自感互感ppt课件

分。
变压器
在交流电路中,电感元件可以组 成变压器,实现电压和电流的变
换,以及电气隔离。
无功补偿
在交流电网中,电感元件可以用 于无功补偿,提高电网的功率因
数,改善电能质量。
电感元件在滤波电路中的应用
低通滤波器
电感与电容元件可以组成低通滤波器,允许低频信号通过,抑制 高频信号。
高通滤波器
利用电感元件,可以组成高通滤波器,用于消除低频噪声,提取高 频信号。
电工学自感互感ppt课件
• 自感现象 • 互感现象 • 电感元件的特性 • 电感元件的应用 • 自感和互感的实验研究
01 自感现象
自感现象的定义
自感现象
当一个线圈中的电流发生变化时 ,会在自身产生一个感应电动势 ,阻碍电流的变化,这种现象称 为自感现象。
产生原因
由于磁场的变化导致线圈中的磁 通量发生变化,从而产生感应电 动势。
03 电感元件的特性
电感元件的电压电流关系
总结词
电感元件的电压和电流之间存在相位差,即电压超前电流90 度。
详细描述
当交流电通过电感元件时,由于磁场的变化,会产生感应电 动势,这个电动势会阻碍电流的变化。因此,电感元件的电 压和电流之间存在相位差,即电压超前电流90度。
电感元件的功率损耗
总结词
带通滤波器与带阻滤波器
通过调整电感与电容的参数,还可以实现带通或带阻滤波,允许或 抑制特定频段的信号通过。
电感元件在谐振电路中的应用
1 2 3
串联谐振
在串联谐振电路中,电感与电容的阻抗相互抵消 ,使得整个电路呈现纯阻性。此时,电流最大, 而电压与电阻成正比。
并联谐振
在并联谐振电路中,电感与电容的电流相互抵消 ,总电流为零。此时,电压最大,而电流与电阻 成正比。
变压器
在交流电路中,电感元件可以组 成变压器,实现电压和电流的变
换,以及电气隔离。
无功补偿
在交流电网中,电感元件可以用 于无功补偿,提高电网的功率因
数,改善电能质量。
电感元件在滤波电路中的应用
低通滤波器
电感与电容元件可以组成低通滤波器,允许低频信号通过,抑制 高频信号。
高通滤波器
利用电感元件,可以组成高通滤波器,用于消除低频噪声,提取高 频信号。
电工学自感互感ppt课件
• 自感现象 • 互感现象 • 电感元件的特性 • 电感元件的应用 • 自感和互感的实验研究
01 自感现象
自感现象的定义
自感现象
当一个线圈中的电流发生变化时 ,会在自身产生一个感应电动势 ,阻碍电流的变化,这种现象称 为自感现象。
产生原因
由于磁场的变化导致线圈中的磁 通量发生变化,从而产生感应电 动势。
03 电感元件的特性
电感元件的电压电流关系
总结词
电感元件的电压和电流之间存在相位差,即电压超前电流90 度。
详细描述
当交流电通过电感元件时,由于磁场的变化,会产生感应电 动势,这个电动势会阻碍电流的变化。因此,电感元件的电 压和电流之间存在相位差,即电压超前电流90度。
电感元件的功率损耗
总结词
带通滤波器与带阻滤波器
通过调整电感与电容的参数,还可以实现带通或带阻滤波,允许或 抑制特定频段的信号通过。
电感元件在谐振电路中的应用
1 2 3
串联谐振
在串联谐振电路中,电感与电容的阻抗相互抵消 ,使得整个电路呈现纯阻性。此时,电流最大, 而电压与电阻成正比。
并联谐振
在并联谐振电路中,电感与电容的电流相互抵消 ,总电流为零。此时,电压最大,而电流与电阻 成正比。
大学物理 12-4 自感和互感

l
μ0
S
l
互感系数计算举例
M Ψ12 I2
N1 N 2 l2
lS
n1n2V
③互感 M与自感L1 ,L2 的关系。
L1 n12V
L2 n22V
M L1L2
在此例中,线圈1的磁通全部通过线圈2,称为无 磁漏。
在一般情况下: M K L1L2
称K 为耦合系数 0 < K <1
自感
2、自感电动势:
dΦ
L N dt
d (NΦ ) dΨ
dt
dt
d (LI ) L dI I dL
dt
dt dt
若回路几何形状、尺寸不变,周围无铁磁性物质,则:
dL 0 dt
L
L
dI dt
自感
【讨论】:1、 L 的定义:可用下两式之一定义
H 2r NI
I
H NI 2r
B NI 2r
dm
B dS
NI 2r
hdr
R2 R1
h
r dr
dm
B dS
NI 2r
hdr
m
dm
NIh பைடு நூலகம்
R2 dr R1 r
NIh ln(
R2
)
2
R1
Nm
N 2 Ih
Lo
L l
2
ln(
R2 R1
)
R1
R2
I
I
l
rdr
§12-4 自感和互感
二、互感
μ0
S
l
互感系数计算举例
M Ψ12 I2
N1 N 2 l2
lS
n1n2V
③互感 M与自感L1 ,L2 的关系。
L1 n12V
L2 n22V
M L1L2
在此例中,线圈1的磁通全部通过线圈2,称为无 磁漏。
在一般情况下: M K L1L2
称K 为耦合系数 0 < K <1
自感
2、自感电动势:
dΦ
L N dt
d (NΦ ) dΨ
dt
dt
d (LI ) L dI I dL
dt
dt dt
若回路几何形状、尺寸不变,周围无铁磁性物质,则:
dL 0 dt
L
L
dI dt
自感
【讨论】:1、 L 的定义:可用下两式之一定义
H 2r NI
I
H NI 2r
B NI 2r
dm
B dS
NI 2r
hdr
R2 R1
h
r dr
dm
B dS
NI 2r
hdr
m
dm
NIh பைடு நூலகம்
R2 dr R1 r
NIh ln(
R2
)
2
R1
Nm
N 2 Ih
Lo
L l
2
ln(
R2 R1
)
R1
R2
I
I
l
rdr
§12-4 自感和互感
二、互感
大学物理自感和互感

Ψ自 LI
L
d自 dt
d ( LI ) dI dL L I dt dt dt
若回路几何形状、 尺寸不变,周围介 质的磁导率不变 自感系数描述线圈 电磁惯性的大小
dL 0 dt
dI L L dt
负号表示自感电动势 总是要阻碍线圈回路 本身电流的变化。
3
单位:亨利,1H=1Wb/A 辅助单位:
B
I
2 πr
R1 Q
R
如图在两圆筒间取一长 为 l 的面 PQRS, 并将其分 成许多小面元.
I
I r
P
R2
l
S
dr
则 dΦ B dS Bldr
Φ dΦ
R2 R1
I
2πr
l dr
10 - 4 自感和互感
第十章 电磁感应
Il R dr R 2 r
2 1
Il R2 ln( ) 2 R1
R1 Q
R
Φ l R L ln( ) I 2 R
2 1
I
I r
P
R2
l
S
dr
单位长度的自感为:
L R2 Lo ln( ) l 2 R1
10 - 4 自感和互感 自感的利用
第十章 电磁感应
在通路时,自感对电流的变化起抑制作用, 可稳定电路中的电流(扼流圈\镇流器等). 在断路时,自感电动势可产生一个瞬时高 压,对有些场合(如日光灯的启动和感应圈 的升压)有用。 构成RC\RCL谐振电路,滤波器等
答: 如图,双线绕制,可确保自感系数为零
0 L
I
0
10 - 4 自感和互感 二、互感(mutual induction)
大学物理第27章_自感互感

科学成就:亨利在物理学方面的主要成就是对电 磁学的独创性研究。
①强电磁铁的制成,为改进发电机打下了基础。
1829年亨利对英国发明家威廉史特京(17831850)发明的电磁铁作了改进,他把导线用丝绸 裹起来代替史特京的裸线,使导线互相绝缘并且 在铁块外缠绕了好几层,使电磁铁的吸引作用大 大增强。
亨利最初制作的电磁铁能吸起三百公斤铁,后 来他制作的一个体积不大的电磁铁能吸起一吨重 的铁块 。
(a) 什么也没发生——电容器仍然保持充满电的状态Q Q0 。
(b) 电容器很快放电,直至最终放完电( Q 0)。
(c) 回路中有电流通过,直至电容器反向充电,周而复始。
(d)
最初储存在电容器中的静电能(U E 圈当中,并一直保存在线圈中。
1 2
Q02
/C
)转移到线
(e) 储存在电容器中的一半能量转移到线圈中,并保存在线
1
M
dI 2 dt
2
M
dI1 dt
练习B 如图27-3所示,哪个螺线管-线圈系统的互 感系数最大?假设螺线管均完全相同。
图27-3
互感的应用:变压器
互感现象不仅发生于绕在同一铁芯 上的两个线圈之间,且可发生于任何 两个相互靠近的电路之间。在电力 工程和电子电路中,互感现象有时 会影响电路的正常工作,这时要设 法减小电路间的互感。
互感的应用:心脏起搏器、变压器等
M 的存在有利有弊 在变压器中:M 越大,能量损失越小。 在电子线路中:M 越大,相互干扰越大。
§27-2 自感
自感现象:当一个
线圈(或者螺线管)中
的电流发生变化时,则
通过该线圈自身的磁通
i
量将发生变化,从而在
大学物理,电磁感应12.4自感和互感

要求自感电动势,应先求出自感系数。
9
12.3 自感和互感
自感应用:
第12章 电磁感应
日光灯镇流器;高频扼流圈;自感线圈与电 容器组合构成振荡电路或滤波电路。 通电后,启辉器辉光放电,金属片受热形变 互相接触,形成闭合回路,电流流过,日光灯灯 丝加热释放电子。 同时,启辉器接通辉光熄灭, 金属片冷却断开,电路切断,镇流器线圈中产生 比电源电压高得多的自感电动势,使灯管内气体 电离发光。 自感危害:电路断开时,产生自感电弧。
dI 1 dI 1 dΨ21 M 21 M ε 21 dt dt dt
当线圈 2 中的电流变化时,在线圈 1 中产生的 互感电动势为:
dΨ12 dI 2 dI 2 ε12 M 12 M dt dt dt
20
12.3 自感和互感
第12章 电磁感应
ε12
dI 2 = -M dt
4
12.3 自感和互感
2、自感系数 L
根据毕奥—萨尔定律: μ0 Idl r dB 4π r 3
第12章 电磁感应
I
B
线圈中的电流在空间任意一点激发的磁感应 强度的大小与线圈中的电流强度成正比,即: 穿过线圈自身总的磁通量与电流 I 成正比,
写成:
Φ LI
L 为自感系数。
解:设长直导线中电流 I ,
矩形线圈平面上的磁链数为: dr I
N B dS
M I
0 I N ldr a 2r 0 NIl a b ln 2 a 0 Nl a b ln 2 a
s ab
r
l
a
b
24
12.3 自感和互感
思考? 若已知矩形线圈中有电流:
9
12.3 自感和互感
自感应用:
第12章 电磁感应
日光灯镇流器;高频扼流圈;自感线圈与电 容器组合构成振荡电路或滤波电路。 通电后,启辉器辉光放电,金属片受热形变 互相接触,形成闭合回路,电流流过,日光灯灯 丝加热释放电子。 同时,启辉器接通辉光熄灭, 金属片冷却断开,电路切断,镇流器线圈中产生 比电源电压高得多的自感电动势,使灯管内气体 电离发光。 自感危害:电路断开时,产生自感电弧。
dI 1 dI 1 dΨ21 M 21 M ε 21 dt dt dt
当线圈 2 中的电流变化时,在线圈 1 中产生的 互感电动势为:
dΨ12 dI 2 dI 2 ε12 M 12 M dt dt dt
20
12.3 自感和互感
第12章 电磁感应
ε12
dI 2 = -M dt
4
12.3 自感和互感
2、自感系数 L
根据毕奥—萨尔定律: μ0 Idl r dB 4π r 3
第12章 电磁感应
I
B
线圈中的电流在空间任意一点激发的磁感应 强度的大小与线圈中的电流强度成正比,即: 穿过线圈自身总的磁通量与电流 I 成正比,
写成:
Φ LI
L 为自感系数。
解:设长直导线中电流 I ,
矩形线圈平面上的磁链数为: dr I
N B dS
M I
0 I N ldr a 2r 0 NIl a b ln 2 a 0 Nl a b ln 2 a
s ab
r
l
a
b
24
12.3 自感和互感
思考? 若已知矩形线圈中有电流:
自感与互感

自感现象
R=RL,
自感应:
回路中因自身电流变 化引起的感应电动势
现象
(a)
:
S1与S2是两个相同的灯泡;
接通K瞬间,S1比S2先亮 (b) 断开瞬间,灯泡突然亮一下 为什么?
接通K或切断K,由于电流变化导致磁场变化
B I (t ) I (t ) I (t )(N匝线圈 )
并维持1中电流I1 不变(可用一个 外接可调电源平衡掉2对1的互感)外接电源需要 抵抗互感电动势所做的功——互感电动势
2005.4 北京大学物理学院王稼军编
外接电源需要抵抗互感电动势所做的功
维持线圈1内 电流不变
A
0
0
21 I1dt
0
di2 I1M 21 dt dt
M 21I1di2 M 21I1I 2
无漏磁 漏磁 无耦合
k1k2 L1L2
令k k1k2 M k1k2 L1L2 k L1L2
2005.4
耦合系数
北京大学物理学院王稼军编
两个线圈串联的自感系数
L1+L2 =?L 一般情况不等,与串联方式有关 串联方式
串联顺接:1尾与2头接 串联反接:1尾与2尾接
2005.4
2005.4
M21= M12=M
北京大学物理学院王稼军编
两个线圈系统总磁能
1 1 2 2 Wm L1 I1 L2 I 2 MI 1 I 2 2 2
总 磁 能 1、2的自感磁能, 大于零 互感磁能, 可正可负 对 称 形 式
推广到k个线圈的普遍情况
1 1 1 1 2 2 Wm L1 I1 L2 I 2 M 12 I1 I 2 M 21 I1 I 2 2 2 2 2 i、j线圈 1 k 1 k 第i个线 2 之间的M 圈的自感 Wm Li I i M ij I i I j 2 i 1 2 i 1 系数
R=RL,
自感应:
回路中因自身电流变 化引起的感应电动势
现象
(a)
:
S1与S2是两个相同的灯泡;
接通K瞬间,S1比S2先亮 (b) 断开瞬间,灯泡突然亮一下 为什么?
接通K或切断K,由于电流变化导致磁场变化
B I (t ) I (t ) I (t )(N匝线圈 )
并维持1中电流I1 不变(可用一个 外接可调电源平衡掉2对1的互感)外接电源需要 抵抗互感电动势所做的功——互感电动势
2005.4 北京大学物理学院王稼军编
外接电源需要抵抗互感电动势所做的功
维持线圈1内 电流不变
A
0
0
21 I1dt
0
di2 I1M 21 dt dt
M 21I1di2 M 21I1I 2
无漏磁 漏磁 无耦合
k1k2 L1L2
令k k1k2 M k1k2 L1L2 k L1L2
2005.4
耦合系数
北京大学物理学院王稼军编
两个线圈串联的自感系数
L1+L2 =?L 一般情况不等,与串联方式有关 串联方式
串联顺接:1尾与2头接 串联反接:1尾与2尾接
2005.4
2005.4
M21= M12=M
北京大学物理学院王稼军编
两个线圈系统总磁能
1 1 2 2 Wm L1 I1 L2 I 2 MI 1 I 2 2 2
总 磁 能 1、2的自感磁能, 大于零 互感磁能, 可正可负 对 称 形 式
推广到k个线圈的普遍情况
1 1 1 1 2 2 Wm L1 I1 L2 I 2 M 12 I1 I 2 M 21 I1 I 2 2 2 2 2 i、j线圈 1 k 1 k 第i个线 2 之间的M 圈的自感 Wm Li I i M ij I i I j 2 i 1 2 i 1 系数
大学物理 74自感与互感 能量
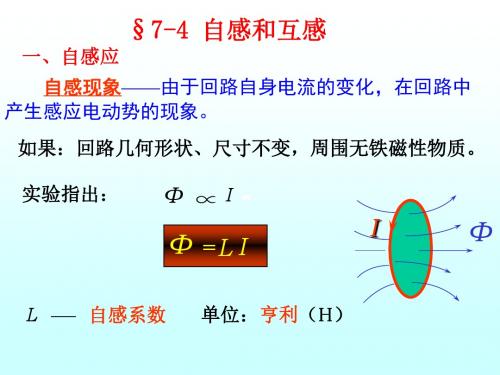
[例] 求同轴传输线之磁能
B= r H = 2 2 π πr dV = 2 π r l dr 1 2 Wm = V wmdV = V 2 μ H dV R 1 ( I )2 = R μ 2 l r r d π 2 2 πr
2
I
μI
R2 R1 I l I
1
I l ln ( R 2 ) μ = 4 R1 π
H2
Φ = s B . dS
M=
N2 μ = B 2S = 0 I 2S 12 l μ 0N 1N 2 I 2S Ψ12 = N 1Φ 12= l Ψ12 = μ 0N 1N 2 l S =μ 0 n 1n 2V I2 l
2
B 2 Φ12 Ψ 12 H 2 = n 2I 2 = N 2 I 2 l N μ μ 0 2 I2 B 2 = 0H 2 = l
dI 2 M 12 = dt 则有: 12 = M
在式
ε
ε
中,若 d I 2 = 1 dt 即:
互感系数在数值上等于当第二个回路电流变化率 为每秒一安培时,在第一个回路所产生的互感电动势 的大小。
[例1] 有两个直长螺线管,它们绕在同一个 圆柱面上 。 已知: N 1、 μ 0、 N 2、 S、 l 求:互感系数
自感系数在数值上等于回路中通过单位电流时,通 过自身回路所包围面积的磁通链数。
自感电动势:
ε
L
= =
(NΦ ) d Φ d d Ψ N = = dt dt dt I I dL d (L I ) d = L dt dt dt
dt
若回路几何形状、尺寸不变,周围无铁磁性
物质,则: d L = 0 自感电动势
...
M =K L 1 L 2 0 < K <1
2自感和互感
2
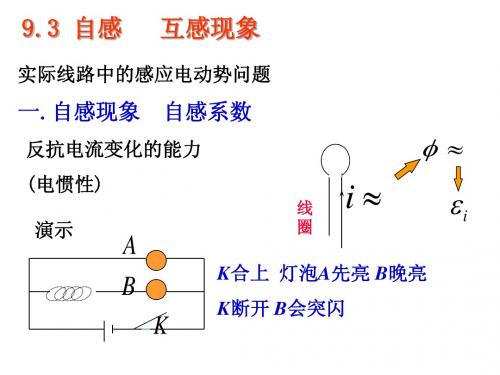
匀速直线运动的点电荷的磁场分布: 匀速直线运动的点电荷的磁场分布:
v2 (1 − 2 ) q c B= ⋅E = ⋅(v ×r ) 2 3 2 3 4πε 0 c r v 2 ( 1 − 2 sin θ ) 2 c
稳恒磁场
类比
C
1 2 We = CV 2
1 2 W m = LI 2
L
通过平板电容器得 出下述结论 存在场 中 在电磁场中
通过长直螺线管得 出下述结论
1 we = D ⋅ E 2
1 wm = B ⋅ H 2
磁能密度 普遍适用 各种电场 磁场
w = we + wm
1 1 w = D⋅E + B⋅H 2 2
b
ψ
21
= Nφ= N
∫
S
B ⋅dS
o
r0 + b
x
µ 0 I1 adx 2π x
ψ 21= Nφ = N ∫ B ⋅ dS = N Bds = N
∫
S
∫
S
r0
Nµ 0 I1a r0 + b ln = 2π r0
µ0 NI1a r0 + b = ln 2π b
µ0 Na r0 + b M= = ln I1 2π b
载流线圈周围无铁磁质, 无变化。 载流线圈周围无铁磁质,且 µ 无变化。 1、当载流线圈中的电流从0 增加到 I 时,且线圈的 当载流线圈中的电流从0 则线圈中会产生感应电动势 自感为 L ,则线圈中会产生感应电动势
di 电源克服自感电动势作功, 电源克服自感电动势作功, ε L = − L dt
在线圈建立自感电动势的 过程中, 过程中,电源在 d t 时间 作功为 内作功为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
M12
N 2Φ21 I1
0n1n2l(πr12 )
代入 B1 计算得 N2Φ21
0n1n2l(πr12 )I1
第八章 电磁感应 电磁场
13
物理学
第五版
8-3 自感和互感
例 4 在磁导率为 的均匀无限大的磁
介质中, 一无限长直导线与一宽、长分别为b
和 l 的矩形线圈共面,直导线与矩形线圈的
M
第八章 电磁感应 电磁场
11
物理学
第五版
8-3 自感和互感
解 先设某一线圈中通以电流 I 求
出另一线圈的磁通量 Φ
M
设半径为 r1 的线
圈中通有电流 I1, 则
B1
0
N1 l
I1
0n1I1
第八章 电磁感应 电磁场
12
物理学
第五版
8-3 自感和互感
则穿过半径为 r2 的线圈的磁通匝数为
N2Φ21 N2B1(π r12 ) n2lB1(πr12 )
x M Φ l ln(b d )
I 2π d
第八章 电磁感应 电磁场
15
S
lE
(4)自感的应用 稳流 , LC 谐振电路 滤波电路, 感应圈等
第八章 电磁感应 电磁场
4
物理学
第五版
8-3 自感和互感
例 2 有两个同轴圆筒形导体 , 其半径分
别为 R1和 R2 , 通过它们的电流均为 I ,
但电流的流向相反.设在
两圆筒间充满磁导率为
R1
的均匀磁介质 , 求其自感 L .
第八章 电磁感应 电磁场
6
物理学
第五版
8-3 自感和互感
Φ
dΦ
R2 R1
I ldr
2π r
Φ Il ln R2
2π R1
L Φ l ln R2
I 2π R1
I
单位长度的自感为
R1 Q R
Ir l
L ln R2
l 2π R1
P
S
R2
dr
第八章 电磁感应 电磁场
7
物理学
I Ir l
R2
第八章 电磁感应 电磁场
5
物理学
第五版
8-3 自感和互感
解 两圆筒之间 B I
2πr 如图在两圆筒间取一
长为 l 的面 PQRS , 并将
其分成许多小面元.
则
dΦ
B dS
Bldr
I
R1 Q R
Ir l
2 R1
I ldr
2π r
P
S
R2
dr
Φ12 I2
注意 互感仅与两个线圈形状、大小、匝
数、相对位置以及周围的磁介质有关.
B1
I1
B2
I2
第八章 电磁感应 电磁场
9
物理学
第五版
8-3 自感和互感
(2)互感电动势
E12
M
dI 2 dt
E21
M
dI1 dt
互感系数 M E21 E12
dI1 dt dI2 dt
一侧平行,且相距为 d .
I
b
求二者的互感系数.
d
l
o
x
第八章 电磁感应 电磁场
物理学
第五版
8-3 自感和互感
解 设长直导线通电流 I
B I
2π x
dΦ
B
ds
I
ldx
2π x
b
Φ db I ldx d 2π x
I
d
l
Il ln(b d )
2π d
o x dx
得H B Φ L
nN l
S
lE
B H nI NΦ NBS
第八章 电磁感应 电磁场
3
物理学
第五版
8-3 自感和互感
NΦ NBS N N IS
l
L N 2 S V lS L n2V
I
l
(一般情况可用下式测量自感)EL
L
dI dt
物理学
第五版
8-3 自感和互感
一 自感电动势 自感
(1)自感
Φ LI L Φ I
若线圈有 N 匝,
NΦ 磁通匝数
IB
自感 L I
注意 无铁磁质时, 自感仅与线圈形 状、磁介质及 N 有关.
第八章 电磁感应 电磁场
1
物理学
第五版
8-3 自感和互感
(2)自感电动势
EL
dΦ dt
(L
dI dt
I
dL ) dt
当
dL dt
0
时,
IB
E
L
L
dI dt
自感
L EL
dI dt
第八章 电磁感应 电磁场
2
物理学
第五版
8-3 自感和互感
(3)自感的计算方法
例1 如图的长直密绕螺线管,已知
l, S, N, , 求其自感 L(忽略边缘效应) .
解 先设电流 I 根据安培环路定理求
第五版
8-3 自感和互感
二 互感电动势 互感
I1 在 I2电流回路中所产生的磁通量
Φ21 M 21I1
I2 在 I1 电流回路 中所产生的磁通量
Φ12 M12I2
B1
I1
B2
I2
第八章 电磁感应 电磁场
物理学
第五版
8-3 自感和互感
(1 )互感系数
M12
M 21
M
Φ21 I1
问:下列几种情况互感是否变化?
O (1)线框平行直导线移动;
(2)线框垂直于直导线移动;
C (3)线框绕 OC 轴转动;
(4)直导线中电流变化.
第八章 电磁感应 电磁场
10
物理学
第五版
8-3 自感和互感
例3 两同轴长直密绕螺线管的互感 有两个长度均为l,半径分别为r1和r2( r1<r2 ), 匝数分别为N1和N2的 同轴长直密绕螺线管. 求它们的互感 .
