中考数学专项练习常用角的单位及换算(含解析)
八年级数学角度单位换算专题

八年级数学角度单位换算专题介绍本文档将介绍八年级数学中的角度单位换算专题。
角度是几何学中的重要概念,了解角度的不同单位及其相互转换对于解决相关问题非常有帮助。
角度单位在数学中,我们常用四种角度单位:度(°)、弧度(rad)、百分度(%)和直角度(gon)。
度(°)度是最常见的角度单位,一个圆可以分为360等份,每一份就是一度。
例如,直角角度是90度,半圆角度是180度。
弧度(rad)弧度是另一种常用的角度单位,它是用弧长等于半径的圆对应的角度定义的。
一个圆的弧长等于圆周长的2π,所以一个圆的角度等于2π弧度。
例如,直角角度是π/2弧度,半圆角度是π弧度。
百分度(%)百分度是用百分数表示的角度单位。
一个圆等分为400份,每一份就是一百分度。
例如,直角角度是100%,半圆角度是200%。
直角度(gon)直角度也是用百分数表示的角度单位。
一个圆等分为400份,每一份就是一直角度。
例如,直角角度是100gon,半圆角度是200gon。
角度单位换算为了进行角度单位换算,我们可以使用下面的公式:- 度与弧度的换算:角度(°) = 弧度(rad)× 180 / π- 度与百分度的换算:角度(°) = 百分度(%) × 90 / 100- 度与直角度的换算:角度(°) = 直角度(gon) × 9 / 10通过这些换算公式,我们可以方便地在不同单位之间进行转换。
结论通过学习本专题,我们了解了八年级数学中的角度单位换算。
掌握角度单位的不同定义和相互转换,能够帮助我们更好地理解和解决相关数学问题。
祝各位同学学习进步!。
2023年中考数学----三角形的综合知识回顾与专项练习题(含答案解析)

知识回顾2023年中考数学----三角形的综合知识回顾与专项练习题(含答案解析)1. 角平分线的性质:①平分角。
②角平分线上任意一点到角两边的距离相等。
2. 角平分线的判定:角的内部到角两边相等的点一定在角平分线上。
3. 角平分线的尺规作图:具体步骤:①以角的顶点O 为圆心,一定长度为半径画圆弧,圆弧与角的两边分别交于两点M 、N 。
如图①。
②分别以点M 与点N 为圆心,大于MN 长度的一半为半径画圆弧,两圆弧交于点P 。
如图②。
③连接OP ,OP 即为角的平分线。
4. 垂直平分线的性质:①垂直且平分线段。
②垂直平分线上任意一点到这条线段两个端点的距离相等。
5. 垂直平分线的判定:到线段两端点距离相等的点一定在线段的垂直平分线上。
6. 垂直平分线的吃规作图:具体步骤:①以线段两个端点为圆心,大于线段长度的一半为半径画圆弧,两圆弧在线段的两侧别分交于M 、N 。
如图①②连接MN ,过MN 的直线即为线段的垂直平分线。
如图②7.中位线的性质:三角形的中位线平行且等于第三边的一半。
8. 等腰三角形的性质:①等腰三角形的两腰相等。
②等腰三角形的两底角相等。
(简称“等边对等角”)③等腰三角形底边的中线、高线以及顶角平分线相互重合。
(简称底边上三线合一)9. 等腰三角形的判定:①有两条边相等的三角形是等腰三角形。
②有两个底角相等的三角形是等腰三角形。
(等角对等边)③若一个三角形某一边上存在“三线合一”,则三角形是等腰三角形。
10. 等边三角形的性质:①等边三角形的三条边都相等,三个角也相等,且三个角都等于60°。
②等边三角形三条边都存在“三线合一”③等腰三角形是一个轴对称图形,有三条对称轴。
④等腰三角形的面积等于243a (a 为等腰三角形的边长)。
11. 等腰三角形的判定:①三条边都相等的三角形是等边三角形。
②三个角都相等(两个角是60°)的三角形是等腰三角形。
③底和腰相等的等腰三角形是等边三角形。
角的度数换算练习题

角的度数换算练习题角度是我们日常生活和数学中常用的一个概念。
在几何学中,角是由两条射线所围成的区域。
而角度则是用来度量角的大小的单位。
角的度数换算是学习角度概念的重要一环,下面我们来通过一些练习题来加深对角度换算的理解。
1. 将30°转换为弧度制。
角度和弧度是用来度量角的两种不同方式,弧度制角度是通过弧长与半径的比值来度量的。
假设一个圆的半径为R,圆心角的弧长为S,则圆心角的弧度数为S/R。
而整周角的弧度数为2π,因为整周角对应的弧长就是整个圆的周长,即2πR。
因此,将30°转换为弧度制,我们可以通过以下公式进行计算:弧度数= (30 × 2π) / 360 = π / 6所以30°等于π/6弧度。
2. 将π/3弧度转换为度数。
将弧度转换为角度时,我们需要用到公式:角度 = (弧度数× 360) / 2π将π/3弧度转换为度数,我们可以进行如下计算:角度= (π/3 × 360) / (2π) = 60°所以π/3弧度等于60°。
3. 如果一个角的度数是150°,那么它的补角是多少度?补角是指两个角度相加为90°的角。
根据定义,我们可以通过以下计算求得:补角度数 = 90° - 角度 = 90° - 150° = -60°由于补角的度数应该是正值,所以-60°的补角度数为300°。
4. 如果一个角的度数是210°,那么它的余角是多少度?余角是指两个角度相加为180°的角。
根据定义,我们可以通过以下计算求得:余角度数 = 180° - 角度 = 180° - 210° = -30°由于余角的度数应该是正值,所以-30°的余角度数为330°。
5. 将一个直角的弧度数和度数分别表示出来。
备战中考数学(北师大版)专项练习直角三角形的角边关系(含解析)

备战中考数学(北师大版)专项练习直角三角形的角边关系(含解析)一、单选题1.如图在Rt△ABC中,∠C=90°,AB=15,sinA=,则BC等于()A.45B.5C.D.2.如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是()A.B.C.D.23.如图,△ABC中,∠C=90°,CD⊥AB ,若AC=3,AB=4,则A D=()A.1B.D.54.的值为()A.B.C.D.15.如图,在△ABC中,AC=8,∠ABC=60°,∠C=45°,AD⊥BC,垂足为D,∠ABC的平分线交AD于点E,则AE的长为()A.B. 2C.D. 36.在Rt△ABC中,∠C=90°,AC=5,∠A=α,那么BC的长是()A.5cotαB.5tanαC.D.7.三角形在方格纸中的位置如图所示,则tanα的值是()A.B.C.D.8.因为sin30°=,sin210°=−,因此sin210°=sin(180°+30°)=-sin30°;因为sin45°=,sin225°=−,因此sin225°=sin(180°+45°)=-sin45°,由此猜想,推理知:一样地当α为锐角时有sin(180°+α)=-sinα,由此可知:sin240°=()A.-B.C.-D.9.如图,小颖利用一个锐角是30°的三角板测量一棵树的高度,已知她与树之间的水平距离BE为5m,AB为1.5m(即小颖的眼睛距地面的距离),那么这棵树高是()A.4mB.m C.(5 + )m D.(+ )m10.三角形在正方形网格纸中的位置如图所示.则sinα的值是()A.B.C.D.二、填空题11.如图,在Rt△ABC中,∠C=90°,AB=2BC,则sinB的值为_____ ___12.如图,P(12,a)在反比例函数图象上,PH⊥x轴于H,则tan∠POH的值为________.13.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sinA=,则DE=________ . [MISSING IMAGE: , ]14.如图,某公园入口原有一段台阶,其倾角∠BAE=30°,高DE=2m,为方便残疾人士,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是________m .15.若sinα=,则α=________°.16.如图,等边△ABC的边长为8,D、E两点分别从顶点B、C动身,沿边BC、CA以1个单位/s、2个单位/s的速度向顶点C、A运动,DE的垂直平分线交BC边于F点,若某时刻tan∠CDE= 时,则线段CF的长度为________.17.如图,△ABC的顶点是正方形网格的格点,则tanA的值为_______ _.18.王小勇操纵一辆遥控汽车从A处沿北偏西60°方向走10m到B处,再从B处向正南方走20m到C处,现在遥控汽车离A处________m.19.在Rt△ABC中,∠C=90°,假如AC=4,sinB=,那么AB=____ ____三、运算题20.已知α是锐角,且cos(α-15°)= ,运算-6cosα+(3-π)0+t anα-( )-1的值.21.运算:3sin60°﹣2cos30°﹣tan60°•cot45°22.运算:﹣cot30°.四、解答题23.高铁给我们的出行带来了极大的方便.如图,“和谐号”高铁列车座椅后面的小桌板收起时,小桌板的支架的底端N与桌面顶端M的距离MN =75cm,且能够看作与地面垂直.展开小桌板使桌面保持水平,AB⊥MN,∠MAB=∠MNB=37°,且支架长BN与桌面宽AB的长度之和等于MN的长度.求小桌板桌面的宽度AB(结果精确到1cm,参考数据:sin37°≈0. 6,cos37°≈0.8,tan37°≈0.75)五、综合题24.为测山高,在点A处测得山顶D的仰角为30°,从点A向山的方向前进140米到达点B,在B处测得山顶D的仰角为60°(如图①).(1)在所给的图②中尺规作图:过点D作DC⊥AB,交AB的延长线于点C(保留作图痕迹);(2)山高DC是多少(结果保留根号形式)?25.如图所示,某工程队预备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观看对面山顶上的一座铁塔,测得塔尖C的仰角为31°,塔底B的仰角为2 6.6°.已知塔高BC=40米,塔所在的山高OB=240米,OA=300米,图中的点O、B、C、A、P在同一平面内.求:(1)P到OC的距离.(2)山坡的坡度tanα.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin31°≈0.52,tan37°≈0. 60)答案解析部分一、单选题1.【答案】B【考点】解直角三角形【解析】【解答】解:∵sinA=,∴BC=AB•sinA=15×=5,故选:B.【分析】依照锐角三角函数的概念sinA=,代入已知数据运算即可.2.【答案】C【考点】解直角三角形【解析】【解答】解:设(2,1)点是B,作BC⊥x轴于点C.则OC=2,BC=1,则tanα==.故选C.【分析】设(2,1)点是B,作BC⊥x轴于点C,依照三角函数的定义即可求解.3.【答案】B【考点】解直角三角形【解析】解答:如图,∵CD⊥AB ,∴∠ADC=90°,又∵∠C=90°,∴∠ACD=∠B(同角的余角相等).又∵∠A=∠A ,∴△ACB∽△ADC ,∴,即,∴AD= .故选:B.分析:利用两角法证得△ACB∽△ADC ,然后由该相似三角形的对应边成比例来求AD的长度.4.【答案】C【考点】专门角的三角函数值【解析】【解答】sin60°= ,故答案为:C.【分析】依照专门角的三角函数值求解。
中考数学题型专项训练:角度问题(含答案)
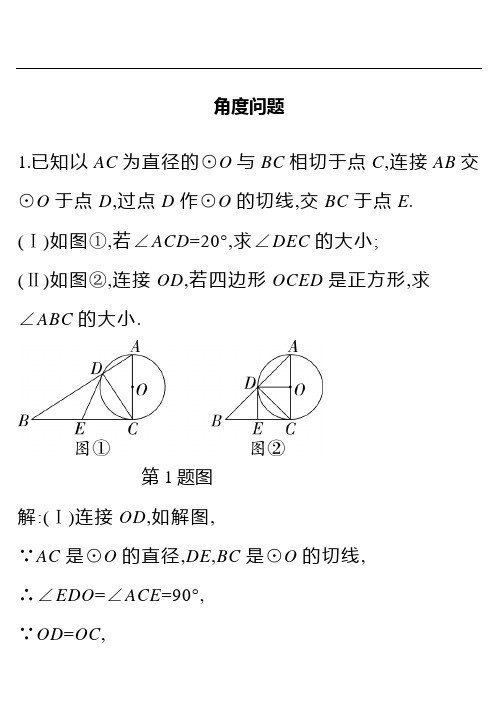
角度问题1.已知以AC 为直径的⊙O 与BC 相切于点C ,连接AB 交⊙O 于点D ,过点D 作⊙O 的切线,交BC 于点E.(Ⅰ)如图①,若∠ACD =20°,求∠DEC 的大小;(Ⅱ)如图②,连接OD ,若四边形OCED 是正方形,求 ∠ABC 的大小.第1题图解:(Ⅰ)连接OD ,如解图,∵AC 是⊙O 的直径,DE ,BC 是⊙O 的切线,∴∠EDO =∠ACE =90°,∵OD =OC ,∴∠ODC=∠OCD=20°,∴∠DOC=140°,∴∠DEC=40°;第1题解图(Ⅱ)如图②,∵四边形ODEC是正方形,∴DE=CE,∠DEC=90°,∴∠DCE=45°,∵AC是⊙O的直径,∴∠BDC=∠ADC=90°,∴∠ABC=45°.2.已知,在⊙O中,AB是⊙O的直径,点C、P在AB的两侧,AC =12AB ,连接CP ,BP . (Ⅰ)如图①,若CP 经过圆心,求∠P 的大小;(Ⅱ)如图②,点D 是PB 上一点,CD ⊥PB ,若CP ⊥AB ,求∠BCD 的大小.第2题图解:(Ⅰ)∵AB 是⊙O 的直径,∴∠ACB =90°,∵AC =12AB , ∴∠ABC =30°,∴∠A =90°-∠ABC =60°,∴∠P=∠A=60°;(Ⅱ) ∵AB是⊙O的直径,AC=12 AB,∴∠A=60°,∴∠BPC=∠A=60°,∵CD⊥PB,∴∠PCD=90°-∠BPC=30°,∵CP⊥AB,AB是⊙O的直径,∴BC BP,∴BC=BP,∴∠P=∠BCP=60°,∴∠BCD=∠BCP-∠PCD=60°-30°=30°.3.如图①,在△ABC中,点D在边BC上,∠ABC:∠ACB: ∠ADB=1:2:3,⊙O是△ABD的外接圆.(Ⅰ)求证:AC是⊙O的切线;(Ⅱ)当BD是⊙O的直径时(如图②),求∠CAD的度数.第3题图(Ⅰ)证明:如解图,连接OA、OD,设∠ABD=x,∵∠ABC:∠ACB:∠ADB=1:2:3,∴∠ADB=3x,∠ACB=2x,∴∠DAC=∠ADB-∠ACB=x,∠AOD=2∠ABC=2x,18022x=90°∴∠OAC=90°-x+x=90°, ∴OA⊥AC,∴AC是⊙O的切线;(Ⅱ)解:∵BD 是⊙O 的直径,∴∠BAD =90°,∴∠ABC +∠ADB =90°,∵∠ABC :∠ACB :∠ADB =1:2:3,∴4∠ABC =90°,∴∠ABC =22.5°,∴∠ADB =67.5°, ∠ACB =45°,∴∠CAD =∠ADB -∠ACB =22.5°.第3题解图上,以O 为圆心OA 为半径的⊙O 交AB 于点E .(Ⅰ)⊙O 过点E 的切线与BC 交于点F ,当0<OA <6时,求∠BFE 的度数;(Ⅱ)设⊙O 与AB 的延长线交于点M ,⊙O 过点M 的切线交BC 的延长线于点N ,当6<OA <12时,利用备用图作出图形,求∠BNM 的度数.解:(Ⅰ)连接OE ,如解图①,∵四边形ABCD 为正方形,∴∠2=45°,∵OE =OA ,∴∠1=∠2=45°,∵EF 为⊙O 的切线,∴OE⊥EF,∴∠OEF=90°,∴∠BEF=45°,∵∠B=90°,∴∠BFE=45°;(Ⅱ)连接OM,如解图②,∵OM=OA,∴∠OMA=∠OAM=45°,∵MN为⊙O的切线,∴OM⊥MN, ∴∠OMN=90°,∴∠BMN=45°,∵∠MBN=90°,∴∠BNM=45°.图① 图②第4题解图 5.四边形ABCD 内接于⊙O ,AC 为其中一条对角线. (Ⅰ)如图①,若∠BAD =70°,BC =CD ,求∠BAC 的大小;(Ⅱ)如图②,若AD 经过圆心O ,连接OC ,AB =BC ,OC ∥AB ,求∠OCD 的大小.第5题图解:(Ⅰ)∵四边形ABCD 内接于⊙O ,BC =CD ,∴∠BAC=∠CAD,∵∠BAD=70°,∴∠BAC=∠CAD=35°;(Ⅱ) 连接BD,如解图,∵AB=BC,∴∠BAC=∠BCA,∵OC∥AB,∴∠BAC=∠OCA,∵OA=OC,∴∠OAC=∠OCA,∵∠ADB=∠ACB,∴∠BAC=∠CAO=∠ADB=∠ACO, ∵AD是⊙O的直径,∴∠ABD=∠ACD=90°,∴∠ADB +∠BAD =90°,即3∠ACO =90°,∴∠ACO =30°,∴∠OCD =∠ACD -∠ACO =90°-30°=60°.第5题解图6.在△ABC 中,AB =AC ,以AB 为直径的⊙O 交BC 于点D ,交AC 于点E .(Ⅰ)如图①,过点D 作DF ⊥AC ,垂足为F ,求证:直线DF 与⊙O 相切;(Ⅱ)如图②,过点B 作⊙O 的切线,与AC 的延长线交于点G ,若∠BAC =35°,求∠CBG 的大小.第6题图解:(Ⅰ)如解图①,连接OD,∵AB=AC, ∴∠B=∠C,∵OD=OB,∴∠B=∠ODB,∴∠C=∠ODB,∴OD∥AC.∴∠CFD=∠FDO,∵∠CFD=90°,∴∠FDO=90°,∴DF⊥OD,∵OD为⊙O的半径,∴直线DF与⊙O相切;(Ⅱ)如解图②,连接AD,∵AB为⊙O的直径,∴∠ADB=90°,∴AD⊥BC,∵AB=AC,∴AD平分∠CAB,∵∠BAC=35°,∴∠DAB=17.5°,∴∠CBA=90°-∠DAB=90°-17.5°=72.5°, ∵BG与⊙O相切,∴∠ABG=90°,∴∠CBG=90°-∠CBA=90°-72.5°=17.5°.图①图②第6题解图7.在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,DF为⊙O的切线,(Ⅰ)如图①,求∠DFC的度数;(Ⅱ)如图②,过点A作BC的平行线交BE的延长线于点G,连接CG,当△ABC为等边三角形时,求∠AGC的度数.第7题图解:(Ⅰ)连接AD,OD,如解图,∵AB是⊙O的直径,∴AD⊥BC.∵AB=AC,∴BD=DC,又∵AO=BO,∴OD是△ABC的中位线,∴OD∥AC.∵DF是⊙O的切线,∴DF⊥OD,∴DF⊥AC,∴∠DFC=90°;(Ⅱ)∵AB是⊙O的直径,∴BG⊥AC.∵△ABC 是等边三角形,∴BG 是AC 的垂直平分线,∴GA =GC .又∵AG ∥BC ,∠ACB =60°,∴∠CAG =∠ACB =60°.∴△ACG 是等边三角形.∴∠AGC =60°.第7题解图8.已知AB 是半圆O 的直径,点C 是半圆O 上的动点,点D 是线段AB 延长线上的动点,在运动过程中,保持CD =OA .(Ⅰ)当直线CD与半圆O相切时(如图①),求∠ODC的度数;(Ⅱ)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,求∠ODC的度数.第8题图解:(Ⅰ)如解图①,连接OC, ∵OC=OA,CD=OA,∴OC=CD,∴∠ODC=∠COD,∵CD是⊙O的切线,∴∠OCD=90°,∴∠ODC=45°;(Ⅱ)如解图②,连接OE.∵CD=OA,∴CD=OC=OE=OA,∴∠1=∠2,∠3=∠4,∠5=∠6,∵AE∥OC,∴∠2=∠3.设∠ODC=∠1=x,则∠2=∠3=∠4=x.又∵∠6是△COD的外角,∴∠5=∠6=∠1+∠2=2x.∵OE=OC,∴∠5=∠6=2x.∵AE∥OC,∴∠4+∠5+∠6=180°,即:x+2x+2x=180°, ∴x=36°.∴∠ODC=36°.第8题解图9.如图①,AB是⊙O的直径,AC是弦,直线EF和⊙O相切于点C,AD⊥EF,垂足为D.(Ⅰ)求证:∠DAC=∠BAC;(Ⅱ)若直径AB=4,AD=3,试求∠BAC的度数.第9题图(Ⅰ)证明:如解图,连接OC, 则OC=OA,∴∠BAC=∠OCA,∵EF切⊙O于点C,∴OC⊥EF,∵AD⊥EF,∴OC∥AD,∴∠OCA=∠DAC,∴∠DAC=∠BAC;(Ⅱ)解:如解图,连接BC,∵AB是⊙O的直径,AD⊥EF, ∴∠ACB=∠ADC=90°,由(Ⅰ)知∠DAC=∠BAC,∴△ADC∽△ACB,∴AC2=AD•AB=3×4=12,∴∠BAC =30° .第9题解图10.已知⊙O 是△ABC 的外接圆,过点A 作⊙O 的切线,与CO 的延长线交于点P ,CP 与⊙O 交于点D .(Ⅰ)如图①,若∠P =38°,求∠B的大小;(Ⅱ)如图②,若AP ∥BC ,∠B =72°,求∠BAC 的大小.第10题图解:(Ⅰ)如解图①,连接OA,∵PA与⊙O与相切,∴∠PAO=90°,∴∠POA=90°-∠P=90°-38°=52°,∴∠AOC=180°-∠POA=180°-52°=128°,(Ⅱ)如解图②,连接BD.∵DC为⊙O的直径,∴∠DBC=90°,∴∠ABD=90°-∠ABC=90°-72°=18°,∵∠ABD=∠ACD,∴∠ACD=18°,∴∠AOD=2∠ACD=36°,又∵∠PAO =90°,∴∠P =54°,∵AP ∥BC ,∴∠PCB =∠P =54°,∴∠CDB =90°-54°=36°,∴∠BAC =∠BDC =36°.图① 图②第10题解图 11.已知⊙O 中,A C 为直径,D A 、D B 分别切⊙O 于点A 、B . (Ⅰ)如图①,若∠D =50°,求∠C 的大小;(Ⅱ)如图②,过点B 作B E ⊥A C 于点F ,交⊙O 于点E ,若B D =B E ,求∠C 的大小.第11题解图解:(Ⅰ)如解图①,连接A B ,∵A D ,B D 为⊙O 的切线,∴A D =B D ,∴∠D A B =∠D B A ,∵∠D =50°,∴∠B A D =65°,∵A D 与⊙O 相切,∴A D ⊥A C ,∴∠D A C 为直角,∴∠C A B=25°,∵A C为直径,∴∠A B C=90°,∴∠C=90°-25°=65°; (Ⅱ)如解图②,连接A B、A E,∵直径A C垂直于弦B E,∴A为优弧BAE的中点,∴A B=A E,∵A D为圆O的切线,∴A D⊥A C,又∵B E⊥A C,∴A D∥B E,∵B D=A D,B D=B E,∴B E=A D,∴四边形A D B E 为平行四边形, 又∵B D =B E ,∴四边形A D B E 为菱形,∴B E =A E ,∴A B =A E =B E ,即△A B E 为等边三角形, ∴∠E =60°,∴∠C =∠E =60°.图① 图② 第11题解图。
中考数学复习----《图形初步认识之角》知识点总结与练习题(含答案解析)

中考数学复习----《图形初步认识之角》知识点总结与练习题(含答案解析)知识点总结1.方向角:方向角的表示方法为角度+距离。
在表达时将北或南放在前,然后加上偏离方向与角度。
如北偏东50°。
2.角的计算:即角的度数的计算。
3.余角和补角:若∠A+∠B=90°,则∠A与∠B互余,其中一个角是另一个的余角;若∠A+∠B=180°,则∠A与∠B互补,其中一个角是另一个的补角;练习题1、(2022•烟台)如图,某海域中有A,B,C三个小岛,其中A在B的南偏西40°方向,C在B的南偏东35°方向,且B,C到A的距离相等,则小岛C相对于小岛A的方向是()A.北偏东70°B.北偏东75°C.南偏西70°D.南偏西20°【分析】根据题意可得∠ABC=75°,AD∥BE,AB=AC,再根据等腰三角形的性质可得∠ABC=∠C=75°,从而求出∠BAC的度数,然后利用平行线的性质可得∠DAB=∠ABE=40°,从而求出∠DAC的度数,即可解答.【解答】解:如图:由题意得:∠ABC=∠ABE+∠CBE=40°+35°=75°,AD∥BE,AB=AC,∴∠ABC=∠C=75°,∴∠BAC=180°﹣∠ABC﹣∠C=30°,∵AD∥BE,∴∠DAB=∠ABE=40°,∴∠DAC=∠DAB+∠BAC=40°+30°=70°,∴小岛C相对于小岛A的方向是北偏东70°,故选:A.2、(2022•益阳)如图,PA,PB表示以P为起点的两条公路,其中公路PA的走向是南偏西34°,公路PB 的走向是南偏东56°,则这两条公路的夹角∠APB=°.【分析】根据题意可得∠APC=34°,∠BPC=56°,然后进行计算即可解答.【解答】解:如图:由题意得:∠APC=34°,∠BPC=56°,∴∠APB=∠APC+∠BPC=90°,故答案为:90.3、(2022•百色)如图摆放一副三角板,直角顶点重合,直角边所在直线分别重合,那么∠BAC的大小为°.【分析】根据三角形外角定理进行计算即可得出答案.【解答】解:根据题意可得,∠BAC=90°+45°=135°.故答案为:135.4、(2022•湘潭)如图,一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,已知∠AOB =120°,∠CDB=20°,则∠AEF=.【分析】根据平面镜反射的规律得到∠EDO=∠CDB=20°,∠AEF=∠OED,在△ODE中,根据三角形内角和定理求出∠OED的度数,即可得到∠AEF=∠OED的度数.【解答】解:∵一束光沿CD方向,先后经过平面镜OB、OA反射后,沿EF方向射出,∴∠EDO=∠CDB=20°,∠AEF=∠OED,在△ODE中,∠OED=180°﹣∠AOB﹣∠EDO=180°﹣120°﹣20°=40°,∴∠AEF=∠OED=40°.故答案为:40°.5、(2022•甘肃)若∠A=40°,则∠A的余角的大小是()A.50°B.60°C.140°D.160°【分析】根据互余两角之和为90°计算即可.【解答】解:∵∠A=40°,∴∠A的余角为:90°﹣40°=50°,故选:A.6、(2022•玉林)已知:α=60°,则α的余角是°.【分析】根据如果两个角的和等于90°,就说这两个角互为余角,即其中一个角是另一个角的余角即可得出答案.【解答】解:90°﹣60°=30°,故答案为:30.7、(2022•连云港)已知∠A的补角为60°,则∠A=°.【分析】根据补角的定义即可得出答案.【解答】解:∵∠A的补角为60°,∴∠A=180°﹣60°=120°,故答案为:120.。
专练06 三角形中有关角的计算与证明-2021年中考数学压轴题专项高分突破训练(全国通用)(解析版)

专练06三角形中有关角的计算与证明1.已知△ABC ,点P 为其内部一点,连结PA 、PB 、PC ,在△PAB ,△PBC 和△PAC 中,如果存在一个三角形,其内角与△ABC 的三个内角分别相等,那么就称点P 为△ABC 的等角点.(1)判断以下两个命题是否为真命题,若为真命题,则在相应横线内写“真”;反之,则写“假”. ①内角分别为30°、60°、90°的三角形存在等角点;________命题; ②任意的三角形都存在等角点;________命题.(2)如图 ①,点P 是△ABC 的等角点,若∠BAC=∠PBC ,探究图 ①中∠BPC ,∠ABC ,∠ACP 之间的数量关系,并说明理由;(3)如图②,在△ABC 中,∠BAC<∠ABC<∠ACB ,若△ABC 的三个内角的角平分线的交点P 是该三角形的等角点,直接写出△ABC 三个内角的度数.【答案】 (1) ①内角分别为30°、60°、90°的三角形存在等角点,是真命题; ②任意的三角形都存在等角点是假命题,如等边三角形不存在等角点; 故答案为:1、真,2、假.(2)解:如图①,∵△ABC 中, ∠BPC=∠ABP+∠BAC+∠ACP , ∠BAC=∠PBC ,∴∠BPC=∠ABP+∠PBC+∠ACP =∠ABC+∠ACP. (3)∵P 为三角形内角平分线的交点, ∵∠PBC=12∠ABC ,∠PCB=12∠ACB , ∵P 为△ABC 的等角点,∴∠PBC=∠A,∴∠ABC=2∠PBC=2∠A,∴∠BCP=∠ABC=2∠A,∴∠ACB=2∠BCP=4∠A,又∵∠A+∠ABC+∠ACB=180°,∴∠A+2∠A+4∠A=180°,∴∠A=180°7,∴该三角形的三个内角的度数分别为:180°7,360°7,720°7.故答案为:180°7,360°7,720°7.2.将一块直角三角板XYZ放置在AABC上,使得该三角板的两条直角边XY,XZ恰好分别经过点B,C.(1)如图1,当∠A=45°时,∠ABC+∠ACB=________度,∠ABX+∠ACX=________度.(2)如图2,改变直角三角板XYZ的位置,使该三角板的两条直角边XY,XZ仍然分别经过点B,C,那么∠ABX+∠ACX的大小是否发生变化?若变化,请举例说明,若没有变化,请探究∠ABX+∠ACX与∠A的关系.【答案】(1)在三角形ABC中,∵∠A=45°∴∠ABC+∠ACB=180°-45°=135°∵∠A=45°∴∠ABC+∠ACB=180°-∠A=180°-45°=135°∵∠YXZ=90°∴∠XBC+∠XCB=90°∴∠ABX+∠ACX=135°-90°=45°(2)解:不变化,∠ABX+∠ACX =90°-∠A,理由如下∵∠x =90°,∴∠XBC+∠XCB =90°∵∠A+∠ABC+∠ACB =180°,∴∠ABX+∠ACX =(∠ABC-∠XBC)+(∠ACB-∠XCB)=(∠ABC+∠ACB)-(∠XBC+∠XCB)=180°-∠A-90°=90°-∠A3.如图(1)如图,请证明∠A+∠B+∠C=180°(2)如图的图形我们把它称为“8字形”,请证明∠A+∠B=∠C+∠D(3)如图,E在DC的延长线上,AP平分∠BAD,CP平分∠BCE,猜想∠P与∠B、∠D之间的关系,并证明(4)如图,AB∥CD,PA平分∠BAC,PC平分∠ACD,过点P作PM、PE交CD于M,交AB于E,则①∠1+∠2+∠3+∠4不变;②∠3+∠4﹣∠1﹣∠2不变,选择正确的并给予证明.【答案】(1)证明:如图1,延长BC到D,过点C作CE∥BA,∵BA∥CE,∴∠B=∠1,∠A=∠2,又∵∠BCD=∠BCA+∠2+∠1=180°,∴∠A+∠B+∠ACB=180°;(2)证明:如图2,在△AOB中,∠A+∠B+∠AOB=180°,在△COD中,∠C+∠D+∠COD=180°,∵∠AOB=∠COD,∴∠A+∠B=∠C+∠D;(3)解:如图3,∵AP平分∠BAD,CP平分∠BCD的外角∠BCE,∴∠1=∠2,∠3=∠4,∵(∠1+∠2)+∠B=(180°﹣2∠3)+∠D,∠2+∠P=(180°﹣∠3)+∠D,∴2∠P=180°+∠D+∠B,∴∠P=90°+ 1(∠B+∠D);2(4)解:②∠3+∠4﹣∠1﹣∠2不变正确.理由如下:作PQ∥AB,如图4,∵AB∥CD,∴PQ∥CD,由AB∥PQ得∠APQ+∠3+∠4=180°,即∠APQ=180°﹣∠3﹣∠4,由PQ∥CD得∠5=∠2,∵∠APQ+∠5+∠1=90°,∴180°﹣∠3﹣∠4+∠2+∠1=90°,∴∠3+∠4﹣∠1﹣∠2=90°.4.如图,在△ABC中,AB=AC,D为直线BC上一动点(不与点B,C重合),在AD的右侧作△ACE,使得AE=AD,∠DAE=∠BAC,连接CE.(1)当D在线段BC上时,①求证:△BAD≌△CAE.②请判断点D在何处时,AC⊥DE,并说明理由.(2)当CE∥AB时,若△ABD中最小角为26°,求∠ADB的度数.【答案】(1)解:①∵∠DAE=∠BAC,∴∠DAB=∠EAC,在△ABD和△ACE中,{AB=AC∠DAB=∠EACAD=AE,∴△BAD≌△CAE(SAS);②如图,连接DE,若AC⊥DE,又∵AD=AE,∴AC平分∠DAE,∴∠DAB=∠CAE=∠CAD,∴AD平分∠CAB,又∵AB=AC,∴BD=CD,∴当点D在BC中点时,AC⊥DE;(2)解:当CE∥AB时,则有∠ABC=∠ACE=∠BAC=60°,∴△ABC为等边三角形,①如图1:此时∠BAD=26°,∴∠ADB=180°﹣∠BAD﹣∠B=180°﹣26°﹣60°=94°.②如图2,此时∠ADB=26°,③如图3,此时∠BAD=26°,∠ADB=60°﹣26°=34°.④如图4,此时∠ADB=26°.综上所述,满足条件的∠ADB的度数为26°或34°或94°5.如图,P是等腰△ABC内一点,AB=BC,连接PA,PB,PC.图1 图2(1)如图1,当∠ABC=90°时,PA=2,PB=4,PC=6,求∠APB.(2)如图2,当∠ABC=60°时,PA=3,PB=4,PC=5,求∠APB.【答案】(1)解:将△APB沿点B顺时针旋转90°,得到△BCP′,连接PP′,可得∠P′BP=90°,且BP=BP′=4,∴△BPP′为等腰直角三角形,∴∠BP′P=45°,PP′=4√2,在△PP′C中,PC2=62=36,P′C2+P′P2=22+(4√2)2=4+32=36,∴PC2=P′C2+P′P2,∴△PP′C为直角三角形且∠PP′C=90°,∴∠BP′C=90°,∴∠BP′C=∠BP′P+∠BP′C=45°+90°=135°,又∵旋转,∴∠APB=∠BP′C=135°(2)解:将△APB沿点B顺时针旋转60°得到△BCP′,连接PP′,可得:BP′=BP=4,∠PBP′=60°∴△PBP′为等边三角形,∴∠BP′P=60°,PP′=4,在△PP′C中,PP′2+P′C2=42+32=25,CP2=52=25,∴△PP′C为直角三角形且∠PP′C=90°,∴∠BP′C=∠BP′P+∠PP′C=60°+90°=150°,∴∠APB=∠BP′C=150°6.如图,CA=CB,CD=CE,∠ACB=∠DCE=40°,AD、BE交于点H,连接CH.(1)求证:ΔACD≌ΔBCE;(2)求证:CH 平分∠AHE;(3)求∠CHE的度数.【答案】(1)证明;∵∠ACB=∠DCE=40°,∴∠ACD=∠BCE,在△ACD和△BCE中,{CA=CB∠ACD=∠BCECD=CE,∴△ACD≌△BCE(SAS)(2)证明;过点C作CM⊥AD于M,CN⊥BE于N,∵△ACD≌△BCE,∴∠CAM=∠CBN,在△ACM和△BCN中,{∠CAM=∠CBN∠AMC=∠BNC=90°AC=BC,∴△ACM≌△BCN(AAS),∴CM=CN,∴CH平分∠AHE(3)解;∵△ACD≌△BCE,∴∠CAD=∠CBE,∵∠AMC=∠AMC,∴∠AHB=∠ACB=40°,∴∠AHE=180°-40°=140°,∠AHE=70º∴∠CHE= 127.我们将内角互为对顶角的两个三角形称为“对顶三角形”.例如,在图1中,△AOB的内角∠AOB与△COD的内角∠COD互为对顶角,则△AOB与△COD为对顶三角形,根据三角形内角和定理知“对顶三角形”有如下性质:∠A+∠B=∠C+∠D.(1)性质理解:如图2,在“对顶三角形” △AOB与△COD中,∠EAO=∠C,∠D=2∠B,求证:∠EAB=∠B;(2)性质应用:①如图3,则∠A+∠B+∠C+∠D+∠E的度数为;②如图4,在△ABC中,点D,E分别在AB,AC上,∠BOD=∠A.若∠ECD比∠DBE大20∘,求∠BDO的度数;(3)拓展提高:如图5,已知BE,CD是△ABC的角平分线,且∠BDC和∠BEC的平分线DP和EP相交于点P,设∠A=α,求∠P的度数(用α表示∠P).【答案】(1)证明:据题意,得∠BAO+∠B=∠C+∠D,∴∠BAO−∠C=∠D−∠B,∵∠EAO=∠C,∠D=2∠B,∴∠BAE=∠B(2)解:①∠A+∠B+∠C+∠D+∠E=∠A+∠C+∠B+∠E+∠D=∠FGD+∠GFD+∠D=180°;故答案为:180°;②由题意得∠ECD−∠DBE=20°,由(1)得∠EBD+∠BDO=∠ECO+∠OEC,∴∠BDO−∠OEC=20°,∵∠BOD=∠A,∴∠A+∠DOE=180°,故∠ADO+∠AEO=180°,∵∠AEO+∠CEO=∠BDO+∠ADO=180°,∴∠BDO=∠AEO,∴∠BDO+∠CEO=180°,∵∠BDO−∠OEC=20°,∴∠BDO=100°;(3)解:∠P=180∘−α4,理由如下:∵∠BDC和∠BEC的平分线DP和EP相交于点P,∴∠BDP=∠CDP,∠BEP=∠CEP,由(1)得∠BDP+∠DBE=∠BEP+∠P①,∠CDP+∠P=∠CEP+∠DCE②,由①−②得∠DBE−∠P=∠P−∠DCE,∴∠P=12(∠DBE+∠DCE),即∠P=14(∠ABC+∠ACB),∴∠P=14(180°−∠A)=180°−α48.已知点C为线段AB上一点,分别以AC、BC为边在线段AB同侧作△ACD和△BCE,且CA=CD,CB=CE,∠ACD=∠BCE,直线AE与BD交于点F,(1)如图1,若∠ACD=60°,则∠AFB=________;如图2,若∠ACD=90°,则∠AFB=________;如图3,若∠ACD=120°,则∠AFB=________;(2)如图4,若∠ACD=α,则∠AFB=________(用含α的式子表示);(3)将图4中的△ACD绕点C顺时针旋转任意角度(交点F至少在BD、AE中的一条线段上),变成如图5所示的情形,若∠ACD=α,则∠AFB与α的有何数量关系?并给予证明.【答案】(1)如图1,CA=CD,∠ACD=60°,所以△ACD是等边三角形.∵CB=CE,∠ACD=∠BCE=60°,所以△ECB是等边三角形.∵AC=DC,∠ACE=∠ACD+∠DCE,∠BCD=∠BCE+∠DCE,又∵∠ACD=∠BCE,∴∠ACE=∠BCD.∵AC=DC,CE=BC,∴△ACE≌△DCB.∴∠EAC=∠BDC.∠AFB是△ADF的外角.∴∠AFB=∠ADF+∠FAD=∠ADC+∠CDB+∠FAD=∠ADC+∠EAC+∠FAD=∠ADC+∠DAC=120°.如图2,∵AC=CD,∠ACE=∠DCB=90°,EC=CB,∴△ACE≌△DCB.∴∠AEC=∠DBC,又∵∠FDE=∠CDB,∠DCB=90°,∴∠EFD=90°.∴∠AFB=90°.如图3,∵∠ACD=∠BCE,∴∠ACD﹣∠DCE=∠BCE﹣∠DCE.∴∠ACE=∠DCB.又∵CA=CD,CE=CB,∴△ACE≌△DCB.∴∠EAC=∠BDC.∵∠BDC+∠FBA=180°﹣∠DCB=180°﹣(180﹣∠ACD)=120°,∴∠FAB+∠FBA=120°.∴∠AFB=60°.故答案为:120°,90°,60°;(2)∵∠ACD=∠BCE,∴∠ACD+∠DCE=∠BCE+∠DCE.∴∠ACE=∠DCB.∴∠CAE=∠CDB.∴∠DFA=∠ACD.∴∠AFB=180°﹣∠DFA=180°﹣∠ACD=180°﹣α.故答案为:180°﹣α;(3)解:∠AFB=180°﹣α;证明:∵∠ACD=∠BCE=α,则∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB.在△ACE和△DCB中{AC=DC∠ACE=∠DCBCE=CB,则△ACE≌△DCB(SAS).则∠CBD=∠CEA,由三角形内角和知∠EFB=∠ECB=α.∠AFB=180°﹣∠EFB=180°﹣α.9.己知∠ABC=90°,AB=2,BC=3,AD∥BC,P为线段BD上的动点,点Q在射线AB上,且满足PQPC=AQAB(如图1所示)(1)当AD=2,且点Q与点B重合时(如图2所示),求线段PC的长;(2)在图1中,联结AP,当AD= 32,且点Q在线段AB上时,设点B、Q之间的距离为x,S△APQS△PBC=y,其中S△APQ表示S△APQ的面积,S△PBC表示△PBC的面积,求y关于x的函数关系式,并写出函数定义域;(3)当AD<AB,且点Q在线段AB的延长线上时(如图3所示),求∠QPC的大小【答案】(1)解:∵AD∥BC,∠ABC=90°,∴∠BAD=∠ABC=90°,当AD=2时,AD=AB,∴∠D=∠ABD=45°,∴∠PQC=∠D=45°,∵PQPC =AQAB,∴PQ=PC,∴∠C=∠PQC=45°,∴∠BPC=90°,∴PC=BC·sin45°=3√22(2)解:如图,作PE⊥AB于E,PF⊥BC于F,∵∠ABC=90°, ∴四边形EBFP 是矩形, ∴PF=BE , 又∵∠BAD=90°, ∴PE ∥AD ,∴Rt △BEP ∽Rt △BAD , ∴BE BA =EPAD , ∴BEEP =BAAD =232=43, 设BE=4k ,则PE=3k , ∴PF=BE=4k ,∵BQ=x ,AQ=AB-BQ=2-x ,∴S △APQ =12AQ·PE=12(2-x )·3k ,S △PBC =12BC·PF=12×3×4k=6k , ∵S △APQS △PBC=y ,∴12(2−x )·3k 6k =y ,∴y=2−x 4(0≤x ≤78);(3)解:∵Rt △BEP ∽Rt △BAD , ∴BE BA =EPAD ,∴BEEP =BAAD ∴PFEP =BAAD , ∵PCPQ =BAAD , ∴PFEP =PCPQ , ∴Rt △PCF ∽Rt △PQE , ∴∠FPC=∠EPQ ,∵∠EPQ+∠QPF=∠EPF=90°,∴∠FPC+∠QPF=90°,即∠QPC=90°。
角的度量练习题带答案

角的度量练习题带答案角的度量是数学中的一个重要概念,它涉及到角度的计算和度量单位。
以下是一些角的度量练习题及其答案,以帮助学生更好地理解和掌握这一概念。
练习题1:一个角的度数是30°,另一个角是它的两倍,求另一个角的度数。
答案:30° × 2 = 60°练习题2:如果一个角的度数是90°,它是一个直角。
那么一个角的度数是45°,它是什么角?答案:45°是一个锐角。
练习题3:一个角的度数是120°,它比直角大多少度?答案:120° - 90° = 30°练习题4:一个角的度数是360°,它是一个周角。
如果将它平均分成4个相等的角,每个角的度数是多少?答案:360° ÷ 4 = 90°练习题5:一个角的度数是180°,它是一个平角。
如果将它平均分成3个相等的角,每个角的度数是多少?答案:180° ÷ 3 = 60°练习题6:一个角的度数是15°,它是一个锐角。
如果将它扩大到原来的3倍,新的角的度数是多少?答案:15° × 3 = 45°练习题7:一个角的度数是150°,它是一个钝角。
如果将它缩小到原来的一半,新的角的度数是多少?答案:150° ÷ 2 = 75°练习题8:如果一个角的度数是75°,它是一个钝角。
那么一个角的度数是75°的三分之一,这个角的度数是多少?答案:75° ÷ 3 = 25°练习题9:一个角的度数是300°,它是一个周角的四分之三。
求这个周角的度数。
答案:300° ÷ (3/4) = 400°练习题10:一个角的度数是40°,另一个角的度数是它的补角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学专项练习常用角的单位及换算(含解析)【一】单项选择题1.把10.26°用度分秒表示为〔〕A.10°15′36" B.10°2 0′6" C.1 0°14′6"D.10°26".2.以下关系式正确的选项是〔〕A.35.5°=35°5′B.35.5°=35°50′ C.35.5°<3 5°5′ D.35.5°>35°5′3.将21.54°用度、分、秒表示为〔〕A.21°54′ B.2 1°50′24″ C.2 1°32′40″ D.2 1°32′24″4.下面等式成立的是〔〕A.83.5°=83°50′B.37°12′36″=37.48° C.24°24′24″=24.44° D.41.25°=41°15′5.0.25°等于〔〕分.A.6B.15C.9D.3606.以下计算错误的选项是〔〕A.0.25°=900″B. 1.5°=90′C.1000″=〔〕° D.125.45°=1254.5′7.∠1=45゜24′,∠2=45.3゜,∠3=45゜18′,那么〔〕A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.以上都不对8.∠1=37°36′,∠2=37.36°,那么∠1与∠2的大小关系为〔〕A.∠1<∠2B.∠1=∠2C.∠1>∠2D.无法比较9.以下计算错误的选项是〔〕A.0.25°=900″B. 1.5°=90′C.1000″=〔〕° D.125.45°=1254.5′10.∠1=18°18′,∠2=18.18°,∠3=18.3°,以下结论正确的选项是〔〕A.∠1=∠3 B.∠1 =∠2C.∠2=∠3 D.∠1 =∠2=∠311.:∠A=25°12′,∠B=25.12°,∠C=25.2°,以下结论正确的选项是〔〕A.∠A=∠B B.∠B=∠C C.∠A=∠C D.三个角互不相等12.以下算式正确的选项是〔〕①33.33°=33°3′3″②33.33°=33°19′48″③50°40′33″=50.43°④50°40′33″=50.675°A.①和②B.①和③C.②和③D.②和④【二】填空题13.34.37°=34°________′________″.14.0.5°=________′=________″;1800″=________°=_______ _′.15.计算:180°﹣20°40′=________.16.8.31°=________°________′________″.17.计算,________18.计算:33.21°=________°________′________″.19.角度换算:26°48′=________°.【三】计算题20.计算:〔1〕46゜39′+57゜41;〔2〕90゜﹣77゜29′32″;〔3〕31゜17′×5;〔4〕176゜52′÷3〔精确到分〕21.计算以下各题:〔1〕153°19′42″+26°40′28″;〔2〕90°3″﹣57°21′44″;〔3〕33°15′16″×5;〔4〕175°16′30″﹣47°30′÷6+4°12′50″×3.22.计算:〔1〕13°29’+78°37‘〔2〕62°5’-21°39‘(3)22°16′×5〔4〕42°15′÷5【四】解答题23.把65°28′45″化成度.24.3.5°与3°5′的区别是什么?25.计算:〔1〕22°18′×5;〔2〕90°﹣57°23′27″.【五】综合题26.计算:〔1〕40°26′+30°30′30″÷6;〔2〕13°53′×3﹣32°5′31″.27.综合题。
〔1〕把41.27°用度、分、秒表示;〔2〕把56°25′l2″化为度.【一】单项选择题1.把10.26°用度分秒表示为〔〕A.10°15′36" B.10°2 0′6" C.1 0°14′6"D.10°26".【考点】度分秒的换算【解析】【解答】10.26°=10°+0.26×60’=10°+15.6‘=0.6×60"=10°15’36",所以A正确.【分析】度分秒之间的换算为60进制的.2.以下关系式正确的选项是〔〕A.35.5°=35°5′B.35.5°=35°50′ C.35.5°<3 5°5′ D.35.5°>35°5′【考点】度分秒的换算3.将21.54°用度、分、秒表示为〔〕A.21°54′ B.2 1°50′24″ C.2 1°32′40″ D.2 1°32′24″【考点】度分秒的换算4.下面等式成立的是〔〕A.83.5°=83°50′B.37°12′36″=37.48° C.24°24′24″=24.44° D.41.25°=41°15′【考点】度分秒的换算【解析】【解答】解:A、83.5°=83°50′,错误;B、37°12′=37.48°,错误;C、24°24′24″=24.44°,错误;D、41.25°=41°15′,正确.应选D、【分析】进行度、分、秒的加法、减法计算,注意以60为进制.5.0.25°等于〔〕分.A.6B.15C.9D.360【考点】度分秒的换算【解析】【解答】0.25°=0.25×60′=15′.应选B.【分析】角的度、分、秒是60进制的,1°=60′,所以0.25°=0.25×6 0′=15′.6.以下计算错误的选项是〔〕A.0.25°=900″B. 1.5°=90′C.1000″=〔〕° D.125.45°=1254.5′【考点】度分秒的换算7.∠1=45゜24′,∠2=45.3゜,∠3=45゜18′,那么〔〕A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.以上都不对【考点】度分秒的换算8.∠1=37°36′,∠2=37.36°,那么∠1与∠2的大小关系为〔〕A.∠1<∠2B.∠1=∠2C.∠1>∠2D.无法比较【考点】度分秒的换算9.以下计算错误的选项是〔〕A.0.25°=900″B. 1.5°=90′C.1000″=〔〕° D.125.45°=1254.5′【考点】度分秒的换算【解析】【解答】解:A、0.25°=900″,正确;B、1.5°=90′,正确;C、1000″=〔〕°,正确;D.125.45°=7527′,故本选项错误;应选:D、【分析】根据1°=60′,1′=60″,进行转换,即可解答.10.∠1=18°18′,∠2=18.18°,∠3=18.3°,以下结论正确的选项是〔〕A.∠1=∠3 B.∠1 =∠2C.∠2=∠3 D.∠1 =∠2=∠3【考点】度分秒的换算11.:∠A=25°12′,∠B=25.12°,∠C=25.2°,以下结论正确的选项是〔〕A.∠A=∠B B.∠B=∠C C.∠A=∠C D.三个角互不相等【考点】度分秒的换算12.以下算式正确的选项是〔〕①33.33°=33°3′3″②33.33°=33°19′48″③50°40′33″=50.43°④50°40′33″=50.675°A.①和②B.①和③C.②和③D.②和④【考点】度分秒的换算【解析】【解答】解:①33.33°=33°19′48″,故错误;②33.33°=33°19′48″,故正确;③50°40′33″=50.675°,故错误;④50°40′33″=50.675°,故正确.应选D、【分析】进行度、分、秒的转化运算,注意以60为进制.【二】填空题13.34.37°=34°________′________″.【考点】度分秒的换算14.0.5°=________′=________″;1800″=________°=_______ _′.【考点】度分秒的换算15.计算:180°﹣20°40′=________.【考点】度分秒的换算16.8.31°=________°________′________″.【考点】度分秒的换算17.计算,________【考点】度分秒的换算18.计算:33.21°=________°________′________″.【考点】度分秒的换算19.角度换算:26°48′=________°.【考点】度分秒的换算【三】计算题20.计算:〔1〕46゜39′+57゜41;〔2〕90゜﹣77゜29′32″;〔3〕31゜17′×5;〔4〕176゜52′÷3〔精确到分〕【考点】度分秒的换算【解析】【分析】〔1〕利用度加度、分加分进行计算,再进位即可;〔2〕把90°化为89°59′60″,再利用度减度,分减分,秒减秒进行计算;〔3〕利用度和分分别乘以5,再进位即可;〔4〕分别度除以3,再分除以3即可.21.计算以下各题:〔1〕153°19′42″+26°40′28″;〔2〕90°3″﹣57°21′44″;〔3〕33°15′16″×5;〔4〕175°16′30″﹣47°30′÷6+4°12′50″×3.【考点】度分秒的换算【解析】【分析】进行度、分、秒的加法、减法.乘除法计算,度与度,分与分,秒与秒对应相加,分的结果假设满60,那么转化为度;度与度,分与分,秒与秒对应相乘除,分的结果假设满60,那么转化为度.22.计算:〔1〕13°29’+78°37‘〔2〕62°5’-21°39‘(3)22°16′×5〔4〕42°15′÷5【考点】度分秒的换算【解析】【解答】(1)13°29′+78°37′=13°+78°+29′+37′=91°+66′=92°6′;〔2〕62°5′-21°39′=61°-21°+65′-39′=40°+26′=40°26′;〔3〕22°16′×5=22°×5+16′×5=110°+80′=111°20′;〔4〕42°15′÷5=42°÷5+15′÷5=8.4°+3′=8°+0.4×60′+3′=8°27′【分析】这里的加减乘除运算,一度等于60分,一分等于60秒;加法运算时,如果和中秒值大于60,就要向分进一,同理,如果分值大于60,也要向度进1;减法运算时,如果秒不够减,可向分借一作为60秒加上原先的秒值再与减数中的秒值相减,分进行减法时类似〔向度借一作60〕。
