模式识别报告
模式识别上机实验报告

实验一、二维随机数的产生1、实验目的(1) 学习采用Matlab 程序产生正态分布的二维随机数 (2) 掌握估计类均值向量和协方差矩阵的方法(3) 掌握类间离散度矩阵、类内离散度矩阵的计算方法(4) 熟悉matlab 中运用mvnrnd 函数产生二维随机数等matlab 语言2、实验原理多元正态分布概率密度函数:11()()2/21/21()(2)||T X X d p X eμμπ---∑-=∑其中:μ是d 维均值向量:Td E X μμμμ=={}[,,...,]12Σ是d ×d 维协方差矩阵:TE X X μμ∑=--[()()](1)估计类均值向量和协方差矩阵的估计 各类均值向量1ii X im X N ω∈=∑ 各类协方差矩阵1()()iTi iiX iX X N ωμμ∈∑=--∑(2)类间离散度矩阵、类内离散度矩阵的计算类内离散度矩阵:()()iTi iiX S X m X m ω∈=--∑, i=1,2总的类内离散度矩阵:12W S S S =+类间离散度矩阵:1212()()Tb S m m m m =--3、实验内容及要求产生两类均值向量、协方差矩阵如下的样本数据,每类样本各50个。
1[2,2]μ=--,11001⎡⎤∑=⎢⎥⎣⎦,2[2,2]μ=,21004⎡⎤∑=⎢⎥⎣⎦ (1)画出样本的分布图;(2) 编写程序,估计类均值向量和协方差矩阵;(3) 编写程序,计算类间离散度矩阵、类内离散度矩阵; (4)每类样本数增加到500个,重复(1)-(3)4、实验结果(1)、样本的分布图(2)、类均值向量、类协方差矩阵根据matlab 程序得出的类均值向量为:N=50 : m1=[-1.7160 -2.0374] m2=[2.1485 1.7678] N=500: m1=[-2.0379 -2.0352] m2=[2.0428 2.1270] 根据matlab 程序得出的类协方差矩阵为:N=50: ]0628.11354.01354.06428.1[1=∑ ∑--2]5687.40624.00624.08800.0[N=500:∑--1]0344.10162.00162.09187.0[∑2]9038.30211.00211.09939.0[(3)、类间离散度矩阵、类内离散度矩阵根据matlab 程序得出的类间离散度矩阵为:N=50: ]4828.147068.147068.149343.14[=bS N=500: ]3233.179843.169843.166519.16[b =S根据matlab 程序得出的类内离散度矩阵为:N=50:]0703.533088.73088.71052.78[1=S ]7397.2253966.13966.18975.42[2--=S ]8100.2789123.59123.50026.121[=W SN=500: ]5964.5167490.87490.86203.458[1--=S ]8.19438420.78420.70178.496[2=S ]4.24609071.09071.06381.954[--=W S5、结论由mvnrnd 函数产生的结果是一个N*D 的一个矩阵,在本实验中D 是2,N 是50和500.根据实验数据可以看出,当样本容量变多的时候,两个变量的总体误差变小,观测变量各个取值之间的差异程度减小。
模式识别实验报告

模式识别实验报告————————————————————————————————作者:————————————————————————————————日期:实验报告实验课程名称:模式识别姓名:王宇班级: 20110813 学号: 2011081325实验名称规范程度原理叙述实验过程实验结果实验成绩图像的贝叶斯分类K均值聚类算法神经网络模式识别平均成绩折合成绩注:1、每个实验中各项成绩按照5分制评定,实验成绩为各项总和2、平均成绩取各项实验平均成绩3、折合成绩按照教学大纲要求的百分比进行折合2014年 6月实验一、 图像的贝叶斯分类一、实验目的将模式识别方法与图像处理技术相结合,掌握利用最小错分概率贝叶斯分类器进行图像分类的基本方法,通过实验加深对基本概念的理解。
二、实验仪器设备及软件 HP D538、MATLAB 三、实验原理 概念:阈值化分割算法是计算机视觉中的常用算法,对灰度图象的阈值分割就是先确定一个处于图像灰度取值范围内的灰度阈值,然后将图像中每个像素的灰度值与这个阈值相比较。
并根据比较的结果将对应的像素划分为两类,灰度值大于阈值的像素划分为一类,小于阈值的划分为另一类,等于阈值的可任意划分到两类中的任何一类。
最常用的模型可描述如下:假设图像由具有单峰灰度分布的目标和背景组成,处于目标和背景内部相邻像素间的灰度值是高度相关的,但处于目标和背景交界处两边的像素灰度值有较大差别,此时,图像的灰度直方图基本上可看作是由分别对应于目标和背景的两个单峰直方图混合构成。
而且这两个分布应大小接近,且均值足够远,方差足够小,这种情况下直方图呈现较明显的双峰。
类似地,如果图像中包含多个单峰灰度目标,则直方图可能呈现较明显的多峰。
上述图像模型只是理想情况,有时图像中目标和背景的灰度值有部分交错。
这时如用全局阈值进行分割必然会产生一定的误差。
分割误差包括将目标分为背景和将背景分为目标两大类。
实际应用中应尽量减小错误分割的概率,常用的一种方法为选取最优阈值。
模式识别 实验报告一

402
132
识别正确率
73.36
84.87
99.71
70.31
82.89
86.84
结果分析:
实验中图像3的识别率最高,图像1和图像2的识别率次之。图像1和图像2的分辨率相对图像3更低,同时图像2有折痕影响而图像1则有大量噪声。通过阈值处理能较好的处理掉图像1的噪声和图像2的折痕,从而使得图像1的识别率有所提升,而图像2的识别率变化不大。从而可以得出结论,图像3和图像2识别率不同的原因主要在于图像分辨率,而图像2和图像1识别率的不同则在于噪声干扰。
实验报告
题目
模式识别系列实验——实验一字符识别实验
内容:
1.利用OCR软件对文字图像进行识别,了解图像处理与模式识别的关系。
2.利用OCR软件对文字图像进行识别,理解正确率的概念。
实验要求:
1.利用photoshop等软件对效果不佳的图像进行预处理,以提高OCR识别的正确率。
2.用OCR软件对未经预处理和经过预处理的简体和繁体中文字符图像进行识别并比较正确率。
图像4内容既有简体又有繁体,从识别结果中可了解到错误基本处在繁体字。
遇到的问题及解决方案:
实验中自动旋转几乎没效果,所以都是采用手动旋转;在对图像4进行识别时若采用系统自己的版面分析,则几乎识别不出什么,所以实验中使用手动画框将诗的内容和标题及作者分开识别。
主要实验方法:
1.使用汉王OCR软件对所给简体和繁体测试文件进行识别;
2.理,再次识别;
实验结果:
不经过图像预处理
经过图像预处理
实验图像
图像1
图像2
图像3
图像4
图像1
图像2
字符总数
458
武汉理工大学,模式识别实验报告,带数据!带代码!

武汉理工大学模式识别实验报告姓名:班级:学号:姓名:班级:学号:实验一总体概率密度分布的非参数方法一、实验目的1.了解使用非参数方法估计样本概率密度函数的原理。
2.了解Parzen窗法的原理及其参数h1,N对估计结果的影响。
3.掌握Parzen窗法的算法并用Matlab实现。
4.使用Matlab分析Parzen窗法的参数h1,N对估计结果的影响。
二、实验数据一维正态分布样本,使用函数randn生成。
三、实验结果选取的h1=0.25,1,4,N=1,16,256,4096,65536,得到15个估计结果,如下图所示。
由下面三组仿真结果可知,估计结果依赖于N和h1。
当N=1时,是一个以样本为中心的小丘。
当N=16和h1=0.25时,仍可以看到单个样本所起的作用;但当h1=1及h1=4时就受到平滑,单个样本的作用模糊了。
随着N的增加,估计量越来越好。
这说明,要想得到较精确的估计,就需要大量的样本。
但是当N取的很大,h1相对较小时,在某些区间内hN趋于零,导致估计的结果噪声大。
分析实验数据发现在h1=4,N=256时,估计结果最接近真实分布。
附录:1.Parzen窗法函数文件parzen.m function parzen=parzen(N,h1,x) %ParzenhN = h1/sqrt(N);num_x = numel(x);parzen = zeros(1, num_x);for u = 1:num_xfor i=1:Nparzen(u) = parzen(u)+exp(((x(u)-x(i))/hN).^2/-2);endparzen(u)=parzen(u)/sqrt(2*pi)/h1/sqrt(N);end2.例程文件parzen_sample.mx = randn(1,10000);%Normally distributed pseudorandom numberspx = normpdf(x,0,1);%Normal probability density function - normpdf(X,mu,sigma)h1 = [0.25, 1, 4];N = [1, 16, 256, 1024, 4096];num_h1 = numel(h1);%Number of array elementsnum_N = numel(N);figure('Name', '总体概率密度分布的非参数方法');%遍历h1for i_h1 = 1:length(h1)h1_offset = (i_h1-1)*(num_N+1)+1;%绘图位置的偏移量subplot(num_h1, num_N+1, h1_offset);plot(x, px, '.');ylabel(sprintf('%s%4.2f', 'h1=', h1(i_h1)));title('正态分布样本的概率密度函数')%遍历Nfor i_N = 1 : length(N)pNx=parzen(N(i_N), h1(i_h1), x);subplot(num_h1, num_N+1, h1_offset+i_N);plot(x, pNx, '.');title(sprintf('%s%d', 'N=', N(i_N)));endend姓名:班级:学号:实验二感知器准则算法实验一、实验目的1.了解利用线性判别函数进行分类的原理。
关于学习了解模式识别技术报告

关于了解学习模式识别技术报告谈起模式识别,我们首先想到的是人工智能。
模式识别是人工智能的一个分支,是电脑应用内容的一部分。
要想了解学习模式识别,首先要懂得人工智能。
第一篇人工智能什么是人工智能呢?人工智能主要用人工的方法和技术,模仿,延伸和扩展人的智能,实现机器智能。
人工智能的长期目标是实现到达人类智力水平的人工智能。
〔摘自《人工智能》史忠植编著,第一章绪论〕简单来说就是使机器拥有类人行为方法,类人思维方法和理性行为方法。
让机器像人一样拥有自主思维的能力,拥有人的生存技能,甚至在某方面超过人类,用所拥有的技能,更好的为人类服务,解放人类的双手。
简单了解了人工智能的概念,接下来将介绍人工智能的起源与发展历史。
说到历史,很多人可能有点不大相信。
人类对智能机器的梦想和追求可以追溯到三千多年前。
也许你会有疑问,三千多年前,人类文明发展都不算成熟,怎么可能会有人对机器有概念。
当然,那时候的机器并非现在的机器概念。
在我国,早在西周时代〔公元前1066~公元前771年〕,就流传有关巧匠偃师献给周穆王艺伎的故事。
东汉〔公元25~公元220年〕张衡发明的指南车是世界上最早的机器人雏形。
〔摘自《人工智能》史忠植编著,第一章绪论〕现在你也许已经笑掉大牙了。
那样一个简易工具竟然说是机器人雏形。
但是事实就是这样,现在对机器人的概念依旧模糊,有些人觉得机器人必须先有像人一样的外形。
其次是有人一样的思维。
这个描述是没有错的,但是有点片面了,只顾及到字面意思了。
机器人的概念是自动执行工作的机器装置。
所以机器可以自动执行工作都叫机器人。
在国外也有案例:古希腊斯吉塔拉人亚里士多德〔公元前384年~公元前322年〕的《工具论》,为形式逻辑奠定了基础。
布尔创立的逻辑代数系统,用符号语言描述了思维活动中推理的基本法则,被后世称为“布尔代数”。
这些理论基础对人工智能的创立发挥了重要作用。
〔摘自《人工智能》史忠植编著,第一章绪论〕人工智能的发展历史,可大致分为孕育期,形成期,基于知识的系统,神经网络的复兴和智能体的兴起。
《模式识别》实验报告K-L变换特征提取

《模式识别》实验报告K-L变换特征提取基于K-L 变换的iris 数据分类⼀、实验原理K-L 变换是⼀种基于⽬标统计特性的最佳正交变换。
它具有⼀些优良的性质:即变换后产⽣的新的分量正交或者不相关;以部分新的分量表⽰原⽮量均⽅误差最⼩;变换后的⽮量更趋确定,能量更集中。
这⼀⽅法的⽬的是寻找任意统计分布的数据集合之主要分量的⼦集。
设n 维⽮量12,,,Tn x x x =x ,其均值⽮量E=µx ,协⽅差阵()T x E=--C x u)(x u ,此协⽅差阵为对称正定阵,则经过正交分解克表⽰为x =TC U ΛU ,其中12,,,[]n diag λλλ=Λ,12,,,n u u u =U 为对应特征值的特征向量组成的变换阵,且满⾜1T-=UU。
变换阵TU 为旋转矩阵,再此变换阵下x 变换为()T -=x u y U ,在新的正交基空间中,相应的协⽅差阵12[,,,]xn diag λλλ==x U C U C。
通过略去对应于若⼲较⼩特征值的特征向量来给y 降维然后进⾏处理。
通常情况下特征值幅度差别很⼤,忽略⼀些较⼩的值并不会引起⼤的误差。
对经过K-L 变换后的特征向量按最⼩错误率bayes 决策和BP 神经⽹络⽅法进⾏分类。
⼆、实验步骤(1)计算样本向量的均值E =µx 和协⽅差阵()T xE ??=--C x u)(x u5.8433 3.0573 3.7580 1.1993??=µ,0.68570.0424 1.27430.51630.04240.189980.32970.12161.27430.3297 3.1163 1.29560.51630.12161.29560.5810x----=--C (2)计算协⽅差阵xC 的特征值和特征向量,则4.2282 , 0.24267 , 0.07821 , 0.023835[]diag =Λ-0.3614 -0.6566 0.5820 0.3155 0.0845 -0.7302 -0.5979 -0.3197 -0.8567 0.1734 -0.0762 -0.4798 -0.3583 0.0755 -0.5458 0.7537??=U从上⾯的计算可以看到协⽅差阵特征值0.023835和0.07821相对于0.24267和4.2282很⼩,并经计算个特征值对误差影响所占⽐重分别为92.462%、5.3066%、1.7103%和0.52122%,因此可以去掉k=1~2个最⼩的特征值,得到新的变换阵12,,,newn k u u u -=U。
《模式识别》线性分类器设计实验报告
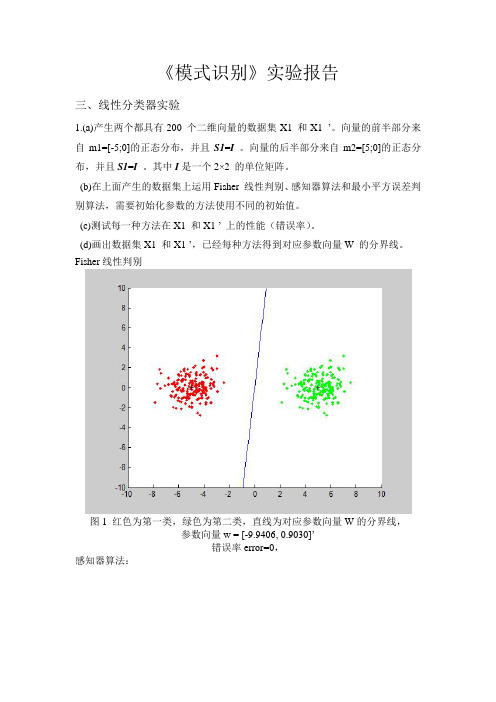
《模式识别》实验报告三、线性分类器实验1.(a)产生两个都具有200 个二维向量的数据集X1 和X1 ’。
向量的前半部分来自m1=[-5;0]的正态分布,并且S1=I 。
向量的后半部分来自m2=[5;0]的正态分布,并且S1=I。
其中I是一个2×2 的单位矩阵。
(b)在上面产生的数据集上运用Fisher 线性判别、感知器算法和最小平方误差判别算法,需要初始化参数的方法使用不同的初始值。
(c)测试每一种方法在X1 和X1 ’ 上的性能(错误率)。
(d)画出数据集X1 和X1 ’,已经每种方法得到对应参数向量W 的分界线。
Fisher线性判别图1 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数向量w = [-9.9406, 0.9030]’错误率error=0,感知器算法:图2 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[0.1;0.1];迭代次数iter=2参数向量w = [-4.8925, 0.0920]’错误率error=0图3 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[1; 1];迭代次数iter=2参数向量w = [-3.9925, 0.9920]’错误率error=0图4 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[10; 10];迭代次数iter=122参数向量w = [-5.6569, 7.8096]’错误率error=0图5 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[50; 50];迭代次数iter=600参数向量w = [-27.0945, 37.4194]’错误率error=0图6 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[50; 100];迭代次数iter=1190参数向量w = [-54.0048, 74.5875]’错误率error=0最小平方误差判别算法:图7 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[0.1; 0.1];参数向量w = [-0.1908, -0.0001]’错误率error=0图8 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[0.5; 0.5];参数向量w = [-0.1924, 0.1492]’错误率error=0图9 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[1; 0.5];参数向量w = [-0.1914, 0.0564]’错误率error=0图10 红色为第一类,绿色为第二类,直线为对应参数向量W的分界线,参数的初始值为[1; 1];参数向量w = [-0.1943, 0.3359]’错误率error= 0.00502.重复1.中的实验内容,数据集为X2 和X2 ’。
模式识别实验报告iris

一、实验原理实验数据:IRIS 数据。
分为三种类型,每种类型中包括50个思维的向量。
实验模型:假设IRIS 数据是正态分布的。
实验准备:在每种类型中,选择部分向量作为训练样本,估计未知的均值和方差的参数。
实验方法:最小错误判别准则;最小风险判别准则。
实验原理:1.贝叶斯公式已知共有M 类别M i i ,2,1,=ω,统计分布为正态分布,已知先验概率)(i P ω及类条件概率密度函数)|(i X P ω,对于待测样品,贝叶斯公式可以计算出该样品分属各类别的概率,叫做后验概率;看X 属于哪个类的可能性最大,就把X 归于可能性最大的那个类,后验概率即为识别对象归属的依据。
贝叶斯公式为M i P X P P X P X P Mj jji i i ,2,1,)()|()()|()|(1==∑=ωωωωω该公式体现了先验概率、类条件概率、后验概率三者的关系。
其中,类条件概率密度函数)|(i X P ω为正态密度函数,用大量样本对其中未知参数进行估计,多维正态密度函数为)]()(21exp[)2(1)(12/12/μμπ---=-X S X SX P T n 式中,),,(21n x x x X =为n 维向量; ),,(21n μμμμ =为n 维均值向量; ]))([(TX X E S μμ--=为n 维协方差矩阵; 1-S是S 的逆矩阵;S 是S 的行列式。
大多数情况下,类条件密度可以采用多维变量的正态密度函数来模拟。
)]}()(21exp[)2(1ln{)|()(1)(2/12/i i X X S X X S X P i T in i ωωπω---=- i i T S n X X S X X i i ln 212ln 2)()(21)(1)(-----=-πωω )(i X ω为i ω类的均值向量。
2.最小错误判别准则① 两类问题有两种形式,似然比形式:⎩⎨⎧∈⇒⎩⎨⎧<>=211221)()()|()|()(ωωωωωωX P P X P X P X l 其中,)(X l 为似然比,)()(12ωωP P 为似然比阈值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
标签比例信息最重要的应用:在 non-full bag 情况下,利用比例 信息,可以减少分配的种数。例如有 C 个标签,以及与其对应的有 个未被标记的样本,如果没有标签比例,那么可能分配的种类数有
C
mi
个, 分配后的标签比例也有很多种; 但是如果提前知道标签比例,
那么只有满足标签比例的分配情况才是有效的。如果用
包 Bi 中的样本属于不同的类(
个样本的类标签是未知的,这种包叫做非全包(non-full bags ) , Non-full bag 的情况增加了分类时的不确定性,当标签是均匀分布 时,non-full bag B i 的不确定度更高, 之间的差异最小。
三、贝叶斯网络分类器
在出现数据丢失时,结构期望最大化策略(Structural EM )提 供了一个合适的框架来学习贝叶斯网络。 它包括网络结构和模型参数 的学习。 贝叶斯网络是一种概率网络,它是基于概率推理的图形化网络, 而贝叶斯公式则是这个概率网络的基础。 贝叶斯网络是基于概率推理 的数学模型,所谓概率推理就是通过一些变量的信息来获取其他的概 率信息的过程,基于概率推理的贝叶斯网络(Bayesian network)是为 了解决不定性和不完整性问题而提出的, 它对于解决复杂设备不确定 性和关联性引起的故障有很的优势,在多个领域中获得广泛应用。 贝叶斯网络的建造是一个复杂的任务, 需要知识工程师和领域专 家的参与。在实际中可能是反复交叉进行而不断完善的。 面向设备故 障诊断应用的贝叶斯网络的建造所需要的信息来自多种渠道, 如设备 手册,生产过程,测试过程,维修资料以及专家经验等。首先将设备 故障分为各个相互独立且完全包含的类别 (各故障类别至少应该具有 可以区分的界限) ,然后对各个故障类别分别建造贝叶斯网络模型, 需要注意的是诊断模型只在发生故障时启动, 因此无需对设备正常状 态建模。 通常设备故障由一个或几个原因造成的, 这些原因又可能由 一个或几个更低层次的原因造成。建立起网络的节点关系后,还需要 进行概率估计。 具体方法是假设在某故障原因出现的情况下,估计该 故障原因的各个节点的条件概率, 这种局部化概率估计的方法可以大 大提高效率。
NB (1)朴素贝叶斯模型
TAN
KDB
朴素贝叶斯模型是一个概率分类器, 它假定预测变量之间都是相 互独立的,每个预测变量都只有一个父类,即类变量 C。这个分类器 可以用下式定义:
c
c arg max p C c p X i xi C c
n
其中 Xi 是第 i (
当提供一个数据集时, 学习贝叶斯网络模型的方法通常需要实现 两步:网络结构的提取和模型参数的估计。在本文中,我们使用贝叶 斯网络模型作为概率分类器。 贝叶斯网络分类器主要分为三种, 朴素 贝叶斯 NB(naive Bayes) 、TAN(tree augmented naive Bayes)和 KDB (K-dependence Bayesian network )分类器。朴素贝叶斯分类器的网 络机构是最简单的,但是它在许多领域都有很好的应用。TAN 和 KDB 是考虑到网络结构复杂度和预测变量之间的条件依赖关系而进一步 得到的。这三种贝叶斯网络模型如下图所示:
环。该算法的伪代码如下:算法 1
1. procedureStructureEM ( D, max P, max S ) 2. D initializeData ( D ) 3. G0 structuralLearning ( D ) 4. i 0 5. repeat 6. 7. 8. 9. 10. 11. 12. 13. 14. 15.
e (e1 , e2 ,...emi ) 表示一个联合分配(joint assignment) 情况,当 e 满足
给定的标签比例时称为有效完成(valid completion) ,其集合记为 Z。此时该有效完成的联合概率为:
1 mi
1e
j 1
mi
j
c
pic
p e | Bi p C e j | X 1 x j1 ,..., X n x jn
0 parametricLearning ( D, Gi )
j0 repeat D completeData ( D, j , Gi )
i 1 parametricLearning ( D, Gi )
j j 1 until (diff ( j , j 1 ) )or ( j max P ) D completeData ( D, j , Gi ) Gi 1 findMaxNeighborStructure( D , Gi ) i i 1
在经典的有监督的分类中,目的是从标记的样本数据集中建立一 个预测的模型,然后给出一个新的未被标记的样本,模型将给其分配 一个已知的类标签。但是也有一些情况,获得标记的样本是困难的。 本文主要研究了利用标签比例学习的分类问题, 提供的数据集是由没 有标记的样本组成,并且这些样本被分成不相关的若干组。每组中属 于某一类的样本比例是已知的。 本文将采用依据 Structural EM 策略的 方法来学习贝叶斯网络分类器并且处理这个分类问题。
j 1
mi
五、基于 SEM 学习贝叶斯网络的四种改进算法
这四种算法是用在 completeData 阶段 (程序第 9 行和 13 行) 的。 PEM:E 是一个概率完成(probabilistic completion), 它表示将样 本 xi 分配给类标签 c,其概率为 Ejc,;PEM 算法就是利用前面的联合 概率公式以及所有的有效完成 e,建立一个概率有效完成 E, 用来填补 丢失数据。Complete Data 需要满足的条件就是 Ejc=Pic. NPEM:在初始化阶段, 样本与类标签配对是随机采用一个有效完成 e。 在数据完成阶段, 考虑所有的有效完成 e,然后选出联合概率最高的, 根据选择的这个有效完成 e,将样本与类标签配对。 MCEM 算法:在遇到样本量更大更复杂的情况下,前两种方法的计算 量就非常大,所以给出了 MCEM 算法。它是采用 Mark Chain Monte Carlo(MCMC)过程在数据完成阶段获得一个近似的概率完成。
c arg max p C c p X i xi i i , C c
c n
其中 i 是 X i 的 K 个父类预测变量的一个集合。
i 1
四、SEM 算法原理
在经典有监督的学习中,所有的训练数据都有已知的类标签,所 有的模型参数都可以用极大似然估计来估计。 对于学习贝叶斯网络模 型的特殊情况, 如果网络结构事先是不知道的,那么我们需要增加一 步结构的学习,另外,数据的缺失也增加了学习的复杂度。 在本文中, 我们主要对类变量缺失数据的贝叶斯网络进行参数和 结构的学习。 SEM (Structural Expectation-Maximization)是在传统的 EM (Expectation-Maximization)算法上增加了结构的学习, 可以同时学习 模型的结构和参数。 (1)EM 算法 EM 算法在统计中被用于寻找,依赖不可观察的隐性变量的概率 模型中,参数的最大似然估计。它是一个迭代过程,可以在缺失部分 数据的情况下获得最大似然参数,也可以用来填补缺失的数据。 每一 次迭代包括两个步骤,y 被认为是观测变量,x 被看做完整数据,θ 被看做是模型参数的实际向量,是未知的。第 k+1 次迭代如下, E 步骤,利用参数的当前估计值获得对数似然函数的期望, θ θ 直到参数估计值收敛到一个稳定值。 θ (2)SEM 算法 它是在传统 EM 算法的参数学习循环外部加了一个结构学习的循 θ θ θ θ M 步骤, 最大化期望, 获得参数的下一次估计值, 如此反复迭代,
) 个预测变量,C 是类变量, c 是一个类标签。
i 1
对于这个模型,参数的学习仅仅包括概率 p(c)的学习和条件概率 p(xi∣c)的学习,朴素贝叶斯模型不需要进行结构学习,因为它有固 定的结构。 (2)TAN 模型 TAN 模型允许预测变量间有依赖关系,但是每个预测变量最多只 有两个父类,一个是类变量,另一个是预测变量。分类规则可以被定 义为下式:
PMEM:是一个综合的方法,当样本量较少时,采用 PEM 方法,当样本 量大时,采用 MCEM 方法。 六、本次收获 通过这次模式识别算法的学习, 让我们了解到了书上所没有的一 些算法, 对模式识别的算法有了更进一步的认识, 在完成课程设计的 过程中,我们遇到了很多困难,包括贝叶斯网络模型的学习,还有 SEM 算法的实现,我们都花费了很多时间去学习,然后我们的能力也 都得到了一定的提升,对 matlab 的使用也更加熟练,为以后的学习 和研究都有很大的帮助,同时感谢梁老师这个学期对我们的辅导,让 我们在学习上得到了提升, 我们以后会更加努力学习, 掌握专业技能, 争取在研究生阶段学到更多的知识,使自己得到最大的提升。
模式识别报告
题 目: Learning Bayesian network classifiers from label proportions 组 员: *** ***
Learning Bayesian network classifiers from label proportions 利用标签比例学习贝叶斯网络分类器 一、内容简介
c arg max p C c p X i xi X j x j , C c
c n
其中 Xj 是 Xi 的预测变量父类。 (3)KDB 模型
i
KDB 结构依据朴素贝叶斯分类器,但是除了类变量作为父类以外,仍 允许每个预测变量最多有 K 个预测变量作为父类。由此,可以得到 TAN 分类器可以被看做是 1DB 分类器,朴素贝叶斯分类器可以被看做 是 0DB。它可以用下式定义:
16. until (Gi Gi 1 )or (i max S ) 17. return{Gi 1, j } 18.end procedure
