单因素方差分析软件操作
spss软件操作步骤
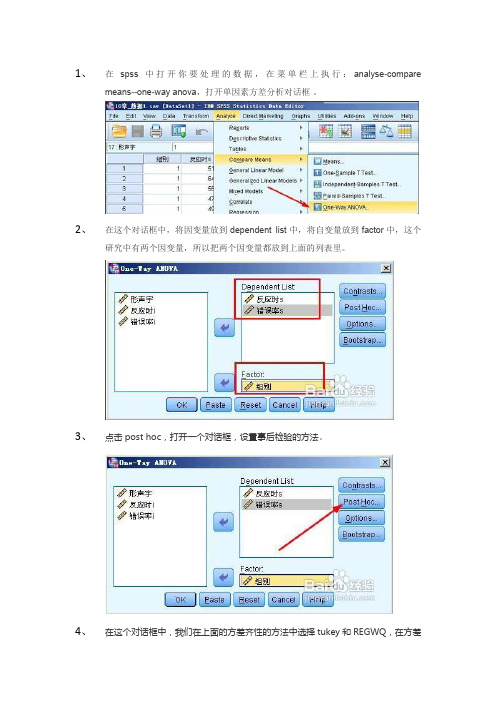
1、在spss中打开你要处理的数据,在菜单栏上执行:analyse-comparemeans--one-way anova,打开单因素方差分析对话框。
2、在这个对话框中,将因变量放到dependent list中,将自变量放到factor中,这个研究中有两个因变量,所以把两个因变量都放到上面的列表里。
3、点击post hoc,打开一个对话框,设置事后检验的方法。
4、在这个对话框中,我们在上面的方差齐性的方法中选择tukey和REGWQ,在方差不齐性的方法中选择dunnetts,点击continue继续。
5、回到了anova的对话框,点击options按钮,设置要输出的基本结果。
6、这里选择描述统计结果和方差齐性检验,点击continue按钮。
7、点击ok按钮,开始处理数据。
8、我们看到的结果中,第一个输出的表格就是描述统计,从这个表格里我们可以看到均值和标准差,在研究报告中,通常要报告这两个参数。
9、接着看方差齐性检验,方差不齐性的话是不能够用方差齐性的方法来检验的,还好,这里显示,显著性都没有达到最小值0.05,所以是不显著的,这证明方差是齐性的。
10、接着看单因素方差分析表,反应时sig值不显著,而错误率达到了显著的水平,这说明实验处理对错误率产生了影响,但是对反应时没有影响。
11、接着看事后检验,因为反应时是没有显著差异的,所以就不必再看反应时的事后检验,直接看错误率的事后检验,从图中标注的红色方框可以看到,第一组和二三组都有显著的差异,而第二组和第三组没有显著差异。
关于dunnet方法,它适合在方差不齐性的时候使用,因为方差齐性,不必去看这个方法的检验结果了。
12、最后我们看这个表格,这里有两个检验方法都是在方差齐性的时候使用的,我们从红色方框可以看出第一组分为一组,第二三组分为一组,它的意思是上面的结果是一致的。
单因素方差分析spss

单因素方差分析spss
一、什么是单因素方差分析
单因素方差分析(ANOVA)是一种统计技术,用于检测是否存在任何
显著差异,以及这些差异在哪里。
它旨在测定两个或更多样本之间的
差异,样本是来自不同类别的几个组的变量,这些组别被称为因素。
二、单因素方差分析的作用
单因子方差分析的作用是确定某一变量的一个或多个不同水平之间的
统计性差异。
当检验不同类别内的水平差异时,单因素方差分析是最
常用的技术。
三、单因素方差分析使用SPSS
SPSS是一个很容易使用的统计分析软件,可以应用单因素方差分析来
检验样本之间的差异。
下面是使用SPSS进行单因素方差分析的步骤:
1. 打开SPSS,打开新建数据表,输入各个组别的名称以及对应的分数。
2. 在“分析”菜单中,点选“生成”,然后选择“单因素方差分析”。
3.在“因变量”框中输入需要分析的变量,在“因素”框中输入需要比较的分组。
4. 点击OK运行,等待完成,结果就直接在SPSS统计屏幕上显示出来了。
五、结论
单因素方差分析是一种强大的统计技术,可以用来帮助研究人员确定是否存在任何显著差异。
使用SPSS来完成单因素方差分析也是比较简单的,只需要正确输入变量,点击“分析”和“生成”,等待报告显示结果就可以了。
SPSS单因素方差分析步骤-图文

SPSS单因素方差分析步骤-图文SPSS(Statistical Package for the Social Sciences)是一种常用的统计分析软件,可以用于进行各种统计分析,包括单因素方差分析。
单因素方差分析是一种用于比较三个或更多组之间平均值差异的统计方法。
下面是使用SPSS进行单因素方差分析的步骤:1.载入数据:打开SPSS软件,并导入数据文件。
可以通过“File”菜单中的“Open”选项来导入已有的数据文件,或是通过“File”菜单中的“New Data”选项创建新的数据文件。
2.数据检查:在进行方差分析之前,需要对数据进行检查,确保数据符合方差分析的假设要求。
主要包括以下几个方面:- 数据的正态性:使用“Explore”功能可以进行直方图和正态性检验。
在菜单栏中选择“Analyze”-“Descriptive Statistics”-“Explore”,然后选择需要检查的变量,并将其拖放到“Dependent List”框中。
点击“Plots”选项卡,勾选“Normality plots with tests”,然后点击“OK”进行正态性检验。
- 数据的同方差性:使用“Explore”功能可以进行散点图和相关统计检验。
同样地,在“Explore”对话框的“Plots”选项卡中,勾选“Scatter/Matrix”选项,并在“Options”选项卡中勾选“Flagextreme cases”,然后点击“OK”进行散点图和异常值检查。
-异常值:通过观察数据的散点图或是通过计算异常值统计量,可以确定是否存在异常值。
3.单因素方差分析:使用“Analyze”菜单中的“General Linear Model”选项来进行单因素方差分析。
在“General Linear Model”对话框中,将需要进行分析的因变量拖到“Dependent Variable”框中,将独立变量拖到“Fixed Factor(s)”框中,然后点击“OK”进行分析。
Excel进行单因素方差分析的步骤

Excel进行单因素方差分析的步骤Excel是一种功能强大的电子表格软件,可以用于进行各种数据分析,包括单因素方差分析。
单因素方差分析是一种常用的统计方法,用于比较不同组之间的均值是否存在显著差异。
下面是在Excel中进行单因素方差分析的步骤:步骤1:准备数据首先,需要准备好用于分析的数据。
假设我们有一个实验,分为三个组,每个组有若干个观测值。
我们需要将这些观测值依次输入到Excel的一些工作表中。
步骤2:计算各组的均值和总均值在Excel中,可以使用平均值函数(AVERAGE)计算每个组的均值。
将这些均值记录在另一列或另一个工作表中。
然后,使用平均值函数计算所有组的总均值。
步骤3:计算组内平方和和组间平方和使用Excel的平方和函数(SUMSQ)来计算每个组的组内平方和。
组内平方和可以通过将每个观测值与其对应组的均值之差的平方相加来计算。
然后,使用平方和函数计算组间平方和。
组间平方和可以通过将每个组的均值与总均值之差的平方乘以该组的观测数量相加来计算。
步骤4:计算均方计算组内平方和和组间平方和的均方,即将组内平方和除以自由度(观测数量减去组数)得到组内均方,将组间平方和除以组数减1得到组间均方。
步骤5:计算F值使用Excel的F分布函数(FDIST)来计算F值。
F值可以通过将组间均方除以组内均方来计算。
步骤6:确定显著性水平和临界值根据实验设计和显著性水平的设置,确定F分布的临界值。
在Excel 中,可以使用F分布的临界值函数(FINV)来计算临界值。
步骤7:进行假设检验根据F值和临界值的比较结果,进行假设检验。
如果F值大于临界值,则可以拒绝原假设,即组均值存在显著差异。
如果F值小于等于临界值,则不能拒绝原假设,即组均值没有显著差异。
步骤8:进行事后比较(可选)如果在步骤7中发现组均值存在显著差异,可以使用Excel的多重比较方法,如Bonferroni校正、Tukey HSD等,进行事后比较。
单因素方差分析spss

单因素方差分析 SPSS简介SPSS(统计软件包社会科学)是一款功能强大的统计软件,广泛应用于社会科学研究领域。
在此文档中,我们将介绍如何使用SPSS进行单因素方差分析(One-way ANOVA)。
单因素方差分析单因素方差分析是一种统计方法,用于比较两个或更多个组之间的均值差异。
它的基本原理是将总体均值差异分解为组内变异和组间变异两部分。
通过比较组间变异与组内变异的大小,我们可以判断组之间是否存在显著差异。
在进行单因素方差分析之前,我们需要满足以下前提条件: 1. 数据应该来自正态分布的总体。
2. 等方差性:各组之间的方差应该是相等的。
3. 独立性:不同组之间的个体应该是相互独立的。
SPSS使用步骤以下是在SPSS中进行单因素方差分析的步骤。
步骤1:导入数据首先,打开SPSS软件并导入包含需要进行单因素方差分析的数据的文件。
选择“打开文件”选项,然后选择相应的数据文件。
步骤2:设置变量在SPSS中,我们需要将需要进行单因素方差分析的变量设置为“因子变量”(Factor Variable)。
选择“数据”菜单中的“变量视图”,然后选择需要进行单因素方差分析的变量,在“类型”一栏中选择“因子”。
步骤3:进行单因素方差分析选择“分析”菜单中的“比较手段”选项,然后选择“单因素方差”。
步骤4:指定变量在单因素方差分析对话框中,将需要进行分析的因子变量移动到“因子”框中。
步骤5:选项设置在单因素方差分析对话框中,可以设置一些可选参数,如:显示描述性统计信息、绘制盒须图等。
根据需要对这些选项进行设置。
步骤6:结果解读点击“确定”按钮后,SPSS将执行单因素方差分析并生成结果输出。
在输出窗口中,可以看到各组的均值、标准差和方差等统计指标。
同时,还会显示组间变异和组内变异的F统计量、p值和显著性水平。
结论单因素方差分析是一种用于比较多个组间均值差异的统计方法。
通过SPSS软件,我们可以轻松地进行单因素方差分析,并获取分析结果。
spss方差分析报告操作示范-步骤-例子

第五节方差分析的SPSS操作一、完全随机设计的单因素方差分析1.数据采用本章第二节所用的例1中的数据,在数据中定义一个group变量来表示五个不同的组,变量math表示学生的数学成绩。
数据输入格式如图6-3(为了节省空间,只显示部分数据的输入):图 6-3 单因素方差分析数据输入将上述数据文件保存为“6-6-1.sav”。
2.理论分析要比较不同组学生成绩平均值之间是否存在显著性差异,从上面数据来看,总共分了5个组,也就是说要解决比较多个组(两组以上)的平均数是否有显著的问题。
从要分析的数据来看,不同组学生成绩之间可看作相互独立,学生的成绩可以假设从总体上服从正态分布,在各组方差满足齐性的条件下,可以用单因素的方差分析来解决这一问题。
单因素方差分析不仅可以检验多组均值之间是否存在差异,同时还可进一步采取多种方法进行多重比较,发现存在差异的究竟是哪些均值。
3.单因素方差分析过程(1)主效应的检验假如我们现在想检验五组被试的数学成绩(math)的均值差异是否显著性,可依下列操作进行。
①单击主菜单Analyze/Compare Means/One-Way Anova…,进入主对话框,请把math选入到因变量表列(Dependent list)中去,把group选入到因素(factor)中去,如图6-4所示:图6-4:One-Way Anova主对话框②对于方差分析,要求数据服从正态分布和不同组数据方差齐性,对于正态性的假设在后面非参数检验一章再具体介绍;One-Way Anova可以对数据进行方差齐性的检验,单击铵钮Options,进入它的主对话框,在Homogeneity-of-variance项上选中即可。
设置如下图6-5所示:图6-5:One-Way Anova的Options对话框点击Continue,返回主对话框。
③在主对话框中点击OK,得到单因素方差分析结果4.结果及解释(1)输出方差齐性检验结果Test of Homogeneity of VariancesMATHLevene Statistic df1 df2 Sig.1.238 4 35 .313上表结果显示,Levene方差齐性检验统计量的值为1.238,Sig=0.313>0.05,所以五个组的方差满足方差齐性的前提条件,如果不满足方差齐性的前提条件,后面方差分析计算F统计量的方法要稍微复杂,本章我们只考虑方差齐性条件满足的情况。
用SPSS进行单因素方差分析和多重比较

用SPSS进行单因素方差分析和多重比较在SPSS中进行单因素方差分析和多重比较可以帮助研究人员分析各组之间的差异,并确定是否存在显著性差异。
本文将详细介绍如何使用SPSS进行单因素方差分析和多重比较。
一、单因素方差分析1.数据准备首先,将数据导入SPSS软件。
确保每个观测值都位于独立的行中,并且将每个因素作为一个变量列。
确保每个变量的测量水平正确设置。
对于要进行单因素方差分析的变量,应该是连续型变量。
2.描述性统计在执行方差分析之前,我们需要进行描述性统计,以了解每个组的均值、标准差和样本数量。
在SPSS中,可以通过选择“统计”菜单,然后选择“描述统计”来执行描述性统计。
在弹出的对话框中,选择想要分析的变量,并选择“均值”和“标准差”。
3.单因素方差分析要进行单因素方差分析,在SPSS中选择“分析”菜单,然后选择“一元方差分析”。
在弹出的对话框中,将要分析的变量移入“因素”框中。
然后,点击“选项”按钮,选择想要输出的结果,如方差分析表和均值表。
最后,点击“确定”执行单因素方差分析。
4.结果解读方差分析表提供了重要的统计信息,包括组间和组内的平方和、自由度、均方、F值和p值。
其中,F值表示组间变异性和组内变异性的比值。
p值表示在原假设下观察到的差异是否显著。
如果p值小于设定的显著性水平(通常为0.05),则可以拒绝原假设,即存在显著差异。
二、多重比较当在单因素方差分析中发现存在显著组间差异时,下一步是进行多重比较,以确定哪些组之间存在显著差异。
1.多重比较检验在SPSS中,可以使用多种方法进行多重比较检验,如Tukey HSD、Bonferroni、LSD等。
这些方法可以通过选择“分析”菜单,然后选择“比较手段”来执行。
在弹出的对话框中,选择要进行比较的变量和方法。
点击“确定”执行多重比较检验。
2.结果解读多重比较结果表提供了各组之间的均值差异估计、标准误差、置信区间和p值。
根据p值,可以确定哪些组之间存在显著差异。
SPSS——单因素方差分析报告详解

SPSS——单因素方差分析来源:李大伟的日志单因素方差分析单因素方差分析也称作一维方差分析。
它检验由单一因素影响的一个(或几个相互独立的)因变量由因素各水平分组的均值之间的差异是否具有统计意义。
还可以对该因素的若干水平分组中哪一组与其他各组均值间具有显著性差异进行分析,即进行均值的多重比较。
One-Way ANOVA过程要求因变量属于正态分布总体。
如果因变量的分布明显的是非正态,不能使用该过程,而应该使用非参数分析过程。
如果几个因变量之间彼此不独立,应该用Repeated Measure 过程。
[例子]调查不同水稻品种百丛中稻纵卷叶螟幼虫的数量,数据如表1-1所示。
表1-1 不同水稻品种百丛中稻纵卷叶螟幼虫数数据保存在“data1.sav”文件中,变量格式如图1-1。
图1-1分析水稻品种对稻纵卷叶螟幼虫抗虫性是否存在显著性差异。
1)准备分析数据在数据编辑窗口中输入数据。
建立因变量“幼虫”和因素水平变量“品种”,然后输入对应的数值,如图1-1所示。
或者打开已存在的数据文件“data1.sav”。
2)启动分析过程点击主菜单“Analyze”项,在下拉菜单中点击“Compare Means”项,在右拉式菜单中点击“0ne-Way ANOVA”项,系统打开单因素方差分析设置窗口如图1-2。
图1-2 单因素方差分析窗口3)设置分析变量因变量:选择一个或多个因子变量进入“Dependent List”框中。
本例选择“幼虫”。
因素变量:选择一个因素变量进入“Factor”框中。
本例选择“品种”。
4)设置多项式比较单击“Contrasts”按钮,将打开如图1-3所示的对话框。
该对话框用于设置均值的多项式比较。
图1-3 “Contrasts”对话框定义多项式的步骤为:均值的多项式比较是包括两个或更多个均值的比较。
例如图1-3中显示的是要求计算“1.1×mean1-1×mean2”的值,检验的假设H0:第一组均值的1.1倍与第二组的均值相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
单因素方差分析表
(基本结构)
误差来源
平方和 自由度 (SS) (df)
均方 (MS)
F值
P值
F 临界值
组间
MSA
(因素影响) SSA
k-1
MSA MSE
组内 (误差)
SSE
n-k MSE
总和 SST n-1
用Excel进行方差分析
(Excel分析步骤)
第1步:选择“数据 ”下拉菜单 第2步:选择【数据分析】选项 第3步:在分析工具中选择【单因素方差分析】 ,
航空业与家电业均值有显著差异
感谢下 载
2. 计算检验的统计量: xi x j
3. 计算LSD
LSD t 2
MSE
1 ni
1 nj
4. 决策:若 xi x j LS,D拒绝H0;若 xi x j LSD, 不拒绝H0
多重比较分析
(例题分析)
第1步:提出假设
▪ ▪ ▪ ▪ ▪ ▪
检检检检检检验验验验验验123456::::::HHHHHH00000::: 0: ::mmmmmm232111
检验3: 检验4:
x1 x4
49 59
Hale Waihona Puke 10▪ 检验5: x2 x3 48 35 13
▪ 检验6: x2 x4 48 59 11
x3 x4 35 59 24
方差分析中的多重比较
(例题分析)
第3步:计算LSD
▪ 检验1:
11
▪ 检验2:LSD1 2.093 ▪ 检验3:LSD2 2.093
m2 m3 m4 m3 m4 m4
,H1:m1 ,H1:m1
,H1:m1 ,H1:m 2 ,H1:m2
,H1:m3
m2 m3 m4 m3 m4 m4
方差分析中的多重比较
(例题分析)
第2步:计算检验统计量
▪ 检验1:
▪ ▪ ▪
检验2:
x1
x1
x2
x3
49 48
49 35
1
14
5
1) 5
15.80
方差分析中的多重比较
(例题分析)
第4步:作出决策
x1 x2 1 13.90
x1 x3 14 14.63 x1 x4 10 14.63 x2 x3 13 15.13 x2 x4 11 15.13
x3 x4 24 15.80
不能认为零售业与旅游业均值之间有显 著差异 不能认为零售业与航空公司均值之间有 显著差异 不能认为零售业与家电业均值之间有显 著差异 不能认为旅游业与航空业均值之间有显 著差异 不能认为旅游业与家电业均值之间有显 著差异
2. 可采用Fisher提出的最小显著差异方法,简写 为LSD
3. LSD方法是对检验两个总体均值是否相等的t 检验方法的总体方差估计加以修正(用MSE来 代替)而得到的
多重比较的步骤
1. 提出假设 ▪ H0: mi=mj (第i个总体的均值等于第j个总体的均值)
▪ H1: mimj (第i个总体的均值不等于第j个总体的均值)
142.526316 ( ) 13.90 76
142.526316 (1 1) 14.63 75
▪ 检验4:LSD3 LSD2 ▪ 检验5:LSD4 2.093
14.63
142.526316
(
1 6
1) 5
15.13
▪ 检验6:LSD5 LSD6
LSD4 15.13 2.093 142.526316 (1
然后选择【确定】 第4步:当对话框出现时
在【输入区域 】方框内键入数据单元格区域 在【】方框内键入0.05(可根据需要确定) 在【输出选项 】中选择输出区域
方差分析中的多重比较
(multiple comparison procedures)
多重比较的意义
1. 通过对总体均值之间的配对比较来进一步检 验到底哪些均值之间存在差异
