面面垂直的判定习题详细答案

合集下载

面面垂直答案

1.已知如图， P 平面ABC PA=PB=PC / APB=/ APC=60，/ BPC=90 ° 求证：平面 ABC!平面 PBC线，然后证明直线与另一平面 D,证明AD 垂直平PBC 即可证明：取BC 中点D 连结AD PD •/ PA=PB / APB=60•••△ PAB 为正三角形同理△ PAC 为正三角形设 PA=a在 RT A BPC 中, PB=PC=a BC= -2a在 A ABC 中 AD= AB 2 BDA D+P[5= —a=a =AP•A APD 为直角三角形即AD 丄DP 又••• AD 丄 BC • AD 丄平面PBC •平面ABCL 平面PBC12 .如图（1）在直角梯形 ABCD 中, AB//CD , AB AD 且AB=AD^ CD=1现以 AD 为一边向梯形外作正方形 ADEF 然后沿AD 将正方形翻拆，使平面 ADEF 与平面ABCD 互相垂直如图（2）。

【答案】【解析】要证明面面垂直，要在其呈平面内找一条垂直即可。

显然 BC 中点(1) 求证平面BDE 平面BEC(2) 求直线BD 与平面BEF 所成角的正弦值。

又在 BCD 中，DB BC 2， DC 2，三边满足勾股定理， BC BD 。

由线面垂直的判定定理即证得结论。

(2)因为DB ,2,只需求出点D 到平面BEF 的距离也是点 A 到平面BEF 的距离,易证出 AD//EF ， AD 平面BEF ，由面面垂直的判定定理得平面ABF 平面BEF ， ABF 中BF 边上的高就是点 A 到平面BEF 的距离。

根据线面角的定义可求直线BD与平面BEF 所成角的正弦值。

(1)求证：EF//平面CBD ; (2)求证：平面 CAAC 丄平面CBD . 【答案】(I)略(H )略【解析】(1 )证明：连结 BD 在长方体AC 1中BD// B 1D 1.又 Q E 、F 为棱 AD AB 的中点，/. EF//BD . /• EF//B 1D 1. ................ 4 分又 BD 平面 CB 1D 1, EF 平面 CBD ,： EF//平面 CBD................ 7 分 (2) Q 在长方体 AC 1中，AA 丄平面A B 1C 1D ，而BD 平面ABC D ,「. AA 丄B D .…9分又Q 在正方形 A B C D 中，A C X B 1 D ，: B D 丄平面CAAC . 又Q B 1 D 平面CBD ,：平面 CAAC 丄平面 CBD .……1 4分 4 .如图，四棱锥P ABCD 中，底面ABCD 为平行四边形，AB 2AD 2, BD .3, PD 丄底面 ABCD .【答案】⑴证见解析⑵sinAH 1 BD 2【解析】(1 )由折前折后线面的位置关系得ED平面ABCD ，所以EDBC ，3 •(本小题满分14分)如图，在正方体 ABC B A i BiGD 中，E 、F 为棱 AD AB 的中点. EA 1D 1FBC（i）证明：平面PBC 平面PBD ；【解析】本试题主要是考查了面面垂直的证明和二面角与线面角的求解的综合运用。

平面与平面垂直的判定基础练习题含答案解析

2.3.2 平面与平面垂直的判定基础练习题（含答案解析）1．如果一个二面角的两个半平面分别平行于另一个二面角的两个半平面，则这两个二面角的关系是()A．相等B．互补C．相等或互补D．不能确定解析：选C.当这两个二面角的两个面均同向或均异向时，它们相等；当这两个二面角的两个面中，一组同向，另一组异向时，它们互补．2．在四棱锥P－ABCD中，已知P A⊥底面ABCD，且底面ABCD为矩形，则下列结论中错误的是()A．平面P AB⊥平面P ADB．平面P AB⊥平面PBCC．平面PBC⊥平面PCDD．平面PCD⊥平面P AD解析：选C.由面面垂直的判定定理知：平面P AB⊥平面P AD，平面P AB⊥平面PBC，平面PCD⊥平面P AD，A、B、D正确．3．如果直线l、m与平面α、β、γ之间满足：l＝β∩γ，l∥α，m⊂α和m⊥γ，那么() A．α⊥γ且l⊥m B．α⊥γ且m∥βC．m∥β且l⊥m D．α∥β且α⊥γ解析：选A.如图，平面α为平面AD1，平面β为平面BC1，平面γ为平面AC，∵m⊂α，m⊥γ，由面面垂直的判定定理得α⊥γ，又m⊥γ，l⊂γ，由线面垂直的性质得m⊥l.4.在正四面体P－ABC中，D、E、F分别是AB、BC、CA的中点，则下面四个结论中不成立的是()A．BC∥平面P DFB．DF⊥平面P AEC．平面PDF⊥平面ABCD．平面P AE⊥平面ABC解析：选C.可画出对应图形(图略)，则BC∥DF，又DF⊂平面PDF，BC⊄平面PDF，∴BC∥平面PDF，故A成立；由AE⊥BC，BC∥DF，知DF⊥AE，DF⊥PE，∴DF⊥平面P AE，故B成立；又DF⊂平面ABC，∴平面ABC⊥平面P AE，故D成立．5．(2013·德州高一检测)已知P A⊥矩形ABCD所在的平面，如图所示，图中互相垂直的平面有()A．1对B．2对C．3对D．5对解析：选D.∵DA⊥AB，DA⊥P A，AB∩P A＝A，∴DA⊥平面P AB，同理BC⊥平面P AB，AB⊥平面P AD，DC⊥平面P AD，∴平面AC⊥平面P AD，平面AC⊥平面P AB，平面PBC⊥平面P AB，平面PDC⊥平面P AD，平面P AB⊥平面P AD.6．若P是△ABC所在平面外一点，而△PBC和△ABC都是边长为2的正三角形，P A ＝6，那么二面角P－BC－A的大小为________．解析：取BC的中点O，连接OA，OP，则∠POA为二面角P－BC－A的平面角，OP ＝OA＝3，P A＝6，所以△POA为直角三角形，∠POA＝90°.答案：90°7.如图所示，在四棱锥P－ABCD中，P A⊥底面ABCD，且底面各边都相等，M是PC上的一动点，当点M满足________时，平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)解析：连接AC，则AC⊥BD.∵P A⊥底面ABCD，BD⊂面ABCD，∴P A⊥BD.∵P A∩AC＝A，∴BD⊥面P AC，∴BD⊥PC.∴当DM⊥PC(或BM⊥PC)时，即有PC⊥平面MBD，而PC⊂平面PCD，∴平面MBD⊥平面PCD.答案：DM⊥PC(或BM⊥PC等)8．经过平面α外一点和平面α内一点与平面α垂直的平面有________个．解析：设面外的点为A，面内的点为B，过点A作面α的垂线l，若点B恰为垂足，则所有过AB的平面均与α垂直，此时有无数个平面与α垂直；若点B不是垂足，则l与点B 确定唯一平面β满足α⊥β.答案：1或无数9．点P是菱形ABCD所在平面外一点，且P A＝PC，求证：平面P AC⊥平面PBD.证明：如图所示，连接AC，BD交于点O，连接PO，∵四边形ABCD是菱形，∴BD⊥AC，又∵AO＝OC，P A＝PC，∴PO⊥AC.∵BD∩PO＝O，∴AC⊥平面PBD.又AC⊂平面P AC，∴平面P AC⊥平面PBD.10．如图所示，四边形ABCD是平行四边形，直线SC⊥平面ABCD，E是SA的中点，求证：平面EDB⊥平面ABCD.证明：连接AC，交BD于点F，连接EF，∴EF是△SAC的中位线，∴EF∥SC.∵SC⊥平面ABCD，∴EF⊥平面ABCD.∵EF⊂平面EDB，∴平面EDB⊥平面ABCD.。

立体几何第六讲面面垂直练习题(含答案)

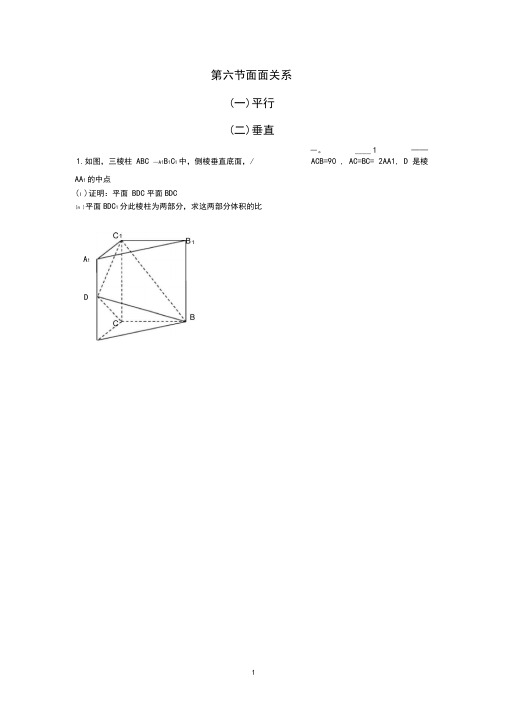
第六节面面关系(一)平行(二)垂直―。

____ 1 ——ACB=90 , AC=BC= 2AA1, D 是棱1.如图，三棱柱ABC —A1B1C1中，侧棱垂直底面，/AA1的中点(I )证明：平面BDC平面BDC(n )平面BDC1分此棱柱为两部分，求这两部分体积的比A1D2.12012高考江西文19](本小题满分12分)如图，在梯形ABCD中，AB //CD, E, F是线段AB上的两点，且DE^AB, CFXAB ,AB=12 , AD=5 , BC=4 后,DE=4.现将△ ADE , △ CFB 分别沿 DE, CF折起，使A, B两点重合与点G,得到多面体CDEFG.(1)求证：平面DEGL平面CFG;(2)求多面体CDEFG的体积。

3.如图，已知空间四边形. ______ .中，BC AC,AD BD , E是AB的中点。

求证：(1) AB 平面CDE;(2)平面CDE 平面ABC。

4.如图，在正方体ABCD ABQ1D1中，E是AA1的中点.(1)求证：A1C//平面BDE；(2)求证：平面A1AC 平面BDE .5.已知四棱锥P—ABCD ,底面ABCD 是菱形, DAB 60 , PD 平面ABCD , PD=AD ,点E为AB中点，点F为PD中点.(1)证明平面PEDL平面PAB;(2)求二面角P—AB—F的平面角的余弦值第六节面面关系答案（一）平行（二）垂直1 .【命题意图】本题主要考查空间线线、线面、面面垂直的判定与性质及几何体的体积计算，考查空间想象能力、逻辑推理能力，是简单题^【解析】（I ）由题设知 BC± CC i ,BC±AC, CC 1 AC C , BC 面 ACC 1A 1,又・ DC 1 面 ACC 1A ，•一 DC 1 BC ,由题设知 A 1DC 1 ADC 450, /. CDC 1=900,即 DC 1 DC ,又 DC BC C , DC 1L 面 BDC , DC 1 面 BDC 1,，面 BDC ，面 BDC 1 ;1121 (n)设棱锥B DACC 1的体积为V 1, AC =1,由题意得，V 1 = — —— 11=—,3 22由三棱柱ABC A 1B 1C 1的体积V =1 ,・♦・平面BDC 1分此棱柱为两部分体积之比为 1:1.2 .【解析】（1）由已知可得 AE=3 , BF=4,则折叠完后 EG=3 , GF=4 ,又因为EF=5,所以可得EG GFEG ,即EG 面CFG 所以平面DEG ，平面CFG.••• (V V 1):V 1=1:1, 又因为CF 底面EGF ,可得CF过G 作GO 垂直于EF , 侑CC1 12二 S 正方形DECF GO -55 — 3 3 53.证明：(1) BC AC CEAE BE GO 即为四棱锥 G-EFCD20AB 的高，所以所求体积为同理, AD AE BD BEDE AB又「 CE DE EAB 平面CDE（2）由（1）有AB平面CDE又「 AB 平面ABC ,，平面CDE 平面ABC4 .证明：（1）设 AC BD 0,E 、O 分别是AA 、AC 的中点，AC // EO又 BD AC , AC 1AAA, BD 平面 A i AC , BD 平面 BDE , 平面 BDE平面A i AC5 . (1)证明：连接BD.AB AD, DAB 60 , ADB 为等边三角形. E 是AB 中点， AB DE.PD 面 ABCD, AB 面 ABCD , AB PD.DE 面 PED, PD 面 PED, DE PD D, AB 面 PED.AB 面 PAB, 面PED 面 PAB.(2)解： AB 平面 PED, PE 面 PED, AB 连接 EF, EF PED, AB EF.PEF 为二面角P —AB —F 的平面角.设 AD=2,那么 PF=FD=1, DE=V 3. 在 PEF 中,PE J7,EF 2, PF 1,即二面角P —AB —F 的平面角的余弦值为 27.14又AC 平面BDE , EO 平面BDE ,A i C //平面 BDE⑵••• AA 平面 ABCD , BD平面 ABCD , AA 1 BDcos PEF(17) 2 22 1 5J ； 2 2.7 14PE.。

面面垂直的性质习题详细答案

变种2
如果一个平面内的两条相交直线与另一个平面垂直，求证这两个平面垂直。
提高题
如果一个平面内的两条相交直线与另一个平面垂直，求证这两个平面的交线与原直线垂直。
综合பைடு நூலகம்解析与解答
• 综合题1：已知一个平面内的两条相交直线与另一个平面垂直，求证这两个平面的交线与原直线垂直。
综合题解析与解答
面面垂直的性质习题详细答案
contents
目录
• 面面垂直的性质概述 • 习题解析 • 习题解答技巧 • 面面垂直的性质习题答案 • 习题拓展与提高
01 面面垂直的性质概述
定义与定理
定义
两个平面互相垂直，当且仅当一个平面内的任意直线都与另一个平面垂直。
定理
如果两个平面互相垂直，那么其中一个平面内的任意直线都与另一个平面垂直。
机械工程
在机械设计中，面面垂直的性质常常用于确定零件的安装角度和位置，以确保机器的正常运转。
地理学
在地理学中，地球的经纬线分布和角度计算也涉及到面面垂直的性质，例如在计算地球上的纬度、经度等数值时，需要利用到面面
垂直的性质。
02 习题解析
基础习题解析
总结词
掌握基础概念
题目
两个平面垂直，其中一个平面内有一条直线，那么这条直线与另一个平面的关系是什么？
由于直线a⊥平面α，且直线b⊥直线a，根据面面垂直的性质定理，直线b必然在平面 α内。
中等难度习题答案
总结词
中等难度习题在考察面面垂直性质的基础上，增加了对空间想象能力和推理能力的考察。
题目3
已知平面α与平面β互相垂直，点A属于平面α，点B属于平面β，且AB与两平面的交线分别交于C和D两点，若AC=CD，求证线段BD的长度。

面面垂直证明例题

数学面面垂直例题
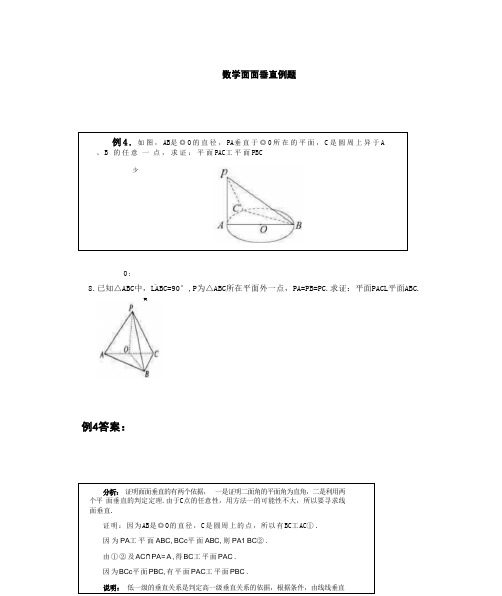
例4.如图，AB是◎O的直径，PA垂直于◎0所在的平面，C是圆周上异于A、B的任意一点，求证：平面PAC工平面PBC
少
8.已知△ABC中，LABC=90°,P为△ABC所在平面外一点，PA=PB=PC.求个依据，一是证明二面角的平面角为直角，二是利用两个平面垂直的判定定理.由于C点的任意性，用方法一的可能性不大，所以要寻求线面垂直.
证明：因为AB是◎O的直径，C是圆周上的点，所以有BC工AC①.
因为PA工平面ABC,BCc平面ABC,则PA1BC②.
由①②及AC∩PA=A,得BC工平面PAC.
因为BCc平面PBC,有平面PAC工平面PBC.
说明：低一级的垂直关系是判定高一级垂直关系的依据，根据条件，由线线垂直一线面垂直→面面垂直.通过这个例题展示了空间直线与平面的位置关系的内在联系，垂直关系的判定和性质共同构成了一个完整的知识体系.
例8答案：取AC的中点为O,连接OP、OB。
AO-OC,PA=PC,故PO垂直AC

面面垂直的判定

三、两个平面互相垂直
两个平面相交,如果它们所成的二面角是直二面角，就说这两个平面相互垂直.Βιβλιοθήκη 记作:
（表示两平面的平行四边形有一组边互相垂直）

问题：
如何检测所砌的墙面和地面是否垂直？
问题：
如何检测所砌的墙面和地面是否垂直？
猜想：
如果一个平面经过了另一个平面的一条垂线，那么这两个平面互相垂直.
A
l
O
10
B

以二面角的棱上任意一点为端点，在两个面上分别引垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角。
O l
O

B
A

B
A
? AOB AOB==
注:（1）二面角的平面角与点的位置无关，只与二面角的张角大小有关。（2）二面角是用它的平面角来度量的，一个二面角的平面角多大，就说这个二面角是多少度的二面角。（3）平面角是直角的二面角叫做直二面角。等角定理：如果一个角的两边和另（4）二面角的取值范围一般规定一个角的两边分别平行，并且方向相为[0°,180°]。同，那么这两个角相等。
又∵CE∩BE=E,
∴SA⊥平面BCE.∵BC 平面BCE，
图2-4-2
∴SA⊥BC.
又∵AD⊥BC,AD∩AS=A,
∴BC⊥平面SAD. ∵SH
平面SAD，∴SH⊥BC.
又∵SH⊥AD,AD∩BC=D, ∴SH⊥平面ABC. 【评析】证明线面垂直，需先有线线垂直，抓住条件中两个等腰三角形共用一条边，抓住公共边的中点，通过作辅助平面，找到所需要的另一条直线.
P C A

的平面，C是圆周上不同于 A,B的任意一点，求证：

面面垂直的性质习题详细答案

2.如图所示，正四棱柱ABCD-A1B1C1D1中，底面边长为2 侧棱长为4，E，F分别为棱AB,BC的中点，EF∩BD=G.
(1)求证：平面B1EF2⊥，平面BDD1B1；
(2)求点D1到平面B1EF的距离.
2.(1)连接AC.∵正四棱柱ABCD-A1B1C1D1的底面是正方形，∴AC⊥BD. 又AC⊥DD1,且BD∩DD1=D,故AC⊥平面BDD1B1， ∵E，F分别为棱AB,BC的中点，故EF∥AC， ∴EF⊥平面BDD1B1， ∴平面B1EF⊥平面BDD1B1.
3a ,
求证:(1)AB⊥平面BCD; (2)平面ACD⊥平面ABD.
【解析】1.∵AD⊥DE,平面ADE⊥平面BCDE, 且平面ADE∩平面BCDE=DE, ∴AD⊥平面BCDE.又BC⊂平面BCDE, ∴AD⊥BC.又BC⊥CD,CD∩AD=D, ∴BC⊥平面ACD,又BC⊂平面ABC, ∴平面ABC⊥平面ACD. 答案：平面ABC⊥平面ACD
4.如图所示，已知平面α⊥平面β， α∩β=l，A∈l，B∈l，AC⊂α， BD⊂β,AC⊥l，BD⊥l，且AB=4， AC=3，BD=12，则CD=_____. 【解析】连接BC,∵AC⊥l,∴BC= 又∵平面α⊥平面β，α∩β=l，BD⊥l, ∴BD⊥平面α，∴BD⊥BC，∴CD= 答案：13
2.∵a∥α,过a作平面γ交α于a′， ∴a′⊥AB. ∵α⊥β，α∩β=AB， ∴a′⊥β， ∴a⊥β.
【思考】在应用面面垂直的性质定理时应注意哪几点？提示：应特别注意三点：(1)两个平面垂直是前提条件；(2)直线必须在其中一个平面内；(3)直线必须垂直于它们的交线.
与面面垂直有关的计算【技法点拨】与面面垂直有关的计算的方法 (1)求角的大小.由所给面面垂直的条件先转化为线面垂直，再转化为线线垂直，一般转化为在三角形中的计算问题. (2)求线段的长度、点到直线或平面的距离以及几何体的体积.求几何体的体积时要注意应用转换顶点法，求线段的长度或点到平面的距离时往往也应用几何体中的转换顶点(等体积)法.

线线垂直、线面垂直、面面垂直的习题及答案解析

线线垂直、线⾯垂直、⾯⾯垂直的习题及答案解析线线垂直、线⾯垂直、⾯⾯垂直部分习及答案1．在四⾯体ABCD 中，△ABC 与△DBC 都是边长为4的正三⾓形．(1)求证：BC ⊥AD ；2如图，在三棱锥S —ABC 中，SA ⊥平⾯ABC ，平⾯SAB ⊥平⾯SBC ．（1）求证：AB ⊥BC ；3.如图，四棱锥P —ABCD 的底⾯是边长为a 的正⽅形，PA ⊥底⾯ABCD ，E 为AB 的中点，且PA=AB ．（1）求证：平⾯PCE ⊥平⾯PCD ；（2）求点A 到平⾯PCE 的距离．4. 如图2-4-2所⽰，三棱锥S —ABC 中，SB=AB ，SC=AC ，作AD ⊥BC 于D ，SH ⊥AD 于H ，求证：SH ⊥平⾯ABC. (第1题)5. 如图所⽰，已知Rt△ABC所在平⾯外⼀点S，且SA=SB=SC，点D 为斜边AC的中点.(1)求证：SD⊥平⾯ABC；(2)若AB=BC，求证：BD⊥平⾯SAC.6. 证明：在正⽅体ABCD－A1B1C1D1中，A1C⊥平⾯BC1DAC7. 如图所⽰，直三棱柱中，∠ACB=90°，AC=1，，侧棱，侧⾯的两条对⾓线交点为D，的中点为M.求证：CD⊥平⾯BDM.8.在三棱锥Ａ－BCD中，BC＝AC，AD＝BD，作BE⊥CD，Ｅ为垂⾜，作AH⊥BE于Ｈ．求证：AH⊥平⾯BCD．9. 如图，过S引三条长度相等但不共⾯的线段SA、SB、SC，且∠ASB=∠ASC=60°，∠BSC=90°，求证：平⾯ABC⊥平⾯BSC．10.如图，在长⽅体ABCD—A1B1C1D1中，AB＝2，BB1＝BC＝1，E为D1C1的中点，连结ED，EC，EB和DB．(1)求证：平⾯EDB⊥平⾯EBC；(2)求⼆⾯⾓E－DB－C的正切值.11：已知直线PA垂直于圆O所在的平⾯，A为垂⾜，AB为圆O的直径，C是圆周上异于A、B的⼀点。

求证：平⾯PAC 平⾯PBC。

2023高考数学复习专项训练《面面垂直的判定》(含解析)

2023高考数学复习专项训练《面面垂直的判定》一、单选题（本大题共12小题，共60分）1.（5分）已知A={ x|3a−1<x<2a+3}，B={ x|x2−x−2⩽0}，A⊆B，则a的取值范围为()A. { a|a⩽−12} B. { a|a⩽12或a⩾0}C. { a|a⩾4}D. { a|a⩽0或a⩾4}2.（5分）定义：设函数f(x)的定义域为D，如果[m,n]⊆D，使得f(x)在[m,n]上的值域为[m,n]，则称函数f(x)在[m,n]上为“等域函数”，若定义域为[1e,e2]的函数g(x)= c x(c>0,c≠1)在其定义域的某个区间上为“等域函数”，则实数c的取值范围为()A. [2e2,1e) B. [2e2,1e]C. [e2e2,e1e] D. [e2e2,e1e)3.（5分）设x、y∈R，则“x≥2且y≥2”是“x2+y2≥4”.（）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既非充分又非必要条件4.（5分）命题p：关于x的不等式ax2+ax−x−1<0的解集为(−∞,−1)∪(1a,+∞)的一个充分不必要条件是().A、a⩽−1B、a>0C、−2<a<0D、a<−2A. a⩽−1B. a>0C. −2<a<0D. a<−25.（5分）函数y=loga (2x−3)+√22(a>0且a≠1)的图像恒过定点P，且点P在幂函数f(x)的图像上，则f(4)=()A. 2B. 12C. 14D. 166.（5分）设ab>0，下面四个不等式：①|a+b|>|a|；②|a+b|<|b|；③|a+b|<|a−b|；④|a+b|>|a|−|b|；正确的是()A. ①和②B. ①和③C. ①和④D. ②和④7.（5分）已知ΔABC 的三个内角A ，B ，C 所对的边分别为a ，b ，c ，若b 2+c 2<a 2，且cos 2A −3sin A +1=0，则sin (C −A)+√32cos (2A −B)的取值范围为 ( )A. (−12,−√34) B. (−12,−√34] C. [0,√34] D. (−23,−12) 8.（5分）函数y =x 2+ln |x|的图象大致为( )A. B.C.D.9.（5分）已知函数f(x)=x 1−|x|(x ∈D)，有下列四个结论：①对任意x ∈D ，f(−x)+f(x)=0恒成立；②对任意m ∈(0,1)，方程|f(x)|=m 有两个不相等的实数根； ③存在函数g(x)使得g(x)的图象与f(x)的图象关于直线y =x 对称； ④对任意k ∈(1,+∞)，函数g(x)=f(x)−kx 在D 上有三个零点．则上述结论中正确的个数为()A. 1B. 2C. 3D. 410.（5分）已知函数f (x )的定义域为R ，f (x +2)为偶函数，f (2x +1)为奇函数，则( )A. f (−12)=0B. f (−1)=0C. f (2)=0D. f (4)=011.（5分）已知定义在R 上的奇函数f(x)，且当x ∈[0,+∞)时，f(x)单调递增，则不等式f(2x +1)+f(1)⩾0的解集是()A. (−∞,1)B. (−1,+∞)C. [−1,+∞)D. (−∞,1]12.（5分）已知集合A ={x|1<x <3}，集合B ={x|log 2(x +1)⩽2}，则A ∪B =()A 、{x|1<x <3}B 、{x|x ⩽3}C 、{x|−1<x <3}D 、{x|1−<x ⩽3} A. {x|1<x <3} B. {x|x ⩽3} C. {x|−1<x <3}D. {x|1−<x ⩽3}二、填空题（本大题共5小题，共25分）13.（5分）函数f(x)=x−1x中，若f（x）=0，则x=__________.14.（5分）某班有36名同学参加数学、物理、化学竞赛小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26，15，13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则只参加物理小组的有__________人，同时参加数学和化学小组的有__________人．15.（5分）写出一个同时具有下列性质①②③的函数f(x)： ______ .①f(x1x2)=f(x1)f(x2)；②当x∈(0,+∞)时，f′(x)>0；③f′(x)是奇函数.16.（5分）已知函数f(x)满足以下条件：①在R上单调递增；②对任意x1，x2，均有f(x1)⋅f(x2)=4f(x1+x2)，则f(x)的一个解析式为 ______.17.（5分）已知等式sin230°+sin230°+sin30°⋅sin30°=34sin220°+sin240°+sin20°⋅sin40°=34sin210°+sin250°+sin10°⋅sin50°=34请你写出一个具有一般性的等式，使你写出的等式包含了已知的等式，这个等式是______.三、解答题（本大题共6小题，共72分）18.（12分）已知集合A={x|1⩽x−1⩽4}，B={x|−2<x⩽3}，C={x|2a−1< x<2a+1}.(1)若x∈C是“x∈A”的充分条件，求实数a的取值范围；(2)若(A∩B)⊆C，求实数a的取值范围．19.（12分）已知函数f(x)=√3sinx+mcosx(m∈R).(Ⅰ)若m=1，求f(π12)的值；(Ⅰ)若m=√6，且f(x)=0，求tan2x.20.（12分）立德中学高一年级共有200名学生报名参加学校团委与学生会组织的社团组织．据统计，参加艺术社团组织的学生有103人，参加体育社团组织的学生有120人(并非每个学生必须参加某个社团).求在高一年级的报名学生中，同时参加这2个社团的最多有多少人？最少有多少人？21.（12分）已知sin(α−β)=12，sin(α+β)=13.(1)证明：tanα+5tanβ=0；(2)计算：tan(α−β)−tanα+tanβtan2α·tan(α−β)的值．22.（12分）在①两个相邻对称中心的距离为π2，②两条相邻对称轴的距离为π2，③两个相邻最高点的距离为，这三个条件中任选一个，补充在下面问题中，并对其求解．问题：函数f(x)=cos(ωx+φ)(ω>0,0<φ<π2)的图象过点(0,12)，且满足________，当α∈(0,π2)时，f(α2)=−√22，求sinα的值．23.（12分）已知函数f(x)=ax−2b x 2+1是定义在[−1,1]上的奇函数，且f(1)=1.(1)求a ，b 的值；(2)判断函数f(x)的单调性并用定义加以证明；(3)求使f(m −1)+f(2m −1)<0成立的实数m 的取值范围．四、多选题（本大题共5小题，共25分） 24.（5分）下列说法正确的是()A. “a >1”是“1a <1”的充分不必要条件B. 命题“∀x >1，x 2<1”的否定是“∃x <1，x 2⩾1”C. “x >1”是“(x −1)(x +2)>0”的必要条件D. 设a ，b ∈R ，则“a ≠0”是“ab ≠0”的必要不充分条件 25.（5分）设a >1，b >1且ab −(a +b)=1，那么( )A. a +b 有最小值2+2√2B. a +b 有最大值2+2√2C. ab 有最小值3+2√2D. ab 有最大值1+√226.（5分）已知x ，y ∈R ，x >0，y >0，且x +2y =1.则下列选项正确的是()A. 1x +1y 的最小值为4√2 B. x 2+y 2的最小值为15 C.x−2y x 2+y 2>1D. 2x+1+4y ⩾427.（5分）已知M 、N 均为实数集R 的子集，且N ∩∁R M =∅，则下列结论中正确的是( )A. M ∩∁R N =∅B. M ∪∁R N =RC. ∁R M ∪∁R N =∁R MD. ∁R M ∩∁R N =∁R M28.（5分）已知函数f(x)=2cos (ωx +ϕ)(ω>0,|ϕ|<π2)的图象上，对称中心与对称轴x =π12的最小距离为π4，则下列结论正确的是( )A. f (x )+f (5π6−x)=0 B. 当x ∈[π6,π2]时，f (x )⩾−√3C. 若g(x)=2cos2x ，则g (x −π6)=f (x )D. 若sin 4α−cos 4α=−45，α∈(0,π2)，则f (α+π4)的值为4−3√35答案和解析1.【答案】C;【解析】解：由题意知B ={ x |−1⩽x ⩽2}， (1)A =∅时，3a −1⩾2a +3，解得a ⩾4，满足题意；(2)A ≠∅时，a <4，由A ⊆B ，即有{2a +3⩽2，解得{a ⩽−12，可得a ∈∅；综上，a ⩾4. 故选：C.分别讨论A 是否为空集，结合集合的关系，可得a 的不等式组，解不等式可得所求范围．此题主要考查集合关系中的含参问题，注意对集合A 分空集和不是空集2种情况进行讨论，属于较易问题．2.【答案】D;【解析】解：由题意得，函数g(x)的图象与直线y =x 在[1e ,e 2]上有两个交点，即方程c x =x 在[1e,e 2]上有两个不等实根，即lnc =lnx x在[1e ,e 2]上有两个不等实根．设函数ℎ(x)=lnx x(1e⩽x ⩽e 2)，ℎ′(x)=1−lnx x 2，当1e⩽x <e 时，ℎ′(x)>0，函数ℎ(x)单调递增；当e <x ⩽e 2时，ℎ′(x)<0，函数ℎ(x)单调递减．所以ℎ(x)在x =e 处取得极大值，也是最大值，为ℎ(e)=1e .又ℎ(1e )=−e,ℎ(e 2)=2e 2，故2e 2⩽lnc <1e ，解得e 2e 2⩽c <e 1e.故选：D.由题意可得函数g(x)的图象与直线y =x 在[1e ,e 2]上有两个交点，即lnc =lnx x在[1e ,e 2]上有两个不等实根．构造函数，通过导数求函数的最值与区间端点值，数形结合求解即可．此题主要考查了导数的新定义问题，考查转化思想，属于中档题．3.【答案】A; 【解析】略4.【答案】null; 【解析】此题主要考查了一元二次不等式的解法，充分必要条件的应用，属于中档题. 先根据命题p 成立的充要条件，求出a 的取值范围，然后根据充分不必要条件的定义结合各选项可得答案.解：由题意命题p 即(ax −1)(x +1)<0的解集为(−∞,−1)∪(1a ,+∞)，即充要条件为{a <0−1⩽1a ，解得a ⩽−1，因为(−∞,−2)⫋(−∞,−1]所以a <−2是a ⩽−1的一个充分不必要条件，故选D.5.【答案】B; 【解析】此题主要考查了对数的恒过定点问题以及幂函数的解析式和求值，属于基础题.将定点代入幂函数解析式，可得a ，进而可求f(4).解：可知函数y =log a (2x −3)+√22(a >0且a ≠1)的图象恒过定点P(2,√22)，令幂函数为f(x)=x a ，代入P 点坐标，可得√22=2a ，则a =−12， f(x)=x −12，则f(4)=4−12=12.故选B.6.【答案】C;【解析】此题主要考查了不等式与绝对值不等式，根据ab >0，逐项判断即可得到答案.解：∵ab >0，∴a 、b 同号，∴ |a +b|>|a|，|a +b|=|a|+|b|，∴①④正确，故选C.7.【答案】A; 【解析】此题主要考查了二倍角公式，解三角形，以及三角恒等变换等内容，需要学生熟练掌握并巧妙变换．由题意，利用二倍角公式将cos2A −3sin A +1=0化成关于sin A 的一元二次方程，解出sin A 的值，利用cos A <0求出A 的取值；将A 的值和B =π−A −C 代入并化简，可以得到关于C 的三角函数，利用三角函数单调性求出值域，即所求．解：因为cos2A −3sin A +1=0，所以1−2sin2A −3sin A +1=0，所以sin A =12或−2(舍)，又因为cos A <0，所以A =5π6，所以sin (C −A)+√32cos (2A −B)=sin (C −5π6)+√32cos [2×−(π−5π6−C)]=sin (C −5π6)+√32sin C =−12cos C ，又因为C ∈(0,π6)，所以cos C ∈(√32,1)，所以−12cos C ∈(−12,−√34) .故选A.8.【答案】A;【解析】此题主要考查了函数图象的识别，关键是掌握函数的奇偶性和函数的单调性和函数值的变化趋势，属于基础题．先求出函数为偶函数，再根据函数值的变化趋势或函数的单调性即可判断．解：∵f(−x)=x 2+ln |x|=f(x)， ∴y =f(x)为偶函数，∴y =f(x)的图象关于y 轴对称，故排除B ，C ，当x >0时，y =x 2+ln x 为增函数，故排除D. 故选A .9.【答案】C;【解析】解：①函数的定义域是{x|x ≠±1},f(−x)+f(x)=−x 1−|−x|+x 1−|x|=0，故①正确；②y =|f(x)|=|x1−|x||={x x−1,x >1x 1−x ,0<x <1−x1+x,−1<x <0−x x+1,x <−1，函数的图象如图所示：y =m 与函数图象有2个交点，故②正确；③设函数g(x)上的任一点为P(x,y)关于y =x 的对称点为(y,x)在函数f(x)上，则x =y 1−|y|，当y >0时，y =xx+1，当y ⩽0时，y =x 1−x，当x =2时，y =23或y =−2，存在一个x 对着两个y 的值，所以不存在函数g(x)使得g(x)的图象与f(x)的图象关于直线v =x 对称，故③不正确； ④x1−|x|−kx =0，当x =0时，满足方程，所以方程的一个实数根是x =0，当x ≠0时，k =11−|x|,|x|=1−1k ，当k >1时，1−1k >0,x =±(1−1k )，)，所以函数有3个零所以满足方程g(x)=f(x)−kx=0的有三个实数根据0,±(1−1k点，故④正确．故正确的个数有3个．故选：C.①根据解析式计算f(−x)+f(x)=0；②画出函数y=|f(x)|的图象，由图象的交点个数判断实数根的个数；③假设存在函数g(x)满足条件，再根据函数的定义，判断选项；④根据f(x)−kx=0，求方程的实数根的个数，再判断定义域上的零点个数．此题主要考查函数的图象和性质，零点，重点考查数形结合分析问题的能力，推理能力，属于中档题型．10.【答案】B;【解析】本题是对函数奇偶性和周期性的综合考查，属于拔高题.推导出函数f(x)是以4为周期的周期函数，由已知条件得出f(1)=0，结合已知条件可得出结论.解：因为函数f(x+2)为偶函数，则f(2+x)=f(2−x)，可得f(x+3)=f(1−x)，因为函数f(2x+1)为奇函数，则f(1−2x)=−f(2x+1)，所以，f(1−x)=−f(x+1)，所以，f(x+3)=−f(x+1)=f(x−1)，即f(x)=f(x+4)，故函数f(x)是以4为周期的周期函数，因为函数F(x)=f(2x+1)为奇函数，则F(0)=f(1)=0，故f(−1)=−f(1)=0，其它三个选项未知.故选B.11.【答案】C;【解析】此题主要考查综合运用函数的单调性与奇偶性解不等式，属于中档题.解：因为函数在[0,+∞)上是增函数，且函数是奇函数，所以函数在(−∞,0)上是增函数，函数在x=0处连续，所以函数在R上是增函数，又f(−1)=−f(1)，所以不等式可化为f(2x+1)⩾−f(1)=f(−1)，所以2x+1⩾−1，解得x⩾−1，即不等式的解集为[−1,+∞).故选C.12.【答案】null;【解析】解：集合A={x|1<x<3}，集合B={x|log2(x+1)⩽2}={x|−1<x⩽3}，则A∪B={x|−1<x⩽3}.故选：D.求出集合A，集合B，利用并集定义能求出A∪B.此题主要考查集合的运算，考查并集定义、不等式性质等基础知识，考查运算求解能力，是基础题．13.【答案】1或-1;【解析】略14.【答案】5;8;【解析】此题主要考查运用集合间的关系确定元素个数问题以及venn图的运用，属于基础题．把集合间的关系利用方程表示出来，再解方程即可．解：由条件知，每名同学至多参加两个小组，故不可能出现一名同学同时参加数学、物理、化学小组，因为参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，所以只参加物理的有15−6−4=5人．设同时参加数学和化学小组的人数有x人，则只参加数学的有26−6−x=20−x，只参加化学的有13−4−x=9−x.又总人数为36人，即20−x+x+6+4+5+9−x=36，所以44−x=36，解得x=8.即同时参加数学和化学小组的人数有8人，15.【答案】f(x)=x2;【解析】此题主要考查了幂函数的求导公式，奇函数的定义及判断，考查了计算能力，属于基础题．函数f(x)=x 2，f(x 1x 2)=(x 1x 2)2=x 12x 22=f(x 1)f(x 2)满足①，求出导函数，可判断满足②③．解：f(x)=x 2时，f(x 1x 2)=(x 1x 2)2=x 12x 22=f(x 1)f(x 2)；当x ∈(0,+∞)时，f′(x)=2x >0；f′(x)=2x 是奇函数．故答案为：f(x)=x 2.16.【答案】f （x ）=2x+2;【解析】解：因为函数f(x)满足对任意x 1，x 2，均有f(x 1)⋅f(x 2)=4f(x 1+x 2)，故考虑基本初等函数中的指数函数，又f(x)在R 上单调递增，则指数函数的底数大于1，所以f(x)的一个解析式为f(x)=2x+2. 故答案为：f(x)=2x+2.由条件②，考虑为基本初等函数中的指数函数，再利用单调性，即可得到答案．此题主要考查了基本初等函数性质的理解与应用，指数函数性质的理解与应用，考查了逻辑推理能力，属于基础题．17.【答案】si n 2α+si n 2（60°-α）+sinα•sin （60°-α）=34;【解析】解：等式的右边为常数34，等式左边的两个角之和为60°，故由归纳推理可知，满足条件的一个结论可以是：sin 2α+sin 2(60°−α)+sinα⋅sin(60°−α)=34.故答案为：sin 2α+sin 2(60°−α)+sinα⋅sin(60°−α)=34.根据两个等式的特点，确定角和角之间的关系，然后利用归纳推理归纳出结论．此题主要考查归纳推理的应用，根据归纳推理，先从条件中确定等式的规律是解决此类问题的基本思路，属于基础题．18.【答案】解：（1）集合A={x|1≤x -1≤4}={x|2≤x≤5}，C={x|2a-1＜x ＜2a+1}， ∵x ∈C 是“x ∈A”的充分条件，∴{2a +1≤52a −1≥2，解得32≤a ≤2， ∴实数a 的取值范围是[32，2]；（2）∵集合A={x|1≤x -1≤4}={x|2≤x≤5}，B={x|-2＜x≤3}，C={x|2a-1＜x ＜2a+1}， ∴A∩B={x|2≤x≤3}，（A∩B ）⊆C ，∴{2a −1<22a +1>3，解得1＜a ＜32， ∴实数a 的取值范围是（1，32）．;【解析】(1)求出集合A ，利用x ∈C 是“x ∈A ”的充分条件，列出不等式组，由此能求出实数a 的取值范围；(2)利用交集定义求出A ∩B ，利用(A ∩B)⊆C ，列出不等式组，由此能求出实数a 的取值范围．此题主要考查集合的运算，考查充分条件、子集、交集定义、不等式性质等基础知识，考查运算求解能力，是基础题．19.【答案】解：（Ⅰ）若m=1，则函数f （x ）=√3sinx+cosx=2sin （x+π6）， ∴f （π12）=2sin π4=√2．（Ⅱ）∵m=√6，f （x ）=√3sinx+√6cosx=0， ∴√3sinx-=-√6cosx ，∴tanx=-√2， ∴tan2x=2tanx 1−tan 2x =2√2．;【解析】(Ⅰ)由题意，利用两角和差的三角公式化简函数f(x)的解析式，从而得到f(π12)的值．(Ⅰ)先由题意求得tanx 的值，再利用二倍角的正切公式，计算tan2x 的值．此题主要考查两角和差的三角公式，二倍角的正切公式，属于基础题．20.【答案】解：由题意：当艺术社团组织的103名学生都参加体育社团组织时，同时参加这2个社团的学生最多，且有103人；当每个学生都参加某个社团时，同时参加这2个社团的学生最少，且有103+120-200=23人，所以同时参加这2个社团的最多有103名学生，最少有23名学生．; 【解析】由题可知当艺术社团组织的学生都参加体育社团组织时，同时参加这2个社团的人数最多，当每个学生都参加某个社团时，同时参加这2个社团的学生最少．此题主要考查集合的应用，考查运算求解能力，属于基础题．21.【答案】解：（1）证明：由条件sin(α−β)=12，sin(α+β)=13，即sinαcosβ−cosαsinβ=12，sinαcosβ+cosαsinβ=13，解得sinαcosβ=512，cosαsinβ=−112，可得tanαtanβ=-5，从而可得tanα=-5tanβ，tanα+5tanβ=0得证．（2）由tan(α−β)=tanα−tanβ1+tanαtanβ，可得tanα-tanβ=tan （α-β）（1+tanαtanβ），∴原式=tan(α−β)−tanα+tanβtan 2αtan(α−β)=tan(α−β)−tan(α−β)(1+tanαtanβ)tan 2αtan(α−β)=−tan(α−β)·tanαtanβtan 2αtan(α−β)=−tanβtanα=15．;【解析】(1)由题意，把所给条件利用两角和差的三角公式展开，化简可得结论． (2)由题意，把两角差的正切公式展开变形，代入要求的式子化简，可得结论．此题主要考查两角和差的三角公式的应用，同角三角函数的基本关系，属于中档题．22.【答案】解：由函数f(x)=cos(ωx +φ)的图象过点(0,12)，得f(0)=cosφ=12，又因为0<φ<π2，所以φ=π3，在①②③三个条件中任选一个，可知最小正周期T =π，根据T =2π|ω|，得ω=2，所以f(x)=cos(2x +π3)，由f(α2)=−√22，得cos(α+π3)=−√22，由α∈(0,π2)，得α+π3∈(π3,5π6)，所以sin(α+π3)=√1−cos 2(α+π3)=√22， sinα=sin[(α+π3)−π3]=sin(α+π3)cos π3−cos(α+π3)sin π3 =√22×12−(−√22)×√32=√2+√64. ;【解析】此题主要考查三角恒等变换和三角函数的图象和性质，属于中档题. 先由f(0)=12求出φ，由三个条件中任选一个，可知最小正周期T =π，得ω=2，求出f(x) ，结合条件以及同角三角函数关系求得sin(α+π3)，再利用两角差的正弦公式即可求解.23.【答案】null; 【解析】(1)由奇函数的性质可得f(0)=0，可求得b 的值，再由f(1)=1可求得a 的值，从而可得a ，b 的值；(2)f(x)在[−1,1]上是增函数，利用增函数的定义即可证明；(3)根据函数的奇偶性与单调性将不等式转化为关于m 的一次不等式，求解即可．此题主要考查函数奇偶性与单调性的综合，考查不等式的解法，考查转化思想与运算求解能力，属于中档题．24.【答案】AD;【解析】解：对于A ：当“a >1”时“1a <1”成立，反之不成立，故“a >1”是“1a <1”的充分不必要条件，故A 正确；对于B ：命题“任意x >1，都有x 2<1”的否定是“存在x >1，使得x 2⩾1”故B 不正确；对于C ：x >1，则(x −1)(x +2)>0，但由(x −1)(x +2)>0，不能推出x >1，故“x >1”是“(x −1)(x +2)>0”的充分不必要条件，故C 不正确；对于D ：设a ，b ∈R ，则“a ≠0”推不出“ab ≠0”，由“ab ≠0”能够推出“a ≠0”，故“a ≠0”是“ab ≠0”的必要不充分条件，故D 正确．故选：AD.直接利用充分条件和必要条件，命题的否定，简易逻辑中的相关知识的应用判断A 、B 、C 、D 的结论此题主要考查的知识要点：充分条件和必要条件，命题的否定，简易逻辑，主要考查学生的运算能力和数学思维能力，属于基础题．25.【答案】AC;【解析】解：∵a >1，b >1， ∴ab =1+(a +b)⩽(a+b 2)2(当且仅当a =b >1时，取等号)，即(a +b)2−4(a +b)−4⩾0且a +b >2， ∴a +b ⩾2+2√2，∴a +b 有最小值2+2√2，即选项A 正确，B 错误；由ab −(a +b)=1，得ab −1=a +b ⩾2√ab (当且仅当a =b >1时，取等号)，即ab −2√ab −1⩾0且ab>1， ∴ab ⩾3+2√2，∴ab 有最小值3+2√2，即选项C 正确，D 错误．故选：AC ．由(a +b)⩽(a+b 2)2，可推出a +b 的最小值；由a +b ⩾2√ab ，可推出ab 的最小值．该题考查基本不等式的应用，熟练掌握基本不等式的各种变形是解答该题的关键，考查学生的逻辑推理能力和运算能力，属于基础题．26.【答案】BD;【解析】解：对于A ：已知x ，y ∈R ，x >0，y >0，且x +2y =1，所以1x +1y =x+2y x+x+2y y=1+3+2y x+xy ⩾4+2√2，当且仅当x 2=2y 2等号成立，故A 错误；对于B ：x 2+y 2=(1−2y)2+y 2=5y 2−4y +1=5(y −25)2+15，当y =25时，最小值为15；故B 正确；对于C ：当x =12，y =14时，x−2yx 2+y 2>1不成立，故C 错误；对于D ：2x+1+4y =2x+1+22y ⩾2√2x+2y+1=4，当且仅当y =12时，等号成立，故D正确．故选：BD.直接利用不等式的性质和基本不等式的应用判断A、B、C、D的结论．此题主要考查的知识要点：不等式的性质，基本不等式的应用，主要考查学生的运算能力和数学思维能力，属于中档题．27.【答案】BD;【解析】解：因为N∩∁R M=∅，所以N⊆M，所以M∩∁R N≠∅，选项A错误；M∪∁R N=R，选项B正确；∁R M∪∁R N=∁R N，选项C错误；∁R M∩∁R N=∁R M，选项D正确．故选：BD.根据题意知N⊆M，利用交集、并集和补集的定义，判断正误即可．此题主要考查了集合的定义与运算问题，也考查了推理与判断能力，是基础题．28.【答案】BD;【解析】此题主要考查了余弦函数的图象及性质，同角三角函数关系及两角差的余弦公式，属于中档题.根据对称中心与对称轴的最小距离求出周期T，得到ω=2，再根据对称轴方程求出ϕ=−π6，再根据余弦函数的图象及性质对四个选项一一判断即可，选项D先利用同角三角函数关系及二倍角公式化简，再求出f(α+π4).解：由题有T=π，则ω=2，又由对称轴x=π12可得，2×π12+ϕ=kπ，k∈Z，又|ϕ|<π2，则ϕ=−π6，故f(x)=2cos(2x−π6)，对于A，因为f(x)+f(5π6−x)=2cos(2x−π6)+2cos(53π−2x−π6)=2cos(2x−π6)−2sin2x=2cos2x cosπ6+2sin2x sinπ6−2sin2x=√3cos2x−sin2x则f(x)+f(5π6−x)=0错误，故A选项不正确.对于B，x∈[π6,π2]，则2x−π6∈[π6,5π6]，则f(x)∈[−√3,√3]，故B选项正确；对于C，f(x)=2cos2(x−π12)，应将g(x)=2cos2x的图象向右平移π12个单位，故C选项错误．对于D，sin4α−cos4α=−cos2α=−45，且α∈(0,π2)，则2α∈(0,π)，故cos2α=45，sin2α=35，而f (α+π4)=2cos (2α+π3)=cos 2α−√3sin 2α=4−3√35，故D 选项正确；故选BD .。

面面垂直证明例题（最终定稿）

面面垂直证明例题（最终定稿）第一篇：面面垂直证明例题数学面面垂直例题例4答案：例8答案：取AC的中点为O，连接OP、OB。

AO=OC,PA=PC,故PO垂直AC第二篇：怎么证明面面垂直怎么证明面面垂直证明一个面上的一条线垂直另一个面;首先可以转化成一个平面的垂线在另一个平面内,即一条直线垂直于另一个平面然后转化成一条直线垂直于另一个平面内的两条相交直线也可以运用两个面的法向量互相垂直。

这是解析几何的方法。

证:连接AC,BD.PD垂直面ABCD=>PD垂直AC.ABCD为正方形=>AC垂直BD.而BD是PB在面ABCD内的射影=>PB垂直AC.PD 垂直AC=>AC垂直面PBD.AC属于面ACE=>面PBD垂直面ACE 2 1利用直角三角形中两锐角互余证明由直角三角形的定义与三角形的内角和定理可知直角三角形的两个锐角和等于90°，即直角三角形的两个锐角互余。

2勾股定理逆定理3圆周角定理的推论：直径所对的圆周角是直角，一个三角形的一边中线等于这边的一半，则这个三角形是直角三角形。

二、高中部分线线垂直分为共面与不共面。

不共面时，两直线经过平移后相交成直角，则称两条直线互相垂直。

1向量法两条直线的方向向量数量积为0 2斜率两条直线斜率积为-1 3线面垂直，则这条直线垂直于该平面内的所有直线一条直线垂直于三角形的两边，那么它也垂直于另外一边4三垂线定理在平面内的一条直线，如果和穿过这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

5三垂线定理逆定理如果平面内一条直线和平面的一条斜线垂直，那么这条直线也垂直于这条斜线在平面内的射影。

3高中立体几何的证明主要是平行关系与垂直关系的证明。

方法如下(难以建立坐标系时再考虑)：Ⅰ.平行关系：线线平行：1.在同一平面内无公共点的两条直线平行。

2.公理4(平行公理)。

3.线面平行的性质。

4.面面平行的性质。

5.垂直于同一平面的两条直线平行。

(完整版)面面垂直的判定+性质定理(例题)

面面垂直的判定1、如图,棱柱111C B A ABC -的侧面11B BCC 是菱形，且11B C A B ⊥证明：平面1AB C ⊥平面11A BC2、如图，AB 是 ⊙O 的直径，PA 垂直于⊙O 所在的平面，C 是圆周上不同于A ，B 的任意一点,求证：平面PAC ⊥平面PBC.3、如图所示，四棱锥P-ABCD 的底面ABCD 是菱形，∠BCD ＝60°，E 是CD 的中点，PA ⊥底面ABCD ，求证：平面PBE ⊥平面PAB ；4、如图，在四面体ABCD 中，CB ＝CD ，AD ⊥BD ,点E 、F 分别是AB 、BD 的中点．求证：(1）直线EF ∥平面ACD ；(2）平面EFC ⊥平面BCD .5、如图,在四棱锥S-ABCD中，底面ABCD是正方形,SA⊥底面ABCD，SA=AB，点M是SD的中点，AN⊥SC，且交SC于点N.(I）求证:SB∥平面ACM；（II）求证:平面SAC⊥平面AMN.面面垂直的性质1、S是△ABC所在平面外一点，SA⊥平面ABC，平面SAB⊥平面SBC，求证AB ⊥BC.2、在四棱锥中,底面ABCD 是正方形，侧面VAD 是正三角形,平面VAD ⊥底面ABCD 证明:AB ⊥平面VAD3、如图,平行四边形ABCD 中，60DAB ︒∠=,2,4AB AD ==将CBD ∆沿BD 折起到EBD ∆的位置，使平面EDB ⊥平面ABD 。

求证:AB DE ⊥ w 。

w 。

k 。

s 。

5.u 。

c 。

o 。

m4、如图，在四棱锥ABCD P -中,平面PAD ⊥平面ABCD ，AB=AD ，∠BAD=60°，E 、F 分别是AP 、AD 的中点求证：（1）直线EF ‖平面PCD ；（2）平面BEF ⊥平面PADV D C BA SA CB5、如图所示，在四棱锥PABCD 中，平面PAD ⊥平面ABCD ，AB ∥DC ，△PAD 是等边三角形，已知BD ＝2AD ＝8,AB ＝2DC ＝4错误!.M 是PC 上的一点，（1)证明：平面MBD ⊥平面PAD 。

高中数学必修二 8 6 3 平面与平面垂直(第2课时)平面与平面垂直的性质练习(含答案)

8.6.3 平面与平面垂直第2课时平面与平面垂直的性质一、选择题1．设α，β是两个不同的平面，l ，m 是两条不同的直线，且l α⊂，m β⊂（） A ．若l β⊥，则αβ⊥B ．若αβ⊥，则l m ⊥C ．若//l β，则//αβD ．若//αβ，则//l m【答案】A【解析】试题分析：由面面垂直的判定定理：如果一个平面经过另一平面的一条垂线，则两面垂直，可得l β⊥，l α⊂ 可得αβ⊥2．如图所示，在平行四边形ABCD 中，AB BD ⊥，沿BD 将ABD △折起，使平面ABD ⊥平面BCD ，连接AC ，则在四面体ABCD 的四个面中，互相垂直的平面的对数为（）A ．1B ．2C ．3D ．4【答案】C【解析】 ∵面ABD ⊥面BCD ，AB ⊥BD ，∴AB ⊥面BCD ，又AB ⊂面ABC ，∴面ABC ⊥面BCD ，同理，面ACD ⊥面ABD.故四面体ABCD 中互相垂直的平面有3对．3．如图所示，三棱锥P ABC -的底面在平面α内，且AC PC ⊥，平面PAC ⊥平面PBC ，点P A B ，，是定点，则动点C 的轨迹是（）A ．一条线段B ．一条直线C ．一个圆D ．一个圆，但要去掉两个点【答案】D【解析】因为平面PAC ⊥平面PBC ，AC ⊥PC ，平面PAC∩平面PBC=PC ，AC ⊂平面PAC ，所以AC ⊥平面PBC.又因为BC ⊂平面PBC ，所以AC ⊥BC.所以∠ACB=90°.所以动点C 的轨迹是以AB 为直径的圆，除去A 和B 两点.选D.4．已知平面α⊥平面β，n αβ=，点A α∈，A n ∉，直线AB n ，直线AC n ⊥，直线m α，m β，则下列四种位置关系中，不一定成立的是（）A ．AB m ∥B ．AC m ⊥ C ．AB β∥D ．AC β⊥【答案】D【解析】如图所示：由于//m α，//m β，n αβ=，所以//m n ，又因为//AB n ，所以//AB m ，故A 正确，由于AC n ⊥，//m n ，所以AC m ⊥，故B 正确，由于//AB n ，n β⊂，AB 在β外，所以//AB β，故C 正确；对于D ，虽然AC n ⊥，当AC 不一定在平面α内，故它可以与平面β相交、平行，不一定垂直，所以D 不正确；故答案选D5．（多选题）给定下列四个命题：A.若一个平面内的两条直线与另一个平面都平行，则这两个平面相互平行；B.若一个平面经过另一个平面的垂线，则这两个平面相互垂直；C.垂直于同一直线的两条直线相互平行；D.若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直．其中，为真命题的是( )A ．①和②B ．②和③C ．③和④D ．②和④【答案】BD【解析】当两个平面相交时，一个平面内的两条直线也可以平行于另一个平面，故A 错误；由平面与平面垂直的判定可知B 正确；空间中垂直于同一条直线的两条直线还可以相交或者异面，故C 错误；若两个平面垂直，只有在一个平面内与它们的交线垂直的直线才与另一个平面垂直，故D 正确．综上，真命题是BD. 故选：BD6．（多选题）如图所示，在直角梯形BCEF 中，90CBF BCE ︒∠=∠=，,A D 分别是,BF CE 上的点，AD BC ∥，且22AB DE BC AF ===(①).将四边形ADEF 沿AD 折起，连接,,BE BF CE (②).在折起的过程中，下列说法中正确的是（）A ．AC 平面BEFB ．,,,BC E F 四点不可能共面C ．若EF CF ⊥，则平面ADEF ⊥平面ABCDD ．平面BCE 与平面BEF 可能垂直【答案】ABC【解析】选项A 中，连接AC ，取AC 的中点O ，BE 的中点M ，连接,MO MF ，MO DE 且12MO DE =，而AF DE ∥且12AF DE =，所以AF MO 且AF MO =所以四边形AOMF 是平行四边形，所以AC FM ∥，而AC ⊄平面BEF ，FM⊂平面BEF ，所以AC 平面BEF ，所以A 正确；选项B 中，设,,,B C E F 四点共面，因为BC AD ∥，BC ⊄平面ADEF ，AD ⊂平面ADEF ，所以BC ∥平面ADEF ，而BC ⊂平面BCEF ，平面BCEF平面ADEF EF =，所以BC EF ∥，所以AD EF ，这与已知相矛盾，故B C E F ，，，四点不可能共面，所以B 正确；选项C 中，连接,CF DF ，在梯形ADEF 中，易得EF FD ⊥，又EF CF ⊥，,FD CF ⊂平面CDF ，FDCF F =，所以EF ⊥平面CDF而CD ⊂平面CDF ，所以CD EF ⊥，而CD AD ⊥，,EF AD ⊂平面ADEF ，且EF 与AD 必有交点，所以CD ⊥平面ADEF ，因为CD ⊂平面ABCD ，所以平面ADEF ⊥平面ABCD ，所以C 正确；选项D 中，延长AF 至G ，使得AF FG =，连接,BG EG ， AD AF ⊥，AD AB ⊥，,AF AB ⊂平面ABF ，AF AB A ⋂=，所以AD ⊥平面ABF ，而BC AD ∥，所以BC ⊥平面ABF ，因为BC ⊂平面BCE ，所以平面BCE ⊥平面ABF ，过F 作FN BG ⊥于N ，FN ⊂平面ABF ，平面BCE 平面ABF BG =，若平面BCE ⊥平面BEF ，则过F 作直线与平面BCE 垂直，其垂足在BE 上，故前后矛盾，所以D 错误.故选：ABC.二、填空题7．如图，四面体P ABC -中，13PA PB ，平面PAB ⊥平面ABC ，90ACB ∠=︒，86AC BC ，，则PC _______.【答案】13【解析】取AB 的中点E ，连接,PE EC .因为90,8ACB AC ，6BC =，所以10AB =，所以5CE =. 因为13PA PB ，E 是AB 的中点，所以,12PEAB PE . 因为平面PAB ⊥平面ABC ，平面PAB ⋂平面ABC AB =，PE ⊂平面PAB ，因为CE ⊂平面ABC ，所以PE CE ⊥.在Rt PEC ∆中，2213PC PE CE .8．如图所示，A B C D ，，，为空间四点，在ABC 中，2AB AC BC ===，ADB 以AB 为轴运动，当平面ADB ⊥平面ABC 时，CD =________.【答案】2.【解析】取AB 的中点E ，连接DE CE ，.因为ADB △是等边三角形，所以DE AB ⊥.当平面ADB ⊥平面ABC 时，因为平面ADB ⋂平面ABC AB =，且DE AB ⊥，所以DE ⊥平面ABC ，故DE CE ⊥.由已知可得1DE EC ==，在Rt DEC △中，2CD ==.9．平面α⊥平面β，l αβ=，n β⊂，n l ⊥，直线m α⊥（m ，n 是两条不同的直线），则直线m 与n 的位置关系是______.【答案】//m n【解析】解：因为平面α⊥平面β，l αβ=，n β⊂，n l ⊥，由面面垂直的性质可得n α⊥，又m α⊥，所以//m n .故答案为：//m n10．已知PA ⊥正方形ABCD 所在的平面，垂足为A ，连接PB ，PC ，PD ，则平面PAB ，平面PAD ，平面PCD ，平面PBC ，平面ABCD 中，互相垂直的平面有对.【答案】5【解析】,,PA ABCD PAB ABCD PAD ABCD ⊥∴⊥⊥平面平面平面平面，又,,,CD AD PADABCD AD CD PAD ⊥=∴⊥平面平面平面PCD PAD ∴⊥平面平面，同理，平面PAB ⊥平面PAD ，平面PBC ⊥平面PAB ，所以互相垂直的平面共有5对.三、解答题11．已知P 是ABC 所在平面外的一点，且PA ⊥平面ABC ，平面PAC ⊥平面PBC .求证:BC AC ⊥.【答案】证明见解析【解析】如图，在平面PAC 内作AD PC ⊥于点D ，∵平面PAC ⊥平面PBC ，平面PAC 平面PBC PC =，AD ⊂平面PAC ，且AD PC ⊥，AD ∴⊥平面PBC ，又BC ⊂平面PBC ，AD BC ∴⊥.PA ⊥平面ABC ，BC ⊂平面ABC ，PA BC ∴⊥，AD PA A =，,AD PA ⊂平面PAC ，BC ∴⊥平面PAC ，又AC ⊂平面PAC ，BC AC ∴⊥.12．如图，三棱锥P ABC -中，已知ABC 是等腰直角三角形，90ABC ︒∠=，PAC 是直角三角形，90PAC ︒∠=，平面PAC ⊥平面ABC .求证：平面PAB ⊥平面PBC .【答案】证明见解析【解析】证明 ∵平面PAC ⊥平面ABC ，平面PAC 平面ABC AC =，又PAC 是直角三角形，所以PA AC ⊥， PA ∴⊥平面ABC .又BC ⊂平面ABC ，PA BC ∴⊥.AB BC ⊥，AB PA A ⋂=，AB 平面PAB ，PA ⊂平面PAB ， BC ∴⊥平面PAB .又BC ⊂平面PBC ，故平面PAB ⊥平面PBC .。

平面与平面垂直的判定试题含答案

平面与平面垂直的判定学校：__________ 班级：__________ 姓名：__________ 考号：__________1. PA垂直于正方形ABCD所在平面，连接PB，PC，PD，AC，BD，则下列垂直关系正确的是（）①面PAB⊥面PBC②面PAB⊥面PAD③面PAB⊥面PCD④面PAB⊥面PAC．A.①②B.①③C.②③D.②④2. 如图，在正方体ABCD−A1B1C1D1中，二面角D1−BC−D的大小为( )A.π6B.π4C.π3D.π23. 如图，以等腰三角形ABC的斜边BC上的高AD位折痕，将△ABD和△ACD折起，使折起后的△ABC成等边三角形，则二面角C−AB−D的余弦值等于（）A.√22B.√63C.13D.√334. 如图，四棱锥P−ABCD的侧面PAB⊥底面ABCD，△PAB为等边三角形，AB=AD=2BC=2，AB⊥AD，AD//BC，点H为PB的中点，则直线HD与底面ABCD所成的角的正弦值为( )A.√2114B.5√714C.√77D.√335. 两个平面平行的条件是（）A.一个平面内一条直线平行于另一个平面B.一个平面内两条直线平行于另一个平面C.一个平面内的无数条直线平行于另一个平面D.一个平面内的任意一条直线平行于另一个平面6. 已知两条不同直线m、l，两个不同平面α、β，在下列条件中，可得出α⊥β的是（）A.m⊥l，l // α，l // βB.m⊥l，α∩β，m⊂αC.m // l，m⊥α，l⊥βD.m // l，l⊥β，m⊂α7. 已知PD⊥矩形ABCD所在的平面，图中相互垂直的平面有（）A.2对B.3对C.4对D.5对8. 棱锥的正视图和侧视图都是正三角形，俯视图是正方形，则其侧面与底面所成二面角的大小是（）A.30∘B.45∘C.60∘D.90∘9. 把正三角形ABC沿高AD折成二面角B−AD−C后，BC=12AB，则二面角B−AD−C为（）A.30∘B.45∘C.60∘D.90∘10. 在正方体ABCD−A1B1C1D1中，平面A1BD与平面C1BD所成二面角的余弦值为（）A.1 2B.13C.√32D.√3311. 如图，在四棱锥P−ABCD中，底面四边形ABCD是矩形，PA⊥平面ABCD，PA=AD，则二面角P−CD−B的大小是________．12. 面面垂直的判定定理：文字语言：________；符号语言：________．13. 设a、b是异面直线，α、β是两个平面，且a⊥α，b⊥β，a⊄β，b⊄α，则当________（填上一种条件即可）时，有α⊥β．14. 边长为1的等边三角形ABC中，沿BC边高线AD折起，使得折后二面角B−AD−C为60∘，则点A到BC的距离为________，点D到平面ABC的距离为________．15. 已知E，F分别是棱长为1的正方体ABCD−A1B1C1D1的棱BC，CC1的中点，则截面AEFD1与底面ABCD所成二面角的正弦值是________．16. 如图，等腰梯形ABCD中，AB//CD, AD=AB=BC=1, CD=2，E为CD中点，AE与BD交于点O，将△ADE沿AE折起，使点D到达点P的位置（P∉平面ABCE）.(1)证明：平面POB⊥平面ABCE；(2)若直线PB与平面ABCE所成的角为π4，求二面角A−PE−C的余弦值.17. 如图，已知AB⊥平面ACD，DE⊥平面ACD，三角形ACD是正三角形，且AD=DE=2AB，F是CD的中点．（1）求证：平面CBE⊥平面CDE；（2）求二面角C−BE−F的余弦值．18. 如图，在Rt△ABC中，AC=BC，PA⊥平面ABC，PB与平面ABC成60∘角.(1)求证：平面PBC⊥平面PAC；(2)求二面角C−PB−A的正切值．19. 如图，四棱锥P−ABCD中，底面ABCD为菱形，AC与BD交于点G，PB=PD．(1)求证：平面PAC⊥平面ABCD；(2)若∠ABC=60∘，PA=PC=AB=2，E为PD的中点，求二面角E−AC−D的大小．20. 如图三棱锥P−ABC中，平面PAB⊥平面ABC，AC⊥BC，BC=√3AC=2√3，PB=3√2，且PB与平面ABC所成的角为45∘，求二面角P−BC−A的正切值．21. 如图，在四面体ABCD中，CB＝CD，AD⊥BD，点E，F分别是AB，BD的中点．求证：(1)直线EF // 面ACD；(2)平面EFC⊥平面BCD.22. 如图，在四棱锥P−ABCD中，PD⊥ABCD，ABCD为正方形．AD=PD=2，E，F，GPC，PD，CB，AP // EGF，求二面角G−EF−D的大小．23. 在如图所示的几何体中，四边形ABCD为正方形，PA⊥平面ABCD，PA // BE，AB ＝PA＝2BE＝4．(Ⅰ)求证：CE // 平面PAD；(Ⅱ)在棱AB上是否存在一点F，使得平面DEF⊥平面PCE？如果存在，求AF的值；如果AB不存在，说明理由．24. 如图平面SAC⊥平面ACB，△SAC是边长为4的等边三角形，△ACB为直角三角形，∠ACB=90∘，BC=4√2，求二面角S−AB−C的余弦值．25. 以正方形ABCD的对角线BD为棱折成直二面角，连接AC，求二面角A−CD−B的余弦值．26. 如图，在直三棱柱ABC−A1B1C1中，AB=1，AC=AA1=√3，∠ABC=60∘．(1)求异面直线AB与A1C的距离；(2)求二面角A−A1C−B的余弦值．27. 已知正方体ABCD−A′B′C′D′中，E是AA′棱的中点．求平面BEC′与平面ABCD所成的角的余弦值．28. 在四面体ABCD中，AB=3，AC=AD=2，且∠DAC=∠BAC=∠BAD=60∘，求证：平面BCD⊥平面ADC．29. 在四棱锥P−ABCD中，AD // BC，∠ABC=∠APB=90∘，点M是线段AB上的一点，且PM⊥CD，AB=BC=2PB=2AD=4BM．(1)证明：面PAB⊥面ABCD；(2)求平面PAB与平面PCD的二面角的正弦值．30. 如图，已知AB⊥平面BCD，BC⊥CD．请指出图中所有互相垂直的平面，并说明理由．31. 如图，AB为圆O的直径，点E，F在圆O上，AB // EF，矩形ABCD和圆O所在的平面互相垂直，已知AB=2，EF=1.(1)求证：平面DAF⊥平面CBF；(2)当AD的长为何值时，二面角D−FE−B的大小为60∘.32. 在三棱柱ABC−A1B1C1中，AA1⊥BC，∠A1AC=60∘，A1A=AC=BC=1，A1B=√2．（1）求证：平面A1BC⊥平面ACC1A1；（2）如果D为AB中点，求证：BC1 // 平面A1CD．33. 如图，直三棱柱ABC−A1B1C1中，AC=BC=1，∠ACB=90∘，AA1=√2，D是A1B1中点．（1）求证C1D⊥平面AA1B1B；（2）当点F在BB1上什么位置时，会使得AB1⊥平面C1DF？并证明你的结论．34. 如图，在正方体ABCD−A1B1C1D1中，E、F、G分别是AB、AD、C1D1的中点．求证：平面D1EF // 平面BDG．35. 如图，三棱锥P−ABC中，PA⊥面ABC，AC⊥BC，求证：面PAC⊥面PBC．36. 在四棱锥P−ABCD中，侧面PDC是边长2的正三角形且与底面ABCD垂直，底面ABCD是面积为2√3的菱形，∠ADC为锐角．(1)求证：PA⊥CD(2)求二面角P−AB−D的大小．37. 如图，已知空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．求证：（1）AB⊥平面CDE；（2）平面CDE⊥平面ABC．38. 如图，在四棱锥P−ABCD中，PA⊥AD，底面四边形ABCD为直角梯形，AD＝λBC，AD // BC，∠BCD＝90∘，M为线段PB上一点．(Ⅰ)若λ=1，则在线段PB上是否存在点M，使得AM // 平面PCD？若存在，请确定M3点的位置；若不存在，请说明理由；(Ⅱ)已知PA＝2，AD＝1，若异面直线PA与CD成90∘角，二而角B−PC−D的余弦值为−√10，求CD的长．1039. 如图，已知直三棱柱ABC−A1B1C1中，AC=BC=2，M、N分别是棱CC1、AB的中点．求证：平面MCN⊥平面ABB1A1．40. 如图1所示，Rt△ABC中，BC=2，CA=3，点P在线段AB上，将△BPC沿CP折成直二面角S−CP−A（点B与点S重合），且SA=√7（图2）．（1）求∠SCP的度数；（2）求二面角P−SC−A的余弦值．参考答案与试题解析平面与平面垂直的判定一、选择题（本题共计 10 小题，每题 3 分，共计30分）1.【答案】A【考点】平面与平面垂直【解析】由于PA垂直于正方形ABCD所在平面，所以PA所在的平面与底面垂直，又ABCD为正方形，故又存在一些线线垂直关系，从而可以得到线面垂直，进而可以判定面面垂直．【解答】证明：由于BC⊥AB，由PA垂直于正方形ABCD所在平面，所以BC⊥PA，易证BC⊥平面PAB，则平面PAB⊥平面PBC；又AD // BC，故AD⊥平面PAB，则平面PAD⊥平面PAB．2.【答案】B【考点】二面角的平面角及求法【解析】此题暂无解析【解答】解：∵因为几何体ABCD−A1B1C1D1是正方体，∴D1C⊥BC，DC⊥BC，∴∠D1CD是二面角D1−BC−D的平面角．∵∠D1CD=π，4∴二面角D1−BC−D的大小为π.4故选B.3.【答案】D【考点】二面角的平面角及求法【解析】设AB中点为E，AD=a，连接CE，DE，则∠CED为所求二面角，证明CD⊥DE，即可求得二面角C−AB−D的余弦值．【解答】解：设AB中点为E，AD=a，连接CE，DE，∵AD=DB，CA=CB∴AB⊥DE，AB⊥CE∴∠CED为所求二面角，∵AD=a，∴DE=√22a，CE=√32AB=√62a，CD=a，∴CE2=CD2+DE2∴CD⊥DE∴cos∠CED=DECE =√22a√62a=√33故选D．4.【答案】A【考点】二面角的平面角及求法【解析】此题暂无解析【解答】解：作HE⊥AB于E，连接ED，BD，∵侧面PAB⊥底面ABCD，∴HE⊥底面ABCD，∵ED⊂底面ABCD，∴HE⊥ED，∴∠HDE即为直线HD与底面ABCD所成的角，设AB=AD=2BC=2，又∵△PAB为等边三角形，∴BH=12BP=12AB=1，BE=14AB=12，∴HE=√32，BD=√AB2+AD2=2√2，∴HD=√BD2−BH2=√7，∴sin∠HDE=HEHD =√2114.故选A.5.【答案】D【考点】平面与平面垂直的判定【解析】排除法，逐一检验答案，①②③可通过特例说明是错误的．④说明两个平面无公共点，是正确的．【解答】解：①如图l // β，l⊂α，但α，β却相交．①错②如图l // β，l⊂α，m // β，m⊂α但α，β却相交．②错③类似于②在α内有无数与l平行的直线，它们均与β平行，但α，β却相交，③错④可知，两个平面无公共点，它们平行．④对故选D．6.【答案】D【考点】平面与平面垂直的判定【解析】对每一个答案进行逐一判定，将由条件可能推出的其它的结论也列举出来．即可得到答案．【解答】解：对于A；l // α，l // β，α与β可以平行，相交；故A不正确．对于B；α与β可以平行，相交；故B不正确．对于C；m // l，m⊥α⇒l⊥α；l⊥β⇒α // β．故C不正确．对于D:m // l，l⊥β⇒m⊥β，m⊂α⇒α⊥β．故D正确．故选：D．7.【答案】D【考点】平面与平面垂直的判定【解析】直接利用面面垂直的判定定理判断即利用题目中的条件找出线面垂直即可．【解答】解：∵PD⊥矩形ABCD所在的平面且PD⊆面PDA，PD⊆面PDC，∴面PDA⊥面ABCD，面PDC⊥面ABCD，又∵四边形ABCD为矩形∴BC⊥CD，CD⊥AD∵PD⊥矩形ABCD所在的平面∴PD⊥BC，PD⊥CD∵PD∩AD=D，PD∩CD=D∴CD⊥面PAD，BC⊥面PDC，AB⊥面PAD，∵CD⊆面PDC，BC⊆面PBC，AB⊆面PAB，∴面PDC⊥面PAD，面PBC⊥面PCD，面PAB⊥面PAD综上相互垂直的平面有5对故答案选D8.【答案】C【考点】二面角的平面角及求法【解析】利用棱锥的三视图，可知该棱锥是正四棱锥，则正视图的底角即为侧面与底面所成二面角．【解答】解：因为棱锥的正视图和侧视图都是正三角形，俯视图是正方形，所以该棱锥是正四棱锥，如图：过G作底面的射影O，则△GEF为正视图，且GE=EF，因为EF⊥BC，所以GE⊥BC，即∠GEO为侧面和底面所成的二面角．因为△GEF为正三角形，所以∠GEF=60∘，所以侧面与底面所成二面角的大小是60∘．故选C．9.【答案】C【考点】二面角的平面角及求法【解析】根据AD⊥BC于D，易得沿AD折成二面角B−AD−C后，∠BDC即为二面角B−AD−C的平面角，解△BDC即可求出二面角B−AD−C的大小．【解答】解：∵ AD ⊥BC ，∴ 沿AD 折成二面角B −AD −C 后，AD ⊥BD ，AD ⊥CD故∠BDC 即为二面角B −AD −C 的平面角又∵ BD =CD =BC =12AB ，∴ ∠BDC =60∘故选C ．10.【答案】B【考点】二面角的平面角及求法【解析】根据正方体分段性质得出∠A 1OC 1为平面A 1BD 与平面C 1BD 所成二面角的夹角，在△A 1OC 1中运用余弦定理求解即可．【解答】解：取BD 中的O ，连接，OB ，OA 1，A 1C 1，∵ 在正方体ABCD −A 1B 1C 1D 1中，设棱长为1，∴ A 1C 1=√2，OB =OA 1=√62，根据正方体的几何性质得出BD ⊥OA ，BD ⊥OC ，BD ⊥AA 1，BD ⊥CC 1， ∴ BD ⊥面OAA 1，BD ⊥平面OCC 1，OA 1⊂面OAA 1，OC 1⊂平面OCC 1，∴ BD ⊥OA 1，BD ⊥OC 1，∴ ∠A 1OC 1为平面A 1BD 与平面C 1BD 所成二面角的夹角，∴ 在△A 1OC 1中，cos ∠A 1OC 1=32+32−22×√62×√62=13故选：B二、填空题（本题共计 5 小题，每题 3 分，共计15分）11.【答案】45∘【考点】二面角的平面角及求法【解析】直接利用已知条件求出二面角的平面角，再进一步求出结果【解答】解：在四棱锥P −ABCD 中，底面四边形ABCD 是矩形，PA ⊥平面ABCD ，所以：PA ⊥CD ，CD ⊥AD ，CD ⊥平面PAD ，所以：PD ⊥CD ，∠PDA 即为二面角P −CD −B 的平面角，由于PA =AD ，所以：∠PDA =45∘，即二面角P −CD −B 的大小是45∘．故答案为：45∘．12.【答案】一个平面过另一平面的垂线，则这两个平面相互垂直,{a ⊂αa ⊥β⇒α⊥β【考点】平面与平面垂直的判定【解析】平面与平面垂直的判定定理：需要两个条件，线面垂直，线在面内，可得面面垂直．进而用符号语言表示后，可得答案．【解答】解：平面与平面垂直的判定定理：一个平面过另一平面的垂线，则这两个平面相互垂直，用符号语言表示为：{a ⊂αa ⊥β⇒α⊥β，故答案为：一个平面过另一平面的垂线，则这两个平面相互垂直，{a ⊂αa ⊥β⇒α⊥β．13.【答案】a ⊥b【考点】平面与平面垂直的判定【解析】从条件a ⊥α结合α⊥β，则有a // β或a ⊂β，再由b ⊥β，a ⊄β，可得a ⊥b ．【解答】解：∵ a ⊥α，α⊥β∴ a // β或a ⊂β又∵ b ⊥β，a ⊄β∴ a ⊥b故答案为：a ⊥b14.【答案】√154,√1510【考点】二面角的平面角及求法【解析】根据条件确定AE 为点A 到直线BC 的距离，DH 为点D 到面ABC 的距离，然后利用边长关系进行求值即可．【解答】解：如图，过D 点作DE ⊥BC ，连AE ，则AE ⊥BC∴ AE 为点A 到直线BC 的距离在直角三角形ADE 中，AE =√AD 2+DE 2=√(√32)2+(12⋅√32)2=√154．又BC 面ADE ，且BC ⊂面ABC ，∴ 面ABC ⊥面ADE ，AE 为高线，作DH ⊥AE 于H ，则DH ⊥面ABC∴ DH 为点D 到面ABC 的距离，由DH ⋅AE =AD ⋅DE 得DH =√32⋅√34√154=√1510．故答案为：√154，√1510．15.【答案】√53【考点】二面角的平面角及求法【解析】以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系，利用向量法能求出截面AEFD 1与底面ABCD 所成二面角的正弦值．【解答】解：以D 为原点，DA 为x 轴，DC 为y 轴，DD 1为z 轴，建立空间直角坐标系， A(1, 0, 0)，E(12,1,0)，F(0, 1, 12)，AE →=(−12, 1, 0)，AF →=(−1, 1, 12)，设平面AEFD 1的法向量n →=(x, y, z)，则{n →⋅AF →=−x +y +12z =0˙，取x =2，得n →=(2, 1, 2)，平面ABCD 的法向量m →=(0, 0, 1)，截面AEFD 1与底面ABCD 所成二面角为θ，cos θ=|m →|⋅|n →|˙=23， ∴ sin θ=√1−(23)2=√53． ∴ 截面AEFD 1与底面ABCD 所成二面角的正弦值是√53．故答案为：√53．三、解答题（本题共计 25 小题，每题 10 分，共计250分）16.【答案】(1)证明：在△PAE 中，OP ⊥AE ，在△BAE 中，OB ⊥AE ，又OP ∩OB =O ，∴ AE ⊥平面POB ，又AE ⊂平面ABCE ，∴ 平面POB ⊥平面ABCE .(2)在平面POB 内作PQ ⊥OB 与Q ，∴ PQ ⊥平面ABCE . ∴ 直线PB 与平面ABCE 夹角为∠PBQ =π4，又∵ OP =OB ，∴ OP ⊥OB ，O ，Q 两点重合，即OP ⊥平面ABCE ，以O 为原点，OE 为x 轴，OB 为y 轴，OP 为z 轴，建立空间直角坐标系O −xyz ，由题意得P (0,0,√32), E (12,0,0), C (1,√32,0)， ∴ PE →=(12,0,−√32), EC →=(12,√32,0)，设平面PCE 的一个法向量为n →1=(x,y,z)，则{PE →⋅n 1→=0EC →⋅n 1→=0，即{12x −√32z =012x +√32y =0，不妨设x =√3，则y =−1，z =1，得n 1→=(√3,−1,1)，同理得平面PAE 的一个法向量n 2→=(0,1,0)，设二面角A −P −EC 为α，|cos α|=|n 1→⋅n 2→||n 1→∥n 2→|=1⋅√5=√55. 即二面角A −P −EC 为α的余弦值为−√55. 【考点】二面角的平面角及求法平面与平面垂直的判定【解析】此题暂无解析【解答】(1)证明：在△PAE 中，OP ⊥AE ，在△BAE 中，OB ⊥AE ，又OP ∩OB =O ，∴ AE ⊥平面POB ，又AE ⊂平面ABCE ，∴ 平面POB ⊥平面ABCE .(2)在平面POB 内作PQ ⊥OB 与Q ，∴ PQ ⊥平面ABCE .∴ 直线PB 与平面ABCE 夹角为∠PBQ =π4，又∵ OP =OB ，∴ OP ⊥OB ，O ，Q 两点重合，即OP ⊥平面ABCE ，以O 为原点，OE 为x 轴，OB 为y 轴，OP 为z 轴，建立空间直角坐标系O −xyz ，由题意得P (0,0,√32), E (12,0,0), C (1,√32,0)， ∴ PE →=(12,0,−√32), EC →=(12,√32,0)，设平面PCE 的一个法向量为n →1=(x,y,z)，则{PE →⋅n 1→=0EC →⋅n 1→=0，即{12x −√32z =012x +√32y =0，不妨设x =√3，则y =−1，z =1，得n 1→=(√3,−1,1)，同理得平面PAE 的一个法向量n 2→=(0,1,0)，设二面角A −P −EC 为α，|cos α|=|n 1→⋅n 2→||n 1→∥n 2→|=1⋅√5=√55. 即二面角A −P −EC 为α的余弦值为−√55. 17. 【答案】（1）证明：因为DE ⊥平面ACD ，DE ⊂平面CDE ，所以平面CDE ⊥平面ACD ．在底面ACD 中，AF ⊥CD ，由面面垂直的性质定理知，AF ⊥平面CDE ．取CE 的中点M ，连接BM 、FM ，由已知可得FM =AB 且FM // AB ，则四边形FMBA 为平行四边形，从而BM // AF ．所以BM ⊥平面CDE ．又BM⊂平面BCE，则平面CBE⊥平面CDE．…（2）解：过F作FN⊥CE交CE于N，过N作NH⊥BE，连接HF，则∠NHF就是二面角C−BE−F的平面角．在Rt△FNH中，NH=√62√5，FH=√5，所以cos∠NHF=NHFH =3√68故二面角C−BE−F的余弦值为3√68…【考点】二面角的平面角及求法平面与平面垂直的判定【解析】（1）取CE的中点M，连接BM、FM，通过证明BM⊥平面CDE，利用平面与平面垂直的判定定理证明平面BCE⊥平面CDE．（2）过F作FN⊥CE交CE于N，过N作NH⊥BE，连接HF，则∠NHF就是二面角C−BE−F的平面角．【解答】（1）证明：因为DE⊥平面ACD，DE⊂平面CDE，所以平面CDE⊥平面ACD．在底面ACD中，AF⊥CD，由面面垂直的性质定理知，AF⊥平面CDE．取CE的中点M，连接BM、FM，由已知可得FM=AB且FM // AB，则四边形FMBA为平行四边形，从而BM // AF．所以BM⊥平面CDE．又BM⊂平面BCE，则平面CBE⊥平面CDE．…（2）解：过F作FN⊥CE交CE于N，过N作NH⊥BE，连接HF，则∠NHF就是二面角C−BE−F的平面角．在Rt△FNH中，NH=√62√5，FH=√5，所以cos∠NHF=NHFH =3√68故二面角C−BE−F的余弦值为3√68…18.【答案】(1)证明：∵PA⊥平面ABC，BC⊂平面ABC，∴BC⊥PA，又∵BC⊥AC，且AC∩PA=A，∴BC⊥平面PAC，而BC⊂平面PBC，∴平面PBC⊥平面PAC；(2)解：取AB的中点D，过D作DE⊥PB交PB于E，连接CE，∵PA⊥平面ABC，∴平面PAB⊥平面ABC，∴CD⊥平面PAB，而PB⊂平面PAB，∴PB⊥CD，∴∠CED就是C−PB−A的二面角，令AC=2，则BC=2，在Rt△ABC中，AC=BC，∴AB=2√2，∴CD=√2，又∵PB与平面ABC成60∘角，PA⊥平面ABC，∴∠PBA=60∘，∴PB=4√2，PA=2√6，易知△PAB∼△DEB，∴DE=√62，在Rt△CDE中，tan∠CED=CDDE =√2√62=2√33．∴二面角C−PB−A的正切值为2√33．【考点】二面角的平面角及求法平面与平面垂直的判定【解析】（1）证明BC⊥PA，然后证明BC⊥平面PAC，利用平面与平面垂直的判定定理证明平面PBC⊥平面PAC；（2）取AB的中点D，过D作DE⊥PB交PB于E，连接CE，说明∠CED就是二面角C−PB−A的平面角，通过在Rt△CDE中，求出二面角C−PB−A的正切值．【解答】(1)证明：∵PA⊥平面ABC，BC⊂平面ABC，∴BC⊥PA，又∵BC⊥AC，且AC∩PA=A，∴BC⊥平面PAC，而BC⊂平面PBC，∴平面PBC⊥平面PAC；(2)解：取AB的中点D，过D作DE⊥PB交PB于E，连接CE，∵PA⊥平面ABC，∴平面PAB⊥平面ABC，∴CD⊥平面PAB，而PB⊂平面PAB，∴PB⊥CD，∴∠CED就是C−PB−A的二面角，令AC=2，则BC=2，在Rt△ABC中，AC=BC，∴AB=2√2，∴CD=√2，又∵PB与平面ABC成60∘角，PA⊥平面ABC，∴∠PBA=60∘，∴PB=4√2，PA=2√6，易知△PAB∼△DEB，∴DE=√62，在Rt△CDE中，tan∠CED=CDDE =√2√62=2√33．∴二面角C−PB−A的正切值为2√33．19.【答案】(1)证明：连接PG，∵底面ABCD为菱形，∴G为BD的中点.又PB=PD，∴BD⊥PG.又BD⊥AC，AC，PG⊂平面PAC，AC∩PG=G，∴BD⊥平面PAC.又BD⊂平面ABCD，∴平面PAC⊥平面ABCD．(2)解：连接EG，∵PA=PC，且G为AC的中点，∴PG⊥AC.又BD⊥AC，BD，PG⊂平面PBD，BD∩PG=G，∴AC⊥平面PBD.∵EG⊂平面PBD，∴AC⊥EG，∴∠EGD是二面角E−AC−D的平面角，由题意PG=DG=√3.在Rt△PGD中，GE=DE=√62，∴tan∠EGD=DEGE=1.∵∠EGD∈(0, π2)，∠EGD=π4，∴二面角E−AC−D的大小为π4．【考点】平面与平面垂直的判定二面角的平面角及求法【解析】（1）连结PG，推导出BD⊥PG，BD⊥AC，从而BD⊥平面PAC，由此能证明平面PAC⊥平面ABCD．（2）连结EG，推导出PG⊥AC，BD⊥AC，从而AC⊥平面PBD，进而∠EGD是二面角E−AC−D的平面角，由此能求出二面角E−AC−D的大小．【解答】(1)证明：连接PG，∵底面ABCD为菱形，∴G为BD的中点.又PB=PD，∴BD⊥PG.又BD⊥AC，AC，PG⊂平面PAC，AC∩PG=G，∴BD⊥平面PAC.又BD⊂平面ABCD，∴平面PAC⊥平面ABCD．(2)解：连接EG，∵PA=PC，且G为AC的中点，∴PG⊥AC.又BD⊥AC，BD，PG⊂平面PBD，BD∩PG=G，∴AC⊥平面PBD.∵EG⊂平面PBD，∴AC⊥EG，∴∠EGD是二面角E−AC−D的平面角，由题意PG=DG=√3.在Rt△PGD中，GE=DE=√62，∴tan∠EGD=DEGE=1.∵∠EGD∈(0, π2)，∠EGD=π4，∴二面角E−AC−D的大小为π4．20.【答案】解：过点P在平面PAB内作PD⊥AB于D，过D点在平面ABC内作DE⊥BC于E，连结PE−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−∵平面PAB⊥平面ABC，且平面PAB⊥平面ABC=AB∴PD⊥平面ABC∴∠PBC即直线PB与平面ABC所成的角，且PD⊥BC∴∠PBC=45∘−−−−−−−−−−−−−−−−−−−−−−−−−−−∴在Rt△PDB中，由PB=3√2得：PD=BD=3又∵DE⊥BC，且PD⊥BC∴BC⊥平面PDE∴BC⊥PE∴∠PED即二面角P−BC−A的平面角，------------------又∵△ABC中，AC⊥CB，BC=√3AC=2√3知，∠CBA=30∘∴在Rt△DBE中：DE=12BD=32．∴在Rt△PDE中：tan∠PDE=PDDE =332=2，即二面角P−BC−A的正切值为2．----------【考点】二面角的平面角及求法【解析】过点P在平面PAB内作PD⊥AB于D，过D点在平面ABC内作DE⊥BC于E，连结PE，可得∠PBC即直线PB与平面ABC所成的角，结合已知可证得∠PED即二面角P−BC−A的平面角，解△ABC，Rt△DBE和Rt△PDE可得答案．【解答】解：过点P在平面PAB内作PD⊥AB于D，过D点在平面ABC内作DE⊥BC于E，连结PE−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−∵平面PAB⊥平面ABC，且平面PAB⊥平面ABC=AB∴PD⊥平面ABC∴∠PBC即直线PB与平面ABC所成的角，且PD⊥BC∴∠PBC=45∘−−−−−−−−−−−−−−−−−−−−−−−−−−−∴在Rt△PDB中，由PB=3√2得：PD=BD=3又∵DE⊥BC，且PD⊥BC∴BC⊥平面PDE∴BC⊥PE∴∠PED即二面角P−BC−A的平面角，------------------又∵△ABC中，AC⊥CB，BC=√3AC=2√3知，∠CBA=30∘∴在Rt△DBE中：DE=12BD=32．∴在Rt△PDE中：tan∠PDE=PDDE =332=2，即二面角P−BC−A的正切值为2．----------21.【答案】证明：(1)在△ABD 中，E ，F 分别是AB ，BD 的中点，EF//AD ，又AD ⊂平面ACD ，EF ⊄平面ACD ，直线EF//平面ACD .(2)在△ABD 中，∵ AD ⊥BD ，EF//AD ，∴ EF ⊥BD ，在△BCD 中，CD =CB ，F 为BD 的中点，∴ CF ⊥BD ，∵ CF ∩EF =F ，∴ BD ⊥平面EFC ，又BD ⊂平面BCD ，∴ 平面EFC ⊥平面BCD ．【考点】直线与平面平行的判定平面与平面垂直的判定【解析】（1）只要证明EF/AD ，利用线面平行的判定解答；（2）只要证明BD 平面EFC 即可【解答】证明：(1)在△ABD 中，E ，F 分别是AB ，BD 的中点，EF//AD ，又AD ⊂平面ACD ，EF ⊄平面ACD ，直线EF//平面ACD ．(2)在△ABD 中，∵ AD ⊥BD ，EF//AD ，∴ EF ⊥BD ，在△BCD 中，CD =CB ，F 为BD 的中点，∴ CF ⊥BD ，∵ CF ∩EF =F ，∴ BD ⊥平面EFC ，又BD ⊂平面BCD ，∴ 平面EFC ⊥平面BCD ．22.【答案】解：建立空间直角坐标系D −xyz ，则P(0, 0, 2)，C(0, 2, 0)，G(1, 2, 0)，E(0, 1, 1)，F(0, 0, 1)，A(2, 0, 0)． ∴ AP →=(−2,0,2)，EF →=(0,−1,0)，EG →=(1,1,−1)设平面EFG 的法向量为：n →=(x,y,z)所以：{n →⋅EG →=0˙解得：n →=(1,0,1)∵ 底面ABCD 是正方形∴ AD ⊥CD∵ PD ⊥ABCD∴ AD ⊥PD∴ AD ⊥平面PCD∴ DA →是平面PCD 的法向量，DA →=(2,0,0)所以：cos <DA ¯，n →>=|DA →|⋅|n →|˙=√22 所以：二面角G −EF −D 的大小为45∘【考点】二面角的平面角及求法【解析】首先建立空间直角坐标系，进一步求出平面EFG 的法向量，再利用DA →是平面PCD 的法向量，利用向量的数量积求出二面角的大小．【解答】解：建立空间直角坐标系D −xyz ，则P(0, 0, 2)，C(0, 2, 0)，G(1, 2, 0)，E(0, 1, 1)，F(0, 0, 1)，A(2, 0, 0)． ∴ AP →=(−2,0,2)，EF →=(0,−1,0)，EG →=(1,1,−1)设平面EFG 的法向量为：n →=(x,y,z)所以：{n →⋅EG →=0˙解得：n →=(1,0,1)∵ 底面ABCD 是正方形∴ AD ⊥CD∵ PD ⊥ABCD∴ AD ⊥PD∴ AD ⊥平面PCD∴ DA →是平面PCD 的法向量，DA →=(2,0,0)所以：cos <DA ¯，n →>=|DA →|⋅|n →|˙=√22所以：二面角G −EF −D 的大小为45∘23. 【答案】（1）证明：BE // PA ，PA ⊂平面PAD ，BE ⊄平面PAD ；∴ BE // 平面PAD ；同理，∵ ABCD 为正方形，∴ BC // AD ，∴ BC // 平面PAD ；又BC ∩BE ＝B ；∴ 平面EBC // 平面PAD ，CE ⊂平面EBC ；∴ CE // 平面PAD ；（2）分别以边AB ，AD ，AP 所在直线为x ，y ，z 轴，建立如图所示空间直角坐标系，则：B(4, 0, 0)，C(4, 4, 0)，E(4, 0, 2)，P(0, 0, 4)，D(0, 4, 0)；∴ PC →=(4,4,−4)，PE →=(4,0,−2)，PD →=(0,4,−4)；设平面PCE 的一个法向量为m →=(x,y,z)；∴ {m →⋅PC →=0m →⋅PE →=0⇒{x +y −z =02x −z =0 ；令x ＝1，则{x =1y =1z =2，∴ m →=(1,1,2)；可设F(a, 0, 0)，则FE →=(4−a,0,2)，DE →=(4,−4,2)；设平面DEF 的一个法向量为n →=(x,y,z)，则{n →⋅DE →=0n →⋅FE →=0⇒{2x −2y +z =0(4−a)x +2z =0 ；令x ＝2，则{x =2y =a 2z =a −4，∴ n →=(2,a2,a −4)；由平面DEF ⊥平面PCE ，得m →⋅n →=0，即2+a2+2a −8=0，a =125<4；∴ 点F(125,0,0)；∴ AFAB =35．【考点】直线与平面平行平面与平面垂直【解析】(Ⅰ)根据已知条件便可证明平面BCE // 平面PAD ，从而便得到CE // 平面PAD ； (Ⅱ)首先分别以AB ，AD ，AP 三直线为x ，y ，z 轴，建立空间直角坐标系，要使平面DEF ⊥平面PCE ，便有这两平面的法向量垂直，设F(a, 0, 0)，平面PCE 的法向量为m →=(x,y,z)，根据{m →⋅PC →=0m →⋅PE →=0 即可求出m →，同样的办法表示出平面DEF 的法向量n →，根据m →⋅n →=0即可求出a ，从而求出AFAB ．【解答】（1）证明：BE // PA ，PA ⊂平面PAD ，BE ⊄平面PAD ； ∴ BE // 平面PAD ；同理，∵ ABCD 为正方形，∴ BC // AD ，∴ BC // 平面PAD ；又BC ∩BE ＝B ；∴ 平面EBC // 平面PAD ，CE ⊂平面EBC ； ∴ CE // 平面PAD ；（2）分别以边AB ，AD ，AP 所在直线为x ，y ，z 轴，建立如图所示空间直角坐标系，则：B(4, 0, 0)，C(4, 4, 0)，E(4, 0, 2)，P(0, 0, 4)，D(0, 4, 0)； ∴ PC →=(4,4,−4)，PE →=(4,0,−2)，PD →=(0,4,−4)；设平面PCE 的一个法向量为m →=(x,y,z)； ∴ {m →⋅PC →=0m →⋅PE →=0 ⇒{x +y −z =02x −z =0 ；令x ＝1，则{x =1y =1z =2，∴ m →=(1,1,2)；可设F(a, 0, 0)，则FE →=(4−a,0,2)，DE →=(4,−4,2)；设平面DEF 的一个法向量为n →=(x,y,z)，则{n →⋅DE →=0n →⋅FE →=0⇒{2x −2y +z =0(4−a)x +2z =0 ；令x ＝2，则{x =2y =a 2z =a −4，∴ n →=(2,a2,a −4)；由平面DEF ⊥平面PCE ，得m →⋅n →=0，即2+a2+2a −8=0，a =125<4；∴ 点F(125,0,0)； ∴ AFAB =35． 24.【答案】解：过S 点作SD ⊥AC 于D ，过D 作DM ⊥AB 于M ，连接SM ，则∵ 平面SAC ⊥平面ACB ∴ SD ⊥平面ACB ∴ SM ⊥AB 又∵ DM ⊥AB∴ ∠DMS 为二面角S −AB −C 的平面角在△SAC 中SD =4×√32=2√3在△ACB 中过C 作CH ⊥AB 于H∵ AC =4，BC =4√2 ∴ AB =4√3∵ S =12AB ⋅CH =12AC ⋅BC ∴ CH =AC⋅BC AB =4⋅4√24√3=4√2√3∵ DM // CH 且AD =DC ∴ DM =12CH =2√2√3∵ SD ⊥平面ACB ，DM ⊂平面ACB ∴ SD ⊥DM在RT △SDM 中，SM =√SD 2+DM 2=√(2√3)2+(2√2√3)2=2√113，∴ cos ∠DMS =DM SM=√2211．【考点】二面角的平面角及求法【解析】过S 点作SD ⊥AC 于D ，过D 作DM ⊥AB 于M ，连接SM ，则∠DMS 为二面角S −AB −C 的平面角，求出DM ，SM ，即可得出结论．【解答】解：过S 点作SD ⊥AC 于D ，过D 作DM ⊥AB 于M ，连接SM ，则∵ 平面SAC ⊥平面ACB ∴ SD ⊥平面ACB ∴ SM ⊥AB 又∵ DM ⊥AB∴ ∠DMS 为二面角S −AB −C 的平面角在△SAC 中SD =4×√32=2√3在△ACB 中过C 作CH ⊥AB 于H∵ AC =4，BC =4√2 ∴ AB =4√3∵ S =12AB ⋅CH =12AC ⋅BC∴ CH =AC⋅BC AB=4⋅4√24√3=4√2√3∵ DM // CH 且AD =DC ∴ DM =12CH =2√2√3∵ SD ⊥平面ACB ，DM ⊂平面ACB ∴ SD ⊥DM在RT △SDM 中，SM =√SD 2+DM 2=√(2√3)2+(2√2√3)2=2√113，∴ cos ∠DMS =DM SM=√2211． 25.【答案】解：∵ 正方形ABCD 的对角线BD 为棱折成直二面角， ∴ 平面ABD ⊥平面BCD ，又∵ AO ⊥BD ，平面ABD ∩平面BCD =BD ，AO ⊂平面ABD ， ∴ AO ⊥平面BCD ，则OC ，OA ，OD 两两互相垂直. 如图，以O 为原点，建立空间直角坐标系O −xyz ．则O(0, 0, 0)，A(0, 0, √22)，C(√22, 0, 0)，B(0, −√22, 0)，D(0, √22, 0)，OA →=(0, 0, √22)是平面BCD 的一个法向量． AC →=(√22, 0, −√22)，BC →=(√22, √22, 0)，设平面ABC 的法向量n →=(x, y, z)，则n →⋅BC →=0，n →⋅AC →=0．即√22x −√22z =0，且√22x +√22y =0，所以y =−x ，且z =x ，令x =1，则y =−1，z =1，解得n →=(1, −1, 1)．从而cos <n →，OA →>=|n →|⋅|OA →|˙=√33，二面角A −BC −D 的余弦值为√33．【考点】二面角的平面角及求法【解析】由已知可得AO ⊥平面BCD ，则OC ，OA ，OD 两两互相垂直，以O 为原点，建立空间直角坐标系O −xyz ，分别求出平面ACD 和平面BCD 的法向量，代入向量夹角公式，即可得到二面角A −CD −B 的余弦值．【解答】解：∵ 正方形ABCD 的对角线BD 为棱折成直二面角， ∴ 平面ABD ⊥平面BCD ，又∵ AO ⊥BD ，平面ABD ∩平面BCD =BD ，AO ⊂平面ABD ， ∴ AO ⊥平面BCD ，则OC ，OA ，OD 两两互相垂直. 如图，以O 为原点，建立空间直角坐标系O −xyz ．则O(0, 0, 0)，A(0, 0, √22)，C(√22, 0, 0)，B(0, −√22, 0)，D(0, √22, 0)， OA →=(0, 0, √22)是平面BCD 的一个法向量． AC →=(√22, 0, −√22)，BC→=(√22, √22, 0)，设平面ABC 的法向量n →=(x, y, z)，则n →⋅BC →=0，n →⋅AC →=0．即√22x −√22z =0，且√22x +√22y =0，所以y =−x ，且z =x ，令x =1，则y =−1，z =1，解得n →=(1, −1, 1)．从而cos <n →，OA →>=|n →|⋅|OA →|˙=√33，二面角A −BC −D 的余弦值为√33． 26. 【答案】解：(1)∵ AC =√3，AB =1，∠ABC =60∘，∴ ∠BAC =90∘， ∴ BA ⊥AC ．∵ AA 1⊥平面ABC ，∴ BA ⊥AA 1且AC ∩AA 1=A ， ∴ BA ⊥平面AA 1C 1C ．取A 1C 的中点M ，连结AM ，如图所示，则BA ⊥AM .又∵ AA 1=AC ，∴ A 1AC 为等腰三角形， ∴ AM ⊥A 1C ，∴ AM 即为异面直线AB 与A 1C 的距离． ∵ AA 1=√3， ∴ AM =√62． (2)连结BM ，如图所示，由(1)可知AM ⊥A 1C .又∵ AA 1=AC =√3，AB =1， AA 1⊥AB ，AB ⊥AC ， ∴ A 1B =BC =2．∴ △A 1BC 为等边三角形，∴ BM ⊥A 1C ，则∠AMB 即为二面角A −A 1C −B 的平面角． ∵ AB =1，AM =√62，BM =√102， ∴ cos ∠AMB =AM BM=√155． ∴ 二面角A −A 1C −B 的余弦值为√155. 【考点】直线与平面垂直的判定点、线、面间的距离计算二面角的平面角及求法【解析】（1）利用线面垂直判定定理证明 BA ⊥平面AA 1C 1C ，然后取A 1C 中点M 连结AM ．证明AM 即为异面直线AB 与A 1C 的距离．（2）由（1）可知AM ⊥A 1C ，证明BM ⊥A 1C ，则∠AMB 即为所求角．求余弦值即可．【解答】解：(1)∵ AC =√3，AB =1，∠ABC =60∘， ∴ ∠BAC =90∘， ∴ BA ⊥AC ．∵ AA 1⊥平面ABC ，∴ BA ⊥AA 1且AC ∩AA 1=A ， ∴ BA ⊥平面AA 1C 1C ．取A 1C 的中点M ，连结AM ，如图所示，则BA ⊥AM .又∵ AA 1=AC ，∴ A 1AC 为等腰三角形， ∴ AM ⊥A 1C ，∴ AM 即为异面直线AB 与A 1C 的距离． ∵ AA 1=√3， ∴ AM =√62． (2)连结BM ，如图所示，由(1)可知AM ⊥A 1C .又∵ AA 1=AC =√3，AB =1， AA 1⊥AB ，AB ⊥AC ， ∴ A 1B =BC =2．∴ △A 1BC 为等边三角形，∴ BM ⊥A 1C ，则∠AMB 即为二面角A −A 1C −B 的平面角． ∵ AB =1，AM =√62，BM =√102， ∴ cos ∠AMB =AMBM =√155． ∴ 二面角A −A 1C −B 的余弦值为√155. 27.【答案】解：以D 为原点，分别以DA 、DC 、DD′为x ，y ，z 轴，建立空间直角坐标系，设正方体的棱长为2，则B(2, 2, 0)，E(2, 0, 1)，C ‘(0, 2, 2)， ∴ BE →=(0,−2,1)，BC ′→=(−2,0,2)，设平面BEC′的法向量n →=(x,y,z)，则{n →⋅BC ′→=−2x +2z =0˙，取x =1，得n →=(2,1,2)，由题意知平面ABCD 的法向量m →=(0,0,1)，设平面BEC′与平面ABCD 所成的角的平面角为θ，则cos θ=cos <m →，n →>=√4+1+4=23．∴ 平面BEC′与平面ABCD 所成的角的余弦值为23．【考点】二面角的平面角及求法【解析】以D 为原点，分别以DA 、DC 、DD′为x ，y ，z 轴，建立空间直角坐标系，利用向量法能求出平面BEC′与平面ABCD 所成的角的余弦值．【解答】解：以D 为原点，分别以DA 、DC 、DD′为x ，y ，z 轴，建立空间直角坐标系，设正方体的棱长为2，则B(2, 2, 0)，E(2, 0, 1)，C ‘(0, 2, 2)， ∴ BE →=(0,−2,1)，BC ′→=(−2,0,2)，设平面BEC′的法向量n →=(x,y,z)，则{n →⋅BC ′→=−2x +2z =0˙，取x =1，得n →=(2,1,2)，由题意知平面ABCD 的法向量m →=(0,0,1)，设平面BEC′与平面ABCD 所成的角的平面角为θ，则cos θ=cos <m →，n →>=√4+1+4=23． ∴ 平面BEC′与平面ABCD 所成的角的余弦值为2．328.【答案】证明：取CD的中点E，连接BE∵AC=AD，CE=ED，∠DAC=60∴AE⊥CD，AC=AD=CD∴CD=2，CE=ED=1CD=1，AE2=AC2−CE2=4−1=32BC2=BD2=AC2+AB2−2AC⋅BCcs∠BAC=4+9−2⋅2⋅3⋅cos60∘=7，△BCD是等腰三角形．∴BE⊥CD，BE∩AE=E，∴CD⊥平面ABE，且BE2=BC2−CE2=7−1=6∴AE2+BE2=3+6=9=AB2∴BE⊥AE，∴AE⊥面BCD∴平面BCD⊥平面ADC．【考点】平面与平面垂直的判定【解析】取CD的中点E，连接BE，通过计算证明BE⊥CD，AE⊥CD，推出AE⊥面BCD，推出平面BCD⊥平面ADC．【解答】证明：取CD的中点E，连接BE∵AC=AD，CE=ED，∠DAC=60∴AE⊥CD，AC=AD=CD∴CD=2，CE=ED=1CD=1，AE2=AC2−CE2=4−1=32BC2=BD2=AC2+AB2−2AC⋅BCcs∠BAC=4+9−2⋅2⋅3⋅cos60∘=7，△BCD是等腰三角形．∴BE⊥CD，BE∩AE=E，∴CD⊥平面ABE，且BE2=BC2−CE2=7−1=6∴AE2+BE2=3+6=9=AB2∴BE⊥AE，∴AE⊥面BCD∴平面BCD⊥平面ADC．29.【答案】(1)证明：∵AB=2PB=4BM，∴PM⊥AB，又∵PM⊥CD，且AB∩CD，∴PM⊥面ABCD.∵PM⊂面PAB，∴面PAB⊥面ABCD；(2)解：由(1)知：面ABCD⊥面PAB，延长BA与CD交于一点H，作AN⊥PH，连接ND，则∠AND就是平面PAB与平面PCD的二面角的平面角，令AB=BC=2PB=2AD=4BM=4t，∵ADBC =AHBH，解得AH=4t.又AM=3t，PM=√3t，PH=2√13t，△HNA∼△HMP，∴ANPM =AHPH，∴ AN=2√3913t，DN=8√1313，∴sin∠AND=√134，∴平面PAB与平面PCD的二面角的正弦值是√134．【考点】二面角的平面角及求法平面与平面垂直的判定【解析】（1）由已知条件推导出PM⊥AB，从而得到PM⊥面ABCD，由此能证明面PAB⊥面ABCD．（2）延长AB与CD交于一点H，作AN⊥PH，连接ND，则∠AND就是平面PAB与平面PCD的二面角的平面角，由此能求出平面PAB与平面PCD的二面角的正弦值．【解答】(1)证明：∵AB=2PB=4BM，∴PM⊥AB，又∵PM⊥CD，且AB∩CD，∴PM⊥面ABCD.∵PM⊂面PAB，∴面PAB⊥面ABCD；(2)解：由(1)知：面ABCD⊥面PAB，延长BA与CD交于一点H，作AN⊥PH，连接ND，则∠AND就是平面PAB与平面PCD的二面角的平面角，令AB=BC=2PB=2AD=4BM=4t，∵ADBC =AHBH，解得AH=4t.又AM=3t，PM=√3t，PH=2√13t，△HNA∼△HMP，∴ANPM =AHPH，∴ AN=2√3913t，DN=8√1313，∴sin∠AND=√134，∴平面PAB与平面PCD的二面角的正弦值是√134．30.【答案】解：如下图所示：因为AB⊥平面BCD，AB⊂平面ABC，所以平面ABC⊥平面BCD．②平面ABD⊥平面BCD．因为AB⊥平面BCD，AB⊂平面ABD，所以平面ABD⊥平面BCD．③平面ABC⊥平面ACD．因为AB⊥平面BCD，CD⊂平面BCD，所以AB⊥CD；又BC⊥CD，且AB∩BC=B，所以CD⊥平面ABC．又CD⊂平面ACD，所以平面ABC⊥平面ACD．【考点】平面与平面垂直的判定【解析】由已知中已知AB⊥平面BCD，BC⊥CD，结合线面垂直及面面垂直的判定定理，我们对三棱锥的四个平面：平面ABC，平面ABD，平面BCD和平面ACD之间的关系逐一进行判断，即可得到结论．【解答】解：如下图所示：①平面ABC⊥平面BCD．因为AB⊥平面BCD，AB⊂平面ABC，所以平面ABC⊥平面BCD．②平面ABD⊥平面BCD．因为AB⊥平面BCD，AB⊂平面ABD，所以平面ABD⊥平面BCD．③平面ABC⊥平面ACD．因为AB⊥平面BCD，CD⊂平面BCD，所以AB⊥CD；又BC⊥CD，且AB∩BC=B，所以CD⊥平面ABC．又CD⊂平面ACD，所以平面ABC⊥平面ACD．31.【答案】(1)证明：∵平面ABCD⊥平面ABEF，CB⊥AB，平面ABCD∩平面ABEF=AB，∴CB⊥平面ABEF．∵AF⊂平面ABEF，∴AF⊥CB.又∵AB为圆O的直径，∴AF⊥BF，∴AF⊥平面CBF．∵AF⊂平面DAF，(2)解：过点A作AM⊥EF，交EF的延长线于点M，连接DM，过点F作FH⊥AB，垂足为H.由(1)可知，DA⊥平面ABEF，又AM∩DA=A，∴ EF⊥平面DAM，则DM⊥EF，∴∠DMA为二面角D−FE−B的平面角，即∠DMA=60∘．在Rt△AFH中，易得AH=12，AF=1，∴FH=√32．又∵四边形AMFH为矩形，∴MA=FH=√32，∴ AD=MA⋅tan∠DMA=√32×√3=32，因此，当AD的长为32时，二面角D−FE−B的大小为60∘．【考点】平面与平面垂直的判定二面角的平面角及求法【解析】（1）欲证平面DAF⊥平面CBF，先证直线与平面垂直，由题意可得：CB⊥平面ABEF，所以AF⊥CB，又在底面圆中AF⊥BF，所以AF⊥平面CBF，进一步易得平面DAF⊥平面CBF（2）本题的设问是递进式的，第（1）问是为第（2）问作铺垫的．根据（1）的证明，有AF⊥平面CBF，所以FB为AB在平面CBF上的射影，则∠ABF为直线AB与平面CBF所成的角．（3）二面角的度量关键在于找出它的平面角，构造平面角常用的方法就是三垂线法．由DA⊥平面ABEF可知：过点A作AM⊥EF，交EF的延长线于点M，连接DM，所以∠DMA为二面角D−FE−B的平面角，∠DMA＝60∘．【解答】(1)证明：∵平面ABCD⊥平面ABEF，CB⊥AB，平面ABCD∩平面ABEF=AB，∴CB⊥平面ABEF．∵AF⊂平面ABEF，∴AF⊥CB.又∵AB为圆O的直径，。

《平面与平面垂直的判定》习题

《平面与平面垂直的判定》一、选择题:1、若三条直线OA 、OB 、OC 两两垂直，则直OA 垂直于（ )A 平面OAB B 平面OAC C 平面OBCD 平面ABC2、设α、γβ、为不同的平面，l 、m 为两条不同的直线,则下列条件中不能推出α⊥β的是（ )A l ⊥m,l ⊥α，m ⊥βB l ⊥m ，l ⊆α，m ⊆βC α⊥γ，β∥γD l ∥m ，l ⊥α，m ⊆β3、在四棱锥P －ABCD 中，底面ABCD 是矩形，若PA ⊥平面ABCD ，则在此四棱锥的五个面中互相垂直的平面共有( ）A 3对B 4对C 5对D 6对4、已知直线m 、n 与平面α β ∧⎥ *}若m ∥α,n ∥α，则m ∥n ；②若m ∥α,n ⊥α,则n ⊥m ；③若m ⊥α，m ∥β，则α⊥β．其中真命题的个数是( ）A 0B 1C 2D 35、设α、β 为两个不同的平面，l 、m 为两条不同的直线，且l ⊂α,m ⊂β，有如下的两个命题:①若α∥β，则l ∥m ；②若l ⊥m ，则α⊥β．那么( ）A ①是真命题，②是假命题B ①是假命题，②是真命题C ①②都是真命题D ①②都是假命题6、在正四面体P －ABC 中,D ，E ,F 分别是AB ，BC ，CA 的中点，下面四个结论中不成立．．．的是（ )A BC //平面PDFB DF ⊥平面P AEC 平面PDF ⊥平面ABCD 平面P AE ⊥平面ABC二、填空题7、已知平面βα,和直线，给出条件：①α//m ;②α⊥m ；③α⊂m ;④βα⊥;⑤βα//。

(i ）当满足条件时,有β//m ；(ii)当满足条件时，有β⊥m 。

(填所选条件的序号）8、已知直线AO ⊥平面α于O ，直线OB ⊥AO,则OB 与平面α的关系是。

9、直角三角形ABC 的斜边在平面α内,两条直角边分别与平面α成30°和45°，则这个直角三角形所在的平面与平面所成二面角为。

面面垂直答案

1.已知如图，Pe 平面 ABC, PA=PB 二PC, ZAPB=ZAPC=60° , ZBPC 二90 ° 求证：平而 ABe 丄平而PBC【答案】【解析】要证明面面垂直，只线，然后证明直线与另一平面∏,证明An 垂直平PBC 即可证明：取BC 中点D 连结Am PnTPA=PB; Z APB=6O β .,.ΔPAB 为正三角形同≡ΔPAC 为正三角形设 PA=a在RTΔBPC 中，PB=PC=aBC=∖2a √2 .,.p∏=——a 2 ⅛ΔABC 中AΓ)=√AB 2-BD 2=a 2=AP 2.∙∙ΔAP∏为直角三角形即AD 丄DP 又 √AΓ)±BC.,.AΓ)丄平面PBC・・・平面ABC 丄平面PBC2.如图 ⑴ 在直角梯形ABCr)中，AB∕∕CP, AB 丄AD 且AB=AD=-CP=I, ≡以2AD 为一边向梯形外作正方形ADEF,然后沿AD 将正方形翻拆，使平面AnEF 与平面 ABCr)互相垂直如图(2)o要在其呈平面内找一条垂直即可。

显然BC 中点√2 VEE(1)求证平面BDE丄平面BEC(2)求直线BD与平面BEF所成角的正弦值。

AH 1【答案】⑴证见解析⑵Sin^ =-DD 2【解析】(1)由折前折后线面的位直关系得ED丄平面ABCD^ UED丄BC, 又在MCD中，DB = BC =近,DC = 2,三边满足勾股定理,:.BC丄BD°由线面垂宜的判定定理即证得结论。

(2)因为DB = Jl,只雲求出点D到平面BEF的距离也是点A到平面BEF的距宵，易证出AD//EF , AQ丄平面B由面面垂直的判定定理得平面A3F丄平面BEF y WF中3F边上的高就是点A到平面BEF的距离。

根据线面角的定义可求直线Bn与平面BEF所成角的正弦值。

3・(本小题满分14分)如图，在正方体ABCD-A X B X C X n X中，E、F为棱人∕λ的中点・(1)求证：EF"平面CB(2)求证：平面CAA}C}丄平面CB I D}・【答案】(I )晒(∏ )略【解析】(1 )证明：连结处在长方体AG中，BDHB x D x. ......... 2 分又・・・E、F为棱AD. AB的中点，/. EFIIBD . . EFI IBp・........ 4分又民D平面CB l D l, EFg平面CBwEFH平面CBa. .......... 7分(2)•••在长方体AC中，£4】丄平面AAGr＞、,而厲门平面A l B I C.∖AA l丄Bm…9分又・・•在正方形 Zee中，内G丄5C,・・・5C丄平面CAA I C l・又・・・51P1平面CBU・平面CAA X G丄平面CB X D X・……14分4 .如图，四棱锥P-ABCD中，底面ABCD为平行四边形，AB = 2AD=2i BD =忑，PD丄底面ABCD.⑴证明：平面PBC 丄平面PBZ )；(2)若二面角P-BC-D 为2,求4P 与平面PBC 所成角的正弦值。

线面垂直与面面垂直答案OK

线面垂直与面面垂直答案第一部分1、答案 C解析①为假命题，m不一定与平面Q垂直，所以平面P与Q不一定垂直．命题②与③为假命题，②中两平面可以相交，③没有任何实质意义．只有④是真命题，因为两平面的垂线所成的角与两平面所成的角相等或互补．2.答案 B解析据题意可知对于命题p，显然与一平面都垂直的两平面的位置关系是平行或相交，如将一本书打开，每一张纸所在平面都与桌面垂直，但这些平面相交，即命题p是假命题；对命题q，只需使平面α内的两点连线与平面β平行，使第三点与这两点的连线与平面β的交点为线段的中点即可满足条件，故命题q 是假命题；A.由于p和q都是假命题，因此命题：“p且q”应为假命题；B.由于p和q都是假命题，故“p或q”应为假命题．故B正确；C错误；D.由于p 和q都是假命题，故非p和非q都是真命题，从而“非p或非q”为真命题，故D是错误的．3.答案 A解析∵AD⊥DF，AB⊥BE∵B、C、D重合记为H∴AH⊥HF，AH⊥HE∴AH⊥面EFH.4.答案①③④解析①③④正确．②中，可能有m∥β，故②不正确．5.答案 D解析根据面面垂直的性质定理，得选项B、C正确．对于A，由于过点P 垂直于平面α的直线必平行于β内垂直于交线的直线，因此平行于平面β.因此A 正确．6.答案 A解析∵CA⊥AB，CA⊥BC1，AB∩BC1＝B，∴CA⊥平面ABC1.∴平面ABC⊥平面ABC1.∴过C1作垂直于平面ABC的直线在平面ABC1内，∴H∈AB.7、答案(1)(2)解析(1)α内两条相交直线分别平行于平面β，则两条相交直线确定的平面α平行于平面β，正确．(2)平面α外一条直线l与α内的一条直线平行，则l平行于α，正确．(3)如图，α∩β＝l，a⊂α，a⊥l，但不一定有α⊥β，错误．(4)直线l与α垂直的充分必要条件是l与α内的两条相交直线垂直，而该命题缺少“相交”两字，故为假命题．综上所述，真命题的序号为(1)(2)．8、答案 ①②③解析由题意知P A ⊥平面ABC ，∴P A ⊥BC .又AC ⊥BC ，P A ∩AC ＝A ，∴BC ⊥平面P AC .∴BC ⊥AF .∵AF ⊥PC ，BC ∩PC ＝C ，∴AF ⊥平面PBC ， ∴AF ⊥PB ，AF ⊥BC .又AE ⊥PB ，AE ∩AF ＝A ， ∴PB ⊥平面AEF .∴PB ⊥EF .故①②③正确9、如图所示，取CD 的中点G ，连结EG 、FG 、EF . ∵E 、F 分别为AD 、BC 的中点，∴EG 綊12AC ，FG 綊12BD .又AC ＝BD ，∴FG ＝12AC .∴在△EFG 中，EG 2＋FG 2＝12AC 2＝EF 2.∴EG ⊥FG .∴BD ⊥AC .又∠BDC ＝90°，即BD ⊥CD ，AC ∩CD ＝C ，∴BD ⊥平面ACD .10、解析 (1)由长方体ABCD －A 1B 1C 1D 1知，AE ⊥平面AA 1D 1D ， ∵A 1D ⊂平面AA 1D 1D ，∴AE ⊥A 1D .又∵AD ＝AA 1，∴四边形AA 1D 1D 是正方形，∴A 1D ⊥AD 1.又∵AD 1∩AE ＝A ，∴A 1D ⊥平面AD 1E ，又∵D 1E ⊂平面AD 1E ，∴D 1E ⊥A 1D .(2)设点E 到平面ACD 1的距离为h ，在△ACD 1中，AC ＝CD 1＝5，AD 1＝2，AD 1上的高为(5)2－(22)2，∴S △AD 1C ＝12 ·2·(5)2－(22)2＝32，而S △AEC ＝12AE ·BC ＝12，∵VD 1－AEC ＝13S △AEC ·DD 1＝13S △AD 1C ·h ，∴12×1＝32×h ，∴h ＝13，∴点E 到平面ACD 1的距离是13.11、证明 (1)取CE 中点P ，连结FP 、BP ，∵F 为CD 的中点，∴FP∥DE，且FP＝12DE.又AB∥DE，且AB＝12DE，∴AB∥FP，且AB＝FP，∴ABPF为平行四边形，∴AF∥BP.又∵AF⊄平面BCE，BP⊂平面BCE，∴AF∥平面BCE.(2)∵△ACD为正三角形，∴AF⊥CD. ∵AB⊥平面ACD，DE∥AB，∴DE⊥平面ACD.又AF⊂平面ACD，∴DE⊥AF.又AF⊥CD，CD∩DE＝D，∴AF⊥平面CDE.又BP∥AF，∴BP⊥平面CDE.又∵BP⊂平面BCE，∴平面BCE⊥平面CDE.12、解析(1)设AC与BD交于点G.因为EF∥AG，且EF＝1，AG＝12AC＝1，所以四边形AGEF为平行四边形，所以AF∥EG.因为EG⊂平面BDE，AF⊄平面BDE，所以AF∥平面BDE.(2)连结FG.因为EF∥CG，EF＝CG＝1，且CE＝1，所以四边形CEFG为菱形，所以CF⊥EG.因为四边形ABCD为正方形，所以BD⊥AC，又因为平面ACEF⊥平面ABCD，且平面ACEF∩平面ABCD＝AC，所以BD⊥平面ACEF.所以CF⊥BD.又BD∩EG＝G，所以CF⊥平面BDE.13、证明(1)∵P A⊥底面ABCD，∴CD⊥P A，又CD⊥AC，P A∩AC＝A，故CD⊥平面P AC，AE⊂平面P AC，故CD⊥AE.(2)∵P A＝AB＝BC，∠ABC＝60°，故P A＝AC.∵E是PC的中点，故AE⊥PC.由(1)知CD⊥AE，。

面面垂直的判定习题详细答案

题目二解析
题目二
在四面体$P-ABC$中，已知$angle APB = angle BPC = angle CPA = 90^{circ}$，求证：平面$PAB perp$平面$PBC$。
解析
首先，由于$angle APB = angle BPC = angle CPA = 90^{circ}$，我们可以得出$PA perp PB$、$PB perp PC$和$PC perp PA$。根据空间直线与平面的垂直关系，我们可以得出$PA perp$平面$PBC$、$PB perp$平面$PAC$和$PC perp$平面$PAB$。由于平面$PAB cap$平面$PBC = PB$，根据两平面垂直于第三
解析
题目三
对于结论$①$
由于正方体的性质，我们知道AC₁和AE都经过点A，所以它们是共面的。因此，
AC₁E不是异面直线。结论$①$不正确。
对于结论$③$
由于正方体的性质，我们知道AC₁不在平面ABCD内。所以结论$③$是正确的。
对于结论$②$
由于AC₁不在平面BDE内，所以结论$②$ 是正确的。
平面内的直线
一条直线如果在某个平面上，则称这条直线为该平面的内直
线。
THANKS FOR WATCHING
感谢您的观看
质，我们可以得出平面 ABDtextsuperscript{⊥}平面BCD。
04 知识点总结
面面垂直的判定定理
判定定理
如果一个平面内的一条直线与另一个平面垂直，则这两个平面互相垂直。
推论
如果两个平面互相垂直，则其中一个平面内的一条直线与另一个平面垂直。
解题技巧和注意事项
技巧
在解题时，首先确定已知条件和未知量，然后根据判定定理和推论，构建数学模型和方程。

面面垂直的判定习题详细答案

面面垂直答案

平面与平面垂直的判定基础练习题含答案解析

立体几何第六讲面面垂直练习题(含答案)

面面垂直的性质习题详细答案

面面垂直证明例题

面面垂直的判定

面面垂直的性质习题详细答案

线线垂直、线面垂直、面面垂直的习题及答案解析

2023高考数学复习专项训练《面面垂直的判定》(含解析)

面面垂直证明例题（最终定稿）

(完整版)面面垂直的判定+性质定理(例题)

高中数学必修二 8 6 3 平面与平面垂直(第2课时)平面与平面垂直的性质 练习(含答案)

平面与平面垂直的判定试题含答案

《平面与平面垂直的判定》习题

面面垂直答案

线面垂直与面面垂直答案OK

面面垂直的判定习题详细答案

高中数学必修二 8 6 3 平面与平面垂直(第2课时)平面与平面垂直的性质练习(含答案)