初中数学基础测试专项训练: 特殊四边形相关的折叠问题(含答案)
特殊四边形中的旋转、翻折问题

专题02 特殊四边形中的旋转、翻折问题题型一 菱形中的旋转、翻折问题1.如图,在菱形纸片ABCD 中,60A Ð=°,点E 在BC 边上,将菱形纸片ABCD 沿DE 折叠,点C 落在AB 边的垂直平分线上的点C ¢处,则DEC Ð的大小为( )A .30°B .45°C .60°D .75°【解答】解:连接BD ,如图所示:Q 四边形ABCD 为菱形,AB AD \=,60A Ð=°Q ,ABD \D 为等边三角形,120ADC Ð=°,60C Ð=°,P Q 为AB 的中点,DP \为ADB Ð的平分线,即30ADP BDP Ð=Ð=°,90PDC \Ð=°,\由折叠的性质得到45CDE PDE Ð=Ð=°,在DEC D 中,180()75DEC CDE C Ð=°-Ð+Ð=°.故选:D .2.如图,在平面直角坐标系中,四边形OABC 是菱形,120AOC Ð=°,点B 的坐标为(6,0),点D 是边BC 的中点,现将菱形OABC 绕点O 顺时针旋转,每秒旋转60°,则第2021秒时,点D 的坐标为( )A .9(2B .9(2-,C .9(2,D .9(2-【解答】解:如图,连接OD ,过点C 作CH OB ^于H ,Q 四边形OABC 是菱形,120AOC Ð=°,点B 的坐标为(6,0),6OB \=,OC BC =,60BOC Ð=°,BOC \D 是等边三角形,6OC OB BC \===,Q 点D 是BC 中点,OD BC \^,3BD =,OD \==,CH OB ^Q ,60COB Ð=°,3OH BH \==,CH ==,\点(3,C -,Q 点D 是BC\点9(2D ,,Q 将菱形OABC 绕点O 顺时针旋转,每秒旋转60°,\第1秒后,点1D 坐标为(0,-,第2秒后,点2D 坐标为9(2-,,第3秒后,点3D 坐标为9(2-,,第4秒后,点4D 坐标为(0,,第5秒后,点5D 坐标为9(2,第6秒后,点6D 坐标为9(2,,¼由上可知,点D 的坐标每6个为一组依次循环着,202163715\¸=¼,\第2021秒时,点D 的坐标为9(2,故选:A .3.如图,菱形OABC 的一边OA 在x 轴上,将菱形OABC 绕原点O 逆时针旋转105°至111OA B C 的位置,若2OA =,120C Ð=°,则点1B 的坐标为( )A .(-B .(3,C .(D .【解答】解:连接AC 与OB 相交于点E ,过点1B 作1BF x ^轴,垂足为F ,Q 四边形OABC 为菱形,120C Ð=°,OA OC =,60AOC \Ð=°,2OC OA AC ===,AC OB ^Q ,\在Rt OAE D 中,2OA =,112AE AC ==,OE \===,OB \=,又1302AOB AOC Ð=Ð=°Q ,1105BOB Ð=°,111801803010545B OF AOB BOB \Ð=°-Ð-Ð=°-°-°=°,在Rt △1B OF 中,1OB OB ==,1OF B F =,22211OF B F OB \+=,可得1OF B F ==,Q 点1B 在第二象限,\点1B 的坐标为(.故选:C .4.如图,在正方形ABCD 中,顶点A ,B ,C ,D 在坐标轴上,且(4,0)B ,以AB 为边构造菱形ABEF ,将菱形ABEF 与正方形ABCD 组成的图形绕点O 顺时针旋转,每次旋转45°,则第164次旋转结束时,点164F 的坐标为( )A .(4-,B .(4,--C .,4)-D .(-,4)-【解答】解:Q 点(4,0)B ,4OB \=,4OA \=,AB \==,Q 四边形ABEF 是菱形,AF AB \==,\点F ,4),由题意可得每次8旋转一个循环,1648204\¸=¼,\点164F 的坐标与点F 坐标关于原点对称,\点164F 的坐标(-,4)-,故选:D .5.如图,已知菱形ABCD 的边长2,60A Ð=°,点E 、F 分别在边AB 、AD 上,若将AEF D 沿直线EF 折叠,使得点A 恰好落在CD 边的中点G 处,则EF【解答】解:延长CD ,过点F 作FM CD ^于点M ,连接GB 、BD ,作FH AE ^交于点H ,如图所示:60A Ð=°Q ,四边形ABCD 是菱形,60MDF \Ð=°,30MFD \Ð=°,设MD x =,则2DF x =,FM =,1DG =Q ,1MG x \=+,222(1))(22)x x \++=-,解得:0.3x =,0.6DF \=, 1.4AF =,10.72AH AF \==,sin 1.4FH AF A =Ð==g ,CD BC =Q ,60C Ð=°,DCB \D 是等边三角形,G Q 是CD 的中点,BG CD \^,2BC =Q ,1GC =,BG \=,设BE y =,则2GE y =-,222(2)y y \+=-,解得:0.25y =,1.75AE \=,1.750.7 1.05EH AE AH \=-=-=,EF \===.6.已知菱形ABCD 中,120ABC Ð=°,12AB =,点E ,F 分别在边AD ,AB 上,将AEF D 沿着直线EF 折叠,使得点A 落在G 点.(1)如图1,若点G 恰好落在AC 上,且3CG =,求DE 的长;(2)如图2,若点G 恰好落在BD 上,且3BG =,求DE 的长.【解答】解:(1)连接BD ,交AC 于点O ,Q 四边形ABCD 是矩形,1602ABD ABC \Ð=Ð=°,90AOB Ð=°,2AC AO =,在Rt AOB D 中易得到AO =,AC =Q 菱形ABCD 中,AD DC =,DAC DCA \Ð=Ð,Q 点A 与点G 关于EF 轴对称,AE EG \=,DAC EGA \Ð=Ð,DCA EGA \Ð=Ð,//EG DC \,\DE CG AD AC =,\12DE =,DE \=.(2)Q菱形ABCD中,120ABCÐ=°,AD AB\=,60AÐ=°,ABD\D是等边三角形,60EDG FBGÐ=Ð=°,又由翻折可得60EGF AÐ=Ð=°,又EGB EGF FGB DEG EDG Ð=Ð+Ð=Ð+Ð,FGB DEG\Ð=Ð.DEG BGF\D D∽,\DE DG EG BG BF FG==,设DE x=,则12EG AE x==-,\9123x xBF FG-==,27BFx\=,363x FGx-=,又12 AB AF BF FG BF=+=+=,\2736312xx x-+=,解得:215x=,即215 DE=.7.四边形ABCD为菱形,BD为对角线,在对角线BD上任取一点E,连接CE,把线段CE绕点C顺时针旋转得到线段CF,使得ECF BCDÐ=Ð,点E的对应点为点F,连接DF.(1)如图1,求证:BE DF=;(2)如图2,若2DFC DBCÐ=Ð,在不添加任何辅助线的前提下,请直接写出五对线段,使每对线段的和等于(BD BE和DE除外).【解答】(1)证明:Q 四边形ABCD 为菱形,BC CD \=,Q 把线段CE 绕点C 顺时针旋转得到线段CF ,CE CF \=,ECF BCD Ð=ÐQ ,BCE DCF \Ð=Ð,在BCE D 与DCF D 中,BC CD BCE DCF CE CF =ìïÐ=Ðíï=î,()BCE DCF SAS \D @D ,BE DF \=.(2)解:BCE DCF D @D Q ,BE DF \=,BEC DFC Ð=Ð,CB CD =Q ,CBD CDE \Ð=Ð,2DFC CBD Ð=ÐQ ,2BEC CDE \Ð=Ð,CEB CDE ECD Ð=Ð+ÐQ ,EDC ECD \Ð=Ð,ED EC CF \==,BD BE EC BE CF DF DE DF CE DF CF \=+=+=+=+=+.8.如图,平行四边形ABCD 中,AB AC ^,1AB =,BC =,对角线AC ,BD 相交于点O ,将直线AC 绕点O 顺时针旋转,分别交BC ,AD 于点E ,F .(1)证明:当90AOF Ð=°时,四边形ABEF 是平行四边形;(2)试说明在旋转过程中,AF 与CE 总保持相等;(3)在旋转过程中,四边形BEDF 可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AOF Ð度数.【解答】(1)证明:当90AOF Ð=°时,//AB EF ,//AF BE Q ,\四边形ABEF 是平行四边形.(2)证明:Q 四边形ABEF 是平行四边形,AO CO \=,//AF EC ,FAO ECO \Ð=Ð,在AOF D 和COE D 中,FAO OCE OA OCAOF COE Ð=Ðìï=íïÐ=Ðî,AOF COE \D @D ,AF CE \=.(3)解:结论:四边形BEDF 可能是菱形.AOF COE D @D Q ,OE OF \=,EF \与BD 互相平分,\四边形BEDF 是平行四边形,\当EF BD ^时,四边形BEDF 是菱形,在Rt ABC D 中,2AC =,1OA AB \==,AB AC ^Q ,45AOB \Ð=°,45AOF \Ð=°,\当四边形BEDF 是菱形时,45AOF Ð=°.9.如图,在平面直角坐标系中,O 是菱形ABCD 对角线BD 的中点,//AD x 轴且4AD =,60A Ð=°,将菱形ABCD 绕点O 旋转,使点D 落在x 轴上,则旋转后点C 的对应点的坐标是( )A .(0,B .(2,4)-C .0)D .(0,或(0,-【解答】解:根据菱形的对称性可得:当点C 旋转到y 轴负半轴时,A 、B 、C 均在坐标轴上,如图,60BAD Ð=°Q ,4AD =,30OAD \Ð=°,2OD \=,AO OC \====,\点C 的坐标为(0,-,同理:当点C 旋转到y 轴正半轴时,点C 的坐标为,\点C 的坐标为或(0,-,故选:D .10.如图,在菱形ABCD 中,1AB =,60DAB Ð=°,把菱形ABCD 绕点A 顺时针旋转30°得到菱形AB C D ¢¢¢,其中点C 的运动路径为 CC ¢,则图中阴影部分的面积为 342p +【解答】解:连接CD ¢和BC ¢,60DAB Ð=°Q ,30DAC CAB \Ð=Ð=°,30C AB Т¢=°Q ,A \、D ¢、C 及A 、B 、C ¢分别共线.AC \=\扇形ACC ¢4p =,AC AC =¢Q ,AD AB¢=\在OCD D ¢和△OC B ¢中,CD BC ACO AC D COD C OB ¢=¢ìïÐ=Т¢íïТ=ТîOCD \D ¢@△()OC B AAS ¢.OB OD \=¢,CO C O=¢60CBC Т=°Q ,30BC O Т=°90COD \Т=°1CD AC AD ¢=-¢=-Q 1OB C O +¢=\在Rt BOC D ¢中,222(1)1)BO BO +-=解得12BO =,32C O ¢=-,1324OC B S BO C O ¢\=¢=-V g \图中阴影部分的面积为:3242OC B ACC S S p¢¢-=+V 扇形.故答案为:342p+-题型二 矩形中的旋转、翻折问题11.如图,在平面直角坐标系中,矩形OABC 的两边OA ,OC 分别在x 轴和y 轴上,并且5OA =,3OC =.若把矩形OABC 绕着点O 逆时针旋转,使点A 恰好落在BC 边上的1A 处,则点C 的对应点1C 的坐标为( )A .9(5-,12)5B .12(5-,95C .16(5-,125D .12(5-,16)5【解答】解:过点1C 作1C N x ^轴于点N ,过点1A 作1A M x ^轴于点M ,由题意可得:1190C NO A MO Ð=Ð=°,123Ð=Ð=Ð,则△1A OM ∽△1OC N ,5OA =Q ,3OC =,15OA \=,13A M =,4OM \=,\设3NO x =,则14NC x =,13OC =,则22(3)(4)9x x +=,解得:35x =±(负数舍去),则95NO =,1125NC =,故点C 的对应点1C 的坐标为:9(5-,12)5.故选:A .12.如图,在矩形ABCD 中,3AB =,4BC =,将矩形ABCD 绕点C 旋转,点A 、B 、D 的对应点分别为A ¢、B ¢、D ¢,当A ¢落在边CD 的延长线上时,边A D ¢¢与边AD 的延长线交于点F ,联结CF ,那么线段CF【解答】解:Q 四边形ABCD 是矩形,3AB CD \==,4AD BC ==,90ADC Ð=°,90A DF CDF ¢\Ð=Ð=°,由旋转的性质得:3CD CD ¢==,4A D AD ¢¢==,90ADC A D C ¢¢Ð=Ð=°,5A C ¢\==,532A D A C CD ¢¢\=-=-=,在Rt CDF D 和Rt △CD F ¢中,CF CF CD CD =ìí¢=î,Rt CDF Rt \D @△()CD F HL ¢,DF D F ¢\=,设DF D F x ¢==,则4A F x ¢=-,在Rt △A DF ¢中,由勾股定理得:2222(4)x x +=-,解得:32x =,32DF \=,CF \===.13.如图,矩形纸片ABCD 中,6AD =,E 是CD 上一点,连结AE ,ADE D 沿直线AE 翻折后点D 落到点F ,过点F 作FG AD ^,垂足为G .若3AD GD =,则DE 的值为( )A B .52C D 【解答】解:过点E 作EH FG ^,交FG 于点H ,如图,由题意:AEF AED D @D ,则6AF AD ==,DE EF =.6AD =Q ,3AD GD =,2GD \=.624AG AD DG \=-=-=.FG AD ^Q ,FG \===.Q 四边形ABCD 是矩形,90D \Ð=°,FG AD ^Q ,EH FG ^,\四边形GHED 为矩形.GH DE \=,2HE GD ==.设DE x =,则GH EF x ==,HF x =,在Rt HEF D 中,222HF HE EF +=Q ,\222)2x x -+=.解得:x =DE \=故选:C .14.如图,点E 在矩形ABCD 边CD 上,将ADE D 沿AE 翻折,点D 恰好落在BC 上的点F 处,若2AB CF =,3CE =,连接DF ,与AE 交于H 点,连接BH ,则点F 到BH 的距离为【解答】解:根据折叠的性质知:AD AF BC ==,DE EF =,AE 是线段DF 的垂直平分线,H 是DF 的中点,设DE EF x ==,则3DC AB x ==+,11(3)22FC AB x ==+,在Rt EFC D 中,222FC EC EF +=,即2221[(3)]32x x ++=,解得:5x =或3x =-(舍去),538DC AB \==+=,4FC =,设AD AF BC y ===,则4BF y =-,在Rt ABF D 中,222AB BF AF +=,即2228(4)y y +-=,解得:10y =,6BF \=,过H 作HN BC ^于N ,过F 作FM BH ^于M ,Q 四边形ABCD 是矩形,//HN CD \,142HN CD \==,122FN FC ==,8BN BF FN \=+=,由勾股定理得:BH ==,1122BHF S BF HN BH FM D =´=´Q ,BF HN FM BH ´\===15.如图,在平面直角坐标系中,四边形OABC 是矩形,6OA =,将ABC D 沿直线AC 翻折,使点B 落在点D 处,AD 交x 轴于点E ,若30BAC Ð=°,则点D 的坐标为( )A .2)-B .3)-C .3)-D .(3,-【解答】解:过D 点作DF x ^轴,垂足为F ,则//DF y 轴,Q 四边形AOCB 为矩形,90OAB AOC B \Ð=Ð=Ð=°,6BC AO ==,AB OC =,\=,OC AB12AC==,由折叠可知:30Ð=Ð=°,AD ABDAC BAC==,\Ð=°,OAE30OE\=,AE=,\=,ED//Q轴,DF y\Ð=Ð=°,30EDF EAODF=,\=,3EF\=+=,OF OE EF-,\点坐标为,3)D故选:B.16.如图,四边形ABCD中,//AD BC,AB BCBCDÐ=°,将CD绕点D逆时针旋转90°至ED,^,45延长AD交EC于点F.(1)求证:四边形ABCF是矩形;AD=,3(2)若2BC=,求AE的长.【解答】(1)证明://BCDÐ=°,^,45Q,AB BCAD BCBCD FDCÐ=Ð=°,\Ð=Ð=°,4590B BAFQ将CD绕点D逆时针旋转90°至ED,Ð=°,EDCDE DC\=,90EDF FDC\Ð=°=Ð,45\^,DF CE\Ð=°,AFC90即90Ð=Ð=Ð=°,B BAF AFC\四边形ABCF是矩形;(2)解:Q四边形ABCF是矩形,\==,AF BC3\=-=,321DFQ,90Ð=°,DFEÐ=°45EDF\Ð=Ð=°,45DEF EDF\==,1DF EF在Rt AFED中,由勾股定理得:AE===.AB=,217.如图,矩形OABC中,1¢¢,则AO=,将矩形OABC绕点O按顺时针转90°,得到矩形OA B CBB¢【解答】解:如图所示:Q矩形OABC中,1AB=,2AO=,将矩形OABC绕点O按顺时针转90°,得到矩形OA B C¢¢,B D¢=,\=,13BD则BB¢==..AB=,618.如图,在矩形ABCD中,4D沿AE折叠,使点B落在矩形BC=,点E为BC的中点,将ABE内点F处,连接CF,则CF的长为( )A .95B .125C .165D .185【解答】解:连接BF ,6BC =Q ,点E 为BC 的中点,3BE \=,又4AB =Q ,5AE \==,由折叠知,BF AE ^(对应点的连线必垂直于对称轴)125AB BE BH AE ´\==,则245BF =,FE BE EC ==Q ,90BFC \Ð=°,185CF \==.故选:D .19.已知,如图,四边形ABCD 中,90D Ð=°,AB AC =,DAC B Ð=Ð,点E 是BC 的中点.(1)求证:四边形AECD 是矩形;(2)若8AD =,6CD =,点F 是AD 上的点,连接CF ,把D Ð沿CF 折叠,使点D 落在点G 处.当AFG D 为直角三角形时,求CF 的长度.【解答】解:(1)证明:AB AC =Q ,B ACB \Ð=Ð.DAC B Ð=ÐQ ,DAC ACB \Ð=Ð.//AD EC \.AB AC =Q ,E 是BC 的中点,AE BC \^.90AEC \Ð=°.18090EAD AEC \Ð=°-Ð=°.90D Ð=°Q ,\四边形AECD 为矩形.(2)当90AGF Ð=°时,G 在AC 上,如图,8AD =Q ,6CD =,10AC \==.CG CD =Q ,4AG AC CG \=-=.设DF x =,则8AF x =-,GF DF x ==,由勾股定理得:222AG GF AF +=.2224(8)x x \+=-.解得:3x =.\CF ===当90AFC Ð=°时,G 在CE 上,此时四边形CDFG 为正方形,如图:CF \=;当90FAG Ð=°时,G 在AB 上,此时6CG CD ==,而8CE AD ==,Q斜边大于直角边,\不可能在AB边上.G综上,CF=.20.矩形ABCD绕点A顺时针旋转至矩形AEFG,使B点正好落在CD上的点E处,连BE.(1)求证:2Ð=Ð;BAE CBE(2)如图2,连BG交AE于M,点N为BE的中点,连MN、AF,试探究AF与MN的数量关系,并证明你的结论.【解答】(1)证明:Q四边形ABCD是矩形,\Ð=Ð=°,C CBA90CBE ABE\Ð+Ð=°,90Q将矩形ABCD绕点A顺时针旋转至矩形A点正好落在CD上的点E处,=,Ð=°,AE AB\=,90BC AGEAG\Ð=Ð,ABE AEBQ,Ð+Ð+Ð=°BAE ABE AEB180\Ð+Ð=°,ABE BAE2180Q,Ð+Ð=°CBE ABE90\Ð+Ð=°,CBE ABE22180\Ð=Ð.BAE CBE2(2)2=,AF MN证明:过B作BO AE^于O,连接EG,Q四边形AEFG是矩形,Ð=Ð=°,MAG BOM\=,90AF EG90C CBA Ð=Ð=°Q ,90AEB ABE CBE \Ð=Ð=°-Ð,90CEB CBE Ð=°-Ð,CEB OEB \Ð=Ð,在CBE D 和OBE D 中,90CBE OBE C BOE BE BE Ð=ÐìïÐ=Ð=°íï=î,()CBE OBE AAS \D @D ,EC OE \=,BO BC AD AG ===,在BOM D 和GAM D 中,AMG BME BOM GAM BO AG Ð=ÐìïÐ=Ðíï=î,()BOM GAM AAS \D @D ,BM GM \=,Q 点N 为BE 的中点,12MN EG \=,EG AF =Q ,2AF MN \=.题型三 正方形中的旋转、翻折问题21.如图,在正方形ABCD 中,E 是BC 边上的一点,将正方形边AB 沿AE 折叠到AF ,延长EF 交DC于G ,连接AG ,则EAG Ð= 45 度.【解答】解:Q 四边形ABCD 是正方形,AB AD \=,90ABE BAD ADG Ð=Ð=Ð=°,由翻折可知:AB AF =,90ABE AFE AFG Ð=Ð=Ð=°,BAE EAF Ð=Ð,90AFG ADG Ð=Ð=°Q ,AG AG =,AD AF =,Rt AGD Rt AGF(HL)\D @D ,GAF GAD Ð=Ð,1()452EAG EAF GAF BAF DAF \Ð=Ð+Ð=Ð+Ð=°.故答案为:45.22.如图,正方形ABCD 的边长为1,将其绕顶点C 按逆时针方向旋转一定角度到如图所示的位置,使得点B 落在对角线CF 1- .【解答】解:方法一:正方形ABCD 的边长为1,将其绕顶点C 按逆时针方向旋转一定角度到CEFG 位置,使得点B 落在对角线CF 上,1EF CE \==,CF \=,1BF \=-,45BFE Ð=°Q ,\阴影部分的面积211111)122=´´-´=-;方法二:Q 过E 点作//MN BC 交AB 、CD 于M 、N 点,设AB 与EF 交于点P 点,连接CP ,如下图所示,B Q 在对角线CF 上,45DCE ECF \Ð=Ð=°,1EC =,ENC \D 为等腰直角三角形,MB CN \===,又BC AD CD CE ===,且CP CP =,PEC D 和PBC D 均为直角三角形,Rt PEC Rt PBC(HL)\D @D ,PB PE \=,又45PFB Ð=°,45FPB MPE \Ð=°=Ð,MPE \D 为等腰直角三角形,设MP x =,则EP BP ==,MP BP MB +=Q ,\x +=x =,1BP \==-,\阴影部分的面积12211)12PBC S BC BP D ==´´´=´-=-.1.23.如图,将边长为3的正方形ABCD 绕点A 逆时针方向旋转30°后得到正方形AB C D ¢¢¢,则图中阴影部分面积为 9-【解答】解:连接AE ,如图所示:由旋转的性质可知:AB AB =¢.在Rt △AB E ¢和Rt ADE D 中,AE AE AB AD =ìí¢=î,Rt \△Rt ADE(HL)AB E ¢@D .DAE B AE \Ð=Т,ADE AB E S S D ¢=V .30BAB Т=°Q ,1(9030)302DAE \Ð=´°-°=°.又3AB =Q ,DE AB \==132ADE S D \==,又239ABCD S ==Q 正方形,929S \=-=-阴影.故答案为:9-.24.如图是一张正方形纸片ABCD ,将其对折使AB 与DC 重合,折痕EF 分别与BC ,AD 交于点E ,F ,再将点D 对折到线段AE 上,折痕AG 交DC 于点G ,则DC GC【解答】解:如图,连接EG ,设DG D G x ¢==,2AB a =,由折叠得:BE EC a ==,2AD AD a ¢==,2CG a x \=-,由勾股定理得:AE ==,2D E a ¢\=-,在Rt EGD ¢D 和Rt EGC D 中,2222(2)2)a a x x a +-=+-,解得1)x a =-,\DC GC =..25.如图,将边长为12的正方形纸片ABCD 折叠,点A 与CD 边中点M 重合,折痕交AD 于点E ,交BC 于点F ,边AB 折叠后与BC 交于点G ,则DE 长度为 92 ,BG 与BC 的数量关系为 .【解答】解:过A 作AH MG ^于H ,连接AG ,如图:设DE x =,则12AE ME x ==-,Rt DME D 中,162DM DC ==,222DM DE ME +=,2226(12)x x \+=-,解得92x =,92DE \=,Q 正方形纸片ABCD 折叠,点A 与CD 边中点M 重合,MAB AMG \Ð=Ð,//DC AB Q ,DMA MAB \Ð=Ð,DMA AMG \Ð=Ð,在ADM D 和AHM D 中,90,D AHM DMA AMG AM AMÐ=Ð=°ìïÐ=Ðíï=î,()ADM AHM AAS \D @D ,AD AH \=,6MH MD ==,AH AD AB \==,在Rt AHG D 和Rt ABG D 中,AH ABAG AG =ìí=î,Rt AHG Rt ABG(HL)\D @D ,HG BG \=,设BG y =,则HG y =,12CG y =-,Rt CMG D 中,162CM DC ==,6MG MH HG y =+=+,222CM CG MG +=,2226(12)(6)y y \+-=+,解得245y =,245BG \=,\2425125 BGBC==,25BG BC\=.故答案为:92,25BG BC=.26.如图,已知正方形ABCD的边长为6,以点C为直角顶点的等腰Rt CEFD绕C旋转一圈,且保持2CE=,过点C作CH DE^于H交直线BF于M,连AM,则AM的最小值为 1- .【解答】解:如图1中,作//BT CF交CM分延长线于T.//BT CFQ,T FCM\Ð=Ð,CH DE^Q,ECFD是等腰直角三角形,90CHE ECF\Ð=Ð=°,90FCM ECH\Ð+Ð=°,90ECH DECÐ+Ð=°,DEC FCM T\Ð=Ð=Ð,90DCB DHCÐ=Ð=°Q,90BCT DCH \Ð+Ð=°,90DCH CDE Ð+Ð=°,TCB CDE \Ð=Ð,CB CD =Q ,()BCT DCE AAS \D @D ,BT EC CF \==,TMB CMF Ð=ÐQ ,T MCF Ð=Ð,()TBM CFM AAS \D @D ,BM FM \=,如图2中,取BC 的中点N ,连接AN ,MN .Q 四边形ABCD 是正方形,6AB BC \==,90ABN Ð=°,3BN NC ==Q ,AN \===,BM MF =Q ,BN NC =,112MN CF \==,AM AN MN -Q …,1AM \…,AM \的最小值为1-.故答案为:1-.27.在正方形ABCD 中,E 、F 分别为BC 、CD 的中点,AE 与BF 相交于点G .(1)如图1,求证:AE BF ^;(2)如图2,将BCF D 沿BF 折叠,得到BPF D ,延长FP 交BA 的延长线于点Q ,若4AB =,求QF 的值【解答】(1)证明:E Q ,F 分别是正方形ABCD 边BC ,CD 的中点,CF BE \=,在ABE D 和BCF D 中,AB BC ABE BCFBE CF =ìïÐ=Ðíï=îRt ABE Rt BCF(SAS)\D @D ,BAE CBF \Ð=Ð,又90BAE BEA Ð+Ð=°Q ,90CBF BEA \Ð+Ð=°,90BGE \Ð=°,AE BF \^;(2)解:Q 将BCF D 沿BF 折叠,得到BPF D ,FP FC \=,PFB BFC Ð=Ð,90FPB Ð=°,//CD AB Q ,CFB ABF \Ð=Ð,ABF PFB \Ð=Ð,QF QB \=,设QF x =,4PB BC AB ===,2CF PF ==,QB x \=,2PQ x =-,在Rt BPQ D 中,222(2)4x x \=-+,解得:5x=,QF=.即528.如图,四边形ABCD是正方形,点E是BC边上的动点(不与点B、C重合),将射线AE绕点A按逆时针方向旋转45°后交CD边于点F,AE、AF分别交BD于G、H两点.(1)当55Ð的度数;BEAÐ=°时,求HADÐ的大小;(2)设BEA aÐ=,试用含a的代数式表示DFAÐ有怎样的数量关系,并说明理由.(3)点E运动的过程中,试探究BEAÐ与FEA【解答】解:(1)Q四边形ABCD是正方形,90\Ð=Ð=°,EBA BAD\Ð=°-Ð=°-°=°,90905535EAB BAE\Ð=Ð-Ð-Ð=°-°-°=°;90453510HAD BAD EAF EAB(2)Q四边形ABCD是正方形,\Ð=Ð=Ð=°,90EBA BAD ADF\Ð=°-Ð=°-,9090EAB BAE a\Ð=Ð-Ð-Ð=°-°-°-=-°,DAF BAD EAF EAB a a9045(90)45\Ð=°-Ð=°--°=°-;9090(45)135DFA DAF a aÐ=Ð,理由如下:(3)BEA FEA=,连接AI.延长CB至I,使BI DFQ四边形ABCD是正方形,\=,90AD ABÐ=Ð=°,ADF ABC90\Ð=°,ABIQ,又BI DF=\D@D,()DAF BAI SASÐ=Ð,\=,DAF BAIAF AIEAI BAI BAE DAF BAE EAF\Ð=Ð+Ð=Ð+Ð=°=Ð,45D的公共边,D与EAFQ是EAI又AEEAI EAF SAS\D@D,()\Ð=Ð.BEA FEA=,过D作DG EF29.在正方形ABCD中,点E、F分别在边BC、AD上,DE EF^于点H,交AB边于点G.(1)如图1,求证:DE DG=;(2)如图2,将EF绕点E逆时针旋转90°得到EK,点F对应点K,连接KG,EG,若H为DG中点,EG.在不添加任何辅助线及字母的情况下,请直接写出图中所有与EG长度相等的线段(不包括)【解答】解:(1)Q四边形ABCD是正方形,DAG DCEÐ=Ð=°,AD BC,90AD DC\=,//\Ð=Ð,DEC EDFQ,DE EF=\Ð=Ð,EFD EDF\Ð=Ð,EFD DECQ于H,DG EF^\Ð=°,GHF90AGH AFH\Ð+Ð=°,180Q,Ð+Ð=°AFH EFD180DGA EFD DEC \Ð=Ð=Ð,在DAG D 和DCE D 中:DGA DEC DAG DCEDA DC Ð=ÐìïÐ=Ðíï=î()DAG DCE AAS \D @D ,DG DE \=.(2)KE EF ^Q ,DG EF ^,//KE DG \,且DG EF KE DE ===,\四边形KEDG 是平行四边形,且DG DE =,\四边形KEDG 是菱形,GK DG KE DE \===,DG EF ^Q ,H 是DG 的中点,EG DE \=,EG DE DG GK KE EF \=====.30.如图,已知正方形ABCD 的边长是2,EAF m Ð=°,将EAF Ð绕点A 顺时针旋转,它的两边分别交BC 、CD 于点E 、F ,G 是CB 延长线上一点,且始终保持BG DF =.(1)求证:ABG ADF D @D ;(2)求证:AG AF ^;(3)当EF BE DF =+时:①求m 的值;②若F 是CD 的中点,求BE的长.【解答】解:(1)证明:在正方形ABCD 中,2AB AD BC CD ====,90BAD C D ABC ABG Ð=Ð=Ð=Ð=Ð=°.BG DF =Q ,在ABG D 和ADF D 中,AB AD ABG ADF BG DF =ìïÐ=Ðíï=î,()ABG ADF SAS \D @D ;(2)证明:ABG ADF D @D Q ,GAB FAD \Ð=Ð,GAF GAB BAF\Ð=Ð+Ð90FAD BAF BAD =Ð+Ð=Ð=°,AG AF \^;(3)①解:ABG ADF D @D ,AG AF \=,BG DF =.EF BE DF =+Q ,EF BE BG EG \=+=.AE AE =Q,。
特殊平行四边形的翻折折叠问题(含答案)
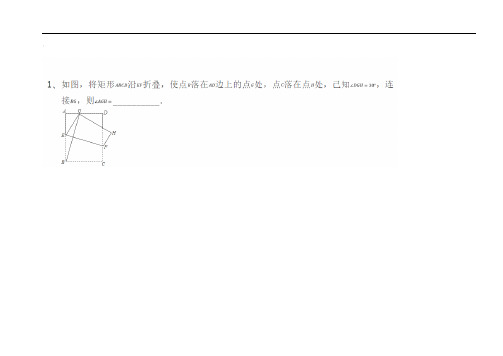
,;【解析】分析:根据翻折的性质可得∠B=∠AB 1E=90°,AB=AB 1,然后求出四边形ABEB 1是正方形,再根据正方形的性质可得BE=AB ,然后根据CE=BC-BE ,代入数据进行计算即可得解. 详解:∵沿AE 对折点B 落在边AD 上的点B 1处,∴∠B=∠AB 1E=90°,AB=AB 1,,又∵∠BAD=90°,∴四边形ABEB1是正方形,∴BE=AB=6cm,∴CE=BC-BE=8-6=2cm.故选:D.点睛:本题考查了矩形的性质,正方形的判定与性质,翻折变换的性质,判断出四边形ABEB1是正方形是解题的关键.,。
【>【解析】分析:先判断出△BFC是直角三角形,再利用三角形的外角判断出A正确,进而判断出AE=CE,得出CE 是△ABC的中位线判断出B正确,利用等式的性质判断出D正确.详解:如图,连接CF,∵点D是BC中点,∴BD=CD,由折叠知,∠ACB=∠DFE,CD=DF,∴BD=CD=DF,?∴△BFC是直角三角形,∴∠BFC=90°,∵BD=DF,∴∠B=∠BFD,∴∠EAF=∠B+∠ACB=∠BFD+∠DFE=∠AFE,∴AE=EF,故A正确,由折叠知,EF=CE,∴AE=CE,[∵BD=CD,∴DE是△ABC的中位线,∴AB=2DE,故B正确,∵AE=CE,∴S△ADE=S△CDE,由折叠知,△CDE≌△△FDE,∴S△CDE=S△FDE,∴S△ADE=S△FDE,故D正确,~∴C选项不正确,故选:C.*~*。
中考数学专题复习《四边形的折叠问题》测试卷-附带答案

中考数学专题复习《四边形的折叠问题》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一 单选题1.如图所示 在长方形ABCD 中 610AD AB ==, 若将长方形ABCD 沿DE 折叠 使点C 落在AB 边上的点F 处 则线段CE 的长为( )A .13B .1730C .103D .102.如图 在ABCD 中 将ADC △沿AC 折叠后 点D 恰好落在DC 延长线上的点E 处.若=60B ∠︒ 1AB = 则ABCD 的周长为( )A .4B .43C .6D .33.如图 在ABC 中 已知8AB = 点DE 、分别在边AC AB 、上 现将ADE 沿直线DE 折叠 使点A 恰好落在点F 处 若将线段BC 向左平移刚好可以与线段EF 重合 连接CF 若215BC CF += 则2BC CF -的值为( )A .4B .5C .6D .74.如图 矩形ABCD 中 3AB = 4BC = 点E 是BC 边上一点 连接AE 把B ∠沿AE折叠 使点B 落在点B '处 当CEB '为直角三角形时 BE 的长为( )A .2B .3C .2或3D .3或1.55.如图 将长方形纸片ABCD 沿EF 折叠后 若170=︒∠ 则2∠的度数为( )A .110︒B .115︒C .120︒D .125︒6.如图 在平面直角坐标中 矩形ABCD 的边5,:1:4AD OA OD == 将矩形ABCD 沿直线OE 折叠到如图所示的位置 线段1OD 恰好经过点B 点C 落在y 轴的点1C 位置 点E 的坐标是( )A .()1,2B .1,2C .)1,2D .()12 7.如图 在平面直角坐标系中 已个纸片OACB 顶点10006A B (,),(,)点P 为BC 边上的动点 将OBP 沿OP 折叠得到OPD 连接CD AD 、.则下列结论中:①当45BOP ∠=︒时 四边形OBPD 为正方形 ①当30BOP ∠=︒时 OAD 的面积为15 ①当P 在运动过程中CD 的最小值为5 ①当OD AD ⊥时 2BP =.其中结论正确的有( )A .1个B .2个C .3个D .4个 8.如图 把一张长方形纸片沿对角线折叠 若30EDF ∠= 则长方形纸片的长宽比为( )A .2:1B 2:1C 31D .23二 填空题9.在平行四边形ABCD 中 点E F 在BC 边上 把ABE 沿直线AE 折叠 CDF 沿直线DF 折叠 使点B C 落在对角线AC 上的点G 处 若110AGD ∠=︒ 则B ∠的度数为 .10.如图 点O 是矩形ABCD 的中心 E 是边AB 上的点 沿CE 折叠后 点B 恰好与点O 重合 若9BC = 则折痕CE 长度为 .11.如图 将长方形ABCD 沿EF 折叠得到两个全等的小长方形 1210AB BC ==,, 点G 在AB 上运动 当点 A 关于DG 的对称点A '落在右侧长方形BCEF 内部(含边界)时 则AG 的长度 m 的取值范围为 .12.如图 菱形ABCD 的边5AB = 高4CE = F 是边CD 上一动点 将四边形AEFD 沿直线EF 折叠 A 点的对应点为P 当CP 的长度最小时 CF 的长为 .13.如图 把正方形纸片ABCD 进行如下操作:对折正方形ABCD 得折痕EF 连接CE 将CB 折叠到CE 上 点B 对应点H 得折痕CG .那么AG BG= .三 解答题14.如图1 点E 为矩形ABCD 边BC 上一点 且CE CD = 把ABE 沿着AE 折叠 点B 的对应点F 恰好落在线段DE 上.(1)求证:≌AFD DCE(2)如图2 延长CF 交AE 于点G 交AB 于点H .①求证:GE DF GF CD ⋅=⋅①求:GH GA 的值.15.如图 沿折痕AE 折叠矩形ABCD 的一边 使点D 落在BC 边上一点F 处.若6AB = 且ABF △的面积为24 则:(1)BF 的长为_______________(2)BC 的长为________________(3)求EC 的长.16.如图1 已知长方形纸片ABCD 点E 在边AD 上 F 为AB 上的一个动点 G 为DC 上的一个动点 将长方形ABCD 沿直线EF EG 、折叠 点A D 、的对应点分别是点A '和点D .(1)如图2 当点A '落在ED 上时 求FEG ∠的度数(2)如图3 若54A ED ''∠=︒ 求FEG ∠的度数(3)如图4 若10A ED ''∠=︒ 求FEG ∠的度数(4)若A ED n ''∠=︒直接写出FEG ∠的度数(用含n 的代数式表示)17.如图 在Rt ABC △中 90BAC ∠=︒ 30C ∠=︒ 点D 是ABC 外一点连接AD BD将ABD △沿DB 折叠使点A 落在边BC 上的点1A 处 连接1A D 若1A D AC ⊥.(1)求证:四边形1ABA D 是菱形(2)连接1AA DC 若2AB = 求四边形1ADCA 的面积.18.综合探究:如图 四边形ABCD 是正方形 点M 在边AD 上 直线MN AB ∥.将正方形沿MN 折叠 点A 落在A '处 点B 落在点B '处 MN 与BD 交于点P 连接AP A P ' A P '交CD 与点F .(1)连接PC 猜想PC 与PA '的数量关系为________ A PC '∠=________°(2)连接B D ' CA ' 两线段交于点O 移动直线MN 若CD 平分PCA '∠ 求证:CP B D '∥(3)移动直线MN 若6=BC 2B C '= 直接写出PAD ∠的度数.参考答案:1.C2.C3.B4.D5.D6.D7.C8.C9.75︒10.11.10103m ≤≤ 12.41314.(1)解:证明:CD CE =CDE ∴为等腰直角三角形45CDE FDA ︒∴∠=∠= ABE 沿AE 折叠得到AEF △ 且四边形ABCD 是矩形 AB AF CD ∴== 90AFE AFD B ∠=∠=∠=︒ 在AFD △与ECD 中AFD ECD CDE FDA AF CE ∠=∠⎧⎪∠=∠⎨⎪=⎩()AAS AFD DCE ∴≌.(2)①证明:AFD DCE ≌△△AD DE ∴= AF DF DC CE ===()11804567.52DCF DFC ∴∠=∠=︒-︒=︒ 45DEC ∠=︒ 180135BED DEC167.52AEF AEB BEF ∴∠=∠=∠=︒ GEF DCF ∴∠=∠ GFE DFC ∠=∠GEF DCF ∴∽GE GF DC DF∴= GE DF GF CD ∴⋅=⋅.①在Rt CED 中 45CDE ∠=︒DE ∴=DF DC CE ==)()2121EF DE DF CD CE ∴=-== 21EF CE ∴ 由①知:67.5BEA DFC ∠=∠=︒18067.5112.5EFC GEC ∴∠=∠=︒-︒=︒ECF GCE ∠=∠CEG CFE ∴△∽△21GE EF GC CE∴==. 15.(1)由矩形的性质可得:90B C ∠=∠=︒ 6AB CD == ABF △的面积为24 ①1242ABF S AB BF =⨯⨯= ①24224286BF AB ⨯⨯=== 故答案为:8(2)在(1)中已得8BF =由矩形的性质可得:90B C ∠=∠=︒ 6AB CD == AD BC = 由折叠的性质可得:AF AD BC == 由勾股定理可得:22228610BC AF BF AB =++= 故答案为:10(3)由(1)(2)可得2CF BC BF =-=根据折叠的性质有:EF DE =设CE x = 则6EF DE x ==-在Rt CEF △中 222CE CF EF +=即()22226x x +=- 解得83x = 即83CE =.16.(1)解:由翻折得:12A EF AEA ''∠=∠ 12D EG DED ''∠=∠ ①180AEA DED ''∠+∠=︒ ①()111809022FEG A EF D EG AEA DED ''''∠=∠+∠=∠+∠=⨯︒=︒(2)解:由 (1) 知12A EF AEA ''∠=∠ 12D EG DED ''∠=∠ ①54A ED ''∠=︒①126AEA DED ''∠+∠=︒①()1632A EF D EG AEA DED ''''∠+∠=⨯∠+∠=︒ ①5463117FEG A ED A EF D EG ''''∠=∠+∠+∠=︒+︒=︒ (3)解:①10A ED ''∠=︒ ①()()11180109522A EF D EG AEA DED ''''∠+∠=∠+∠=︒+︒=︒ ①951085FEG A EF D EG A ED ''''∠=∠+∠-∠=︒-︒=︒ (4)解:如图3 ①A ED n ''∠=︒①()180180AEA DED A ED n ''''∠+∠=︒-∠=-︒ ①2A EF AEA ''∠=∠ 2D EG DED ''∠=∠ ①1802n A EF D EG ︒-︒''∠+∠= ①18018022n n FEG A EF D EG A ED n ︒-︒︒+︒''''∠=∠+∠+∠=+︒= 如图4 ①180AEA DED A ED ''''∠+∠-∠=︒ ''A ED n ∠=︒ ①180AEA DED n ''∠+∠=︒+︒①2A EF AEA ''∠=∠ 2D EG DED ''∠=∠ ①1802n A EF D EG ︒+︒''∠+∠= ①18018022n n FEG A EF D EG A ED n ︒+︒︒-︒''''∠=∠+∠-∠=-︒= 综上 FEG ∠的度数为1802n ︒+︒或 1802n ︒-︒. 17.(1)证明:如图1 连接1AA 设1A D 交AC 于点E由折叠的性质得:1AB A B = 1AD A D =90BAC ∠=︒ 30C ∠=︒903060ABC ∴∠=︒-︒=︒1ABA ∴是等边三角形1AB AA ∴= 160BAA ∠=︒11906030CAA BAC BAA ∴∠=∠-∠=︒-︒=︒1A D AC ⊥190AEA ∴∠=︒1903060AA D ∴∠=︒-︒=︒∴1AA D △是等边三角形1AD AA ∴=11AB A B AD A D ∴===∴四边形1ABA D 是菱形(2)解:如图2由(1)可知 四边形1ABA D 是菱形 12A D AB ∴==90BAC ∠=︒ 30ACB ∠=︒24BC AB ∴==22224223AC BC AB ∴--1A D AC ⊥∴四边形1ADCA 的面积=1AA C ADC S S + 111111232232222AC A E AC DE AC A D =⋅+⋅=⋅=⨯= 18.(1)解:①四边形ABCD 是正方形 ①AB BC CD DA === 90BAD ABC BCD CDA ∠∠∠∠====︒ 四边形ABCD 是轴对称图形 BD 所在直线是其一条对称轴①45ADP ∠=︒ PA PC = PAM PCF ∠∠= ①MN AB ∥①90PMD BAD ∠∠==︒①MN AD ⊥18090A DF CDA '∠=︒-∠=︒①将正方形沿MN 折叠 点A 落在A '处 点B 落在点B '处 ①MN AA '⊥①点A D A '三点共线同理:点B C B '三点共线①将正方形沿MN 折叠 点A 落在A '处 点B 落在点B '处 ①PA PA '= PA D PAM PCF '∠=∠=∠ 90CB A B A D ABC BAD ''''∠=∠=∠=∠=︒ ①PC PA '=①90A DF '∠=︒ 180A DF PA M DFA PCF PFC A PC ''''∠+∠+∠=∠+∠+∠=︒ PA M PCF '∠=∠ DFA PFC '∠=∠ ①90A D A PC F '∠=︒'∠=故答案为:PC PA '= 90(2)证明:由(1)得PC PA '= 90A PC '∠=︒ ①45PCA PA C ''∠=∠=︒①CD 平分PCA '∠①22.5OCD PCD ∠=∠=︒①90CB A B A D ''''∠=∠=︒ 90A DF '∠=︒ ①四边形A B CD ''是矩形①OA OD OB OC ''===①ODC OCD ∠∠==22.5︒①45A ODC O A OD PC CD ''∠=︒=∠+∠=∠ ①CP B D '∥(3)解:如图 在AN 上取一点N 使得AN =①四边形A B CD ''是矩形 ①2,A D B C ''=①将正方形沿MN 折叠 点A 落在A '处 点B 落在点B '处 ①MN 垂直平分AA ' ①62MA MA +'== 90PMD PMN ∠∠==︒ ①MN AM AN =-=6232662+-=①45PDM ∠=︒ ①904545MPD PDM ∠∠=︒-︒=︒= ①PM DM AD AM ==-62626+-==①在Rt PMN 中6232tan 326PM PNM MN -∠===-①30PNM ∠=︒ ①262N PN PM A === ①PAD APN ∠∠==130152⨯︒=︒.。
2024年中考数学总复习考点培优训练第七章专项5与特殊四边形有关的折叠问题

(2)若DE=5,△GDF的周长为20,求四边形BCDE的周长.
(2)解:由折叠的性质得GF=CF,DG=DC,
∵△GDF的周长为20,
∴GF+FD+GD=20,
∴CF+DF+DC=20.
∵四边形BFDE是平行四边形,DE=5,
∴BE=DF,BF=DE=5,
第7题图
∴四边形BCDE的周长为BC+CD+DE+BE=BF+
5 )2,
∴点F到AB的距离为1;
第5题解图
专项5 与特殊四边形有关的折叠问题
(2)求CE的长. (2)由(1)知FM=1,
∴AM=BM=2,FN= 5-1.
∵∠BFE=90°,∴∠BFM+∠EFN=90°.
∵MN⊥CD,∴∠FNE=90°,
∴∠EFN+∠FEN=90°,∴∠BFM=∠FEN.
∵∠BMF=∠FNE=90°,∴△BMF∽△FNE,
专项5 与特殊四边形有关的折叠问题
5. 如图,在矩形ABCD中,AB=4,BC= 5 ,E为CD边上一点,将
△BCE沿BE折叠,使得点C落到矩形内点F的位置,连接AF,tan ∠BAF
=
1 2
.
(1)求点F到AB的距离;
解:(1)如解图,过点F作MN∥AD,分别交AB,
CD于点M,N,则MN⊥AB,MN⊥CD. 由折叠的性质,得EC=EF,BC=BF= 5 ,
第4题图
专项5 与特殊四边形有关的折叠问题
解题关键点 观察设问:求DE的长; 观察题干:▱ABCD,AB=6,BC=8,∠ABC=120°,△ABE折叠得 △A′BE,点A′落在EC上; 关键点:如图,过点C作CH⊥AD交AD的 延长线于点H,构造Rt△CDH求得HC的 长;连接EC,构造Rt△ECH求得DE的长.
专题07 特殊的平行四边形中折叠问题(解析版)八年级数学下册期末综合复习专题提优训练(人教版)

2020-2021学年八年级数学下册期末综合复习专题提优训练(人教版)专题07 特殊的平行四边形中折叠问题【典型例题】1.如图所示,长方形纸片ABCD 的长AD =8cm ,宽AB =4cm ,将其折叠,使点D 与点B 重合. (1)求证:BE =BF ;(2)求折叠后DE 的长;(2)求以折痕EF 为边的正方形面积.【答案】(1)证明见解析;(2)5cm ;(3)20cm 2.【详解】(1)在长方形ABCD 中,AD //BC ,DEF EFB ∴∠=∠,DEF BEF ∠=∠,EFB BEF ∴∠=∠,∴ BE =BF ,设DE =x cm ,则BE =x cm ,AE =()8x cm -,在Rt ABE △中,由勾股定理()22248x x +-=, ∴5x =,即DE 的长为5cm .(2)过E 作EH BF ⊥于点H ,则EH =AB =4,BH =AE =3,∴ HF =BF -BH =5-3=2,∴2222420EF =+=,∴ 以EF 为边长的正方形的面积为220cm .【专题训练】一、选择题1.如图,将菱形纸片ABCD 折叠,使点A 恰好落在菱形的对称中心O 处,折痕为EF .若菱形ABCD 的边长为4,120B ∠=︒,则EF 的值是( )A B .2 C .D .4【答案】B【分析】 根据菱形的性质证明∴ABD 是等边三角形,求得BD =4,再证明EF 是∴ABD 的中位线即可得到结论.【详解】解:连接AC ,BD∴四边形ABCD 是菱形,∴AC BD ⊥,BD 平分∴ABC ,4AB BC CD DA ==== ∴∴111206022ABD ABC ︒=∠=⨯=︒ ∴AB AD =∴∴ABD 是等边三角形,∴ 4.BD =由折叠的性质得:EF AO ⊥,EF 平分AO ,又∴BD AC ⊥,∴//EF BD∴EF 为∴ABD 的中位线, ∴122EF BD == 故选:B .【点睛】本题考查了折叠性质,菱形性质,主要考查学生综合运用定理进行推理和计算的能力.2.如图,把正方形纸片ABCD 沿对边中点所在的直线对折后展开,折痕为MN ,再过点C 折叠纸片,使点C 落在MN 上的点F 处,折痕为BE .若AB 的长为1,则FM 的长为( )A .1B .2C .2D .12【答案】B【分析】根据翻折得到1FB BC ==,12BM =,在Rt BFM 中,可利用勾股定理求出FM 的值. 【详解】 解:四边形ABCD 是正方形, 1AB BC ∴==,由折叠的性质可知,1FB BC ==,1122BM AB ==, 在Rt BFM 中,由勾股定理得:2FM ===. 故选:B .【点睛】本题考查翻折、正方形的性质、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键. 3.将矩形纸片ABCD 按如图所示的方式折叠,得到菱形AECF .若AB =3,则BC 的长为( )A .1B .2CD 【答案】D【分析】 根据菱形及矩形的性质可得到∴BAC 的度数,从而根据直角三角形的性质求得BC 的长.【详解】解:∴四边形AECF 为菱形,∴∴FCO =∴ECO ,EC =AE ,由折叠的性质可知,∴ECO =∴BCE ,又∴FCO +∴ECO +∴BCE =90°,∴∴FCO =∴ECO =∴BCE =30°,在Rt ∴EBC 中,EC =2EB ,又∴EC =AE ,AB =AE +EB =3,∴EB=1,EC=2,∴Rt∴BCE中,BC ,故选:D.【点睛】本题主要考查了菱形的性质以及矩形的性质,解决问题的关键是根据折叠以及菱形的性质发现特殊角,根据30°的直角三角形中各边之间的关系求得BC的长.4.如图,在正方形ABCD中,AB=6,点E,F分别在边AB,CD上,∴EFC=120°.若将四边形EBCF沿EF 折叠,点B恰好落在AD边上,则AE的长度为()A.2B C D.1【答案】A【分析】依据正方形的性质以及折叠的性质,即可得到∴AEB'=60°,再根据含30°角的直角三角形的性质,即可得到AE的长.【详解】解:∴四边形ABCD是正方形,∴AB∴CD,∴A=90°,∴∴BEF=180°-∴EFC=60°,∴将四边形EBCF沿EF折叠,点B恰好落在AD边上,∴∴BEF=∴FEB'=60°,BE=B'E,∴∴AEB'=180°-∴BEF-∴FEB'=60°,∴∴AB'E=30°,∴B'E=2AE,设AE=x,则B'E=2x=BE,∴AB=6,∴x+2x=6,解得x=2.故选:A.【点睛】本题考查了正方形的性质,折叠的性质,含30°角的直角三角形的性质等知识点,能综合性运用性质进行推理是解此题的关键.5.如图,菱形ABCD中,∴ABC=60°,AB=4,E是边AD上一动点,将∴CDE沿CE折叠,得到∴CFE,则∴BCF 面积的最大值是()A.8B.C.16D.【答案】A【分析】由三角形底边BC是定长,所以当∴BCF的高最大时,∴BCF的面积最大,即当FC∴BC时,三角形有最大面积.【详解】解:在菱形ABCD中,BC=CD=AB=4又∴将∴CDE沿CE折叠,得到∴CFE,∴FC=CD=4由此,∴BCF的底边BC是定长,所以当∴BCF的高最大时,∴BCF的面积最大,即当FC∴BC时,三角形有最大面积∴∴BCF面积的最大值是11448 22BC FC=⨯⨯=故选:A.【点睛】本题考查菱形的性质和折叠的性质,掌握三角形面积的计算方法和菱形的性质正确推理计算是解题关键. 6.如图,有一张矩形纸条ABCD ,AB =5cm ,BC =2cm ,点M ,N 分别在边AB ,CD 上,CN =1cm .现将四边形BCNM 沿MN 折叠,使点B ,C 分别落在点B ′,C ′上.在点M 从点A 运动到点B 的过程中,若边MB '与边CD 交于点E ,则点E 相应运动的路径长为( )cm .A 32B .52CD .32【答案】A【分析】探究点E 的运动轨迹,寻找特殊位置解决问题即可.【详解】解:如图1中,∴四边形ABCD 是矩形,∴AB ∴CD ,∴∴1=∴3,由翻折的性质可知:∴1=∴2,BM =MB ′,∴∴2=∴3,∴MB ′=NB ′,∴NB '==cm ),∴BM NB '==(cm ).如图2中,当点M 与A 重合时,同理可得:AE =EN ,设AE =EN =x cm ,在Rt ∴ADE 中,则有2222(4)=+-x x ,解得x =52, ∴53422DE =-=(cm ), 如图3中,当点M 运动到MB ′∴AB 时,DE ′的值最大,DE ′=5-1-2=2(cm ),如图4中,当点M 运动到点B ′落在CD 时,DB ′(即DE ″)51(4=-=(cm ),∴点E 的运动轨迹E →E ′→E ″,运动路径3322(4)22EE E B '''=+=-+-=(cm ). 故选:A .【点睛】本题考查了翻折变换,矩形的性质,勾股定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考填空题中的压轴题.二、填空题7.如图a 是长方形纸带,∴DEF =22°,将纸带沿EF 折叠成图b ,再沿BF 折叠成图c ,则图c 中的∴CFE 的度数是________°.【答案】114°【分析】根据两直线平行,内错角相等可得∴EFB=∴DEF,再根据翻折的性质,图c中∴EFB处重叠3层,然后根据∴CFE=180°-3∴EFB代入数据行计算即可得解【详解】∴∴DEF =22°长方形ABCD的对边AD//BC∴∴EFB=∴DEF=22°由折叠,∴EFB处折叠了3层∴∴CFE=180° -3∴EFB=180°—3 × 22°=114°故答案为:114°【点睛】本题考查折叠问题,熟知折叠中蕴含着全等,有相等的角与边进行分析是关键.8.如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC 边上的点F处,则CE=_____.【答案】4 3【分析】由折叠求出BF和CF,再设CF=x,在∴CEF中用勾股定理列方程即可得答案.【详解】解:∴矩形ABCD沿AE折叠,AB=3,AD=5,∴AF=AD=5,∴B=∴C=90°,DE=EF,∴BF4,∴CF=BC﹣BF=1,设CE=x,则EF=DE=3﹣x,在Rt∴CEF中,CE2+CF2=EF2,∴x2+12=(3﹣x)2,解得x=43,∴CE=43.故答案为:43.【点睛】本题考查矩形性质及勾股定理应用等知识,解题的关键是在Rt∴CEF中用勾股定理列方程.9.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN,若32NEC FMN∠=︒∠=,_____︒.【答案】119【分析】根据正方形的性质得到∴A=∴C=∴D=90°,根据折叠的性质得到∴F=∴A=90°,∴FEN=∴C=90°,∴DNM=∴ENM,根据平角的定义得到∴ENM=12(180°-∴ENC)=12(180°-58°)=61°,根据四边形的内角和即可得到结论.【详解】解:∴四边形ABCD是正方形,∴∴A=∴C=∴D=90°,∴将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,∴∴F=∴A=90°,∴FEN=∴D=90°,∴DNM=∴ENM,∴∴NEC=32°,∴∴ENC=58°,∴∴ENM=12(180°-∴ENC)=12(180°-58°)=61°,∴∴FMN =360°-90°-90°-61°=119°,故答案为:119.【点睛】本题考查了角的计算,翻折变换的问题,折叠问题其实质是轴对称,对应线段相等,对应角相等,找到相等的角是解决本题的关键.10.对角线长分别为6和8的菱形ABCD 如图所示,点O 为对角线的交点,过点O 折叠菱形,使B ,B '两点重合,MN 是折痕.若1B M '=,则CN 的长为_______.【答案】4【分析】连接AC 、BD ,如图,利用菱形的性质得132OC AC ==,142OD BD ==,90COD ∠=︒,再利用勾股定理计算出5CD =,接着证明OBM ODN ∆≅∆得到DN BM =,然后根据折叠的性质得1BM BM'==,从而有1DN =,于是计算CD DN -即可.【详解】解:连接AC 、BD ,如图,点O 为菱形ABCD 的对角线的交点,132OC AC ∴==,142OD BD ==,90COD ∠=︒, 在Rt COD ∆中,5CD ==,//AB CD ,MBO NDO ∴∠=∠,在OBM ∆和ODN ∆中MBO NDO OB ODBOM DON ∠=∠⎧⎪=⎨⎪∠=∠⎩, OBM ODN ∴∆≅∆,DN BM ∴=,过点O 折叠菱形,使B ,B ′两点重合,MN 是折痕,1BM BM'∴==, 1DN ∴=,514CN CD DN ∴=-=-=,故答案为:4.【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了菱形的性质.11.如图,矩形ABCD 中,6,8AB BC ==,点E 是BC 边上一点,连接AE ,把ABE △沿AE 折叠,使点B 落在点F 处,当CEF △为直角三角形时,CF 的长为________.【答案】4或【分析】当CEF △为直角三角形时,有两种情况:①当点F 落在矩形内部时,如答图1所示.连接AC ,先利用勾股定理计算出10AC =,根据折叠的性质得90AFE B ∠=∠=︒,而当CEF △为直角三角形时,只能得到90EFC ∠=︒,所以点A 、F 、C 共线,即B 沿AE 折叠,使点B 落在对角线AC 上的点F 处,则,6EB EF AB AF ===,可计算出CF ; ②当点F 落在AD 边上时,如答图2所示.此时ABEF 为正方形,根据勾股定理计算出CF .【详解】解:当CEF △为直角三角形时,有两种情况:①当点F 落在矩形内部时,如答图1所示.连接AC ,在Rt ABC 中,6,8AB BC ==,∴10AC =,∴B 沿AE 折叠,使点B 落在点F 处,∴90AFE B ∠=∠=︒,当CEF △为直角三角形时,只能得到90EFC ∠=︒,∴点A 、F 、C 共线,即B 沿AE 折叠,使点B 落在对角线AC 上的点F 处,∴,6EB EF AB AF ===,∴1064CF =-=;②当点F 落在AD 边上时,如答图2所示.此时ABEF 为正方形,∴6,862BE AB CE ===-=,∴CF =综上所述,CF 的长为4或.故答案为:4或.【点睛】本题考查折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理.解题的关键是要注意本题有两种情况,需要分类讨论,避免漏解.12.如图,在正方形ABCD 中,12AB =,点E 在边CD 上,3CD DE =.将ADE 沿AE 对折至AFE △,延长EF 交边BC 于点G ,连接AG ,CF .有下列结论:①ABG AFG ≅;②BG GC =;③//AG CF ;④6FGC S =△.其中正确的结论是__________.(填序号)【答案】①②③【分析】由正方形的性质和折叠的性质得出AB =AF ,∴AFG =90°,由HL 证明Rt ∴ABG ∴Rt ∴AFG ,得出①正确;设BG =FG =x ,则CG =12-x .由勾股定理得出方程,解方程求出BG ,得出GC ,即可得出②正确;由全等三角形的性质和三角形内角和定理得出∴AGB =∴AGF =∴GFC =∴GCF ,得出AG ∴CF ,即可得出③正确;通过计算三角形的面积得出④错误;即可得出结果.【详解】解:①正确.理由如下:四边形ABCD 是正方形,12AB BC CD AD ∴====,90B GCE D ∠=∠=∠=︒,由折叠的性质得:AF AD =,90AFE D ∠=∠=︒,90AFG ∴∠=︒,AB AF =,在Rt ABG △和Rt AFG △中,AG AG AB AF=⎧⎨=⎩, Rt Rt (HL)ABG AFG ∴≅△△;②正确.理由如下: 由题意得:143EF DE CD ===,设BG FG x ==,则12CG x =-. 在直角ECG 中,根据勾股定理,得222(12)8(4)x x -+=+,解得:6x =,6BG ∴=,1266GC ∴=-=,BG GC ∴=;③正确.理由如下:CG BG =,BG GF =,CG GF ∴=,FGC ∴△是等腰三角形,GFC GCF ∠=∠.又∴Rt Rt ABG AFG ≅△△,AGB AGF ∴∠=∠,218022+==︒-=+==∠∠∠∠∠∠∠∠AGB AGF AGB FGC GFC GCF GFC GCF ,AGB AGF GFC GCF ∴∠=∠=∠=∠,//AG CF ∴;④错误;理由如下:11682422GCE S GC CE =⋅=⨯⨯=△, 6GF =,4EF =,GFC 和FCE △等高,:3:2GFC FCE S S ∴=△△,37224655GFC S ∴=⨯=≠△. 故④不正确.∴正确的个数有①②③.故答案为:①②③.【点睛】本题考查的是翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算等知识;本题综合性强,有一定的难度.三、解答题13.如图,矩形纸片 ABCD 的长 AD =10cm ,宽 AB =5cm ,将其折叠,使点 D 与点 B 重合,那么折叠后AE 的长是多少?【答案】154cm【分析】设DE =x ,根据折叠的性质可得BE =x ,表示出AE =10−x ,然后在Rt ∴ABE 中,利用勾股定理列式计算即可得解.【详解】解:设 DE =xcm ,则BE =xcm ,∴AE =(10﹣x )cm ,∴在 Rt ∴ABE 中,AB 2+AE 2=BE 2,∴52+(10﹣x )2=x 2,∴解得:x =254, ∴AE =10﹣254=154cm 答:折叠后AE 的长是154cm . 【点睛】本题考查了矩形的性质,折叠的性质,勾股定理的应用,根据勾股定理列出方程是解题的关键. 14.如图,在菱形ABCD 中,120ABC ∠=︒,将菱形折叠,使点A 恰好落在对角线BD 上的点G 处(不与B D ,重合),折痕为EF ,若26DG BG ==,,求AF 的长.【答案】AF 的长为267. 【分析】 作FH BD ⊥于点H ,通过菱形的性质和折叠的性质证明ABD △为等边三角形,设AF x =,则FG x =,8DF x =-,在Rt DFH 中,利用特殊角表示出DH ,FH ,最后在Rt FHG 中利用勾股定理即可求解.【详解】如图,作FH BD ⊥于点H .由折叠的性质可知,FG FA =.由题意,得8BD DG BG =+=.∴ 四边形ABCD 是菱形. ∴1602AD AB ABD CBD ABC =∠=∠=∠=︒,, ∴ABD △为等边三角形,∴8AD BD ==.设AF x =,则FG x =,8DF x =-,在Rt DFH 中,∴60FDH ∠=︒,∴()118422DH x x =-=-,)822FH x x =-=, ∴1222HG DH x =-=-. 在Rt FHG 中,222FG FH GH =+,即222122x x x ⎛⎫⎛⎫=+- ⎪ ⎪ ⎪⎝⎭⎝⎭, 解得267x =, ∴AF 的长为267. 【点睛】本题主要考查菱形的性质,含30°的直角三角形的性质,折叠的性质,勾股定理,掌握菱形的性质,勾股定理及方程的思想是解题的关键.15.如图,正方形纸片ABCD 的边长为6,点E 、F 分别在边BC 、CD 上,将AB 、AD 分别沿AE 、AF 折叠,点B 、D 恰好都在点G 处,已知2BE =,求FC 的长.【答案】3【分析】因为正方形ABCD 的边长为6,由图形折叠可得=2BE EG =,624EC =-=,6DF FG x ==-, 再利用勾股定理进行计算即可.【详解】解:设FC x =,由图形折叠可得=2BE EG =,624EC =-=,6DF FG x ==-,在直角ECF ∆中,∴222EF EC CF =+,∴222(426)x x +-=+,解得3x =,∴3=FC .【点睛】此题考查了折叠问题,解题的关键是找准不变的线段,利用勾股定理求解线段.16.如图,AC 为矩形ABCD 的对角线,将边AB 沿AE 折叠,使点B 落在AC 上的点M 处,将边CD 沿CF 折叠,使点D 落在AC 上的点N 处.(1)求证:四边形AECF 是平行四边形;(2)若AB =6,AC =10,求四边形AECF 的面积.【答案】(1)证明见解析;(2)30.【解析】试题分析:(1)首先由矩形的性质和折叠的性质证得AB =CD ,AD ∴BC ,∴ANF =90°,∴CME =90°,易得AN =CM ,可得∴ANF∴∴CME(ASA),由平行四边形的判定定理可得结论;(2)由AB=6,AC=10,可得BC=8,设CE=x,则EM=8-x,CM=10-6=4,在Rt∴CEM中,利用勾股定理可解得x,由平行四边形的面积公式可得结果.试题解析:(1)证明:∴折叠,∴AM=AB,CN=CD,∴FNC=∴D=90°,∴AME=∴B=90°,∴∴ANF=90°,∴CME=90°,∴四边形ABCD为矩形,∴AB=CD,AD∴BC,∴AM=CN,∴AM﹣MN=CN﹣MN,即AN=CM,在∴ANF和∴CME中,{FAN EMC AN CMANF CME∠=∠=∠=∠,∴∴ANF∴∴CME(ASA),∴AF=CE,又∴AF∴CE,∴四边形AECF是平行四边形;(2)解:∴AB=6,AC=10,∴BC=8,设CE=x,则EM=8﹣x,CM=10﹣6=4,在Rt∴CEM中,(8﹣x)2+42=x2,解得:x=5,∴四边形AECF的面积的面积为:EC•AB=5×6=30.17.如图1.将矩形ABCD沿DE折叠使点A落在A'处,然后将矩形展平,沿EF折叠使点A落在折痕DE 上的点G处,再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处,如图2.(1)求证:EG=CH;(2)已知AF∴CDE的面积.【答案】(1)见解析;(2)∴CDE的面积=4+【分析】(1)由折叠的性质及矩形的性质可得AD AE BC ==,AE EG =,BC CH =,可得结论;(2)由折叠的性质可知45ADE ∠=︒,90FGE A ∠=∠=︒,AF =,那么DG =,利用勾股定理求出2DF =,于是可得2AD AF DF =+=;再利用AAS 证明AEF BCE △≌△,得到AF BE =,于是22AB AE BE =+=+=,即可求解.【详解】(1)证明:四边形ABCD 是矩形, AD BC ∴=,将矩形ABCD 沿DE 折叠使点A 落在A '处,AD A D '∴=,AE A E '=,45ADE A DE '∠=∠=︒,45ADE AED ∴∠=∠=︒,AD AE ∴=,AE BC ∴=,由折叠的性质可得AE EG =,BC CH =,EG CH ∴=;(2)45ADE ∠=︒,90FGE A ∠=∠=︒,AFDG ∴=2DF =,2AD AF DF ∴=+;由折叠知AEF GEF ∠=∠,BEC HEC ∠=∠,90GEF HEC ∴∠+∠=︒,90AEF BEC ∠+∠=︒,90∠+∠=︒AEF AFE ,BEC AFE ∴∠=∠,在AEF 与BCE 中,90AFE BEC A B AE BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩, ()AEF BCE AAS ∴△≌△,AF BE∴=,22AB AE BE CD ∴=+=+==,CDE ∴的面积11(2(24 22CD AD=⨯⨯=⨯+⨯=+【点睛】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了全等三角形的判定与性质,矩形的性质,勾股定理等知识.18.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处,将边CD沿CF 折叠,使点D落在AC上的点N处.(1)求证:四边形AECF是平行四边形;(2)当∴BAE为多少度时,四边形AECF是菱形?请说明理由.【答案】(1)证明见解析(2)当∴BAE=30°时,四边形AECF是菱形【分析】(1)首先证明∴ABE∴∴CDF,则DF=BE,然后可得到AF=EC,依据一组对边平行且相等四边形是平行四边形可证明AECF是平行四边形;(2)由折叠性质得到∴BAE=∴CAE=30°,求得∴ACE=90°-30°=60°,即∴CAE=∴ACE,得到EA=EC,于是得到结论.【详解】(1)∴四边形ABCD为矩形,∴AB=CD,AD∴BC,∴B=∴D=90°,∴BAC=∴DCA.由翻折的性质可知:∴EAB=12∴BAC,∴DCF=12∴DCA.∴∴EAB=∴DCF.在∴ABE和∴CDF中B DAB CDEAB DCF ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴∴ABE∴∴CDF(ASA),∴DF=BE.∴AF=EC.又∴AF∴EC,∴四边形AECF是平行四边形;(2)当∴BAE=30°时,四边形AECF是菱形,理由:由折叠可知,∴BAE=∴CAE=30°,∴∴B=90°,∴∴ACE=90°-30°=60°,即∴CAE=∴ACE,∴EA=EC,∴四边形AECF是平行四边形,∴四边形AECF是菱形.【点睛】本题主要考查了菱形的判定,全等三角形的判定和性质,折叠的性质、矩形的性质、平行四边形的判定定理和勾股定理等,综合运用各定理是解答此题的关键.19.探究:如图①点E、F分别在正方形ABCD的边BC、CD上,连结AE、AF、EF,将∴ABE、∴ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与∴AEF完全重合的三角形.若BE=2,DF=3,求AB的长;拓展:如图②点E、F分别在四边形BACD的边BC、CD上,且∴B=∴D=90°.连结AE、AF、EF将∴ABE、∴ADF分别沿AE、AF折叠,折叠后的图形恰好能拼成与∴AEF完全重合的三角形.若∴EAF=30°,AB=4,则∴ECF的周长是.【答案】探究:AB=6;拓展:.3【分析】探究:设:正方形的边长为a,则EC=a-2,CF=a-3,则由勾股定理得:EF2=EC2+CF2,即可求解;拓展:证明∴ABC∴∴ADC,∴BAE+∴DAF=∴EAF=30°,则∴BAD=60°,∴BAC=∴DAC=12(∴BAD)=30°,CD=BC=ABtan∴BAC,即可求解.【详解】探究:设:正方形的边长为a,则EC=a﹣2,CF=a﹣3,则EF=BE+DF=5,则EF2=EC2+CF2,即:25=(a﹣2)2+(a﹣3)2,解得:a=6或﹣1(舍去﹣1),故AB=6;拓展:由题意得:AB=CD=4,连接AC,∴AB=CD,AC=AC,∴∴ABC∴∴ADC,∴BC=CD,∴BAC=∴DAC,∴点E、F分别在四边形BACD的边BC、CD上,故:∴BAE+∴DAF=∴EAF=30°,则∴BAD=60°,∴∴BAC=∴DAC=12(∴BAD)=30°,CD=BC=ABtan∴BAC=4∴ECF的周长=EF+EC+FC=AE+FD+EC+FC=AC+CD=2CD,故答案为:3. 【点睛】 本题考查的是翻折变换(折叠问题),涉及到正方形的性质、三角形全等等,其中(2)证明∴ABC ∴∴ADC ,是本题解题的关键.20.(1)如图1,将矩形ABCD 折叠,使AB 落在对角线AC 上,折痕为AE ,点B 落在点1B 处,若66DAC ∠=︒,则BAE ∠= º;(2)小丽手中有一张矩形纸片,9AB =,4=AD .她准备按如下两种方式进行折叠:①如图2,点F 在这张矩形纸片的边CD 上,将纸片折叠,使点D 落在边AB 上的点1D 处,折痕为FG ,若5DF =,求AG 的长;②如图3,点H 在这张矩形纸片的边AB 上,将纸片折叠,使HA 落在射线HC 上,折痕为HK ,点A ,D 分别落在1A ,2D 处,若73DK =,求1AC 的长. 【答案】(1)12;(2)①AG =32;②13A C = 【分析】 (1)由折叠的性质可得∴BAE =∴CAE =12°;(2)①过点F 作FH ∴AB 于H ,可证四边形DFHA 是矩形,可得AD =FH =4,由勾股定理可求D 1H =3,由勾股定理可求AG 的长;②首先证明CK =CH ,利用勾股定理求出BH ,可得AH ,再利用翻折不变性,可知AH =A 1H ,由此即可解决问题.【详解】解:(1)∴∴DAC =66°,∴∴CAB =24°∴将矩形ABCD 折叠,使AB 落在对角线AC 上,∴∴BAE=∴CAE=12°故答案为:12;(2)如图2,过点F作FH∴AB于H,∴∴D=∴A=90°,FH∴AB∴四边形DFHA是矩形∴AD=FH=4,∴将纸片ABCD折叠∴DF=D1F=5,DG=D1G,∴D 1H2225163FH,∴AD1=2∴AG2+D1A2=D1G2,∴AG2+4=(4−AG)2,∴AG=32;②∴DK=73,CD=9,∴CK=9−73=203,∴四边形ABCD是矩形,∴DC∴AB,∴∴CKH=∴AHK,由翻折不变性可知,∴AHK=∴CHK,∴∴CKH=∴CHK,∴CK=CH=203,∴CB=AD=4,∴B=90°,∴在Rt∴CDF中,BH22400161693BC,∴AH=AB−BH=11 3,由翻折不变性可知,AH=A1H=11 3,∴A1C=CH−A1H=3.【点睛】本题考查四边形综合题、矩形的性质、翻折变换、勾股定理,解题的关键是灵活运用所学知识解决问题,学会利用翻折不变性解决问题,属于中考压轴题.。
(完整版)中考数学几何图形折叠试题典题及解答
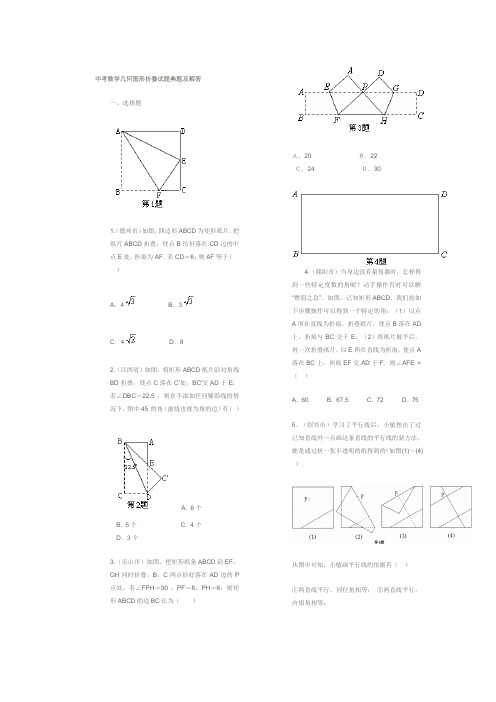
中考数学几何图形折叠试题典题及解答一、选择题1.(德州市)如图,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于()A.4B.3C.4D.82.(江西省)如图,将矩形ABCD纸片沿对角线BD折叠,使点C落在C′处,BC′交AD于E,若∠DBC=22.5°,则在不添加任何辅助线的情况下,图中45°的角(虚线也视为角的边)有()A.6个B.5个C.4个D.3个3.(乐山市)如图,把矩形纸条ABCD沿EF,GH同时折叠,B,C两点恰好落在AD边的P 点处,若∠FPH=90°,PF=8,PH=6,则矩形ABCD的边BC长为()A.20B.22C.24D.304.(绵阳市)当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD,我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD 上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A 落在BC上,折痕EF交AD于F.则∠AFE =()A.60°B.67.5°C.72°D.75°5. (绍兴市)学习了平行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)).从图中可知,小敏画平行线的依据有()①两直线平行,同位角相等;②两直线平行,内错角相等;③同位角相等,两直线平行;④内错角相等,两直线平行.A.①②B.②③C.③④D.①④6.(贵阳市)如图6-1所示,将长为20cm,宽为2cm的长方形白纸条,折成图6-2所示的图形并在其一面着色,则着色部分的面积为()A.34cm2 B.36cm2C.38cm2 D.40cm2二、填空题7.(成都市)如图,把一张矩形纸片ABCD沿E F折叠后,点C,D分别落在C′,D′的位置上,EC′交AD于点G.已知∠EFG=58°,那么∠B EG°.8. (苏州市)如图,将纸片△ABC沿DE折叠,点A落在点A′处,已知∠1+∠2=100°,则∠A的大小等于____________度.三、解答题9.(荆门市)如图1,在平面直角坐标系中,有一张矩形纸片OABC,已知O(0,0),A(4,0),C(0,3),点P是OA边上的动点(与点O、A不重合).现将△PAB沿PB翻折,得到△PDB;再在OC边上选取适当的点E,将△POE沿PE翻折,得到△PFE,并使直线PD、PF重合.设P(x,0),E(0,y),求y关于x的函数关系式,并求y的最大值;如图2,若翻折后点D落在BC边上,求过点P、B、E的抛物线的函数关系式;在(2)的情况下,在该抛物线上是否存在点Q,使△P EQ是以PE为直角边的直角三角形?若不存在,说明理由;若存在,求出点Q的坐标.10. (济宁市)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ.求证:△PBE∽△QAB;你认为△PBE和△BAE相似吗?如果相似给出证明,如不相似请说明理由;如果沿直线EB折叠纸片,点A是否能叠在直线EC 上?为什么?11.(威海市)如图,四边形ABCD为一梯形纸片,AB∥CD,AD=BC.翻折纸片ABCD,使点A与点C重合,折痕为EF.已知CE⊥AB.(1)求证:EF∥BD;(2)若AB=7,CD=3,求线段EF的长.12. (烟台市)生活中,有人喜欢把传送的便条折成形状,折叠过程是这样的(阴影部分表示纸条的反面):如果由信纸折成的长方形纸条(图①)长为2 6 cm,宽为xcm,分别回答下列问题:为了保证能折成图④的形状(即纸条两端均超出点P),试求x的取值范围.(2)如果不但要折成图④的形状,而且为了美观,希望纸条两端超出点P的长度相等,即最终图形是轴对称图形,试求在开始折叠时起点M与点A的距离(用x表示).13. 将平行四边形纸片ABCD按如图方式折叠,使点C与A重合,点D落到D′处,折痕为EF.(1)求证:△ABE≌△AD′F;(2)连接CF,判断四边形AECF是什么特殊四边形?证明你的结论.14.(孝感市)在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:第一步:对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开(如图1);第二步:再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN(如图2).请解答以下问题:(1)如图2,若延长MN交BC于P,△BMP 是什么三角形?请证明你的结论.(2)在图2中,若AB=a,BC=b,a、b满足什么关系,才能在矩形纸片ABCD上剪出符合(1)中结论的三角形纸片BMP ?(3)设矩形ABCD的边AB=2,BC=4,并建立如图3所示的直角坐标系. 设直线BM′为y=kx,当∠M′BC=60°时,求k的值.此时,将△ABM′沿BM′折叠,点A是否落在EF上(E、F分别为AB、CD中点)?为什么?15.(邵阳市)如图①,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C 重合(图②).(1)在图①中画出折痕所在的直线l.设直线l 与AB,AC分别相交于点D,E,连结CD.(画图工具不限,不要求写画法)(2)请你找出完成问题(1)后所得到的图形中的等腰三角形.(不要求证明)16.(济宁市)如图,先把一矩形ABCD纸片对折,设折痕为MN,再把B点叠在折痕线上,得到△ABE.过B点折纸片使D点叠在直线AD上,得折痕PQ. 求证:△PBE∽△QAB;你认为△PBE和△BAE相似吗?如果相似给出证明,如补相似请说明理由;(3)如果直线EB折叠纸片,点A是否能叠在直线EC上?为什么?17.(临安市)如图,△OAB 是边长为的等边三角形,其中O是坐标原点,顶点B在y轴正方向上,将△OAB 折叠,使点A落在边OB上,记为A′,折痕为EF.(1)当A′E//x轴时,求点A′和E的坐标;(2)当A′E//x轴,且抛物线经过点A′和E时,求抛物线与x轴的交点的坐标;(3)当点A′在OB上运动,但不与点O、B重合时,能否使△A′EF成为直角三角形?若能,请求出此时点A′的坐标;若不能,请你说明理由.18.(南宁市)如图,在锐角△ABC中,BC=9,AH⊥BC于点H,且AH=6,点D为AB边上的任意一点,过点D作DE∥BC,交AC于点E.设△ADE的高AF为x(0<x<6),以DE为折线将△ADE翻折,所得的△A′DE与梯形DBCE重叠部分的面积记为y(点A关于DE的对称点A′落在AH所在的直线上).(1)分别求出当0<x≤3与3<x<6时,y与x 的函数关系式;(2)当x取何值时,y的值最大?最大值是多少?19.(宁夏回族自治区)如图,将矩形纸片ABCD沿对角线B D折叠,点C落在点E处,BE交AD于点F,连结AE.证明:(1)BF=DF;(2)AE∥BD.参考答案一、1.A 2.B 3.C 4.B 5.C 6.B二、7.648.50°三、9. 解:(1)由已知PB平分∠APD,PE平分∠OPF,且PD、PF重合,则∠OPE+∠APB= 90°.又∠APB+∠ABP=90°,∴∠OPE=∠PBA.∴Rt△POE∽Rt△BPA.∴.即.∴.且当x=2时,y 有最大值.由已知,△PAB、△POE均为等腰直角三角形,可得P(1,0),E(0,1),B(4,3).……6分设过此三点的抛物线为y=ax2+bx+c ,则∴y=.由(2)知∠EPB=90°,即点Q与点B重合时满足条件.直线PB为y=x-1,与y轴交于点(0,-1).将PB向上平移2个单位则过点E(0,1),∴该直线为y=x+1.由得∴Q(5,6).故该抛物线上存在两点Q(4,3)、(5,6)满足条件.10. 证明:(1)∵∠PBE+∠ABQ=180°-90°=90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.又∵∠BPE=∠AQB=90°,∴△PBE~△QAB.(2)∵△PBE~△QAB ,∴∵B Q=P B,∴.又∵∠ABE=∠BPE=90°,∴△PBE~△BAE.(3)点A能叠在直线EC上.由(2)得,∠AE B=∠CEB,∴EC和折痕AE重合.11. 解:(1)证明:过C点作CH∥BD,交AB的延长线于点H;连结AC,交EF于点K,则AK=CK.∵AB∥CD,∴BH=CD,BD=CH.∵AD=BC,∴AC=BD=CH.∵CE⊥AB,∴AE=EH.∴EK是△AHC的中位线.∴EK∥CH.∴EF∥BD.(2)解:由(1)得BH∥CD,EF∥BD,∴∠AEF=∠ABD.∵AB=7,CD=3,∴AH=10.∵AE=CE,AE=EH,∴AE=CE=EH=5.∵CE⊥AB,∴CH=5=BD.∵∠EAF=∠BAD,∠AEF=∠ABD,∴△AFE∽△ADB.∴.∴.12. 解:(1)由折纸过程知0<5x<26,,0<x <.(2)图④为轴对称图形,∴A M =.即点M与点A的距离是(13-x)cm.13. 证明:⑴由折叠可知:∠D=∠D′,CD=A D′,∠C=∠D′AE.∵四边形ABCD是平行四边形,∴∠B=∠D,AB=CD,∠C=∠BAD.∴∠B=∠D′,AB=AD′,∠D′AE=∠BAD,即∠1+∠2=∠2+∠3.∴∠1=∠3.∴△ABE ≌△AD′F.⑵四边形AECF是菱形.由折叠可知AE=EC,∠4=∠5.∵四边形ABCD是平行四边形,∴AD∥BC.∴∠5=∠6.∴∠4=∠6.∴AF=AE.∵AE=EC,∴AF=EC.又∵AF∥EC,∴四边形AECF是平行四边形.∵AF=AE,∴四边形AECF是菱形.14. 解:(1)△BMP是等边三角形.证明:连结AN.∵EF垂直平分AB,∴AN = BN.由折叠知AB = BN ,∴AN = AB = BN,∴△ABN为等边三角形.∴∠ABN =60°. ∴∠PBN =30°.又∵∠ABM =∠NBM =30°,∠BNM =∠A =9 0°.∴∠BPN =60°.∠MBP =∠MBN +∠PBN =60°.∴∠BMP =60°∴∠MBP =∠BMP =∠BPM =60°.∴△BMP为等边三角形 .(2)要在矩形纸片ABCD上剪出等边△BMP,则BC ≥BP.在Rt△BNP中,BN = BA =a,∠PBN =30°,∴BP =. ∴b≥. ∴a≤b .∴当a≤b时,在矩形上能剪出这样的等边△BMP.(3)∵∠M′BC =60°,∴∠ABM′=90°-60°= 30°.在Rt△ABM′中,tan∠ABM′ =. ∴tan3 0°=. ∴AM′ =.∴M′(,2). 代入y=kx中,得k== .设△ABM′沿BM′折叠后,点A落在矩形ABCD 内的点为A′.过A′作AH ⊥BC交BC于H.∵△A′BM′ ≌△ABM′,∴∠A′BM′=∠ABM′=3 0°, A′B = AB =2.∴∠A′BH=∠M′BH-∠A′BM′=30°.在Rt△A′BH中,A′H =A′B =1 ,BH=,∴.∴A'落在EF上.(图2)(图3)15.解:(1)如图.等腰三角形DAC.16.(1)证明:∵∠PBE+∠ABQ=180°-90°=90°,∠PBE+∠PEB=90°,∴∠ABQ=∠PEB.又∵∠BPE=∠AQB,∴△PBE∽△QAB.(2)∵△PBE∽△QAB,∴. ∵B Q=P B,∴.又∵∠ABE=∠BPE=90°,∴△PBE~△BAE.(3)点A能折叠在直线EC上.由(2)得,∠AEB=∠CEB,∴EC和折痕AE 重合.17. 解:(1)由已知可得∠A'OE=60o , A'E= AE.由A′E//x轴,得△OA'E是直角三角形.设A′的坐标为(0,b),则AE=A'E=b,OE=2b.∵b+2b=2+,∴b=1.∴A'、E的坐标分别是(0,1)与(,1).(2)因为A'、E在抛物线上,所以所以函数关系式为y =.由=0得,.与x轴的两个交点坐标分别是(-,0)与(,0).(3)不可能使△A'EF成为直角三角形.∵∠FA'E=∠FAE=60o,若△A'EF成为直角三角形,只能是∠A'EF=90o或∠A'FE=90o.若∠A'EF=90o,利用对称性,则∠AEF=90o, A'、E、A三点共线,O与A重合,与已知矛盾.同理若∠A'FE=90o也不可能.所以不能使△A′EF成为直角三角形.18. 解:(1)①当0<x≤3时,由折叠得到的△A'ED落在△ABC内部如图10(1),重叠部分为△A'ED.∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.∴△ADE∽△ABC.∴.∴,即.又∵FA'=FA=x,∴y=DE·A'F=·x·x.∴(0<x≤3).②当3<x<6时,由折叠得到的△A'ED有一部分落在△ABC外,如图10(2),重叠部分为梯形EDPQ.∵FH=6-AF=6-x, A'H=A'F-FH=x-(6-x)=2x-6,又∵DE∥PQ,∴△A'PQ∽△A'DE.∴.∴∴.(2)当0<x≤3时,y的最大值;当3<x<6时,由,可知当x=4时,y的最大值y2=9.∵y1<y2,∴当x=4时,y有最大值y最大=9.19. 证明:(1)能正确说明∠ADB=∠EBD(或△ABF≌△EDF),∴BF=DF.(2)能得出∠AEB=∠DBE(或∠EAD=∠BD A),∴AE∥BD.。
中考数学专题复习《特殊平行四边形中的折叠问题》测试卷-附带答案

中考数学专题复习《特殊平行四边形中的折叠问题》测试卷-附带答案学校:___________班级:___________姓名:___________考号:___________一 单选题1.如图 在矩形纸片ABCD 中 将BCD △沿BD 折叠 C 点落在C '处 则图中共有全等三角形( )A .2对B .3对C .4对D .5对2.如图 对折矩形纸片ABCD 使AB 与DC 重合得到折痕EF 将纸片展平 再一次折叠 使点D 落到EF 上点G 处 并使折痕经过点A 展平纸片后DAG ∠的大小为( )A .40︒B .60︒C .55︒D .75︒3.如图 在矩形ABCD 中 5AB = 8BC = 点E 和F 是边BC 上的两点 连结AE DF 、 将ABE 和CDF 沿AE DF 、折叠后 点B 和点C 重合于点M 则EF 的长是( )A .2.5B .3C .1.5D .44.如图 在矩形纸片ABCD 中 已知8AD = 折叠纸片使AB 边与对角线AC 重合 点B 落在点F 处 折痕为AE 且3EF = 则ABE 的面积为( )A .10B .9C .8D .75.如图 在矩形OABC 中 9OA = 15AB = E 是BC 上一点 沿AE 折叠 使点B 恰好落在x 轴的点D 处.E 点坐标是( )A .()5,15B .()3,15C .()15,2D .()15,4 6.如图 在矩形ABCD 中 点E 是边CD 的中点 将ADE 沿AE 折叠后得到AFE △ 且点F 在矩形ABCD 的内部 将AF 延长后交边BC 于点G 且45CG GB = 则AB AD 的值为( )A .43B .56C .1D .77.如图 把矩形纸片ABCD 沿对角线BD 折叠 设重叠部分为EBD △ 则下列结论不一定成立的是( )A .AB CD = B .BAE DCE ≌△△C .EB ED = D .30ABE ∠=︒ 8.如图 在一张菱形纸片ABCD 中 2AB = 30B ∠=︒ 点E 在BC 边上(不与B C 重合)将ABE 沿直线AE 折叠得到AFE △ 连接BF EF DF 有以下四个结论:AE EF =① 105BFD ∠=︒② ③当AE BC ⊥时 FD AC = ④当FE 平分AFB ∠时 则23FD = 其中正确的结论个数是( )A .1B .2C .3D .4二 填空题9.如图 正方形纸片ABCD 的边长为12 E 是边CD 上一点 连接AE 折叠该纸片 使点A 落在AE 上的点G 并使折痕经过点B 得到折痕BF 点F 在AD 上.若5DE = 则GE 的长为 .10.将一张长方形纸片ABCD 按如图所示方式折叠 AE AF 为折痕 点B D 折叠后的对应点分别为B' 'D 若''4B AD ∠=︒ 则EAF ∠的度数为 .11.如图 在长方形ABCD 中 3AD = 2AB = 点F 是AB 上一点 1AF = 点E 是BC 上一动点 连接EF 将BEF △沿EF 折叠 记点B 的对应点为点B ' 连接DB ' 则FB DB '+'的最小值是 .12.如图 在矩形ABCD 中 5AB = 8AD = 边AD 上有一动点P 连结BP 把ABP沿BP 折叠当点A 的对应点A '刚好落在BC 的垂直平分线上时 点A '到AD 的距离为 .13.如图所示 在完全重合放置的两张矩形纸片ABCD 中 8AB = 16BC = 将上面的矩形纸片折叠 使点C 与点A 重合 折痕为EF 点D 的对应点为点G 连接DG 则图中阴影部分的面积为 .三 解答题14.如图 正方形纸片ABCD 的边长12AB = E 是DC 上一点 5CE = 折叠正方形纸片 使点B 和点E 重合 折痕为FG 试求FG 的长.15.如图 把一张长方形纸片ABCD 折叠起来 使其对角顶点A 与C 重合 D 与G 重合 若长方形的长BC 为8 宽AB 为4(1)求DE 的长(2)求阴影部分的面积.16.如图1 将矩形纸片()ABCD AD AB >折叠 使点C 刚好落在线段AD 上 且折痕分别与边BC AD 相交 设折叠后点C D 的对应点分别为点G H 折痕分别与边BC AD 相交于点E F .(1)求证:四边形CEGF 是菱形(2)如图2 若3AB = 9BC = 当点G 与点A 重合时 求折痕EF 的长.17.如图 在四边形纸片ABCD 中 AD BC ∥ AD CD > 将纸片沿过点D 的直线折叠 使点C 落在AD 上的点C '处 折痕DE 交BC 于点E 连接C E '.(1)请确定四边形CDC E '的形状 并说明理由(2)若30BCD ∠=︒ 2CE = 过点C '作C F BC '⊥于F 连接CC '交DE 于点M 连接FM : ①四边形CDC E '的面积为①2FM = .18.已知矩形ABCD 中 4AB = 6AD = 点P 是边AD 的中点.(1)如图1 连接BP 并延长 与CD 的延长线交干点F 问:线段CF 上是否存在点Q 使得PFQ △是以PF 为腰的等腰三角形 若存在 请直接写出DQ 的长 若不存在 请说明理由.(2)①如图2 把矩形ABCD 沿直线MN 折叠 使点B 落在点D 上 直线MN 与AD BD BC 、、的交点分别为M H N 求折痕MN 的长.①如图3:在①的条件下 以点A 为原点 分别以矩形ABCD 的两条边AD AB 、所在的直线为x 轴和y 轴建立平面直角坐标系 若点R 在x 轴上 在平面内是否存在点S 使以R M N S 为顶点的四边形是菱形?若存在 请求出点S 的坐标 若不存在 请说明理由.(3)如图4:若点E 为CD 边上的一个动点 连结PE 以PE 为边向下方作等边PEG △ 连结AG 则AG 的最小值是______.(请直接写出答案)参考答案:1.C2.B3.B4.B5.D6.A7.D8.B9.491310.43︒111012.213.72514.解:如图 过点F 作FM BC ⊥ 垂足为M 连接BE .①四边形ABCD 为正方形①AB BC CD AD === 90A ABC C D ∠=∠=∠=∠=︒①90A ABC BMF ===︒∠∠∠①四边形ABMF 为矩形①12MF AB BC ===①将正方形纸片ABCD 折叠 使点B 落在边CD 上的点E 折痕为FG ①90C FMG ∠=∠=︒ BE FG ⊥①90BNG C ∠=∠=︒①90MGF CBE BEC CBE ∠+∠=∠+∠=︒ ①MGF CEB ∠=∠在FMG 和BCE 中 MGF CEB FMG C FM BC ∠=∠⎧⎪∠=∠⎨⎪=⎩①()AAS FMG BCE ≌①MG CE =.又①5CE =①5MG =.在Rt MFG 中 根据勾股定理得13FG == 即FG 的长是13.15.(1)设DE EG x == 则8AE x =- 在Rt AEG △中 222AG EG AE +=所以()22168x x +=-解得:3x =即3DE =(2)过点G 作GM AD ⊥于M 则1122AG GE AE GM ⨯=⨯4AG AB == 5AE = 3GE = 所以1143522GM ⨯⨯=⨯⨯所以125GM = 所以11825CED S GM DE =⨯=△. 16.解:(1)证明:①四边形ABCD 是矩形 ①AD ①BC①①GFE =①FEC①图形翻折后点G 与点C 重合 EF 为折线 ①①GEF =①FEC FG =FC EG =EC ①①GFE =①FEG①GF =GE①GE =EC =CF =FG①四边形CEGF 为菱形(2)当G 与A 重合时 由折叠的性质得AE =CE ①①B =90° AB =3 BC =9 BE =9-CE ①Rt ①ABE 中 AE 2=AB 2+BE 2即CE 2=32+(9-CE )2解得 CE =5.AC 222239310AB BC ++=由(1)知四边形CEGF 为菱形 ①12CEGF S EF AC CE AB =⨯=⨯菱形 ①10310EF == 17.(1)解:四边形CDC E '是菱形 理由如下: 根据折叠的性质可得:CD C D C DE CDE '∠=∠ CE C E '= ①AD BC ∥①C DE CED '∠=∠①CDE CED ∠=∠①CD CE =①CD C D C E CE ''===①四边形CDC E '为菱形(2)①①四边形CDC E '是菱形 ①2C E CE '== C E CD '∥ CM C M '= ①30C EF DCB '∠=∠=︒ ①C F BE '⊥ ①112C F C E ''== EF F '=①四边形CDC E '的面积212CE C F '=⨯=⨯= 故答案为:2①①EF = 2CE =①2CF =①(2222218C C C F CF ''=+=+=+①C F BC CM C M ''⊥=, ①12FM C C '=①22124FM C C '==故答案为:2 18.(1)解:存在 理由如下: 四边形ABCD 是矩形 90A ADC ∴∠=∠=︒ AB CD = 90FDP ∴∠=︒点P 是边AD 的中点 AP DP ∴=又APB DPF ∠=∠ ()ASA ABP DFP ∴△≌△ PF PB ∴= AB DF = 4,6AB AD ==4DF AB ∴== 132AP PD AD === 90A ∠=︒在Rt ABP 中:2222345PB AB AP +=+=5PF ∴=PFQ △为等腰三角形 以PF 为腰的等腰三角形分为两种情形: ①当PF PQ =时 此时点Q 与点C 重合 故4DQ DC == ①当FP FQ =时 如图:5PF = 5FQ = FD =4541DQ FQ FD =-=-=综合①① DQ 的长为:4或1(2)解:①如图:连接BM DN根据题意可知:MN 垂直平分BD ,MN BD BH DH ∴⊥= ,NB ND MB MD == 四边形ABCD 是矩形AD BN ∴MDH HBN ∴∠=∠ 又MHD NHB ∠=∠MHD NHB ∴△≌△MH HN ∴= MD NB =∴四边形MBND 是菱形设AM b = 则6MD MB b ==-在Rt AMB △中222BM AM AB =+即:222(6)4b b -=+ 解得:53b = 5513,6333AM BM ∴==-= 在Rt △ABD 中BD 12BH BD ∴=MH BD ⊥∴在Rt MHB △中MH ==2MN MH ∴== ①建立平面直角坐标系如图:由①知:53AM = 133BN MD MB ===4AB = MN = ①5130433M N ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,,, R M N S 为顶点的四边形是菱形 点R 在x 轴上当MR 为对角线时 MR NS ⊥,M R 都在x 轴上 ∴,N S 关于x 轴对称 1343S ⎛⎫∴ ⎪⎝⎭, 当MN 为对角线时 MN RS ⊥ 由(2)知 四边形MBND 是菱形 则S 与点B 重合 ∴此时(0,4)S -当MS 为对角线时 则MR SN ∥ MR SN =MN = 13(,4)3N -①1343S ⎛⎫- ⎪ ⎪⎝⎭综上可知 存在点S 使得以R M N S 为顶点的四边形是菱形 点S 坐标为:134134⎫--⎪⎪⎝⎭ 134134⎫+-⎪⎪⎝⎭ 13,43⎛⎫⎪⎝⎭ (0,4)- (3)解:如图:分别以PD PC 为边向下方作等边,PDF PCH △△ 过点F 作FI AD ⊥垂足为I 连接AF HF P 为AD 中点 ∴132AP PD AD ===PDF △为等边三角形1322PI PD ∴== 60DPF ∠=︒ PD PF =PA PF = 60DPF ∠=︒30PAF PFA ∴∠=∠=︒120APF ∴∠=︒92AI AP PI ∴=+=点E 为CD 边上的一个动点 以PE 为边向下方作等边PEG △ 当点E 与点D 重合时 点G 与点F 重合 当点E 与点C 重合时 点G 与点H 重合 ∴点G 在线段FH 上运动 当AG HF ⊥时 AG 最小 PEG △为等边三角形60EPG ∴∠=︒ PE PG =60 FPG FPE FPE EPD∴∠+∠=∠+∠=︒FPG DPE∴∠=∠∴FPG DPE△≌△PDE PFG∴∠=∠90PDE∠=︒∴90PFG∠=︒PF FH∴⊥当AG HF⊥时AG PF120,30APF PAF∠=︒∠=︒18012060PAG∴∠=︒-︒=︒603030 FAG PAG PAF∠=∠-∠=︒-︒=︒IAF GAF∴∠=∠FI AD⊥90AIF∴=︒在AFI和AFI中AIF AGFAF AFFAG FAI∠=∠⎧⎪=⎨⎪∠=∠⎩∴()ASAAFI AFI≌AG AI∴=∴当AG HF⊥时92AG AI==故答案为:92.。
2023学年北师大版九年级数学上学期专项讲练1-24 特殊平行四边形折叠(基础篇)

专题1.24 特殊平行四边形折叠专题(基础篇)(专项练习)一、单选题【知识点一】菱形折叠问题1.如图,将长方形纸片折叠,使A点落BC上的F处,折痕为BE,若沿EF剪下,则折叠部分是一个正方形,其数学原理是()A.邻边相等的矩形是正方形B.对角线相等的菱形是正方形C.两个全等的直角三角形构成正方形D.轴对称图形是正方形AB=,则2.如图,将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF,若6BC的长为()A.2B.C.4D.3.如图,把菱形ABCD沿AH折叠,使B点落在BC上的E点处,若70∠=︒,则EDCB∠的大小为().A.15︒B.20︒C.30D.25︒4.如图,在菱形纸片ABCD中,60A∠=︒,点E是边BC上的一点,将纸片沿DE折叠,点C落在C'处,DC'恰好经过AB的中点P,则DEC∠的度数是()A.75︒B.60︒C.45︒D.78︒【知识点二】矩形将折叠问题5.如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为()A.28°B.31°C.62°D.56°6.如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将∠DAE沿DE折叠,使点A落在对角线BD上的点A′处,则AE的长为()A.103B.203C.3D.47.如图,把矩形OABC放入平面直角坐标系中,点B的坐标为(10,8),点D是OC 上一点,将∠BCD沿BD折叠,点C恰好落在OA上的点E处,则点D的坐标是()A.(0,4)B.(0,5)C.(0,3)D.(0,2)8.如图,将矩形ABCD沿EF折叠,使点B落在边AD上的点M处,点C落在点N处,已知∠DMN=30°,连接BM,则∠AMB的度数为()A.60°B.75°C.80°D.85°【知识点三】正方形折叠问题9.如图,将正方形纸片ABCD折叠,使顶点B落在边AD上的点E处,折痕交AB于点F,交CD于点G.若1AE=,30∠=︒,则AB的长为()AFEA.2B.1C.D.2+10.如图,AC是正方形ABCD的对角线,E是BC上的点,1BE=,将ABE△沿AE折叠,使点B落在AC上点F处,则AB的长为()A.2B.3C.1D.111.把一个面积为4的正方形,通过沿虚线折叠得到一个新正方形,它的边长是()A.2 B C .1 D .1.41412.将一张正方形纸片ABCD 按如图所示的方式折叠,CE 、CF 为折痕,点B 、D 折叠后的对应点分别为B '、D ',若∠ECF =21°,则∠B 'CD '的度数为( )A .35°B .42°C .45°D .48°二、填空题【知识点一】菱形折叠问题13.如图,在菱形纸片ABCD 中,60A ︒∠=,折叠菱形纸片ABCD ,使点C 落在DP (P 为AB 的中点)所在的直线上,得到经过点D 的折痕DE ,则DEC ∠的度数为________.14.如图,在菱形ABCD 中,E 是AD 上一点,沿BE 折叠ABE △,点A 恰好落在BD 上的点F 处,连接CF ,若110DFC ∠=︒,则A ∠=__________.15.将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为_____.16.如图,将平行四边形ABCD进行折叠,折叠后AD恰好经过点C得到AD',若∠=︒==,则线段AC的长度为_________.90,5,4BAC DE CE【知识点二】矩形将折叠问题17.如图所示,把一张矩形纸片按如图所示方法进行两次折叠,得到等腰Rt∠ABC,若S△ABC=2,则S△ACD=__.18.如图,将矩形纸片ABCD折叠(AD>AB),使AB落在AD上,AE为折痕,然后将矩形纸片展开铺在一个平面上,E点不动,将BE边折起,使点B落在AE上的点G处,连接DE,若DE=EF,CE=1,则AD=________.19.如图,在矩形ABCD中,AB=4,BC=6,点E是BC的中点,点F在AD上运动,沿直线EF折叠四边形CDFE,得到四边形GHFE,其中点C落在点G处,连接AG,AH,则AG的最小值是__.20.矩形ABCD中,AB=5,AD=3,P为CD上一点,将∠ADP沿AP所在的直线折叠,得到∠AEP,当B、E、P三点共线时,tan∠DAP=_______【知识点三】正方形折叠问题21.如图,小明将一张正方形纸片对折,使得AB与CD重合,折痕为EF,展开后再沿BH折叠,使得点C刚好落在折痕EF上的C′处,若CH=1cm,则BC= _____cm.22.如图.将正方形纸片ABCD折叠,使边AB、CB均落在对角线BD上,得折痕BE、BF,则∠EBF的大小为_____.23.如图,在一次综合实践活动中,小明将一张边长为10cm的正方形纸片ABCD,沿着BC 边上一点E 与点A 的连线折叠,点B '是点B 的对应点,延长EB '交DC 于点G ,经测量2cm BE =,20cm 3B G '=,则ECG 的面积为______2cm .24.如图,先将正方形纸片对折,折痕为MN ,再把B 点折叠在折痕MN 上,折痕为AE ,点B 在MN 上的对应点为H ,则HBC ∠的度数为______.三、解答题25.如果我们身旁没有量角器或三角尺,又需要作60°,30°,15°等大小的角,该怎么办呢?小西进行了以下操作研究(如图1):第1步:对折矩形纸片ABCD ,使AD 与BC 重合,得到折痕EF ,把纸片展平. 第2步:再次折叠纸片,使点A 落在EF 上,并使折痕经过点B ,得到折痕BM ,同时得到了线段BN .小雅在小西研究的基础上,再次动手操作(如图2):将MN 延长交BC 于点G ,将△BMG 沿MG 折叠,点B 刚好落在AD 边上点H 处,连接GH ,把纸片再次展平.请根据小西和小雅的探究,完成下列问题:∠直接写出BE和BN的数量关系:;∠根据定理:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角是30°,请求出∠ABM的度数;∠求证:四边形BGHM是菱形.26.如图所示,在矩形ABCD中,AB=5,AD=8,点E,F分别是边AD,BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,使点C落在点G处,点D落在点H处,若EH与CB的延长线交于点P.(1)求证:PH=PB;(2)若∠PEA=45°,求AE的长度.27.【教材呈现】人教八年级下册数学教材第59页的部分内容.如图1,把一张矩形纸片按如图那样折一下,就可以裁出正方形纸片,为什么?(1)【问题解决】如图1,已知矩形纸片ABCD(AD>AB),将矩形纸片沿过点A的直线折叠,使点B落在边AD上,点B的对应点为F,折痕为AE,点E在BC上.求证:四边形ABEF是正方形.(请完成以下填空)证明:∠四边形ABCD是矩形,∠∠BAD=∠B=90°,∠折叠,∠AFE=∠B=90°,∠四边形ABEF是矩形()∠折叠,∠AB=(),∠四边形ABEF是正方形()(2)【问题拓展】如图2,已知平行四边形纸片ABCD(AD>AB),将平行四边形纸片沿过点A的直线折叠,使点B落在边AD上,点B的对应点为F,折痕为AE,点E在边BC上.∠求证:四边形ABEF是菱形.∠连结BF,若AE=5,BF=10,求菱形ABEF的面积.28.如图,E、F分别是正方形ABCD边AB、AD的中点,将△ABF沿BF折叠,点A 落在点Q处,连接FQ并延长,交DC于G点.(1)求证:CE=BF;(2)若AB=4,求GF的值.参考答案1.A【分析】将长方形纸片折叠,使A点落BC上的F处,可得到BA=BF,折痕为BE,沿EF剪下,故四边形ABFE为矩形,且有一组邻边相等,故四边形ABFE为正方形.解:∠将长方形纸片折叠,A落在BC上的F处,∠BA=BF,∠折痕为BE,沿EF剪下,∠四边形ABFE为矩形,∠四边形ABEF为正方形.故用的判定定理是;邻边相等的矩形是正方形.故选:A.【点拨】本题考查了正方形的判定定理,关键是根据邻边相等的矩形是正方形和翻折变换解答.2.D【分析】根据菱形及矩形的性质可得到∠BAC的度数,从而根据直角三角形的性质求得BC的长.解:∠四边形AECF为菱形,∠∠FCO=∠ECO,EC=AE,由折叠的性质可知,∠ECO=∠BCE,又∠FCO+∠ECO+∠BCE=90°,∠∠FCO=∠ECO=∠BCE=30°,在Rt∠EBC中,EC=2EB,又∠EC=AE,AB=AE+EB=6,∠EB=2,EC=4,∠Rt∠BCE中,BC故选:D.【点拨】本题主要考查了菱形的性质以及矩形的性质,解决问题的关键是根据折叠以及菱形的性质发现特殊角,根据30°的直角三角形中各边之间的关系求得BC 的长.3.A【分析】根据菱形的性质,已知菱形的对角相等,故推出70ADC B ∠=∠=︒,从而得出AED ADE ∠=∠.又因为//AD BC ,故DAE AEB ∠=∠,ADE AED ∠=∠,易得解.解:根据菱形的对角相等得70ADC B ∠=∠=︒.AD AB AE ==,AED ADE ∴∠=∠.根据折叠得70AEB B ∠=∠=︒.//AD BC ,70DAE AEB ∴∠=∠=︒,(180)255ADE AED DAE ∴∠=∠=︒-∠÷=︒.705515EDC ∴∠=︒-︒=︒.故选:A .【点拨】此题要熟练运用菱形的性质得到有关角和边之间的关系.在计算的过程中,综合运用了等边对等角、三角形的内角和定理以及平行线的性质.注意:折叠的过程中,重合的边和重合的角相等.4.A【分析】连接BD ,由菱形的性质及∠A =60°,得到三角形ABD 为等边三角形,P 为AB 的中点,利用三线合一得到DP 为角平分线,得到∠ADP =30°,∠ADC =120°,∠C =60°,进而求出∠PDC =90°,由折叠的性质得到∠CDE =∠PDE =45°,利用三角形的内角和定理即可求出所求角的度数.解:连接BD ,∠四边形ABCD为菱形,∠A=60°,∠∠ABD为等边三角形,∠ADC=120°,∠C=60°,∠P为AB的中点,∠DP为∠ADB的平分线,即∠ADP=∠BDP=30°,∠∠PDC=90°,∠由折叠的性质得到∠CDE=∠PDE=45°,在∠DEC中,∠DEC=180°−(∠CDE+∠C)=180°−(45°+60°)=75°.故选:A.【点拨】本题考查了折叠问题,菱形的性质,等边三角形的性质,以及内角和定理,熟练掌握折叠的性质是解本题的关键.5.D【分析】先利用互余计算出∠FDB=28°,再根据平行线的性质得∠CBD=∠FDB=28°,接着根据折叠的性质得∠FBD=∠CBD=28°,然后利用三角形外角性质计算∠DFE的度数.解:∠四边形ABCD为矩形,∥,∠ADC=90°,∠AD BCBDC62,∠FDB=90°-∠BDC=90°-62°=28°,∥,∠AD BC∠∠CBD=∠FDB=28°,∠矩形ABCD沿对角线BD折叠,∠∠FBD=∠CBD=28°,∠∠DFE=∠FBD+∠FDB=28°+28°=56°.故选:D.【点拨】本题考查了平行线的性质,轴对称的性质,矩形的性质,三角形的外角的性质,熟练的利用轴对称的性质得到相等的角是解本题的关键.6.A【分析】首先利用勾股定理计算出BD 的长,再根据折叠可得AD =A ′D =5,进而得到A ′B 的长,再设AE =x ,则A ′E =x ,BE =12-x ,再在Rt ∠A ′EB 中利用勾股定理可得方程:(12-x )2=x 2+82,解出x 的值,可得答案.解:∠AB =12,BC =5,∠AD =5,∠BD =13,根据折叠可得:AD =A ′D =5,∠A ′B =13-5=8,设AE =x ,则A ′E =x ,BE =12-x ,在Rt △A ′EB 中:(12-x )2=x 2+82,解得:x =103. 故选:A .【点拨】此题主要考查了图形的翻折变换,关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.7.C【分析】由题意可得AO =BC =10,AB =OC =8,DE =CD ,BE =BC =10,在Rt ABE △中,由勾股定理可求得6AE =,OE =4,设OD =x ,则DE =CD =8-x ,然后在Rt ODE △中,由勾股定理即可求得OD =3,继而求得点D 的坐标.解:∠点B 的坐标为(10,8),∠AO =BC =10,AB =OC =8,由折叠的性质,可得:DE =CD ,BE =BC =10,在Rt ABE △中,由勾股定理得:6AE =,∠OE =AO -AE =10-6=4,设OD =x ,则DE =CD =8-x ,在Rt ODE △中,由勾股定理得:222OD OE DE +=,即:()22248x x +=-,解得:3x =,∠OD =3,∠点D 的坐标是(0,3).故选:C.【点拨】本题主要考查了矩形的性质、折叠的性质、勾股定理,熟练掌握折叠的性质是解题的关键.8.B【分析】由四边形ABCD 是矩形,得∠A =∠ABC =90°,根据矩形ABCD 沿EF 折叠,使点B 落在边AD 上的点M 处,点C 落在点N 处,得∠NME =∠ABC =90°,ME =BE ,而∠DMN =30°,即知∠AME =60°,∠AEM =30°,即∠EMB +∠EBM =30°,可得∠EMB =∠EBM =15°,故∠AMB =∠AME +∠EMB =75°.解:∠四边形ABCD 是矩形,∠∠A =∠ABC =90°,∠矩形ABCD 沿EF 折叠,使点B 落在边AD 上的点M 处,点C 落在点N 处,∠∠NME =∠ABC =90°,ME =BE ,∠∠DMN =30°,∠∠AME =180°-∠NME -∠DMN =60°,∠∠AEM =90°-∠AME =30°,∠∠EMB +∠EBM =30°,∠ME =BE ,∠∠EMB =∠EBM =15°,∠∠AMB =∠AME +∠EMB =75°,故选:B .【点拨】本题考查了矩形中的折叠问题,解题的关键是掌握折叠的性质:折叠前后能够重合的线段相等、能够重合的角相等.9.D【分析】先求出AF和EF的长,再根据翻折变换的知识得到EF=BF,进而求出AB的长.解:∠四边形ABCD是正方形,∠∠A= 90°,AE= 1,∠AFE= 30°∠EF= 2,AF∠正方形纸片ABCD折叠,使顶点B落在边AD上的点E处,EF= BF,BF= 2,∠AB= AF+ BF故选:D.【点拨】本题主要考查了翻折变换以及正方形的性质,解题的关键是根据翻折变换得到EF=BF,此题难度不大.10.C【分析】∠BCD=45°,由折叠的性由正方形的性质得AB=BC,∠BCD=∠B=90°,∠ECF=12质得∠AFE=∠B=90°,FE=BE=1,证出△CEF是等腰直角三角形,则CE FE进而得出答案.解:∠四边形ABCD是正方形,∠BCD=45°,∠AB=BC,∠BCD=∠B=90°,∠ECF=12由折叠的性质得:∠AFE=∠B=90°,FE=BE=1,∠∠CFE=90°,∠∠CEF是等腰直角三角形,FE,∠CE=BE+CE=1∠AB=BC=1故选:C.【点拨】本题考查了翻折变换的性质、正方形的性质、等腰直角三角形的判定与性质等知识;熟练掌握翻折变换和正方形的性质是解题的关键.11.B由原正方形的面积是4,可求得原正方形的边长为2,由勾股定理可出新正方形边长.解:∠原正方形的面积是4,∠原正方形的边长,∠由折叠可得四角是等腰直角三角形,其腰长为1,由勾股定理得:新正方形边长,故选:B.【点拨】本题考查折叠问题,正方形的性质,勾股定理,掌握运用勾股定理是解题的关键.12.D【分析】可以设∠ECB'=α,∠FCD'=β,根据折叠可得∠DCE=∠D'CE,∠BCF=∠B'CF,进而可求解.解:设∠ECB'=α,∠FCD'=β,根据折叠可知:∠DCE=∠D'CE,∠BCF=∠B'CF,∠∠ECF=21°,∠∠D'CE=21°+β,∠B'CF=21°+α,∠四边形ABCD是正方形,∠∠BCD=90°,∠∠D'CE+∠ECF+∠B'CF=90°∠21°+β+21°+21°+α=90°,∠α+β=27°,∠∠B'CD'=∠ECB'+∠ECF+∠FCD'=α+21°+β=21°+27°=48°则∠B'CD'的度数为48°.故选:D.【点拨】本题考查了正方形与折叠问题,解决本题的关键是熟练运用折叠的性质.13.75°连接BD ,先证明ABD △为等边三角形,然后根据三线合一定理得到30ADP BDP ∠=∠=即可得到90PDC ∠=,则45CDE PDE ∠=∠=,再根据三角形内角和定理求解即可.解:连接BD ,∠四边形ABCD 为菱形,∠AD =AB ,60C A ∠==∠,AB∠CD ,∠180A ADC ∠+∠=,∠120ADC ∠=∠60A ∠=,∠ABD △为等边三角形,∠P 为AB 的中点,∠DP 为ADB ∠的平分线,即30ADP BDP ∠=∠=,∠90PDC ∠=,由折叠的性质得到45CDE PDE ∠=∠=,在DEC 中,()18075DEC CDE C ∠=-∠+∠=.故答案为:75°.【点拨】本题主要考查了菱形的性质,等边三角形的性质与判定,折叠的性质,三角形内角和定理,解题的关键在于能够熟练掌握相关知识进行求解.14.100︒【分析】根据菱形的性质得到AB =BC =CD =DA ,AD//BC ,∠ADB =∠CBF =∠ABD ,再根据折叠的性质得到∠BFC =∠BCF ,由三角形内角和与外角的性质得到结果.解:∠四边形ABCD 是菱形,∠AB =BC =CD =DA ,AD//BC ,∠∠ADB =∠CBF =∠ABD ,∠E 是AD 上一点,沿BE 折叠ABE △,点A 恰好落在BD 上的点F 处,∠BA =BF ,∠A =∠BFE ,∠BF =BC ,∠∠BFC =∠BCF ,∠110DFC ∠=︒,∠∠BFC =∠BCF =70°,∠∠ADB =∠CBF =40°,∠∠A =180°-2∠ADB =180°-80°=100°,故答案为:100︒.【点拨】本题主要考查了菱形的基本性质与折叠的基本性质,根据菱形的基本性质与折叠的基本性质得到边相等是解题的关键.15.23√【分析】根据菱形AECF ,得∠FCO =∠ECO ,再利用∠ECO =∠ECB ,可通过折叠的性质,结合直角三角形勾股定理求得BC 的长,则利用菱形的面积公式即可求解.解:∵四边形AECF 是菱形,AB =3,∴设BE =x ,则AE =3﹣x ,CE =3﹣x ,∵四边形AECF 是菱形,∴∠FCO =∠ECO ,∵∠ECO =∠ECB ,∴∠ECO =∠ECB =∠FCO =30°,∴2BE =CE ,∴CE =2x ,∴2x =3﹣x ,解得:x =1,∴CE =2,利用勾股定理得出:BC 2+BE 2=EC 2,BC 3=√又∵AE =AB ﹣BE =3﹣1=2,则菱形的面积=AE •BC =23√.故答案为23√.【点拨】此题主要考查了折叠问题以及勾股定理等知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.16.12【分析】由平行四边形的性质可得AD =BC ,AB =CD =DE +CE =9,AB //CD ,可得∠ECD '=90°,由折叠的性质可得D 'E =DE =5,AD =AD ',由勾股定理可求CD '的长,AC 的长.解:∠四边形ABCD 是平行四边形∠AD =BC ,AB =CD =DE +CE =9,AB //CD∠∠BAC =∠ACD =90°∠∠ECD '=90°∠将平行四边形ABCD 进行折叠,折叠后AD 恰好经过点C 得到AD ',∠D 'E =DE =5,AD =AD '∠CD '3∠AD '=AC +3=AD =BC∠BC 2=AB 2+AC 2,∠(AC +3)2=81+AC 2,∠AC =12故答案为:12.【点拨】本题考查了翻折变换,平行四边形的性质,求出CD '的长是本题的关键. 17.【分析】根据折叠的性质可得ACD DEC S S =,分别求出DE ,EC ,求出DEC S ,即可得出ACD S .解:如图:过点A 作AF DE ⊥于点F ,ABC 是等腰直角三角形,2ABC S =, 1·22ABC S AB BC ∴==,即2AB BC ==,AC ∴==折叠,AC CE ∴==DAC DEC SS =,纸片为矩形, ∴折叠后45FDA ∠=︒,90DFA ∠=︒,DFA ∴是等腰直角三角形,2DF FA EC CB ∴==+=,2AB EF ==,224DE DF FE ∴=+=+=+(114422ACD DEC S S DE EC ∴==⨯=⨯+⨯,故答案为:4.【点拨】本题考查了折叠问题,矩形的性质,等腰直角三角形,三角形的面积,勾股定理,通过折叠得出ACD DEC S S =是解题的关键.18.22+【分析】证明Rt △EBF ∠Rt △EB ′D (HL ),推出BF =DB ′,再证明DB ′=EC =BF =1,想办法求出AB ′,可得结论.解:由翻折的性质可知,EB =EB ′,∠B =∠AB ′E =∠EB ′D =90°,在Rt△EBF和Rt△EB′D中,EB EB EF ED'=⎧⎨=⎩,∠Rt△EBF∠Rt△EB′D(HL),∠BF=DB′,∠四边形ABCD是矩形,∠∠C=∠CDB′=∠EB′D=90°,∠四边形ECDB′是矩形,∠DB′=EC=1,∠BF=EC=1,由翻折的性质可知,BF=FG=1,∠F AG=45°,∠EGF=∠B=∠AGF=90°,∠AG=FG=1,∠AF∠AB=AB∠AD=AB′+DB故答案为:.【点拨】本题考查翻折变换,矩形的性质,全等三角形的判定和性质,等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.19.2【分析】如图,当A、G、E共线时,AG最小,先求出AE,根据AG=AE﹣EG即可解决问题.解:如图,依题意:点G在以点E为圆心,12BC长为半径的圆上运动,当A、G、E共线时,AG最小,∠四边形ABCD 是矩形,∠∠B =90°,BE =EC =3,AB =4,∠AE5.此时AG =AE ﹣EG =5﹣3=2.故答案为2.【点拨】本题考查了矩形的性质,勾股定理,点到圆的距离,明确点和圆的位置关系是解决本题的关键.20.13【分析】由翻折可得AD =AE ,在Rt ∠ABE 中可求出BE ,设DP =EP =x ,表示出BP 和CP ,在Rt ∠BCP 中,通过勾股定理即可列出等式,解出方程,从而求出答案.解:矩形ABCD 中,AB =5,AD =3,则CD =5,BC =3,∠ADP 沿AP 所在的直线折叠,得到∠AEP ,且B 、E 、P 三点共线,∠易证∠ADP ∠∠AEP ,∠AE =AD ,DP =EP ,∠ADP =∠AEP =90°,在Rt ∠ABE 中,AB =5,AE =3,∠BE =4;设DP =EP =x ,则BP =4x +,CP=5x -,在Rt ∠BCP 中,222+BC CP BP =,即()()2223+54x x -=+,解得1x =,∠DP =1,在Rt ∠ADP 中,tan∠DAP =13DP AD =.故答案为:13.【点拨】本题主要考查翻折问题,直角三角函数和勾股定理,找准线段之间的关系,并准确计算是解题的关键.21【分析】连接CC′,证明∠BCC′是等边三角形,再由折叠的性质得到∠HBC=∠HBC′=30°,利用含30度角的直角三角形的性质求解即可解决问题.解:如图,连接CC′,由折叠的性质知,折痕为EF是BC的垂直平分线,∠BC′=CC′,又由折叠的性质知,BC= BC′,∠HBC=∠HBC′,∠BC′=CC′=BC,∠∠BCC′是等边三角形,∠∠C′BC=60°,∠∠HBC=∠HBC′=30°,在Rt△HBC中,∠HBC=30°,CH=1cm,∠HB=2cm,∠BCcm),【点拨】本题考查了翻折变换的性质,等边三角形的判定和性质,勾股定理,解决本题的关键是掌握翻折的性质.22.45°##45度【分析】首先根据正方形的性质可得∠1+∠2+∠3+∠4=∠ABC=90°,再根据折叠可得∠1=∠2=1 2∠ABD ,∠3=∠4=12∠DBC ,进而可得∠2+∠3=45°,即∠EBF =45°.解:∠四边形ABCD 是正方形,∠∠ABC =90°,根据折叠可得∠1=∠2=12∠ABD ,∠3=∠4=12∠DBC ,∠∠1+∠2+∠3+∠4=∠ABC =90°,∠∠2+∠3=45°,即∠EBF =45°,故答案为:45°.【点拨】此题主要考查了图形的翻折变换和正方形的性质,关键是找准图形翻折后,哪些角是相等的.23.403##1133 【分析】根据题意,BE B E '=,进而求得EC ,勾股定理求得CG ,即可求得ECG 的面积. 解:折叠,∴BE B E '=2cm BE =,20cm3B G '=, 2023EG ∴=+263=cm ,8EC BC BE =-=cm ∠四边形ABCD 是正方形∠90C ∠=︒Rt EGC △中103CG ==cm . 11104082233ECG S EC CG ∴=⨯⨯=⨯⨯=△2cm .故答案为:40 3【点拨】本题考查了折叠的性质,勾股定理,掌握勾股定理是解题的关键.24.15°【分析】由翻折的性质AH=AB,MN垂直平分AD,于是得到DH=AH=AB=AD,故此∠ADH 为等边三角形,由∠ADH为等边三角形可知∠HAB=30°,在∠ABH中可求得∠ABH=75°,故此可求得∠HBC=15°.解:∠MN垂直平分AD,∠DH=AH.由翻折的性质可知:AH=AB.∠正方形ABCD中,∠AH=AD=DH.∠∠ADH是一个等边三角形.∠∠DAH=60°.∠∠HAB=30°.∠AB=AH,∠∠ABH=12×(180°−30°)=75°.∠∠HBC=∠ABC−∠ABH=90°−75°=15°.故答案是:15°.【点拨】本题主要考查的是翻折的性质、线段垂直平分线的性质、等边三角形的性质和判定、等腰三角形的性质,正方形的性质,证得∠ADH是一个等边三角形是解题的关键.25.∠BE=12BN;∠∠ABM=30°;∠见分析.【分析】(1)根据折叠的性质可得BE=12AB,从而得到BE=12BN,即可求解;(2)根据在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角是30°,可得∠BNE=30°,即可求解;(3)由∠得∠ABM=30°,从而得到∠BMG是等边三角形,进而得到BM=BG,再有折叠的性质,即可求证.解:∠解:∠对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,AB,∠BE=12∠再次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到了线段BN.∠AB=BN,BN;∠BE=12∠解:∠由折叠的性质得:∠BEN=∠AEN=90°,BN,∠BE=12∠∠BNE=30°,∠∠ABN=60°,∠ABN=30°;由折叠的性质得:∠ABM=12∠证明:由∠得∠ABM=30°,∠四边形ABCD是矩形,∠∠A=∠ABC=90°,∠∠AMB=∠BMN=60°,∠MBG=60°,∠∠BMG是等边三角形,∠BM=BG,由折叠得BM=MH,BG=GH,∠BM=MH=BG=GH,∠四边形BGHM是菱形.【点拨】本题主要考查了图形的变换——折叠,矩形的性质,菱形的判定等,熟练掌握图形折叠前后对应边相等,对应角相等是解题的关键.26.(1)见分析(2)AE【分析】(1)根据∠PEF=∠PFE,证明PE=PF,再根据折叠的性质ED=EH,DE=BF,进一步计算即可证明PH=PB;(2)先证明△AEQ和△BPQ都是等腰直角三角形,设AE=CF=x,则EQ x,PQ(5-x) ,利用PE=PF代出方程求解即可.解:(1)证明:∠四边形ABCD是矩形,∠AD∠BC,∠∠DEF=∠PFE,由翻折变换可知,∠DEF=∠PEF,∠∠PEF=∠PFE,∠PE=PF;∠AD=BC,AE=FC,∠ED=BF.由折叠性质得ED=EH,∠BF=EH,∠PE-EH=PF-BF,∠PH=PB;(2)解:设PE交AB于点Q,设AE=CF=x,则DE=BF=8-x,∠∠PEA=45°,∠A=∠ABC=∠ABP=90°,∠∠AEQ=∠AQE=∠PBQ=∠QPB=45°,∠△AEQ和△BPQ都是等腰直角三角形,∠BQ=PB=5-x,由勾股定理得:EQ,PQ-x) ,∠PE=PF,∠PQ+EQ=PB+BF-x=5-x+8-x,解得:x∠AE【点拨】本题考查了翻折变换,等腰直角三角形的判定和性质,勾股定理等知识,解答本题的关键是明确题意,找出所求问题需要的条件.27.(1)有三个角是直角的四边形是矩形;AF;一组邻边相等的矩形是正方形.(2)∠证明见详解;∠菱形ABEF的面积为25【分析】(1)由矩形的性质得∠BAD=∠B=90°,再由折叠的性质得:∠AFE=∠B=90°,AB=AF,则四边形ABEF是矩形,然后由AB=AF,即可得出结论;(2)∠由平行四边形的性质得AD∠BC,则∠F AE=∠BEA,再证AB=BE,则AF=BE,得四边形ABEF是平行四边形,然后由AF=AB即可得出结论;∠由菱形面积公式得S菱形ABEF=12AE•BF,即可得出答案.(1)解:∠四边形ABCD是矩形,∠∠BAD=∠B=90°,由折叠的性质得:∠AFE=∠B=90°,∠四边形ABEF是矩形(有三个角是直角的四边形为矩形),由折叠的性质得:AB=AF,∠四边形ABEF是正方形(有一组邻边相等的矩形是正方形),故答案为:有三个角是直角的四边形为矩形;AF;有一组邻边相等的矩形是正方形;(2)∠证明:∠四边形ABCD是平行四边形,∠AD∠BC,∠∠F AE=∠BEA,由折叠的性质得:AF=AB,∠BAE=∠F AE,∠∠BEA=∠BAE,∠AB=BE,∠AF=BE,∠四边形ABEF是平行四边形,又∠AF=AB,∠平行四边形ABEF是菱形;∠解:如图,∠四边形ABEF是菱形,AE=5,BF=10,∠S菱形ABEF=12AE•BF=12×5×10=25,故菱形ABEF的面积为25.【点拨】本题是四边形综合题目,考查了矩形的判定与性质、正方形的判定、菱形的判定与性质、平行四边形的判定与性质、等腰三角形的判定、折叠的性质、平行线的性质等知识,本题综合性强,熟练掌握折叠的性质、矩形的判定与性质是解题的关键.28.(1)见分析(2)GF的值为103.【分析】(1)先判断出AF=BE,进而得出△F AB∠∠EBC(SAS),即可得出结论;(2)连接BG,根据HL证明Rt△BQG∠Rt△BCG,得QG=GC,设QG=b,在Rt△DFG 中,根据勾股定理列方程可得b,从而可得结论.解:(1)证明:∠四边形ABCD是正方形,∠AB=AD,∠A=∠ABC=90°,∠E、F分别是正方形ABCD边AB、AD的中点,∠AF=BE,∠∠F AB∠∠EBC(SAS),∠CE=BF;(2)解:如图,连接BG,由折叠得:AB=BQ,∠BQF=∠A=90°,∠AB=BC,∠BC=BQ,∠BG=BG,∠Rt△BQG∠Rt△BCG(HL),∠QG=GC,∠AB=4,F是正方形ABCD边AD的中点,设QG=b,则DF=AF=FQ=2,FG=2+b,DG=4-b,在Rt△DFG中,∠DF2+DG2=FG2,∠2222(4)(2)b b+-=+,∠b=43,即QG=43,∠GF=FQ+QG=2+43=103.∠GF的值为103.【点拨】此题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,正确作辅助线是本题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊四边形相关的折叠问题 一、选择题
1. 如图,将▱ABCD 沿对角线AC 折叠,使点B 落在B ′处,若∠1=∠2=44°,则∠B 为( )
A .66°
B .104°
C .114°
D .124°
2.如图,在矩形ABCD 中,AB=3,BC=5,点E 在边CD 上,连接BE ,将△BCE 沿BE 折叠,若点C 恰好落在AD 边上的点F 处,则CE 的长为( )
A. 53
B. 35
C. 43
D.3
4
3.如图,正方形ABCD 的边长为9,将正方形折叠,使顶点D 落在BC 边上的点E 处,折痕为GH .若BE :EC=2:1,则线段CH 的长是( )
A.3
B. 4
C. 5
D.6
二、填空题
4. 如图,折叠矩形纸片ABCD ,得折痕BD ,再折叠使AD 边与对角线BD 重合,得折痕DF .若AB=4,BC=2,则AF= _________.
5. 如图,长方形ABCD 中,AB=3cm ,AD=9cm ,将此长方形折叠,使点B 与点D 重合,折痕为EF ,则△ABE 的面积为________ cm 2.
6.如图,正方形ABCD 的边长为4,E 为BC 上的一点,BE=1,F 为AB 上的一点,AF=2,P 为AC 上一个动点,则PF+PE 的最小值为_______.
三、解答题
7.在平行四边形ABCD 中,将△BCD 沿BD 翻折,使点C 落在点E 处,BE 和AD 相交于点O.
求证:OA=OE
8.如图,将□ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点'D 处,折痕l 交CD 边于点E ,连接BE
(1)求证:四边形'BCED 是平行四边形
(2)若BE 平分∠ABC ,求证:2
22BE AE AB +=
9. 如图,AC 为矩形ABCD 的对角线,将边AB 沿AE 折叠,使点B 落在AC 上的点M 处,将边CD 沿CF 折叠,使点D 落在AC 上的点N 处。
(1)求证:四边形AECF 是平行四边形;
(2)若AB=6,AC=10,求四边形AECF 的面积。
10.将矩形ABCD 折叠使A ,C 重合,折痕交BC 于E ,交AD 于F ,
(1)求证:四边形AECF 为菱形;
(2)若AB=4,BC=8,
①求菱形的边长;
②求折痕EF 的长.
A B C D E
O
参考答案
1. C .【解析】∵四边形ABCD 是平行四边形,
∴AB ∥CD ,∴∠ACD=∠BAC ,
由折叠的性质得:∠BAC=∠B ′AC ,∴∠BAC=∠ACD=∠B ′AC=∠1=22°,
∴∠B=180°-∠2-∠BAC=180°-44°-22°=114°.
2.B 【解析】设CE=x .
∵四边形ABCD 是矩形,
∴AD=BC=5,CD=AB=3,∠A=∠D=90°.
∵将△BCE 沿BE 折叠,使点C 恰好落在AD 边上的点F 处,
∴BF=BC=5,EF=CE=x ,DE=CD-CE=3-x . 在Rt △ABF 中,由勾股定理得:
AF 2=52-32=16,
∴AF=4,DF=5-4=1.
在Rt △DEF 中,由勾股定理得:
EF 2=DE 2+DF 2,
即x 2=(3-x )2+12,
解得x=3
5. 3.B[解析]由题意设CH=xcm ,则DH=EH=(9-x )cm ,
∵BE :EC=2:1,∴CE=BC=3cm
∴在Rt △ECH 中,EH 2=EC 2+CH 2,
即(9-x )2=32+x 2,
解得x=4,即CH=4cm .
4.-1
5. 6【解析】∵将此长方形折叠,使点B 与点D 重合,
∴BE=ED .
∵AD=9cm=AE+DE=AE+BE .
∴BE=9-AE ,
根据勾股定理可知:AB 2+AE 2=BE 2.
∴32+AE 2=(9-AE )2.
解得AE=4cm .∴△ABE 的面积为×3×4=6(cm2).
17E 关于直线AC 的对称点E ′,连接E ′F ,则E ′F 即为所求,
过F 作FG ⊥CD 于G ,
在Rt △E ′FG 中,GE ′=CD-BE-BF=4-1-2=1,GF=4,
7.证明:∵四边形ABCD 为平行四边形,∴AD ∥BC ,且AD=BC ,∴∠ADB=∠CBD ,由折叠可知∠EBD=∠CBD ,BE=BC ,∴∠EBD=∠ADB ,∴BO=DO ,∵AD= BE ,∴AD - DO = BE- BO ,即OA=OE.
8.证明:(1)∵将▱ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点D ′处,
∴∠DAE=∠D ′AE ,∠DEA=∠D ′EA ,∠D=∠AD ′E ,
∵DE ∥AD ′,
∴∠DEA=∠EAD ′,
∴∠DAE=∠EAD ′=∠DEA=∠D ′EA ,
∴∠DAD ′=∠DED ′,
∴四边形DAD ′E 是平行四边形,
∴DE=AD ′,
∵四边形ABCD 是平行四边形,
∴四边形BCED ′是平行四边形;
(2)∵BE 平分∠ABC ,
∴∠CBE=∠EBA ,
∵AD ∥BC ,
∴∠DAB+∠CBA=180°,
∵∠DAE=∠BAE ,
∴∠EAB+∠EBA=90°,
∴∠AEB=90°,
∴AB2=AE2+BE2.
9.解:(1)证明:因为四边形ABCD 是矩形,那么AD ∥BC ,AB ∥CD ,所以∠FAC=∠ACE ,∠BAC=∠DCA 。
由折叠可得∠BAE=∠EAC=21∠BAC ,∠DCF=∠NCF=21
∠DCA ,所以∠EAC=∠FCA 。
又因为AC=CA ,所以△CAE △ACF ,所以CE=AF 。
即四边形AECF 是平行四边形。
(2)因为AB=6,AC=10,由勾股定理,得BC=8.设EM=x ,那么BE=EM=x ,所以CE=BC-BE=8-x ,CM=AC-AM=AC-AB=10-6=4.在Rt △CEM 中,由勾股定理,得EM2+CM2=CE2,所以x2+42=(8-x)2,解得x=3。
所以四边形AECF 的面积=2△ACE 的面积=2×21
AC ×EM=30.
10. 证明:(1)∵矩形ABCD 折叠使A ,C 重合,折痕为EF ,
∴OA=OC ,EF ⊥AC ,EA=EC ,
∵AD∥AC,
∴∠FAC=∠ECA,在△AOF和△COE中,
∴△AOF≌△COE,
∴OF=OE,
∵OA=OC,AC⊥EF,
∴四边形AECF为菱形;
(2)①设菱形的边长为x,则BE=BC-CE=8-x,AE=x,在Rt△ABE中,∵BE2+AB2=AE2,
∴(8-x)2+42=x2,解得x=5,
即菱形的边长为5;
②在Rt△ABC中,
∴OA=AC=2,
在Rt△AOE中,AE=5,
∴EF=2OE=2.。
