流体力学习题答案2分解
(完整版)流体力学习题解析
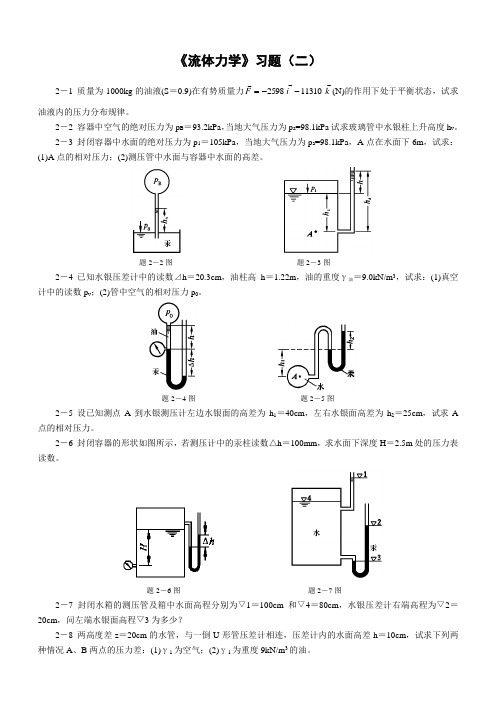
《流体力学》习题（二）2－1 质量为1000kg 的油液(S ＝0.9)在有势质量力k i F 113102598--=(N)的作用下处于平衡状态，试求油液内的压力分布规律。
2－2 容器中空气的绝对压力为p B ＝93.2kPa ，当地大气压力为p a =98.1kPa 试求玻璃管中水银柱上升高度h v 。
2－3 封闭容器中水面的绝对压力为p 1＝105kPa ，当地大气压力为p a =98.1kPa ，A 点在水面下6m ，试求：(1)A 点的相对压力；(2)测压管中水面与容器中水面的高差。
题2－2图 题2－3图 2－4 已知水银压差计中的读数⊿h ＝20.3cm ，油柱高h ＝1.22m ，油的重度γ油＝9.0kN/m 3，试求：(1)真空计中的读数p v ；(2)管中空气的相对压力p 0。
题2－4图 题2－5图 2－5 设已知测点A 到水银测压计左边水银面的高差为h 1＝40cm ，左右水银面高差为h 2＝25cm ，试求A 点的相对压力。
2－6 封闭容器的形状如图所示，若测压计中的汞柱读数△h ＝100mm ，求水面下深度H ＝2.5m 处的压力表读数。
题2－6图 题2－7图 2－7 封闭水箱的测压管及箱中水面高程分别为▽1＝100cm 和▽4＝80cm ，水银压差计右端高程为▽2＝20cm ，问左端水银面高程▽3为多少？2－8 两高度差z ＝20cm 的水管，与一倒U 形管压差计相连，压差计内的水面高差h ＝10cm ，试求下列两种情况A 、B 两点的压力差：(1)γ1为空气；(2)γ1为重度9kN/m 3的油。
题2－8图题2－9图2－9 有一半封闭容器，左边三格为水，右边一格为油(比重为0.9)。
试求A、B、C、D四点的相对压力。
2－10 一小封闭容器放在大封闭容器中，后者充满压缩空气。
测压表A、B的读数分别为8.28kPa和13.80kPa，已知当地大气压为100kPa，试求小容器内的绝对压力。
流体力学第二章习题解答
第 2 章流体静力学大气压计的读数为100.66kPa(755mmHg)，水面以下 7.6m 深处的绝对压力为多少？知： P a a水1000 kg / m3求：水下h 处绝对压力PP P a gh 解：1000175KP a烟囱高H=20m，烟气温度t s=300℃，压力为p s，确立惹起火炉中烟气自动流通的压力差。
烟气的密度可按下式计算： p=（1.25-0.0027t s）kg/m3，空气ρ3。
解：把 t s300 C 代入s s)kg / m3得s(1.25 0.0027t s) kg / m30.0027 300)kg / m30.44kg / m3压力差p=（a -s） gH ，把a 1.29kg / m3，s/ m3， g9.8N / kg ，H20m 分别代入上式可得p=（ a -s）gH=(1.29-0.44)9.8 20Pa2已知大气压力为。
求以水柱高度表示时：（1）绝对压力为22时的相对压力；（2）绝对压力为时的真空值各为多少？解：p =p-p m2（1）相对压力：a大气以水柱高度来表示：a/g =19.62*1033）h= p/（ 9.807*10（2）真空值：p v=p a68.5=29.6 KN / m 2以水柱高度来表示：h= a/g =29.6*103/ （9.807*103）p以下图的密封容器中盛有水和水银，若A 点的绝对压力为300kPa ，表面的空气压力为 180kPa ，则水高度为多少？压力表B 的读数是多少？解：水的密度1000 kg/m3，水银密度13600 kg/m3A 点的绝对压力为：p Ap 0h 2o ghHgg(0.8)300 10 3 =180103 +1000 9.8 h+13600求得： h=压力表 B 的读数p g p p a (300 101)KPa 199KPa以下图，在盛有油和水的圆柱形容器的盖上加载F=5788N 已知 h 1 =50cm ，h 2=30cm ，，油密度ρ 油=800kg/m 3 水银密度ρ Hg =13600kg/m 3，求 U 型管中水银柱的高度差 H 。
流体力学课后习题及答案
第二章2-2解：由P gh ρ=得h 水 =Pg ρ水=3350101109.8⨯⨯⨯=5.1m 335010=3.21.6109.8Ph m gρ⨯==⨯⨯四氯化碳四氯化碳 335010=0.37513.6109.8Ph m g ρ⨯==⨯⨯水银水银2-3 解：（1）体积弹性模量 /dpEv d ρρ=+在重力场中流体的压强形式为：dpg dzρ=- d dp gdz Evρρρ∴=-=两边积分，带入边界条件：00,0,z p ρρ===0lnEvp Ev Ev ghρ∴=- 11222212.5*160N F *40000NF L L s F s ==⎛⎫=== ⎪⎝⎭题解：有杠杆原理知：F 所以： 6、如题2-6图所示，封闭容器中盛有ρ=800kg/3m的油，1300h mm =，油下面为水，2500h mm =，测压管中水银液位读数400hmm =，求封闭容器中油面上的压强p 的大小。
解：12g 0p h gh gh ρρρ++-=油水水银12g p gh h gh ρρρ=--水银油水333313.6109.840010109.8500100.8--=⨯⨯⨯⨯-⨯⨯⨯-⨯=44.6110pa ⨯2-7：解：（1）、2224F gh s 10009.81001010101098Nρ--==⨯⨯⨯⨯⨯=2）m 121216G [s h h s h ]1000199109.81.95g Nρ-=⨯⨯=⨯⨯⨯=（-）+02h（3）因为在21h h -处谁对容器有向上的压力2-8，解：由同一液面压强相等可列：(0)()gh sin /6p(0)1239.21/^3p p h l kn m θθπ===∴=液2-9 解：设A 点距左U 形管测压计水银页面高度为H 则B 点距右U 型管测压计水银高度为H+hB A B h gh g H h gh gh gh m ag ρρρρρρA P -P -+P P -P =-=-⨯⨯P 水水水水则（+）=则（）=（13600-1000）9.80.3=370442.10，解：选取右侧U 形管汞柱高作为等压面，有：1132()m B P g h h gh gh gh p ρρρρ++-+=+酒汞汞水B p 42.7410pa =-⨯2-11解:左边液面压强与右边液面压强相等知，.66g .66.89g .82g .8211g ⨯+-⨯=⨯+-⨯未知水未知水）（）（ρρρρ解得333102.31m kg 103.85⨯=⋅⨯=-未知ρ3m kg -⋅2-12 解：设左支管液面到另一液体分界面的距离为1h ，右支管为2h ，则有：1112222P gh P gh gh ρρρ+=++或121122121221()()P P g h h ghP P gh gh ghρρρρρρ-=--+-=-+=-得 1221()P P h gρρ-=-2-13解：gh P gh ρρ+=水水银P=gh gh ρρ∴-水银水127400.07891.8F PS N∴==⨯=2-14解：以闸门与液面交点为O 点，沿闸门向下方向建立坐标S ，取微元ds ，在面积bds 内，液体压力对链轴取矩()()0.2sin600.2dM ghbds s g s sdsρρ=-+=-+ 所以)0sin 600.2Mgb s sds ρ=-+Q对链轴取矩)cos600.2Q M Q =由力矩平衡得 0Q M M +=化简)1.*1.9320.302Q -=得 26778Q N=()()D 33352.151y y *1132***2*4121232,8832**10*10*12*89.6*10xcC c xc cD c I y sI b a y s d y F g h s ρ=+==========题解：依题意知又即:*16、一个很长的铅垂壁面吧海水和淡水隔开，海水深7m ；试确定淡水多深时壁面所受液体作用力合力为零。
华中科技大学流体力学课后习题答案完整版
解： v |(1,2) =
v
2 x
+
v
2 y
|(1,2) = 30.41m / s ；
a=
a
2 x
+
a
2 y
|(1,2) =
(∂vx / ∂x ⋅ vx )2 + (∂vy / ∂x ⋅ vx + ∂vy / ∂y ⋅ vy )2 = 167.71m / s2 。
2.4 （1） ax = 35, a y = 15 ；（2）260。
直立部分： P2
=
ρg⎜⎛ h ⎝
+
h ⎟⎞ ⋅ hB 2⎠
=
3 2
ρgh 2 B
方向向左；作用点距离水平面为
yD
=
3 2
h+
Bh3 12 3h 2 ⋅ Bh
=
14 h 9
⇒ L2 = 2h −14h 9 = 4h 9 M 2 = P2 ⋅ L2 = 2ρgh3 B 3
于是关闭闸门所需的力 P 由力矩平衡方程
H2
− h2
设此合力的作用点距底部 x 处，则
( ) R ⋅ x = P1 ⋅ H 3 − P2 ⋅ h 3 = ρgB H 3 − h3 6
将 H = 7.5m
⇒
x
=
H
2 + Hh + h2
3(H + h)
h = 3m B = 5m 代入得 R = 1160KN
x = 2.79m
1.29 解：闸门自动开启，此时压力中心 D 应与 O 点重合；水位超过 H，则压力中心 D 高
解：（1） ax |(2,1) = (∂vx / ∂x ⋅ vx + ∂vx / ∂y ⋅ v y ) |(2,1) = 35 ，
流体力学三版第2章课后答案
第一章 流体的基本概念1-1 单位换算：1.海水的密度ρ=1028公斤/米3，以达因/厘米3，牛/米3为单位，表示此海水的重度γ值。
解：2.酒精在0℃时的比重为0.807，其密度ρ为若干公斤/米3 ? 若干克/厘米3 ? 其重度γ为若干达因/厘米3 ? 若干牛/米3 ? 解：l-2 粘度的换算：1.石油在50℃时的重度γ=900达因/厘米3，动力粘度μ=58.86×10-4牛.秒/米2。
求此石油的运动粘性系数ν。
解：2.某种液体的比重为1.046，动力粘性系数μ=1.85厘泊，其运动粘性系数为若干斯? 解：3.求在1大气压下，35℃时空气的动力粘性系数μ及运动粘性系3323333w /8.790/7908/8.9/807 0.807g/cm 807kg/m 1000kg/m cm dy m N s m m kg ==⨯===⨯γ酒精√sm s cm cmdy s cm cm s dy g /104.6/1064 /900/)/980101086.58( 26233224--⨯=⨯=⨯⋅⨯==∴γμν)(/017686.0 /1046.1/1085.1 232w 斯比重s cm cmg cm s g =⨯⋅⨯=⨯=∴-ρμν33235/44.1007/4.10074/8.9/1028 101 ; cm dy m N s m m kg dyN g ==⨯=∴==γργ数ν之值。
解：1-3 相距10毫米的两块相互平行的板子，水平放置，板间充满20℃的蓖麻油(动力粘度μ=9.72泊)。
下板固定不动，上板以1.5米/秒的速度移动，问在油中的切应力τ是多少牛/米2? 解：1-4 直径为150毫米的圆柱，固定不动。
内径为151.24毫米的圆筒，同心地套在圆柱之外。
二者的长度均为250毫米。
柱面与筒内壁之间的空隙充以甘油。
转动外筒，每分钟100转，测得转矩为9.091牛米。
假设空隙中甘油的速度按线性分布，也不考虑末端效应。
流体力学课后习题答案第二章
第二章 流体静力学2-1 密闭容器测压管液面高于容器内液面h=1.8m,液体密度为850kg/m3, 求液面压强。
解：08509.8 1.814994Pa p gh ρ==⨯⨯=2-2 密闭水箱，压力表测得压强为4900Pa,压力表中心比A 点高0.4米，A 点在液面下1.5m ，液面压强。
解：0()490010009.8(0.4 1.5) 49009800 1.15880PaM B A p p g h h ρ=+-=+⨯⨯-=-⨯=-2-3 水箱形状如图，底部有4个支座。
试求底面上的总压力和四个支座的支座反力，并讨论总压力和支座反力不相等的原因。
解：底面上总压力（内力，与容器内的反作用力平衡）()10009.81333352.8KN P ghA ρ==⨯⨯+⨯⨯=支座反力支座反力（合外力）3312()10009.8(31)274.4KN G g V V ρ=+=⨯⨯+=2-4盛满水的容器顶口装有活塞A ，直径d=0.4m ，容器底直径D=1.0m ，高h=1.8m 。
如活塞上加力为2520N(包括活塞自重)。
求容器底的压强和总压力。
解：压强2252010009.8 1.837.7kPa (0.4)/4G p gh A ρπ=+=+⨯⨯= 总压力 237.71/429.6KN P p A π=⋅=⨯⋅=2-5多管水银测压计用来测水箱中的表面压强。
图中高程单位为m ，试求水面的绝对压强。
解：对1-1等压面02(3.0 1.4)(2.5 1.4)p g p g ρρ+-=+-汞对3-3等压面 2(2.5 1.2)(2.3 1.2)a p g p g ρρ+-=+-汞将两式相加后整理0(2.3 1.2)(2.5 1.4)(2.5 1.2)(3.0 1.4)264.8kPap g g g g ρρρρ=-+-----=汞汞绝对压强 0.0264.8+98=362.8kPa abs a p p p =+=2-6水管A 、B 两点高差h 1=0.2m ，U 形管压差计中水银液面高差h 2=0.2m 。
《流体力学》课后习题答案.pdf
得：T1 = t1 + 273 = 50 + 273 = 323K ，T2 = t2 + 273 = 78 + 273 = 351K
根据
p
=
mRT V
，有：
p1
=
mRT1 V1
，
p2
=
mRT2 V2
得： V2 V1
=
p1 p2
T2 T1
=
9.8067 104 5.8840 105
351 323
=
0.18
设管段长度 l，管段表面积： A = dl
单位长度管壁上粘滞力： = A u = dl u − 0 = 3.14 0.025 0.03
l y l
0.001
1-8 解： A = 0.8 0.2 = 0.16m2 ，u=1m/s， = 10mm ， = 1.15Pa s
T = A u = A u − 0 = 1.15 0.16 1 = 18.4N
1
=
T1 b
=
A b
u
−0 −h
=
0.7 0.06b b
15 − 0 0.04 − 0.01
=
21N
/m，方向水平向左
下表面单位宽度受到的内摩擦力：
2
=
T2 b
=
Au−0 b h−0
=
0.7 0.06b 15 − 0
b
0.01− 0
= 63N
/m，方向水平向左
平板单位宽度上受到的阻力：
= 1 + 2 = 21+ 63 = 84N ，方向水平向左。
h1 = 5.6m
2.4 解：如图 1-2 是等压面，3-4 是等压面，5-6 段充的是空气，因此 p6 = p5 ，6-7 是等压面，
工程流体力学习题分解
⼯程流体⼒学习题分解⼯程流体⼒学习题第⼀部分流体及其物理性质1、按连续介质的概念，流体质点是指：A 、流体的分⼦；B 、流体内的固体颗粒；C 、⼏何的点；D 、⼏何尺⼨同流动空间相⽐是极⼩量，⼜含有⼤量分⼦的微元体。
2、与⽜顿内摩擦定律有关的因素是：A 、压强、速度和粘度；B 、流体的粘度、切应⼒与⾓变形率；C 、切应⼒、温度、粘度和速度；D 、压强、粘度和⾓变形。
3、在研究流体运动时，按照是否考虑流体的粘性，可将流体分为：A 、⽜顿流体及⾮⽜顿流体；B 、可压缩流体与不可压缩流体；C 、均质流体与⾮均质流体；D 、理想流体与实际流体。
4、理想液体的特征是：A 、粘度为常数B 、⽆粘性C 、不可压缩D 、符合RT p ρ=。
5、流体运动黏度υ的国际单位是：A 、m 2/s ；B 、N/m 2；C 、 kg/m ；D 、N·s/m 2。
6、液体黏度随温度的升⾼⽽____，⽓体黏度随温度的升⾼⽽_____。
A 、减⼩，升⾼；B 、增⼤，减⼩；C 、减⼩，不变；D 、减⼩，减⼩7、下列说法正确的是：A 、液体不能承受拉⼒，也不能承受压⼒B 、液体不能承受拉⼒，但能承受压⼒C 、液体能承受拉⼒，但不能承受压⼒D 、液体能承受拉⼒，也能承受压⼒。
8、下列流体哪个属⽜顿流体：A 、汽油；B 、纸浆；C 、⾎液；D 、沥青。
9、液体的黏性主要来⾃于液体：A 、分⼦热运动；B 、分⼦间内聚⼒；C 、易变形性；D 、抗拒变形的能⼒。
10、流体是⼀种物质。
A 、不断膨胀直到充满容器的；B 、实际上是不可压缩的；C 、不能承受剪切⼒的；D 、在任⼀剪切⼒的作⽤下不能保持静⽌的。
11、如图所⽰为压⼒表校正器。
器内充满压缩系数为βp ＝4.75×10－10 1/Pa 的油液，器内压⼒为105Pa 时油液的体积为200mL 。
现⽤⼿轮丝杆和活塞加压，活塞直径为1cm ，丝杆螺距为2mm ，当压⼒升⾼⾄20MPa 时，问需将⼿轮摇多少转？12、在相距1mm的两平⾏平板之间充有某种黏性液体，当其中⼀板以1.2m/s的速度相对于另⼀板作等速移动时，作⽤于板上的切应⼒为3 500 Pa。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
5-2. 有一水箱水面保持恒定（5m ），箱壁上开一孔口，孔口直径d=10cm,（1）如果箱壁厚度为3mm ，求通过孔口的流速和流量。
（2）如箱壁厚度为40mm ，求通过孔口的流速和流量。
解：（1）薄壁孔口：02Q A gH μ= 对薄壁孔口，μ=0.6~0.6224430.01(0.60.62)2*9.8*5 4.6710 4.8210/4Q m s π--⋅∴=⋅⋅=⨯⨯通过孔口的流速02Qv gH Aμ== (0.60.62)2*9.8*5 5.946.14/v m s ∴=⋅=（2）厚壁孔口2430.010.822*9.8*5 6.3810/4Q m s π-⋅∴=⋅⋅=⨯通过孔口的流速0.822*9.8*58.12/v m s =⋅=5-3．图示水箱用隔板分为左右两个水箱，隔板上开一直径401=d mm 的薄壁小孔口，水箱底接一直径302=d mm 的外管嘴，管嘴长1.0=l m ，31=H m 。
（1）分析出流恒定性条件（2H 不变的条件）（2）在恒定出流时，B 箱中水深2H 等于多少？（3）水箱流量1Q 为何值？⎡⎤⎣⎦解（1）12Q Q =时，2H 恒定不变。
（2）20.13~4l m d ==为管嘴出流，1d 为孔口出流。
取10.6μ=()()111222222A g H H A g H l μμ-=-()()222212220.6230.8220.1A g H A g H -=-⎡⎤⎡⎤⎣⎦⎣⎦()()()222422222222410.820.820.330.10.10.590.10.60.60.4A H H H H A ⨯-=+=+=+⨯ ()2230.05910.59 1.59H H -=+=2 2.9411.851.59H m == （3）()32311220.60.042 1.15 3.58104m Q A g H H g sπμ-=-=⨯⨯⨯⨯=⨯5-7．某恒温室采用多孔板送风，风道中的静压为200Pa ，孔口直径为20mm ，空气温度为020C ，μ=0.8，要求送风量为31ms。
问需要布置多少孔口？⎡⎤⎣⎦解在通风工程中，对于多孔板送风，流量系数采用μ=0.8 3231220020.8(0.02) 4.5861041.2pm Q A gs πμγ-∆⨯==⨯⨯=⨯1Q nQ = 1312184.58610Q n Q -===⨯（个）5-11. 如图孔板流量计，输送20℃空气，测量h=100mmH 2O,0.62μ=,d=100mm,求Q 。
解：323220.19.8100.620.14 1.20.197p Q Am sμρπ=⨯⨯⨯=⨯⨯⋅=5-15．两水池用虹吸管连通，上下游水位差2H m =，管长1233,5,4l m l m l m ===，直径200d mm =，上游水面至管顶高度1h m =，已知0.026,10, 1.5λζζ===入口弯头，1.0ζ=出口，求（a ）虹吸管中的流量。
（b ）管中压强最低点的位置及其最大负压值。
⎡⎤⎣⎦解写上下游水面的能量方程，得2222212()(0.02102 1.51)15.222220.22l v v v l v v H d g g g d g gλζλζ=+=+=++⨯+=∑∑hp 1p 2220.1315215.215.2v H g === 20.1315 1.6m v g s=⨯=3220.2 1.65104mQ Av sπ-==⨯⨯=⨯压强最低点在2l 末端，则222120(10 1.5)222cp l l v v v h g d g g λγ⎡⎤+=+++++⎢⎥⎣⎦281(12.50.02)(10.131513.3) 2.7520.2cp v m gγ⎡⎤=-++=-+⨯=-⎢⎥⎣⎦ 5-16．如图所给水泵抽水系统，管长，管径单位为米，ζ给于图中，流量334010m Q s-=⨯，0.03λ=。
求（1）吸水管和压水管的S 数（2）求水泵所需水头。
⎡⎤⎣⎦解（1）S 数251124241208()8(0.03 3.2)0.25118/0.25ld S s m d g g λζππ+⨯+===⨯∑ 2522242422608()8(0.030.7)0.22052/0.2ld S s m d g gλζππ+⨯+===⨯∑ （2）2232122170(4010) 3.5h S QS Q m -=+=⨯=∑17320Z m =+=20 3.523.5H Z h m =+=+=∑5-20．有一简单并联管路如下图，总流量338010m Q s-=⨯，0.02λ=，求各管段间的流量及二节点间的水头损失。
第一支路1200d mm =，1600l m =，第二支路2200d mm =，2360l m =。
⎡⎤⎣⎦解12S S S = 1124251880.0260030900.2l d S d g gλππ⨯⨯===⨯ 2224252880.0236018600.2ld S d g gλππ⨯⨯===⨯ 110.01820.02320.041455.54330901860S ==+=+=215820.0414S ==节点间的水头损失225820.08 3.72h SQ m ==⨯=311 3.720.03503090h m Q s S ===322 3.720.0451860h m Q s S === 校核3120.08mQ Q s+=5-22．如图所示管路，设其中的流量30.6/,0.02,A Q m s λ==不计局部损失。
其它已各条件如，求A 、D 二点间的水头损失。
⎡⎤⎣⎦解22222322220.6100012040.027.67220.60.622(0.6)2(0.6)44ABl v l Q l h md g d gA d g g g λλλπππ⨯====⨯⨯==BC 段的损失为2BC h SQ =423S S S S =+22424880.0211003440.350.35ld S d g g λππ⨯⨯===⨯⨯⨯32424880.028005380.350.35ld S d g g λππ⨯⨯===⨯⨯⨯ 42424880.029001440.350.35ld S d g g λππ⨯⨯===⨯⨯⨯1110.08330.04320.0540.181223.218.5144538344S ==++=++= 所以21()310.18S == 2310.611.15AB h m =⨯=222452150040.630160.360.02 5.30.720.70.72CDh m g g ππ⨯⨯⨯=⨯==⨯⨯7.6711.15 5.324.12AD AB BC CD h h h h m =++=++=5-25．三层供水管路，各管段的S 值均为，层高为5m 。
设a 点的压力水头20m ，求1Q 、2Q 、3Q ，并比较三流量，得出结论来。
⎡⎤⎣⎦解211h SQ H == 348120 4.461010H m Q s S -===⨯ 以二、三层楼分支点，分别写能量方程，设分支点水头为1H则 对二层2112H S Q = 121H Q S =对三层211352H S Q =+ 13152H Q S -=写上述分支点，a 点的能量方程211235()H H S Q Q =+++2211231235()15()H H S Q Q S Q Q =--+=-+上式代入2Q 及3Q ，则211111155()2H H H H S S S -=--21111111115515(2)22H H H H S S S S S --=-+115152H H -=--133522H =--111335()53522244H H H --==-222111112255(5)353535(5)2()22444444H H H H H ⎡⎤-=-=-⋅⋅+⎢⎥⎣⎦222111115(3535025)32H H H H -=-+ 2211710350H H --=114H m =342 3.7410m Q s -==⨯343 2.1210m Q s -====⨯ 123Q Q Q >>6-2：某体育馆的圆柱形送风口，00.6d m =，风口距赛区为60m ，要求比赛区风速（质量平均风速）不得超过0.3m s ，求送风口的送风量应不超过多少3ms？⎡⎤⎣⎦解00.30.6720.672 2.520.0860 2.52n r s m a ==⨯=>2000223000.230.1470.30.230.08600.1470.610.6310.630.63/44v aS v d v mv s Q v d m sππ=+∴=⨯+∴=∴=⨯=⨯⨯=所以，计算断面在主体段，a 值为0.086-3：岗位送风所设风口向下，距地面4m 。
要求在工作区（距地1.5m 高范围）造成直径为1.5m 的射流,限定轴心速度为2m s.求喷嘴直径及风口流量。
⎡⎤⎣⎦解采用圆形喷嘴0.08a =00000 1.50.08 2.56.8(0.147) 6.8(0.147)0.14D aS d d d d d m⨯=+⇒=+∴= 00.070.6720.6720.588 2.50.08n r S S a ==⨯=<=，为主体段。
0000223000.4820.480.08 2.50.1470.1470.146.56 6.560.140.101/44m v aS v v d m v sQ v d m sππ=⇒=⨯++∴=∴=⨯=⨯⨯=6-9：高出地面5m 处设一孔口00.1d m =，以2ms速度向房间水平送风，送风温度0010t C =-，室内温度027e t C =。
试求距出口3m 处的2v 、2t 及弯曲轴心坐标。
⎡⎤⎣⎦解2222100227270.230.230.230.083102737 2.5470.1470.1470.123.7e e T T T t t aS T T T d t C-∆--======⨯∆---++∴= 320200(0.510.35)e g T a y S S v T d ∆'=+()3229.827310(27327)0.08(0.5130.353)2(27327)0.14.28m--+⎡⎤⎣⎦=⨯+⨯+=- 220020.230.230.08320.1470.1470.10.181v v aS v d mv s=⇒=⨯++∴=9-12：有一收缩型喷嘴，如图9-2，已知p 1=140kPa(abs), p 2=100kPa(abs), v 1=80m/s, T 1=293k,求2-2断面的速度v 2。