玻璃材料的弹性模量评价技术和影响因素
CAE常用各种材料的弹性模量及泊松比
CAE常用各种材料的弹性模量及泊松比弹性模量（Young's modulus）是描述材料在受力作用下发生弹性变形程度的物理量，常用符号为E。
弹性模量表示单位面积的材料受力后的伸长或收缩程度，单位为帕斯卡（Pa）或兆帕（MPa）。
泊松比（Poisson's ratio）表示材料在受力作用下的横向收缩与纵向伸长的比例，无单位。
本文将介绍一些常用材料的弹性模量和泊松比。
1.金属材料：-铜：弹性模量为110-130GPa，泊松比为0.33-0.36-铝：弹性模量为68-79GPa，泊松比为0.33-钢（低碳钢）：弹性模量为200-210GPa，泊松比为0.27-0.30。
-钛：弹性模量为95-120GPa，泊松比为0.292.玻璃材料：-常规玻璃：弹性模量为60-90GPa，泊松比为0.20-0.27-硼硅酸盐玻璃：弹性模量为80-90GPa，泊松比为0.20-0.25-石英玻璃：弹性模量为70-80GPa，泊松比为0.173.塑料材料：-聚乙烯：弹性模量为0.1-0.3GPa，泊松比为0.42-聚丙烯：弹性模量为0.8-1.6GPa，泊松比为0.40-0.45-聚氯乙烯（PVC）：弹性模量为2.5-3.0GPa，泊松比为0.42-0.45 -聚苯乙烯（PS）：弹性模量为3.0-3.5GPa，泊松比为0.35-0.384.复合材料：-碳纤维增强复合材料：弹性模量为200-400GPa，泊松比为0.2-0.3 -玻璃纤维增强复合材料：弹性模量为25-40GPa，泊松比为0.255.高分子材料：-聚苯乙烯（PS）：弹性模量为3.0-3.5GPa，泊松比为0.35-0.38-聚氨酯：弹性模量为15-30GPa，泊松比为0.30-0.45-聚酰胺（尼龙）：弹性模量为2.5-4.0GPa，泊松比为0.35-0.42需要注意的是，在实际工程中，材料的弹性模量和泊松比可能会因具体材料牌号、制造工艺和温度等因素而有所差异。
常用材料的弹性模量与泊松比
常用材料的弹性模量与泊松比弹性模量是一个材料对外加力产生形变的抵抗能力的度量，而泊松比是衡量材料在拉伸或压缩时横向收缩或扩展程度的因素。
不同材料的弹性模量和泊松比对于工程设计和材料选择非常重要。
以下是一些常用材料的弹性模量和泊松比的示例：1.金属材料：金属具有较高的弹性模量和较低的泊松比，使其具有很好的强度和刚性。
-钢：弹性模量通常在200-220GPa之间，泊松比约为0.3-铝：弹性模量约为70-80GPa，泊松比约为0.33-铜：弹性模量约为110-140GPa，泊松比约为0.342.陶瓷材料：陶瓷材料通常是非金属的，具有高硬度和低弹性模量。
-瓷砖：弹性模量约为60-80GPa，泊松比约为0.2至0.3-氧化铝陶瓷：弹性模量约为350-400GPa，泊松比约为0.2至0.25 -碳化硅陶瓷：弹性模量约为400-500GPa，泊松比约为0.1至0.2 3.高分子材料：高分子材料具有较低的弹性模量和较高的泊松比，使其具有较好的延展性和柔韧性。
-聚乙烯：弹性模量约为0.1-0.3GPa，泊松比约为0.42至0.49-聚丙烯：弹性模量约为0.8-2.0GPa，泊松比约为0.36至0.42-聚苯乙烯：弹性模量约为2.5-3.5GPa，泊松比约为0.39至0.43 4.合成材料：合成材料通常由不同类型的材料组合而成，其弹性模量和泊松比可能因组合方式而有所不同。
-碳纤维增强复合材料：弹性模量约为130-330GPa，泊松比约为0.2至0.4-玻璃纤维增强复合材料：弹性模量约为20-45GPa，泊松比约为0.2至0.3-聚合物混凝土：弹性模量约为20-40GPa，泊松比约为0.17至0.22需要注意的是，上述数值仅为常见材料的一般范围，具体数值可能会因材料的制备方法、组分和结构等因素而有所不同。
另外，弹性模量和泊松比还可以通过实验测量来获取，因此具体的数值可以在实验室中精确测定。
玻璃工艺学复习材料
玻璃工艺学复习重点第一章绪论狭义的玻璃定义为：玻璃是一种熔融物冷却、凝固的非结晶（在特定条件下也能成为晶体）无机物质，是过冷的液体。
广义的玻璃定义是：结构上完全表现为长程无序的、性能上具有玻璃转变特性的非晶态固体。
玻璃是一种具有无规则结构的非晶态固体。
玻璃具有如下的特性：1、各向同性；2、无固定熔点；3、亚稳性（介稳性）4、变化的可逆性；5、可变化性。
晶子学说是由门捷列夫于1921年提出的。
晶子学说的成功之处在于它解开了玻璃是我微观结构不均匀性和近程有序的结构特性。
无规则网络学说：其排列是无序的，缺乏对称性和周期性重复，因而其内能大于晶体。
无规则网络学说宏观上强调了玻璃中多面体相互排列的连续性，统计均匀性和无序性。
晶子学说以玻璃结构的近程有序为出发点，而无规则网络学说则强调了玻璃结构的连续性、统计均匀性和无序性。
准晶是具有准周期平移格子构造的固体，其中的原子常呈定向有序排列，但不做周期性平移重复，其对称要素包含与晶体空间格子不相容的对称（如5次对称轴）。
液晶：在一定温度范围出现液晶相，在较低温度为正常传晶的物质。
从宏观物理性质看：液晶既有液体的可流动性、粘滞性，又具有晶体的各向异性。
从微观结构上看，晶体具有一定的长程有序性，即分子按某一从优方向排列，这是其物理性质各向异性的主要原因。
然而，液晶又是平移无序或部分平移无序的，因而也具有某些类似液体的性质。
网络形成体（玻璃形成体）氧化物能单独形成玻璃。
网络外体（玻璃整体）氧化物不能单独形成玻璃。
网络中间体（玻璃中间体）氧化物一般不能单独生成玻璃。
第二章玻璃的主要性质粘度是度量流体粘性大小的物理量。
粘度的物理意义是指面积为A的两平行液层，以一定的速度梯度dv/dx移动时需要克服的摩擦力。
石英颗粒的溶解、扩散速度加快，有利于玻璃的快速形成。
在璃的澄清过程中，气泡在玻璃液中的上升速度与玻璃液的粘度成反比。
在玻璃的均化过程中，不均质体的扩散速度也与玻璃的粘度成反比关系，因此玻璃粘度的降低，可加速不均物质和气泡的扩散，加快玻璃液的均化过程。
玻璃产品的技术性能参数及设计
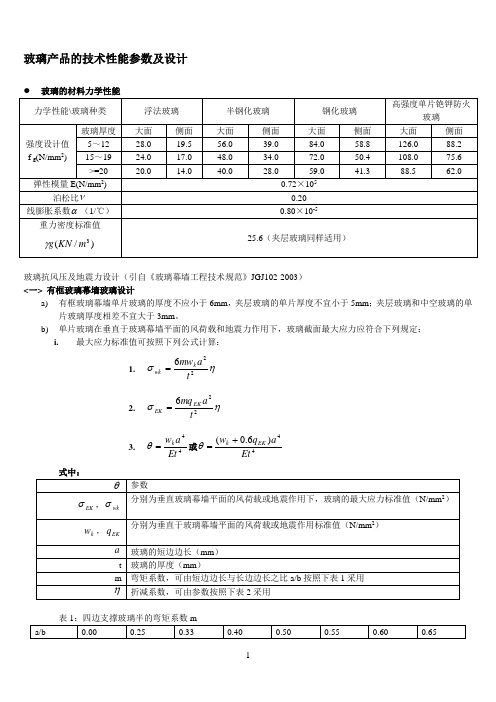
玻璃产品的技术性能参数及设计玻璃抗风压及地震力设计（引自《玻璃幕墙工程技术规范》JGJ102-2003） <一> 有框玻璃幕墙玻璃设计a) 有框玻璃幕墙单片玻璃的厚度不应小于6mm ，夹层玻璃的单片厚度不宜小于5mm ；夹层玻璃和中空玻璃的单片玻璃厚度相差不宜大于3mm 。
b) 单片玻璃在垂直于玻璃幕墙平面的风荷载和地震力作用下，玻璃截面最大应力应符合下列规定： i. 最大应力标准值可按照下列公式计算：1.ησ226t a mw k wk=2.ησ226ta mq EK EK= 3. 44Et a w k =θ或44)6.0(Eta q w EK k +=θ表2：折减系数ηc) 单片玻璃的刚度和跨中挠度应符合以下规定：1. 单片玻璃的刚度D ，按照：)1(1223v Et D -=计算。
2. 玻璃跨中挠度u 可按照下式计算：ημDa w u k 4=四边支撑板的挠度系数：3. 在风荷载标准值作用下，四边支撑玻璃的最大挠度u 不宜大于其短边尺寸的1/60d ） 夹层玻璃可按照下列规定进行计算：1. 作用于夹层玻璃上的风荷载和地震作用可按下列公式分配到两片玻璃上：3231311t t t w w kk +=（1）3231322t t t w w kk +=（2）3231311t t t q q Ek EK +=（3）3231322t t t q q EkEK +=（4）2. 两片玻璃可各自按照第1，2条的规定分别进行单片玻璃的应力计算；3. 夹层玻璃的挠度可按照第1，3条的规定进行计算，但在计算刚度D 时，应采用等效厚度t et e 可按照下式计算：32313t t t e +=（5）其中：t 1,t 2分别为各单片玻璃的厚度（mm ）e) 中空玻璃可按照下列规定进行计算1． 作用于中空玻璃上的风荷载标准值可按下列公式分配到两片玻璃上：i. 直接承受风荷载作用的单片玻璃：32313111.1t t t W W k k +=（1.5-1）ii.不直接承受风荷载作用的单片玻璃：32313221.1t t t W W k k +=（1.5-2）2. 作用于中空玻璃上的地震作用标准值，可根据各单片玻璃的自重计算。
常用材料的弹性模量与泊松比
常用材料的弹性模量与泊松比弹性模量（Young's modulus）和泊松比（Poisson's ratio）是材料力学性质的重要参数，用于描述材料的弹性行为和变形特性。
弹性模量是衡量材料抵抗形变的刚度的物理量。
它表示单位面积内的应力（力与单位面积的比值）与应变（形变与初始尺寸的比值）之间的比例关系。
弹性模量的单位为帕斯卡（Pa）或兆帕（MPa）。
不同材料的弹性模量差异很大。
下面是一些常见材料的弹性模量范围：-铁：200-211GPa-钢：200-210GPa-铝：68.9GPa-铜：110-128GPa-钛：116GPa-水泥：14-40GPa-玻璃：65-85GPa泊松比是描述材料体积在受力同时沿一个轴向收缩而沿另一个轴向膨胀的能力的无量纲物理量。
一般来说，泊松比的值在0到0.5之间。
常见材料的泊松比一般在以下范围内：-铁：0.28-0.33-钢：0.27-0.30-铝：0.33-0.34-铜：0.33-钛：0.34-0.37-水泥：大于0.05小于0.3-玻璃：0.2-0.3需要注意的是，这些数值是一个大致的估计范围，因为弹性模量和泊松比会受到很多因素的影响，例如材料的微结构、温度等。
有了弹性模量和泊松比的数值，我们可以通过应力-应变关系来计算材料在外力作用下的变形行为。
例如，对于线弹性材料，可以根据胡克定律（Hooke's law）来计算应力和应变之间的关系：应力=弹性模量×应变同时，泊松比也可以用于描述应变在材料中的传播情况。
例如，当材料拉伸时，在拉伸方向上产生的应变将会导致在垂直方向上的压缩应变，而泊松比可以描述这种相互作用的程度。
总之，弹性模量和泊松比是常用材料力学性质的重要参数，能够在工程设计和材料选择过程中提供有价值的信息。
然而，不同材料的实际弹性模量和泊松比还会受到更多因素的影响，包括应力状态、变形速率和温度等。
因此，在具体的工程应用中，还需要对具体材料的力学性质进行更详细的研究和测试。
玻璃的力学性能及热学性能
1.4.1 玻璃密度与成分的关系 • 不同组成玻璃密度差别很大。
• 一般单组分玻璃的密度最小，添加网络外体密度增大。
• 玻璃中引入R2O和RO氧பைடு நூலகம்物，随离子半径的增大，玻璃密度
增加。
• 同一氧化物配位状态改变，对密度也产生影响。
• B2O3从[BO3]到[BO4]密度增加；
• 中间体从网络内四面体[RO4]转变为网络外八面体[RO6]密度增加；
• 定义：当负荷超过玻璃的极限强度时，不产生明显 的塑性变形而立即破裂的性质。 • 表示方法：
• 破坏时受到的冲击强度
• 脆弱度——玻璃抗压强度与抗冲击强度之比 S
Ph V
• 脆裂负荷——测定显微硬度时压痕发生破裂时的负荷值
C D S
1.4 玻璃的密度
• 玻璃的密度主要取决于构成玻璃原子的质量、原子 堆积紧密程度以及配位数有关，是表征玻璃结构的 一个标志。 • 实际生产中，通过测定玻璃的密度来控制工艺过程， 借以控制玻璃成分。
不同热处理情况下玻璃瓶密度的变化
热处理情况 成形后未退火 退火较差 退火良好 d/(g/cm3) 2.5000 2.5050 2.5070 Δd 0 0.005 0.007
1.4.3 玻璃密度与压力的关系 • 一定温度下，随压力的增加玻璃的密度随之增大。 • 密度变化的幅度与加压方法、玻璃组成、压力大小、 加压时间有关。
• 一是渗入裂纹像楔子一样使裂纹扩展； • 二是与玻璃起化学作用破坏结构。
• 活性介质中玻璃的强度降低。 • 玻璃强度的测定最好在真空或液氮中进行，以免受活性介 质的影响。
• 温度
• 低温和高温对玻璃强度的影响是不同的； • 接近绝对零度至200℃，强度随温度升高而降低； • 200℃为强度最低点； • 高于200℃，强度逐渐增大。
包装材料学习题库
习题库一、填空题1、玻璃的结构特点为短程有序、长程无序。
2、影响玻璃强度的主要因素有：表面状况、温度、周围介质、玻璃的静态疲劳。
3、玻璃的弹性参数主要有弹性模量E、剪切模量G、泊松比μ和体积压缩模量K，这些参数中，只有弹性模量E和泊松比μ是独立的。
4、玻璃的硬度指玻璃抵抗其他物体浸入的能力，它主要取决于其组分与结构。
5、影响玻璃粘度的主要因素是温度和化学组成。
6、玻璃的原料，根据它们的作用和用量可分为主要原料和辅助原料两大类，主要原料对玻是指往玻璃中引入各种氧化物的原料。
按其向玻璃中引入的氧化物的性质，可分为酸性氧化物原料、碱金属氧化物原料、碱土金属和二价氧化物原料及多价氧化物原料。
按这些氧化物在玻璃结构中的作用，又将其分为玻璃形成体氧化物原料（有SiO2、B2O3、P2O5等）、玻璃中间体氧化物原料（Al2O3、ZnO、PbO等）和玻璃改变体氧化物原料（Li2O、Na2O、K2O、CaO、MgO、BaO等）。
7、脱色剂按其作用原理，可分为化学脱色剂和物理脱色剂两种。
8、碎玻璃常用作玻璃原料的助熔剂。
9、硼硅酸盐玻璃体系中，当Na2O/B2O3的摩尔比大于1时，B2O3以[SiO4]结构形式存在，而摩尔比小于1时，就会产生[BO3]三角平面结构，进而产生分相。
10、玻璃包装容器按制造方法可分为模制瓶和管制瓶。
11、玻璃瓶依瓶口内径大小可分为窄口瓶和广口瓶，两者瓶口内径以30mm来分界。
12、玻璃包装容器按容积分为小型瓶和大型瓶，以容量5L为分界。
13、玻璃的密度主要决定于构成玻璃的原子质量，也与原子的堆积及配位数有关。
14、玻璃的硬度主要决定于原子半径、电荷大小及堆积密度。
15、粘度对玻璃的熔制、成型、加工与退火等各工艺过程都有很大的影响，低的粘度值有利于降低玻璃熔制温度，加快熔制速度。
16、按照玻璃料性的不同，可以将玻璃分为长性玻璃和短性玻璃。
17、玻璃粘度的对数与温度的倒数呈直线关系。
18、在玻璃生产工艺中，主要的特征温度有熔融温度、成型温度、软化温度、退火温度、转变温度、应变温度。
玻璃的粘度,表面性质,力学和热学性质
C 玻璃的硬度主要取决于化学组成和结构，还与温度和 D 热处理历史有关。对玻璃冷加工影响非常大。 S
抗冲击强度
测量方法：落球法，压痕破坏法
5.1.4
玻璃的密度
密度主要取决于构成玻璃原子的质量， 也与原子的堆积紧密程度及配位数有关。
网络形成体
体积： [BO4]<[SiO4]<[AlO4]
影响热导率因素：
玻璃内部的导热包括：热传导，热辐射
低温时，热传导占主要地位，其大小主要取决 于玻璃的化学组成：键强越大，热传导性能越 好
高温时，热辐射占主要地位，温度越高，传导 性能越高。玻璃的颜色越深，导热性越差。
5.2.4
玻璃的热稳定性
玻璃经受剧烈的温度变化而不破坏的性能。
P K E cd
第4章
玻璃的粘度和表面性质
4.1
玻璃的粘度
定义 粘度是指面积为S的两平行液面，以一定的速 度梯度dV/dx移动时所需克服的内摩擦阻力f。 f=ηS dV
dx
粘度在玻璃生产过程中的作用
在熔制过程中，原料的溶解、气泡的排除、各组分的扩散均化
影响粘度的因素：化学组成、温度、热处理时间 在成形过程中，不同的成型方法与成形速度要求不同的粘度和料性
4.1.3
粘度与组成的关系
有利于形成大阴离子基团的组成使粘度增大（SiO2、 Al2O3、ZrO2等）
提供游离氧，破坏网络结构的，则使粘度减小；场 氧硅比较大，意味着大型的[SO4] 强较大的可能产生复杂的作用：高温降粘，低温增 群分解为小型[SO4]群，粘滞活化能降 粘 氧硅比 键强、离子的极化（R2O－SiO2） 结构的对称性（B2O3、P2O5、SiO2） 配位数（B2O3、Al2O3） 总体来说，键强大，则粘度大
玻璃制造的应变与弹性模量分析
影响因素：温度、压力、 时间等对应变与弹性模量
的关系有影响
应变与弹性模量是玻 璃制造过程中重要的 参数，直接影响玻璃
的性能和品质。
应变与弹性模量的测量和 计算方法对玻璃制造工艺 的优化具有重要意义，可 以帮助制造商提高生产效
率和产品质量。
通过控制应变与弹性模量， 可以调整玻璃的强度、硬 度、透明度等性能，以满 足不同应用场景的需求。
应变优化的目标 ：提高玻璃制品 的强度、硬度和 韧性
应变优化的策略 ：通过调整制造 工艺参数和材料 成分，实现应变 的优化控制
弹性模量：材料在应力作用下的应 变与应力的比值，反映了材料的刚 性程度
影响因素：材料的成分、结构、温 度、湿度等
添加标题
添加标题
添加标题
添加标题
测量方法：可以通过拉伸试验、压 缩试验、剪切试验等方法进行测量
应变对玻璃强度 的影响：应变越 大，玻璃强度越 高
应变对玻璃硬度 的影响：应变越 大，玻璃硬度越 高
应变对玻璃韧性 的影响：应变越 大，玻璃韧性越 高
应变对玻璃光学 性能的影响：应 变越大，玻璃光 学性能越好
应变控制的重要 性：保证玻璃制 品的质量和性能
应变控制的方法： 采用先进的制造 工艺和设备，如 热处理、冷加工 等
汇报人：
应变的概念：物 体在外力作用下 产生的形状和尺 寸变化
应变的类型：线 性应变、剪切应 变、体积应变等
应变的测量方法 ：光学法、电测 法、超声波法等
应变的影响因素 ：温度、湿度、 加载速率等
玻璃制造过程中，由于温度变化、 压力变化、剪切力作用等因素，会 导致玻璃产生应变。
应变的产生会影响玻璃的力学性能、 光学性能和热学性能等，因此需要 对应变进行精确分析和控制。
材料物理性能
2、弹性模量E随原子间距R的减小，近似的存在以下关系：E=k/R m3、并联：E=E A S A/S+E B S B/S 串联：1/E=L A/E A L+L B/E B L4、弹性系数Ks的大小实质上反映了原子间势能曲线极小值尖峭度的大小。
对于一定的材料它是个常数，它代表了对原子间弹性位移的抵抗力，即原子结合力。
5、影响裂纹扩展的因素：①首先应使作用应力不超过临界应力，这样裂纹就不会扩展。
②其次在材料中设置吸收能量的机构也阻碍裂纹扩展。
③此外，人为地在材料中造成大量极微细的裂纹（小于临界尺寸）也能吸收能量，阻止裂纹扩展。
6、杜隆-珀替定律——元素的热容定律：恒压下元素的原子摩尔热容为25J/(K*mol),即3R7、热膨胀：物体的体积或长度随温度的升高而增大的现象称为热膨胀。
8、固体材料的热膨胀机理：①固体材料的热膨胀本质，归结为点阵结构中质点间平均距离随温度升高而增大。
②晶体中各种热缺陷的形成造成局部点阵的畸变和膨胀。
9、影响金属热导率的因素：①温度的影响②晶粒大小的影响③立方晶系的热导率与晶向无关；非立方晶系的热导率表现出各向异性④杂质将强烈影响热导率10、影响无机非金属材料热导率的因素：温度的影响；化学组成的影响；显微结构的影响:a.结晶构造的影响b.各向异性晶体的热导率c.多晶体与单晶体的热导率d.非晶体的热导率11、热稳定性：是指材料承受温度的急剧变化而不致破坏的能力，故又称抗热震性。
12、晶体和非晶体热导率曲线比较：①在不考虑光子导热的贡献的任何温度下λ非晶体<λ晶体。
②高温时，非晶体的热导率和晶体的热导率比较接近。
③两者的λ-T曲线的重大区别在于非晶体的λ-Ｔ曲线无λ的峰值点ｍ。
13、热应力引起的材料断裂破坏，还涉及材料的散热问题，散热使热应力得以缓解。
与此有关的因素包括：材料的热导率λ；传热的途径；材料表面散热速率14、提高材料抗热冲击断裂性能的措施：①提高材料强度、减小弹性模量，使σ/E提高；②提高材料的热导率，使R、提高；减小材料的热膨胀系数；③减小表面热传递系数；减小产品厚度15、光子与固体材料相互作用，实际上是光子与固体材料中的原子、离子、电子等的相互作用，出现以下两重要结果：①电子极化；②电子能态转变。
玻璃的弹性模量
玻璃的弹性模量
玻璃是一种既有美感又易于加工的自然材料，早在古人就开始使用它。
它的质量轻，有较大的弹性模量，所以能够成为很多高质量产品的材料。
玻璃的弹性模量是它性能的关键参数之一，而且它是一个复杂的物理量，因此理解弹性模量对改善玻璃的性能和研究新型玻璃材料至关重要。
弹性模量是一个物理量，它反映了物体受外力影响时对力的反应。
换句话说，弹性模量是物体抗拉力的强度，即物体抗扭转时的强度。
它可以用弹性模量的不同数值来表示，一般而言，模量越高，物体的抗力就越大，因此，理解弹性模量对研究玻璃材料有重要意义。
玻璃的弹性模量主要取决于玻璃的组成元素、结构和厚度等因素。
对玻璃的改性可以通过添加少量的元素及其复合物，从而改变其化学组成和结构而影响其弹性模量。
此外，研究人员还研究了玻璃的厚度对其弹性模量的影响，认为厚度增加可以提高玻璃的弹性模量。
当然，玻璃的弹性模量不仅取决于玻璃的组成，还受玻璃的物理性质的影响，如热膨胀系数、热传导系数和抗剥落性等。
这些性质在玻璃加工过程中起着重要作用，因此很重要。
玻璃的弹性模量受到温度的影响也是一个重要话题。
实验表明，玻璃的弹性模量随温度的升高而降低，而当温度升高到一定程度时，玻璃的弹性模量将急剧降低，这是因为温度升高时玻璃的分子结构会发生变化，影响玻璃的弹性模量。
综上所述，玻璃的弹性模量是一个复杂的物理量，它受玻璃的组
成、结构、厚度和物理性质以及温度等多个因素的影响。
因此，理解玻璃的弹性模量对改善玻璃性能及应用发挥玻璃本身的优势具有重要意义。
玻璃材料力学性能及断裂韧度研究
玻璃材料力学性能及断裂韧度研究玻璃作为一种常见的材料，在我们日常生活中随处可见。
然而，虽然玻璃看起来脆弱，但它实际上具有一定的力学性能和断裂韧度。
本文将探讨玻璃材料的力学性能以及与断裂韧度相关的研究。
首先，我们来了解一下玻璃的力学性能。
玻璃是一种非晶态固体，其分子结构不规则，没有长程有序性。
这使得玻璃具有高度的均匀性和透明性。
然而，由于其分子结构的不规则性，玻璃缺乏晶体的结晶点，因此也就没有明确的熔点。
玻璃的力学性能主要包括弹性模量、屈服强度和断裂韧度。
弹性模量是衡量材料在受力后恢复原状能力的指标。
对于玻璃来说，由于其非晶态结构，其弹性模量较低，一般在50-90 GPa之间。
屈服强度则是材料在受力后开始发生塑性变形的临界点。
对于玻璃来说，由于其分子结构的不规则性，其屈服强度较低，一般在50-150 MPa之间。
这也是为什么玻璃容易破碎的原因之一。
然而，尽管玻璃具有较低的弹性模量和屈服强度，它却具有较高的断裂韧度。
断裂韧度是衡量材料在受力后抵抗断裂的能力的指标。
对于玻璃来说，由于其非晶态结构，其断裂韧度较高，一般在0.5-1.5 MPa·m^0.5之间。
这意味着玻璃在受到外力作用时，能够相对较好地抵抗断裂，而不会立即破碎。
研究玻璃材料的断裂韧度是一个重要的课题，因为它对于玻璃的使用和应用具有重要意义。
在建筑和工程领域，玻璃常被用作窗户和墙体材料。
在这些应用中，玻璃需要具备一定的断裂韧度，以抵抗外界的冲击和压力。
因此，研究如何提高玻璃的断裂韧度，是一个备受关注的课题。
目前，研究者们采用了多种方法来提高玻璃的断裂韧度。
其中一种方法是添加强化剂。
强化剂可以改变玻璃的分子结构，增加其断裂韧度。
例如，添加氧化锆等强化剂可以显著提高玻璃的断裂韧度。
另一种方法是采用热处理技术。
通过热处理，可以使玻璃分子结构发生变化，从而增加其断裂韧度。
此外，还有一些新型材料的研究，如金属玻璃和有机玻璃等，这些材料具有更高的断裂韧度和力学性能。
玻璃钢杨氏模量
玻璃钢杨氏模量介绍玻璃钢是一种由玻璃纤维和树脂组成的复合材料，具有优异的力学性能和化学稳定性。
杨氏模量是描述材料刚度的一个重要参数，用于衡量材料在受力时的变形能力。
本文将深入探讨玻璃钢的杨氏模量及其影响因素。
玻璃钢的性质玻璃钢是一种具有绝缘性、耐腐蚀性和优异机械性能的复合材料。
由于其良好的化学稳定性和高强度，玻璃钢被广泛应用于船舶、化工、储罐、桥梁等领域。
其独特的结构使其具有优异的抗张、抗压和抗弯性能。
杨氏模量的定义杨氏模量，又称弹性模量，是描述材料在受力时的刚度的物理量。
它定义为单位应力下材料单位截面内的应变，可以用来描述材料在正应力下的变形能力。
影响玻璃钢杨氏模量的因素玻璃钢杨氏模量受到多个因素的影响，包括纤维体积分数、纤维长度、纤维排列方式等。
以下是一些常见影响因素的详细介绍：1. 纤维体积分数纤维体积分数是指复合材料中纤维的体积占总体积的百分比。
在玻璃钢中，提高纤维体积分数可以增加杨氏模量。
这是因为纤维具有较高的刚度，增加纤维含量可以增加整体材料的刚度。
2. 纤维长度纤维长度是指纤维的长度大小。
较长的纤维可以提供更多的强度，从而提高玻璃钢的杨氏模量。
随着纤维长度的增加，杨氏模量也会相应增加。
3. 纤维排列方式玻璃钢中的纤维排列方式可以分为单向排列和随机排列两种。
单向排列的纤维使得材料在受力时具有更高的刚度和强度，从而提高杨氏模量。
而随机排列的纤维则降低了材料的刚度，导致杨氏模量减小。
4. 树脂性能树脂作为玻璃钢的粘结剂，在杨氏模量中也发挥着重要的作用。
优质的树脂可以增强纤维与基体的粘结强度，提高材料的整体刚度。
玻璃钢杨氏模量的测量方法测量玻璃钢杨氏模量的常用方法有拉伸试验、弯曲试验和共振频率法。
以下是这些测量方法的详细介绍：1. 拉伸试验拉伸试验是最常用的测量杨氏模量的方法之一。
通过在拉伸机上施加一定的拉应力，测量材料在拉伸过程中的应变，可以得到杨氏模量。
2. 弯曲试验弯曲试验是另一种常用的测量方法，适用于较长的玻璃钢试样。
玻璃的抗拉伸性实验
断裂强度：样 品在拉伸过程 中，应力达到 最大值，样品 断裂，此时的 应力称为断裂 强度
05
应变：单位长度上的变形量， 表示材料变形的程度
弹性模量：应力与应变的比 值，表示材料抵抗弹性变形
的能力
泊松比：横向应变与纵向应 变的比值，表示材料在拉伸
过程中横向变形的程度
应力：单位面积上的力，表 示材料抵抗变形的能力
4
实验方法：采用拉伸试验 机进行测试
实验结果：玻璃在不同温 度下的抗拉伸性能
评估标准：根据实验结果， 评估玻璃的抗拉伸性能
结论：玻璃的抗拉伸性能 与其成分、温度等因素有
关
玻璃的材质：不 同材质的玻璃， 其抗拉伸性不同
玻璃的厚度：玻 璃的厚度越大， 其抗拉伸性越强
玻璃的温度：温 度越高，玻璃的
抗拉伸性越弱
根据实验数据处理结果，得出实验结论， 并撰写实验报告
实验数据：拉 伸强度、断裂 伸长率、弹性 模量等
数据整理：使 用Excel等软件 进行数据整理 和图表绘制
数据分析：使 用统计分析方 法，如方差分 析、回归分析 等
结果解释：根 据数据分析结 果，解释玻璃 的抗拉伸性能 和影响因素
0
0
0
0
1
2
3
玻璃的材质和结构有关。
项标题
建筑行业：提高玻 璃的抗拉伸性，增
强建筑安全性
项标题
汽车行业：提高汽 车玻璃的抗拉伸性，
提高汽车安全性
项标题
航空航天行业：提 高飞机、航天器玻 璃的抗拉伸性，提
高飞行安全性
项标题
电子行业：提高电 子设备玻璃盖板的 抗拉伸性，提高设
备耐用性
项标题
科研领域：为研究 新材料、新工艺提 供参考，推动科技
玻璃弹性模量
玻璃弹性模量
玻璃是一种非晶质材料，具有特殊的物理性质，可以作为研究材料，在许多应用中发挥重要作用。
它是一种脆性材料，易于破坏，具有较强的耐热性能。
在玻璃的力学性能的研究中，玻璃弹性模量是最重要的参数之一。
它是一个称为弹性模量的度量，可以用来衡量材料内部的均衡能力，以及材料在受力之后的形变能力。
玻璃的弹性模量受到许多因素的影响，包括温度、湿度、沉积工艺以及表面处理，这些因素都会影响玻璃的弹性模量。
首先，温度对玻璃弹性模量具有重要作用。
随着温度的升高，玻璃的弹性模量会降低，但是玻璃的弹性模量在-200摄氏度到200摄氏度范围内变化很小。
其次，湿度也会影响玻璃弹性模量，湿度越高，玻璃的弹性模量会越小。
玻璃的沉积工艺也会影响玻璃的弹性模量，沉积的玻璃的弹性模量通常比原始玻璃的弹性模量要高。
此外，表面处理也会影响玻璃的弹性模量，经过一定的表面处理，玻璃的弹性模量会发生很大的变化。
因此，玻璃的弹性模量是一个重要的参数，可以反映玻璃材料性能的变化。
在玻璃研究中，我们可以通过测量玻璃弹性模量来分析玻璃材料的性质，从而更好地提高玻璃的强度和韧性。
但是，测量玻璃的弹性模量本身却是一件复杂的事情。
它的测量方法通常依赖于光非弹性散射技术，通过测量玻璃样品的振动行为，利用弹性模量计算公式，计算出玻璃样品的弹性模量。
此外，还可以采用X射线衍射技术或热扩散技术来测量玻璃样品的弹性模量。
最后，玻璃的弹性模量是我们研究玻璃所必须考虑的重要参数，可以用来衡量玻璃材料内部的均衡能力，及其在受力之后的形变能力。
因此，在使用玻璃的应用中，应该重视测量玻璃弹性模量的任务，确保玻璃的性能。
材料力学与材料弹性模量的关系
材料力学与材料弹性模量的关系材料力学是研究材料在受力作用下的力学行为和性能的一门学科。
材料弹性模量是描述材料在弹性变形时所表现出来的刚度的物理量。
此两者之间存在着密切而复杂的关系。
本文将探讨材料力学与材料弹性模量之间的关系，以及该关系对实际应用的影响。
1. 弹性模量的定义及测定方法弹性模量是衡量材料刚度的重要指标。
根据弹性模量的定义，材料受力后产生的弹性变形与外力成正比，而且在去除外力时能够恢复到原始形状。
常见的弹性模量有弹性体积模量、剪切模量和杨氏模量等。
测量材料的弹性模量可以通过多种方法进行，例如压缩试验、拉伸试验和剪切试验等。
其中最常用的是拉伸试验，通过施加拉力使试样延长，然后根据受力和变形的关系计算弹性模量。
2. 材料力学对弹性模量的影响材料力学性质对弹性模量有着重要影响。
首先，杨氏模量与材料的抗拉强度密切相关。
对于强度较高的材料，其分子间结合力也较大，因此具有较高的弹性模量。
其次，材料的结晶度也对弹性模量产生影响。
结晶度高的材料通常在晶格间有更多的键合，因此具有更高的弹性模量。
此外，材料的孔隙率和含水率对弹性模量也有一定影响。
孔隙率高的材料内部存在较多空隙，导致其分子间相互作用减弱，从而降低了弹性模量。
含水率高的材料在水分的作用下容易发生蠕变，这也会导致弹性模量的下降。
3. 弹性模量对工程应用的重要性弹性模量在工程领域具有重要的应用价值。
首先，在材料选择和设计中，弹性模量是评价材料刚度和变形能力的重要参数。
根据不同的工程需求，可以选择合适的材料以满足强度和刚度的要求。
其次，弹性模量对材料的应力分布和变形性能的影响不可忽视。
在材料的设计过程中，需要合理估计和预测材料的弹性行为，以确保结构在工作条件下的稳定性和安全性。
此外，在材料力学研究中，材料的弹性模量也是进行模拟和计算的基础。
通过对材料力学行为和弹性模量的深入研究，可以提高材料的设计和生产效率，促进新材料的开发和应用。
总结材料力学与材料弹性模量之间存在着密切的关系。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
1 前言
弹性模量是反映材料抵抗外界作用力而引起变形的能 力，是材料及构件中最为重要的力学性能之一[1]。 一直以来全 世界的材料和力学科学家都在寻找一种既简单又能准确测 量弹性模量的评价技术。 目前，常用的测量方法有应力-应变 法、弯曲法、位移敏感压痕法、声共振法和超声波等。 应力-应 变法通常需要在样品上安装应变片，然后对样品施加一定的 载荷， 通过获得的应力-应变曲线计算出材料的弹性模量[1]。 弯曲法是通过测量试样在一定载荷作用下的弯曲挠度和样 品尺寸计算材料的弹性模量[2]。 位移敏感压痕技术 需 要 特 定 的设备，如纳米硬度计等，对样品进行加载卸载实验，通过在 加载卸载曲线上卸载起始点的斜率并结合载荷值就可以计 算出材料的弹性模量[3～4]。 声共振法和超声波法都是利用声波 或 超 声 波 在 材 料 中 传 播 的 阻 尼 特 性 而 得 到 弹 性 模 量[5～6]，实 验 设备和计算公式都较为复杂。
比，通常 Ei、vi 和 v 已知，故求得 Er 后，即可获得 E。
图 2 残余压痕剖面图
在一个光滑的弹性半无限平面上加、卸载时，卸载过程
载荷和压头的位移用幂函数对初始卸载部分数据进行拟合，
得到卸载曲线方程，见公式（1）。
P=α（h-hf）m
（1）
式中:
P— — — 载 荷 值 ；
h— — — 压 入 深 度 ；
部品与原材料专栏·玻璃
一项。 位移敏感压痕技术中用来确定接触弹性模量的公式为
（5）。
Er= 姨π S
（5）
2β 姨A
对具有轴对称的压头，常数 β=1。
在弹性接触理论中，试样的弹性模量和接触模量关系为：
2
1 = 1-v2 + 1-vi
（6、E、vi 和 v— ——分 别 为 压 头 和 试 样 的 弹 性 模 量 和 泊 松
hf— — — 残 余 压 痕 深 度 ； α 与 m 由最小二乘法确定。
卸载曲线在最大载荷 Pmax 下，即位移最大值 hm 时的斜率 定义为接触刚度 S。
S=[ dP dh
]h=hm=αm（hm-hf）m-1
（2）
关键词： 玻璃； 弹性模量； 痕迹法； 静态弯曲法； 声共振法； 超声波法 Abstract: Elastic modulus reflects the stiffness to withstand an applied load, which is commonly seen as one of the most important material properties in fracture mechanics for engineering materials. In this work, four different methods, viz., indentation depth method, static load -deflection, sonic -resonance method and unltrasonic speed method, are utilized to measure the elastic modulus of float glass. It is indicated that the scatter of the measured elastic modulus by indentation depth method and unltrasonic speed method is dispersive. Although the results by static load -deflection method are steady, the operation is complex. Sonic resonance method may be a suitable method because it is a lossless testing method and the measured results are reliable. Key words: glass, elastic modulus, indentation depth method, static load -deflection method, sonic -resonance method, unltrasonic speed method
部品与原材料专栏·玻璃
玻璃材料的弹性模量评价技术和 影响因素分析
万德田 包亦望 刘小根 田 远
中国建筑材料科学研究总院 中国建材检验认证集团股份有限公司
摘 要： 弹性模量是反映材料抵抗外界作用力而引起变形的能力，是材料的基本力学性能之一。 本文利用痕迹法、静态弯 曲法、声共振法和超声波法等四种方法测量了普通浮法玻璃的弹性模量，并结合普通浮法玻璃在工程上应用的特点，比较了各 种评价技术的优缺点。 实验结果表明，痕迹法和超声波法虽然操作简单，且可在线测量，但影响弹性模量测量准确性的因素较 多，离散性也比较大。 静态弯曲法实验结果稳定但操作比较复杂。 声共振法测量结果准确可靠，离散性极小，而且是一种无损测 试技术，具有广泛的应用前景。
本文利用痕迹法、静态弯曲法、声共振法和超声波法等
2012.08
四种方法测量了普通浮法玻璃的弹性模量，并结合普通玻璃 在工程上应用的特点，比较了各种评价技术在工程应用中的 优缺点。
2 实验方法 2.1 痕迹法评价材料的弹性模量
图 1 典型的加载-卸载曲线图
31
痕 迹 法 的 基 本 原 理 是 以 Oliver-Pharr 模 型 为 基 础 位 移 敏感压痕技术来测得材料的硬度和弹性模量 。 [3，4] 一个完整的 压痕过程包括两个步骤， 即所谓的加载过程与卸载过程，如 图 1 所示。 以一定的载荷速率给压头施加载荷，使之压入样 品表面，随着载荷的增大，压头压入样品的深度也随之增加， 当载荷达到最大值时，以同样的载荷速率移除外载，样品表 面会存在残留的压痕痕迹，如图 2 所示。 通过残余痕迹的形 貌，测量压痕的深度和几何尺寸，确定材料的弹性模量 [7-8]。