直方图实际应用
直方图与几率分布念

直方图的绘制方法
01
02
03
04
收集数据
首先需要收集要进行统计分析 的数据。
确定分组
将数据按照一定的规则分成若 干个组,每个组的范围称为一
个箱子或区间。
计算频数
统计每个组内数据值的数量或 出现次数。
绘制条形
模拟数据直方图分析
模拟数据生成
使用随机数生成器模拟一组年龄分布数据,模拟了1000个年龄在 18-60岁之间的人的身高数据。
直方图绘制
同样使用Excel或Python等工具绘制直方图,将身高分为若干个区 间,统计每个区间内的人数。
分析结果
通过直方图可以直观地看出身高的分布情况,发现身高的主要分布区 间和异常值,为后续的统计分析提供基础。
案例比较与讨论
比较分析
比较实际数据和模拟数据的直方图,分析它们的相似性和差异性。
讨论
探讨造成这种差异的原因,如数据来源、样本大小、数据质量等。同时,也可以讨论如何根据分析结果进行进一 步的统计分析或预测。
06
总结与展望
直方图与几率分布的重要意义
直观展示数据分布
直方图能够直观地展示 数据的分布情况,帮助 我们快速了解数据的集 中趋势、离散程度和异 常值。
04
直方图与几率分布的实际应用
在数据分析中的应用
数据可视化
直方图可以用于展示数据的分布情况,帮助分析 者直观地了解数据特征和变化趋势。
数据清洗
在数据分析之前,通过直方图可以初步判断数据 的异常值和缺失值,为数据清洗提供依据。
数据分组
直方图可以用于对数据进行分组,以便进一步分 析不同组别的数据特征和规律。
直方图的理解与应用
直方图的理解与应用
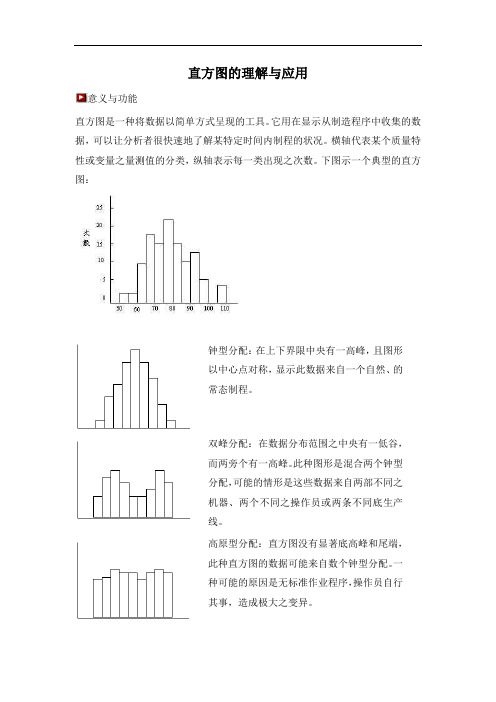
意义与功能
直方图是一种将数据以简单方式呈现的工具。
它用在显示从制造程序中收集的数据,可以让分析者很快速地了解某特定时间内制程的状况。
横轴代表某个质量特
性或变量之量测值的分类,
纵轴表示每一类出现之次数。
下图示一个典型的直方图:
钟型分配:在上下界限中央有一高峰,且图形
以中心点对称,显示此数据来自一个自然、的
常态制程。
双峰分配:在数据分布范围之中央有一低谷,
而两旁个有一高峰。
此种图形是混合两个钟型
分配,可能的情形是这些数据来自两部不同之
机器、两个不同之操作员或两条不同底生产
线。
高原型分配:直方图没有显著底高峰和尾端,
此种直方图的数据可能来自数个钟型分配。
一
种可能的原因是无标准作业程序,操作员自行
其事,造成极大之变异。
质量管理工具-直方图

组中直 3.40 3.43 3.46 3.49
x 0 = 3.52 3.55 3.58 3.61 3.64 3.67
注:x 0为频数一栏的组中值
频数核对
频数f i 1 2 13 19
26
16 12 7 3 1 ∑f i = 100
三、直方图的范例
直方图
9. 画直方图,如下图所示。 直方图的横坐标表示质量特性值,纵坐标表示频数。横坐标上标明分组
四、直方图的观察分析
TL
TU
x TM
(h)
直方图
能力富裕型:
直方图的公布在公差范围内,且两边有过大 的余地.这种情况表明虽然不会出现不合格品, 但很不经济,属于过剩质量,除特殊精密、主要 的零件外,一般应适当放宽材料、工具与设备 的精度要求,或放宽检验频次以降低鉴定成本。
五、直方图在应用中常见的问题
(注:从全体数据中寻找最大值与最小值是比较困难的。为此可以找数据表各列(或各列)数据打最大值与最
小值,进而再从中找出全体数据的最大值和最小值。)
3. 确定组数k K值可以从下表选取,本例取k=10组。
由N求k的表
数据个数N
分组k
一般使用k
50~100
6~10
100~250
7~12
10
250以上
10~20
分析与判断 双峰型:
直方图出现两个顶峰,往往是由于把不同材 料、不同加工者、不同操作方法、不同设备生 产批次的产品混在一起而造成的。
这时若分层作一下直方图就能发现其差异。
锯齿型(包括掉齿型):
直方图象锯齿一样凹凸不平(某几组直方柱的 频数少于两边紧邻组的频数),大多是由于分组不 当或是检测数据不准而造成的,应查明原因,采取 措施,重新作图分析。
QC七手法之直方图应用

QC七手法之直方图应用直方图一、前言现场工作人员经常都要面对许多的数据,这些数据均来自于生产过程中抽样或检查所得的某项产品的质量特性。
如果我们应用统计绘图的方法,将这些数据加以整理,则生产过程中的质量散布的情形及问题点所在及过程、能力等,均可呈现在我们的眼前;我们即可利用这些信息来掌握问题点以采取改善对策。
通常在生产现场最常利用的图表即为直方图。
二、直方图的定义⒈什么是直方图:即使诸如长度、重量、硬度、时间等计量值的数值分配情形能容易地看出的图形。
直方图是将所收集的测定值特性值或结果值,分为几个相等的区间作为横轴,并将各区间内所测定值依所出现的次数累积而成的面积,用柱子排起来的图形。
因此,也叫做柱状图。
⒉使用直方图的目的:⑴了解分配的形态。
⑵研究制程能力或计算制程能力。
⑶过程分析与控制。
⑷观察数据的真伪。
⑸计算产品的不合格率。
⑹求分配的平均值与标准差。
⑺用以制定规格界限。
⑻与规格或标准值比较。
⑼调查是否混入两个以上的不同群体。
⑽了解设计控制是否合乎过程控制。
3.解释名词:⑴次数分配将许多的复杂数据按其差异的大小分成若干组,在各组内填入测定值的出现次数,即为次数分配。
⑵相对次数第1页共19页在各组出现的次数除以全部的次数,即为相对次数。
⑶累积次数(f)自次数分配的测定值较小的一端将其次数累积计算,即为累积次数。
⑷极差(R)在所有数据中最大值和最小值的差,即为极差。
⑸组距(h)极差/组数=组距 ⑹算数平均数(X)数据的总和除以数据总数,通常一X X-bar )表示。
⑺中位数(X)将数据由大至小按顺序排列,居于中央的数据为中位数。
若遇偶位数时,则取中间两数据的平均值。
⑻各组中点的简化值(μ)⑼众数(M)次数分配中出现次数最多组的值。
例:次数最多为24,不合格数是9,故众数为9。
⑽组中点(m)一组数据中最大值与最小值的平均值, (上组界+下组界)÷ 2=组中点 ⑾标准差(σ)X= X 1+X 2+ …… +X nn X= ∑μfnX 0+h~ μ= , X i - X 0 组距(h) X 0=次数最多一组的组中点 X i =各组组中点 nn f f 2)μ(2μ∑-∑12)μ(2μ-∑-∑n n f f n Xi ni ∑=1=QC 七手法之直方图应用第3页共19页⑿样本标准差(S)三、直方图的制作 ⒈直方图的制作方法步骤1:收集数据并记录收集数据时,对于抽样分布必须特别注意,不可取部分样品,应全部均匀地加以随机抽样。
统计调查-直方图

数据预测
通过对直方图的观察和分析,可以对 未来的数据变化趋势进行预测,为决 策提供依据。
直方图的局限性
对数据量要求较高
直方图适用于数据量较大的情况,对于少量数据,直方图的分布 可能不够稳定,难以准确描述数据的分布特征。
对数据的处理方式较为简单
直方图只是一种简单的数据处理方法,对于一些复杂的数据分布情 况可能无法准确描述。
颜色区分
使用不同的颜色或标记来区分不同的数据系列或类别,以便更直观地比较。
强调异常值
对于异常值或关键点,可以使用不同的颜色或标记来突出显示,以便引起关注。
05
直方图与其他统计图的比较
柱状图与直方图的区别
柱状图主要用于展示分类数据的频数分布,而直 方图则主要用于展示连续变量的频数分布。
柱状图的柱子是互相独立的,而直方图中的柱子 是连续的,表示数据在某个范围内的频数分布。
考虑数据量
对于大量数据,应选择较小的分组间 距,以便更好地观察数据分布;对于 少量数据,则可以适当增大分组间距 。
合理设置坐标轴和刻度
刻度设置
坐标轴的刻度应与分组间距相匹配,以便准确反映数据分布 情况。
标签和标题
在直方图上添加适当的标签和标题,以清晰地说明数据的含 义和比较的基准。
使用适当的颜色和标记
直方图的绘制方法
确定数据范围和分组
将数据分成若干个组,每组的 数据范围称为组距。
计算每组的频数
统计每个组内数据的数量。
计算每组的组中值
组中值是该组中间位置的数值 ,用于代表该组的平均水平。
绘制条形图
根据频数和组中值绘制条形图 ,条形的高度代表该组的频数 ,条形的长度代表该组的组距
。
直方图的应用场景
七大手法之散布图与直方图

散布图应用案例
案例一
某工厂生产线上,发现产品不合格率异常升高。通过绘制散布图,将产品不合格率与生产过程中的关 键变量(如温度、压力、时间等)进行关联分析,发现温度是影响产品不合格率的主要因素。通过调 整温度参数,产品不合格率得到有效控制。
案例二
某医院对患者的病情状况与治疗效果进行评估。通过绘制散布图,将患者病情状况与治疗效果进行关 联分析,发现治疗效果与患者病情状况存在一定的相关性。这为医生制定治疗方案提供了有价值的参 考信息。
质量控制
用于分析产品质量数据,了解产品特性的变化趋势,找出潜在问题。
统计分析
用于探索两个变量之间的关系,判断是否存在关联性。
实验设计
用于实验数据的初步分析,了解实验因素与结果之间的关联。
预测与决策
用于预测未来趋势,辅助决策制定。
02
直方图介绍
直方图的定义
直方图是一种用于表示数据分布的图 形,它将一组数据按照一定的分类方 式进行整理,并使用矩形条表示各类 别的频数或频率。
直方图应用案例
案例一
某电商网站对用户购买行为进行分析。 通过绘制直方图,将用户购买量与商品 价格进行关联分析,发现商品价格在某 个区间内购买量最高。这为电商网站制 定价格策略提供了有力支持,有助于提 高销售额。
VS
案例二
某制造企业对其生产线上各工序的加工时 间进行分析。通过绘制直方图,将各工序 加工时间进行统计展示,发现某工序加工 时间过长,影响了整体生产效率。企业针 对此问题进行了工艺优化和设备更新,有 效提高了生产效率。
制作条形图
根据整理后的数据,使用矩形 条表示各类别的频数或频率, 并按照分类方式进行排列。
添加标题和注释
在图表上添加标题和必要的注 释,以帮助读者更好地理解图 表内容。
数学直方图知识点总结
数学直方图知识点总结直方图是一种用来表示数据分布的图形,它以长方形的高度来表示相应的数据频数或频率。
直方图可以清晰地显示数据的分布规律和特点,因此在统计学中有着广泛的应用。
在本文中,我将对直方图的相关知识点进行总结,包括直方图的构成要素、绘制方法、应用场景等方面进行详细介绍。
一、直方图的构成要素1. 数据频数和频率直方图是由一系列长方形组成的,每个长方形的高度代表相应数据的频数或频率。
频数是指某个数值在数据集中出现的次数,而频率是指该数值在数据集中出现的频率。
频数和频率是直方图的基本构成要素,它们能够直观地反映数据的分布情况。
在绘制直方图时,我们通常选择频率作为纵轴的标度,以便更好地比较不同数据集之间的分布情况。
2. 数据区间直方图的横轴通常表示数据的区间范围,每个长方形代表一个数据区间。
在确定数据区间时,我们需要根据数据的大小和分布情况来选择合适的区间宽度,以便更好地呈现数据的分布规律。
通常情况下,数据区间的宽度应该尽量相同,这样才能使直方图更加准确地显示数据的分布情况。
3. 坐标轴和标题直方图通常由横轴、纵轴和标题组成。
横轴表示数据的区间范围,纵轴表示数据的频率或频数,而标题则说明直方图所表示的数据集名称或相关信息。
正确设置坐标轴和标题对于理解直方图所要传达的信息非常重要,因此在绘制直方图时,我们需要注重这些构成要素的设置。
二、直方图的绘制方法1. 确定数据区间在绘制直方图前,我们首先要确定数据的区间范围。
通常情况下,我们需要根据数据的分布情况选择合适的区间宽度,然后确定各个数据区间的范围。
在确定数据区间时,我们需要确保每个区间的宽度尽量相同,以便更好地呈现数据的分布规律。
2. 绘制长方形绘制直方图时,我们需要根据数据的频率或频数来确定每个长方形的高度。
一般来说,长方形的高度代表相应数据的频率或频数,而长方形的宽度则代表数据的区间范围。
在绘制长方形时,我们需要确保相邻的长方形之间没有空隙,以便更好地显示数据的分布情况。
血细胞直方图和散点图的临床意义
网织红细胞参数
网织红细胞绝对值计数更能反映骨髓增生,它是网织红细胞百分数与红细胞计数的乘积,参考值为(24~84)×109/L。
溶血时,由于大量网织红细胞进入血循环,网织红细胞可增至6%~8%以上,急性溶血时,可高达20%左右,严重者可在50%以上,绝对值常超过100× 109/L。
肾衰竭
WBC 3.9 MCV 108.7
RBC 2.90 MCH 36.9
HGB 10.7 MCHC 34.0
HCT 31.5 RDW 29.7 R
高脂血症
WBC 7.4 MCV 78.1
HGB 15.7 MCHC 34.6
血细胞直方图和散点图的临床意义
一、什么是直方图?
直方图是通过血细胞计数仪测量而提供的血细胞体积分布图形,这些图形可以表示出细胞群体分布情况。
库尔特原理
1
检测区域
点击此处添加正文
2
红细胞
点击此处添加正文
3
红细胞通过小孔
点击此处添加正文
4
Oscilloscope
点击此处添加正文
5
示波镜
点击此处添加正文
VCS检测
V 是以库尔特原理检测细胞的体积 获得的是完全的细胞体积
VCS - DC
01
02
体积检测(V)
2
1
C 运用高频探针检测细胞的内部结构 获得细胞核复杂程度的信息 区分分叶核和非分叶核细胞
VCS - RF
细胞内部结构检测(C)
VCS - Laser
S 是运用一个宽角度的散射范围(10 -70)来测量细胞的颗粒特性 更好地根据颗粒特性区分淋巴细胞、中性粒细胞和嗜酸细胞
直方图在管理中的应用护理课件
避免将直方图作为唯一的决策 依据,应结合其他统计方法和 实际经验进行综合判断。
PART 05
案例分享
病患护理质量提升的案例
总结词
通过直方图分析,优化病患护理流程, 提高护理质量。
详细描述
某医院采用直方图对病患护理质量进 行监控,发现护理过程中的薄弱环节, 并针对性地优化流程,如加强护理人 员培训、完善交接制度等,最终实现 护理质量的显著提升。
直方图的组成
01
02
03
横轴
表示数据的区间范围,通 常以等距的方式进行划分。
纵轴
表示每个区间内的数据点 数量,通常以直方柱状的 形式表示。
坐标轴
表示数据的实际数值,通 常在直方图的旁边标注。
直方图的绘制方法
数据整理
区间划分
将原始数据按照大小顺序进行排序,并计 算出数据的最大值、最小值、平均值等统 计指标。
通过标准化处理,将数据转换为统一的尺度,便于比较和分析,提高直方图的解释 价值。
标准化处理的方法包括最小-最大缩放、均值标准化、分位数标准化等,应根据具体 情况选择合适的方法。
直方图的解读与误用
正确解读直方图,避免对数据 的误读和误解。
注意直方图的形状、分布、异 常值等特征,结合实际情况进 行分析和解释。
PART 03
直方图与其他管理工具的 结合
直方图与PDCA循环
总结词
直方图与PDCA循环结ห้องสมุดไป่ตู้,有助于提高管理效率和护理质量。
详细描述
在PDCA循环中,直方图可以用于展示护理过程中的数据分布和变化情况,帮助管理者发现问题并制 定改进措施。通过直方图,可以直观地比较不同阶段的数据,评估改进效果,持续优化护理过程。
直方图在护理管理中的应用
直方图在护理管理中的应用一、引言在现代护理管理中,数据的收集与分析是提升护理质量的重要手段。
直方图作为一种有效的数据可视化工具,在护理管理中有着广泛的应用。
通过直方图,护理管理者能够直观地了解护理工作中的各种数据特征,从而制定更为科学的管理决策。
二、直方图基础知识2.1 直方图的定义直方图是一种图形表示方法,用于表示数据的分布情况。
通过将数据分组并绘制成矩形条的高度来表示每个组内数据的频数,直方图可以帮助我们直观地了解数据的集中趋势、离散程度以及数据的分布形态。
2.2 直方图的构成直方图主要由横轴和纵轴组成:横轴(X轴):表示数据的分组区间。
纵轴(Y轴):表示每个分组的频数或频率。
2.3 直方图的类型直方图主要分为以下几种类型:单峰直方图:数据呈现出一个主要的集中峰值。
多峰直方图:数据有多个峰值,显示多种集中趋势。
偏态直方图:数据分布不对称,向一侧倾斜。
三、护理管理中的数据分析需求在护理管理中,数据分析的需求主要体现在以下几个方面:3.1 护理质量监测护理质量是医院服务的重要组成部分,通过对护理质量相关数据的分析,可以发现问题并进行改进。
3.2 护理成本控制护理成本的控制是医院管理的重要目标,通过对护理成本数据的分析,可以有效地进行预算和成本控制。
3.3 患者满意度评估患者满意度是医院服务质量的重要指标,护理管理者需要通过数据分析了解患者的满意度变化,以便采取相应措施。
四、直方图在护理管理中的具体应用4.1 护理质量监测在护理质量监测中,可以利用直方图对各类护理事件的发生频率进行分析。
例如,某医院在一段时间内收集了护理不良事件的数据,通过绘制直方图,可以清楚地看到不同护理事件的发生频率。
4.1.1 数据收集数据收集是进行护理质量监测的第一步。
需要收集的护理事件数据包括但不限于:药物错误感染事件跌倒事件4.1.2 数据分析通过直方图分析不同类型护理事件的发生频率,可以识别出高发的护理事件。
例如,在分析药物错误事件时,如果直方图显示某些药物错误发生频率较高,护理管理者可以针对性地进行培训和教育,提升护理人员的用药安全意识。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
12
制程能力解释
n1 Pp Cp加工制品数据离散分布的好坏
Pa Ca加工制品数据中心分布的好坏 Ppk Cpk加工制品数据中心分布与离散分布的好坏
A 1.67≤Cpk B 1.33 ≤Cpk< 1.67 C 1.00 ≤Cpk< 1.33 D Cpk< 1.00
USL=规格上限、 LSL=规格下限、 μ=规格中心值、 T=USL-LSL、
n 1 =推定群体标准差、 X =总取样样本平均值
不属于常态分配之数据,以Pp、Cp值或依客户指定方式来表示制程能力, 如:偏肉、真圆度、圆筒度、心振、心差等。
3 n1
= X LSL
3 n1
= X
T /2
(双边规格适用) (望小规格适用) (望大规格适用)
(双边规格适用)
制程能力 精确度
Ppk
Cpk
= Cp(1-Ca)
A 1.90 ≤Cp B 1.52 ≤Cp< 1.90 C 1.15 ≤Cp< 1.52 D Cp< 1.15
A B C
Ca≤ 0.125 0.125 < Ca≤0.25 0.25<Ca
偏态型是指图的顶峰有时偏向左侧、 有时偏向右侧。由于某种原因使下限受到 限制时发生偏左型。 由于某种原因使上 限受到限制时发生偏右型。或由于工作习 惯都会造成偏态型。也出现在单边规格时
平顶型没有突出的顶峰,一般有三种
原因。 A与双峰型类似,由多个总体、多
分布混在一起。 B由于生产过程中某中缓
慢的倾向在起作用,如工具的磨损、操
A
2
直方图的作用: 直方图作用,
通过直方图的观察与分析,可了解产品质量的波动情况, 掌握质量特性的分布规律,以便对质量状况进行分析判 断。同时可通过质量数据特征值的计算,估算施工生产 过程总体的不合格品率,评价过程能力等
直方图的判定:
ห้องสมุดไป่ตู้
加工制品数据好坏
正常型是指过程处于稳定的图型,它 的形状是中间高、两边低,左右近似对 称。近似是指直方图多少有点参差不齐, 主要看整体形状及与异常型直方图比较 而言。
无富余型样本分布中心 与公差中心M近似重 合,但两边与规格的上、下限紧紧相连,没有 余地,表明过程能力已到极限,非常容易出现 失控,造成不合格。因此,要立即采取措施, 提高过程能力,减少标准偏差。
A
6
直方图与规格界限的比较
能力富余型样本分布中心 与公差中心M近似一致, 但两边与规格上、下限有很大距离,说明工序能力 出现过剩,经济性差。因此,可考虑改变工艺,放 宽加工精度或减少检验频次,以降低成本。
A
3
直方图判图
孤岛型在直方图旁边有孤立的小岛出 现,当这种情况出现时过程中有异常原 因。如:原料发生变化,不熟练的新工 人替人加班,测量有误等,应及时查明 原因、采取措施。
双峰型当直方图中出现了两个峰,这是由 于观测值来自两个总体,两个分布的数据混 合在一起造成的。如:两种有一定差别的原 料所生产的产品混合在一起,或者两部机台、 两种产品混在一起,此时应当加以分层或减 少差异。
折齿型当直方图出现凹凸不平的形状, 这是由于作图时数据分组太多,测量仪器 误差过大或观测数据不准确等造成的,此 时应重新收集数据和整理数据。
A
4
直方图判图 陡壁型当直方图像高山的陡壁向一边 倾斜时,通常在质量较差时为了符合标 准而进行全检,剔除不合格品。剔除了 不合格品的产品数据作直方图时容易产 生这种陡壁型,这是一种非自然形态。
直方图实际应用
A
1
直方图制作
制作直方图的步骤:
(1)收集数据。一般应大于50个。 (2)确定数据的极差(R)。用数据的最大值减去最小值 求得。 (3)确定组数K=1+3.322*LN(N);或:
N=50~100 K=6~10、N=100~250 K=7~12、N>250 K=10~20; 组数要适当,太少会较大计算误差;太多分组规律不明显性工作量大。 (4)确定组距(h)。以此组数去除极差,可得直方图每组的宽度,即组距。 (5 )确定各组的界限值。为避免数据值与组界限值重合而造成不便,组的界限 值单位应取最小测量单位的1/2。分组时应把最大值和最小值包括在内。 (6)编制频数分布表,即数据分组。 (6)按数据值比例画出横坐标。 (7)按频数值比例画纵坐标。以观测值数目或百分数表示。 (8)画直方图。在直方图上应标注出公差范围(T)、公差中心线 样本容量(n)、样本平均值(x)、样本标准偏差值(s)和x的位置等。---后续
准确度、精密度、精确度-----------类似量测部分的数据好坏
Ca
Cp Cpk
制程能力指数(Cpk)、机器能力指数(CmK)、初期制程能 力指数(Ppk),仅抽样时机、顺序、数量不同
A
11
制程能力公式
项目 代号
计算公式
等级
基准
精密度 Pp Cp 准确度 Pa Ca
T
= 6 n1 = USL X
生产中直方图应用
日 报 单、
A
8
生产中直方图应用
机 台 作 业 画 面
A
9
生产中直方图应用
成 绩 表
A
10
直方图与制程能力
直方图评价→加工能力好坏评价: 平均值与规格中心比较、数据的离散分布状况
制程能力是指工序在一定时间里,处于控制状态(稳定状态) 的实际工作能力。制程能力指数是指制程能力满足产品质量 标准要求(规格范围等)的程度,或是工序在一定时间里, 处于控制状态(稳定状态)下的实际加工能力。
作者的疲劳等。 C、质量指标在某个区间
中A 均匀变化
5
直方图与规格界限的比较
理想型图型对称分布,样本分布中心与公差 中心M近似重合,分布在公差范围内且两边有 一定余量,是理想状态。因此,可保持状态水 平加以监督。
偏向型样本分布中心比公差中心M有较大偏 移,这种情况下,稍有不慎就会出现不合格。 因此要调整分布中心与公差中心近似重合。
能力不足型样本中心与公差中心M近似重合,但分 布已超出上、下限。这时不合格已经出现。因此, 要采取措施提高加工精度,减少标准偏差。
能力不足,左、右超限样本中心 与公差中心M有偏 移且分布有部分已超出上、下限。这种情况比较复 杂。首先,调整分布中心与公差中心重合,调整后, 不合格消失,说明是由于某个系统原因造成的,这 时,再深入分析过程能力是否要继续提升等。其次, 如果经调整分布中心与公差中心已近似重合但仍有 不合格,则说明过程能力已严重不足,样本分散程 度过大,要A继续提高加工精度,减少标准偏差。7
