TDDFT简介
密度泛函理论(DFT)
一、 计算方法密度泛函理论（DFT ）、含时密度泛函理论（TDDFT ）二、 计算方法原理1． 计算方法出处及原理本计算方法设计来源于量子化学理论中的Born–Oppenheimer 近似，给近似下认为原子核不动, 这样电子就相当于在一个由核产生的外部的静态势场 V 中运动。
那么一个固定的电子态可以用波函数 Ψ(1r , · · · ,N r ), 并且满足多 N 电子体系薛定谔方程:()()22ˆˆˆˆ,2N N N i i j i i i i j H T V U V r U r r E m <⎡⎤⎡⎤ψ=++ψ=-∇++ψ=ψ⎢⎥⎣⎦⎣⎦∑∑∑ (2-3) 其中，● Ĥ, 哈密顿算符;● E , 体系总能量;● ˆT, 动能项; ● ˆV, 由带正电的原子核引起的外场势能项; ● Û, 电子电子相互作用能。
通常把 ˆT和 Û 叫做通用算符, 因为对于任何一个 N 电子体系, 表达式都相同.而势能函数 ˆV与体系密切相关。
由于电子相互作用项 Û 的存在, 复杂的多体系的薛定谔方程公式 2-3并不能拆分为简单的单电子体系的薛定谔方程。
根据 DFT 的核心理念, 对于一个归一化的波函数 Ψ, 电子的密度 n(r ) 可以定义为:333*231212()(,,)(,,)N N N n r N d r d r d r r r r r r r =⋅⋅⋅ψ⋅⋅⋅ψ⋅⋅⋅⎰⎰⎰ (2-4)更重要的是, DFT 的核心理念告诉我们, 对于一个给定的基态, 如果基态的电子密度0()n r 是知道的话, 那么基态的波函数012(,,)N r r r ψ⋅⋅⋅就唯一确定。
也就是说, 基态的波函数0ψ是基态电子密度0n 的泛函[11], 表达为:[]00n ψ=ψ (2-5)既然有以上的假定, 那么对于基态的任何一个观测量ˆO, 它的数学期望就应该是0n 的泛函:[][][]000ˆO n n O n =ψψ (2-6) 特别的, 基态的能量也是0n 的泛函:[][][]0000ˆˆˆE E n n T V U n ==ψ++ψ (2-7) 这里外部势能的贡献[][]00ˆn V n ψψ可以通过基态的电子密度0n 来精确表达：300[]()()V n V r n r d r =⎰ (2-8)或者外部势能ˆVψψ可以用电子密度 n 来表达: 30[]()()V n V r n r d r =⎰ (2-9)泛函 T [n ] 和 U [n ] 被称作通用泛函, 而势能泛函 V [n ] 被称做非通用泛函, 因为它与当前研究的系统息息相关。
【国家自然科学基金】_tddft计算_基金支持热词逐年推荐_【万方软件创新助手】_20140802
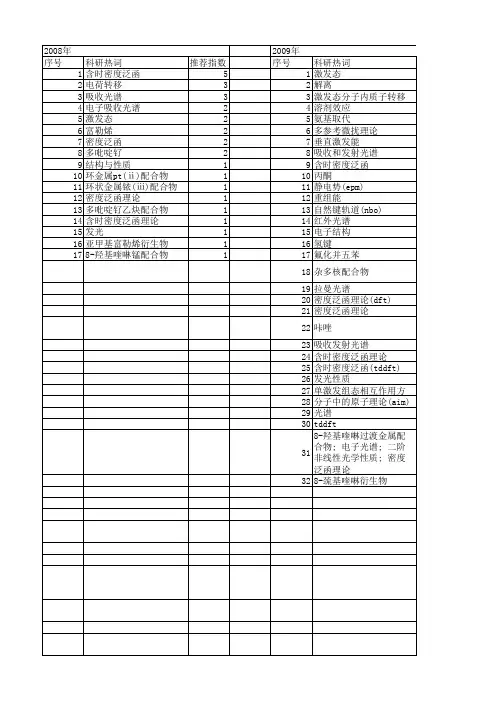
推荐指数 5 3 3 2 2 2 2 2 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32
科研热词 激发态 解离 激发态分子内质子转移 溶剂效应 氨基取代 多参考微扰理论 垂直激发能 吸收和发射光谱 含时密度泛函 丙酮 静电势(epm) 重组能 自然键轨道(nbo) 红外光谱 电子结构 氢键 氟化并五苯 杂多核配合物 拉曼光谱 密度泛函理论(dft) 密度泛函理论 咔唑 吸收发射光谱 含时密度泛函理论 含时密度泛函(tddft) 发光性质 单激发组态相互作用方法 分子中的原子理论(aim) 光谱 tddft 8-羟基喹啉过渡金属配合物; 电子光谱; 二阶 8-巯基喹啉衍生物
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词 含时密度泛函 电荷转移 吸收光谱 电子吸收光谱 激发态 富勒烯 密度泛函 多吡啶钌 结构与性质 环金属pt(ⅱ)配合物 环状金属铱(ⅲ)配合物 密度泛函理论 多吡啶钌乙炔配合物 含时密度泛函理论 发光 亚甲基富勒烯衍生物 8-羟基喹啉锰配合物
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48
科研热词 推荐指数 密度泛函理论 3 吸收光谱 2 光吸收谱 2 黄曲霉素b1 1 镁细菌叶绿素a 1 锌细菌叶绿素a 1 量子化学理论方法 1 量子化学 1 连续极化模型 1 表面增强预共振拉曼光谱 1 表面增强拉曼散射 1 荧光分子 1 离解能 1 电荷差异密度 1 电离 1 电子结构 1 氧化还原势 1 有机染料分子p1和p4 1 扩展卟啉 1 态密度 1 外电场 1 复合物afb1-agn（n=2，4，6）： 1 含时密度泛函理论(tddft) 1 含时密度泛函理论 1 含时密度泛函 1 取代基 1 发射光谱 1 前线区域轨道 1 分子设计 1 分子线 1 分子电离 1 分子动力学 1 分子内电荷转移 1 从头计算 1 五氯酚 1 zinc-bacteriochlorophylla 1 uv电子光谱 1 tddft 1 surface-enhanced resonance raman 1 spectrum surface-enhanced raman scattering 1 redox potential 1 magnesium-bacteriochlorophylla1 dissociation energy 1 dft 1 density functional theory 1 complexesafb1-ag. （n=2, 4, 6） 1 aflatoxin b1 1 absorption spectrum 1
XANES谱及分析基础-陈栋梁
X射 线 吸 收 谱 学 实 验 和数据分析讲习班
XAFS
XAFS谱、XANES谱
XANES谱:划分
XANES:-20 ~ +50eV (-几十eV ~ + 几十 eV) 区域：边前（pre-edge）+边（edge）+边后（post-edge）
EXAFS
北 京同步辐射装置 Beijing Synchrotron Radiation Facility
北 京同步辐射装置 Beijing Synchrotron Radiation Facility
X射 线 吸 收 谱 学 实 验 和数据分析讲习班
XANES谱分析实例
XANES谱基本原理
北 京同步辐射装置 Beijing Synchrotron Radiation Facility
X射 线 吸 收 谱 学 实 验 和数据分析讲习班
XANES谱分析的关键：终态！包括什么态才是可以允许跃迁 的（跃迁规则），及能够跃迁多少（态密度）。
XANES谱基本原理
北 京同步辐射装置 Beijing Synchrotron Radiation Facility
X射 线 吸 收 谱 学 实 验 和数据分析讲习班
定性判定：凝聚态体系
试着：Cr2O3，Cr K-边XANES
X射 线 吸 收 谱 学 实 验 和数据分析讲习班
X射 线 吸 收 谱 学 实 验 和数据分析讲习班
定性判定：单原子/连续体
单原子：对于电偶极跃迁
K 边： 初态为1s (n=1，l=0，m=0)； LⅠ边：初态为2s (n=2，l=0，m=0)； LⅡ边：初态为2p1/2 (n=2，l=1，j=1/2)； LⅢ边：初态为2p3/2 (n=2，l=1，j=3/2)；
傅里叶变换t dt f df
傅里叶变换t dt f df傅里叶变换是一种数学工具，它在信号处理、图像处理以及物理学等领域中有着广泛的应用。
它的主要作用是将一个函数在时间域中的描述转换为频域中的描述，从而帮助我们更好地理解信号的特性。
傅里叶变换的基本思想是将一个函数分解成不同频率的正弦和余弦函数的叠加。
通过将函数在时间域中的描述转换为频域中的描述，我们可以得到函数的频谱信息，即函数中不同频率的成分的强度和相位。
在傅里叶变换中，t表示时间，dt表示时间的微小变化量。
f表示频率，df表示频率的微小变化量。
通过对函数进行傅里叶变换，我们可以得到函数在不同频率上的能量分布情况。
傅里叶变换的应用十分广泛。
在通信领域，傅里叶变换可以帮助我们理解信号的频谱特性，从而实现信号的传输和解调。
在图像处理领域，傅里叶变换可以帮助我们分析图像的频域特征，如边缘和纹理等。
在物理学领域，傅里叶变换可以帮助我们研究物体的振动和波动等现象。
虽然傅里叶变换在数学上是一个严谨的理论，但我们可以通过直观的例子来理解它的基本原理。
比如，假设我们要分析一段音乐的频谱特性。
我们可以将这段音乐信号进行傅里叶变换，得到它在不同频率上的能量分布情况。
通过分析这个频谱图，我们可以了解这段音乐信号中不同乐器的成分和它们的强度。
总的来说，傅里叶变换是一种非常重要的数学工具，它帮助我们理解和分析信号的频域特性。
通过对函数进行傅里叶变换，我们可以得到函数在不同频率上的能量分布情况，从而更好地理解信号的特性。
无论是在通信领域、图像处理领域还是物理学领域，傅里叶变换都有着广泛的应用。
通过深入学习和理解傅里叶变换，我们可以更好地应用它来解决实际问题，并推动科学技术的发展。
dtft,dft和z变换的关系
dtft,dft和z变换的关系
DTFT、DFT和Z变换都是信号处理领域中常见的变换方法。
它们可以将时域信号转换为频域信号，或将离散时间域信号转换为复平面上的Z域信号。
虽然它们之间有些区别，但它们的本质都是通过数学方法来描述信号的频域特性。
DTFT是离散时间傅里叶变换的一种形式，可以将一个离散时间域信号转化为连续频域信号。
通过DTFT可以得到一个信号的频谱，从而分析信号的频域特性。
DTFT的公式是一个无限长的求和式，需要对信号进行无限次的积分，因此需要消耗大量的计算资源。
DFT是离散傅里叶变换的一种形式，它可以将一个N点离散时间域信号转化为N点频域信号。
相比于DTFT，DFT的计算量更小，因为它只需要对N个采样点进行有限次的计算。
因此，DFT常常用于实际信号处理中，比如在数字音频中进行频谱分析。
Z变换是一种复变函数的变换，可以将一个离散时间域信号转换为复平面上的Z域信号。
Z变换的主要应用是在数字控制系统和数字滤波器中。
通过Z变换，可以将差分方程转换为代数方程，从而进行系统分析和设计。
Z变换的公式类似于DTFT的无限长求和式，需要进行无限次的积分或求和。
综上所述，DTFT、DFT和Z变换都是信号处理中常用的变换方法，它们可以将时域信号转换为频域信号或复平面上的Z域信号。
虽然它们的应用场景和计算方法略有不同，但它们的本质都是描述信号的频域特性。
gaussian09 计算旋轨耦合
根据您提供的主题，我将为您撰写一篇关于Gaussian09计算旋轨耦合的文章。
Gaussian09是一个广泛使用的量子化学计算软件，它可以用于研究分子的结构、能量、振动频率等性质。
旋轨耦合是指自旋轨道相互作用，它在研究分子的磁性质和光学性质时具有重要作用。
在本文中，我们将探讨如何使用Gaussian09计算旋轨耦合，以及其在理论化学研究中的应用。
一、Gaussian09简介1. Gaussian09是由Gaussian, Inc.开发的一款用于量子化学计算的软件，它可以进行从量子力学到分子动力学等多种计算。
2. Gaussian09具有强大的功能和灵活的使用方式，广泛应用于理论化学、生物化学、材料科学等领域。
二、旋轨耦合的理论基础1. 旋轨耦合是量子力学中的重要概念，它描述了自旋和轨道运动之间的相互作用。
2. 在分子中，电子的自旋和轨道运动相互作用会导致分子的磁性质和光学性质发生变化，因此对旋轨耦合的研究具有重要意义。
三、Gaussian09计算旋轨耦合的方法1. 在Gaussian09中，可以通过设置适当的计算参数来进行旋轨耦合的计算。
2. 通过在输入文件中指定旋轨耦合的计算方法和相关的分子结构信息，可以使用Gaussian09进行旋轨耦合的计算。
四、旋轨耦合在理论化学研究中的应用1. 旋轨耦合的计算结果可以用于研究分子的磁性质和光学性质，为理论化学研究提供重要的参考数据。
2. 通过对旋轨耦合进行计算和分析，可以揭示分子中电子的运动规律和相互作用机制，为理论化学研究提供重要的理论基础。
五、结论通过对Gaussian09计算旋轨耦合的方法和应用进行探讨，我们可以看到旋轨耦合在理论化学研究中的重要性和应用前景。
使用Gaussian09进行旋轨耦合的计算不仅可以为理论化学研究提供重要的数据支持，也为研究者提供了一个强大的工具和评台，有助于推动理论化学研究的发展。
致力于提供高质量的理论化学研究工具和支持，Gaussian09的不断发展和完善将为理论化学研究提供更多的可能性和机遇。
DFT_DFT设计概述
DFT_DFT设计概述DFT（Design-for-Test）是面向测试的设计，它是一种在集成电路设计阶段就考虑测试需求的方法，以便在芯片制造之前提前规划和设计测试，从而提高芯片测试的效率和可靠性。
DFT能够帮助简化测试流程，减少测试时间和成本，提高测试覆盖率和可靠性，从而提高整体产品质量。
DFT设计的目标是通过在芯片设计中引入一些特殊的硬件或软件功能，使得对芯片进行测试和故障定位更加容易。
DFT的设计方法主要包括逻辑插入、测试模式设计、故障模拟和故障定位等。
逻辑插入是在芯片设计过程中将一些专用的硬件逻辑插入到设计中，以便在测试过程中对芯片进行控制和观测。
这种逻辑包括扫描链（Scan chain）、BIST（Built-In Self-Test）和观测点（Observation Point）等。
扫描链是一种顺序逻辑的测试结构，它可以将芯片内的寄存器连接成一个长链，便于故障检测和故障调试。
BIST是一种自测试的结构，它可以通过内部的特殊逻辑来生成测试模式，执行测试和判断测试结果。
观测点是一种在设计中添加的特殊信号，用于观察芯片内部的状态和信号。
测试模式设计是指在设计阶段就考虑如何生成和应用测试模式，以便对芯片进行测试。
测试模式是一种特殊的输入序列，它可以刺激芯片的输入，以检测芯片的功能和故障。
测试模式设计需要考虑测试目标、测试覆盖率和测试时间等因素。
常用的测试模式包括全覆盖测试模式、随机测试模式和伪随机测试模式等。
故障模拟是指在设计阶段通过特殊的软件工具对芯片进行故障注入和故障模拟，以评估芯片的可测试性和可靠性。
故障注入是通过在芯片设计中引入一些故障模型和故障点，以模拟芯片内部的故障。
故障模拟是通过软件工具模拟故障注入后的芯片行为，以评估故障检测和故障定位的能力。
故障定位是指在测试过程中通过观察测试结果和相应的故障模式，定位芯片内部的故障。
故障定位需要对测试结果进行分析和处理，并结合故障模型和故障点信息来确定故障的位置。
dft 概述
dft 概述
离散傅里叶变换（Discrete Fourier Transform，DFT）是一种数字信号处理技术，用于将离散时间信号转换为频域表示。
它是傅里叶变换在离散时间信号上的推广，广泛应用于数字信号处理、图像处理、通信系统等领域。
DFT 的基本思想是将离散时间信号表示为一系列复数系数的组合，这些复数系数表示信号在不同频率上的幅度和相位。
DFT 可以通过快速傅里叶变换（Fast Fourier Transform，FFT）算法高效地计算，其中 FFT 是一种利用分治法和周期性的算法，能够将 DFT 的计算复杂度降低到 O(n log n)，其中 n 是信号的长度。
DFT 的应用包括信号分析、信号合成、数字滤波器设计、图像压缩、通信系统中的调制和解调等。
它在处理信号的频率特性、时频分析、信号识别等方面具有重要作用。
DFT 是数字信号处理的基础工具之一，对于理解和处理数字信号具有重要意义。
1。
第一性原理简介
简介：ABINIT的主程序使用赝势和平面波，用密度泛函理论计算总能量，电荷密度，分子和周期性固体的电子结构，进行几何优化和分子动力学模拟，用TDDFT（对分子）或GW近似（多体微扰理论）计算激发态。
此外还提供了大量的工具程序。
程序的基组库包括了元素周期表1-109号所有元素。
ABINIT适于固体物理，材料科学，化学和材料工程的研究，包括固体，分子，材料的表面，以及界面，如导体、半导体、绝缘体和金属。
功能：可以计算很多物理属性：A. 计算倒格子中核与电子的总能量。
A.1. 计算使用平面波和赝势。
A.2. 总能量的计算使用密度泛函理论（DFT）。
可以使用大多数重要的局域密度近似(LDA)，包括Perdew-Zunger近似。
可以使用两种不同的局域自旋密度(LSD)，包括Perdew Wang 92和M. Teter的LSD。
还可以使用Perdew-Burke-Ernzerhof，revPBE，RPBE和HCTH等GGA (自旋极化和非极化)。
A.3. 自恰场计算生成DFT基态，以及相关的能量和密度。
此后的非自恰计算可以对能带结构的大量k-点产生本征能量。
态密度的计算即可以用四面体方法，也可以用模糊技术。
A.4. 程序可以使用多种不同的赝势。
对整个周期表适用的有两种：Troullier-Martins型和Goedecker型（这种类型包括自旋-轨道耦合）。
如果需要的话，有四个代码可以产生新的赝势。
A.5. 程序本身可以处理金属和绝缘体系。
A.6. 晶胞可以是正交或者非正交。
计算可以输入任何对称性及相应的k-点集。
A.7. 电子体系可以用自旋极化和自旋非极化计算。
一个特殊的选项可以有效地处理反铁磁性。
可以对总能量计算非共线的磁性（不能用于力，张量，相应函数...）。
可以禁止晶胞的总磁矩。
A.8. 总能量，力，张量和电子结构的计算可以考虑自旋-轨道耦合。
A.9. 能量可分解为不同的成分（局域势，XC，Hartree...）。
论量子化学计算中的密度泛函理论
论量子化学计算中的密度泛函理论摘要：本文简要介绍了密度泛函理论的基本理论，同时着重介绍了相对论含时密度泛函理论及其在相关计算方面的应用。
关键词：密度泛函理论弱作用体系强相关体系1引言随着量子理论的建立和计算机技术的发展,人们希望能够借助计算机对微观体系的量子力学方程进行数值求解,然而量子力学的基本方程———Schrdinger 方程的求解是极其复杂的。
克服这种复杂性的一个理论飞跃是电子密度泛函理论(DFT)的确立[1 ,2 ]。
电子密度泛函理论是上个世纪60年代在Thomas-Fermi理论的基础上发展起来的量子理论的一种表述方式。
传统的量子理论将波函数作为体系的基本物理量,而密度泛函理论则通过粒子密度来描述体系基态的物理性质,这使得密度泛函理论将3N维波函数问题简化为3维粒子密度问题,十分简单直观。
另外,粒子密度通常是可以通过实验直接观测的物理量。
粒子密度的这些优良特性,使得密度泛函理论具有诱人的应用前景。
经过几十年的发展,密度泛函理论体系及其数值实现方法都有了很大的发展, 这使得密度泛函理论被广泛地应用在化学、物理、材料和生物等学科中, Kohn也因为他对密度泛函理论的贡献获得1998年的诺贝尔化学奖[3]。
下面,我们将在本文中对密度泛函理论基本理论和它越来越广泛的应用作一个简单的回顾:首先介绍密度泛函理论的基本原理，最后用一些实例说明密度泛函理论的广泛应用。
2密度泛函理论的基本原理现代密度泛函理论的建立，提出了电子体系的物理性质，完全可以由体系基态的电子密度决定，而电子密度的定义是这样的：ρ(r1) = N |ψ(r1, r2, · · · , rN)|2dr2, · · · , rN(2-1) 其物理意义是在r1点找到电子的总几率密度(不管其它电子在何处)。
很明显，电子密度ρ(r1)仅仅是一个三维坐标的函数，其复杂度远远小于电子的多体波函数。
含时密度泛函
含时密度泛函含时密度泛函（TimeDensityFunctionalTheory，TDDFT）是一种基于密度泛函理论（Density Functional Theory，DFT）的时间域计算方法，可以解决物理系统激发态能量水平的问题。
TDDFT可以用来在相对较低的计算成本下，快速准确地求解物理系统中激发态能量水平。
首先，让我们从原子和分子物理中的激发态理论开始。
在原子和分子物理学中，很多情况下，我们会发现系统的激发态具有更高的能量，而基态的能量却较低。
激发态的存在意味着，以一种更低的能量状态存在的原子或分子，可以分子激发到更高的能量状态。
但是，由于原子和分子的激发态总是非常多，因此激发态的理论和计算工作一直是很棘手的。
另一方面，DFT是一种统一的理论框架，可以用来描述原子和分子的几何和能量状态，但是它的局限性在于，它只能预测基态的能量，而不能预测激发态的能量。
为了解决这个问题，就有了TDDFT的发展。
TDDFT的主要思想是，把DFT的本征态解的原则，扩展到时域，从而可以用来求解短暂时间内（几个离子周期）物理系统的激发态能量水平。
TDDFT建立在DFT理论的基础上，它通过引入一个新的变量电子密度的时间变化，从而为量子力学中激发态的研究提供了一种新的方法。
TDDFT建立在几个基本原理上：第一，电子-核相互作用是一种局部可调的势能；第二，电子在时间空间中的运动可以用相对较少的参数来描述；第三，在一定条件下，电子的态密度是一个时间不变的量。
TDDFT的实现需要以下几个关键步骤：第一，建立泛函，以描述电子-核相互作用；第二，将电子的运动轨迹离散化，以便计算电子的态密度；第三，建立一个相应的时间密度泛函，以描述电子的时间变化；最后，用该时间密度泛函解算出激发态能量水平。
TDDFT有许多优点，其中最显著的是，在解决激发态能量水平问题时，可以节省很多计算成本，比静态DFT方法节省很多时间。
另外，与基于求解Schrdinger方程的他方法相比，TDDFT的计算步骤更简单，可以节省更多计算成本。
tddft计算激发态下的分子结构
tddft计算激发态下的分子结构
TDDFT（时间依赖的密度泛函理论，Time-Dependent Density Functional Theory）是一种计算电子激发态的量子化学方法，在化学、材料科学以及生物学等领域都有广泛应用。
其基本思想是将激发态看
作一个“激发的密度”，通过求解电子自相互作用的密度泛函方程（DFT，Density Functional Theory）和时间依赖的Kohn-Sham方程
来得到激发的密度和激发能量等信息。
TDDFT方法可以用来计算分子在光激发下的各种性质，比如激发
能量、吸收光谱等。
通过包含不同的函数形式，TDDFT方法可以很好地处理不同类型的激发态，比如单重态、三重态、有机物和无机物等等。
同时，TDDFT方法还可以考虑溶剂效应、非共价相互作用等复杂情况的影响。
在计算激发态下的分子结构时，TDDFT方法可以用来预测分子在
激发态下的几何结构和反应能力等信息。
这些信息对于化学反应机理
以及新药物的研发等有重要的指导意义。
通过这种方法，可以更好地
理解分子的电子构型和化学性质，推动化学研究的发展。
TDDFT的输出文件的详细解释
--------------------------------------------------------------------1 2 3 8 1 1 0 0 0 0.000000 1.000000 0.000000 0.000000 0.000000 1.000000 0.000000 0.000000 0.000000
52.227-19.
Gaussian, Inc. Carnegie Office Park, Building 6, Pittsburgh, PA 15106 USA
--------------------------------------------------------------Warning -- This program may not be used in any manner that competes with the business of Gaussian, Inc. or will provide assistance to any competitor of Gaussian, Inc. The licensee of this program is prohibited from giving any competitor of Gaussian, Inc. access to this program. By using this program, the user acknowledges that Gaussian, Inc. is engaged in the business of creating and licensing software in the field of computational chemistry and represents and warrants to the licensee that it is not a competitor of Gaussian, Inc. and that it will not use this program in any manner prohibited above. ---------------------------------------------------------------
DTFT和DFT的区别
DTFT和DFT的区别：对于一般的周期信号可以用一系列（有限个或者无穷多了）正弦波的叠加来表示。
这些正弦波的频率都是某一个特定频率的倍数如5hz、2*5hz、3*5hz……（其中的5hz叫基频）。
这是傅立叶级数的思想。
所以说周期信号的频率是离散的。
而且，对于周期信号有一个特点，信号的周期越长，信号的基频越小。
非周期信号可以看作周期无穷大的周期信号，那么它的基频就是无穷小，这样它的频率组成就编程了连续的了。
求这个连续频率的谱线的过程就是傅立叶变换。
包括这样几种：DTFT（时间离散，频率连续）DFT（时间和频率都离散，可在计算机中处理）FFT（DFT的优化算法，计算量减少）幅频响应：信号通过系统之后的输出信号的幅度与它输入时的信号的幅度的比值。
幅频响应曲线：多种不同信号的比值描绘成的曲线，叫做幅频响应曲线。
相频相应：信号通过系统之后的输出信号的相位与它输入时的信号的相位值差。
补充：在放大电路中提到过通频带的概念。
放大电路输出信号的幅度和相位，会随着信号频率的变化发生变化，一般来说，在放大电路的低频段与高频段和中频段相比，信号的幅度会下降，也会产生一定的相移。
这就是放大电路的频率特性，它分为幅频特性和相频特性两方面。
幅频特性是描绘输入信号幅度固定，输出信号的幅度随频率变化而变化的规律，即。
相频特性是描绘输出信号与输入信号之间相位差随信号频率变化而变化的规律，即这些统称放大电路的频率响应。
幅频特性偏离中频值的现象，称为幅度频率失真。
相频特性偏离中频值的现象，称为相位频率失真。
放大电路的幅频特性和相频特性，也称频率响应。
因放大电路对不同频率成分信号的增益不同，从而使输出波形产生失真，称为幅度频率失真简称幅频失真。
放大电路对不同频率成分信号的相移不同，从而使输出波形产生的失真，称为相频失真。
幅频失真和相频失真是线性失真。
本课程重点考虑幅频特性，相频特性只是建立一个概念,不深入研究。
产生频率失真的原因是放大电路中存在电抗性元件，例如耦合电容、旁路电容、分布电容、变压器、分布电感等，并且三极管的电流放大系数b(w)也是频率的函数。
td-wcdma
td-wcdma简介TD-SCDMA（名为中国第三代移动通信制式，英文为Time Division-Synchronous Code Division Multiple Access）是由中国华为、中兴、大唐等企业自主研发的标准第三代移动通信制式之一。
WCDMA（名为宽带无线通信技术，英文为Wideband Code Division Multiple Access）是由3GPP组织制定的标准第三代移动通信制式之一。
TD-WCDMA（即TD-SCDMA+WCDMA）是将TD-SCDMA和WCDMA两种制式进行整合的方案，使得支持TD-WCDMA的终端能够同时兼容TD-SCDMA和WCDMA两种制式。
优势TD-WCDMA制式在许多方面具有以下优势：1.频谱资源利用率高：TD-SCDMA采用时分复用技术（TDD），能够灵活地根据网络需求进行上下行链路的分配，从而最大限度地提高频谱资源的利用率。
2.兼容性强：TD-WCDMA终端既可以支持TD-SCDMA网络，也可以支持WCDMA网络，从而能够在不同网络环境下提供更好的移动通信服务。
3.抗干扰能力强：TD-SCDMA采用了分集和分集组合技术，有效抵抗多径衰落、多路径干扰等信道问题，从而提高了系统的抗干扰能力。
4.支持高速数据传输：TD-WCDMA制式能够支持更高的数据传输速率，适用于各种多媒体应用和数据业务。
5.系统容量大：由于TD-SCDMA采用了动态分配资源的策略，使得系统容量可以根据用户需求进行动态调整，从而提高了系统的承载能力。
技术细节TD-WCDMA制式的技术细节包括以下几个方面：1.改进的调度算法TD-SCDMA网络中，调度算法是最重要的技术之一。
为了提高系统的带宽利用率和用户体验，TD-WCDMA引入了改进的调度算法。
该算法能够根据用户的业务需求、信道质量和系统负载等因素，灵活地对资源进行分配，从而提高了网络的性能。
2.高速数据传输技术TD-WCDMA制式支持高速数据传输，采用了多输入多输出（MIMO）技术和高阶调制（QAM）技术。
XANES谱及分析基础-陈栋梁
XANES谱分析实例
XAFS谱、XANES谱
XAFS谱:几个缩写名称
XAS： X-ray Absorption Spectroscopy XAFS ： X-ray Absorption Fine Structure EXAFS ：Extended X-ray Absorption Fine Structure XANES： X-ray Absorption Near Edge Structure NEXAFS ：Near Edge X-ray Absorption Fine Structure
XANES谱基本原理
/
原子的选择定则: LS耦合，单电子近似
定性判定：单原子
北 京同步辐射装置 Beijing Synchrotron Radiat 收 谱 学 实 验 和数据分析讲习班
/
/
/
XANES谱基本原理
北 京同步辐射装置 Beijing Synchrotron Radiation Facility
X射 线 吸 收 谱 学 实 验 和数据分析讲习班
定性判定：单原子/连续体
单原子：对于电偶极跃迁
K 边： 初态为1s (n=1，l=0，m=0)； LⅠ边：初态为2s (n=2，l=0，m=0)； LⅡ边：初态为2p1/2 (n=2，l=1，j=1/2)； LⅢ边：初态为2p3/2 (n=2，l=1，j=3/2)；
X射 线 吸 收 谱 学 实 验 和数据分析讲习班
试着：Cr2O3和Na2CrO4，Cr K-边XANES Cr:1s22s22p63s23p63d54s14p0
1s→ 连续态
1s→ 4p（(n+1)p）
DFT介绍
+ Local density
+ Density gradient
+ Inexplicit occupied orbital information
+ Explicit occupied orbital information
+Unoccupied orbital information
jacob's ladder
underestimates Ec but overestimates Ex, resulting in unexpectedly good values of Exc.
So we have:
Fermi and Amaldi1934(the first version of SIC)
固体能隙问题
准粒子方程
零级近似，plasmon-pole模型，自洽
TDKS方程
外场微扰
一阶密度响应响应函数
线性响应方程
交换相关核，绝热局域密度近似
轨道序：
et al.：惩罚泛函
单格点动力学Anderson杂质模型
量子电动力学的单粒子方程：Dirac Dirac-Coulomb（DC）哈密顿量
Dirac-Coulomb-Breit（DCB）哈密顿量
两分量准相对论方法
ECP）方法
冻声方法，分子动力学谱分析方法
赝势（PP）方法
USPP or PAW? (VASP, ABINIT, ...)
提高FD方法的计算效率
多分辨分析
semicardinal）基组
轨道最小化
优基组密度矩阵最小化。
tddft 分子吸收谱
TDDFT分子吸收谱
TDDFT（Time-Dependent Density Functional Theory）是一种用于描述分子系统中电子行为的量子力学方法。
TDDFT 计算可以得到分子的吸收光谱，这是一种描述分子吸收电磁辐射的能力的光谱。
TDDFT计算分子吸收光谱的基本思想是，在给定的分子几何构型下，通过计算体系的电子密度随时间的演化，得到分子吸收电磁辐射的能量转移过程。
具体而言，TDDFT计算可以给出分子的电子密度分布，以及这些密度分布如何随时间变化而引起电子能级的变化。
通过分析这些变化，可以得到分子的吸收光谱，其中吸收峰的位置和强度可以反映分子吸收电磁辐射的能力。
TDDFT计算分子吸收光谱的精度取决于计算所采用的模型和参数。
目前，常用的TDDFT计算方法包括LR-TDDFT 和rt-TDDFT。
其中，LR-TDDFT用于计算体系的静态性质，如波函数、能带等，而rt-TDDFT则用于计算体系的动力学性质，如光谱等。
此外，为了提高TDDFT计算的精度，还可以采用不同的模型和参数，如混合密度泛函、自旋轨道耦合等。
总的来说，TDDFT计算分子吸收光谱是一种非常有用的工具，可以帮助我们更深入地理解分子系统中的电子行为，
以及分子与外界相互作用的本质。
用TDDFT方法模拟氢原子、氢分子和氮分子高次谐波的产生的开题报告
用TDDFT方法模拟氢原子、氢分子和氮分子高次谐
波的产生的开题报告
高次谐波（High-order harmonic generation, HHG）是一种非线性光学现象，指一个原子或分子吸收高强度的激光脉冲后会发射高能量、高频率的紫外或软X射线光子，产生高次谐波频率的现象。
研究高次谐波对于理解分子和固体中的非线性光学性质以及激光精细控制等方面具有重要的理论和实际意义。
TDDFT（Time-dependent Density Functional Theory）方法可以用于模拟物质中的电子结构和光学性质，特别在非线性光学中应用广泛。
本开题报告将使用TDDFT方法模拟氢原子、氢分子和氮分子高次谐波的产生，以研究这些分子在高强度激光作用下的非线性光学响应。
首先，将使用DFT方法计算这些分子的基态结构和总能量，获得其电子密度分布和电子态密度的信息。
接着，将以实验中常用的高强度激光脉冲为输入，结合TDDFT方法模拟有限时间内的分子响应，得到分子的电子态随时间演化的情况，从而计算其高次谐波频率、幅度和相位等信息。
最后，将分析不同分子的高次谐波光谱，比较它们的谐波产生效率和分子结构的影响，揭示分子在高强度激光作用下的动力学机制和光学性质。
该研究将对理解分子非线性光学性质和高次谐波产生机制提供重要的原理和实践指导，对于激光技术的发展和实际应用都具有积极的促进作用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
四、线性响应：
自洽求解响应函数
五、Excitation Energies：
Ziegler, Rauk and Baerends in 1977 The procedure starts with the construction of many-particle states with good symmetry, Ψi, by taking a finite superposition of states：
同样，含时薛定谔方程不好计算，计算量也很大。 考虑将多体问题转化为单体k-s方程。
二、Runge-Gross Theorem
ˆ 定态下：E[] H
含时情况下，显然没有定态的总能量极小的变分， 定义quantum mechanical action ：
A[] dt (t ) i
Runge-Gross Theorem的证明：
目标：
若两个外势只差C(t)，则 uk (r ) 必为常数。 若两个外势的差值不止C(t)，那么有：
又
初态是固定的，所以：
作差之后：
当k=0时，即 v v c(r ) ，显然 (v v) 0，j j 当k>0时，再做k阶导数：
ˆ (1 ) D 1 1 2 2
E ( ) (1 ) E1 E2 n (r ) (1 )n1 (r ) n2 (r )
用 n (r) 作H-K定理然后用K-S方法计算。 注意单体轨道有分数占据态，由 决定。交换 关联能也与 有关。
N 1 N E2 E1
Exc ( ) |n n
Thanks for your listening
TDDFT简介
一、TDDFT
ˆ i (r , t ) H (r , t ) t
H (r , t ) T (r ) W (r ) Vext (r , t )
1 1 1 T ( r ) i 2 , W ( r ) 2 i 2 i j ri rj
t0 t1
ˆ (t ) H t
性质： 1、 A[ ] 中对 (t ) 做变分，可得到薛定谔方程。计算 A[ ] 的驻 点得到的 为薛定谔方程的解。 2、取 时 A[ ] 一直为0。 另外，含时薛定谔方程是初值问题，Runge-Gross Theorem是针对同一个初态来讨论的。
ˆ (t t , t t ) U ˆ 1 (t t , t t ) U 2 2
B式
ˆ (t t , t ) 和 (t t ) ，构建 H (t t ) 先用A式得到 U ˆ (t t , t t ) 。最后用B式得到最终的波函数 (t t ) j
下证：j j, n n
作k+1阶导数：
[n0 (r )uk (r )] 0, 所以有n n
三、含时薛定谔方程：
2 i i (r , t ) [ vKS (r , t )]i (r , t ) t 2
i ci , ＝ ａ ｊ ｊ
ｊ
ˆ ａ 2 E H ｊ j
j
1、建立 ˆ H 2、对 作K-S计算，得到 ˆ ａ 2 E H ｊ j 得到 E j 3、解
j
ensemble DFT： 对基态和激发态做一个混合：
V(r,t)较小时，用线性响应处理也是有效的。 V(r,t)较大时(例如强激光场)，就需要解含时薛定谔 方程。
VTD U en Vlaser
1 i 1
Nn
N
N Z Ef (t )sin wt ri ri R (t ) i 1
近似： 1、经典的激光场，不是量子化的光场。 2、dipole approximation， 波长远大于系统的大小。粒子在光场 周期内的运动距离远小于波长。 3、激光脉冲的时间短，相互作用时，分子不离开激光的范围。
2 n(r , t ) i (r , t ) 0
vKS vext (r , t ) vhartree (r , t ) vxc (r , t ) n(r , t ) vhartree (r , t ) d 3r r r
A xc vxc (r , t ) |n ( r ,t ) n( r , )
交换关联能依然是最大的问题。
xc [n] 用t时刻的n(t)的交换关联能，要 vxc (r, t ) v ALDA： 求系统时间依赖小，离平衡态不远。这个近似在强激 光下不好，还有在算离子势、电子离核远时 不准。
时间演化方案：
A式 Modified Crank–Nicholson Scheme: