异方差性及其检验
异方差定义及检验

4、帕克(Park)检验和戈里瑟(Glejser)检验
2 e x e i • Park检验的辅助模型为: i 2 • 求对数后为: ln(ei ) ln( ) ln xi
(4.1.2)
2 e • Glejser检验以 i 为被解释变量,以原模型的某一解释 变量 x j为解释变量,建立如下方程 :
ei f x ji i (4.1.3) • • f x j 可有多种函数形式。(利用试回归法,选择关于 变量的不同的函数形式,对方程进行估计并进行显著 性检验,如果存在某一种函数形式,使得方程显著成 立,则说明原模型存在异方差性。) • 可利用Eviews软件实现。
2
第二节 异方差的修正
方式2:在方程窗口中点击Estimate\Options\Weighted, 并在权数变量栏输入权数变量;
3)利用White检验判断是否消除了异方差性 权数变量的确定:依据Pack检验和Gleiser检验的结 果,或直接取成1/ei
精品课件!
作业四:
• 第五章3/4/6/8。
步骤:1)将解释变量的样本值按从小到大排序,再利用
ห้องสมุดไป่ตู้ • 检验统计量:
• F服从分布
2 1
n c k 1 2 RSS 2 2 F (4.1.1) 2 2 RSS1 RSS1 n c k 1 2
nc nc F (k 1), (k 1) 2 2
2.戈德菲尔德—匡特(Goldfeld—Quant)检验
原理:适合递增型的异方差,利用方差与解释变量同步增
长的原理,通过检验小方差与大方差是否有明显差异,达 到检验异方差的目的。 OLS求出估计值和残差序列 ei 2)在所有样本点中删去中间的c个点,将余下的点分为两组, 每组样本为 n c 2 个。 3)将两组样本分别作OLS,求得各自的残差平方和,再设计 统计量检验两组残差平方和是否有显著差异,若有,异方 差存在。
实验四异方差性的检验与处理

实验四异方差性的检验与处理集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]实验四 异方差性的检验及处理(2学时)一、实验目的(1)、掌握异方差检验的基本方法; (2)、掌握异方差的处理方法。
二、实验学时:2学时 三、实验要求(1)掌握用MATLAB 软件实现异方差的检验和处理; (2)掌握异方差的检验和处理的基本步骤。
四、实验原理1、异方差检验的常用方法(1) 用X-Y 的散点图进行判断(2). 22ˆ(,)(,)e x e y 或的图形 ,),x )i i y i i ((e 或(e 的图形)(3) 等级相关系数法(又称Spearman 检验)是一种应用较广的方法,既可以用于大样本,也可与小样本。
检验的三个步骤 ① ˆt t y y=-i e②|i x i i 将e 取绝对值,并把|e 和按递增或递减次序排序,计算Spearman 系数rs ,其中:21ni i d =∑s 26r =1-n(n -1)③ 做等级相关系数的显着性检验。
n>8时,/2(2),t t n α>-反之,若||i i e x 说明与之间存在系统关系,异方差问题存在。
(4) 帕克(Park)检验帕克检验常用的函数形式:若在统计上是显着的,表明存在异方差性。
2、异方差性的处理方法: 加权最小二乘法 如果在检验过程中已经知道:222()()()i i i ji u Var u E u f x σσ===则将原模型变形为:121(i i p pi iy x x uf xβββ=+⋅++⋅+在该模型中:即满足同方差性。
于是可以用OLS估计其参数,得到关于参数12,,,pβββ的无偏、有效估计量。
五、实验举例例101i i iy x u=++若用线性模型,研究不同收入家庭的消费情况,试问原数据有无异方差性如果存在异方差性,应如何处理解:(一)编写程序如下:(1)等级相关系数法(详见文件)%%%%%%%%%%%%%%% 用等级相关系数法来检验异方差性 %%%%%%%%[data,head]=xlsread('');x=data(:,1); %提取第一列数据,即可支配收入xy=data(:,2); %提取第二列数据,即居民消费支出yplot(x,y,'k.'); % 画x和y的散点图xlabel('可支配收入x(千元)') % 对x轴加标签ylabel('居民消费支出y(千元)') % 对y轴加标签%%%%%%%% 调用regres函数进行一元线性回归 %%%%%%%%%%%%xdata=[ones(size(x,1),1),x]; %在x矩阵最左边加一列1,为线性回归做准备[b,bint,r,rint,s]=regress(y,xdata);yhat=xdata*b; %计算估计值y% 定义元胞数组,以元胞数组形式显示系数的估计值和估计值的95%置信区间head1={'系数的估计值','估计值的95%置信下限','估计值的95%置信上限'};[head1;num2cell([b,bint])]% 定义元胞数组,以元胞数组形式显示y的真实值,y的估计值,残差和残差的95%置信区间head2={'y的真实值','y的估计值','残差','残差的95%置信下限','残差的95%置信上限'};[head2;num2cell([y,yhat,r,rint])]% 定义元胞数组,以元胞数组形式显示判定系数,F统计量的观测值,检验的P值和误差方差的估计值head3={'判定系数','F统计量的观测值','检验的P值','误差方差的估计值'};[head3;num2cell(s)]%%%%%%%%%%%%% 残差分析 %%%%%%%%%%%%%%%%%%figure;rcoplot(r,rint) % 按顺序画出各组观测值对应的残差和残差的置信区间%%% 画估计值yhat与残差r的散点图figure;plot(yhat,r,'k.') % 画散点图xlabel('估计值yhat') % 对x轴加标签ylabel('残差r') % 对y轴加标签%%%%%%%%%%%% 调用corr函数计算皮尔曼等级相关系数res=abs(r); % 对残差r取绝对值[rs,p]=corr(x,res,'type','spearman')disp('其中rs为皮尔曼等级相关系数,p为p值');(2)帕克(park)检验法(详见文件)%%%%%%%%%%%%%%% 用帕克(park)检验法来检验异方差性 %%%%%%%[data,head]=xlsread(''); %导入数据x=data(:,1);y=data(:,2);%%%%%% 调用regstats函数进行一元线性回归,linear表带有常数项的线性模型,r表残差ST=regstats(y,x,'linear',{'yhat','r','standres'});scatter(x,.^2) % 画x与残差平方的散点图xlabel('可支配收入(x)') % 对x轴加标签ylabel('残差的平方') %对y轴加标签%%%%%%% 对原数据x和残差平方r^2取对数,并对log(x)和log(r^2)进行一元线性回归ST1=regstats(log(.^2),log(x),'linear',{'r','beta','tstat','fstat'})% 输出参数的估计值% 输出回归系数t检验的P值% 输出回归模型显着性检验的P值(3)加权最小二乘法(详见文件)%%%%%%%%%%% 调用robustfit函数作稳健回归 %%%%%%%%%%%%[data,head]=xlsread(''); % 导入数据x=data(:,1);y=data(:,2);% 调用robustfit函数作稳健回归,返回系数的估计值b和相关统计量stats[b,stats]=robustfit(x,y) %调用函数作稳健回归% 输出模型检验的P值%%% 绘制残差和权重的散点图 %%%%%%%plot,,'o') %绘制残差和权重的散点图xlabel('残差')ylabel('权重'(二)实验结果与分析:第一步::用OLS方法估计参数,并保留残差(1)散点图图可支配收入(x)居民消费支出(y)散点图因每个可支配收入x的值,都有5个居民消费收入y与之对应,所以上述散点图呈现此形状。
第五章 异方差性

26
异方差性的检验
问题在于用什么来表示随机误差项的方差 一般的处理方法:
Var(ui ) E(uቤተ መጻሕፍቲ ባይዱ2) ei2
图示检验法
图示检验法
(一)相关图形分析 方差描述的是随机变量取值的(与其均值的)离散程度。因为被解释
变量Y与随机误差项u有相同的方差,所以分析Y与X的相关图,可以初 略地看到Y的离散程度与X之间是否有相关关系。
ui 的某些分布特征,可通过残差 ei 的图形对异方差进行观察。
对于一元回归模型,绘制出ei2 对Xi的散点图,对于多元回归模型,绘制出ei2 对Yi的散点图或ei2 与认为和异方差有关的X的散点图。
31
图示检验法
(二)残差图形分析
e~i 2
e~i 2
X 同方差
e~i 2
X 递增异方差
e~i 2
X 递减异方差
每个企业所处的外部环境对产出量的影响被包含在随机误差项中 每个企业所处的外部环境对产出量的影响程度不同,造成了随机
误差项的异方差性
产生异方差性的原因
产生异方差性的原因
(一)模型设定误差
假设正确的模型是:
Yi 1 2 X2i 3 X3i ui
假如略去了重要的解释变量X3 ,而采用 Yi 1 2 X2i vi
排序,再按戈德菲尔德匡特检验方法回归,否则即使存在异方差,也有可能用戈德菲
尔德匡特方法检验不出来。
用 EViews 给截面数据排序的方法:在 Workfile 窗口点击 Procs 键并选 Sort current page
功能,在打开的 Sort Workfile Series 对话窗填写以哪一个序列为标准(基准序列)排
异方差性的检验及处理方法

异方差性的检验及处理方法异方差性是指随着自变量变化,因变量的方差不保持恒定,即方差存在不均匀的变化趋势。
在统计分析中,如果忽视了异方差性,可能会导致误差的不准确估计,从而影响对因变量的显著性检验和参数估计结果的准确性。
为了避免异方差性给统计分析带来的影响,需要进行异方差性的检验和处理。
下面将介绍几种常用的异方差性检验及处理方法。
一、异方差性的检验方法:1.绘制残差图:绘制因变量的残差(观测值与拟合值之差)与自变量的散点图,观察残差是否随着自变量的变化而存在明显的模式。
如果残差图呈现出锥形或漏斗形状,则表明存在异方差性。
2.帕金森检验:帕金森检验是一种常用的检验异方差性的方法。
该方法的原理是通过对残差进行变换,判断变换后的残差是否与自变量相关。
3. 布罗斯-佩根检验(Breusch-Pagan test):布罗斯-佩根检验是一种常用的检验异方差性的方法。
该方法的原理是通过计算残差与自变量的相关系数,进而判断是否存在异方差性。
4. 品尼曼检验(Leve ne’s test):品尼曼检验是一种非参数的检验方法,可以用于检验不同组别的方差是否存在显著差异。
二、异方差性的处理方法:1.变量转换:通过对因变量和自变量进行变换,可以使数据满足异方差性的假设。
比如可以对因变量进行对数转换或平方根转换,对自变量进行标准化处理等。
2.使用加权最小二乘法(WLS):加权最小二乘法是一种可以处理异方差性的回归分析方法。
该方法的原理是通过对残差进行加权,使得残差的方差与自变量无关。
3.使用广义最小二乘法(GLS):广义最小二乘法是一种可以处理异方差性的回归分析方法。
该方法的原理是通过对残差进行加权,使得残差的方差可以通过自变量的一个线性组合来估计。
4.进行异方差性的鲁棒估计:鲁棒估计是一种对异常值和异方差性具有较好鲁棒性的估计方法。
通过使用鲁棒估计,可以减少异方差性对参数估计的影响。
综上所述,异方差性是统计分析中需要重视的问题。
异方差性的概念、类型、后果、检验及其修正方法含案例

Yi和Xi分别为第i个家庭的储蓄额和可支配收入。
在该模型中,i的同方差假定往往不符合实际情况。对高收 入家庭来说,储蓄的差异较大;低收入家庭的储蓄则更有规律 性(如为某一特定目的而储蓄),差异较小。
因此,i的方差往往随Xi的增加而增加,呈单调递增型变化 。
– 在选项中,EViews提供了包含交叉项的怀特检验“White Heteroskedasticity(cross terms)”和没有交叉项的怀特检 验“White Heteroskedasticity(no cross terms)” 这样两个 选择。
• 软件输出结果:最上方显示两个检验统计量:F统计 量和White统计量nR2;下方则显示以OLS的残差平 方为被解释变量的辅助回归方程的回归结果。
随机误差项具有不同的方差,那么: 检验异方差性,也就是检验随机误差项的方差与解
释变量观测值之间的相关性及其相关的“形式”。 • 各种检验方法正是在这个共同思路下发展起来的。
路漫漫其修远兮, 吾将上下而求索
问题在于:用什么来表示随机误差项的方差? 一般的处理方法:
路漫漫其修远兮, 吾将上下而求索
2.图示检验法
路漫漫其修远兮, 吾将上下而求索
3.模型的预测失效
一方面,由于上述后果,使得模型不具有良好的统计性质;
【书上这句话有点问题】
其中 所以,当模型出现异方差性时,Y预测区间的建立将发生困 难,它的预测功能失效。
路漫漫其修远兮, 吾将上下而求索
三、异方差性的检验(教材P111)
1.检验方法的共同思路 • 既然异方差性就是相对于不同的解释变量观测值,
(注意:其中的2完全可以是1)
第二节 异方差性检验

3.计算 利用求回归估计式得到辅助回归函数的可决系 数 nR2 , n 为样本容量。 4.提出假设 H0 : 2 = ...= 6 = 0, H1 : (j= 2,,3,...,6)不全为零 j
et a0 a1 xt h vt 步骤:
h 1, 2, 1 , 2
1、应用OLS估计回归模型并求残差e t ; 2、分别建立 et 对每个解释变量的各种回归方程; 3、检验每个回归方程参数1的显著性,如果参数1显著不为零, 则随机项存在异方差,反之,随机项具有等方差性。 帕克提出如下假定函数形式: et2 a0 xa1 e vt t 即lnet2 a 0 a1lnx t v t
之间是否有相关关系。 X
如果随着 X 的增加, 的离散程度为逐渐增大(或 Y 减小)的变化趋势,则认为存在递增型(或递减型)的 异方差。
(二)残差图形分析 设一元线性回归模型为:
Yi β1 β2 X i ui
运用OLS法估计,得样本回归模型为:
ˆ ˆ ˆ Yi = β1 + β2 X i
其中vt 为随机误差项。
2 σt2 = α1 +α2 X 2t +α3 X 3t +α4 X 2t +α5 X 32t +α6 X 2t X 3t +vt
1.求回归估计式并计算 ˆ 用OLS估计线性回归模型,计算残差 et Yt - Yt ,并求残差 的平方 et2 。
2.求辅助函数 et2 作为异方差 σ t2 的估计,并建立 用残差平方 2 的辅助回归,即 X 2t , X 3t , X 2t , X 32t , X 2t X 3t
异方差实验报告步骤(3篇)

第1篇一、实验目的1. 掌握异方差性的基本概念和检验方法。
2. 学会运用统计软件进行异方差的检验和修正。
3. 提高对计量经济学模型中异方差性处理能力的实践应用。
二、实验原理1. 异方差性:在回归分析中,若回归模型的误差项(残差)的方差随着自变量或因变量的取值而变化,则称模型存在异方差性。
2. 异方差性的检验方法:图形检验、统计检验(如F检验、Breusch-Pagan检验、White检验等)。
3. 异方差性的修正方法:加权最小二乘法(WLS)、广义最小二乘法(GLS)等。
三、实验步骤1. 数据准备1. 收集实验所需数据,确保数据质量和完整性。
2. 对数据进行初步处理,如剔除异常值、缺失值等。
2. 模型设定1. 根据研究问题,选择合适的回归模型。
2. 利用统计软件(如Eviews、Stata等)进行初步的回归分析。
3. 异方差性检验1. 图形检验:绘制散点图,观察残差与自变量或因变量的关系,初步判断是否存在异方差性。
2. 统计检验:- F检验:检验回归系数的显著性。
- Breusch-Pagan检验:检验残差平方和与自变量或因变量的关系。
- White检验:检验残差平方和与自变量或因变量的多项式关系。
4. 异方差性修正1. 若检验结果表明存在异方差性,则需对模型进行修正。
2. 选择合适的修正方法:- 加权最小二乘法(WLS):根据残差平方与自变量或因变量的关系,计算权重,加权最小二乘法进行回归分析。
- 广义最小二乘法(GLS):根据残差平方与自变量或因变量的关系,选择合适的方差结构,广义最小二乘法进行回归分析。
5. 结果分析1. 对修正后的模型进行回归分析,观察回归系数的显著性、拟合优度等指标。
2. 对实验结果进行分析,解释实验现象,验证研究假设。
6. 实验报告撰写1. 撰写实验报告,包括以下内容:- 实验目的- 实验原理- 实验步骤- 实验结果- 分析与讨论- 结论2. 实验报告应结构清晰、逻辑严谨、语言简洁。
异方差性的检验及处理方法
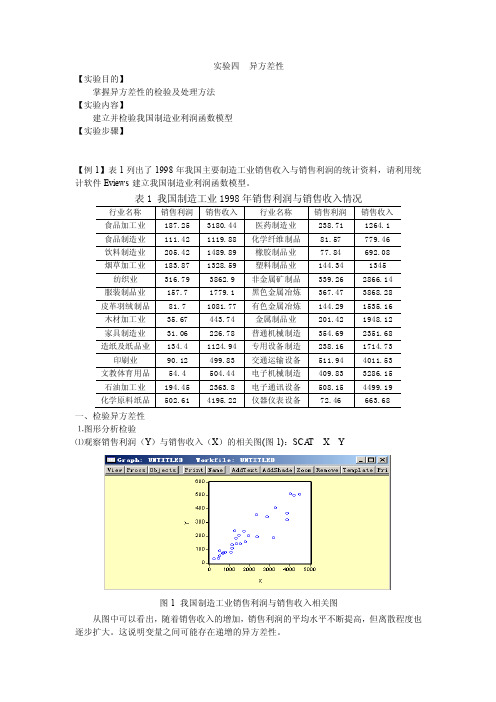
实验四异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
一、检验异方差性⒈图形分析检验⑴观察销售利润(Y)与销售收入(X)的相关图(图1):SCA T X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
在方程窗口中点击Resids按钮就可以得到模型的残差分布图(或建立方程后在Eviews工作文件窗口中点击resid对象来观察)。
图2 我国制造业销售利润回归模型残差分布图2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
⒉Goldfeld-Quant检验⑴将样本按解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)⑵利用样本1建立回归模型1(回归结果如图3),其残差平方和为2579.587。
SMPL 1 10LS Y C X图3 样本1回归结果⑶利用样本2建立回归模型2(回归结果如图4),其残差平方和为63769.67。
SMPL 19 28LS Y C X图4 样本2回归结果⑷计算F 统计量:12/RSS RSS F ==63769.67/2579.59=24.72,21RSS RSS 和分别是模型1和模型2的残差平方和。
取05.0=α时,查F 分布表得44.3)1110,1110(05.0=----F ,而44.372.2405.0=>=F F ,所以存在异方差性⒊White 检验⑴建立回归模型:LS Y C X ,回归结果如图5。
图5 我国制造业销售利润回归模型⑵在方程窗口上点击View\Residual\Test\White Heteroskedastcity,检验结果如图6。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
异方差性及其检验
I 概念
对于多元线性回归模型
同方差性假设为 如果出现
即对于不同的样本点,随机干扰项的方差不再是常数,而是互不相同,不具有等同的分散程度,则认为出现了异方差(Heteroskedasticity ) II 类型
同方差性假定是指,回归模型中不可观察的随机误差项i u 以解释变量X 为条件的方差是一个常数,因此每个i u 的条件方差不随X 的变化而变化,即有
2()i i f X σ=≠常数
在异方差的情况下,总体中的随机误差项i u 的方差 2
i σ不再是常数,
通常它随解释变量值的变化而变化,即
异方差一般可归结为三种类型:
01122 1,2,
,i i i k ki i Y X X X i n ββββμ=+++
++=2(), 1,2,...,i Var i n μσ==2(), 1,2,...,i i Var i n
μσ==2()
i i f X σ=
异方差类型图:
III来源
(1)截面数据(不同样本点除解释变量外其他影响差异大)
(2)时间序列(规模差异)
(3)分组数据、异常值等
(4)模型函数形式设置不正确和数据变形不正确
(5)边错边改学习模型
IV影响
计量经济学模型一旦出现异方差,如果仍然用普通最小二乘法估计模型参数,会产生一系列不良后果。
(1)参数估计量非有效
(2)OLS估计的随机干扰项的方差不再是无偏的
(3)基于OLS估计的各种统计检验非有效
(4)模型的预测失效
V检验
异方差性,即相对于不同的样本点,也就是相对于不同的解释变量观测值,随机干扰项具有不同的方差,那么检验异方差性,也就是检验随机干扰项的方差与解释变量观测值之间的相关性。
一般检验方法如下:
(1)图示检验法
(2)帕克(Park)检验与戈里瑟(Gleiser)检验
(3)G-Q(Goldfeld-Quandt)检验
(4)F检验
(5)拉格朗日乘子检验
(6)怀特检验
(具体步骤随后介绍)
VI修正方法
加权最小二乘法
定义:加权最小二乘法是对原模型加权,使之变成一个新的不存在异方差性的模型,然后采用OLS法估计其参数。
基本思想:在采用OLS方法时,对较小的残差平方2ˆ
e赋予较大的权
i
重,对较大的2ˆ
e赋予较小的权重,以对残差提供的信息的重要程度
i
作一番修正,提高参数估计的精确程度。
不同形式的异方差要求用不同的加权方法来处理:
(一) 异方差为已知的解释变量的某一函数形式时的加权最小二乘
估计
(二)异方差形式未知时的估计—可行的加权最小二乘法
一般情况下,异方差形式是未知的,往往直接运用模型估计后的残差项来确定权重,对模型进行修正,即权重为:
i
i e 1w =
检验方法总结
1.图示检验法
2.Goldfeld - Quandt 检验法
基本步骤
(1)将解释变量排序,从中间去掉/4c n =个观测值
(2)分成两个部分,利用样本1 和样本2 分别建立回归模型 (3)根据回归求出各自残差平方和1RSS 和2RSS (4)在同方差假定下,构造F 统计量:
22
11
//RSS v F RSS v =
与21(,)F v v 进行比较
21(,)F F v v ≥,拒绝同方差假设 21(,)F F v v ≤,接受原假设
适用范围:大样本,递增或递减型异方差 注意:(1)该检验的功效取决于c 值,c 值越大,则大小方差的差异越大,检验功效越好
(2)两个回归所用的观测值的个数是否相等并不重要,因为可以通过公式改变自由度和统计量的计算公式来调整
(3)当模型中包含多个解释变量时,应对每个可能引起方差的解释变量都进行检验
3.Park 或Glesjser 检验
基本步骤:
(1) 对原模型进行OLS 回归,得到残差i e
(2) 以i e 或2i e 为解释变量,以原模型中的某一解释变量为解释
变量,建立两者之间的回归方程:
2()i ji i e f X ε==或者 ()i ji i e f X ε=+
(3) 选择j X 的不同函数形式,对方程进行估计并进行显著性检验。
若存在某种函数形式使方程显著成立,则说明原模型中存在异方差
适用范围:各种类型异方差检验 注意:(1)由于方差形式未知,因此需要进行各种测试
(2)该方法不仅检验出了异方差是否存在,同时给出异方差具体形式
4.White检验
基本步骤:
(1)对原模型进行OLS回归,得到残差
e
i
(2)以2
e为被解释变量,以各种解释变量、个解释变量的平方项、
i
解释变量之间两两交叉项为解释变量建立辅助回归方程,并
估计
(3)根据辅助回归方程估计结果构造并计算统计量2
nR,它服从2
分布(自由度为辅助回归式中解释变量个数)
(4)根据临界值判断,若大于临界值,拒绝同方差假定;小于临界值,则接受同方差假定
适用范围:各种类型异方差检验
注意:(1)辅助回归中可引入解释变量的更高次幂
(2)在多元回归中,由于解释变量个数太多,可去掉辅助回归式中解释变量间的交叉项
附:Eviews实际操作
异方差性检验及存在异方差模型估计
检验使用方法:(1)G-Q检验(2)White 检验
模型估计方法:加权最小二乘法(WLS)
下表为2000年中国部分省市城镇居民每个家庭平均年可支配收入(X)与消费性支出(Y)的统计数据:
一、利用Eviews求出线性模型
可得模型:
ˆ272.2250.755
i i
Y X
=+
(1.705) (32.394) R2=0.9832
二、异方差检验
(1)G-Q检验:首先将可支配收入X升序进行排列,然后去掉中间4个样本,将余下的样本分为容量各为8的两个子样本,并分别进行回归。
大样本小样本样本取值较小的Eviews输出结果如下
残差平方和:RSS1=126528.3
样本取值较大的Eviews输出结果如下:
残差平方和:RSS 2=615073.7
因此统计量为: 2
1
4.8611RSS F RSS ==
在5%的显著性水平下,
0.05(6,6) 4.28F =,4.86>4.28,因此拒绝原假设,存在异方差性。
(2)White 检验:在原模型的最小二乘估计窗口上选择“View\Residual Tests\Heteroskedasticity Tests\White ”得到如下结果:
检验统计量值为12.64768,查询2
0.05(2) 5.99x =,因
此12.6478>5.99,因而拒绝原假设,模型存在异方差。
三、估计存在异方差的经济模型
利用加权最小二乘法(WLS )进行估计:首先在对原模型进行估计后,保存残差,步骤如下:①Quick\Generate Series 再输入“e1=resid ”,得到e1
②Quick\Estimte Equation 再输入“Y C X ” ③选择Options,在“Weighted LS/TLS ”输入“1/abs(e1)”(备注:abs 表示绝对值
)
附:Eviews 实际操作
11
醉客天涯之异方差 得到如下结果;
即采用加权最小二乘估计得到的回归方程: ˆ415.480.7290i i Y X =+
(3.55) (32.50)R 2=0.98 加权结果与不加权结果差别很大。
