(最新整理)2018高考文科数学模拟题1
2018年普通高等学校招生全国统一考试文科数学模拟试题及答案

2018年普通高等学校招生全国统一考试文科数学模拟注意事项:1、答题前,考生务必将自己的姓名、准考证号填写在答题卡上。
2、回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:共12小题,每小题5分,共60分.在每个小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2340A x x x =∈--≤Z ,{}0ln 2B x x =<<,则A B =()A .{}1,2,3,4B .{}3,4C .{}2,3,4D .{}1,0,1,2,3,4-【答案】C【解析】{}{}{}2340141,0,1,2,3,4A x x x x x =∈--≤=∈-≤≤=-Z Z ,{}{}20ln 21e B x x x x =<<=<<,所以{}2,3,4AB =.2.设复数1z =(i 是虚数单位),则z z+的值为()A.B .2C .1D.【答案】B【解析】2z z +=,2z z +=.3.“p q ∧为假”是“p q ∨为假”的()条件.A .充分不必要B .必要不充分C .充要D .既不充分也不必要 【答案】B【解析】由“p q ∧为假”得出p ,q 中至少一个为假.当p ,q 为一假一真时,p q ∨为真,故不充分;当“p q ∨为假”时,p ,q 同时为假,所以p q ∧为假,所以是必要的,所以选B .4.已知实数x ,y 满足约束条件222020x x y x y ≤⎧⎪-+≥⎨⎪++≥⎩,则3x z y =-+的最大值为()A .143- B .2- C .43 D .4【答案】C【解析】作出的可行域为三角形(包括边界),把3x z y =-+改写为3xy z =+,当且仅当动直线3x y z =+过点()2,2时,z 取得最大值为43. 5.据有关文献记载:我国古代一座9层塔共挂了126盏灯,且相邻两层中的下一层灯数比上一层灯数都多n (n 为常数)盏,底层的灯数是顶层的13倍,则塔的底层共有灯()盏. A .2 B .3 C .26 D .27 【答案】C【解析】设顶层有灯1a 盏,底层共有9a 盏,由已知得,则()91991132691262a a a a a =⎧⎪⇒=⎨+=⎪⎩, 所以选C .6.如图是一个算法流程图,若输入n 的值是13,输出S 的值是46,则a 的值可以是() A .8 B .9 C .10 D .11【答案】C 【解析】依次运行流程图,结果如下:13S =,12n =;25S =,11n =;36S =,10n =;46S =,9n =,此时退出循环,所以a 的值可以取10.故选C .7.设双曲线()2222:10,0x y C a b a b-=>>的两条渐近线互相垂直,顶点到一条渐近线的距离为1,则双曲线的一个焦点到一条渐近线的距离为() A .2BC.D .4【答案】B【解析】因为双曲线2222:1x y C a b-=的两条渐近线互相垂直,所以渐近线方程为y x =±,所以a b =.因为顶点到一条渐近线的距离为1,所以12a =,所以a b ==,双曲线C 的方程为22122x y -=,所以双曲线的一个焦点到一条渐近线的距离为b =8.已知数据1x ,2x ,,10x ,2的平均值为2,方差为1,则数据1x ,2x ,,10x 相对于原数据() A .一样稳定 B .变得比较稳定 C .变得比较不稳定 D .稳定性不可以判断 【答案】C【解析】因为数据1x ,2x ,,10x ,2的平均值为2,所以数据1x ,2x ,,10x 的平均值也为2,因为数据1x ,2x ,,10x ,2的方差为1,所以()()102211222111i i x =⎡⎤-+-=⎢⎥⎣⎦∑,所以()10212=11i i x =-∑,所以数据1x ,2x ,,10x 的方差为()102112=1.110i i x =-∑,因为1.11>,所以数据1x ,2x ,,10x 相对于原数据变得比较不稳定.9.设n a 表示正整数n 的所有因数中最大的奇数与最小的奇数的等差中项,数列{}n a 的前n 项和为n S ,那么21n S -=()A .122n n +-- B .11222433n n --+⋅- C .2nn - D .22nn +-【答案】B【解析】由已知得,当n 为偶数时,2n n a a =,当n 为奇数时,12n na +=. 因为12342121n n S a a a a a --=+++++,所以1112342121n n S a a a a a ++--=+++++()()111352462122+n n a a a a a a a a ++--=++++++++()1123211113151212222n n a a a a +-⎛⎫++++-=+++++++++ ⎪⎝⎭()()123211232n n a a a a -=+++++++++()211222n nnS -+=+()211242n nn S -=++, 即()121211242n n n n S S +--=++,所以()()()1112211112121111224242422422233n n n n n n nS S --------=+++++++=+⋅-.10.过抛物线2y mx =()0m >的焦点作直线交抛物线于P ,Q 两点,若线段PQ 中点的横坐标为3,54PQ m =,则m =() A .4B .6C .8D .10【答案】C【解析】因为2y mx =,所以焦点到准线的距离2mp =,设P ,Q 的横坐标分别是1x ,2x ,则1232x x +=,126x x +=,因为54PQ m =,所以125+4x x p m +=,即5624m m +=,解得8m =.11.已知一个三棱锥的三视图如图所示,其中三视图的长、宽、高分别为2,1,12,则此三棱锥外接球的表面积为()A .174π B .214π C .4π D .5π【答案】B【解析】由已知条件及三视图得,此三棱锥的四个顶点位于长方体1111ABCD A BC D -的四个顶点,即为三棱锥11A CB D -,且长方体1111ABCD A BC D -的长、宽、高分别为2,1,12, 所以此三棱锥的外接球即为长方体1111ABCD A BC D -的外接球,半径4R ==,所以三棱锥外接球的表面积为22214444S R ⎛π=π=π= ⎝⎭.12.已知点P 是曲线sin ln y x x =+上任意一点,记直线OP (O 为坐标系原点)的斜率为k ,则下列一定成立的为() A .1k <- B .0k < C .1k < D .1k ≥ 【答案】C【解析】任意取x 为一正实数,一方面sin ln ln 1y x x x =+≤+,另一方面容易证ln 1x x +≤成立,所以sin ln y x x x =+≤,因为sin ln ln 1y x x x =+≤+与ln 1x x +≤中两个等号成立条件不一样,所以sin ln y x x x =+<恒成立,所以1k <,所以排除D ;当2x π≤<π时,sin ln 0y x x =+>,所以0k >,所以排除A ,B .所以选C .第Ⅱ卷本卷包括必考题和选考题两部分。
2018年普通高等学校招生全国统一考试仿真卷 文科数学(一)解析版

绝密 ★ 启用前2018年普通高等学校招生全国统一考试仿真卷文科数学(一)本试题卷共14页,23题(含选考题)。
全卷满分150分。
考试用时120分钟。
★祝考试顺利★注意事项:1、答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型A 后的方框涂黑。
2、选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3、填空题和解答题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4、选考题的作答:先把所选题目的题号在答题卡上指定的位置用2B 铅笔涂黑。
答案写在答题卡上对应的答题区域内,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
5、考试结束后,请将本试题卷和答题卡一并上交。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
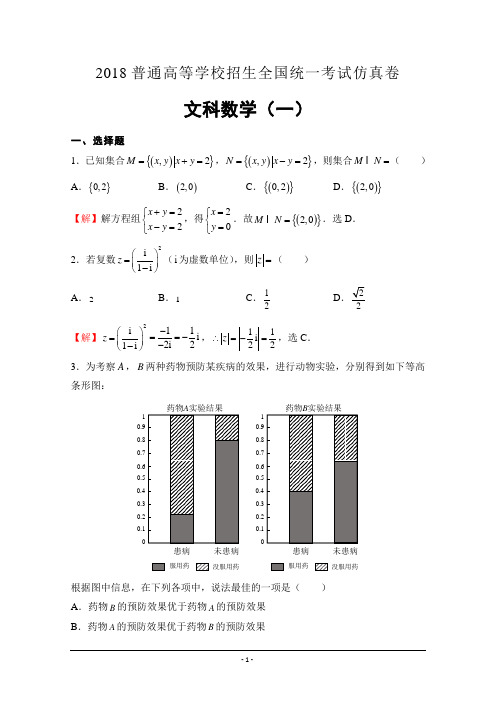
1.[2018·晋城一模]已知集合(){},2M x y x y =+=,(){},2N x y x y =-=,则集合MN =( )A .{}0,2B .()2,0C .(){}0,2D .(){}2,0【答案】D【解析】解方程组22x y x y +=-=⎧⎨⎩,得2x y =⎧⎨=⎩.故(){}2,0MN =.选D .2.[2018·台州期末](i 为虚数单位)) A .2 B .1C .12D【答案】C11i 22z ∴=-=,选C . 3.[2018·南宁二中]为考察A ,B 两种药物预防某疾病的效果,进行动物实验,分别得到如下等高条形图:根据图中信息,在下列各项中,说法最佳的一项是( ) A .药物B 的预防效果优于药物A 的预防效果 B .药物A 的预防效果优于药物B 的预防效果C .药物A 、B 对该疾病均有显著的预防效果D .药物A 、B 对该疾病均没有预防效果 【答案】B【解析】由A 、B 两种药物预防某疾病的效果,进行动物试验,分别得到的等高条形图,知:药物A 的预防效果优于药物B 的预防效果.故选B .4.[2018·滁州期末])A .4-B .4C.13- D .13【答案】C【解析】sin 2costan 2ααα-=-⇒=,C .5.[2018·陕西一模]《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”.已药物A 实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91药物B实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91班级 姓名 准考证号 考场号 座位号此卷只装订不密封知某“堑堵”的三视图如图所示,俯视图中间的实线平分矩形的面积,则该“堑堵”的侧面积为( )A .2 B.4+C.4+D.4+【答案】C【解析】根据题意和三视图知几何体是一个放倒的直三棱柱,底面是一个直角三角形,2,且侧棱与底面垂直,侧棱长是2,∴几何体的侧面积C .6.[2018·滁州期末]设变量x ,y 满足约束条件220220 2x y x y y +--+⎧⎪⎨⎪⎩≥≤≤,则目标函数z x y =+的最大值为( ) A .7 B .6C .5D .4【答案】D【解析】画出不等式组表示的可行域(如图阴影部分所示).由z x y =+,得y x z =-+.平移直线y x z =-+,结合图形可得,当直线(图中的虚线)经过可行域内的点A 时,直线在y 轴上的截距最大,此时z 取得最大值.由2 220y x y =-+=⎧⎨⎩,解得22x y ==⎧⎨⎩,故点A 的坐标为(2,2).∴max 224z =+=,即目标函数z x y =+的最大值为4.选D .7.[2018·蚌埠一模]已知()201720162018201721f x x x x =++++,下列程序框图设计的是求()0f x 的值,在“ ”中应填的执行语句是( )A .2018n i =-B .2017n i =-C .2018n i =+D .2017n i =+【答案】A【解析】不妨设01x =,要计算()120182017201621f =+++++,首先201812018S =⨯=,下一个应该加2017,再接着是加2016,故应填2018n i =-. 8.[2018·达州期末]若函数()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则a 的取值范围为( ) A .()0,4 B .()0,+∞C .()3,4D .()3,+∞【答案】C【解析】如图,若()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则()34a ∈,,故选C .9.[2018·朝阳期末]阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数k (0k >且1k ≠)的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A ,B 间的距离为2,动点P 与A ,B P ,A ,B 不共线时,PAB △面积的最大值是( )A .BC .3D .3【答案】A开始i =1,n =2018结束i ≤2017?是否输入x 0S =2018输出SS =Sx 0S =S+ni =i +1【解析】如图,以经过A ,B 的直线为x 轴,线段AB 的垂直平分线为y 轴,建立直角坐标系;则:()10A -,,()10B ,,设()P x y ,,PA PB=,两边平方并整理得:()222261038x y x x y +-+=⇒-+=.∴PAB △面积的最大值是122⨯⨯=A .10.[2018·孝感八校]已知双曲线E :22221x y a b-=(0,0)a b >>的右顶点为A ,右焦点为F ,B 为双曲线在第二象限上的一点,B 关于坐标原点O 的对称点为C ,直线CA 与直线BF的交点M 恰好为线段BF 的中点,则双曲线的离心率为( )A .12B .15C .2D .3【答案】D【解析】不妨设2,b B c a ⎛⎫- ⎪⎝⎭,由此可得(),0A a ,2,b C c a ⎛⎫- ⎪⎝⎭,(),0F c ,20,2b M a ⎛⎫ ⎪⎝⎭,由于A ,C ,M 三点共线,故222b b a a a a c=--,化简得3c a =,故离心率3e =.11.[2018·昆明一中]设锐角ABC △的三个内角A ,B ,C 的对边分别为a ,b ,c ,且1c =,2A C =,则ABC △周长的取值范围为( )A.(0,2 B.(0,3C .(2++ D .(2+【答案】C【解析】因为ABC △为锐角三角形,cos C <<2A C =, 所以sin 2sin cos A C C =,又因为1c =,所以2cos a C =;由sin sin b cB C=, 即2sin sin34cos 1sin sin c B Cb C C C===-,所以24cos 2cos a b c C C ++=+,令cos t C=, 则(,22t ∈⎭,又因为函数242y tt =+在( ,22⎭上单调递增,所以函数值域为(2+,故选:C .12.[2018·菏泽期末]()2f x mx =+有一个零点,则实数m 的取值范围是( ) A ]{64-+B ]{0,64-+C ]{}632-D ]{0,63-【答案】B【解析】由题意函数()f x 的图象与直线2y mx =+有一个交点.如图是()f x 的图象,1x >时,()21f x x =-,,设切点为()00,x y ,则切线为()()02002211y x x x x -=----,把()0,2代入,02x =;1x ≤时,()2e x f x =-,()e x f x '=-,设切点为()00,x y ,则切线为()()002e e x x y x x --=--,把()0,2代入,解得01x =,又()12e f =-,()11e e f '=-=-,所以由图象知当]{0,42-B .第Ⅱ卷本卷包括必考题和选考题两部分。
2018普通高等学校招生全国统一考试仿真卷文科数学一
2018普通高等学校招生全国统一考试仿真卷文科数学(一)一、选择题1.已知集合(){},2M x y x y =+=,(){},2N x y x y =-=,则集合M N =( )A .{}0,2B .()2,0C .(){}0,2D .(){}2,0【解】解方程组22x y x y +=-=⎧⎨⎩,得20x y =⎧⎨=⎩.故(){}2,0MN =.选D .2(i 为虚数单位)) A .2B .1C .12D11i 22z ∴=-=,选C . 3.为考察A ,B 两种药物预防某疾病的效果,进行动物实验,分别得到如下等高条形图:药物A实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91药物B 实验结果患病未患病服用药没服用药0.10.20.30.40.50.60.70.80.91根据图中信息,在下列各项中,说法最佳的一项是( ) A .药物B 的预防效果优于药物A 的预防效果 B .药物A 的预防效果优于药物B 的预防效果C.药物A、B对该疾病均有显著的预防效果D.药物A、B对该疾病均没有预防效果【解】由A、B两种药物预防某疾病的效果,进行动物试验,分别得到的等高条形图,知:药物A的预防效果优于药物B的预防效果.故选B.4)A.4-B.4C.13-D.13【解】sin2cos tan2ααα-=-⇒=,C.5.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”.已知某“堑堵”的三视图如图所示,俯视图中间的实线平分矩形的面积,则该“堑堵”的侧面积为()A.2 B.4+C.4+D.4+【解】根据题意和三视图知几何体是一个放倒的直三棱柱,底面是一个直角三角2,且侧棱与底面垂直,侧棱长是2,∴几何C.6.设变量x,y满足约束条件2202202x yx yy+--+⎧⎪⎨⎪⎩≥≤≤,则目标函数z x y=+的最大值为A.7 B.6 C.5 D.4【解】画出不等式组表示的可行域(如图阴影部分所示).由z x y =+,得y x z =-+.平移直线y x z =-+,结合图形可得,当直线(图中的虚线)经过可行域内的点A 时,直线在y 轴上的截距最大,此时z 取得最大值.由2 220y x y =-+=⎧⎨⎩,解得22x y ==⎧⎨⎩,故点A 的坐标为(2,2).∴max 224z =+=,即目标函数z x y =+的最大值为4.选D . 7.已知()201720162018201721f x x x x =++++,下列程序框图设计的是求()0f x 的值,在“ ”中应填的执行语句是( )开始i =1,n =2018结束i ≤2017?是否输入x 0S =2018输出SS =Sx 0S =S+ni =i +1A .2018n i =-B .2017n i =-C .2018n i =+D .2017n i =+【解】不妨设01x =,要计算()120182017201621f =+++++,首先201812018S =⨯=,下一个应该加2017,再接着是加2016,故应填2018n i =-. 8.若函数()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则a 的取值范围为( ) A .()0,4B .()0,+∞C .()3,4D .()3,+∞【解】如图,若()24x f x a =--存在两个零点,且一个为正数,另一个为负数,则()34a ∈,,故选C .9.阿波罗尼斯(约公元前262-190年)证明过这样一个命题:平面内到两定点距离之比为常数k (0k >且1k ≠)的点的轨迹是圆.后人将这个圆称为阿氏圆.若平面内两定点A ,B 间的距离为2,动点P 与A ,B,当P ,A ,B 不共线时,PAB △面积的最大值是( ) A.BCD【解】如图,以经过A ,B 的直线为x 轴,线段AB 的垂直平分线为y 轴,建立直角坐标系;则:()10A -,,()10B ,,设()P x y ,,PA PB=两边平方并整理得:()222261038x y x x y +-+=⇒-+=.∴PAB △面积的最大值是122⨯⨯=A .10.已知双曲线E :22221x y a b-=(0,0)a b >>的右顶点为A ,右焦点为F ,B 为双曲线在第二象限上的一点,B 关于坐标原点O 的对称点为C ,直线CA 与直线BF 的交点M 恰好为线段BF 的中点,则双曲线的离心率为( )A .12B .15C .2D .3【解】不妨设2,b B c a ⎛⎫- ⎪⎝⎭,由此可得(),0A a ,2,b C c a ⎛⎫- ⎪⎝⎭,(),0F c ,20,2b M a ⎛⎫ ⎪⎝⎭,由于A ,C ,M 三点共线,故222b b a a a a c=--,化简得3c a =,故离心率3e =.11.设锐角ABC △的三个内角A ,B ,C 的对边分别为a ,b ,c ,且1c =,2A C =,则ABC △周长的取值范围为( ) A.(0,2B.(0,3+C.(2++ D.(2++ 【解】因为ABC △cos C <<因为2A C =,所以sin 2sin cos A C C =,又因为1c =,所以2cos a C =;由sin sin b cB C=, 即2sin sin34cos 1sin sin c B Cb C C C ===-,所以24cos 2cos a b c C C ++=+,令cos t C =,则t ∈⎭,又因为函数242y t t =+在⎭上单调递增,所以函数值域为(2+,故选:C .12()2f x mx =+有一个零点,则实数m 的取值范围是( ) A ]{64-+B ]{0,64-+C ]{}632-D ]{0,63-【解】由题意函数()f x 的图象与直线2y mx =+有一个交点.如图是()f x 的图象,1x >时,()21f x x =-,,设切点为()00,x y ,则切线为()()02002211y x x x x -=----,把()0,2代入,02x =+;1x ≤时,()2e x f x =-,()e x f x '=-,设切点为()00,x y ,则切线为()()002e e x x y x x --=--,把()0,2代入,解得01x =,又()12e f =-,()11e e f '=-=-,所以由图象知当]{0,42-B .13.已知平面向量a 与b 的夹角为.【解】2+=a b ,即224412+⋅+=a a b b ,41cos ⨯⨯a14.已知0a >,0b >,22a b +=,若24a b m +>恒成立,则实数m 的取值范围是__________.【解】,当且仅当1a =,12b =时等号成立,即()min 244a b +=,由恒成立的结论可得:()min 24a b m <+,即实数m 的取值范围是4m <.15.将正整数对作如下分组,第1组为()(){}1,2,2,1,第2组为()(){}1,3,3,1,第3组为()()()(){}1,4,2,3,3,2,4,1,第4组为()()()(){}1,5,2,44,25,1⋅⋅⋅⋅⋅⋅则第30组第16个数对为__________.【解】根据归纳推理可知,每对数字中两个数字不相等,且第一组每一对数字和为3,第二组每一对数字和为4,第三组每对数字和为5,......,第30组每一对数字和为32,∴第30组第一对数为()1,31,第二对数为()2,30,.......,第15对数为()15,17,第16对数为()17,15,故答案为()17,15.16.在三棱椎P ABC -中,底面ABC 是等边三角形,侧面PAB 是直角三角形,且2PA PB ==,PA AC ⊥,则该三棱椎外接球的表面积为________.【解】由于PA PB =,CA CB =,PA AC ⊥,则PB CB ⊥,因此取PC 中点O ,则有OP OC OA OB ===,即O 为三棱锥P ABC -外接球球心,又由2PA PB ==,得三、解答题17.已知数列{}n a 满足2n n S a n =-()*n ∈N . (1)证明:{}1n a +是等比数列; (2)求13521...n a a a a +++++()*n ∈N . 【解】(1)由1121S a =-得:11a =因为()()()11221n n n n S S a n a n ---=----()2n ≥, 所以121n n a a -=+, 从而由()1121n n a a -+=+得1121n n a a -+=+()2n ≥, 所以{}1n a +是以2为首项,2为公比的等比数列. (2)由(1)得21n n a =-,所以()()321135212221n n a a a a n +++++⋅⋅⋅+=++⋅⋅⋅+-+()()1214114n n +-=-+-232353n n +--=. 18.某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了100名学生的体检表,得到如图的频率分布直方图(图1).(1)若直方图中后四组的频数成等差数列,试估计全年级视力在5.0以下的人数; (2)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在1~50名和951~1000名的学生进行了调查,得到图2中数据,根据表中的数据,能否在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系?【解】(1)由图可知,第一组有3人,第二组7人,第三组27人 设后四组的频数构成的等差数列的公差为d , 则()()()2727227363d d d -+-+-=,解得3d =, 所以后四组频数依次为27,24,21,18,所以视力在5.0以下的频数为3+7+27+24+21=82人, 故全年级视力在5.0以下的人数约为1000×0.82=820(人). (2)()2210041183293004.110 3.8415050732773k ⨯⨯-⨯==≈>⨯⨯⨯, 因此能在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系19.如图,在四棱椎E ABCD -中,AE DE ⊥,CD ⊥平面ADE ,AB ⊥平面ADE ,6CD DA ==,2AB =,3DE =.ABCDE(1)求证:平面ACE ⊥平面CDE ;(2)在线段DE 上是否存在一点F ,使AF ∥平面BCE ?若存在,求出EFED的值;若不存在,说明理由.【解】(1)证明:因为CD ⊥平面ADE ,AE ⊂平面ADE ,所以CD AE ⊥,又因为AE DE ⊥,CDDE D =,所以AE ⊥平面CDE ,又因为AE ⊂平面ACE ,所以平面ACE ⊥平面CDE .ABCDEMF(2)结论:在线段DE 上存在一点F ,且13EF ED =,使AF ∥平面BCE . 解:设F 为线段DE 上一点,且13EF ED =,过点F 作FM CD ∥交CE 于M ,则13FM CD =.因为CD ⊥平面ADE ,AB ⊥平面ADE ,所以CD AB ∥. 又因为3CD AB =,所以MF AB =,FM AB ∥, 所以四边形ABMF 为平行四边形,则AF BM ∥.又因为AF ⊄平面BCE ,BM ⊂平面BCE ,所以AF ∥平面BCE .20.已知椭圆2222:1(0)x y C a b a b+=>>的两个焦点与短轴的一个端点连线构成等边三角形,且椭圆C 的短轴长为(1)求椭圆C 的标准方程;(2)是否存在过点()0,2P 的直线l 与椭圆C 相交于不同的两点M ,N ,且满足2OM ON ⋅=(O 为坐标原点)若存在,求出直线l 的方程;若不存在,请说明理由.【解】(1C 的标准方程是22143x y +=(2)当直线l的斜率不存在时,(M,(0,N3OM ON ⋅=-,不符合题意当直线l 的斜率存在时,设直线l 的方程为2y kx =+,()11,M x y ,()22,N x yy 整理得:()22341640k x kx +++=, ()()221616340k k ∆=-+>,解得12k <-或12k >,1221634kx x k+=-+,122434x x k =+, ∴1212OM ON x x y y ⋅=+=()()21212124k x x k x x ++++()222222413216124343434k k k k k k +-=-+=+++ ∵2OM ON ⋅=,∴221612234k k-=+,解得k =,满足0∆>,21.已知函数()()21ln f x a x x =-+,a ∈R .(1)当2a =时,求函数()y f x =在点()()1,1P f 处的切线方程;(2)当1a =-时,令函数()()ln 21g x f x x x m =+-++,若函数()g x有两个零点,求实数m 的取值范围.【解】(1)当2a =时,()()221ln f x x x =-+224ln 2x x x =-++. 当1x =时,()10f =,所以点()()1,1P f 为()1,0P , ,因此()11k f '==. 因此所求切线方程为()0111y x y x -=⨯-⇒=-.(2)当1a =-时,()22ln g x x x m =-+,,所以当()0g x '=时,1x =, 时,()0g x '>;当1e x <<时,()0g x '<; 故()g x 在1x =处取得极大值也即最大值()11g m =-.,()2e 2e g m =+-,()g x 上的最小值为()e g , 故()g x 在区间上有两个零点的条件是所以实数m 22.选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,曲线1C 的参数方程为2cos 2sin x m y αα=+=⎧⎨⎩(α为参数),以坐标原点为极点,x 轴为极轴建立极坐标系,曲线2C 的极坐标为2sin 2cos ρθθ=.(1)求曲线1C 的普通方程和曲线2C 的直角坐标方程;(2)若曲线1C 和曲线2C 有三个公共点,求以这三个公共点为顶点的三角形的面积.【解】(1)由2cos 2sin x m y αα=+=⎧⎨⎩消去参数α,得()224x m y -+=,即为曲线1C 的普通方程.由2sin 2cos ρθθ=得22sin 2cos ρθρθ=,结合互化公式得22y x =,即为曲线2C 的直角坐标方程.(2)因为曲线1C 和曲线2C 都是关于x 轴对称的图形,它们有三个公共点,所以原点是它们的其中一个公共点,所以()224x m y -+=中2m =, 解()22224 2x y y x -+==⎧⎪⎨⎪⎩得三个交点的坐标分别为()0,0,()2,2,()2,2-,23.选修4-5:不等式选讲已知函数()211f x x x =-++(1)解不等式()3f x ≤;(2)记函数()()1g x f x x =++的值域为M ,若t M ∈【解】(1)于是得()13 33x f x x -⎧=⎨-⎩≤≤≤或解得11x -≤≤,即不等式()3f x ≤的解集为{|11}x x -≤≤.(2当且仅当()()21220x x -+≤时,取等号, ∴[)3,M =+∞,∵t M ∈,∴30t -≥,210t +>,。
【高三数学试题精选】2018年高考数学文科模拟试卷(有答案)

2018年高考数学文科模拟试卷(有答案)
5 c 2018届高三高考模拟数学试题
第Ⅰ卷
一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1已知集合,则
A B
c D
2若,则
A B
c D
3已知,则“”是“”的
A 充分不必要条
B 必要不充分条
c 充要条 D 既不充分也不必要条
4一个几何体的三视图如图所示,则该几何体的体积为
A 4 B
c 8 D
5已知两个不重合的平面和两条不同直线,则下列说法正确的是
A 若则
B 若则
c 若则 D 若则
6若,满足的解中的值为0的概率是
A B
c D
7在中,角所对应的边分别为,若,则
A B 3
c 或3 D 3或
8已知定义域为的函数在区间上单调递减,并且函数为偶函数,则下列不等式关系成立的是。
2018届高考数学(文科)模拟测试卷含答案

2018年高考模拟试卷数学(文)一、选择题(本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. 设全集U 0,1,2,3,4,5,集合{1,3},{3,5}A B ,则U ()C A B U =A .{0,4}B .{1,5}C .{2,0,4}D .{2,0,5}2. 复数z 满足23zi i ,复数z 是A .32iB .32iC .32i D.32i3. 下列函数中,在区间0(,)上为增函数的是A.1y xB.sin y xC. 2x yD. 12log (1)y x 4.已知双曲线22:1169x y C ,它的渐近线的方程A .34y xB .43y x C .916y x D .169y x5.等差数列{}n a 中,前n 项和为n S ,公差0d ,且711S S ,若96a ,则10a =A . 0B .6C .10a 的值不确定D .106a 6.直线01)1(:1y a ax l ,02:2ay x l ,则“2a ”是“21l l ”A.充分不必要条件B. 必要不充分条件C.充分必要条件D. 既不充分也不必要条件7. 已知,,a b c 分别为ABC 三个内角,,A B C 的对边,且()(sin sin )()sin a b A B c b C ,则ABC 中A 为A .6B .23C .3D .568. 某电力公司在工程招标中是根据技术、商务、报价三项评分标准进行综合评分的,按照综。
2018年高考文科数学模拟试题及答案

2018年高考文科数学模拟试题注意事项:1.本试卷分第1卷(选择题)和第II 卷(非选择题)两部分。
答题前,考生务必用黑 色碳素笔将自己的姓名、准考证号、考场号、座位号填写在答题卡上,并认真核准 条形码上的准考证号、姓名、考场号、座位号及科目,在规定的位置贴好条形码。
2.回答第1卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其它答案标号。
写在本试卷上无效。
3.回答第II 卷时,将答案写在答题卡上,写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第1卷一、选择题:(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符 合题目要求的)(1)已知i 为虚数单位,复数i z +=21,i z 212-=,则=+21z z ( ) (A)i +1 (B) i -2 (C) i -3 (D) i -(2)设平面向量3(=,)2,x (=,)4-,如果与平行,那么x 等于( ) (A) 6 (B) 3 (C) 3- (D) 6-(3)设n S 是等差数列}{n a 的前n 项和,若2:1:21=a a ,则=21:S S ( ) (A)3:1 (B) 4:1 (C) 5:1 (D) 6:1 (4)设3log 31=a ,31log 21=b , 2)31(=c ,则下列正确的是 ( )(A)c b a << (B)b c a << (C)c a b << (D)a c b <<(5)某商场在今年春节假期的促销活动中,对大年初一9时至14时的销售金额进行统计,并将销售金额按9时至10时、10时至11时、11时至12时、12时至13时、13时至14 时进行分组,绘制成下图所示的频率分布直方图,已知大年初一9时至10时的销售金额为3万元,则大年初-11时至12时的销售金额为 ( ) (A)4万元 (B)8万元 (C) 10万元 (D) 12万元(6)下图是一个空间几何体的三视图(注:正视图也称主视图,侧视图也称左视图),其中 正视图与侧视图都是边长为6的正三角形,俯视图是直径等于6的圆,则这个空间几何体的 表面积为 ( ) (A) π180.400.35 0.30 0.250.200.15 0.100.05(B) π27(C) 382π(D) 383π(7)已知函数x x x x f cos sin cos 3)(2+=,R 是实数集,若R x ∈∃1,R x ∈∃2,R x ∈∀,)()()(21x f x f x f ≤≤,则12x x -的最小值为 ( )(A)π (B)2π (C) 3π (D) 4π(8)在三棱锥ABC P -中,PA 、PB 、PC 两两互相垂直,3=PA ,5=PB ,2=PC ,若三棱锥ABC P -的顶点都在球O 的球面上,则球0的体积等于 ( ) (A) π36 (B) π25 (C) π16 (D)π34 (9)如图所示的程序框图的功能是 ( )(A)求数列}1{n 的前10项和(B)求数列}1{n 的前11项和(C)求数列}21{n 的前10项和(D)求数列}21{n的前11项和(10)下表提供了某工厂节能降耗技术改造后,一种产品的产量x (单位:吨)与相应的生根据上表提供的数据,求得y 关于x 的线性回归方程为35.07.0ˆ+=x y那么表 格中t 的值为 ( )(A) 5.3 (B) 25.3 (C) 15.3 (D) 3(11)已知0>a ,0>b ,双曲线S :12222=-bx a y 的离心率为3,k 是双曲线S 的一条俯视图渐近线的斜率,如果0>k ,那么b ak+的最小值为 ( ) (A) 2 (B) 23 (C) 24 (D) 6(12)已知23)(x x f y +=的图象关于原点对称,若3)2(=f ,函数x x f x g 3)()(-=, 则)2(-g 的值是 ( )(A) 12 (B) -12 C) -21 (D) -27第Ⅱ卷本卷包括必考题和选考题两部分。
2018年高考(文科)数学模拟试题及答案

2018年高考(文科)数学模拟试题及答案一、选择题共8小题,每小题5分,共40分。
(1)若集合A={x|-5<x <2},B={x|-3<x <3},则A B=( )A. -3<x <2B. -5<x <2C. -3<x <3D. -5<x <3(2)圆心为(1,1)且过原点的圆的方程是( )(A )(x-1)2+(y-1)2=1 (B )(x+1)2+(y+1)2=1(C )(x+1)2+(y+1)2=2 (D )(x-1)2+(y-1)2=2(3)下列函数中为偶函数的是( )(A )y=x ²sinx (B )x x y cos 2= (C )x y ln = (D )x y -=2(4)某校老年,中年和青年教师的人数见下表,采用分层抽样的方法调查教师的身体情况,在抽取的样本中,青年教师有320人,则该样本的老年人数为( )(A )90 (B )100 (C )180 (D )300类别 人数老年教师 900中年教师 1800青年教师 1600合计 4300(5)执行如果所示的程序框图,输出的k 值为( )(A )3 (B )4 (C)5 (D)6(6)设a ,b 是非零向量,“a ·b=IaIIbI ”是“a//b ”的( )(A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件 (D )既不充分也不必要条件(7)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为( )(A)1 (B )错误!未找到引用源。
(B )错误!未找到引用源。
(D)2(8)某辆汽车每次加油都把油箱加满,下表记录了该车相邻两次加油时的情况。
注:“累计里程”指汽车从出厂开始累计行驶的路程在这段时间内,该车每100千米平均耗油量为( )(A )6升 (B )8升 (C )10升 (D )12升二、填空题(共6小题,每小题5分,共30分)(9)复数()i i +1的实部为(10)32- , 213 , log 25三个数中最大数的是 (11)在△ABC 中,a=3,b=错误!未找到引用源。
2018年高考模拟卷数学(文)试题Word版含答案

2018年高考模拟卷数学(文)试题Word版含答案2018年高中毕业班教学质量检测高考模拟数学(文科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设复数z满足(1-i)z=1+3i(i为虚数单位),则z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限2.已知全集U=Z,A={x∈Z|x^2-x-2≥0},B={-1,0,1,2},则(C∩A)∩B=()A.{-1,2}B.{-1,0}C.{0,1}D.{1,2}3.若-1<sinα+cosα<1,则()A.sinα<cosαB.cosα<sinαC.tanα<cosαD.cos2α<14.已知点(2,3)在双曲线x^2/a^2-y^2/b^2=1(a>0)的一条渐近线上,则a=()A.3B.4C.2D.235.“a^2=1”是“函数f(x)=lg((2+x)/(1-x))+(a^2-1)/2为奇函数”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.执行以下程序框架,则输出A的值是()int A=0;for(int i=1;i<=6;i++){A=A*10+i;XXX<<A<<endl;A.B.xxxxxxxxC.D.xxxxxxx7.边长为4的正三角形ABC中,点D在边AB上,AD=DB,M是BC的中点,则AM×CD=()A.16B.12√3C.-8/3D.-88.等比数列{a_n}共有2n+1项,其中a_1=1,偶数项和为170,奇数项和为341,则n=()A.3B.4C.7D.99.函数f(x)=x^2cos(x)在(-π/2,π/2)的图象大致是()A。
B。
C。
D。
10.抛物线x^2=4y的焦点为F,过F作斜率为-3的直线l 与抛物线在y轴右侧的部分相交于点A,过A作抛物线准线的垂线,垂足为H,则△AHF的面积是()A.4B.3/3C.4/3D.811.将函数f(x)=sin(ωx)(ω>0)的图象向左平移π/4个单位得到函数g(x)的图象,若函数g(x)的图象关于直线x=ω对称且在区间(-ω,ω)内单调递增,则ω的值为()A.3π/2B.2π/3C.3π/4D.π/212.若函数f(x)={-x-e^(x+1),x≤a。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AC= BC=
1 2 AA1
,D 是侧棱
(Ⅰ)证明:平面 BDC1⊥平面 (Ⅱ)平面 BDC1 分此棱柱为
第 5 页 共 12 页
2018 高考文科数学模拟题 1
cab
(7)某同学想求斐波那契数列 0,1,1,2,3,5 …(从第三项起每一项
S Sc
等于前两项的和)的前 10 项的和,他设计了一个程序框图,那么在
ab
空白矩形框和判断框内应分别填入的语句是( )
i i 1
A. b c,i 10 C. b c,i 9
B. c a,i 10 D. c a,i 9
=( ) (A)
3
(B) 2 3
(C)
(10)如图是 表面积为
A.7π cm2 C.9π cm2
B.8π cm2 D.11π cm2
(11)已知函数
f
x
1 2
a
3
sin
x
3 2
a
1
2018 高考文科数学模拟题 1
到函数 g x 的图象,若对任意 x R
,都有 g x
g
4
成立,则 a 的值为(
(14)已知抛物
线与双曲
线
焦点 F,O 为坐标
有共同的
原点,P 在 X 轴上方且在双曲线
上,则 的最小值为__________________
(15)在某条件下的汽车测试中,驾驶员在一次加满油后的连续行驶过程中从汽车仪表盘
第 4 页 共 12 页
得到如下信息: 时间 油耗(升/100 公里) 10: 9。5 00 11:00 9.6
1 2
, bn1
n 1 2n bn
。
(1)求数列an ,bn 的通项公式;
(2)记
Tn
为数列{bn}的前
n
项和,
ห้องสมุดไป่ตู้
f
(n)
2Sn (2 Tn ) n2
,试问
f
(n)
是否存在最大值,若存
在,求出最大值,若不存在请说明理由.
(18)(本小题满分 12 分)
某班同学利用国庆节进行社会实践,对
岁的人群随机抽取 人进行了一次生活习惯
是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低
碳族”,得到如下统计表和各年龄段人数频率分布直方图:
(Ⅰ)补全频率分布直方图并求 、 、 的值;
(Ⅱ)从年龄段在
的“低碳族”中采用分层
选取 人作为领队,求选取的 名领队中恰有 1 人
(19)(本小题满分 12 分)如图:三棱柱 ABC-A
第 1 页 共 12 页
2018 高考文科数学模拟题 1
016 年全国高考文科数学模拟试题五
注意事项: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷 1 至 3 页,第Ⅱ卷 3 至 5 页. 2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。 3。全部答案在答题卡上完成,答在本试题上无效. 4. 考试结束后,将本试题和答题卡一并交回。
2018 高考文科数学模拟题 1
2018 高考文科数学模拟题 1 编辑整理:
尊敬的读者朋友们: 这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我 们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018 高考文科数学 模拟题 1)的内容能够给您的工作和学习带来便利。同时也真诚的希望收到您的建议和反馈, 这将是我们进步的源泉,前进的动力。 本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快 业绩进步, 以下为 2018 高考文科数学模拟题 1 的全部内容。
)
A. 1
B. 1
C. 2
D. 2
(12)已知函数
f
x
x
1 2
x
0
若函数 g x f x x a 在 R 上恰有两个相异零点,
f x 1 x 0
则实数 a 的取值范围为( )
A.1,
B. 1,
C. , 0
D. ,1
第Ⅱ卷
二、填空题(本大题共 4 小题,每小题 5 分) (13)《九章算术》中有一题:今有女子善织,日自倍,五日织五尺,问日织几何。该女子 首日织布为________________________(尺)
第Ⅰ卷 一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的。 (1)已知全集 U 为实数集,集合 A={x|x2﹣2x﹣3<0},B={x|y=ln(1﹣x)},则图中 阴影部分表示的集合为( )
(2)已知 为虚数单位,若复数 满 足 Z 是复数 Z
2018 高考文科数学模拟题 1
(6)设 关 于 x,y 的 不 等
式组表示的平面区域内存在点 P(x0,y0),
满足 x0-2y0=2,则 m 的取值范围是(
A.(-∞, 4 ) 3
C.(-∞, 2 ) 3
)
B.(-∞, 1 ) 3
D.(-∞, 5 ) 3
出出 a 0,b 1,i 3
S ab
可继续行驶距 300
220
注:
,
. ①行驶了 80 公里; ②行驶不足 80 公里; ③平均油耗超过 9。6 升/100 公里; ④平均油耗恰为 9.6 升/100 公里; ⑤平均车速超过 80 公里/小时. 从以上信息可以推断在 10:00—11:00 这一小时 号).
2018 高考文科数学模拟题 1
A.
B.
C.
D.
(3) 空间四边形 OABC 中,
,
,
的中点,则 =( )
A.
B.
C.
D.
(4)如图,用一边长为 三角形,做成一个蛋巢,将
蛋巢形状保持不变,则鸡
A.{x|1≤x<3} B.{x|x<3}
C.{x|x≤﹣1}
D.{x|﹣1<x<1}
第 2 页 共 12 页
A.
(5)函数
B.
C.
的图象大致是(
出
出 出出 S
出出
(8)若函数 y ax2 1 ( a 0 且 a 1)的图象经过定点 m, n ,且过点 Q m 1, n 的直线 l
第 3 页 共 12 页
被圆 C : x2 y2 2x 2 y 7 0 截得的弦长为 3 2 ,
A. 1或 7
B. 7 或 4
C.
3
(9) 设 ABC 的 内 角 A, B,C 所 对 边 的 长 分 别 为
(16)设 a,b > 0, a +b = 5 ,则 a +1+ b+3 的最大值为 ________。
三、解答题 (本大题共 6 小题,共 70 分.解答应写出文字说明、证明过程或演算步骤.)
(17)(本小题满分 12 分)
已知等差数列an
,的前
n
项和为
Sn,且
a2=2,S5=15,数列bn 满足 b1
