20201128空间向量与立体几何(同步)
高中数学第1章空间向量与立体几何1.1.1空间向量及其线性运算课件新人教A版选择性必修第一册

1.
类型 共线(平行)向量
共面向量
如果表示若干空间向量的有向线段所
在的直线 互相平行或重合 ,那么这些
向量叫做共线向量或平行向量
平行于同一个平面的向量,叫
定义
做共面向量
共线向量也叫平行向量,注意与两直线
重合和平行的区别
如果两个向量a,b不共线,那么
充要 对任意两个空间向量a,b(b≠0),a∥b的充 向量p与向量a,b共面的充要条
1.定义.
在空间,我们把具有 大小 和 方向
小叫做空间向量的 长度或模 .
的量叫做空间向量,空间向量的大
2.空间向量及其模的表示方法.
空间向量用字母a,b,c,…表示.若向量a的起点是A,终点是B,则向量a也可以
记作
,其模记为|a|或 | |.
3.空间向量的相关概念.
对于任意向量a,均有0∥a
算时,务必要注意和向量、差向量的方向,必要时可采用空间向量的自由平
移获得更准确的结果.
(2)化简空间向量的常用思路:
①分组:合理分组,以便灵活运用三角形法则、平行四边形法则进行化简.
②多边形法则:在空间向量的加法运算中,若是多个向量求和,还可利用多
边形法则,若干个向量的和可以将其转化为首尾相接的向量求和.
1
1
+ 2 =-a+b+2c.
规律方法
空间向量线性运算的技巧与思路
(1)空间向量加法、减法运算的两个技巧:
①巧用相反向量:向量加减法的三角形法则是解决空间向量加法、减法运
算的关键,灵活运用相反向量可使有关向量首尾相接,从而便于运算.
②巧用平移:利用三角形法则和平行四边形法则进行向量的加法、减法运
空间向量与立体几何PPT教学课件

3)射影
已知向量 AB=a和轴l,e是l上与l同方向的单位向量。
作点A在l上的射影A1 , 作点B在l上的射影B1,
则 A1B1叫做向量 AB在轴l上的或在e方向上的正射影,
简称射影。 A1B1 AB cosa, e a e
B
e
A1
B1
l
A
注意:AB 是轴l上的正射影,A1B1是一个可正可负的实数, 它的符号代表向量 AB 与l的方向的相对关系,大小代
第二章 《空间向量与立体几何》
一.空间向量的运算
b
OaA
B
b
a
结论:空间任意两个向量都是共面向量,所以它们可用 同一平面内的两条有向线段表示。 因此凡是涉及空间任意两个向量的问题,平面向量中有 关结论仍适用于它们。
类比思想 数形结合思想
平面向量
空间向量
概念 定义 表示法 相等向量
具有大小和方向的量
| b |2 b b b12 b22 b32
注意:此公式的几何意义是表示长方体的对 角线的长度。
(2)空间两点间的距离公式
终点坐标减 在空间直角坐标系中,已知 A起(x1点, y坐1 ,标z1)、
B(x2 , y2 , z2 ) ,则 AB ( x2 x1 , y2 y1 , z2 z1)
PA n d
n
N D1 F
C1
A1
E M B1
D
Cy
A
B
x
立体几何中的向量方法——坐标法
问题1:已知:△ABC为正三角形,EC⊥平面ABC,
且EC,DB在平面ABC同侧,CE=CA=2BD.求证:
平面ADE⊥平面ACE.
z
E
⑴怎样建立适当的空间直角坐标系?
(完整版)空间向量与立体几何知识点归纳总结(2),推荐文档

空间向量与立体几何知识点归纳总结一.知识要点。
1. 空间向量的概念:在空间,我们把具有大小和方向的量叫做向量。
注:(1)向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量。
(2)向量具有平移不变性2. 空间向量的运算。
定义:与平面向量运算一样,空间向量的加法、减法与数乘运算如下(如图)。
;;OB OA AB a b =+=+ BA OA OB a b =-=- ()OP a R λλ=∈运算律:⑴加法交换律:a b b a+=+⑵加法结合律:)()(c b a c b a++=++⑶数乘分配律:ba b aλλλ+=+)(运算法则:三角形法则、平行四边形法则、平行六面体法则3. 共线向量。
(1)如果表示空间向量的有向线段所在的直线平行或重合,那么这些向量也叫做共线向量或平行向量,平行于,记作。
ab b a//(2)共线向量定理:空间任意两个向量、(≠),//存在实数λ,使=λa bb 0 a b a。
b (3)三点共线:A 、B 、C 三点共线<=>AC AB λ=<=>)1(=++=y x OB y OA x OC 其中(4)与共线的单位向量为a a 4. 共面向量(1)定义:一般地,能平移到同一平面内的向量叫做共面向量。
说明:空间任意的两向量都是共面的。
(2)共面向量定理:如果两个向量不共线,与向量共面的条件是存在实,a b p ,a b数使。
,x y p xa yb =+(3)四点共面:若A 、B 、C 、P 四点共面<=>ACy AB x AP +=<=>)1(=++++=z y x OC z OB y OA x OP 其中5. 空间向量基本定理:如果三个向量不共面,那么对空间任一向量,存在,,a b cp 一个唯一的有序实数组,使。
,,x y z p xa yb zc =++若三向量不共面,我们把叫做空间的一个基底,叫做基向量,,,a b c {,,}a b c,,a b c 空间任意三个不共面的向量都可以构成空间的一个基底。
高中数学人教A版选择性必修第一册第一章空间向量与立体几何1.1空间向量及其运算课件

学习重难点
• 重点:理解空间向量的概念
• 难点:掌握空间向量的运算及其应用
空间向量及其运算
向量
平面向量VS空间向量
左图是一个做滑翔运动员的场景,
可以想象在滑翔过程中,飞行员会受到
来自不同方向大小各异的力,例如绳索
的拉力,风力,重力等,显然这些力不
在同一个平内。
向量.
另外,利用向量加法的交换律和结合律,还可
以得到:有限个向量求和,交换相加向量的顺序,其
和不变.
A'
B'
D
A
C
B
知识点二 空间向量的加减运算及运算律
探 对任意两个空间向量与,如果=λ (λ∈R),与有什么位置关系?反过来,
究 与有什么位置关系时,=λ?
类似于平面问量共线的充要条件,对任意两个空间向量, (≠0), ∥
联想,用平面向量解决物理问题的方法,能否把平面向量推广
到空间向量,从而利用向量研究滑翔运动员呢?
下面我们类比平面向量,研究空间向量,先从空间上的概念和
表示开始。
知识点一 空间向量的概念
思考1
类比平面向量的概念,给出空间向量的概念.
在空间,把具有大小和方向的量叫做空间向量。
空间向量的大小叫做向量的长度或模.
―→ ―→ ―→
(2)AA′+ AB +B′C′.
解
→
→
→
→
→
→
AA′ +AB +B′C′ =(AA′ +AB )+B′C′ =
→
→
→
→
→
AB′+B′C′=AC′.向量AD′、AC′如图所示.
课堂检测
如图,E,F分别是长方体ABCD -A'B'C'D'的棱AB,CD的中点.
高中数学选修2-1-空间向量与立体几何
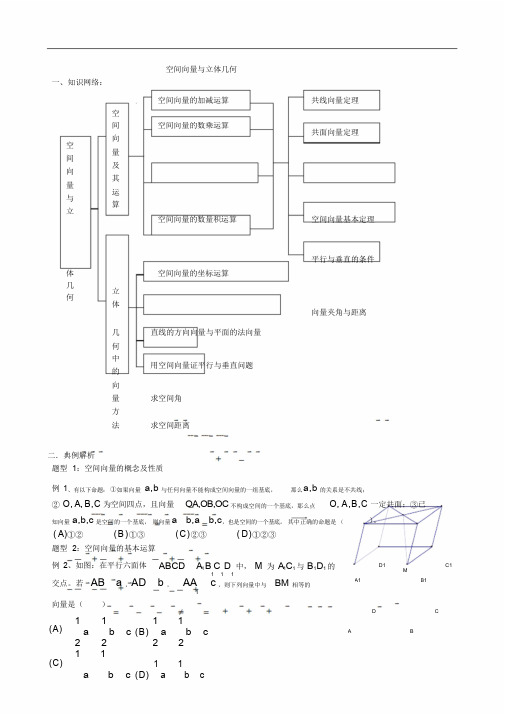
空间向量与立体几何一、知识网络:空间向量的加减运算共线向量定理空空间向量与立间向量及其运算空间向量的数乘运算共面向量定理空间向量的数量积运算空间向量基本定理平行与垂直的条件体空间向量的坐标运算几何立体向量夹角与距离几直线的方向向量与平面的法向量何中的用空间向量证平行与垂直问题向量求空间角方法求空间距离二.典例解析题型1:空间向量的概念及性质例1、有以下命题:①如果向量a,b与任何向量不能构成空间向量的一组基底,那么a,b的关系是不共线;②O, A, B,C 为空间四点,且向量OA,OB,OC不构成空间的一个基底,那么点O, A,B,C 一定共面;③已知向量a,b,c 是空间的一个基底,则向量a b,a b,c,也是空间的一个基底。
其中正确的命题是()。
( A)①②(B)①③(C)②③( D)①②③题型2:空间向量的基本运算例2、如图:在平行六面体A BCD A1B C D 中,M 为A1C1 与B1D1 的1 1 1 D1 C1M交点。
若AB a ,A D b ,A A c ,则下列向量中与BM 相等的1A1 B1向量是()D C(A) 1 1a b c (B)2 21 1a b c2 2A B(C) 1 11 1a b c (D) a b c2 2 2 2例3、已知: a 3m 2n 4p 0,b (x 1)m 8n 2 yp, 且m, n, p不共面. 若a ∥b , 求x, y 的值.例4、底面为正三角形的斜棱柱ABC-A1B1C1 中,D为AC的中点,求证:AB1∥平面C1BD.(三)强化巩固导练1、已知正方体ABCD—A1B1C1D1 中,点 F 是侧面CDD1C1 的中心,若,求x-y 的值.AF AD xAB y AA1 在平行六面体ABCD 中,M为AC与BD的交点,若A1 B1 a,A1 D1 b,A1 A c,则下列向量中A1B C D1 1 12、与相等的向量是( ) 。
B1M1 1 1 1 1 1 1 1A.a+b+c B.a+b+cC. a b+c D. a b+c2 2 2 2 2 2 2 23、(2009 四川卷理)如图,已知正三棱柱ABC A B C的各条棱长都相等,M 是侧棱CC1 的中点,则1 1 1AB和BM异面直线所成的角的大是。
2020版高中数学第三章空间向量与立体几何3.1.1空间向量的线性运算(第1课时)课件

跟踪训练
A
归纳小结
归纳小结
2.熟练应用三角形法则和平行四边形法则 (1)利用三角形法则进行加法运算时,注意“首尾相连” 和向量的方向是从第一个向量的起点指向第二个向量的终点. 进行减法运算时,注意“共起点”,差向量的方向是从减向量 的终点指向被减向量的终点. (2)平行四边形法则一般用来进行向量的加法运算. 注意:平行四边形的两条对角线所表示的向量恰为两邻边 表示向量的和与差.
第三章 空间向量与立体几何
3.1.1 空间向量的线性运算
引入课题
F1
F3
F2
已知|F1|=2000N, |F2|=2000N, |F3|=2000N, 这三个力两两之间的夹角 都为60°, 它们的合力的大小为多少N?
三个力的特点是: 三力既有大小又有方向, 但不在同一平面上. 所以解决这类问题, 需要空间知识.
C
向量的加减法统一 在平行四边形中
知识点五:数乘运算的概念
λ>0 方向
λ<0 大小 运算律
典例分析
[思路探索] 可根据向量相等的两个条件来进行判断, 任何一条不具备,则两向量不相等.
典例分析
【解析】 命题①,
据向量相等的定义,要保证两个向量相等, 不仅模要相等,而且方向还要相同,故①错; 命题②符合两个向量相等的条件,②正确; 命题③正确; 命题④,任意两个单位向量只是模相等, 方向不一定相同,故④错. 【答案】 ②③
空间向量
知识点一:空间向量的概念
(1)定义:空间中具有 大小 和 方向 的量叫做向量.
(2)表示:
B
有向线段
向 量
几何表示
A
的 表 代数表示
示
知识点一:空间向量的概念
新教材高中数学第一章空间向量与立体几何2空间向量在立体几何中的应用3直线与平面的夹角课件新

=
探究点三 利用空间向量求直线与平面的夹角
例 如图,在四棱锥 − 中,底面为直角梯形, ∥ ,∠ = 90∘
,Байду номын сангаас⊥底面,且 = = = 2,,分别为,的中点
.
(1) 求与平面所成的角;
[答案] 如图所示,以为原点,, , 的方向分别为轴,轴,轴的
角.
⒉数学运算——能用向量法求直线
与平面的夹角.
要点一 直线与平面的夹角的概念
1.直线与平面的夹角的定义
如果一条直线与一个平面垂直,则称这条直线与这个平面所成的角为①
∘
90
______;如果一条直线与一个平面平行,或直线在平面内,则称这条直线与
0∘
这个平面所成的角为②_____.
射影
平面的斜线与它在平面内的③_______所成的锐角,称为这条斜线与平面所
⋅
=
0
由൝
得ቊ
取=1,则= − 1,∴ =(1,0, −1),∵
+ = 0,
⋅ = 0
cos⟨, ⟩ =
⋅
||||
=
−2
8× 2
=
1
2
1
− ,
2
∴ sin = |cos < , > | = . 又0∘ ≤ ≤ 90∘ ,∴ = 30∘ .
∵ ∩ 1 = ,,1 ⊂平面1 1 ,
∴ ⊥平面1 1 ,
故∠1 为1 与平面1 1 所成的角.
易知在Rt △ 1 中, =
∴ sin∠1 =
∴ ∠1 =
π
.
6
1
,
2
3
,1
2
高中数学第三章空间向量与立体几何本章整合课件新人教B版选修2

|·|
||
=
综合应用
专题一
专题二
专题三
(2) = (−1,0, 3), = (−1, − 3, 2 3).
设平面 ACM 的法向量为 n1=(x,y,z),
1 ⊥ ,
- + 3 = 0,
由
得
-- 3 + 2 3 = 0,
1 ⊥
解得 x= 3, = , 取n1=( 3, 1,1).
②证明能够在平面内找到一个向量与已知直线的方向向量共线;
③利用共面向量定理,即证明直线的方向向量与平面内的两个不
共线向量是共面向量.
(3)证明面面平行的方法:
①转化为线线平行、线面平行处理;
②证明这两个平面的法向量是共线向量.
综合应用
专题一
专题二
专题三
(4)证明线线垂直的方法是证明这两条直线的方向向量互相垂直.
则 P(0,− 3, 2), (0, − 3, 0), (1,0,0), (0, 3, 0).
所以 = (1, 3, −2), = (0,2 3, 0).
设 PB 与 AC 所成角为 θ,
则 cos θ=
·
||||
=
6
2 2×2 3
=
6
.
4
2
3
真题放送
1
(3)解:由(2)知BC = (−1, 3, 0).
但线段AB 与 A1B1 不重合;
π
②错误.a·b<0,即 cos<a,b><0⇒ <<a,b>≤π,而钝角的取值范
围是
π
,π
2
2
;
③错误.当 λ=0 时,λa=0 不能作为直线 l 的方向向量;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AB AD 2 (Ⅰ)求证: AO 平面 BCD;
(Ⅱ)求异面直线 AB 与 CD 所成角的余弦值; (Ⅲ)求点 E 到平面 ACD 的距离.
A
D O
B
C
E
5、如图,已知 P 为矩形 ABCD 所在平面外一点,PA 平面 ABCD,E、F 分别是 A B.PC 的中点.
(Ⅰ)求证:EF∥平面 PAD;
空间向量与立体几何
1. 已知向量 a (0, 2,1) , b (1,1,2) ,则 a 与 b 的夹角为 (A)0° (B)45° (C)90° (D)180°
()
2、已知向量 a=(1,1,0),b=(-1,0,2),且 k a+b 与 2 a-b 互相垂直,则 k 的值
是(
)
A. 1
B. 1 5
(Ⅱ)求证:EF CD;
6、如图,在棱长为 1 的正方体 ABCD—A1B1C1D1 中,点 E 是棱 BC 的中点,点 F 是棱 CD 的 中点。
(1)求证:D1E⊥平面 AB1F; (2)求二面角 C1—EF—A 的余弦值。
4
7、在直平行六面体 AC1 中, ABCD 是菱形, DAB 60 , AC BD O , AB AA1 .
x
E
y B
图2
2
3、如图,四棱锥 P ABCD 中, 底面 ABCD 为矩形, PD 底面 ABCD,AD=PD,
E,F 分别 CD、PB 的中点。
(Ⅰ)求证:EF 平面 PAB;
xC
F
(Ⅱ)设 AB= 2 BC,求 AC 与平面 AEF 所成角的正弦值。 B
图3
z P
E
D
A y
4、如图,四面体 ABCD 中,O、E 分别是 B D.BC 的中点, CA CB CD BD 2 ,
1
空间向量练习题
1、 在棱长为 1 的正方体 ABCD A1B1C1D1 中, 求(1)平面 ACD1 的法向量 n 。(2)点 A1 到平面 ACD1 的距离。
D1 z A1
C1 B1
(3)直线 AA1 与平面 ACD1 所成角的余弦值。 (4)二面角 D1 AC D 的余弦值。
C
D A
y B
b
=(3,
,
15
)平行,则λ等于
2
6、在棱长为
1
的正方体
ABCD—A1B1C1D1
中,E、F
分别是
D1D,DB
的中点,G
在棱
CD
上
CG=
1 4
CD,
H 是 C1G 的中点.
(1)求证:EF⊥B1C;
(2)求 EF 与 C1G 所成角的余弦值;
(3)求 FH 的长.
7、正方体 ABCD—A1B1C1D1 中,E 为 CD 的中点 (1)求证:EB1⊥AD1;(2)求 D1E 与 A1C 所成角的余弦值.
C. 3 5
D. 7 5
3、已知点 A(3,-5,7),点 B(1,-4,2),则 AB 的坐标是___ _______,AB 中点坐标是 __________。
4.
已知
a
=(3,-3,-1),b
=(2,0,3),c
=(0,0,2),求
a
·(
b
+
c
)=__________。
5.
已知向量
a
=(2,-3,5)与向量
B
O M A
D C
5
x 图1
2、如图,在长方体 ABCD A1B1C1D1 中,AD= AA1 =1,AB=2,
点 E 在棱 AB 上移动。
(Ⅰ)证明: D1E A1D ;
(Ⅱ)当 E 为 AB 的中点时,求点 E 到面 ACD1 的距离;
(Ⅲ)AE
等于何值时,二面角
D1
EC
D
的大小为
4
。
z
D1
C1
A1
B1
C
D A
(1)求证: C1O // 平面 AB1D1 ; (2)求证:平面 AB1D1 平面 ACC1A1 ;
D1 A1
C1 B1
(3)求直线 AC 与平面 AB1D1 所成角的大小.
D
C
A
O B
8、如图,在四棱锥 O ABCD 中,底面 ABCD 是边长为1的菱 形, ABC , OA 底面 ABCD , OA 2 , M 为 4 OA 的中点, N 为 BC 的中点. (Ⅰ)证明:直线 MN // 平面 OCD ; (Ⅱ)求异面直线 AB 与 MD 所成角的大小; (Ⅲ)求点 B 到平面 OCD 的距离.
