神经网络中的反向传播法算法推导及matlab代码实现_20170527
神经网络中的反向传播算法分析与优化

神经网络中的反向传播算法分析与优化神经网络是近年来备受关注的一个领域,其在图像识别、语音识别、自然语言处理、智能机器人等领域有着广泛的应用。
其中,反向传播算法是神经网络训练中最常用的方法之一。
本文将对反向传播算法进行分析,并提出一些优化思路。
一、反向传播算法简介反向传播算法(Backpropagation Algorithm)是一种神经网络的学习算法,它的主要思想是通过误差反向传播来更新每一个权值。
具体来说,对于一个输人样本(input),神经网络先进行前向传播(forward propagation),计算出每一个节点的输出值;然后利用误差反向传播(back propagation of error)算法,计算每一个连接的误差,并根据误差大小更新每一个连接的权值,最终使得网络对输人样本的输出结果更加接近期望结果。
反向传播算法可以分为两个阶段:前向传播和误差反向传播。
前向传播即为输入层到隐层和隐层到输出层的计算,隐层与输出层的计算公式如下:第 j 个输出层节点的输出值为:$$O_j=f(\sum\limits_{i=1}^n w_{ji}O_i)$$其中,$f$ 为激活函数,$w_{ji}$ 是连接权重,$O_i$ 是输入层或者隐层的输出值。
误差函数采用均方误差(MSE)或交叉熵(Cross-entropy)。
均方误差定义为:$$E=\frac{1}{2}\sum\limits_{k=1}^n(y_k-\hat{y}_k)^2$$其中,$n$ 是输出节点数,$y_k$ 是期望输出,$\hat{y}_k$ 是神经网络的输出。
交叉熵定义为:$$E=-\sum\limits_{k=1}^n y_k\log\hat{y}_k+(1-y_k)\log(1-\hat{y}_k)$$误差反向传播算法的具体步骤如下:1. 小批量随机采样训练集;2. 前向传播,计算每个节点的输出值,得到整个网络的输出值;3. 根据误差函数,计算整个网络的误差;4. 求出每个节点的误差,即计算偏导数$\frac{\partial E}{\partial O_j}$;5. 根据链式法则,求出每个连接的误差,即计算偏导数$\frac{\partial E}{\partial w_{ji}}$;6. 利用梯度下降法,更新每个连接的权值,有公式$w_{ji}\leftarrow w_{ji}-\eta\frac{\partial E}{\partial w_{ji}}$,其中$\eta$为学习率。
基于matlab的卷积神经网络(CNN)讲解及代码

基于matlab的卷积神经网络(CNN)讲解及代码转载自:/walegahaha/article/details/516030401.经典反向传播算法公式详细推导2.卷积神经网络(CNN)反向传播算法公式详细推导网上有很多关于CNN的教程讲解,在这里我们抛开长篇大论,只针对代码来谈。
本文用的是matlab编写的deeplearning toolbox,包括NN、CNN、DBN、SAE、CAE。
在这里我们感谢作者编写了这样一个简单易懂,适用于新手学习的代码。
由于本文直接针对代码,这就要求读者有一定的CNN基础,可以参考Lecun的Gradient-Based Learning Applied to Document Recognition和tornadomeet的博文首先把Toolbox下载下来,解压缩到某位置。
然后打开Matlab,把文件夹内的util和data利用Set Path添加至路径中。
接着打开tests 文件夹的test_example_CNN.m。
最后在文件夹CNN中运行该代码。
下面是test_example_CNN.m中的代码及注释,比较简单。
load mnist_uint8; %读取数据% 把图像的灰度值变成0~1,因为本代码采用的是sigmoid激活函数train_x = double(reshape(train_x',28,28,60000))/255;test_x = double(reshape(test_x',28,28,10000))/255;train_y = double(train_y');test_y = double(test_y');%% 卷积网络的结构为 6c-2s-12c-2s% 1 epoch 会运行大约200s,错误率大约为11%。
而100 epochs 的错误率大约为1.2%。
rand('state',0) %指定状态使每次运行产生的随机结果相同yers = {struct('type', 'i') % 输入层struct('type', 'c', 'outputmaps', 6, 'kernelsize', 5) % 卷积层struct('type', 's', 'scale', 2) % pooling层struct('type', 'c', 'outputmaps', 12, 'kernelsize', 5) % 卷积层struct('type', 's', 'scale', 2) % pooling层};opts.alpha = 1; % 梯度下降的步长opts.batchsize = 50; % 每次批处理50张图opts.numepochs = 1; % 所有图片循环处理一次cnn = cnnsetup(cnn, train_x, train_y); % 初始化CNNcnn = cnntrain(cnn, train_x, train_y, opts); % 训练CNN [er, bad] = cnntest(cnn, test_x, test_y); % 测试CNN%plot mean squared errorfigure; plot(cnn.rL);assert(er<0.12, 'Too big error');•1•2•3•4•5•6•7•8•9•10•11•12•13•14•15•16•17•18•19•20•21•22•23•24•25•26•27•28•29•30•31•32•33•34下面是cnnsetup.m中的代码及注释。
神经网络之反向传播算法(BP)公式推导(超详细)

神经⽹络之反向传播算法(BP)公式推导(超详细)反向传播算法详细推导反向传播(英语:Backpropagation,缩写为BP)是“误差反向传播”的简称,是⼀种与最优化⽅法(如梯度下降法)结合使⽤的,⽤来训练⼈⼯神经⽹络的常见⽅法。
该⽅法对⽹络中所有权重计算损失函数的梯度。
这个梯度会反馈给最优化⽅法,⽤来更新权值以最⼩化损失函数。
在神经⽹络上执⾏梯度下降法的主要算法。
该算法会先按前向传播⽅式计算(并缓存)每个节点的输出值,然后再按反向传播遍历图的⽅式计算损失函数值相对于每个参数的偏导数。
我们将以全连接层,激活函数采⽤Sigmoid函数,误差函数为Softmax+MSE损失函数的神经⽹络为例,推导其梯度传播⽅式。
准备⼯作1、Sigmoid 函数的导数回顾sigmoid函数的表达式:\sigma(x) = \frac{1}{1+e^{-x}}其导数为:\frac{d}{dx}\sigma(x) = \frac{d}{dx} \left(\frac{1}{1+e^{-x}} \right)= \frac{e^{-x}}{(1+e^{-x})^2}= \frac{(1 + e^{-x})-1}{(1+e^{-x})^2}=\frac{1+e^{-x}}{(1+e^{-x})^2} - \left(\frac{1}{1+e^{-x}}\right)^2= \sigma(x) - \sigma(x)^2= \sigma(1-\sigma)可以看到,Sigmoid函数的导数表达式最终可以表达为激活函数的输出值的简单运算,利⽤这⼀性质,在神经⽹络的梯度计算中,通过缓存每层的 Sigmoid 函数输出值,即可在需要的时候计算出其导数。
Sigmoid 函数导数的实现:import numpy as np # 导⼊ numpydef sigmoid(x): # sigmoid 函数return 1 / (1 + np.exp(-x))def derivative(x): # sigmoid 导数的计算return sigmoid(x)*(1-sigmoid(x))2、均⽅差函数梯度均⽅差损失函数表达式为:L = \frac{1}{2}\sum_{k=1}^{K}(y_k-o_k)^2其中y_k为真实值,o_k为输出值。
神经网络中的反向传播算法

神经网络中的反向传播算法神经网络是一种模仿人脑神经元工作原理的计算模型,具有自主学习和适应能力,已经成为人工智能领域的前沿技术。
然而,神经网络的训练过程需要大量的数据和时间,常常考验着研究人员的耐心和智慧。
其中最重要的一个算法就是反向传播算法,本文将从以下几个方面进行探讨。
一、神经网络的基本结构及工作原理神经网络是由大量人工神经元构成的,每个神经元接收来自其他神经元的输入信号,通过非线性函数(如sigmoid函数)进行加权求和,并生成一个输出信号。
神经网络通常由输入层、隐藏层和输出层组成,其中输入层通过传递输入信号激活隐藏层,隐藏层通过传递激活后的信号影响输出层。
每层神经元都会有一组权重,用于控制输入信号在这一层中的传播和计算。
而反向传播算法就是通过不断调整神经元间相关的权重,来最小化神经网络对训练数据的误差。
二、反向传播算法的基本思想反向传播算法主要分为两部分:前向传播和反向误差传播。
在前向传播过程中,输入信号会经过各个神经元的加权求和和激活函数处理,计算得到网络的输出。
而在反向误差传播过程中,首先计算网络输出误差,然后分别计算每个神经元权重对误差的贡献,最后反向传回网络,以此来更新权重。
三、反向传播算法的实现过程对于一个有n个训练样本的神经网络,我们需要不断迭代调整权重,达到优化网络的目的。
具体步骤如下:1. 首先将训练数据输入到神经网络中,得到网络输出。
2. 根据网络输出和实际标签计算误差,由于常用的误差函数是均方误差函数,所以误差可以通过网络输出与样本标签的差值平方和来计算。
3. 反向计算误差对每个神经元的输出的贡献,然后再根据误差对该神经元相应权重的贡献来计算梯度下降也就是权重的变化量。
4. 根据得到的梯度下降值,更新每个神经元的权重。
(注意反向传播需要使用到链式法则,要将误差从输出层传递回隐藏层和输入层)5. 重复步骤1到4,直到误差满足收敛条件或者达到预设的最大迭代次数。
四、反向传播算法的优化反向传播算法是一种经典的训练神经网络的方法,但是也有一些需要注意的问题。
神经网络——前向传播与反向传播公式推导

神经⽹络——前向传播与反向传播公式推导概述对于⼀个最原⽣的神经⽹络来说,BP反向传播是整个传播中的重点和核⼼,也是机器学习中的⼀个⼊门算法。
下⾯将以逻辑回归的分类问题为例,从最简单的单个神经元开始引⼊算法,逐步拓展到神经⽹络中,包括BP链式求导、前向传播和反向传播的向量化。
最后利⽤Python语⾔实现⼀个原始的神经⽹络结构作为练习。
需了解的预备知识:代价函数、逻辑回归、线性代数、多元函数微分参考:《ML-AndrewNg》神经元单个神经元是最简单的神经⽹络,仅有⼀层输⼊,⼀个输出。
【前向传播】\[z={{w}_{1}}\cdot {{x}_{1}}+{{w}_{2}}\cdot {{x}_{2}}+{{w}_{3}}\cdot {{x}_{3}}+b=\left[ \begin{matrix} {{w}_{1}} & {{w}_{2}} & {{w}_{3}} \\\end{matrix} \right]\left[ \begin{matrix} {{x}_{1}} \\ {{x}_{2}} \\ {{x}_{3}} \\ \end{matrix} \right]+b \]若激活函数为sigmoid函数,则\[\hat{y}=a =sigmoid(z) \]【代价函数】\[J(W,b)=-[y\log (a)+(1-y)\log (1-a)] \]【计算delta】\[deleta=a-y=\hat{y}-y \]【计算偏导数】\[\frac{\partial J}{\partial w}=\frac{\partial J}{\partial a}\cdot \frac{\partial a}{\partial z}=-(\frac{y}{a}+\frac{y-1}{1-a})a(a-1)=(a-y)x^T=(\hat{y}-y)x^T \]\[\frac{\partial J}{\partial b}=\frac{\partial J}{\partial a}\cdot \frac{\partial a}{\partial z}\cdot \frac{\partial z}{\partial b}=a-y=\hat{y}-y \]【更新权重】\[w = w-\alpha*\frac{\partial J}{\partial w} \]\[b = b-\alpha*\frac{\partial J}{\partial b} \]拓展到神经⽹络假设⽹络结构如上图所⽰,输⼊特征为2个,输出为⼀个三分类,隐藏层单元数均为4,数据如列表中所⽰,共20条。
BP(BackPropagation)反向传播神经网络介绍及公式推导
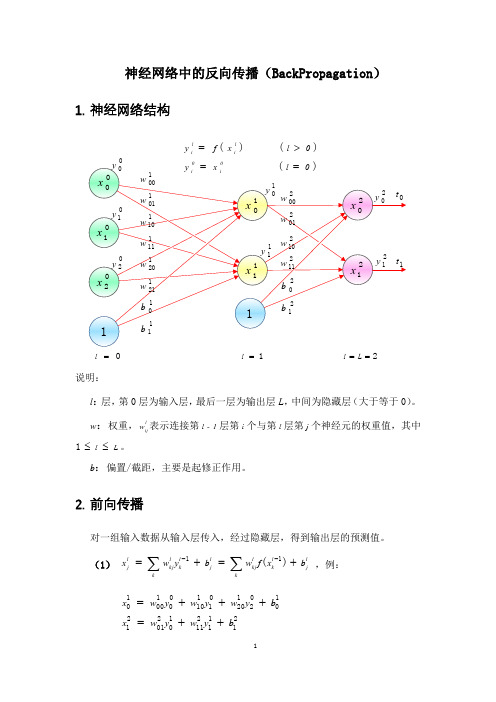
5. 链式法则
如果函数 u (t )及 v (t )都在 t 点可导,复合函数 z f(u,v)在对应点(u,v)具 有连续偏导数,z 在对应 t 点可导,则其导数可用下列公式计算:
dz z du z dv dt u dt v dt
6. 神经元误差
定义 l 层的第 i 个神经元上的误差为 il 即: (7)
5
附:激活函数
非线性: 当激活函数是线性的时候,一个两层的神经网络就可以逼近基 本上所有的函数了。但是,如果激活函数是恒等激活函数的时候(即 f(x)=x) ,就不满足这个性质了,而且如果 MLP 使用的是恒等激活函数, 那么其实整个网络跟单层神经网络是等价的。 可微性: 当优化方法是基于梯度的时候,这个性质是必须的。 单调性: 当激活函数是单调的时候,单层网络能够保证是凸函数。 f(x)≈x: 当激活函数满足这个性质的时候, 如果参数的初始化是 random 的很小的值, 那么神经网络的训练将会很高效; 如果不满足这个性质, 那 么就需要很用心的去设置初始值。 输出值的范围: 当激活函数输出值是 有限 的时候,基于梯度的优化方 法会更加 稳定,因为特征的表示受有限权值的影响更显著;当激活函数 的输出是 无限 的时候, 模型的训练会更加高效, 不过在这种情况小, 一 般需要更小的 learning rate.
l i
j
l 1 E x j x lj 1 xil
j
x lj 1 x
l i
jl 1 ,其中 l L
将公式(1) x j
l 1
w
k
l 1 l kj k
y blj 1
w
k
l 1 kj
f( xkl ) blj 1 ,对 x i 的求导
反向传播算法代码
反向传播算法代码反向传播算法(Backpropagation Algorithm)是深度学习中常用的一种神经网络训练算法,用于优化神经网络的参数。
下面是反向传播算法的代码实现:首先,我们需要定义一些函数,包括神经网络前向传播函数和误差函数(均方差误差函数):```pythonimport numpy as npdef sigmoid(x):return 1 / (1 + np.exp(-x))def relu(x):return np.maximum(0, x)def forward_propagation(X, W1, b1, W2, b2):Z1 = np.dot(X, W1) + b1A1 = relu(Z1)Z2 = np.dot(A1, W2) + b2A2 = sigmoid(Z2)return Z1, A1, Z2, A2def compute_cost(A2, Y):m = Y.shape[0]cost = (-1/m) * np.sum(Y * np.log(A2) + (1 - Y) *np.log(1 - A2))cost = np.squeeze(cost)return cost```下面是反向传播算法的代码实现:```pythondef backward_propagation(X, Y, Z1, A1, Z2, A2, W1, W2, b1,m = Y.shape[0]dZ2 = A2 - YdW2 = (1/m) * np.dot(A1.T, dZ2)db2 = (1/m) * np.sum(dZ2, axis=0, keepdims=True)dA1 = np.dot(dZ2, W2.T)dZ1 = np.multiply(dA1, np.int64(A1 > 0))dW1 = (1/m) * np.dot(X.T, dZ1)db1 = (1/m) * np.sum(dZ1, axis=0, keepdims=True)gradients = {"dW1": dW1,"db1": db1,"dW2": dW2,"db2": db2}return gradients```最后,我们使用梯度下降算法来更新神经网络参数:```pythondef update_parameters(W1, b1, W2, b2, gradients, learning_rate):dW1 = gradients["dW1"]db1 = gradients["db1"]dW2 = gradients["dW2"]db2 = gradients["db2"]W1 = W1 - learning_rate * dW1b1 = b1 - learning_rate * db1W2 = W2 - learning_rate * dW2b2 = b2 - learning_rate * db2parameters = {"W1": W1,"b1": b1,"W2": W2,"b2": b2}return parameters```通过以上代码,我们可以实现反向传播算法来训练神经网络,优化网络参数,从而能够更好地进行分类或回归任务。
神经网络前向传播和反向传播公式详细推导
神经⽹络前向传播和反向传播公式详细推导神经⽹络的前向传播和反向传播公式详细推导本篇博客是对Michael Nielsen 所著的《Neural Network and Deep Learning 》第2章内容的解读,有兴趣的朋友可以直接阅读原⽂。
对神经⽹络有些了解的⼈可能都知道,神经⽹络其实就是⼀个输⼊到输出的映射函数:,函数的系数就是我们所要训练的⽹络参数,只要函数系数确定下来,对于任何输⼊我们就能得到⼀个与之对应的输出,⾄于是否符合我们预期,这就属于如何提⾼模型性能⽅⾯的问题了,本⽂不做讨论。
那么问题来了,现在我们⼿中只有训练集的输⼊和输出,我们应该如何调整⽹络参数使⽹络实际的输出与训练集的尽可能接近? 在开始正式讲解之前,让我们先对反向传播过程有⼀个直观上的印象。
反向传播算法的核⼼是代价函数对⽹络中参数(各层的权重和偏置)的偏导表达式。
这些表达式描述了代价函数值随权重或偏置变化⽽变化的程度。
到这⾥,BP 算法的思路就很容易理解了:如果当前代价函数值距离预期值较远,那么我们通过调整和的值使新的代价函数值更接近预期值(和预期值相差越⼤,则和调整的幅度就越⼤)。
⼀直重复该过程,直到最终的代价函数值在误差范围内,则算法停⽌。
BP 算法可以告诉我们神经⽹络在每次迭代中,⽹络的参数是如何变化的,理解这个过程对于我们分析⽹络性能或优化过程是⾮常有帮助的,所以还是尽可能搞透这个点。
我也是之前⼤致看过,然后发现看⼀些进阶知识还是需要BP 的推导过程作为⽀撑,所以才重新整理出这么⼀篇博客。
前向传播过程 在开始反向传播之前,先提⼀下前向传播过程,即⽹络如何根据输⼊得到输出的。
这个很容易理解,粗略看⼀下即可,这⾥主要是为了统⼀后⾯的符号表达。
记为第层第个神经元到第层第个神经元的权重,为第层第个神经元的偏置,为第层第个神经元的激活值(激活函数的输出)。
不难看出,的值取决于上⼀层神经元的激活:将上式重写为矩阵形式:为了⽅便表⽰,记为了⽅便表⽰,记为每⼀层的权重输⼊,为每⼀层的权重输⼊,式则变为。
神经网络中的反向传播算法详解
神经网络中的反向传播算法详解神经网络是一种模拟人脑神经元网络结构的计算模型,它通过学习和调整权重来实现对输入数据的分类和预测。
而神经网络中的反向传播算法则是实现这一目标的重要工具。
本文将详细解析神经网络中的反向传播算法,包括其原理、步骤和应用。
一、反向传播算法的原理神经网络中的反向传播算法基于梯度下降法,通过计算损失函数对网络中各个权重的偏导数来更新权重。
其核心思想是将输出误差从网络的输出层向输入层进行传播,并根据误差的梯度来调整网络中的权重,以最小化损失函数。
二、反向传播算法的步骤反向传播算法的具体步骤如下:1. 前向传播:将输入数据通过神经网络的各个层,得到输出结果。
2. 计算损失函数:将网络的输出结果与真实值进行比较,计算损失函数的值。
3. 反向传播:从输出层开始,计算损失函数对网络中每个权重的偏导数。
4. 权重更新:根据偏导数的值和学习率,更新网络中的权重。
5. 重复以上步骤:重复执行前向传播、损失函数计算、反向传播和权重更新,直到达到预设的停止条件。
三、反向传播算法的应用反向传播算法在神经网络中的应用非常广泛,以下是几个典型的应用场景:1. 图像分类:神经网络可以通过反向传播算法学习到图像的特征,从而实现对图像的分类。
2. 语音识别:通过训练神经网络,利用反向传播算法,可以实现对语音信号的识别和转录。
3. 自然语言处理:神经网络可以通过反向传播算法学习到文本的语义和语法信息,从而实现对文本的处理和理解。
4. 推荐系统:利用神经网络和反向传播算法,可以根据用户的历史行为和偏好,实现个性化的推荐。
四、反向传播算法的改进虽然反向传播算法在神经网络中得到了广泛应用,但它也存在一些问题,如容易陷入局部最优解、计算量大等。
为了克服这些问题,研究者们提出了许多改进的方法,如随机梯度下降法、正则化、批量归一化等。
五、结语神经网络中的反向传播算法是实现网络训练和权重调整的关键步骤。
通过前向传播和反向传播的结合,神经网络可以通过学习和调整权重,实现对输入数据的分类和预测。
神经网络的正反向传播算法推导
神经⽹络的正反向传播算法推导1 正向传播1.1 浅层神经⽹络为简单起见,先给出如下所⽰的简单神经⽹络:该⽹络只有⼀个隐藏层,隐藏层⾥有四个单元,并且只输⼊⼀个样本,该样本表⽰成⼀个三维向量,分别为为x1,x2和x3。
⽹络的输出为⼀个标量,⽤ˆy表⽰。
考虑该神经⽹络解决的问题是⼀个⼆分类的问题,把⽹络的输出解释为正样本的概率。
⽐⽅说输⼊的是⼀张图⽚(当然图⽚不可能只⽤三维向量就可以表⽰,这⾥只是举个例⼦),该神经⽹络去判断图⽚⾥⾯是否有猫,则ˆy代表该图⽚中有猫的概率。
另外,为衡量这个神经⽹络的分类表现,需要设置⼀个损失函数,针对⼆分类问题,最常⽤的损失函数是log−loss函数,该函数如下所⽰:L(y,ˆy)=−y×log(ˆy)−(1−y)×log(1−ˆy)上式只考虑⼀个样本的情况,其中y为真实值,ˆy为输出的概率。
1.1.1 单样本的前向传播我们把单个输⼊样本⽤向量表⽰为:\boldsymbol{x} = \left[ \begin{matrix} x_1 \\ x_2 \\ x_3 \end{matrix} \right] \tag{2}那么对于隐藏层中的第⼀个单元,如果不考虑激活函数,则其输出可以表⽰为:z^{[1]}_1 = \boldsymbol{w}^{[1]^T}_1\boldsymbol{x} + b^{[1]}_1 \tag{3}上式中,字母右上⾓的⽅括号中的数字代表这是神经⽹络的第⼏层,如果把输⼊层看作是第0层的话,那么这⾥的隐藏层就是第⼀层,字母的下标代表该层的第⼏个单元。
\boldsymbol{w}^{[1]}_1是权重向量,即给输⼊向量的每个元素⼀个权重,这些权重组合起来就形成了\boldsymbol{w}^{[1]}_1向量,把向量和其权重作点乘,再加上⼀个偏置标量b^{[1]}_1,就得到了该神经元的输出z^{[1]}_1。
同理可得隐藏层剩余三个单元的输出为:z^{[1]}_2 = \boldsymbol{w}^{[1]^T}_2\boldsymbol{x} + b^{[1]}_2 \tag{4}z^{[1]}_3 = \boldsymbol{w}^{[1]^T}_3\boldsymbol{x} + b^{[1]}_3 \tag{5}z^{[1]}_4 = \boldsymbol{w}^{[1]^T}_4\boldsymbol{x} + b^{[1]}_4 \tag{6}但是对于每⼀个神经单元,其输出必须有⼀个⾮线性激活函数,否则神经⽹络的输出就是输⼊向量的线性运算得到的结果,这样会⼤⼤限制神经⽹络的能⼒。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
神经网络中的反向传播法算法推导及matlab代码实现
最近在看深度学习的东西,一开始看的吴恩达的UFLDL教程,有中文版就直接看了,后来发现有些地方总是不是很明确,又去看英文版,然后又找了些资料看,才发现,中文版的译者在翻译的时候会对省略的公式推导过程进行补充,但是补充的又是错的,难怪觉得有问题。
反向传播法其实是神经网络的基础了,但是很多人在学的时候总是会遇到一些问题,或者看到大篇的公式觉得好像很难就退缩了,其实不难,就是一个链式求导法则反复用。
如果不想看公式,可以直接把数值带进去,实际的计算一下,体会一下这个过程之后再来推导公式,这样就会觉得很容易了。
说到神经网络,大家看到这个图应该不陌生:
这是典型的三层神经网络的基本构成,Layer L1是输入层,Layer L2是隐含层,Layer L3是隐含层,我们现在手里有一堆数据{x1,x2,x3,...,xn},输出也是一堆数据{y1,y2,y3,...,yn},现在要他们在隐含层做某种变换,让你把数据灌进去后得到你期望的输出。
如果你希望你的输出和原始输入一样,那么就是最常见的自编码模型(Auto-Encoder)。
可能有人会问,为什么要输入输出都一样呢?有什么用啊?其实应用挺广的,在图像识别,文本分类等等都会用到,我会专门再写一篇Auto-Encoder的文章来说明,包括一些变种之类的。
如果你的输出和原始输入不一样,那么就是很常见的人工神经网络了,相当于让原始数据通过一个映射来得到我们想要的输出数据,也就是我们今天要讲的话题。
本文直接举一个例子,带入数值演示反向传播法的过程,公式的推导等到下次写Auto-Encoder的时候再写,其实也很简单,感兴趣的同学可以自己推导下试试:)(注:本文假设你已经懂得基本的神经网络构成,如果完全不懂,可以参考Poll写的笔记:[Mechine Learning & Algorithm] 神经网络基础)
假设,你有这样一个网络层:
第一层是输入层,包含两个神经元i1,i2,和截距项b1;第二层是隐含层,包含两个神经元h1,h2和截距项b2,第三层是输出o1,o2,每条线上标的wi是层与层之间连接的权重,激活函数我们默认为sigmoid函数。
现在对他们赋上初值,如下图:
其中,输入数据 i1=0.05,i2=0.10;
输出数据o1=0.01,o2=0.99;
初始权重 w1=0.15,w2=0.20,w3=0.25,w4=0.30;
w5=0.40,w6=0.45,w7=0.50,w8=0.55
目标:给出输入数据i1,i2(0.05和0.10),使输出尽可能与原始输出o1,o2(0.01和0.99)接近。
Step 1 前向传播
1.输入层---->隐含层:
计算神经元h1的输入加权和:
神经元h1的输出o1:(此处用到激活函数为sigmoid函数):
同理,可计算出神经元h2的输出o2:
2.隐含层---->输出层:
计算输出层神经元o1和o2的值:
这样前向传播的过程就结束了,我们得到输出值为[0.75136079 , 0.772928465],与实际值[0.01 , 0.99]相差还很远,现在我们对误差进行反向传播,更新权值,重新计算输出。
Step 2 反向传播
1.计算总误差
总误差:(square error)
但是有两个输出,所以分别计算o1和o2的误差,总误差为两者之和:
2.隐含层---->输出层的权值更新:
以权重参数w5为例,如果我们想知道w5对整体误差产生了多少影响,可以用整体误差对w5求偏导求出:(链式法则)
下面的图可以更直观的看清楚误差是怎样反向传播的:
现在我们来分别计算每个式子的值:
计算:
计算:
(这一步实际上就是对sigmoid函数求导,比较简单,可以自己推导一下)计算:
最后三者相乘:
这样我们就计算出整体误差E(total)对w5的偏导值。
回过头来再看看上面的公式,我们发现:
为了表达方便,用来表示输出层的误差:
因此,整体误差E(total)对w5的偏导公式可以写成:
如果输出层误差计为负的话,也可以写成:
最后我们来更新w5的值:
(其中,是学习速率,这里我们取0.5)
同理,可更新w6,w7,w8:
3.隐含层---->隐含层的权值更新:
方法其实与上面说的差不多,但是有个地方需要变一下,在上文计算总误差对w5的偏导时,是从out(o1)---->net(o1)---->w5,但是在隐含层之间的权值更新时,是out(h1)---
->net(h1)---->w1,而out(h1)会接受E(o1)和E(o2)两个地方传来的误差,所以这个地方两个都要计算。
计算:
先计算:
同理,计算出:
两者相加得到总值:
再计算:
再计算:
最后,三者相乘:
为了简化公式,用sigma(h1)表示隐含层单元h1的误差:
最后,更新w1的权值:
同理,额可更新w2,w3,w4的权值:
这样误差反向传播法就完成了,最后我们再把更新的权值重新计算,不停地迭代,在这个例子中第一次迭代之后,总误差E(total)由0.298371109下降至0.291027924。
迭代10000次后,总误差为0.000035085,输出为[0.015912196,0.984065734](原输入为[0.01,0.99]),证明效果还是不错的。
88888888888888888888888888888888888888888888888888888888888888
clear all
clc
close all
i1=0.05; i2=0.10;
o1=0.01; o2=0.99;
w1=0.15; w2=0.20; w3=0.25; w4=0.30; b1=0.35;
w5=0.40; w6=0.45; w7=0.50; w8=0.55; b2=0.6;
% alpha=38.9
% epoch=6000;
alpha=0.5
epoch=10000;
for k=1:epoch
% forward:hidden layers
net_h1=w1*i1+w2*i2+b1*1;
out_h1=1/(1+exp(-net_h1));
net_h2=w3*i1+w4*i2+b1*1;
out_h2=1/(1+exp(-net_h2));
%forward:output layer
net_o1=w5*out_h1+w6*out_h2+b2*1;
net_o2=w7*out_h1+w8*out_h2+b2*1;
out_o1=1/(1+exp(-net_o1));
out_o2=1/(1+exp(-net_o2));
% cost function
E_total(k)=((out_o1-o1)^2+(out_o2-o2)^2)/2;
% backward: output layer
dE_dw5=-(o1-out_o1)*out_o1*(1-out_o1)*out_h1;
dE_dw6=-(o1-out_o1)*out_o1*(1-out_o1)*out_h2;
dE_dw7=-(o2-out_o2)*out_o2*(1-out_o2)*out_h1;
dE_dw8=-(o2-out_o2)*out_o2*(1-out_o2)*out_h2;
% backward: hidden layer
dE_douto1=-(o1-out_o1);
douto1_dneto1=out_o1*(1-out_o1);
% dEo1_douth1=-(o1-out_o1)*out_o1*(1-out_o1)
dEo1_dneto1=dE_douto1*douto1_dneto1;
dEo1_douth1=dEo1_dneto1*w5;
dEo1_douth2=dEo1_dneto1*w6;
dE_douto2=-(o2-out_o2);
douto2_dneto2=out_o2*(1-out_o2);
% dEo1_douth1=-(o1-out_o1)*out_o1*(1-out_o1)
dEo2_dneto2=dE_douto2*douto2_dneto2;
dEo2_douth1=dEo2_dneto2*w7;
dEo2_douth2=dEo2_dneto2*w8;
dE_dw1=(dEo1_douth1+dEo2_douth1)*out_h1*(1-out_h1)*i1; dE_dw2=(dEo1_douth1+dEo2_douth1)*out_h1*(1-out_h1)*i2; dE_dw3=(dEo1_douth2+dEo2_douth2)*out_h2*(1-out_h2)*i1; dE_dw4=(dEo1_douth2+dEo2_douth2)*out_h2*(1-out_h2)*i2;
w1=w1-alpha*dE_dw1;
w2=w2-alpha*dE_dw2;
w3=w3-alpha*dE_dw3;
w4=w4-alpha*dE_dw4;
w5=w5-alpha*dE_dw5;
w6=w6-alpha*dE_dw6;
w7=w7-alpha*dE_dw7;
w8=w8-alpha*dE_dw8;
end
v_E_total_k=E_total(k)
plot(E_total)。
