融合马尔科夫链_蒙特卡洛算法的改进通用似然不确定性估计方法在流域水文模型中的应用
马尔可夫链蒙特卡洛方法在生态学建模中的应用案例分析(八)

马尔可夫链蒙特卡洛方法在生态学建模中的应用案例分析引言生态学是研究生物与环境相互作用的学科,它涉及到多种不确定性因素,例如气候变化、生物种群的迁徙和扩散等。
为了更好地理解这些复杂的生态系统,科学家们需要依靠数学模型来进行建模和预测。
近年来,马尔可夫链蒙特卡洛方法在生态学建模中的应用越来越广泛,这种方法能够有效地模拟出生态系统中复杂的动态过程,为科学家们提供了一种强大的工具来研究生态系统的变化和演化。
马尔可夫链蒙特卡洛方法简介马尔可夫链蒙特卡洛方法(Markov Chain Monte Carlo, MCMC)是一种基于马尔可夫链的随机模拟算法。
它通过在状态空间中进行随机抽样,来模拟出系统的演化过程。
MCMC方法最早是由Stanislaw Ulam和John von Neumann在上世纪40年代提出的,后来由Metropolis等人在上世纪50年代发展完善。
MCMC方法的核心思想是通过马尔可夫链的转移矩阵来实现状态的转移和抽样,最终达到对系统进行模拟的目的。
马尔可夫链蒙特卡洛方法在生态学建模中的应用马尔可夫链蒙特卡洛方法在生态学建模中的应用非常广泛,它能够帮助科学家们对生态系统中的种群动态、演化过程和生态系统的稳定性进行深入研究。
例如,在研究生态系统中的食物链结构和物种迁徙过程时,科学家们可以利用MCMC方法来模拟出不同物种之间的相互作用和迁徙规律,从而更好地理解生态系统中的复杂动态过程。
另外,MCMC方法还可以在生态系统中的资源分配和能量流动方面发挥重要作用。
通过模拟不同环境条件下的资源分配和能量流动过程,科学家们可以更好地预测生态系统的稳定性和可持续性,为生态保护和资源管理提供科学依据。
案例分析:MCMC方法在森林生态系统建模中的应用为了更具体地展示马尔可夫链蒙特卡洛方法在生态学建模中的应用,下面将以森林生态系统为例进行案例分析。
森林生态系统是地球上最重要的生态系统之一,它不仅是生物多样性的重要栖息地,也是全球碳循环和气候调节的重要组成部分。
基于马尔可夫链蒙特卡洛方法的数据关联算法研究

基于马尔可夫链蒙特卡洛方法的数据关联算法研究李景熹;王树宗;王航宇【期刊名称】《武汉理工大学学报(交通科学与工程版)》【年(卷),期】2007(031)006【摘要】数据关联是杂波环境下多目标跟踪问题的难点之一.文中提出了一种基于马尔可夫链蒙特卡洛(MCMC)方法的数据关联算法(MCMCDA),该算法通过在相应的关联事件空间中采样,可以有效地估计数据的边际关联概率,而且算法的估计精度可根据需要进行调节.仿真结果表明,在需要跟踪的目标数目较多,探测概率较低、杂波概率较高的情况下,JPDA算法因出现"组合爆炸"问题而难以在实际中应用;MCMCDA算法则能在保持较高估计精度的情况下降低计算负荷,从而能够较好地满足实时跟踪系统的要求.【总页数】4页(P1045-1048)【作者】李景熹;王树宗;王航宇【作者单位】海军工程大学海军兵器新技术应用研究所,武汉,430033;海军驻426厂军代室,大连,116005;海军工程大学海军兵器新技术应用研究所,武汉,430033;海军工程大学电子工程学院,武汉,430033【正文语种】中文【中图分类】TP301.6【相关文献】1.基于数据关联的多雷达点迹融合算法研究 [J], 张昕;张博文;张玉萍;李军侠;燕瑞超2.基于FP-growth关联规则的图书馆数据快速挖掘算法研究 [J], 文芳;黄慧玲;李腾达;王佳斌3.基于FP-growth关联规则的图书馆数据快速挖掘算法研究 [J], 文芳;黄慧玲;李腾达;王佳斌4.基于关联关系的海洋数值预报数据推荐算法研究 [J], 李学强;赵文洋;解玉琪5.基于关联规则与相似度的数据挖掘算法研究 [J], 李英;汤庸因版权原因,仅展示原文概要,查看原文内容请购买。
马尔可夫链蒙特卡洛方法在环境科学中的应用案例分析

马尔可夫链蒙特卡洛方法在环境科学中的应用案例分析介绍马尔可夫链蒙特卡洛方法,简称MCMC,是一种用于模拟概率分布的数值方法,它通过马尔可夫链的随机抽样来生成服从特定概率分布的样本。
在环境科学中,MCMC方法被广泛应用于气象、水文、生态等领域,用于模拟自然系统的复杂动态过程,评估环境风险和预测环境变化。
本文将通过几个实际案例,探讨MCMC方法在环境科学中的应用。
气候变化模拟气候变化对全球环境产生深远影响,因此对气候变化进行准确模拟和预测至关重要。
MCMC方法可以用于气候模型的参数估计和不确定性分析。
例如,研究人员可以利用MCMC方法对气候模型的参数进行贝叶斯估计,从而获得更加可靠的气候模拟结果。
通过对气候系统进行MCMC模拟,可以更好地理解气候变化的概率分布和不确定性,为应对气候变化提供科学依据。
水文模拟与预测水资源是人类生存和发展的重要基础,而气候变化和人类活动对水资源的影响日益显著。
MCMC方法在水文模拟与预测中发挥了重要作用。
例如,通过MCMC方法可以对降雨、蒸发和径流等水文要素的概率分布进行模拟,从而实现对水文过程的准确模拟和预测。
这对于水资源管理、洪涝灾害预警等方面具有重要意义。
生态系统评估生态系统是地球上自然资源的重要组成部分,而生态系统的稳定性和可持续发展对于人类社会的发展至关重要。
MCMC方法可以用于生态系统的评估与管理。
例如,通过MCMC方法可以对生态系统中各种因素之间的概率关系进行建模,从而实现对生态系统动态过程的模拟和预测。
这有助于科学评估生态系统的健康状况,为生态环境保护和资源管理提供科学依据。
结语马尔可夫链蒙特卡洛方法在环境科学中的应用案例众多,涉及气候变化、水文模拟、生态系统评估等多个领域。
通过MCMC方法,可以更好地理解自然环境的复杂动态过程,为环境保护和可持续发展提供科学支持。
随着计算机技术的不断发展和数据的不断积累,MCMC方法在环境科学中的应用前景将更加广阔。
希望本文所介绍的MCMC方法在环境科学中的应用案例,能够为读者提供一些启发和思考。
基于MCMC和ES-MDA方法的地下水数值模型非均质参数场及开采量的反演研究

2023年10月水 利 学 报SHUILI XUEBAO第54卷 第10期文章编号:0559-9350(2023)10-1236-12收稿日期:2023-04-08;网络首发日期:2023-10-19网络首发地址:https:??kns.cnki.net?kcms?detail?11.1882.TV.20231018.1051.001.html基金项目:国家自然科学基金重点项目(U21A2004)作者简介:刘墉达(1998-),硕士生,主要从事地下水数值模拟研究。
E-mail:liuyongda@tju.edu.cn通信作者:陈喜(1964-),博士,教授,主要从事地下水数值模拟研究。
E-mail:xi_chen@tju.edu.cn基于MCMC和ES-MDA方法的地下水数值模型非均质参数场及开采量的反演研究刘墉达,陈 喜,高 满,孟详博,刘维翰,黄日超(天津大学地球系统科学学院表层地球系统科学研究院,天津300072)摘要:马尔科夫链蒙特卡罗方法(MCMC)和多重数据同化集合平滑器方法(ES-MDA)近年来在地下水参数反演得到广泛应用,但对三维多层非均质含水层参数反演精度和计算效率还缺乏对比分析。
本文构建了含有基于Karhunen-Loève展开的非均质参数场的潜水和多层承压水含水层案例,并建立了地下水数值模型和基于Kriging方法的替代模型,模拟含水层分层水头变化,探讨了基于替代模型的MCMC、替代模型和数值模型相结合的两阶段MCMC以及ES-MDA方法反演的含水层渗透系数以及开采量。
结果表明,针对本文算例,在非均质参数和开采量的反演中,相比而言,两阶段MCMC反演参数精度更高,ES-MDA方法计算效率更高。
本研究为地下水数值模型参数反演方法选择提供参考依据。
关键词:MCMC算法;ES-MDA算法;替代模型;地下水参数;地下水数值模拟 中图分类号:TV123文献标识码:Adoi:10.13243?j.cnki.slxb.202301971 研究背景对于复杂的多层含水层,根据有限的地下水水位等观测数据,反演水文地质参数、开采量等通常存在不唯一性、不确定性问题,且在调用地下水数值模型进行参数反演时,随着调用次数和参数维度增加,反演计算成本变高。
河流水文模拟与水资源管理技术研究

河流水文模拟与水资源管理技术研究随着人口的不断增长和城市化进程的不断推进,水资源管理已成为各地政府重点关注的问题。
如何科学地利用和保护水资源,成为了当今社会面临的一大难题。
河流是水资源管理的重要组成部分,而河流水文模拟是研究河流水环境和水资源管理的重要手段之一。
在这篇文章中,我们将探讨河流水文模拟与水资源管理技术研究的现状和未来发展趋势。
一、河流水文模拟的意义河流水文模拟是指利用计算机模拟河流水文过程,包括径流、水位、流速等参数,以分析和优化水文系统的运行。
河流水文模拟能够预测河流水位、洪水、干旱等自然灾害,为水资源管理提供重要的参考依据。
河流水文模拟还能够模拟河流生态系统的运转过程,探究河流水质、水生态环境,为生态保护和河流治理提供科学依据。
二、水资源管理技术的现状水资源管理技术的现状可以从以下几方面进行分析。
1. 水资源综合管理水资源综合管理是指对水资源进行整体规划和管理,从多方面利用和保护水资源。
近年来,各地政府加强了对水资源综合管理的重视,通过制定相关政策和建立管理机制,有效管理和利用水资源。
2. 水污染治理技术水污染治理技术是指采用多种技术手段,对水体中的污染物进行去除和控制。
目前,水污染治理技术已经相当成熟,包括化学混凝沉淀、生物处理、吸附等多种技术手段。
这些技术的应用,有效改善了水环境质量。
3. 智能水利智能水利是指通过应用现代信息技术,构建智能水务系统,实现对水资源管理的智能化。
智能水利技术可以对水资源进行智能化监测、分析、控制和调度,提高水资源利用效率和水环境保护效果。
三、河流水文模拟技术的研究现状河流水文模拟技术的研究现状可以从以下几方面进行分析。
1. 模型建立河流水文模拟的核心是模型建立,建立优质的水文模型对实现精准预测和优化管理至关重要。
目前,有很多流域水文模型,包括SWAT、HSPF等,不同的模型适用于不同的河流和研究需求。
2. 模型参数优化模型参数优化对水文模拟精度和可信度有很大的影响。
蒙特卡洛与马尔可夫方法在降水预测中的应用
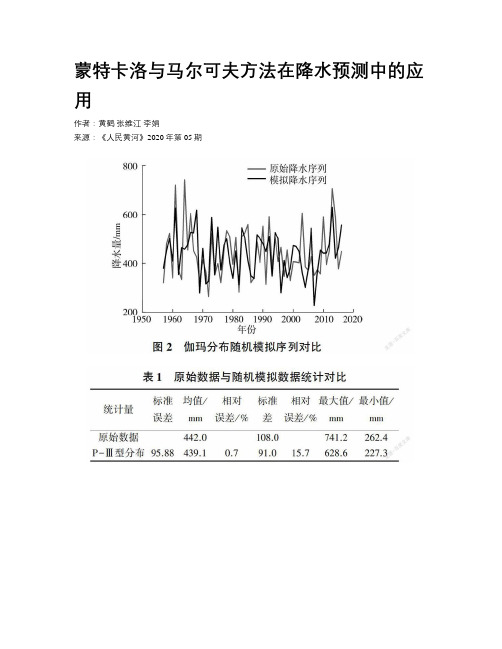
蒙特卡洛与马尔可夫方法在降水预测中的应用作者:黄鹤张维江李娟来源:《人民黄河》2020年第05期摘要:為了更深入地分析原州区的降水特征,为该区域水资源预测提供依据,基于原州区1957—2016年60 a降水资料,采用蒙特卡洛方法推求降水分布,采用K-S检验对模型进行显著性检验,采用基于欧氏距离的层次聚类方法进行状态划分,确定了原州区的降水分布,建立了适用于原州区的滑动平均加权马尔可夫预测模型。
根据已有数据验证了预测结果的有效性,再结合已确定的降水分布,通过K-S检验,检验了未来5 a降水预测的准确性。
结果表明:原州区降水分布符合P-Ⅲ型分布;马尔可夫模型适用于原州区降水预测,且未来5 a的降水预测结果是准确的,分别为508.5、520.8、554.9、451.0、466.6 mm。
关键词:蒙特卡洛方法;马尔可夫模型;随机模拟;降水预测;原州区;K-S检验中图分类号:TV11 文献标志码:Adoi:10.3969/j.issn.1000-1379.2020.05.004Abstract: In order to analyze the characteristics of precipitation in YuanzhouDistrict and provide a basis for water resources prediction in the region, based on the precipitation data from 1957 to 2016 of the district, the Monte Carlo method was used to estimate the precipitation distribution and the K-S test was used to model the significant test. It used the hierarchical clustering method based on Euclidean distance to divide the state, determined the precipitation distribution of the region and established a sliding average weighted Markov prediction model which was suitable for Yuanzhou District. Based on the existing data, the true validity of the prediction results was verified. Combined with the determined precipitation distribution, the accuracy of precipitation prediction for the next 5 years was tested by K-S test. Comparing with Pearson three-type distribution, the results show that the precipitation distribution in Yuanzhou District is more consistent with the log-normal distribution. The Markov model can be applied to the precipitation forecast in the region, and the prediction results of the sliding average precipitation in the next 5 years are real and effective,respectively 508.5, 520.8, 554.9, 451.0 and 466.6 mm.Key words: Monte Carlo method; Markov model; stochastic simulation; precipitation prediction; Yuanzhou District; K-S test1 引言由于客观世界中的一些现象可能与另一种现象存在着某种相似性,因此我们经常从一种现象出发来研究另一种现象。
基于改进马尔柯夫链的区域干旱预测
基于改进马尔柯夫链的区域干旱预测
王志成
【期刊名称】《国际沙棘研究与开发》
【年(卷),期】2018(000)002
【摘要】本文依据阿克苏河支流协和拉水文站1961—2007年降水量资料,采用SPI指数进行干旱分级,在此基础上,建立了适用于研究区的加权马尔科夫链预测模型,并对模型进行改进预测.结果表明:该模型可提高中度以上干旱等级预测精度,为流域干旱预警及抗旱减灾提供了较好的参考价值.
【总页数】3页(P55-57)
【作者】王志成
【作者单位】新疆塔里木河流域管理局,新疆库尔勒 841000
【正文语种】中文
【中图分类】P331
【相关文献】
1.基于改进马尔柯夫链的区域干旱预测 [J], 王志成;
2.基于改进LSTM的区域综合能源系统多元负荷短期预测研究 [J], 田浩含;张智晟;于道林
3.基于典型代表电站和改进SVM的区域光伏功率短期预测方法 [J], 张扬科;李刚;李秀峰
4.基于改进BP神经网络的干旱区芦苇腾发量预测模型 [J], 苏里坦;玉米提;宋郁东
5.基于区域气候模式与作物干旱模式嵌套技术的华北农业干旱监测预测 [J], 邬定荣;刘建栋;刘玲;房世波;姜朝阳;罗立军
因版权原因,仅展示原文概要,查看原文内容请购买。
马尔可夫链蒙特卡洛方法在环境科学中的应用案例分析(Ⅲ)
马尔可夫链蒙特卡洛方法在环境科学中的应用案例分析马尔可夫链蒙特卡洛方法是一种重要的随机模拟技术,广泛应用于金融、生物、物理等领域。
在环境科学领域,马尔可夫链蒙特卡洛方法同样发挥着重要的作用。
本文将通过几个具体的应用案例,介绍马尔可夫链蒙特卡洛方法在环境科学中的应用。
案例一:气候模拟气候模拟是环境科学领域中一个重要的问题。
马尔可夫链蒙特卡洛方法可以用来模拟气候系统的随机性。
通过对气候系统中的各种参数进行采样,并使用马尔可夫链蒙特卡洛方法进行模拟,可以得到气候系统的概率分布。
这对于预测未来气候变化、制定应对气候变化的政策具有重要意义。
案例二:水资源管理在水资源管理中,马尔可夫链蒙特卡洛方法可以用来模拟水文过程中的随机变量,比如降雨量、蒸发量等。
通过对这些随机变量进行采样,并使用马尔可夫链蒙特卡洛方法进行模拟,可以得到水资源的概率分布。
这对于合理利用和管理水资源具有重要意义。
案例三:生态系统建模生态系统是环境科学中一个复杂的系统。
马尔可夫链蒙特卡洛方法可以用来对生态系统进行建模和模拟。
通过对生态系统中的各种参数进行采样,并使用马尔可夫链蒙特卡洛方法进行模拟,可以得到生态系统的概率分布。
这对于保护生态环境、维护生物多样性具有重要意义。
案例四:大气污染模拟大气污染是环境科学中一个严重的问题。
马尔可夫链蒙特卡洛方法可以用来模拟大气污染物的扩散和传播过程。
通过对大气污染物的扩散和传播过程中的各种参数进行采样,并使用马尔可夫链蒙特卡洛方法进行模拟,可以得到大气污染物的概率分布。
这对于预测大气污染的影响范围、制定减排政策具有重要意义。
结论马尔可夫链蒙特卡洛方法在环境科学中具有广泛的应用前景。
通过对环境系统中的各种随机变量进行采样,并使用马尔可夫链蒙特卡洛方法进行模拟,可以得到环境系统的概率分布,为环境科学领域的研究和应用提供重要的参考。
因此,我们有理由相信,马尔可夫链蒙特卡洛方法将在环境科学领域发挥越来越重要的作用。
水文模型参数不确定性分析方法探讨
() , + 一 Ob , , ) =( 6 lO , . . .
( )从指 定的先 验概率 中抽取 : 3 ,
X"dx ,’,此处 =) ,v ≠I ‘ 1 (L )  ̄ :. c j 。
作 者简 介 :陈 昌军 ( 9 4年 一 ) 男 , 高 级 工 程 师 。 17 ,
水 文水 资源
水 利规 划与 设计
2 1 第 3期 0 2年
水 文模 型 参数 不确 定 性 分析 方 法探 讨
陈 昌军 郑雄 伟
( 浙江省水利 水 电勘 测设 计院 杭 州 3 0 0 ) 1 02
【 摘 要 】 应用 基 于马 尔科 夫 链 蒙托 卡 罗 ( a k v C a n M n e C r o M r o h i o t a l )理 论 的 删 ( h e r p l t e M t o o i S
f xY = —— (,) —
2c √ 一 7 1
一
链 收 敛 后 , 两 参 数 散 点 图见 图 2 ,结 果 与 已
一
{ 却
2 t … 19 .
+ )
知 的概率 分布相一致 。 由此可见 ,M H算法可 以 成 功 模 拟 出参 数 后 验 分 布 的强 香 蕉 形 曲线 ,故 可
2 2 模 拟 验 证 . 根 据 以 上 马 尔 科 夫 链 蒙 托 卡 罗 法 的 算 法 原 理 ,采 用 M T A A L B语 言 编 写 计 算 程序 进 行 模 拟 计 算 , 为 测 试 计 算 程 序 的 正 确 性 , 检 验 M ( h H te
M t o o i a t n s l o i h e r p l H s i g a g r t m)算 法 在 不 确 S
地下水模拟不确定性问题的多模型分析
地下水模拟不确定性问题的多模型分析宋凯;刘丹;刘建【摘要】Multiple Model Analysis was applied to study the groundwater modelling uncertainties caused by the deviation of model structure and heterogeneity in aquifer media. According to different natural conditions,two hydrogeological conceptual models were established. Using a large number of model parameter data,obtained through hydrogeological tests,as a priori information and based on the two conceptual models,a series of seepage field models was constructed using the Adaptive Metropolis-Markov Chain Monte Carlo method that acceptance condition was adjusted. Uncertainties of modelling output data are analysed based on corrected Akaike's Information Criteron. Research indicates that the ergodicity and convergence of sample parameters will not be affected by changes in acceptance conditions. The model output data include the following effects:"same results with different parameters"and"same results with different models". Although these effects exist,the model structure is closer to the objective of improving the probability of obtaining a high precision model. The proportion of the primary conceptual model,with a variance between 1 and 2,is 65%. When the model with Delta values greater than 10 is excluded,the top 10 models are retained and the cumulative a posterior probability is 0. 996. The proportion of the second conceptual model,with a variance between 1 and 2,is 46%. When the model with Delta values greater than 10 isexcluded,the top 21 models are retained. The cumulative posterior probability of the top 10 models is only 0.884.%为研究地下水概念模型的构建偏差及水文地质参数非均质性引起的地下水渗流场模拟不确定性问题,首先根据自然条件的差异构建2组概念模型;以大量原位水文地质试验获取的待估参数数据为先验信息,应用接受条件进行调整的马尔科夫链蒙特卡罗方法(MCMC)中的自适应采样算法(A-M)进行参数样本采集,并基于2组概念模型分别构建多组渗流场计算模型;将输出结果基于AICc准则进行相关多模型定量分析.研究结果表明:调整的A-M采样算法,参数样本的遍历性及收敛性未受影响;计算模型中除存在"异参同效",亦存在"异构同效";异构同效虽存在,但更接近客观条件的概念模型结构获取高精度模型的概率较大,1#、2#概念模型中方差值介于1~2的模型比例分别为65%、46%;各概念模型的100组计算模型中,剔除Delta值大于10的计算模型后,1#模型中仅保留排名前10个模型,累计后验概率0.996,2#模型则保留排名前21个模型,而其排名前10的模型累计后验概率仅为0.884.【期刊名称】《西南交通大学学报》【年(卷),期】2018(053)003【总页数】8页(P574-581)【关键词】地下水模拟;不确定性;多模型分析;AM-MCMC【作者】宋凯;刘丹;刘建【作者单位】西南交通大学地球科学与环境工程学院,四川成都610031;西南交通大学地球科学与环境工程学院,四川成都610031;西南交通大学地球科学与环境工程学院,四川成都610031【正文语种】中文【中图分类】P641.2近年来,地下水模拟已成为研究地下水环境各类问题的主要方法,地下水模拟的高度概化、水文地质条件的不协调与研究问题本身的复杂性,致使地下水模拟不确定性问题的出现,直观表征为模拟预报结果与实际情况的偏差.现广泛应用的确定性数值模型仅能获得唯一解,未考虑模拟不确定性对模型预测结果的影响,依据此预测结果进行决策存在风险.因此,十分必要对模型进行不确定分析获取优化模型,提高模型精度.地下水模拟不确定性根据其来源可分为:参数不确定性、模型不确定性和资料不确定性[1].主要通过参数识别方法研究参数不确定性问题,如单纯形法、最速下降法、共轭梯度法、高斯-牛顿法、遗传算法、模拟退火算法、蒙特卡罗法及贝叶斯方法等[2];一般通过多模型方法探讨概念模型不确定性问题;可通过连续长期观测资料,不依赖于某时刻或单一空间数据来克服资料不确定性.地下水模型参数的不确定性问题己经获得了广泛的关注,如Beven和Binley提出的GLUE (generalized likelihood uncertainty estimation)方法对水文模型的参数不确定性进行估计[3-4];马尔科夫链-蒙特卡洛(Markov Chain Monte Carlo, MCMC)也是一种重要的不确定性分析方法,它在蒙特卡洛模拟框架内不断演化马尔科夫链,使采集的样本参数收敛于模型参数的后验概率分布[5-6],能够有效地探索参数分布空间的高概率密度区域,并反映出参数后验概率的分布特征[7].Hassan等[5]使用MCMC方法对Alaska、Amchitka Island的Milrow试验场地下水模型参数进行了不确定性评价.Kuczera和Parent[8]、Rojas[9]、陆乐[2]和刑贞相[10]等依托不同的试验场地及水文模型研究各类参数不确定性对模型的影响,并应用于模型参数的识别及地下水环境的风险分析.有关地下水概念模型的不确定性分析起步较晚,部分研究针对模型结构的不确定性进行了分析,如Rojas等[11]提出了GLUE与贝叶斯模型平均(Bayesian model averaging)结合的方法,分别对模型参数和概念模型的不确定性进行了统计.此外,Neuman[12]、Ye[13]、吴吉春[1]、曾献奎[14]等亦对概念模型不确定性进行了相关研究.这些研究多侧重于对多个概念模型模拟结果的综合分析,以获取输出变量的分布特征;或假设以理想模型的不同边界条件构建多模型进行影响分析研究.然而,各类不确定因素对模型影响的敏感度及概念模型的可靠性等方面缺乏系统的分析研究.本文应用调整接受条件后的自适应采样(adaptive metropolis, A-M)算法,以大量水文地质试验数据为参数分布的先验信息构建多模型,根据模型输出数据进行参数识别,并结合基于AICc准则的多模型分析方法,研究参数不确定性及不同结构概念模型对模拟输出的影响及其敏感性.1 地下水模拟的多模型分析方法1.1 多模型的构建思路传统的多模型分析遵循的主要步骤:(1) 考虑构建模拟区多个可能的模型;(2) 在相同观测数据条件下校正模型;(3) 使用某种准则对模型进行排序;(4) 去掉可能性小的模型;(5) 对余下模型得到的预测值与统计量进行权重分析[15-16].通过调整A-M接受样本条件,对多模型分析步骤进行调整:(1) 将不同概念模型结合服从某分布的随机抽样参数样本,构建研究区多个可能的计算模型;(2) 在相同观测数据条件下,通过调整后A-M采样的样本接受条件,直接剔除预测值与观测值偏差较大模型;(3) 对余下模型得到的预测值与统计量进行权重分析.1.2 AM-MCMC的优化MCMC是一种重要的不确定性分析方法,该方法的效率很大程度上取决于其采样的算法.常用的算法有:metropolis-hastings(M-H)算法、吉布斯(Gibbs)采样[17]、A-M算法[18]及single component adaptive metropolis(SCAM)算法[19]等.相比传统的M-H与Gibbs采样,A-M不再需要确定变量的推荐分布,而是决定于初始抽样的协方差,将先验的推荐分布定义为空间的多维正态分布形式,其初始协方差可根据先验信息确定,因此大量先验数据成为A-M采样算法效率及准确性的基础.A-M及SCAM采样原理相近,但若参数组中包含较多维向量,需要分析全局最优解为多维向量参数组时,A-M算法较SCAM更适用.A-M算法是将参数组看成多维的向量,第i步参数样本推荐服从第i-1次采样所得的向量θi-1为均值,协方差矩阵为Ci的多元正态分布.在初始i0次抽样中,协方差矩阵Ci取固定值C0,C0的确定可依据先验信息,之后自适应更新.协方差矩阵计算如式(1).(1)式中:C0为初始协方差矩阵;COV(θ0,…,θi-1)为已有的所有样本向量的协方差矩阵;ε为较小的正数,本次研究取值10-5,为确保Ci不成为奇异矩阵;sd为比例因子,依赖于参数空间维度d,以确保接受率在一个合适的范围内,sd=2.42/d;Id为d维的单位矩阵[20].Ci+1为参数i+1次采样的协方差矩阵,由式(1)推出协方差公式为(2)式中:和为前i-1和i次的抽样均值;和为向量和的转置.A-M算法采样具体步骤如下:步骤1 按先验分布随机产生初始样本向量θ0;步骤2 利用公式计算Ci;步骤3 产生的参数样本θ*~N(θi,Ci);步骤4 计算接受概率α,(3)若接受产生样本θ*,令θi+1=θ*;传统的参数样本接受与否,通过模型的计算值与实际观测资料计算得来的接受概率判定,如式(3).A-M算法不再依赖于参数的推荐分布,假设参数样本先验及后验分布均服从于多元正态分布,以大量实测参数数据为先验信息,随机采集样本的“失真”及后验分布的不收敛基本可忽略.后期依据AICc 信息量准则统计模型的预测值进行权重分析,获取最优参数区间.为提高采样效率,尝试将原接受条件调整为模型的各项计算值与对应观测值的残差均值在K范围内,对模型进行初步筛选,即将步骤4接受样本条件由式(3)调整为式(4).(4)式中:为残差均值;y1、y2分别为实际观测及模型计算值;n为观测数据个数.步骤5 重复步骤(2)~(4),直到取得足够多的样本.1.3 基于AICc准则的多模型分析基于AICc准则的参数识别是利用模型预测结果来计算模型平均预测值及模型残差,并通过排列模型,计算模型概率或权重来分析模型的最优取值区间.单个模型的权重通常是由信息量准则来确定的.信息量准则是信息理论和似然理论结合的成果,日本统计学家赤池弘次首先提出了赤池信息量准则AIC (Akaike’s information criteron),将信息理论中的Kullback-Leibler距离和Fisher极大似然函数联系起来[21].继AIC之后提出修正的AIC信息量准则(AICc).AICc信息量的计算如式(5)~(7).(5)(6)(7)式中:Ai为AICc信息量的计算值;分别为残差平方和及最优目标函数值的残差平方和;分别为残差平方均值和最优目标函数值的残差平方均值;k为待估参数个数.AICc与AIC的不同仅在于它多了式(5)右边第3项.这项是标识因观测数据较少产生的二阶偏差,当n/k<40时,尤其需要考虑到二阶偏差对多模型分析的影响.在对地下水系统进行建模分析时,n/k<40的情况很普遍[22],因此推荐使用AICc准则.得到AICc值之后,用模型的AICc值减去所有备选模型中的AICc最小值,计算每个模型的Delta值Δi、Δj(i≠j).最后根据Delta值计算模型的后验概率ωi,R是参加多模型分析得到的备选模型总数[23].(8)2 实例计算研究2.1 研究区概况及水文地质条件研究区位于我国西南某平原区,区内主要分布第四系松散沉积砂砾卵石孔隙潜水含水层.模拟区位于该平原区某河流右岸的一级阶地,地下水类型为第四系全新统冲洪积层砂卵砾石孔隙潜水,根据钻探及模拟区原位水文地质试验成果,含水层厚度约为25 m,渗透系数介于31.34~138.96 m/d,东侧为当地最低侵蚀基准面,地下水由西北向东南径流.区内1995年起运营生活垃圾填埋场,2010年停止堆填并采取封场措施,至今原始地形地貌已然发生改变,根据收集的原始地形资料及现有堆填区实测地形数据分析,堆填区经过削坡、整形等封场措施后仍高于原始地形约9 m.地表高程及坡降等因素的改变将对地下水补给条件产生影响,本文将依据上述差异构建2组不同概念的模型.2.2 多模型构建根据原始地形资料及实测的地形数据,构建2组地形存在差异,其余水文地质条件相同的概念模型,1#模型考虑堆填体对原始地形的改变,2#模型为原始地形(图1).依靠先验信息即原位水文地质试验获取的渗透系数数据,生成渗透系数对数的初始平均值及初始方差,依次按AM-MCMC采样方法生成每组样本.每组样本中包含对应网格数的渗透系数对数值,将每组对数值进行转化并输入1#模型进行模拟计算.根据接受条件筛选100组(每组含2 250个数据)参数并获取相应输出数据;将筛选好的100组参数输入2#模型,对应获取相应输出数据;最后依据AICc准则进行多模型分析.2.2.1 模型概化及边界条件设置根据水文地质条件及钻孔信息构建的2组概念模型范围均为X(1 000 m)×Y(900m)(X为南北向,Y为东西向),网格为10 m×10 m,含水层厚度约为25 m,东侧边界为当地最低侵蚀基准面,设置为河流边界,西侧及北侧设置为定水头边界,同时,模拟区内设置14个水位观测孔.以原始地形数据及堆填后实测地形数据分别输入模型来刻画2组模型中地形地貌差异(图1).(a) 1#模型(b) 2#模型图1 根据不同地形地貌条件概化的2组模型Fig.1 Groups hydrogeological conceptual model2.2.2 AM-MCMC采样渗透系数为待估参数,视为随机变量.按前述接受条件调整后的A-M算法进行采样.先验信息是参数随机采样的基础,其来源的可靠性将决定采样的合理性.研究区主要地下水类型为松散堆积孔隙潜水,主要由:山前扇状冲洪积砂砾卵石层孔隙潜水,河道漫滩、一级阶地冲洪积砂卵砾石层孔隙潜水,河间二级阶地冰-水堆积泥质砂砾卵石层孔隙潜水构成,3类孔隙潜水分布于平原坝区,相互叠置,介质类型相似,其间无明显的隔水层,地下水有着密切的水力联系,构成了研究区上部潜水含水层组. 因此,本次先验信息由模拟区周边上述3类含水介质的原位水文地质试验数据构成[24-26],其中包括129个钻孔的174组抽水试验数据(图2)及模拟区5个钻孔的14组数据.经统计,先验信息参数对数取值范围为1.369~5.583,初始参数样本服从均值3.407,协方差C0为0.713的正态分布.依次通过A-M算法采集参数样本,耦合地下水数值模拟软件Modflow输出模拟结果进行不确定性分析.2.3 地下水流场模拟不确定性分析文中A-M算法中的接受条件由似然函数求解的后验概率修正为更直接的残差平方的接受值域范围.基于此接受条件的修改,首先需检验条件改变后参数取值的遍历性及收敛性.注:Q4al+pl为第四系全新统河道漫滩、一级阶地冲洪积砂卵砾石层孔隙潜水;Q4alp为第四系全新统山前扇状冲洪积砂卵砾石层孔隙潜水;Q3fgl+al为第四系上更新统河间二级阶地冰-水堆积泥质砂卵砾石层孔隙潜水;Q1+2fgl+al为第四系中、下更新统泥卵砾石孔隙潜水.图2 研究区同类含水介质水文地质试验孔分布Fig.2 Distribution of boreholes at similar aquifers2.3.1 参数取值遍历性分析采用A-M算法对参数样本进行采样,根据接受条件共筛选100组参数,每组含2 250个样本值.图3(a)、(b)为参数在采样过程中均值与方差的迭代迹线.当取样20组(样本个数达到45 000个以上)时,参数的均值和方差趋于平稳.图3(c)、(d)分别为45 000个参数样本的采样过程中样本值遍历参数的可能取值范围,通过自适应更新,样本值取样波动逐步减弱,采样过程基本稳定.综合考虑均值、方差迭代迹线和样本采样过程,调整接受条件后的A-M采样方法并没有对参数后验分布的遍历性及收敛性产生影响,更直接的接受条件可修正样本取样空间,提高样本采集效率.2.3.2 多模型分析多模型的构建旨在分析参数不确定性与模型不确定性对模拟结果的影响.在剔除不符合接受条件的模型后,2组不同的概念模型分别在其中选取100个计算模型.并依据AICc准则多模型分析方法计算得到各模型的AICc值、Delta值及模型的后验概率ωi.运用AICc准则分析参数不确定性对模拟预测结果的影响时,Burnham和Anderson建议如果模型的后验概率超过0.9时,可视其为最佳模型用于预测.而在地下水模拟不确定性研究中,是不易输出如此高概率模型从而获取单个的最优解,输出的是一系列拟合程度相近的模型,即分析所得的是参数样本的最优取值区间而非唯一解.多模型分析方法可通过对预测平均值或预测值置信区间的分析来反映预测值的范围及其与参数的不确定性关系.运用AICc分析认为Delta值小于2的模型是较好的模型,Delta值介于4~7的模型为经验推荐模型,而Delta值大于10的模型可以舍去[17].甄选1#模型中Delta值小于10的计算模型,对输出观测孔地下水位序列值进行统计分析,可计算各观测孔的众数和置信区间.观测孔水位众数、95%置信区间和实际观测值的序列如图4表示,再进一步剔除Delta值大于10的模型后,剩余计算模型的水位众数与观测值几乎重合.(a) 参数对数均值(b) 方差(c) 随机样本(d) 相对频率图3 采样过程Fig.3 Sampling process根据1#模型与2#模型的输出结果排序,排名前三的参数样本相同,排名前十的计算模型中有6组相同,表明在本文设定的不确定性条件下,较之概念模型的不确定性,参数的不确定性的敏感性更高,对模型输出结果的精度更具控制性.虽地下水流场模拟过程中不仅会出现“异参同效”,甚至存在“异参、异构同效”,但仍能从高精度模型出现频次及最优解区间区间范围等方面分析,考虑地形实际变化的1#模型优于2#,反映模型的不确定性仍对模拟结果有着明显的影响.根据输出结果统计分析:(1) 高精度模型出现频次的不同,1#、2#概念模型分别有65%、46%方差值介于1~2之间;(2) 最优解区间取值范围及概率的不同,剔除Delta值大于10的计算模型后,1#模型中仅保留前10个模型,累计后验概率为0.996;2#模型保留前21个模型,而其前10个模型的累计后验概率仅为 0.884(图5).图4 1#模型计算模型地下水位众数、95%置信区间(阴影区域)与观测值Fig.4 95% confidence intervals (shadow areas), observations and mean values图5 不同精度模型比例Fig.5 Comparative precision of the different models 3 结论地下水模拟不确定性与模型的输入参数、模型结构等因素有关.研究表明:(1) 由于影响因素间的相互补偿致使模型的输出存在“异参同效”甚至“异参、异构同效”,因此,综合考虑参数和模型结构因素而获取的取值区间应是更合理的. (2) 在充实的先验数据及参数分布特征既定的条件下,将A-M采样算法中的接受条件调整为模型输出值与实际值方差的接受值域,不会对参数样本的遍历性及收敛性产生影响.(3) 文中构建的多模型分析方法可识别不同影响因素的敏感性,经过参数样本接受条件及基于AICc准则的多模型分析的双重筛选,能较为高效及准确地获得参数最优区间,同时,亦可完成较优概念模型的甄选识别.参考文献:【相关文献】[1] 吴吉春,陆乐. 地下水模拟不确定性分析[J]. 南京大学学报:自然科学,2011,47(3): 227-234. WU Jichun, LU Le. Uncertainty analysis for groundwater modeling[J]. Journal of Nanjing University: Natural Sciences, 2011, 47(3): 227-234.[2] 陆乐,吴吉春,陈景雅. 基于贝叶斯方法的水文地质参数识别[J]. 水文地质工程地质,2008(5): 58-63.LU Le, WU Jichun, CHEN Jingya. Identification of hydrogeological parameters based on the Bayesian method[J]. Hydrogeology and Engineering Geology, 2008(5): 58-63.[3] BEVEN K, BINLEY A. The future of distributed models-model calibration and uncertainty prediction[J]. Hydrological Processes, 1992, 6(3): 279-98.[4] BEVEN K, FREER J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology[J]. Journal of Hydrology, 2001, 249(1): 11-29.[5] HASSAN A E, BEKHIT H M, CHAPMAN J B. Using Markov Chain Monte Carlo to quantify parameter uncertainty and its effect on predictions of a groundwater flow model[J]. Environmental Moddelling & Software, 2009, 24(6): 749-63.[6] ROJAS R, KAHUNDE S, PETERS L, et al. Application of a multimodel approach to account for conceptual model and scenario uncertainties in groundwater modelling[J]. Journal of Hydrology, 2010, 394(3): 416-35.[7] BLASONE R S, VRUGT J A, MADSEN H, et al. Generalized likelihood uncertainty estimation(GLUE) using adaptive Markov Chain Monte Carlo sampling[J]. Advances in Water Resources, 2008, 31(4): 630-48.[8] KUCZERA G, PARENT E. Monte Carlo assessment of parameter uncertainty inconceptual catchment models: the metropolis algorithm[J]. Journal of Hydrology, 1998, 211(1): 69-85.[9] ROJAS R, FEYEN L, BATCLAAN O, et al. On the value of conditioning data to reduce conceptual model uncertainty in groundwater modeling[J]. Water Resources Research, 2010, 46: W08520-1-W08520-75.[10] 刑贞相,芮孝芳,崔海燕,等. 基于AM-MCMC算法的贝叶斯概率洪水预报模型[J]. 水利学报,2007,38(12): 1500-1506.XING Zhenxiang, RUI Xiaofang, CUI Haiyan, et al. Bayesian probabilistic flood forecasting model based on adaptive metropolis-MCMC algorithm[J]. Journal of Hydraulic Engineering, 2007, 38(12): 1500-1506.[11] ROJAS R, FEYEN L, DASSARGUES A. Conceptual model uncertainty in groundwater modeling: Combining generalized likelihood uncertainty estimation and Bayesian model averaging[J]. Water Resources Research, 2008, 44: 12418.[12] NEUMAN S P. Maximum likelihood Bayesian averaging of uncertain model predictions[J]. Stochastic Environmental Research and Risk Assessment, 2003, 17(5): 291-305.[13] YE M, NEUMAN S P, MEYER P D. Maximum likelihood Bayesian averaging of spatial variability models in unsaturated fractured tuff[J]. Water Resources Research, 2004, 40:W05113-1-W05113-21.[14] 曾献奎,王栋,吴吉春. 地下水流概念模型的不确定性分析[J]. 南京大学学报:自然科学,2012,48(6): 746-752.ZENG Xiankui, WANG Dong, WU Jichun. Uncertainty analysis of groundwater flow conceptual model[J]. Journal of Nanjing University: Natural Sciences, 2012, 48(6): 746-753.[15] NEUMAN S P. Maximum likelihood Bayesian averaging of alternative conceptual mathematical models[J]. Stochastic Environmental Research and Risk Assessment, 2003, 17(5): 291-305.[16] REFSGAARD J C, SLUIJS J P V D , BROWN J, et al. A framework for dealing with uncertainty due to model structure error[J]. Advances in Water Resources, 2006, 29: 1586-1597.[17] GILKS W R, RICHARDSON S, SPIEGELHALTER D J. Markov chain monte carlo in practice[M]. London: Chapman & Hall, 1996: 112-119.[18] HAARIO H, SAKSMAN E, TAMMINEN J. An adaptive metropolis algorithm[J]. Bernoulli, 2001, 7(2): 223-242.[19] HAARIO H, SAKSMAN E, TANMIINEN J. Componentwise adaptation for high dimensional MCMC[J]. Computational Statistics, 2005, 20(2): 265-273.[20] GEHNAN A, CARLIN J B, STREN H.S, et al. Bayesian data analysis[M]. London: Chapmann and Hall, 1995: 142-151.[21] BURNHAM K P, ANDERSON D R. Model selection and multi-model inference: a practical information-theoretic approach[M]. New York: Springer-Verlag, 2002: 163-177.[22] POETER E P, ANDERSON D. Multi-model ranking and inference in groundwater modeling[J]. Ground Water, 2005, 43(4): 597-605.[23] 夏强. 地下水不确定性问题的多模型分析方法及应用[D]. 北京:中国地质大学,2011.[24] 四川省地质局. 成都幅水文地质报告[R]. 成都:四川省地质局,1977.[25] 四川省地质局. 都江堰幅水文地质报告[R]. 成都:四川省地质局,1977.[26] 四川省地质矿产局. 成都平原水文地质工程地质综合勘察评价报告[R]. 成都:四川省地质矿产局,1985.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年4月水 利 学 报SHUILI XUEBAO 第40卷 第4期收稿日期:2008-04-23基金项目:国家自然科学基金重点项目(40730632);教育部新世纪优秀人才支持计划(NCET-05-0624);霍英东青年教师基金资助项目(101077)作者简介:卫晓婧(1984-),女,山西阳泉人,硕士生,主要从事水文水资源方面的研究。
E -mail:hellomuki@to 文章编号:0559-9350(2009)04-0464-10融合马尔科夫链-蒙特卡洛算法的改进通用似然不确定性估计方法在流域水文模型中的应用卫晓婧,熊立华,万 民,刘 攀(武汉大学水资源与水电工程科学国家重点实验室,湖北武汉 430072)摘要:本文在Blasone 研究工作的基础上,进一步提出了基于马尔科夫链-蒙特卡洛算法的改进通用似然不确定性估计方法(Markov Chain -Monte Carlo based Modified Generalized Likelihood Uncertainty Esti mation,MMGLUE)。
该方法结合近年来被广泛用于推求参数后验分布的MC MC 方法,对基于Mon te Carlo 随机取样方法的传统GLUE 方法进行改进,并以预测区间性质最优为标准,对可行参数组阈值进行判断与选择,提出了衡量预测区间对称性的标准,并就预测区间性质与可行参数组个数的相关关系进行了探索。
在汉江玉带河流域的实例研究证明,MMGLUE 方法较传统的GLUE 方法能够推求出性质更为优良的预测区间,从而更真实合理地反映水文模型的不确定性。
关键词:MC MC;GLUE;MMGLUE;预测区间;覆盖率;区间宽度;区间对称性中图分类号:P333文献标识码:A1 研究背景近10年来,流域水文模型的不确定性研究逐渐成为当今水文界广泛研究的热点之一,各国的水文学家就此做了大量的工作[1]。
Beven [2-3]于1992年率先提出了流域水文模型/异参同效性0的观点,并针对流域水文模型的不确定性研究问题提出了通用似然不确定性估计(Generalized Likelihood Uncertainty Estimation,GLUE)方法。
该方法结合Monte Carlo 随机取样技术与Bayesian 框架,对由模型结构、参数冗余及相关性、输入输出误差等因素造成的不确定性进行综合分析。
GLUE 方法原理简单,易于操作,但由于其自身理论结构的缺陷,越来越多的研究者就GLUE 方法提出了质疑[4-5],即并非经典的Bayesian 方法、主观判断参数可行域阈值和推求的参数后验概率分布不具有显著的统计特征。
因此,基于不同假设的其他不确定性研究方法,如:基于经典Bayesian 理论的Ba RE(Bayesian Recursive Estimation)方法[6],基于全局卡尔曼滤波理论的EnKF(Ense mble Kalman Filter )方法[7],多目标方法如MOSCE M (Mult-i objective Shuffled Complex Evolution Metropolis)方法[8]等被用于估计模型的不确定性工作中。
然而,上述方法尽管理论结构相对复杂,应用效果与GLUE 方法相比却并没有明显的提高。
同时期另一种基于经典Bayesian 理论的马尔科夫链-蒙特卡洛(Markov Chain Monte Carlo,MC MC)方法也被广泛应用于推求参数后验分布的研究中。
特别是SCE M -UA (The Shuffled Complex E volutionMetropolis Algorithm)方法[9]能够有效地探索参数空间,使Markov Chain 能够朝着高概率密度区进化,从而推导出具有显著统计特征的水文模型参数的后验分布。
因此,Blasone [10]提出将两种方法结合起来,采用SCE M -UA 采样方法替代传统的GLUE 方法中的)464)Monte Carlo随机取样方法,并根据估计的预测区间的覆盖率来控制可行参数组个数的选择,对传统的GL UE方法进行改进。
本文在Blasone所做工作基础之上,进一步提出以预测区间性质最优为指标来控制可行参数组个数的选取。
2方法211贝叶斯统计推断贝叶斯学派是数理统计中的一个重要学派,其重要观点是[11]:任一未知参数H 都可以看作随机变量,因为任一未知量都有不确定性,因此可以用概率分布来描述。
人们根据先验信息对未知参数H的先验分布P(H),通过实验获得样本x1,x2,,,x n,对H的先验分布进行调整,调整的结果是H的后验分布h(H|x1,x2,,,x n)。
在这个过程中,人们的认识由P(H)调整到h(H|x1,x2,,, x n)。
贝叶斯方法中样本x1,x2,,,x n对H的条件密度p(x,x2,,,x n|H)就是经典方法中H已知时样本的联合密度。
一旦样本已知,就只有H在变化,把联合密度看成参数H的似然函数,用l(H|x1,x2,,, x n)来表示。
参数的后验分布表示为[12]h(H|x1,x2,,,x n)=P(H)l(H|x1,x2,,,x n)Q P(H)l(H|x1,x2,,,x n)d H(1)因为参数的后验分布综合了总体信息、样本信息和先验信息,因此对H的统计推断就应建立在后验分布的基础上。
贝叶斯假设:参数的无信息先验分布P(x)所在的取值范围内是/均匀0分布的。
根据最大熵原则,无信息如果意味着不确定性最大,那么,无信息的先验分布应是最大熵的相应分布,因为只有在分布是均匀时,熵才达到最大值,故本文中两种方法所采用的先验分布都是均匀分布。
经典统计学中处理点估计与区间估计方法不同,但在贝叶斯学派却是统一的。
对于贝叶斯统计中的区间估计,只要存在后验分布,就可以用相应分布的分位点给出参数H的置信区间,就模型参数不确定性分析而言,也就是预测区间。
问题就在于评判估计效果的标准。
本文中采用预测区间覆盖率、区间宽度、区间对称性作为最优后验分布判定的标准。
当后验分布已知时,对于给定的置信概率1-A可以求出很多置信区间。
由于参数H的最大后验区域估计集中了分布密度似然函数值取值尽可能最大的点,因此H的最大后验区间一定是在统一置信概率下区间宽度最狭窄的区间。
进而,推求参数的最大后验估计,成为不确定性分析方法研究的最终目的和手段。
212GL UE方法GLUE方法是目前最常用于不确定性估计的经验频率方法,它的原理与步骤如下:首先假设参数服从某一先验分布,通过Monte Carlo取样方法生成一定数目的可行参数组,然后利用流域降雨、蒸发、径流资料,计算各组参数值的对应的似然值。
那些与实际过程越接近的模型参数被认为具有越高的可信度与似然度。
最后主观选定一阈值,对似然度低于该阈值的参数组,令其相应的似然度为0;对高于该阈值的参数组,按照似然函数值由高到低排序,并标准化,再按照其似然值赋予相应的权重。
通过更新样本信息,从而取得参数的后验分布。
213MC MC方法MC MC是为了获得参数后验分布一系列后验量而发展起来的一种行之有效的计算方法,主要适用于多变量,非标准形式,且各变量间相互不独立时的分布模拟。
显然,MC MC方法非常适用于推求流域水文模型各参数的后验量。
Markov链具有如下特性:(1)无后效性:由随机变量序列组成的Markov链{X(0),X(1),X(2),,},在任一时刻t(t\0),序列中下一时刻处的X(t+1)由条件分布产生,它只依赖于时刻t处的当前状态而与时刻t之前的历史状态{X(0),X(1),,X(t-1)}无关;(2)各态遍历性:从不同的X(0)出发,链经过一段时间的迭代后,历经各种状态的Markov链最终收敛于平稳分布[13]。
MC MC方法的基本原理就是基于建立的平稳分布为P(x)的Markov链来获得P(x)的样本。
产生若干条独立并行的Markov链来探索模型参数空间,通过不断更新样本信息而使Markov链收敛于高概率)465)密度区,也就是Bayesian 方法中的最大后验估计。
MC MC 方法中的SCE M -UA 取样方法能够更有效的探索未知参数空间,因此本文采用该种方法推求实验模型参数的后验分布及其预测区间。
214 MC MC -based Modified GLUE (MMGLUE )方法 MMGLUE 方法,采用SCE M -UA 取样方法代替传统的GL UE 方法中的Monte Carlo 随机取样,并采用预测区间性质作为可行参数组数目x 的选取标准。
从而推求出有统计学意义的、性质优良的预测区间。
方法流程如图1所示,具体步骤如下:图1 MMGLUE 方法结构流程(1)选择实验模型以及相应的流域资料。
(2)确定似然函数,本文采用模型效率系数R 2作为似然函数:R 2=1-E M i =1(Q i -Q ^i )2P E M i =1(Q i - Q )2(2)式中:Q i 为实测径流量;Q ^i 为预测径流量; Q 为实测径流序列的均值;M 表示实测系列长度。
(3)根据先验分布随机产生s 个决策变量H t (t =1,2,,,s )。
(4)将s 个样本点划分为q 个区,每个区采用SCEM -UA[14-18]方法独立并行演化L 次以获得L #q 个样本点。
(5)将这些样本点掺混。
(6)将掺混后的样本点按照似然值由高到低排序。
(7)以预测区间对观测值覆盖率最合理、预测区面宽度最窄、区间对称性最优为标准,选取一合理初值x 带入模型进行预测区间性质检验,调整x 的值,使之达到既定标准。
覆盖率CR [19]及区间宽度IW 计算公式为CR =E M t =1J [Q obs,t ]P M ;IW =E M t =1(Q u p,t -Q low,t )P M (3)其中:J [Q obs,t ]=1,Q low,t <Q obs,t <Q up ,t0,其它式中:Q ob s,t 为时段t 实测径流量;Q low,t 为时段t 预测区间下界;Q up,t 为时段t 预测区间上界。
为了更好的反映预测区间的偏移程度,本文提出预测区间对称性IS 计算公式如下:)466)IS =E M t =1I [Q up,t ]P E M t =1I [Q low,t ](4)其中:I [Q low,t ]=1,Q ob s,t <Q low,t 0,其它; I [Q up,t ]=1,Q obs,t >Q up ,t 0,其它. 由式(4)可以看出,当IS =1时,区间对称,当0[IS <1时,区间较实际观测值偏高,IS >1时,区间偏低。
