电动力学数学基础
需要具备哪些物理和数学基础,才能完全理解狭义和广义相对论?

需要具备哪些物理和数学基础,才能完全理解狭义和广义相对
论?
先说物理基础。
其实很显然,按照历史的发展顺序,爱因斯坦提出狭义相对论的时候,物理学只有经典力学和电动力学,前者包括牛顿力学和分析力学。
一般在物理专业课中是四大力学的第一门《经典力学》,在大学普物课中是《力学》但因为你的目的是“完全理解”,那么我就不提普物了,只提物理学专业课。
后者包括早期电磁学和麦克斯韦方程组,在物理专业课中是四大力学的第三门《电动力学》。
这就是学习相对论之前需要掌握的物理基础。
顺便提一下,物理专业课中是四大力学的第二门是《热力学和统计物理》,这个对学习相对论来说不是必需的,但标准的课程都会按照这个顺序讲,所以还是逃不过一起学,对经典物理学有一个完整印象。
经典力学,电动力学,热力学和统计物理(不含量子统计部分)合称经典物理学。
再说数学基础。
狭义相对论对数学要求其实不高,推导洛伦兹变换甚至连微积分都用不到。
但既然你想完全理解和狭义相对论,还是要具备完整的《高等数学》基础,主要包括微积分,偏微分方程,线性代数三个部分,这都是学习经典物理学必备的工具。
此外,还要学习一门《数理方程》。
更难一些的《复变函数》不是狭义相对论必需的。
但广义相对论对数学的要求就更高了,因为时空不再是简单的欧几里得几何,而是有曲率的黎曼几何,这在数学上就进入了《微分几何》的领域。
想要完全理解广义相对论,不但要把前面的高等数学,数理方程和复变函数统统学一遍,还要增加微分几何内容。
所以这样一趟下来,广义相对论在物理学专业中已经属于研究生课程难度(当然入门知识可以在本科最后一年选修)。
电动力学数学基础 PPT课件

z
Az
散度的物理意义:矢量的散度是通量的体密度,是标量。它是空 间坐标点的函数,代表了矢量场内某点的源的分布特性。
➢ • A> 0 表示点P是流出的源,其值表示源的强度或源密度 ➢ • A< 0 表示点P是吸收的洞,其值表示洞的强度
• A = 0
(正源)
• A = 0 (负源)
➢ • A=0 表示点P是既不是源也不是洞,称矢量场A为无源场
单位矢量——大小(长短)为1的矢量。直角坐标系中
三个坐标轴方向的单位矢量表示为 (i , j , k )
任意方向的单位矢量一般表示为 eˆ A / A
4维矢量: X t x, y,z p E, px , py , pz
(以下不作特殊说明,均指三维矢量)
矢量运算: ➢ 标量积(点积):一个矢量在另一个矢量上的投影
记忆方法:轮换法、爱因斯坦约定*
i jk ex eyez ( y Az z Ay )ex ( z Ax x Az )ey ( x Ay y Ax )ez
yzx zx y x yz
小结:梯度、散度或旋度都是微分运算,它们表示场在 某点附近的变化特性。场中各点的梯度、散度或旋度可 能不同,因此,梯度、散度及旋度描述的是场的点特性 或称为微分特性。函数的连续性是可微的必要条件,因 此在场量发生不连续处,也就不存在前面定义的梯度、 散度或旋度。
nˆ
nˆ 是 = C1的
p
等量面上p点法
线方向的单位
等量面 等量面 矢量,指向
C1 C2 增加的方向。
C1 < C2
梯度是在P点的最大方向导数,也即在P点梯度给出, 在P点沿哪个方向增长最快,及增长最快的速率。
❖ 矢量场:若物理场的物理量是矢量,则为矢量场。矢量场中
电动力学复习

电动⼒学复习第⼀章电磁现象的基本规律1、描写静电场的基本⽅程(积分与微分),各⾃反映静电场的什么性质,以及微分⽅程反映场的局域性质的意义。
2、描写静磁场的基本⽅程(积分与微分),各⾃反映静磁场的什么性质,以及微分⽅程反映场的局域性质的意义。
3、电荷守恒定律的微分形式;欧姆定律的微分形式4、电荷系统单位体积所受电磁场作⽤的⼒密度(即洛伦兹⼒公式)5、1)电介质极化,极化体束缚电荷密度与极化强度的关系,极化⾯电荷密度与极化强度的关系;引⼊辅助量,电位移⽮量,电位移⽮量的定义式;对各向同性线性介质,电位移⽮量的表达式;如:均匀介质内部的体极化电荷密度p ρ总是等于体⾃由电荷密度f ρ的)1(0εε--倍。
2)磁介质磁化,引⼊辅助量,磁场强度,磁场强度的定义式;对各向同性⾮铁磁质,磁场强度的表达式6、电磁场边值关系如:1)介电常数分别为ε1和ε2两种绝缘介质的分界⾯上不带⾃由电荷时,分界⾯上电场线的曲折满⾜什么关系2)⽤边值关系证明:在绝缘介质与导体的分界⾯上,在静电情况下,导体外的电场线总是垂直于导体表⾯,在恒定电流的情况下,导体内电场线总是平⾏于导体表⾯。
7、麦克斯韦⽅程组,两个基本假设:感⽣电场和位移电流。
其中位移电流如何产⽣,位移电流与传导电流的共同点与不同点。
8、1)电磁场和电荷系统的能量转化和守恒定律的微分形式;2)电磁场的能量密度和能流密度表达式9、结合场的微分⽅程的数学上的散度、旋度的计算(如P34 习题3)如:已知电位移⽮量z y x e z e y e x D323++=,求电荷密度;已知电极化强度,求极化电荷密度;x e y e B y x+=是否为能表⽰磁感应强度的⽮量函数;若给出磁感强度为,求m 的值;⽮量是否可能是静电场的解第⼆章静电场1、在静电场中,电场强度 E和电位 ? 之间的关系;如:已知电势222z y x -=?,求电场强度;已知电势,求电场强度等2、静电势的微分⽅程和边值关系(注意导体的静电条件)3、⽤电荷密度和电势表⽰的静电场能量(注意只对总能量计算有意义,不能当做能量密度看待),如计算带电量Q﹑半径为a 的导体球的静电场总能量; 4、唯⼀性定理是解静电学问题的理论基础5、分离变量法解拉普拉斯⽅程(球坐标系下通解的形式,以及问题具有轴对称性以及球对)()23(3mzy e z y e x e B z y x +--+=(2)xyzE yz x e xze xye=-++称性下的简化形式)如:P49-51 例题 2 与例题3补充习题:1)真空中半径为R 的带电球⾯,其电荷⾯密度为σ =σ0cos θ(σ0为常数),试⽤分离变量法求球⾯内外的电势分布。
电动力学——精选推荐

电动⼒学电动⼒学第⼀章静电场⼀、考核知识点1、真空与介质中静电场场⽅程,场的性质、物理特征。
2、电场的边值关系、在两种介质分界⾯上电场的跃变性质。
3、由场⽅程、边值关系,通过电荷分布确定场分布及极化电荷的分布。
4、静电场的势描述。
由势分布确定场分布、荷分布;通过静电势的定解问题,确定静电势的分布、场分布及介质极化性质的讨论。
⼆、考核要求(⼀)、场⽅程、场的确定1、场⽅程,场的边值关系,体、⾯极化电荷密度的确定式等规律的推导。
2、识记:(1)、真空与介质静电场⽅程。
(2)、电场的边值关系。
(3)、体、⾯极化电荷密度的确定式。
3、领会与理解:(1)、静电场的物理特征。
12(2)、P D E ,,与电荷的关系,⼒线分布的区别与联系。
(3)、在介质分界⾯上场的跃变性质。
4、应⽤:通过对称性分析,运⽤静电场的⾼斯定理确定场,讨论介质的极化,正确地由电荷分布画出场的⼒线分布。
(⼆)、静电势1、静电势⽅程、边值关系的推导。
2、识记:静电势的积分表述、势⽅程、势的边值关系、势的边界条件、唯⼀性定理。
3、领会与理解:势的边值关系与边界条件,荷、势与场的关系,解的维数的确定,电像法的指导思想与像电荷的确定。
4、应⽤:求解静电势定解问题的⽅法(分离变量法、电像法)的掌握及应⽤,求解的准确性,场的特征分析及由势对介质极化问题的讨论。
第⼆章稳恒磁场⼀、考核知识点1、电荷守恒定律。
2、稳恒磁场场⽅程,场的性质特点。
3、由场⽅程,通过流分布确定场分布与磁化流。
4、磁场的边值关系。
5、稳恒磁场的⽮势。
6、由磁标势法确定场。
3⼆、考试要求1、规律的推导:真空、介质中稳恒磁场场⽅程,电荷守恒定律的微分表述,体、⾯磁化电流密度的确定式,磁场的边值关系,⽮势⽅程及其积分解,磁标势⽅程和边值关系等。
2、识记:电荷守恒定律,稳恒磁场场⽅程,体、⾯磁化电流密度的确定式,⽮势引⼊的定义式,磁标势引⼊条件,磁场的边值关系,0=f α情况磁标势的边值关系。
第0章 电动力学的数学基础

(2)两个矢量的叉乘 ) 两个矢量的叉乘,乘积是一个矢量, 两个矢量的叉乘,乘积是一个矢量,称为矢积或 外积. 外积.其大小等于以两矢量为邻边所作平行四边 形的面积,方向满足右手螺旋法则. 形的面积,方向满足右手螺旋法则.
a×b
b a
3. 三个矢量的乘积: 三个矢量的乘积
(1)三个矢量的混合积 ) 三个矢量的混合积是一个标量. 三个矢量的混合积是一个标量. 设 则 , ,
(2). 散度 定义: 定义: 矢量场的散度是一个标量 直角坐标系中散度可表示为 直角坐标系中散度可表示为
Ax Ay Az div A = + + x y z
散度定理
∫
V
div A dV = ∫ A dS
S
从数学角度建立了面积分和体积分的关系. 数学角度建立了面积分和体积分的关系. 角度建立了 从物理角度建立了区域 V 中的场和包围区域 V 的边界 S 上的场 物理角度建立了区域 角度建立了 之间的关系. 之间的关系.
算符以及梯度, . 算符以及梯度,散度和旋度的表示 (del operator)
直角坐标系中: 直角坐标系中: = i + j+ k x y z
表示梯度,散度和旋度: 用 表示梯度,散度和旋度:
grad = ,
算符的性质: 算符的性质:
divA = A,
rotA = × A
矢量性——矢算符 按矢量运算规则. 矢量性——矢算符,按矢量运算规则. 矢算符, 微分性——微分运算 按求导规则. 微分性——微分运算,按求导规则. 微分运算,
Laplace算符 标算符,有的书上记为: 算符, 2—Laplace算符,标算符,有的书上记为:
× (× A) = ( A) 2 A
电动力学(数学基础)

散的度强的弱重程要 度性 ,在 当于div,A可 用0 表,征表空示间该各点点有矢散量发场通发量散
的正源;当div A 0 ,表示该点有吸收通量的
负源;当div
A
0
,表示该点为无源场。
在直角坐标系中:
divA A Ax Ay Az x y z
例:设u是空间坐 标A(xu,)y,z的u函数dA,(u证) 明
Operator
设有一标量函数 r x, y, z
d dx dy dz
x y z
x
i
y
j
z
k
dxi dyj dzk
Gx,
y,
z dl
G
n dl
p
n
dn θ
p dl
p
l
0
方向导数:
l
G n el
G
c
os
n
e
G cos
G
l max
n
引进梯度(Gradient)概念:
6 0, A 0
证明:
( )
(
)
ex
x
(
)
ey
y
(
)
ez
z
(
)
ex (
x
x
)
ey (
y
y
)
ez (
z
z
)
(ex
x
ey
y
ez
)
z
(ex x
ey y
ez
) z
§0-5 二阶微分算符
Second-order Differentiation Operator
电动力学内容简介
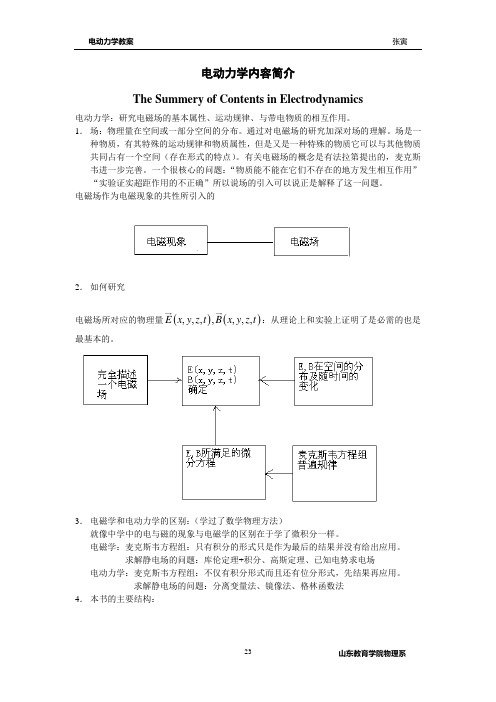
电动力学内容简介The Summery of Contents in Electrodynamics电动力学:研究电磁场的基本属性、运动规律、与带电物质的相互作用。
1. 场:物理量在空间或一部分空间的分布。
通过对电磁场的研究加深对场的理解。
场是一种物质,有其特殊的运动规律和物质属性,但是又是一种特殊的物质它可以与其他物质共同占有一个空间(存在形式的特点)。
有关电磁场的概念是有法拉第提出的,麦克斯韦进一步完善。
一个很核心的问题:“物质能不能在它们不存在的地方发生相互作用” “实验证实超距作用的不正确”所以说场的引入可以说正是解释了这一问题。
电磁场作为电磁现象的共性所引入的2. 如何研究电磁场所对应的物理量()(),,,,,,,E x y z t B x y z t :从理论上和实验上证明了是必需的也是最基本的。
3. 电磁学和电动力学的区别:(学过了数学物理方法)就像中学中的电与磁的现象与电磁学的区别在于学了微积分一样。
电磁学:麦克斯韦方程组:只有积分的形式只是作为最后的结果并没有给出应用。
求解静电场的问题:库伦定理+积分、高斯定理、已知电势求电场电动力学:麦克斯韦方程组:不仅有积分形式而且还有位分形式,先结果再应用。
求解静电场的问题:分离变量法、镜像法、格林函数法4. 本书的主要结构:⎧⎧→⎨⎪⎪⎩→⎨⎧⎪→⎨⎪⎩⎩第二章静电场静第三章静磁场第一章电磁现象的普遍规律第四章电磁场的的传播动第五章电磁场的发射第六章相对论第一章 电磁现象的普遍规律Universal Law of Electromagnetic Phenomenon本章将从基本的电磁实验定律出发建立真空中的Maxwell’s equations 。
并从微观角度论证了存在介质时的Maxwell’s equations 的形式及其电磁性质的本构关系。
继而给出Maxwell’s equat ions 在边界上的形式,及其电磁场的能量和能流,最后讨论Maxwell’s equations 的自洽性和完备性。
高等电动力学汇总.

绪论 INTRODUCTION
宏观电磁理论,即场与波的理论或 Maxwell理论的位置: 波长 >> 器件/系统尺寸:电路理论。
波长 ≈ 器件/系统尺寸,涉及的能量 >> 光子能量: 宏观电磁理论,即场与波的理论或 Maxwell 理论。
波长 << 器件/系统尺寸:传统(几何)光学理论。 波长 ≈ 与能级跃迁相应的波长:量子力学理论。 涉及的能量 ≈ 光子能量:量子电动力学,量子光学。
课程名称:高等电动力学 ADVANCED ELECTRODYNAMICS
性质:研究生学位课程
内容:非相对论宏观电磁理论,微波与光电子学中的场与波 问题。 目的: 1. 在本科“电动力学”的基础上提高一步,打下坚实的电 磁理 论基础。
2. 学会在各种边界限制下,各种媒质中求解电磁场与波的 基本方法。 3. 认识场与波的各种形态。做到融会贯通,触类旁通。 4. 能顺利阅读微波与光电子学领域有关电磁场与波的现代
1.
绪论 INTRODUCTION
2. 什么人需要学习Maxwell理论?随着电子学的发展越来越多 的学者需要学习Maxwell理论。 中期(1940年代以后):微波,波长米到毫米量级,约等于 基于机械加工的器件或系统的尺寸。研究器件或系统的学者 都需要学习Maxwell理论。麦克斯韦理论得以普及。 后期(1970年代以后):光纤光学,导波光学,波长微米量 级,约等于基于微细加工的器件或系统的尺寸。所有研究器 件或系统的学者都需要学习Maxwell理论。 现在(1990 - 2000年代以后):数字电路和计算机的钟频 (Clock frequency)达到GHz,相当于微波的波长。电路内部 出现场与波的问题,研究电路的学者也需要学习Maxwell理 论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
T f Tij ei e j fl el Tij fl ei jl Tij f j ei
张量和矢量的点乘——书P280
ij l
f T fiTij e j
ij
ijl
ij
张量和矢量点乘:结果仍为矢量
单位张量:
a I =I a a ; A I =I A A ;
e1e2 e2 e2 e3 e2
e1e3 e2 e3 e3 e3
下的9个分量,有一个 矩阵A与之对应,记作:
A11 A12 A13 A21 A22 A23 A31 A32 A33
称为3维2阶张量,可记作:
4)旋度(rotation):设想将闭合曲线缩小到其内某 点P附近,则以闭合曲线L为界的面积 S 逐渐缩 小,环量也将逐渐减小,两者比值的极限记作 该极限与闭合曲线的形状无关,而依赖于以 闭合曲线L为界的面积 S 的法线n 的方向。 矢量场A在P点的旋度 rot A 通过下式定义:
( x, t )
4 0 V
1
1)标量场的梯度(gradient) :标量函数的梯度是一个矢量, 直角坐标系中—— 注:矢量微分(哈密顿) u u u grad u i j k u 算符,同时具有矢量特性 x y z 和微分特性,但不是真正 意义的矢量,须对一个函 i j k x y z 数实施作用才有意义。
场的微分运算
物理场:空间区域D的每个点,都对应某个物理量的
一个确定的值(可随时间变化),则称在D上确定了
该物理量的一个场。若场中物理量在各点处的值不随 时间变化,则称稳定场,反之为不稳定场。 标量场:若物理场的物理量是标量,则为标量场。标 量场中每一点的物理量,均可用标量来表示。
0 ( x, t r c ) dV r
A B B A
A
A B C
C
A B
练习:判断矢量C的方向
A B C
B
BABA来自A c a b a b c b c a
两个重要公式:书P275 混合积与双叉乘
A Aij ei e j
上述可推广到n 维 m 阶张量,其分量为:
Aj1 , j2 ,... jm ; j1 , j2 , ... jm : 1 n
分量个数为nm。以下不作特殊说明,均指3维2阶张量。
0阶张量即标量;n维1阶张量即n维矢量
A11 A12 A13 A: A21 A22 A23 A31 A32 A33
量A、B为邻边的平行 四边形面积.
A B ( Ax i Ay j Az k ) ( Bx i B y j Bz k ) ( Ay Bz B y Az )i ( Az Bx Bz Ax ) j ( Ax B y Bx Ay )k
A Ax i Ay j Az k Ax , Ay , Az
单位矢量——大小(长短)为1的矢量。直角坐标系中 三个坐标轴方向的单位矢量表示为 ( i , j , k )
任意方向的单位矢量一般表示为 e A / A ˆ
4维矢量: X t x , y, z p E , p x , p y , pz
3) 矢量与并矢的点积——不对易,结果为矢量
2) 并矢间二次点积——对易,结果为标量
a (cd )=(a c )d ;
(ab ) c a (b c )
张量:张量在并矢基
e1e1 e2 e1 e3 e1
在其它形式的坐标系,如柱坐标、球坐标,梯度的表达式不同。
2)梯度运算公式:类似求导规则
F (u) F (u)u u 1 2 (vu uv ) v v
( )
3)梯度的几何意义:在P点处的梯度方向与通过P点的等量面 (量值相等的点构成的面)在P点的法线n的方向相同,且指向 增加的方向;梯度的模等于在此法线方向的方向导数。
平行六面体体积
把三个矢量进行轮换,其积不变; 只把两矢量对调,其积差一负号。 三矢量共面充要条件:上式=0
c a b c b a c a b a (b c ) b (c a ) c (a b ) 0
矢量的导数和积分:
A( t ) Ax ( t )i Ay ( t ) j Az ( t )k
dA( t ) dAx ( t ) dAy ( t ) dAz ( t ) i j k dt dt dt dt
A(t )dt
A (t )dt
(以下不作特殊说明,均指三维矢量) 矢量运算: 标量积(点积):一个矢量在另一个矢量上的投影
A B Ax Bx Ay B y Az Bz A B cos
结果为标量,平行模相乘;垂直积为0
A 0 or A B 0 B 0 or A B
ˆ n
p
等量面 等量面
是 = C 的 ˆ n 1
等量面上p点法 线方向的单位 矢量,指向 增加的方向。
C1 C2
C1 < C2
梯度是在P点的最大方向导数,也即在P点梯度给出, 在P点沿哪个方向增长最快,及增长最快的速率。
矢量场:若物理场的物理量是矢量,则为矢量场。矢量场中
1 矢量的非法运算: , lnB, A
C , eD
并矢:两个矢量并列,不做任何运算所构成的量
ab (a1e1 +a2e2 a3e3 )(b1e1 b2e2 b3e3 ) a1b1e1e1 a1b2 e1e2 a1b3 e1e3 a2 b1e2 e1 a2 b2 e2 e2 a2b3e2e3 9个分量 a3 b1e3 e1 a3 b2 e3 e2 a3b3e3e3
电动力学中的数学基础
矢量、张量、积分变换、 坐标系、数理方程
标量 矢量 张量
标量(数量):温度T,密度 特点1):只有大小没有方向的物理量 特点2):用正实数或负实数来表示 矢量(向量) 3维矢量:r x i y z k x , y , z j
• A = 0
(正源)
• A = 0 (负源)
• A=0 表示点P是既不是源也不是洞,称矢量场A为无源场
高斯公式:矢量场通过封闭曲面S的流量,等于此封闭曲面包围 的体积V上每一点的散度对V的体积分
S
A dS ( A)dV
V
——面(积分)化体(积分)
B
2 A A A 0
A
矢量积(叉积):结果为矢量;平行积为0,垂直模 相乘. 大小: C A B sin , (0 )
A B C
方向:右手螺旋定则 C A,C B C C矢量的大小等于以矢 B
"张量"一词最初由哈密尔顿在1846年引入,一些物理量如弹性体 的应力、应变以及运动物体的能量动量等都需用张量来表示。爱 因斯坦在其广义相对论中广泛地利用了张量。 1)应力是某点A的坐标的函数,即受力 体内不同点的应力不同。
2)应力是某点A在坐标系 中方向余弦的函数,即同 一点不同方位的截面上的 应力是不同的。
x
i
Ay (t )dt j
Az (t )dt k
矢量的导数和积分的结果仍为矢量,但这些新
矢量与原矢量的方向是否相同?
d ( A B ) dB dA A B dt dt dt d ( A B ) dB dA A B dt dt dt
S
A dS
称矢量 A 沿有向曲面S 的通量。若S 为闭合曲面,则可据
= 0 (无源)
< 0 (有负源)
> 0 (有正源)
正源
负源 无源
3)散度(divergence):在矢量场中,围绕 P点做一闭合面,所围 体积为V,若垂直穿过闭合面的通量与体积之比的极限存在, 则称该极限为矢量场A在 P 点的散度。
每一点的物理量,均可用矢量 A( x , y , z ) 来表示。 A( x , y , z ) Ax ( x , y , z )i Ay ( x , y , z ) j Az ( x , y , z )k
注:每个分量均是(x,y,z)的函数 1) 矢量场的梯度是张量 2) 通量:矢量A 沿有向曲面S 的面积分 通量的大小判断闭合面内源的性质:
对称张量:
Aij Aji
Aji
反对称张量:Aij
任何张量均可分解为一个对称张量与一个反对称张量:
A=As+Aa
(A12 A21 )/2 (A13 A31 )/2 A11 As : (A21 A12 )/2 A22 (A23 A32 )/2 (A31 A13 )/2 (A32 A23 )/2 A33 (A12 A21 )/2 0 Aa :(A21 A12 )/2 0 (A31 A13 )/2 (A32 A23 )/2 (A13 A31 )/2 (A23 A32 )/2 0
(e1 , e2 , e3 ) (i , j , k ) 注意:一般来说,并矢本身不对易 ab ba
